차량 진동에너지 회생을 위한 회전형 발전시스템 Screw Blade 최적설계
Copyright Ⓒ 2020 KSAE / 180-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper illustrates the optimized design of a screw blade, a rotary power generation system, to enhance the harvesting capacity of vehicle vibration energy. The suspension consisted of a screw blade type of turbine for the rotary generator, instead of the commonly-used propeller type, and the number of blade pitch was adjusted. Due to the suspension's fluid motion, a screw blade type of turbine can convert fluid motion into a rotary motion more effectively than a conventional propeller. Also, it can supplement the structural property because it makes it possible to design a shaft with a longer diameter. The researcher then predicted the fluid inflow speed with CarSim-Simulink, derived the T-ω curve by using ANSYS Fluent, and designed the screw blade with optimal generation capacity.
Keywords:
CFD analysis, Design of experiments, Design optimization, Energy harvesting, Rotary generator, Vehicle suspension키워드:
유동해석, 실험계획법, 최적설계, 에너지 하베스팅, 로터리 발전기, 차량용 현가장치1. 서 론
최근 하이브리드카 및 전기자동차의 발전과 보급이 확산되면서 배터리 자가 충전에 대한 연구가 활발히 진행되고 있다. 특히, 자동차 주행 시 상하 진동에너지를 쇼크업저버에 설치한 선형발전기를 이용하여 하베스팅하는 연구가 국내외 연구소 및 일부 대학에서 수행되고 있다.1) 하지만, 선형발전기의 End-Effect로 인해 발전량이 효율적이지 못하며 공심을 정확히 맞춰야 하므로 제작이 까다롭다.2,3) 이에 따라 쇼크업져버의 상하운동을 회전운동으로 변환하여 회전형 발전기를 통한 발전방식이 연구되었다.4) 하지만, 추가적인 기구장치가 요구되어, 설치공간이 방대해지고, 중량도 증가되는 단점이 있다. 본 연구에서 최적 설계한 Screw Blade는 일반적인 차량용 현가장치의 오리피스를 대신하여 감쇠력을 내며 유체의 유동을 회전운동으로 변환시켜 선형 발전기를 통해 전력을 생산한다. 일반적인 Propeller 형태의 Turbine에 비해, 쇼크업져버 내의 유체유동의 특성상 Screw Blade의 형태가 보다 효율적으로 유동에너지를 회전운동으로 변환 시킬 수 있으며 그만큼 쇼크업져버에서 필요한 감쇠력 또한 낼 수 있다. Screw Blade의 주요 설계변수를 설정하고 CATIA를 이용하여 모델링 하여 ANSYS Fluent 프로그램을 사용해 CFD해석을 진행하였다. 실험계획법(Design of Experiments)을 이용하여 설계변수 변경에 따라 계산된 Torque값의 변화를 분석하였으며, 설계문제 정식화에 따라 입력속도에 따른 최적의 블레이드 형상을 설계하여 최적 조건에서의 발전량을 예측하였다.
2. 에너지 하베스팅 쇼크업져버
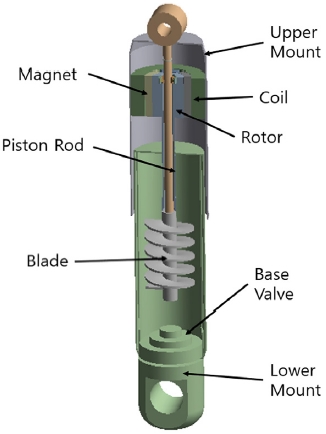
본 연구에서 제안된 에너지 하베스팅 쇼크업져버의 구조는 Fig. 1과 같다. 기본의 복통식 쇼크업져버에 블레이드 및 회전형 발전기를 적용시켜, 차량의 주행에 따른 상하 진동으로 인한 실린더 내부 유체의 유동을 Screw 블레이드에 의한 회전운동으로 변환시키고, 이를 통해 회전형 발전기로 전기에너지를 발생시킨다.
3. Carsim-Simulink를 이용한 유입 속도 계산
차량의 주행 시 발생하는 상하진동에 의해 블레이드로 유입되는 작동 유체의 유입 속도를 시뮬레이션으로 계산하기 위해 Carsim-Simulink 프로그램을 사용하였다. 에너지 하베스팅 쇼크업저버의 설치공간을 고려하여 Fig. 2와 같이 서스펜션 공간이 비교적 큰 SUV차량을 선택하였다. 시뮬레이션에 사용된 SUV 차량의 주요특성은 Table 1에 명기하였다.
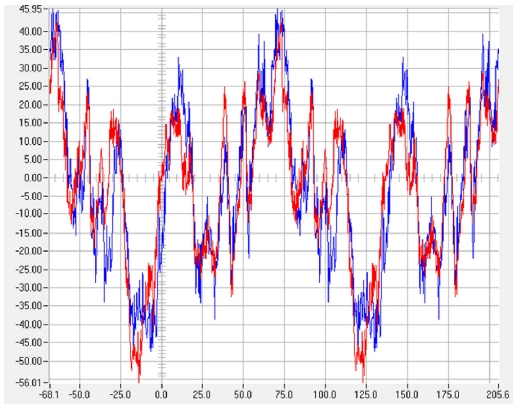
차량의 주행 속도는 80 km/h로 가정하고 지면의 Roughness는 Fig. 3의 데이터를 사용하여 4개 Wheel의 상하운동에 대한 속도를 계산하였다.5) 이를 토대로 Blade내로 유체의 유입속도를 결정하였다.
4. Screw Blade 해석모델
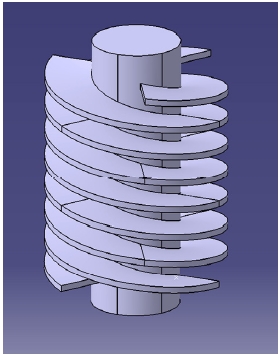
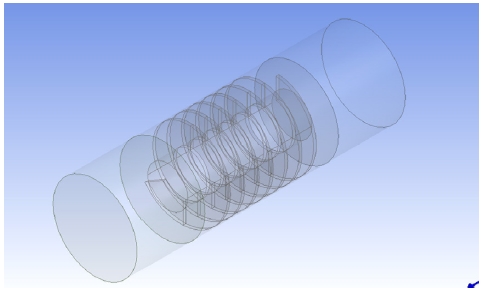
SUV 차량의 기존 쇼크업져버 크기 및 설치 공간 등을 고려하여 쇼크업져버의 내의 블레이드의 직경 및 상하운동 범위를 결정하였고, 블레이드가 받는 압력을 고려하여 블레이드의 두께를 설정하였다. Screw Blade의 형상은 Fig. 4와 같다.
5. 설계문제 정식화
로터리 발전기에서 최대 발전량을 계산하기 위해 최대 Rotational energy를 갖는 블레이드 형상을 찾는 것을 목표로 하였다. 이때, 에너지 변환 과정에서 기계적 손실은 없다고 가정했을 때 Rotational energy인 Pm은 식 (1)과 같이 T*ω로 계산된다. 여기서, T는 Torque(Nm), ω는 Angular velocity(rad/s), V는 전압, I는 전류, PE는 Electric energy이다.
| (1) |
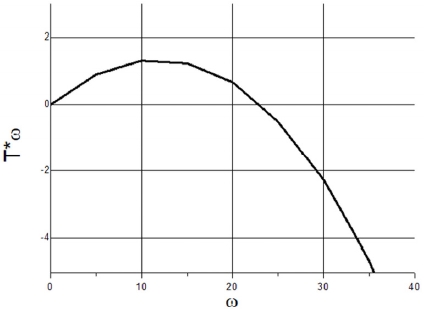
받음각 90°, 2중 블레이드, Pitch 20 mm인 Screw Blade 모델에서의 ω 변경에 따른 T값과 T*ω 계산값은 Table 2와 같고, ω 변경에 따른 T*ω값 변화 추이는 Fig. 5와 같다. Rotational energy를 최대화 할 수 있는 T*ω 최댓값은 Fig. 5에서 결정되며, 해당 최댓값을 Tω_max로 한다.
Screw Blade를 구성하는 설계 요소 중 Rotational energy를 최대화하는데 영향을 줄 수 있을 것으로 판단되는 받음각(Angle), 블레이드 개수(nBlade), 피치(Pitch) 세 가지를 설계변수로 결정하였다.
설계문제를 정식화하면 식 (2)와 같다. 단, 받음각과 피치는 하한값과 상한값을 갖는 연속변수 형태이며, 블레이드 개수는 단일, 2중, 3중으로 이산변수 형태로 정의하였다.
| (2) |
6. ANSYS Fluent를 이용한 CFD해석
CATIA로 Screw Blade를 모델링 하여 stp 파일로 저장한 후, ANSYS에서 Import하여 Fig. 6과 같이 Design Modeler로 블레이드 주변의 유압유체를 모델링 하였다.6)
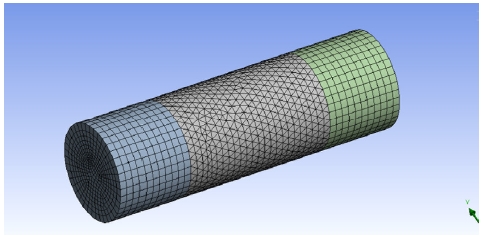
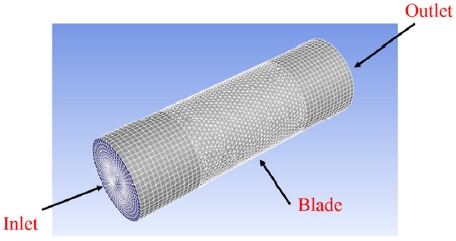
Mesh Size는 5 mm로 설정하여 Fig. 7과 같이 유한요소모델을 생성하였으며, Named Selections로 Inlet과 Outlet을 설정한 해석조건은 Fig. 8과 같다.
일반적인 쇼크업져버에 사용되는 SAE30을 유압유체로 정하였으며, SAE30에 대한 특성은 Table 3과 같다.
해석에 앞서 층류, 천이, 난류 구분을 위해 식 (3)을 이용하여 Reynolds number를 계산하였다.
| (3) |
Reynolds number가 2300 미만으로 계산되므로 해석모델은 Laminar로 설정하였다.7) 과도해석의 Time Step은 0.001초, Step Number는 200으로 설정하였고, Iteration Number는 100회로 설정하여 해석을 진행하였다.
해석 과정에서 ω를 0 rad/s에서 40 rad/s까지 5 rad/s씩 회전속도를 상승시키며 Pressure와 Viscous를 도출하고, Pressure와 Viscous의 합으로 Torque값을 계산하였다. 해석 완료 후 블레이드의 Pressure 분포는 Fig. 9와 같다.
7. 실험계획법을 이용한 Screw Blade 최적설계
본 설계문제에는 블레이드 개수와 같이 이산변수가 포함되어 있기 때문에 효율적인 설계를 위해 실험계획법을 설계 방법론으로 채택하였다.8)
통합최적설계 소프트웨어인 PIAnO에서 제공하는 다양한 실험계획법 중 적은 수의 실험만으로 효율적인 설계 및 분석이 가능한 직교배열(Orthogonal Array, OA)을 선택하였다. 설계인자는 Table 4와 같이 받음각(Angle), 블레이드 개수(nBlade), 피치(Pitch) 이상 3개이며, 각 설계인자를 3수준(3Level)로 정의하였다. 설계 효율성과 설계 개선을 위해 실험 횟수(nEXP)는 식 (4)와 같이 2차 Full Quadratic Polynomial 모델을 생성하는데 필요한 최소한의 실험점 수인 포화점 수(The Number of Saturated Points, nSAT)의 1.5배수 보다 크면서 유사하여야 한다.
| (4) |
여기서, nDV는 설계인자의 개수이다.
직교배열 L18(33)을 이용하여 Table 5와 같이 18개 실험점(Sampling points)을 생성하였으며, 각 실험점의 설계인자값으로 ANSYS Fluent 모델 구성 후 각 해석에 따른 Tw_max값을 계산하였다.
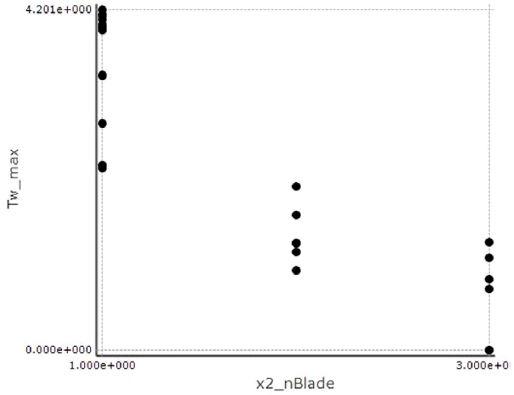
직교배열 L18(33) 실험 결과값을 이용하여 설계인자와 성능지수간의 영향력 및 경향성을 파악하기 위한 Scatter plot은 Fig. 10과 같다. 블레이드 개수(nBlade)가 감소할수록 Tω_max는 증가하는 경향을 보이며, 상관계수(Correlation coefficient)가 -0.86으로 블레이드 개수와 Tω_max가 반비례적인 선형 관계에 있음을 알 수 있다. 즉, Tω_max를 최대화하는 것이 본 연구의 목표이므로 브레이드는 단일 블레이드가 최적일 것으로 판단된다.
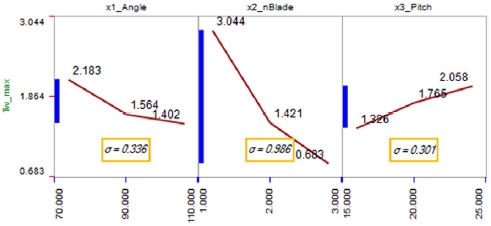
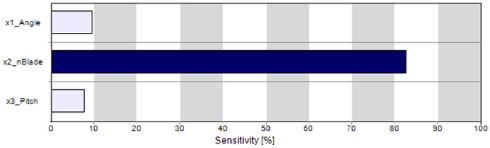
성능지수에 대한 주요설계인자를 분석하기 위해 Fig. 11과 같이 평균분석(ANOM)을 수행하였다. 받음각(Angle)과 블레이드 개수(nBlade)는 감소할수록 Tω_max는 증가하며, 피치(Pitch)는 증가할수록 Tω_max가 증가하는 경향을 볼 수 있다. 특히, ANOM 결과에서 블레이드 개수의 변화에 따라 Tω_max의 변화량의 큰 것으로 보아 블레이드 개수가 주요 설계인자임을 확인할 수 있으며, 민감도(Sensitivity)를 분석하기 위한 Fig. 12의 Sensitivity plot에서도 블레이드 개수의 영향도를 볼 수 있다.
직교배열 L18(33) 실험 결과값에서 Tω_max가 최대가가 되는 실험점을 분석하였다. 초기값(Initial)은 Table 5에서 9번 실험점이며 이때 Tω_max는 1.32이다. Tω_max가 최대가 되는 Best Point(BP)는 2번 실험점으로 Tω_max는 4.15였으며, 초기값 대비 3.14배 향상된 결과이다. 특히 Best Point의 경우 블레이드 개수가 1이어서 실험 결과 분석과 일치함을 확인하였다.
직교배열 L18(33)의 경우 설계 효율성을 위해 최소의 실험만을 진행하였고, 설계영역에서 3수준만을 고려하였기 때문에 직교배열 L18(33)에서 결정한 Best Point 근처 설계 영역에 더 개선된 설계점이 있을 가능성이 높다. 따라서 직교배열 L18(33)의 Best Point 근처에서 설계 영역을 줄여 공간충진성(Space-filling)을 고려한 추가 실험이 필요하다. 하지만 공간충진성을 고려한 추가 실험은 추가 실험 횟수만큼 수준수가 증가하게 되고, 블레이드 개수와 같은 정형화된 이산변수 사용이 불가능하게 된다. 따라서 공간충신성을 고려한 추가 실험을 계획하기 위해 Tω_max를 최대화하는데 가장 영향을 많이 미치는 이산변수인 블레이드 개수를 1로 고정시켜 설계인자에서 제외(Screening)하고, 받음각과 피치만으로 추가 실험을 계획하였다.
추가 실험 설계인자 범위는 식 (2)의 설계문제 정식화에서 정의된 범위의 25 %로서, 직교배열 L18(33)에서 결정된 Best Point의 설계인자 값이 포함될 수 있도록 식 (5)와 같이 설정하였다.
추가 실험은 공간충진성을 보장할 수 있는 실험점 생성 기법인 Augmenting Design을 사용하여 Table 6과 같이 9개의 추가 실험점을 생성하였으며, 추가 실험점에서 해석을 진행하였다. 추가 실험점을 9개로 결정한 이유는 본 연구에서 시도한 전체 실험 횟수를 3인자 3수준 Full Factorial Design 실험 횟수(27개)와 같을 수 있도록 한정하기 위함이다. 분석 결과, 9개의 추가 실험점 중 7번 추가 실험점의 Tω_max값이 4.20으로 최대였고, 1차로 진행된 직교배열 L18(33)의 Best Point값 4.15보다 0.05 증가된 값이었다. 이를 통해 본 연구에서 진행한 추가 실험 방안의 적절함을 확인할 수 있다.
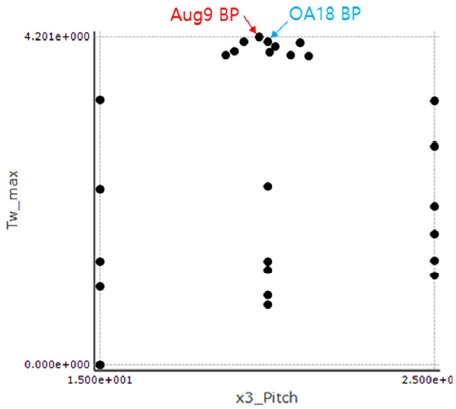
1차로 진행된 직교배열 L18(33)의 Best Point(OA18 BP)와 추가 실험의 Best Point(Aug9 BP)를 Fig. 13에 Scatter plot으로 나타내었다.
두 차례에 걸친 실험계획을 통해 Tω_max를 최대화 할 수 있는 블레이드는 받음각 77.41°, 단일 블레이드, Pitch 19.76 mm이었으며, 바탕으로 발전기 해석을 진행하였다.
| (5) |
8. ANSYS Maxwell을 이용한 발전기 해석
앞서 도출했던 최적 ω값을 입력하여 발전량 생성을 예측하기 위해 ANSYS Maxwell을 이용하여 시뮬레이션을 진행하였다.9)
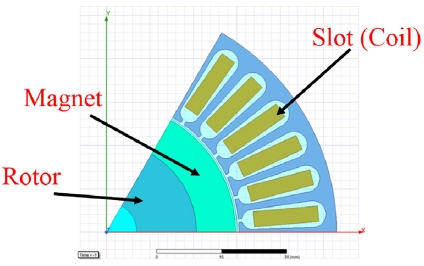
Generator 모델 형상은 Fig. 14와 같다. Rotor의 각속도를 20 rad/s로 설정하였고, Time step은 0.001초로 설정하였으며, 3 ms까지 해석을 진행하였다.
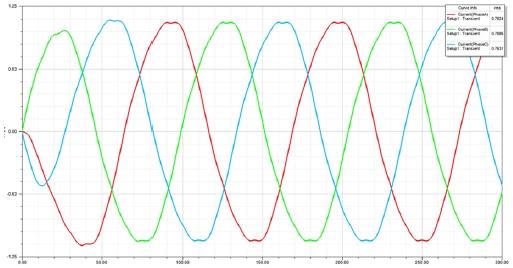
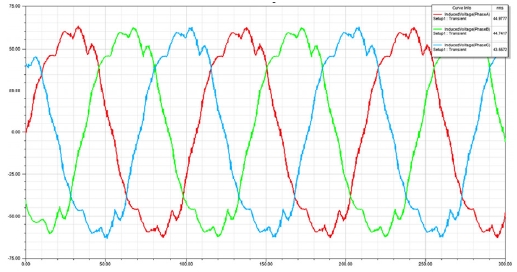
Fig. 15는 발전기에서 생산된 전압을 나태내며 Fig. 16은 생성된 전류를 나타낸다. 3개 상의 전류와 전압을 RMS로 평균값을 낸 후 곱하여 전력 생산량을 계산하였으며, 약 103 Watt의 전력이 생성되는 것으로 계산되었다. 이는 일반적인 Propeller형태의 블레이드에서 동일한 조건에서의 발전량인 10W보다 10배 이상 증가한 결과이다. 비교를 위해 해석에 사용된 블레이드의 형상은 Fig. 17과 같다.
9. 결 론
본 논문에서는 차량의 진동에 의한 쇼크업져버의 유동을 회전운동으로 변환시켜 에너지를 생성하는 에너지 하베스팅 쇼크업져버의 성능향상을 위해 Screw Blade 최적설계를 진행하였다. 에너지 변환 과정에서 블레이드의 최대 T*ω값을 최대화할 수 있도록 받음각과 블레이드 수, 피치를 설계변수 선정하였다. 실험계획법 중의 하나인 직교배열 L18(33)을 이용하여 초기모델 보다 Tω_max를 3.14배 향상시킬 수 있는 블레이드 형상을 결정하였다. Augmenting Design을 이용한 추가 실험을 통해 L18(33)에서 도출된 결과보다 Tω_max가 0.05 증가된 Blade 형상을 최종 결정하여 본 연구에서 적용한 설계 절차의 타당성을 보였다. 최종 블레이드형상이 반영된 Screw Blade의 발전량은 Propeller형태의 블레이드에서의 발전량 보다 약 10배 더 향상됨을 시뮬레이션으로 입증하였다. 그러나 본 연구에서는 유체의 유입속도에 따른 최적값 만을 계산한 것이므로 실제 적용을 위해서는 블레이드가 대체한 현가장치의 Piston Valve만큼의 감쇠력을 가져야하며, 현가장치내 유압유체의 운동 특성에 맞도록 추가적인 장치가 있어야 효율적인 발전이 가능할 것으로 판단된다.
Nomenclature
| T : | torque, Nm |
| ω : | angular velocity, rad/s |
| Re : | reynolds number |
| V : | fluid velocity, m/s |
| D : | characteristic length, m |
| μ : | dynamic viscosity, Pa・s |
| ν : | kinematic viscosity, m2/s |
| ρ : | fluid density, kg/m3 |
Subscripts
| Pm : | rotational energy |
| Pe : | electric energy |
| OA : | orthogonal array |
| Aug : | augmenting design |
Acknowledgments
본 과제(결과물)는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 사회맞춤형 산학협력 선도대학(LINC+) 육성사업의 연구 결과입니다.
References
-
M. Wischke, M. Masur and P. Woias, “A Hybrid Generator for Virbration Energy Harvesting Applications,” IEEE TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference, pp.521-524, 2009.
[https://doi.org/10.1109/SENSOR.2009.5285376]

-
J. H. Kim, Y. J. Shin, Y. D. Chun and J. H. Kim, “Design of 100W Regenerative Vehicle Suspension to Harvest Energy from Road Surfaces,” International Journal of Precision Engineering and Manufacturing, Vol.19, No.7, pp.1089-1096, 2018.
[https://doi.org/10.1007/s12541-018-0129-5]

-
Z. Li, L. Zuo, J. Kuang and G. Luhrs, “Energy-harvesting Shock Absorber with a Mechanical Motion Rectifier,” Smart Materials and Structures, Vol.22, No.2, Article ID 025008, 2012.
[https://doi.org/10.1088/0964-1726/22/2/025008]

-
J. H. Choi, D. B. Shin and J. H. Kim, “Design of Resonance Linear Electric Generator System for Vibration Energy Harvesting in Vehicle Suspension,” Journal of the Korea Academia-Industrial Cooperation Society, Vol.15, No.6, pp.3357-3362, 2014.
[https://doi.org/10.5762/KAIS.2014.15.6.3357]

-
S. Zhao and L. Zhu, “Cruise Control System Based on Joint Simulation of CarSim and Simulink,” Open Access Library Journal, Vol.5, No.7, pp.1-8, 2018.
[https://doi.org/10.4236/oalib.1104724]

-
B. S. Choe “Hydraulic Shock Absorber Analysis Using Fluent Dynamic Mesh Method,” The KSFM Journal of Fluid Machinery, Vol.12, No.3, pp.75-78, 2009.
[https://doi.org/10.5293/KFMA.2009.12.3.075]

-
D. Bhuyan and K. Kumar, “3D CAD Modelling and Computational Fluid Analysis of Piston Valve of Twin Tube Shock Absorbers,” Materials Today: Proceedings, Vol.4, No.8, pp.7420-7425, 2017.
[https://doi.org/10.1016/j.matpr.2017.07.073]

- PIAnO(Process, Integration, Automation and Optimization) 2020 Manuals and Tutorials, PIDOTECH, 2019.
- R. A. Msuya, R. R. M. Kainwa and M. I. Mgwatu, “Design of a Small Scale Wind Generator for Low Wind Speed Areas,” Tanzania Journal of Science, Vol.43, No.1, pp.138-152, 2017.