전자식 사륜 구동 차량의 코너링 성능 향상을 위한 횡방향 거동 제어
Copyright Ⓒ 2020 KSAE / 178-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
A lateral motion control to enhance the cornering performance of electronic-four-wheel drive(e-4WD) vehicles is introduced in this paper. The proposed controller aims to optimally provide the in-wheel motor(IWM) torques to each wheel assisting the vehicle in following the desired trajectories. It includes a yaw rate reference for neutral-steering, which leads to enhanced cornering performance. A smooth sliding mode controller(SMC) is utilized based on a bicycle model to generate the desired yaw moment. Lastly, a torque distribution method with the Daisy-chaining allocation is utilized within an available torque operation area of IWM. Using the CarSim software, the proposed control algorithm is simulated. The effectiveness of the proposed approach is evaluated using various driving scenarios. It is confirmed that some evaluation factors in cornering performance are improved.
Keywords:
Lateral motion control, In-wheel motor, Electronic-four-wheel drive vehicle, Sliding mode control, Torque distribution키워드:
횡방향 거동 제어, 인휠 모터, 전자식 사륜 구동 차량, 슬라이딩 모드 제어, 토크 분배1. 서 론
전동식 구동 시스템을 기반으로 하여 4륜 전체를 차량 구동에 활용하는 전자식 사륜 구동 차량은 고성능차에 대한 소비자 수요가 증가하는 현재 자동차 시장에서 매우 각광받고 있다.1) 특히 휠 내부에 전동식 구동 시스템을 장착한 In-wheel motor(IWM)는 다음의 장점들 덕분에 여러 자동차 회사들에서 전자식 사륜 구동 차량에 적용시키기 위해 연구 중에 있다.2) 1) 정확한 구동 토크의 생성 덕분에 정밀한 차량 샤시 제어의 구현이 가능하다. 2) 정방향 및 역방향 토크 생성이 모두 가능하다. 3) 높은 동력 전달 효율을 가진다. IWM를 전자식 사륜 구동 차량의 횡방향 거동 제어에 활용한다면 더 높은 코너링 민첩성을 이끌어 낼 수 있을 것으로 예상된다. 이와 관련된 기존 연구들이 다음과 같이 존재한다. 차량 요레이트 및 횡방향 슬립각을 동시 제어하는 방식으로 높은 횡방향 슬립각을 유지하는 횡방향 거동 제어 연구가 있었다.3) 하지만 해당 연구는 상용 센서로 측정이 불가능한 횡방향 슬립각을 피드백 제어해야 한다는 어려움을 가지고 있다. 또한 최적 토크 분배 방식을 활용한 횡방향 거동 제어 알고리즘이 개발되었으나, 이는 커다란 계산량 부담을 가져온다는 단점을 가지고 있다.4) 피드백 및 피드포워드 제어를 모두 활용하는 기존의 모델 기반 제어기는 IWM의 특성을 고려하지 않는 토크 분배 방식을 가지고 있었다.5)
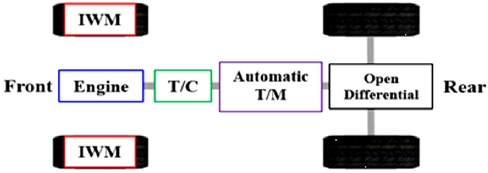
본 논문은 차량 내부 센서 및 상용 GPS를 활용한 전자식 사륜 구동 차량의 요레이트 추종 제어 알고리즘을 소개한다. 요레이트 추종 제어 알고리즘은 차량 코너링 시의 중립 조향 특성을 제어 목표로 설정하며, 이에 따라 기존 로직 대비 더 높은 코너링 민첩성을 유도할 수 있다. 제어 대상은 상용화된 후륜 구동 시스템의 전륜에 IWM를 장착한 전자식 사륜 구동 차량이다(Fig. 1). 전륜의 좌우 IWM들로부터 생성되는 요 모멘트가 제어 입력이 되어 차량 횡방향 거동 제어를 구현한다. 최종적으로는 차량 동역학 시뮬레이션용 소프트웨어인 CarSim을 통해 제안된 알고리즘의 제어 성능이 검증된다.
2. 차량 모델링
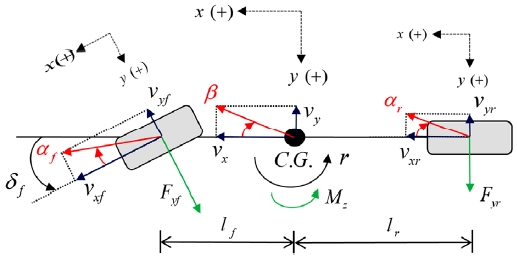
본 논문에서는 평면 상에서의 차량 횡방향 거동을 다루고자 하며, 이를 위해 Bicycle model을 활용한다. 이는 Fig. 2와 같이 좌우 바퀴가 차량 중심선에 합쳐져 놓인다고 가정함으로써, 전륜 및 후륜에서 통합된 횡방향 타이어 힘들을 Fyf, Fyr로 표현한다.6) 차량 Bicycle model의 요 모멘트 및 횡방향 힘 평형식들은 다음과 같다.
| (1) |
| (2) |
이 때, 차량 횡방향 가속도 ay는 다음과 같이 표현 가능하다.
| (3) |
또한 차량의 종방향 속도 변화가 크지 않다는 가정 아래에, 전륜 및 후륜의 타이어 횡방향 미끌림 각들은 아래와 같다.
| (4) |
식 (1) ~ (4)을 종합하여, Bicycle model의 β 및 r에 대한 미분 방정식은 각각 식 (5), (6)과 같다.
| (5) |
| (6) |
3. 제어기 설계
제어기 설계를 위해 차량 횡방향 슬립 각의 추정 값 정보가 필요하며, 이를 위해 기존에 연구된 확장형 칼만 필터 기반의 차량 횡방향 슬립 각 추정기가 활용된다.6) 제어 타겟은 중립 조향 특성 (|αf|=|αr|)에 해당되는 Desire yaw rate rd이며, 이를 통해 언더스티어 조향 특성을 타겟으로 하는 기존의 제어 타겟보다 더욱 민첩한 차량 코너링 주행을 이끌어 낼 수 있다. 본 연구의 제어 타겟 모델은 다음과 같다.
| (7) |
3.1 Smooth Sliding Mode Control (SMC)
단순 피드백 제어만으로 제어기를 구성할 경우, 높은 비례 게인을 취할 시 심하게 진동하는 제어 입력을 발생시킬 우려가 존재한다. 따라서 이러한 진동 현상이 발생하지 않기 위해서는 피드포워드 제어를 동반하는 것이 효과적이다. 이는 제어 정확도 및 제어 응답성 역시도 향상시키는 효과를 가져온다. 본 논문에서는 피드백 제어와 차량 모델 정보 기반의 피드포워드 제어가 동시에 이루어지는 Smooth SMC를 개발하여, 차량의 횡방향 거동의 제어에 활용하고자 한다.
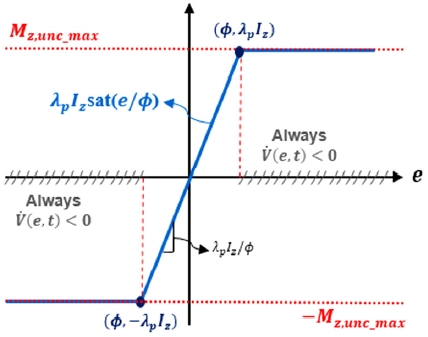
Sign 피드백 텀을 동반하는 일반적인 SMC는 모델 불확실성 및 외란에 대하여 높은 제어 강건성을 가진다는 장점을 가지지만, 제어 입력의 Chattering 현상을 야기할 수 있다는 점이 우려된다.7) 이러한 SMC의 Chattering 현상이 IWM 시스템에서 발생될 경우, 운전자가 느끼는 승차감은 매우 악화될 것으로 예상된다. Fig. 3에서 볼 수 있듯이 본 논문에서 활용하고자 하는 Smooth SMC는 Sign 피드백 텀 대신 Saturation 피드백 텀을 활용하며, 이를 통해 Chattering 현상을 방지할 수 있다. Smooth SMC의 설계 과정은 다음과 같다. 먼저 피드백 오차를 다음과 같이 정의한다.
| (8) |
피드백 오차의 미분 방정식을 Saturation 함수로 표현하면 다음과 같다.
| (9) |
여기서 ϕ와 λp는 각각 Saturation boundary와 피드백 게인을 의미한다. 식 (8)을 시간에 대하여 미분한 뒤, 식 (6)을 대입하면 다음과 같은 식을 유도할 수 있다.
| (10) |
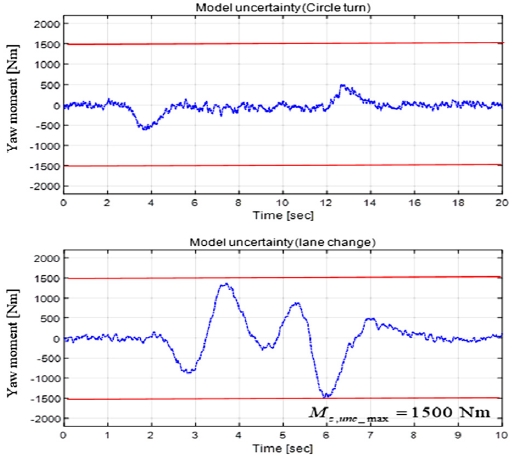
이 때, Mz,unc는 부정확한 모델링에 의해 발생하는 모델 Uncertainty를 의미한다. 다양한 주행 조건에서의 시뮬레이션을 통해 Mz,unc의 범위를 결정할 수 있다: |Mz,unc| ≤ Mz,unc_max.8) Fig. 4에서는 본 논문의 시뮬레이션에서 활용될 Circle turn과 Double lane change 상황에서의 모델 Uncertainty Mz,unc 값을 각각 보여준다. 본 논문에서 Mz,unc_max는 1500 Nm으로 설정된다.
최종적으로 식 (9)를 식 (10)에 대입하면, 아래와 같은 요 모멘트 제어 입력 값이 설계된다.
| (11) |
제어기의 안정성을 검증하기 위해서 임의의 Lyapunov 함수를 다음과 같이 정의한다.
| (12) |
Lyapunov 함수 V(e)의 시간에 대한 미분을 표현하면 식 (13)이 유도된다.
| (13) |
다음으로 식 (10)을 식 (13)에 대입하면 다음과 같다.
| (14) |
λpIz < Mz,unc_max인 경우 을 만족하는 영역은 존재하지 않는다. λpIz ≥ Mz,unc_max인 경우에는 e ≥ ϕ에 해당되는 영역에서 이 만족된다. 이에 따라 요레이트 제어 오차 e는 ϕ라는 Saturation boundary 이내로 최종적으로 수렴함을 증명할 수 있다.7) 이 때, ϕ가 0에 근접할수록 e의 최종 수렴 값 역시도 0에 근접하게 된다. 제어 입력의 Smoothness 및 제어 오차의 수렴성 사이의 Trade-off 관계를 고려하여 적절한 Saturation boundary ϕ를 결정한다.
4. 토크 분배
필요한 요 모멘트 제어량 Mz,des를 실제로 생성하기 위해 전륜 좌우 IWM들에 토크 분배를 실시해야 한다. 이를 위해서는 먼저 IWM의 최대 모터 토크를 정의해야 한다. 먼저 전륜 좌우 바퀴들의 수직방향 타이어 힘들은 다음과 같다.
| (15) |
또한 식 (16)과 식 (17)은 전륜 좌우 바퀴들의 횡방향 타이어 힘들의 합과 비율을 나타낸다.
| (16) |
| (17) |
식 (16)과 식 (17)로부터 전륜 좌우 바퀴 각각의 개별적인 횡방향 타이어 힘을 다음과 같이 정의할 수 있다.
| (18) |
| (19) |
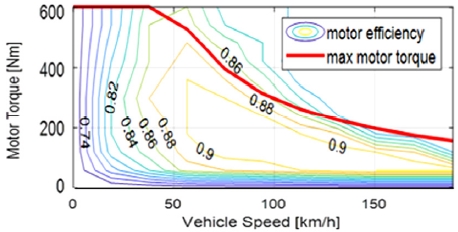
타이어 마찰원 효과에 의한 전륜 바퀴 i의 물리적 최대 모터 토크는 이다. 이와 동시에 IWM의 전기적 특성, 즉 T-N curve를 반드시 고려해주어야 한다. Fig. 5에서는 본 연구에서 활용되는 IWM의 T-N curve를 보여주고 있으며, 휠 속도에 따른 최대 모터 토크 값을 확인 가능하다. 최종적으로 물리적, 전기적 특성을 모두 고려한 전륜 바퀴 i의 최대 IWM 토크 값은 식 (20)과 같이 정의된다 (i = fl, fr).
| (20) |
이에 따라, 전륜 바퀴 i에서 생성할 수 있는 최대 요 모멘트는 다음과 같다.
| (21) |
4.1 Daisy-Chaining Allocation
필요 요 모멘트가 결정된 다음 이를 전륜의 좌/우로 토크 분배를 통해 실제 추가 요 모멘트를 생성해내야 한다. 특정 요 모멘트를 생성해낼 수 있는 좌/우 토크 분배의 조합은 많이 있지만, 본 연구에서는 승차감을 고려하여 Negative 인휠 토크를 최대한 사용하지 않고 꼭 필요한 경우에만 Negative 모터 토크를 생성 하는 방식을 택했다. IWM의 특성을 고려한 토크 분배를 위하여 Daisy-chaining allocation 알고리즘이 본 연구에서 활용된다.9) 이는 여러 개의 Actuator들에 각각 제어량을 분배하는 방식으로서, 전체 제어 요구량의 크기가 증가함에 따라 실제로 사용하는 Actuator의 수를 점차적으로 증가시키는 분배 구조를 가진다.
이와 같은 Daisy-chaining allocation을 본 연구의 IWM 토크 분배에 다음과 같이 적용시키고자 한다. 먼저 Mz,des의 값이 양수일 경우, 오른쪽 IWM에서만 모터 토크를 생성한다. 하지만 Mz,des의 값이 증가하여 Mz_lim,fr < Mz,des이 된 순간부터 반대편의 왼쪽 IWM에서도 Negative 모터 토크를 생성하기 시작한다. Mz,des의 값이 음수인 경우에도 이와 대칭적으로 IWM의 모터 토크 값들을 생성시킨다. 이를 정리하면 식 (22), (23)과 같이 Mz,des의 값에 따른 전륜 좌우 IWM들의 모터 토크 분배량이 표현된다.
| (22) |
| (23) |
결과적으로 요 모멘트 제어 요구량이 적은 Mild cornering 상황(|Mz,des|≤Mz_lim)에서는 하나의 IWM에서만 Positive 모터 토크를 생성한다. 하지만 요 모멘트 요구량이 커지는 Severe cornering 상황(|Mz,des|>Mz_lim)에서는 Negative torque가 생성되고, 즉 두 개의 IWM들이 모두 횡 방향 거동 제어에 활용되며 Positive 및 Negative 모터 토크들이 함께 발생하게 된다.
5. 시뮬레이션 결과
MATLAB/Simulink와 연동된 CarSim 소프트웨어를 활용하여 시뮬레이션 검증이 이루어진다.10) 시뮬레이션 차량의 파라미터 정보는 Table 1에서 확인할 수 있으며, 이는 실제 E-class 세단 차량의 제원 정보를 기반으로 한다.정상 상태 및 과도 상태 코너링 상황에 해당되는 Circleturn test 및 Double lane change test가 진행되며, μmax = 0.9의 고마찰 노면 특성을 가지는 Dry asphalt 노면에서 시뮬레이션이 이루어진다.11) 비교 대상은 Conventional PID 제어를 활용하는 횡방향 거동 제어기이며, 토크 분배는 동일한 알고리즘을 사용하다.
5.1 Circle Turn Test
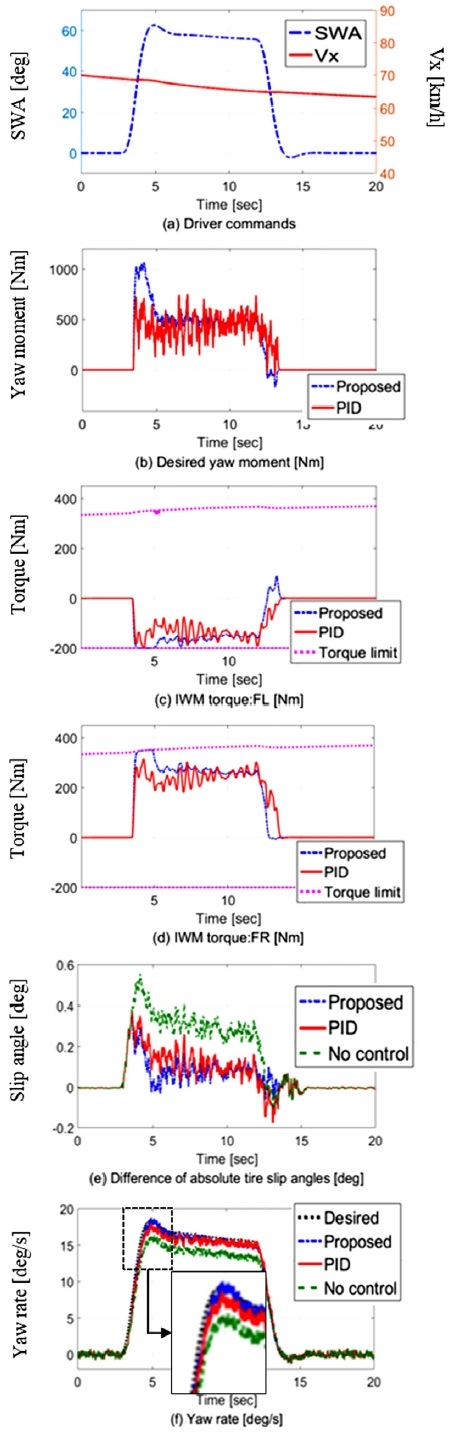
Fig. 6에서는 Circle turn test에서의 시뮬레이션 결과를 소개한다. Fig. 6(a)에서는 60 ~ 70 km/h 사이의 차량 속도와 함께 반시계 방향으로 원형 주행하는 운전자의 명령을 확인할 수 있다. Fig. 6(b)~(d)는 각각 Mz,des, Tm,des_fl, Tm,des_fr을 보여주고 있다. 제안된 Smooth SMC의 제어 입력 값들이 Conventional PID 제어기의 제어 입력 값들보다 진동 현상이 훨씬 더 적음을 확인 가능하다. 또한 Fig. 6(e)는 |αf|-|αr|, 즉 전후륜 타이어 횡방향 슬립각들 사이의 차이를 나타낸다. 제안된 알고리즘은 0에 근접한 값을 나타내고 있고, 이를 통해 |αf|=|αr|, 즉 중립 조향 특성에 가까운 민첩한 코너링 주행이 이루어짐을 확인할 수 있다. 최종적인 요레이트 추종 제어 결과는 Fig. 6(f)에서 소개된다. 제안된 제어 알고리즘이 제어 타겟 rd을 가장 근접하게 추종함을 볼 수 있다.
이와 같은 Circle turn test에서의 시뮬레이션 분석을 통해, 제안된 알고리즘은 기존 Conventional 제어기보다 정상 상태 코너링 상황에서 더욱 높은 코너링 성능을 이끌어 낼 수 있음이 검증된다.
5.2 Double Lane Change Test
Double lane change는 차량의 주행 차선을 빠르게 2번 연속으로 변경하는 상황으로서, 장애물 회피와 같이 높은 코너링 민첩성을 필요로 하는 긴급 상황에서 제안된 횡방향 거동 제어기의 코너링 성능을 검증할 수 있는 주행 시뮬레이션이다.
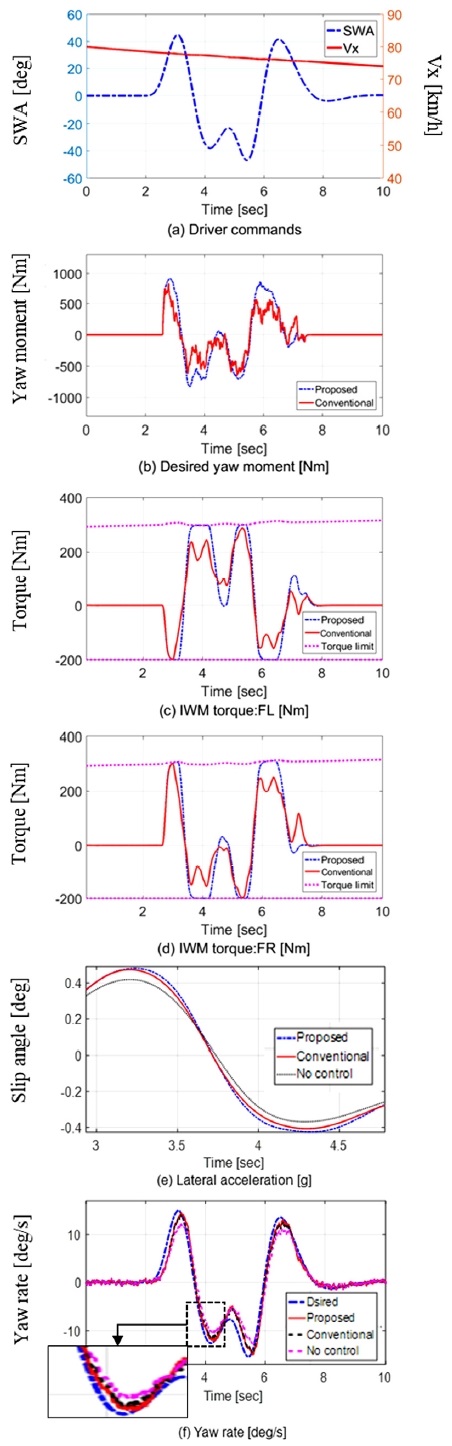
Fig. 7(a)는 70 ~ 80 km/h의 속도 범위에서 Double lane change를 실시하는 운전자 명령을 보여준다. 또한 Fig. 7(b) ~ (d)에서는 앞선 Fig. 6과 마찬가지로 제어 입력 값들을 보여주고 있다. 제안된 Smooth SMC는 차량 모델 정보로 구성된 피드포워드 제어가 동반되기 때문에, 피드백으로만 이루어진 Conventional PID 제어기보다 제어 입력의 반응 속도가 더욱 빠름을 확인할 수 있다. 빠른 제어응답 속도 덕분에 Fig. 7(e)와 같이 동일한 주행 명령에서 더욱 높은 차량 횡가속도 값을 이끌어낼 수 있다. Double lane change test에서의 최종 요레이트 추종 제어 결과는 Fig. 7(f)에서 보여진다.
결론적으로, Double lane change와 같은 과도 상태 코너링 상황에서 제안된 알고리즘은 기존 Conventional 제어기보다 동일 조향 명령 시 더 높은 횡가속도를 이끌어낸다. 이는 긴급 주행 상황에서 높은 코너링 성능과 함께 민첩하게 코너 구간을 탈출할 수 있음을 의미한다.
6. 결 론
본 논문에서는 IWM를 활용한 전자식 사륜 구동 차량의 횡방향 거동 제어기가 개발된다. 먼저 요레이트 제어 타겟을 추종하기 위해 Smooth SMC에서 제어 입력 값을 결정한다. 다음으로는 이에 해당되는 요 모멘트 제어량을 생성하기 위해 전륜 좌우의 IWM들에 Daisy-chaining allocation을 기반으로 한 토크 분배가 이루어진다. 최종적으로 차량에 중립 조향 특성을 가지는 횡방향 거동 제어가 적용됨으로써, 민첩하고 날카로운 차량의 코너링 주행이 실현된다.
본 논문의 제어 알고리즘의 주된 기여들은 다음과 같이 요약된다. 1) 차량 모델 정보를 기반으로 한 Smooth SMC는 제어 입력의 Smoothness 및 제어 수렴성을 모두 고려할 수 있다. 2) 타이어 마찰원 효과 및 IWM의 T-N curve를 모두 고려한 IWM 토크 분배가 이루어진다. 3) 또한 토크 분배는 Daisy-chaining allocation을 기반으로 하기 때문에, Negative 모터 토크를 가능한 적게 활용한다는 장점을 가진다.
결론적으로 본 논문에서 제안된 차량 모델 기반 횡방향 거동 제어 알고리즘은 전자식 사륜 구동 차량의 코너링 성능 향상에 충분히 기여될 수 있음이 확인된다. 더불어 실제 차량 적용 시에 발생하는 문제들에 대응함으로써, 높은 실차 적용 가능성을 보여주고 있다.
Nomenclature
| m : | vehicle mass, kg |
| Iz : | vehicle yaw moment of inertia, Nm |
| r : | vehicle yaw rate, rad/s |
| Mz : | additional yaw moment, Nm |
| vx : | vehicle longitudinal velocity, m/s |
| β : | vehicle sideslip angle, rad |
| lf,lr : | CG-front and CG-rear axle distances, m |
| Tm : | IWM torque, Nm |
| Cf ,Cr : | front and rear tire cornering stiffness, N/rad |
| h : | vehicle CG height, m |
| δf : | front steering angle, rad |
| t : | track width, m |
| Re : | effective tire radius, m |
| αf,αr : | front and rear tire slip angles, rad |
| μmax : | tire-road friction coefficient |
Subscripts
| fl, fr : | front left, front right |
| des : | desired |
References
-
K. Han, M. Choi, B. Lee and S. Choi, “Development of a Traction Control System Using a Special Type of Sliding Mode Controller for Hybrid 4WD Vehicles,” IEEE Transactions on Vehicular Technology, Vol.67, No.1, pp.264-274, 2018.
[https://doi.org/10.1109/TVT.2017.2752704]

-
B. Ren, H. Chen, H. Zhao and L. Yuan, “MPC-based Yaw Stability Control in In-wheel-motored EV via Active front Steering and Motor Torque Distribution,” Mechatronics, Vol.38, pp.103-114, 2016.
[https://doi.org/10.1016/j.mechatronics.2015.10.002]

-
Q. Lu, P. Gentile, A. Tota, A. Sorniotti, P. Gruber, F. Costamagna and J. Smet, “Enhancing Vehicle Cornering Limit through Sideslip and Yaw Rate Control,” Mechanical Systems and Signal Processing, Vol.75, pp.455-472, 2016.
[https://doi.org/10.1016/j.ymssp.2015.11.028]

-
L. Novellis, A. Sorniotti and P. Gruber, “Wheel Torque Distribution Criteria for Electric Vehicles With Torque-Vectoring Differentials,” IEEE Transactions on Vehicular Technology, Vol.63, No.4, pp.1593-1602, 2014.
[https://doi.org/10.1109/TVT.2013.2289371]

-
L. Zhang, H. Ding, Y. Huang, H. Chen, K. Guo and Q. Li, “An Analytical Approach to Improve Vehicle Maneuverability via Torque Vectoring Control: Theoretical Study and Experimental Validation,” IEEE Transactions on Vehicular Technology, Vol.68, No.5, pp.4514-4526, 2019.
[https://doi.org/10.1109/TVT.2019.2903872]

-
G. Park, S. Choi, D. Hyun and J. Lee, “Integrated Observer Approach Using In-vehicle Sensors and GPS for Vehicle State Estimation,” Mechatronics, Vol.50, pp.134-147, 2018.
[https://doi.org/10.1016/j.mechatronics.2018.02.004]

- H. K. Khalil and J. Grizzle, Nonlinear Systems, Prentice Hall, New Jersey, 1996.
-
T. Goggia, A. Sorniotti, L. Novellis, A. Ferrara, P. Gruber, J. Theunissen, D. Steenbeke, B. Knauder and J. Zehetner, “Integral Sliding Mode for the Torque-Vectoring Control of Fully Electric Vehicles: Theoretical Design and Experimental Assessment,” IEEE Transactions on Vehicular Technology, Vol.64, No.5, pp.1701-1715, 2015.
[https://doi.org/10.1109/TVT.2014.2339401]

-
J. Buffington and D. Enns, “Lyapunov Stability Analysis of Daisy Chain Control Allocation,” Journal of Guidance Control and Dynamics, Vol.19, No.6, pp.1226-1230, 1996.
[https://doi.org/10.2514/3.21776]

-
S. Chung and H. Lee, “Vehicle Sideslip Estimation And Compensation For Banked Road,” Int. J. Automotive Technology, Vol.17, No.1, pp.63-69, 2016.
[https://doi.org/10.1007/s12239-016-0005-1]

-
J. Kim and J. Yang, “Understanding Metrics of Vehicle Control Take-Over Requests in Simulated Automated Vehicles,” Int. J. Automotive Technology, Vol.21, No.3, pp.757-770, 2020.
[https://doi.org/10.1007/s12239-020-0074-z]