다종소재 차체 부품의 하이브리드 조인트 설계법에 관한 연구

1. 서 론

최근 자동차 시장의 가장 큰 화두(관심사)는 전기차를 중심으로 한 친환경 차량이다. 북미, 유럽을 중심으로 전기차 생산 및 대중화가 시작되었으며, 이러한 세계적 흐름에 맞춰 국내 자동차 기업들도 전기차에 맞는 다양한 전용 부품들을 개발하고 있다. 앞으로의 시장 전망 또한 2040년에는 전 세계 신규 자동차 판매의 약 50 %를 전기차가 대체할 것으로 예상하고 있다.¹⁾

현 시점에서 전기차가 내연기관 자동차 대비 가장 큰 약점으로 지적 받는 것은 상대적으로 짧은 주행거리로, 한번 충전해서 달릴 수 있는 거리는 배터리의 용량, 차량의 무게와 밀접한 관련이 있다. 이처럼 전기차의 주행거리가 상대적으로 짧은 것은 전기차 구동을 위한 무거운 필수 부품들을 수반하는 것이 근본 원인으로 지적되고 있다. 이에 필수 부품들의 경량화 연구가 활발히 진행 중이나, 실질적인 문제 개선을 위해서는 상당한 시일이 필요할 것으로 내다보고 있다. 이러한 문제를 해결하고자 전기차의 필수 부품 이외 기계적 구조물 (특히 차체) 들에 대한 경량화 요구가 높아지고 있으며, 기존의 철강 소재의 틀에서 벗어나 복합재료를 중심으로 한 경량 소재의 활용 요구가 커지고 있다.^2-4)

자동차에 사용되는 복합재료는 탄소섬유 혹은 유리섬유와 폴리머 기지제를 혼합하여 만들어낸 경량 소재로, 복합재료 내 섬유가 주 하중을 담당하는 특성이 있기 때문에, 섬유의 파단이 발생할 수 있는 기계식 조인트 (Mechanical joint) 기술보다는 폴리머 접착제를 활용한 접착식 조인트(Adhesive joint) 기술이 일반적인 접합 기술로 사용되고 있다.

그러나 접착제는 하중 방향에 따라 각기 다른 특성을 지니며, 강도에 있어 이방성이 존재하기 때문에 하중 방향에 따른 적절한 설계와 공정이 이루어지지 않으면 구조 조인트로서 사용이 매우 제한적인 단점이 있다. 때문에 접착제를 사용하는 대부분의 구조에서는 취약한 Peel 방향 하중이 발생하지 않도록 구조 설계를 하며, 그 관리 또한 엄격하게 이루어지는 것이 특징이다.⁵⁾ 그러나 자동차의 부품들은 매우 다양한 하중 케이스를 극복해야 한다. 실제로 주요 하중 조건들을 특정하여 설계한다 하더라도 설계과정에서 다루어지지 않은 다른 하중 조건들에 노출될 수 있기 때문에 모든 하중에 대한 설계 검토가 이루어지기가 사실상 불가능하다. 이에 예측 가능한 하중 조건을 근거로 신뢰성 높은 조인트를 설계하는 것이 일반적인 조인트 설계 방법이다.

본 연구에서는 Shear 방향 하중을 기반으로 설계되던 기존의 접합부 설계 방법론에서 벗어나, 접착 접합 방식이 수직 방향 하중에 취약한 단점을 극복할 수 있는 하이브리드 조인트 설계 방법을 제안하고자 한다. 이에 Roof cross member의 천장 강도 시험 조건을 활용하여 본 연구에서 제안하는 설계 방법의 예시를 설명하고, FE 모델 해석을 통해 제안된 설계 방법론으로 하이브리드 조인트를 설계 하였다.

2. 조인트 설계 방법론

접착 조인트는 Shear 방향 하중에 대해, 기계식 조인트는 Peel 방향 하중에 대해 효과적으로 조이닝할 수 있는 장점이 있다.

이에 본 연구에서 제안하는 조인트 설계 방법론은 Shear 방향 하중은 접착조인트가, Peel 방향 하중은 기계식 조인트가 담당하도록 하여 설계하는 방식이며, 구조가 운용 도중 발생하는 하중에 대해 각 조인트 형식이 효과적인 대응을 할 수 있도록 하는 것이 특징이다.

이 같은 설계 방법론이 제대로 운용되기 위해서는 다음의 조건이 우선 고려되어야 한다.

• 1. 조인트에 발생하는 하중 성분에 대한 평가가 잘 이루어질 수 있어야 하며, 그 방법론은 비교적 효과적이어야 한다.
• 2. 조인트의 세부 설계 또한 Shear 하중은 접착조인트가, Peel 하중은 기계식 조인트가 담당할 수 있는 구성으로 되어 있어야 한다.

본 연구에서는 우선 고려되어야 할 조건 중에 조인트에 발생하는 하중 성분을 효과적으로 계산 하는 방법과 모델링 방식에 따른 하중 계산 방법을 제시 하는 것으로, 조인트의 세부 설계는 본 논문에서 제안하는 방법론이 적용될 수 있는 구성으로 설계되어 있다고 가정하였다.

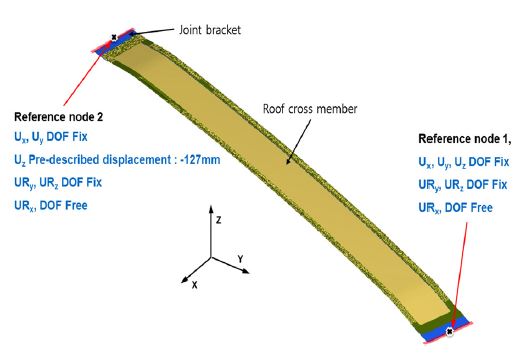
3. Roof Cross Member의 설계 요구 조건

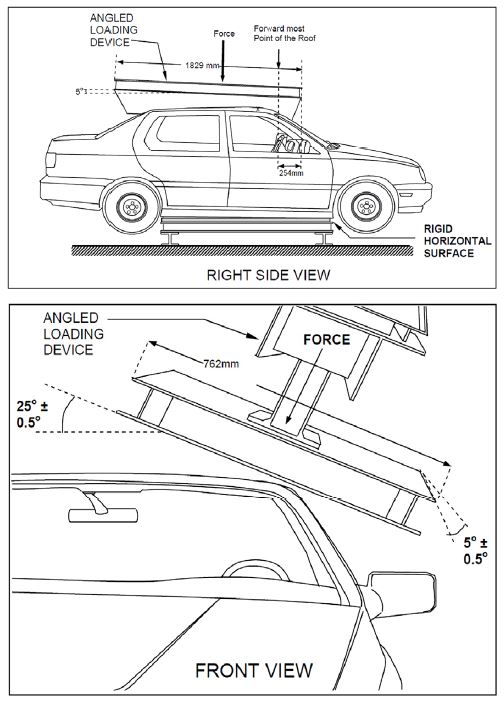
조인트 설계요구도를 도출하기 위해, Roof cross member의 차량안전시험 중 천장강도 시험(FMVSS No.216a)⁶⁾을 활용하였다. Roof cross member가 자동차 운용기간 도중 가장 극심한 하중에 노출되는 케이스로 Roof cross member 조인트 설계요구도 중 가장 가혹한 조건이다.

Fig. 1

Roof crush resistance test (FMVSS No.216a)

시험 조건에 따르면 차량이 전복되었을 경우, 탑승자를 보호하기 위해 차량 무게의 3배 하중이 인가되는 동안 Roof가 최대 5 인치(127 mm) 까지만 변형 되어야 한다. 시험 중 하중이 가해지게 되면, 주변 부품인 Roof, Roof cross member, Roof rail, B-pillar 등으로 하중이 전달되게 된다. 이때 전달되는 하중은 각 차체 부품들의 구조강성 비율에 따라 분산되기 때문에 Roof cross member의 정보만으로 조인트부에 가해지는 하중을 예측할 수 없다.

따라서 본 연구에서는 하중방향으로 Roof cross member를 5 인치(127 mm) 강제 변위 시켰을 때, 지지점에서의 Internal load를 계산하여 조인트의 구조 요구도를 도출하였다. 이 방법은 천장강도 시험 중 하중 부가 장치와 그 장치에 맞닿은 조인트부 위치가 같은 변위를 가진다는 점을 착안한 것으로, 다른 주요 부품들을 따로 모델링 하지 않아도 조인트를 통해 전달되는 하중을 쉽게 예측할 수 있는 장점이 있다. 또한, 이는 Steel로 구성된 기존 차체 구조와 비교, 동등 수준 이상의 구조 건전성을 확보하도록 설계하는데도 유용한 방법이며, Roof rail과 연결되는 조인트에 발생하는 Resultant force로부터 조인트의 구조 요구도를 쉽게 도출 할 수 있다.

4. Modeling & Analysis

4.1 이종 소재의 Internal Load 계산방법

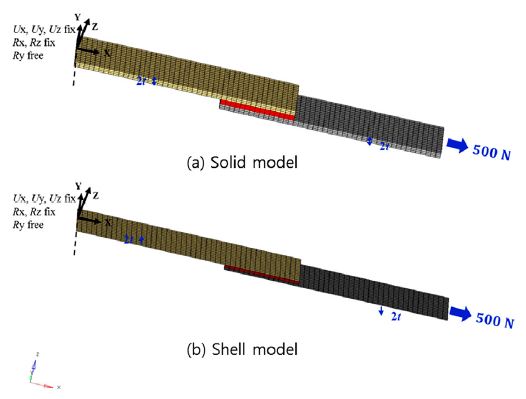
Roof cross member와 Joint bracket 접합부의 Internal load 계산방법을 검증하기 위해, 해당 접합부 연결 방식인 Single-lap joint 구조의 유한요소 해석을 수행하였다. 본 해석의 수행 목적은 크게 두 가지로, 첫 번째는 이종 소재 간 접합부에 발생하는 Internal load와 모재의 구성 차이에 대한 상관관계를 확인(Model verification case 1)하기 위함이고, 두 번째는 FE model의 종류(Solid model과 Shell model)가 해석 결과에 미치는 영향을 확인(Model verification case2)하기 위함이다.

접합부 모델링 방법에는 파손 모드와 거동에 따라 Solid, Shell, CZM(Cohesive Zone Modeling) 혹은 Tie break 방법 등이 있다. 본 연구에서는 접합부 모델링 방법에 따라 조인트에 전달되는 하중이 큰 차이가 없는 점과, 본 연구의 목적이 조인트에 전달되는 하중을 기준으로 접합부 설계 방법론을 개발하는 데 있기 때문에, 접합부의 Internal load를 계산할 수 있는 Solid 및 Shell element를 사용하였다. 또한 전체 모델이 대칭으로 구성되어 있으나, 모델 자체가 단순하고 계산이 비교적 빠르게 수행 될 수 있어 Full model을 사용하였다.

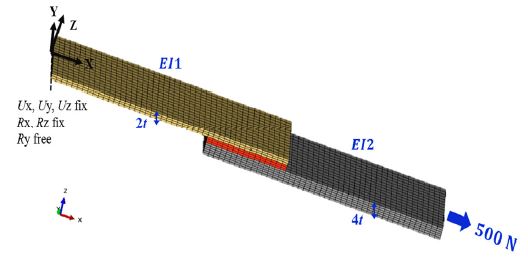
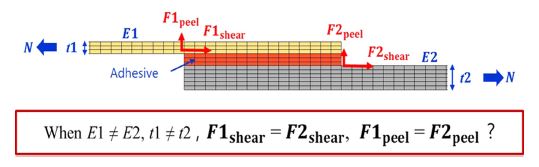
첫 번째로 다종 소재 차체 부품 간 접합부는 접착층을 기준으로 상/하 피접착부의 구성이 다르기 때문에, 접합 경계면에 발생하는 Internal load가 서로 동일한지 확인할 필요가 있다. 이종 소재 간 접합부에 발생하는 Internal load와 피 접착부의 구성에 대한 상관관계를 확인하기 위해 Fig. 2와 같이 접착층을 기준으로 소재 강성과 두께가 다른 피 접착부를 Single-lap shear joint 형태로 모델링 하였고, 3D solid model을 사용하였다.

Fig. 2

Correlation between the internal loads on the adhesive joint part and the stiffness of adherends (Model verification case 1)

접착층을 기준으로 상/하 피접착부의 구조강성을 달리하기 위해, 피접착부 1, 2의 소재와 두께를 각 각 다르게 적용하였다. 피접착부 1은 CFRP Laminate, 2 mm두께로 구성하였고, 피접착부 2는 Steel, 4 mm 두께로 구성하였다. 또한 접착층 두께는 2 mm로 모델링 하였다.

이 때 사용한 소재의 물성은 Table 1, Table 2와 같다. Table 2의 CFRP Laminate 물성은 Carbon prepreg lamina (Table 3)를 Stacking sequence에 따라 계산한 Equivalent laminate 물성이며, Laminate stacking sequence는 [±45/0₂]_s 이다.

Table 1

Material properties (Model verification case 1)

Table 2

Material property : CFRP Laminate

Table 3

Material property : CFRP Lamina

Table 1의 Adhesive 물성은 L社의 필름형 접착제 시편을 ASTM D638-14 규격에 따라 Lab. Test한 결과값을 사용하였고, Steel 물성은 문헌에서 제공하는 값을 인용하였다.⁷⁾ 또한 Table 3의 CFRP Lamina 물성은 NCF UD 직물을 VA-RTM으로 성형하여 만든 복합재 시편을 ASTM D3039와 ASTM D3410 규격에 따라 Lab. Test 한 결과값을 이용하였고, 특히 E₁ 값과 E₂ 값은 인장방향 실험값과 압축방향 실험값을 평균하여 사용하였다.

해석을 위한 경계조건은 Fig. 3과 같이 Single-lap shear joint의 한 쪽 끝 면(Surface) 자유도 중 세 방향 변위(U_x, U_y, U_z)와 두 방향 회전(R_x, R_z)을 고정하고, 다른 쪽 끝 면에 500 N의 x 방향 하중을 부여했다.

Fig. 3

Boundary condition of the single-lap shear joint model (Model verification case 1)

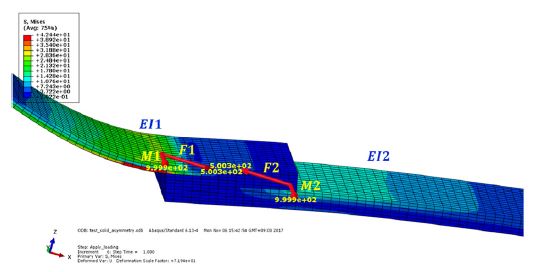
접착층을 기준으로 상/하 피접착부의 경계면에서 산출하는 Internal load를 정의하기 위해, 접착층과 피 접착부 1의 경계면에서 산출한 Resultant moment를 M1, Resultant force를 F1, 접착층과 피 접착부 2의 경계면에서 산출한 Resultant moment를 M2, Resultant force를 F2로 정의했다.

Table 4는 해석을 통해 접합 경계면에서 발생하는 Internal load를 산출한 결과이며, 이로부터 피 접착부 1의 경계면에서 계산한 값과 피 접착부 2의 경계면에서 계산한 값 사이에 식 (1)~(3)과 같은 관계가 성립함을 알 수 있다.

Table 4

Analysis result (Model verification case 1)

Resultant moment

$\[ M1=M2 \]$

(1)

Resultant force

$\[ F{1}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}=F{2}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}} \]$

(2)

$\[ F{1}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}}=F{2}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}} \]$

(3)

여기서 Resultant force의 Tangential 성분은 Shear 하중, Normal 성분은 Peel 하중으로 볼 수 있다. 해석 결과로부터 접합부 경계면에 발생하는 Internal load(Resultant moment, Resultant force)는 상/하 피접착부의 구조 강성 차이와는 관계가 없음을 알 수 있다. Fig. 4는 Model verification case 1의 해석 결과이다.

Fig. 4

Analysis result of single-lap shear joint (Model verification case 1)

두 번째로 차체 구조의 전산해석 모델은 주로 2D shell model을 사용하기 때문에, FE model의 종류(Solid model과 Shell model)가 Internal load 계산 결과에 미치는 영향을 확인할 필요가 있다. 이를 위해 Single-lap shear joint 모델을 Fig. 5와 같이 Solid model과 Shell model로 구성하여 해석을 수행하였다.

Fig. 5

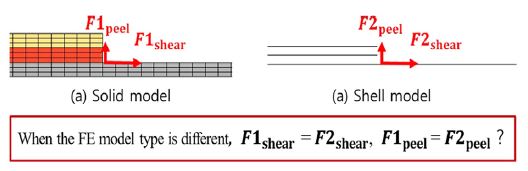
Correlation between the internal loads on the adhesive joint part and FE model type (Model verification case 2)

본 해석은 FE model 종류에 따른 해석결과의 차이를 보는 것이 목적이므로, Model verification case 1과 동일한 소재와 물성을 사용하였다. 또한 접착층을 기준으로 상/하 피접착부의 구조강성 차이를 크게 할 필요가 없기 때문에, 접착층, 피접착부 1, 피접착부 2의 두께는 모두 2 mm로 통일하였다.

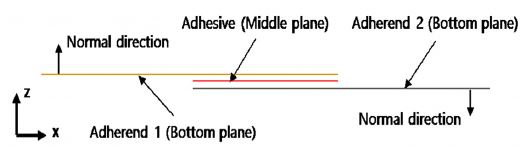
Shell model의 Reference plane 정보는 Table 5와 같고, 각 Part의 Reference plane과 Normal direction 등을 구체적으로 도식화 하면 Fig. 6과 같다.

Table 5

Reference plane of shell model (Model verification case 2)

Fig. 6

Reference plane of shell model (Model verification case 2)

해석을 위한 경계조건은 Fig. 7과 같다. Solid model의 경우 Single-lap shear joint의 한쪽 끝 면(Surface) 자유도 중 세 방향 변위(U_x, U_y, U_z)와 두 방향 회전(R_x, R_z)을 고정하고, 다른 쪽 끝 면에 500 N의 x 방향 하중을 부여했다. Shell mode의 경우 Single-lap shear joint의 한 쪽 끝 Edge 자유도 중 세 방향 변위(U_x, U_y, U_z)와 두 방향 회전(R_x, R_z)을 고정하고, 다른 쪽 끝 Edge에 500 N의 x 방향 하중을 부여했다.

Fig. 7

Boundary condition of the single-lap shear joint model (Model verification case 2)

Solid model로 해석하여 산출한 Resultant moment를 M1, Resultant force를 F1, Shell model로 해석하여 산출한 Resultant moment를 M2, Resultant force를 F2로 정의하였으며, 해석 결과는 Table 6과 같다. Solid model과 Shell model을 이용하여 Internal load를 산출한 결과를 비교하면 식 (4) ~ (6)과 같은 관계를 얻을 수 있다.

Table 6

Analysis result (Model verification case 2)

Resultant moment

$\[ M1=2\times M2 \]$

(4)

Resultant force

$\[ F{1}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}=F{2}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}} \]$

(5)

$\[ F{1}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}}=2\times F{2}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}} \]$

(6)

Solid model을 사용한 경우와 Shell model을 사용한 경우 접합부 경계면에 발생하는 Internal load(Resultant moment, Resultant force) 산출 값이 차이가 있음을 확인할 수 있다. 이는 Solid model의 경우 단면의 Neutral plane을 기준으로 Moment가 계산되지만, Shell model의 경우 Reference plane을 기준으로 Moment가 계산되기 때문에 Reference plane의 위치를 어디로 설정하는지에 따라 해석 결과가 달라지는 것이다.

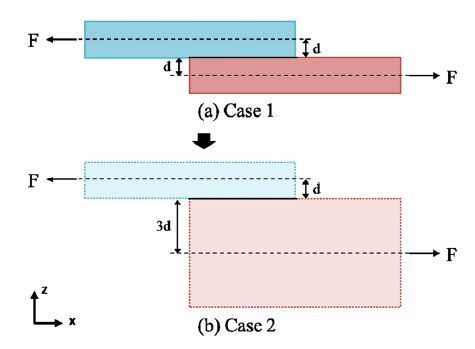
Neutral plane의 위치에 따라 접합부 경계면에 발생하는 Resultant moment와 Peel방향 Resultant force 계산 결과가 어떻게 달라지는 지를 설명하기 위해 Fig. 8과 같이 두 개의 Adherend가 접합되어 있을 때의 단면 그림을 참고한다. Case 1은 두 Adherend의 Neutral plane 간 거리가 2d 로, 여기서 작용하는 Moment arm의 크기는 d 이고, Case 2는 두 Adherend의 Neutral plane 간 거리가 4d 로, 여기서 작용하는 Moment arm의 크기는 2d 이다. 때문에, Case 1, 2에서 계산되는 Moment는 식 (7), (8)과 같다.

$\[ \mathrm{M}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}{\mathrm{t}}_{\left(\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{ }1\right)}=F\cdot d \]$

(7)

$\[ \mathrm{M}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}{\mathrm{t}}_{\left(\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{ }2\right)}=F\cdot 2d \]$

(8)

Fig. 8

Relationship between moment and position of neutral plane

식 (7), (8)로부터 Moment_{(Case 2)}는 Moment_{(Case 1)}의 2배인 것을 확인할 수 있고, 이는 Case 1과 Case 2 의 Moment arm 차이에 의한 것임을 알 수 있다. 또한 접합부 경계면에서 계산되는 Peel 방향 Resultant force가 Moment에 비례하기 때문에 식 (9)를 도출할 수 있다.

$\[ F_{\mathrm{p}\mathrm{e}\mathrm{e}\mathrm{l}\left(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{ }1\right)}=2F_{\mathrm{p}\mathrm{e}\mathrm{e}\mathrm{l}\left(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{ }2\right)} \]$

(9)

결국 Shell model의 경우 Reference plane을 기준으로 Moment가 계산되기 때문에 Reference plane을 Middle plane으로 구성하지 않는 한, 하중이 발생하는 수직 거리가 바뀌게 되고, 바뀐 Moment arm만큼 Resultant moment가 바뀌는 것이다. 또한 이에 비례해서 Resultant force의 Normal 성분인 Peel 방향 Resultant force도 함께 바뀌게 된다(Moment arm과 관계없는 Resultant force의 Tangential 성분은 바뀌지 않는다). 따라서 Shell model을 사용할 경우에는 해당 형상의 두께 정보와 Reference plane의 위치를 고려해서, 산출된 Resultant moment와 Resultant force를 Moment arm 변화만큼 보상해서 결과를 확인해야 한다.

4.2 Roof Cross Member 모델링 및 해석

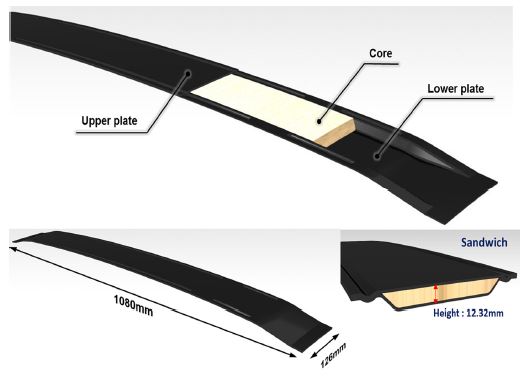
본 연구에서는 복합재료 Sandwich 구조(CFRP + Core)로 대체 설계된 Roof cross member model을 활용하였다. 이는 기존 Steel 부품과 비교하여 동등 이상의 강성/강도를 가지도록 설계된 구조이며 해당 부품의 형상은 Fig. 9와 같다.

Fig. 9

Roof cross member model applied sandwich composite structure

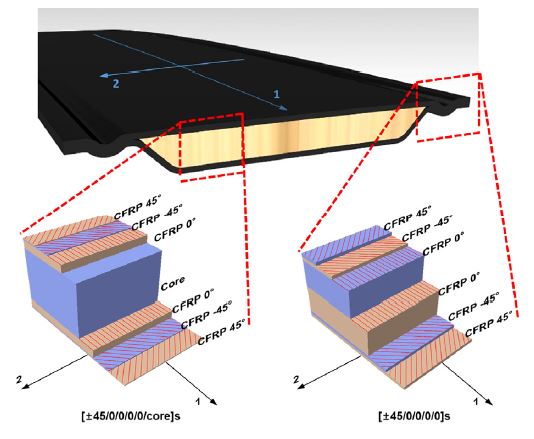
본 부품의 중앙부위에는 Core를 포함한 구조이나, 조인트 부는 CFRP Laminate와 Steel Bracket만 존재 하며, Roof cross member의 CFRP Laminate와 Steel joint bracket은 Shell element로, Roof cross member의 내부 Core는 Solid element로 모델링하였다. 해석을 위해 사용한 소재 중 복합재료 Sandwich 구조 (CFRP + Core)는 Fig. 10과 같고, Core와 맞닿는 면을 기준으로 CFRP Laminate가 [0₄ / ±45]로 적층되어 있다. 이 때 사용된 CFRP Lamina 물성은 Table 3에, Bracket의 Steel 물성은 Table 1에 나타낸 값과 같고, Core 물성은 Table 7에 나타내었다.

Fig. 10

Stacking sequence of core and CFRP lamina

Table 7

Material property : Other materials

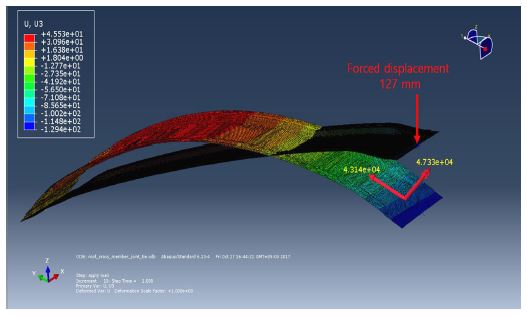
해석 수행을 위해 Fig. 11과 같이, ‘Roof cross member + Joint bracket’의 양쪽 끝 단 각 1열 Node들을 기준으로 경계조건을 부여했고, 한쪽 끝 단은 세 방향 변위(U_x, U_y, U_z)와 두 방향 회전(R_y, R_z)을 고정했다. 다른 쪽 끝 단은 두 방향 변위(U_x, U_y)와 두 방향 회전(R_y, R_z)을 고정하고, -z 방향으로 127 mm 강제 변위를 부여하여 해석을 수행하였다. 해당 경계 조건은 앞서 3장에서 설명한 바와 같이, 자동차 천장강도 시험 조건에 따라 차량이 전복되었을 때 Roof가 최대 5 인치(127 mm)까지만 변형을 허용해야 하는 조건을 고려하여, 해당 변형이 발생했을 때 Joint bracket에 발생하는 Internal load를 확인하기 위함이다.

Fig. 11

Boundary condition of ‘Roof cross member + Joint bracket’ model

Fig. 12는 FE model 해석 수행 결과이며, 4.1절에서 설명한 Shell model의 Internal load 산출 방법에 따라 Joint bracket에 발생하는 Internal load를 산출하면 Table 8과 같은 결과를 얻을 수 있다.

Fig. 12

Analysis result of ‘Roof cross member + Joint bracket’

Table 8

Internal loads at the joint bracket

4.1절에서 설명한 것과 같이 Resultant force의 Tangential 성분은 Shear load, Normal 성분은 Peel load로 볼 수 있고, 이렇게 얻은 Shear load와 Peel load는 Joint 설계를 위한 기준 값으로 활용할 수 있다.

5. Hybrid Joint의 설계

본 연구에서 제시하는 Hybrid joint 설계법은 Joint part에 발생하는 Internal load 중 Shear load는 Adhesive joint가, Peel load는 Mechanical joint가 담당하도록 설계 하는 것이다. 이를 좀 더 상세히 설명하면 아래와 같다.

• ① Shear load capability 요구도를 충족하도록 Adhesive의 Bonding area를 결정한다.
• ② Peel load capability 요구도를 충족하도록 Mechanical joint의 수량을 결정한다.

앞서 4장에서는 자동차 천장강도 시험 조건을 기준으로 ‘Roof cross member + Joint bracket’ 해석 수행을 통해 Joint part에 발생하는 Internal load를 산출하였다. 이렇게 산출된 Internal load에 Safety factor를 적용하여, Joint 설계 요구도를 도출할 수 있다. 4장에서 Internal load를 산출하기 위해 해석한 조건은 차량이 전복되었을 경우에 해당하는 천장강도 시험조건으로, 해당 부품 및 Joint part가 생애 1번만 겪는 조건이다. 또한 Mechanical joint를 함께 적용하여, Adhesive는 Shear load만 견디도록 하는 보수적인 설계이기 때문에, Safety factor는 ‘2’로 선정하였다.

식 (11), (12)에서 얻은 Internal load와 Safety factor 2를 조합하여, Joint part의 설계 요구도를 구하면 Table 9와 같다.

Table 9

Design requirement of the joint bracket

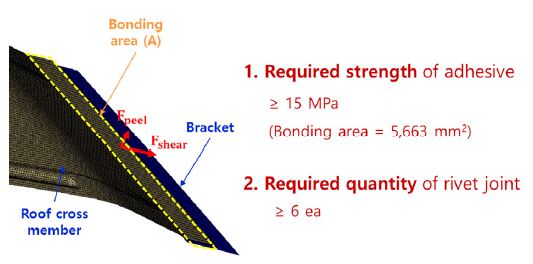
Adhesive joint의 Shear strength를 15 MPa로 가정하고, Mechanical joint(Rivet type) 1개의 Peel 방향 Load capability는 2.5 kN 인 점을 고려하면, 다음과 같은 Hybrid Joint part의 최종 설계 안을 얻을 수 있다.

• ① Adhesive의 Shear strength가 15 MPa인 경우, Bonding area는 5,663 mm²
• ② Mechanical joint (Rivet type)는 6개 이상 사용

Fig. 13

Final design of hybrid joint

6. 결 론

본 연구에서는 이종 소재의 Hybrid joint(접착 + 기계식)에 대해 하중을 기반으로 한 설계 방법론을 제안 하였다. 본 연구에서 제안하는 설계 방법론은 접착 조인트와 기계식 조인트의 장점을 활용하기 위한 설계 방법론으로 Shear 방향 하중은 접착조인트가, Peel 방향 하중은 기계식 조인트가 담당하도록 하는 조인트에 관한 것이다. 위와 같은 설계 방법론이 운용되기 위해 수행 되어야 할 효과적인 하중 성분을 산출하는 방법론을 제안하였으며, 차체의 일반적인 모델링 방법인 Shell model에서는 Reference plane의 위치에 따라 모멘트가 달리 계산되는 점을 고려하여 전달하중을 산출해야 함을 알게 되었다. 또한 본 결과를 Solid model과 shell model과의 비교를 통해 검증하였으며, 정립된 방법론을 통해 Roof cross member의 조인트부에 대해 하중을 산출하고 기본 설계를 수행 하였다.

Acknowledgments

본 연구는 산업통상자원부 산업소재핵심기술개발사업(반응중합을 이용한 자동차용 열가소성 탄소섬유 복합소재/공정 및 이를 활용한 센터플로어 차체 구조의 전주기 개발, 10052724)으로 지원된 연구결과 입니다.

본 연구는 산업통상자원부 산업핵심기술개발사업(금속-복합재 하이브리드 공정(접합-성형) 통합 엔지니어링 기술개발 및 25 % 이상 경량화 사이드 스트럭쳐 상용화 부품 개발, 10077492)으로 지원된 연구결과 입니다.

References

• Colin McKerracher (BloombergNEF), Electric Vehicle Outlook 2019, https://bnef.turtl.co/story/evo2019.pdf, , 2019.
• J. S. Park, J. B. Kim, J. B. Moon, H. K. Jang and S. H. Yoon, “Future Technology for Multi-material Lightweight Carbody Structure,” Machinery and Materials, Vol.28, No.2, pp.42-57, 2016.
• J. B. Moon, J. H. Kim, H. K. Jang and J. S. Park, “A Study on Calculation of Composites Lamina Material Properties through Reverse Engineering of Light Weight Composite Car-body,” Transactions of KSAE, Vol.25, No.1, pp.1-10, 2017. [https://doi.org/10.7467/KSAE.2017.25.1.001]
• J. B. Kim, K. D. Kim, S. J. Kim, D. W. Shin and D. K. Kim, “Development of Carbon Continuous-fiber Composite Frame for Automotive Sun-roof Assembly,” Transactions of KSAE, Vol.25, No.3, pp.350-359, 2017. [https://doi.org/10.7467/KSAE.2017.25.3.350]
• A. J. Kinloch, Adhesion and Adhesive, Chapman and Hall, London, pp.188-194, 1990.
• U. S. Department of Transportation, U.S. Department of Transportation National Highway Traffic Safety Administration Laboratory Test Procedure for FMVSS, No. 216a, ROOF CRUSH RESISTANCE, TP-216a-00, 2009.
• J. M. Gere and S. P. Timoshenko, Mechanics of Materials, 2nd Edn., Brooks, Monterey, California, p.744, 1984.