고속주행시 요 응답성 향상을 위한 후륜 조향 제어 알고리즘

1. 서 론

최근까지 요 모멘트 생성에 도움을 주는 부가적인 요소를 덧붙여 차량의 성능을 향상시키는 연구가 진행되어 왔다. 이러한 연구들은 ESC(Electronic Stability Control), AFS(Active Front Steering), RWS(Rear Wheel Steering)와 같이 차량 횡 방향 움직임에 영향을 주는 구동기를 이용하였으며 그 특성을 고려하여 차량의 안정성을 높이거나 선회 능력을 향상시켰다.^1-3) 가장 대표적으로 ESC는 좌우 차륜에 독립적인 제동을 통해 요 모멘트를 생성하는 장치이다. 하지만 편 제동을 통해 요 모멘트를 생성하므로 운동에너지 손실이 발생하며 승차감이 떨어진다는 단점이 있다. AFS의 경우에는 제동을 사용하지 않으므로 이러한 단점은 없지만, 운전자 조향각에 추가적인 조향각을 더하는 방식으로 작동하기 때문에 전륜 횡력이 쉽게 포화된다. 즉 제어 가능한 영역이 제한적이다. 하지만 RWS는 운전자의 조향과는 상관없이 후륜에서 조향각을 생성하므로 횡력 포화 관점에서 넓은 제어 영역을 가진다.

RWS는 운전자의 조향 입력을 후륜 조향 구동기가 보조하는 조향 시스템이다. 차량이 저속으로 주행할 때는 후륜 조향각을 전륜 조향각에 대해 역상으로 제어하여 차량의 조종성을 향상시킨다. 고속 주행에서는 이를 동상 제어하여 차량의 안정성을 향상시킨다. 하지만 이때 운전자 조향의도에 대해 차량 요 응답 성능이 떨어지는 단점을 가진다.

RWS의 대표적인 제어 방식은 전륜 조향각의 크기에 비례하는 후륜 조향각을 계산하여 차량을 제어하는 것이다. 비율을 결정할 때, Look-up table을 이용하여 속도에 따른 고정 비율을 사용하는 방법과 차량의 횡 방향 동 특성 모델로부터 Neutral-steer 차량의 특성을 갖도록 비율을 계산하는 방법이 이용되었다.^4-6) 하지만 이러한 방법 모두 횡 슬립각을 줄이도록 후륜 조향각을 제어하기 때문에 고속 주행 시 요 응답성이 저하되는 단점이 있다. 또한 Feed-forward 제어를 통해 후륜 조향각을 결정하기 때문에 상황에 따른 차량 상태 변화를 고려할 수 없으며, Disturbance로 인한 제어 오차가 발생한다.

Disturbance에 대해 강인한 제어를 하기 위해 여러 연구가 발표되었다.^7-9) 차량의 상태 변화나 외부 요인들을 고려하기 위하여 요 속도와 횡 슬립각을 Feed-back 하였으며, 목표 요 속도와 목표 횡 슬립각을 추종하도록 후륜 조향각을 결정하였다. 하지만 하나의 제어 입력으로 두 가지의 제어 목표를 추종하기 때문에 성능이 저하되며 마찬가지로 고속 주행시 요 응답성이 저하되는 단점이 존재한다.

이러한 단점을 해결하기 위해 RWS와 추가적인 구동기를 통합하여 사용한 연구들이 발표되었다.^10-13) AFS, ESC와 같은 추가 구동기의 조합을 통해 목표 요 속도, 목표 횡 슬립각을 동시에 추종하는 것이 가능하다. 하지만 추가적인 구동기를 사용한다는 점에서 경제성이 떨어지고, 구동기들 간에 상호 작용을 고려해야 한다는 점에서 제어로직의 복잡도가 올라가므로 양산 차량에 적용하는데 어려움이 있다.

기존의 연구들을 살펴볼 때, RWS 단일 구동기만을 사용할 경우 고속 주행 영역에서 차량 요 응답성이 떨어지며 이를 해결하기 위해 추가 구동기가 필요하다는 것을 알 수 있다. 따라서 본 연구에서는 고속주행시, RWS 단일 구동기만을 이용하여 기존 제어 방법에서 얻을 수 있는 차량 안정성을 유지한 채 요 응답성을 향상시키는 방법을 다루었다.

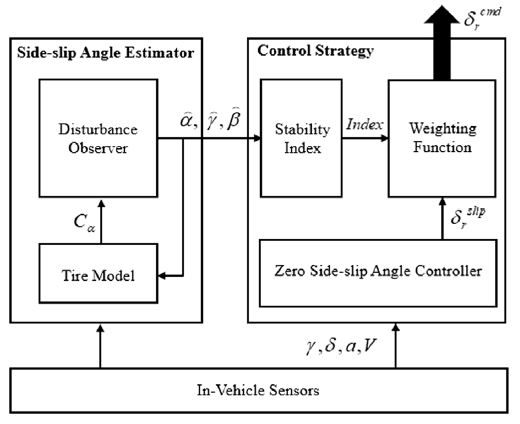
본 논문의 구성은 다음과 같다. 2장에서는 차량 안정성을 관측하기 위해 필요한 Side-slip angle 추정기 설계 방법을 제시한다. 3장에서는 안정성을 유지한 채 요 응답성을 향상시키는 제어 전략을 제안한다. 4장에서 실차 실험 결과를 통해 제안된 방법의 성능을 검증하였고 5장에서 결론을 맺는다. 전체 알고리즘의 구성은 Fig. 1과 같다.

Fig. 1

Overall algorithm architecture

2. Side-slip Angle 추정기

본 논문에서는 차량 안정성 모니터링을 위해 Side-slip angle, β를 추정하였다. 먼저 타이어 모델을 구축하여 전 후륜의 Cornering stiffness, C_α를 추정한다. 또한 Input, Output disturbance를 고려하기 위해 차량 모델과 Disturbance를 통합한 모델을 설계하였다. 통합 모델에 추정된 C_α를 매 샘플 업데이트하고 Kalman filter를 이용하여 β를 추정하였다.

2.1 타이어 모델

타이어 횡방향 힘은 식 (1)과 같다.

$\[ \begin{array}{cc}{F}_{yi}=C_{\alpha i}\cdot {\alpha }_i& where i:f, r\end{array} \]$

(1)

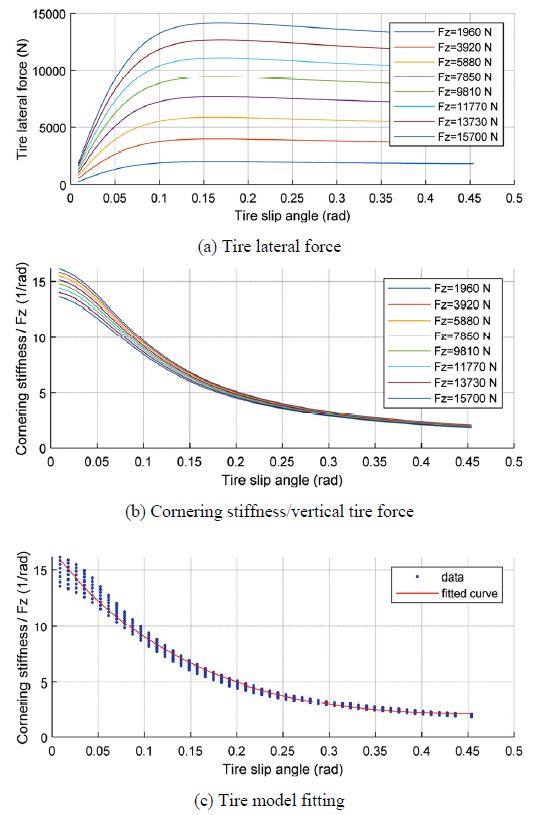
Fig. 2(a)는 타이어 Slip angle, α 에 대한 타이어 횡방향 힘, F_y 의 그래프이다. 이를 살펴보면, α가 작은 영역에서는 α가 증가함에 따라 F_y 도 선형적으로 증가하지만 일정 영역을 벗어나면 비선형적 특성을 보인다. 또한 타이어 수직방향 힘, F_z 가 증가할수록 F_y 또한 증가하는 것을 확인할 수 있다.

Fig. 2

Tire model fitting process

식 (1)의 양 변을 F_z 와 α로 나누고 이를 α에 대한 지수함수 형태로 표현하게 되면 식 (2)와 같다. 식 (2)의 좌변 데이터들을 α에 대해 지수함수 형태로 피팅하게 되면, 지수함수 튜닝 파라미터 c₁, c₂를 결정할 수 있다. 그리고 이를 Fig. 2(b)와 (c)에서 표현하였다.

$\[ \begin{array}{cc}\frac{F_{yi}}{F_{zi}\cdot {\alpha }_i}=\frac{C_{\alpha i}}{F_{zi}}=c_1\exp \left(c_2\cdot {\alpha }_i\right)& where i:f, r\end{array} \]$

(2)

최종적으로 구축한 타이어 모델은 식 (3)과 같다.

$\[ \begin{array}{cc}{C}_{\alpha i}=F_{zi}\cdot c_1\exp \left(c_2\cdot {\alpha }_i\right)& where i:f, r\end{array} \]$

(3)

이때 C_α를 추정하기 위한 F_z 와 α는 다음 식을 통해 계산한다.

$\[ \begin{array}{l}{F}_{zf}=\frac{mg{l}_r-m{a}_{x}h}{l}\\ F_{zr}=\frac{mg{l}_f+m{a}_{x}h}{l}\end{array} \]$

(4)

$\[ \begin{array}{l}{\alpha }_f={\delta }_f-\stackrel{̑}{\beta }-\frac{l_r\widehat{\gamma }}{V_x}\\ {\alpha }_r={\delta }_r-\stackrel{̑}{\beta }+\frac{l_f\widehat{\gamma }}{V_x}\end{array} \]$

(5)

여기서 ^̑ 은 추정 값을 의미하며 챕터 2.2의 추정기 Output 결과를 피드백 하여 사용한다.

2.2 Side-slip Angle 추정 알고리즘

2.2.1 차량 모델

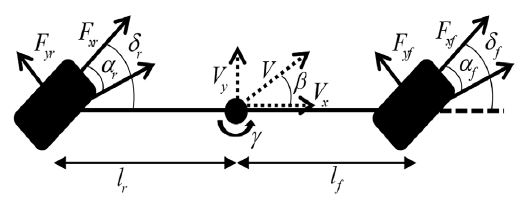
차량의 횡방향 상태를 추정하기 위해 Fig. 3의 2- DOF 차량 모델을 사용하였다. 현재 상태벡터로부터 다음 상태벡터를 예측하는 Process model은 다음과 같다.

$\[ \begin{array}{l}\dot{\mathbf{x}}\left(t\right)=A\mathbf{x}\left(t\right)+B\mathbf{u}\left(t\right)\\ \mathbf{z}\left(t\right)=C\mathbf{x}\left(t\right)\end{array} \]$

(6)

Fig. 3

2-DOF vehicle model

$\[ \begin{array}{l}where\\ A=\left[\begin{array}{cc}-\frac{2\left(C_{\alpha f}+C_{\alpha r}\right)}{m{V}_x}& -1+\frac{2\left({l_{r}C}_{\alpha r}-l_f{C}_{\alpha f}\right)}{m{V}_x^2}\\ \frac{2\left(l_r{C}_{\alpha r}-l_f{C}_{\alpha f}\right)}{I_z}& -\frac{2\left(l_f^2{C}_{\alpha f}+l_r^2{C}_{\alpha r}\right)}{I_z{V}_x}\end{array}\right]\\ B=\left[\begin{array}{cc}\frac{2C_{\alpha f}}{m{V}_x}& \frac{2C_{\alpha r}}{m{V}_x}\\ \frac{2l_f{C}_{\alpha f}}{I_z}& -\frac{2l_r{C}_{\alpha r}}{I_z}\end{array}\right], C=\left[0 1\right]\\ \mathbf{x}={\left[\beta \gamma \right]}^T, \mathbf{u}={\left[{\delta }_f {\delta }_r\right]}^T\end{array} \]$

식 (6)의 Process model을 Sample time, T_s 로 이산화 하면 식 (7)과 같다

$\[ \begin{array}{l}\mathbf{x}\left(k+1\right)=A_d\mathbf{x}\left(k\right)+B_d\mathbf{u}\left(k\right)+\mathbf{w}\left(k\right)\\ \mathbf{z}\left(k\right)=C\mathbf{x}\left(k\right)+\mathbf{v}\left(k\right)\end{array} \]$

(7)

$\[ \begin{array}{cc}where& A_d=I+T_s\cdot A, { B}_d\end{array}=T_s\cdot B \]$

2.2.2 Disturbance Observer

차량 횡방향 상태를 추정하기 위해 2-DOF 차량 모델을 사용하였다. 하지만 간소화된 모델을 사용함으로써 모델 오차가 발생한다. 또한 부정확한 Steering ratio정보로 인해 전륜 타이어 조향각에 오차가 존재한다. 이러한 Input disturbance들이 발생할 경우 추정 성능에 영향을 미치므로 추정기 설계 단계에서 이를 고려하여야 한다. 마찬가지로 차량 운동 상태를 측정하는 센서의 Bias 및 Delay와 같은 Output disturbance들 또한 추정 성능에 영향을 미친다. 따라서 이를 고려하기 위해 Input, Output disturbance를 상태벡터에 추가하여 함께 추정하였다. Disturbance는 시불변이라 가정하면 통합 모델은 식 (8)과 같다.

$\[ \begin{array}{l}\overline{\mathbf{x}}\left(k+1\right)=A_a\overline{\mathbf{x}}\left(k\right)+B_a\mathbf{u}\left(k\right)+{\mathbf{w}}_a\left(k\right)\\ \overline{\mathbf{z}}\left(k\right)=C_a\overline{\mathbf{x}}\left(k\right)+{\mathbf{v}}_a\left(k\right)\end{array} \]$

(8)

$\[ \begin{array}{l}where\\ A_a=\left[\begin{array}{ccc}{A}_d& B_d& \mathbf{0}\\ \mathbf{0}& {\mathbf{I}}_{2\times 2}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathbf{I}}_{1\times 1}\end{array}\right]\\ B_a=\left[\begin{array}{c}{B}_d\\ {\mathbf{0}}_{2\times 2}\\ {\mathbf{0}}_{1\times 2}\end{array}\right], C_a=\left[C {\mathbf{0}}_{1\times 2} {\mathbf{I}}_{1\times 1}\right]\\ \overline{\mathbf{x}}=\left[\begin{array}{c}\mathbf{x}\\ {{\mathbf{d}}^i}_{2\times 1}\\ {{\mathbf{d}}^o}_{1\times 1}\end{array}\right], {\mathbf{W}}_a~\left(0,Q\right), {\mathbf{v}}_a~\left(0,R\right)\end{array} \]$

w_α, v_α는 각각 통합 모델의 Process noise와 Measurement noise를 의미하며 정규분포를 따른다고 가정한다.

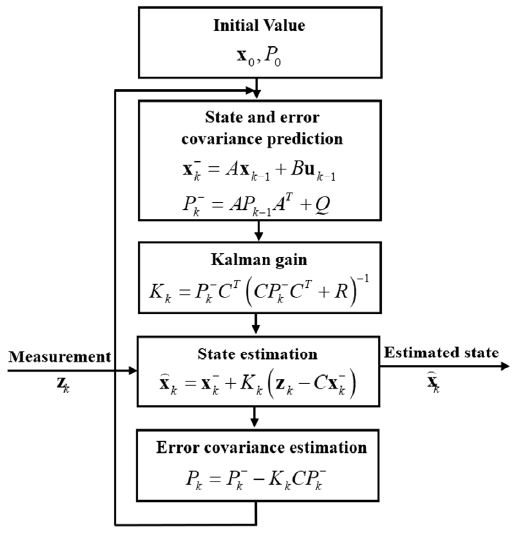
통합 모델을 Fig. 4에서 설명하는 Kalman filter 알고리즘에 적용하여 상태벡터를 추정한다.

Fig. 4

Kalman filter algorithm

3. 후륜 조향 제어 전략

본 논문에서는 고속 주행 시 차량의 안정성을 유지한 채 요 응답성을 향상시키는 방법을 제안한다. 차량의 안정성 유지를 위해 기존의 Zero Side-slip angle을 위한 후륜 조향 제어기를 채용하였다. 하지만 이것을 그대로 사용하지 않고 먼저, 차량 안정성 지표를 선정하였다. 그리고 적절한 가중함수를 도입하여 상황에 따라 필요한 후륜 조향각을 결정하였다.

3.3 가중 함수를 이용한 최종 제어량 결정

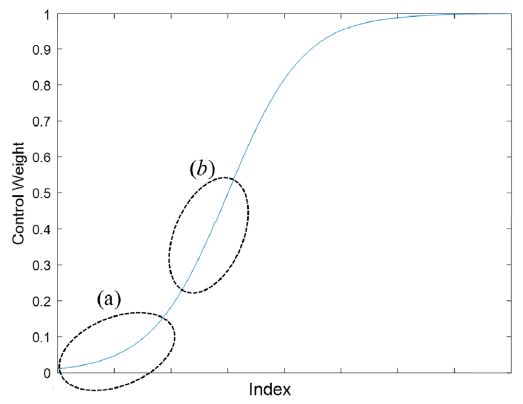
고속주행시 차량 안정성과 요 응답성은 서로 Trade-off관계에 있다. 따라서 Fig. 5(a)부분과 같이 안정하다고 판단될 때는 가중치를 천천히 증가시켜 후륜 조향 제어량을 억제함으로써 요 응답성을 키웠다. 또한 Fig. 5(b)부분과 같이 불안정하다고 판단될 때는 빠르게 제어 입력을 키워 안정성을 향상시켰다. 이러한 특징을 가지는 Sigmoid function을 이용하여 식 (11)과 같이 가중함수를 구성하였다.

$\[ w=\frac{1}{1+\exp \left(-c_3\left(Index-c_4\right)\right)} \]$

(11)

Fig. 5

Weighting function

최종적으로 후륜 조향각 제어 명령값은 식 (12)와 같다.

$\[ {\delta }_r^{cmd}=w\cdot {\delta }_r^{slip} \]$

(12)

4. 실차 실험 결과

제안하는 알고리즘 검증을 위해 실차 실험을 진행하였다. RWS구동기를 장착하여 후륜 조향이 가능한 차량을 이용하여 알고리즘을 검증하였다. 실시간 알고리즘 구현을 위해 dSpace사의 Micro-Autobox 장비를 사용하였다. 또한 Side-slip angle계측 장비는 OxTS사의 RT3000을 사용하였다. 모든 결과는 Vector사의 CANoe 장비를 이용하여 로깅하였다.

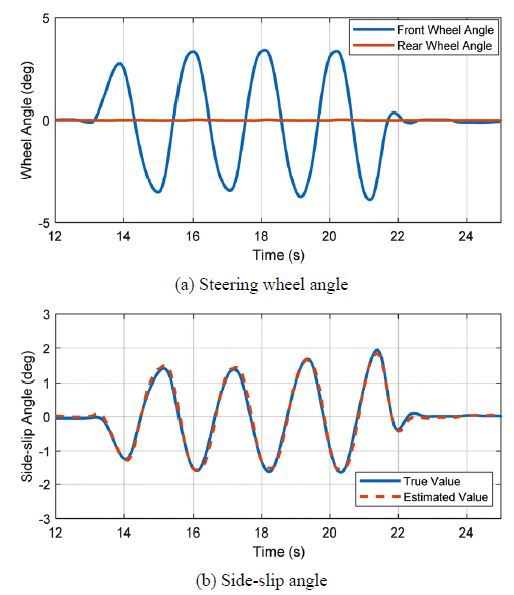
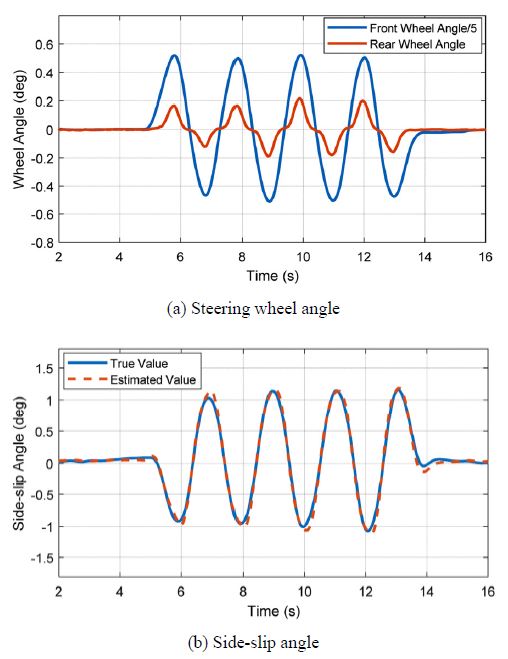
먼저 Side-slip angle 추정기의 성능을 검증하였다. 차량이 100 km/h로 고속 주행할 때 전륜 조향 입력을 Sine wave형태로 인가하였다. Fig. 6은 후륜 조향이 없을 때, Fig. 7은 후륜 조향이 있을 때의 Side-slip angle 추정 결과이다. 각각의 경우에 대해 추정 오차를 RMSE(Root Mean Square Error)로 수치화 하여 도출하였으며 Table 1에 정리하였다. 후륜 조향각 유무에 상관없이 RMSE가 충분히 작다는 것을 통해 Side-slip angle이 잘 추정되고 있음을 확인하였다.

Fig. 6

Estimation result w/o RWS

Fig. 7

Estimation result w/ RWS

Table 1

Side-slip angle estimation RMSE

제어 전략에 따른 후륜 조향 제어 성능을 알아보기 위해 실험을 진행하였다. 제안하는 알고리즘과의 성능 비교를 위해 챕터 3.1의 $$ {\delta }_r^{slip}$$ 을 이용하여 후륜을 제어하는 기존 방법과 제안하는 후륜 조향 제어량, $$ {\delta }_r^{cmd}$$ 을 통해 후륜을 제어하는 방법을 비교하였다.

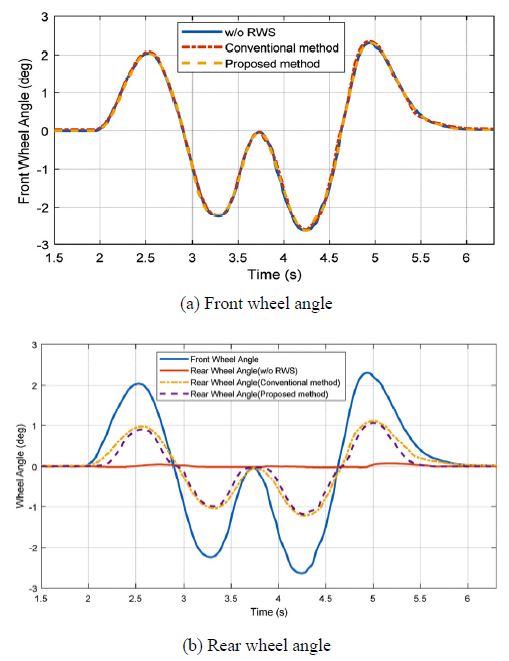
실험은 차량이 100 km/h로 고속 주행하면서 DLC(Double Lane Change)하는 상황에서 수행하였으며 동일한 비교를 위해 조향 로봇을 통하여 같은 전륜 조향 입력을 인가하였다. Fig. 8(a)와 같이, 후륜 조향을 하지 않은 경우, 기존 방법, 제안하는 방법의 세가지 경우에 같은 전륜 조향입력을 인가하였으며 그때 발생한 후륜 조향각은 Fig. 8(b)와 같다. Fig. 8(b)에서 보이듯이 전륜 조향 입력이 인가되었을 때, 기존의 방법에서는 거의 동시에 후륜 조향 제어량이 생성되는 것을 확인할 수 있다. 하지만 제안하는 방법에서는 아직 차량이 안정하다고 판단하고 있으므로 후륜 조향 제어량을 거의 생성하지 않다가 점점 불안정한 상태가 됨에 따라 급격히 제어량을 증가시키는 것을 확인할 수 있다. 이를 통해 앞서 선정한 안정성 지표와 Sigmoid 함수 형태로 설정한 가중함수가 연구 목적에 맞게 잘 작동하고 있음을 확인하였다.

Fig. 8

Control inputs of each method in DLC

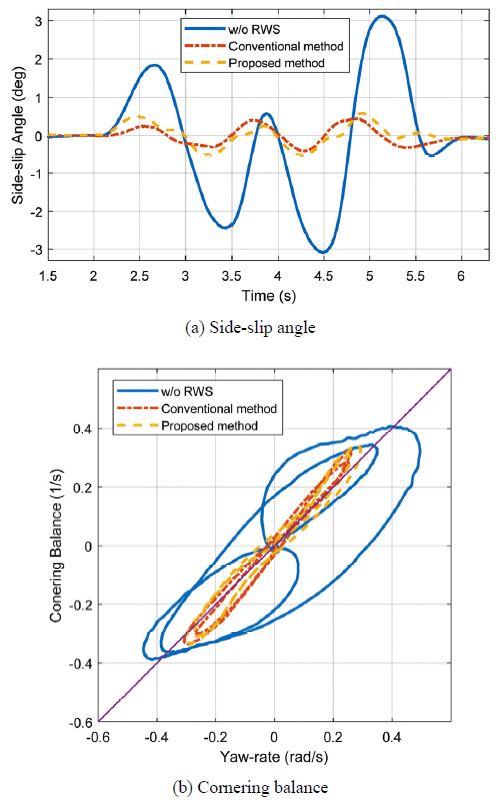
먼저 알고리즘 성능 비교를 위해 차량 안정성 관련 지표들을 확인하였다. Fig. 9(a)에서는 DLC상황에서 계측한 Side-slip angle, 그리고 Fig. 9(b)에서는 Cornering balance를 나타내었다. Cornering balance는 식 (14)의 좌항의 값으로써 횡 가속도를 차량 속도로 나눈 값이다. Yaw-rate을 x축, Cornering balance를 y축에 놓고 비교하였을 때 선형성이 나타날수록 Side-slip angle의 변화율이 작다는 의미이므로 Cornering balance가 좋다고 할 수 있다.

Fig. 9

Experiment results for vehicle stability in DLC

Fig. 9(a)에서 보이듯이 후륜 조향을 하지 않았을 때 Side-slip angle이 가장 많이 발생한다. 그리고 기존의 방법과 제안하는 방법에서는 비슷한 수준으로 Side-slip angle이 발생함을 알 수 있다. 마찬가지로 Fig. 9(b)에서 보이듯이 후륜 조향을 하지 않았을 때 Cornering balance가 가장 나쁘며, 나머지 경우에는 비슷한 수준인 것을 확인할 수 있다. 이를 수치화 하여 비교하기 위해 각각의 경우에 대해 RMSE를 Table 2에 정리하였다. RMSE를 계산할 때 Side-slip angle의 경우 계측량을 Error로 정의하였고, Cornering balance의 경우 기울기 1을 갖는 1차함수와의 거리를 Error로 정의하였다. Side-slip angle과 Cornering balance의 RMSE 수치를 통해 안정성능을 살펴보면, 후륜 조향을 하지 않았을 때보다 기존의 방법으로 제어하였을 때 증가한 차량 안정성 수치에 비해, 제안하는 방법으로 제어하였을 때 각각 1.7 %, 3.7 %의 성능 감소가 있음을 확인하였다.

Table 2

Vehicle stability RMSE

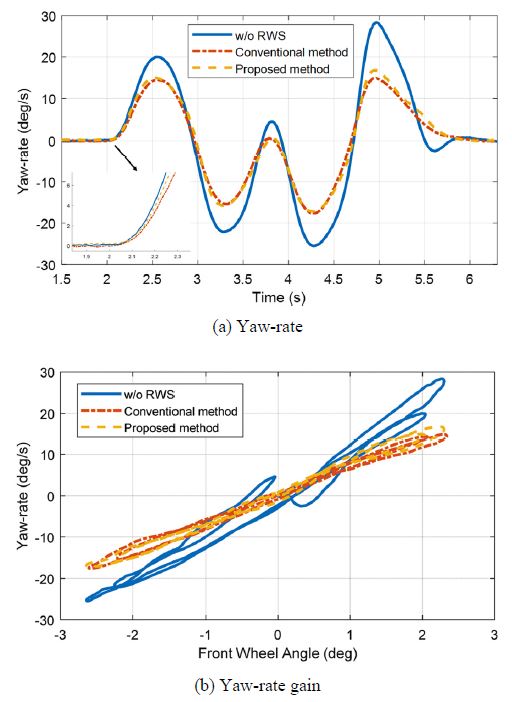
다음으로 알고리즘 성능 비교를 위해 요 응답성 관련 지표들을 확인하였다. Fig. 10(a)에서는 DLC상황에서 계측한 Yaw-rate, 그리고 Fig. 10(b)에서는 Yaw-rate gain을 나타내었다. Yaw-rate gain이란 전륜 조향 입력 증가량 대비 발생한 Yaw-rate의 증가량을 의미한다. 즉 전륜 조향각을 x축, Yaw-rate을 y축으로 놓고 데이터들의 기울기 값을 비교하였을 때 기울기가 클수록 Yaw-rate gain이 크다고 할 수 있다. Fig. 10(a)에서 보이듯이 제안하는 방법이 기존 방법보다 Yaw-rate이 빠르게 증가하는 것을 확인할 수 있다. 또한 Fig. 10(b)에서 보이듯이 제안하는 방법으로 제어했을 때 발생한 데이터들의 기울기가 기존 방법의 그것보다 크다는 것을 통해 제안하는 방법이 더 큰 Yaw-rate gain을 가진다는 것을 확인하였다. 이를 수치화 하여 비교하기 위해 각 방법의 데이터들을 1차함수로 피팅하여 그 기울기 값을 비교하였으며 결과는 Table 3에 정리하였다.

Fig. 10

Experiment results for yaw responsibility in DLC

Table 3

Yaw-rate gain

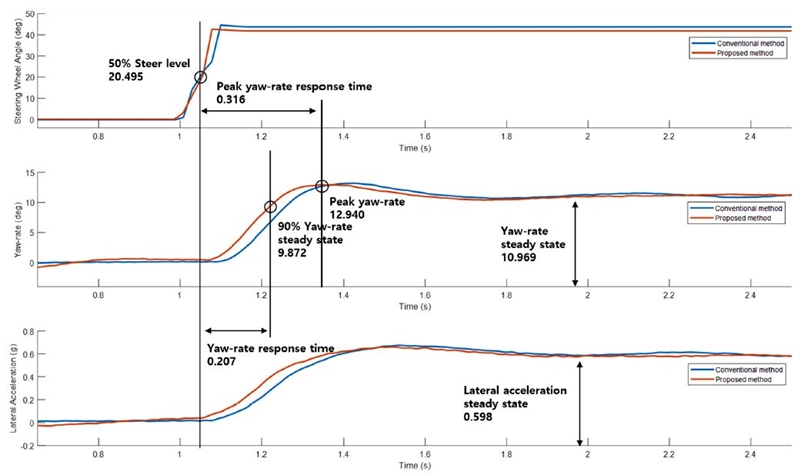
마지막으로, 제안하는 방법과 기존 방법의 핸들링 과도응답 특성을 비교하기 위해 ISO 규격의 Step steer objective 평가를 이용하였다.¹⁴⁾ 이 방법은 차량이 0.6 g의 횡 가속도를 가지도록 전륜 조향각을 Step input으로 인가하였을 때, 발생하는 횡 움직임 정보들을 이용하여 과도응답 특성을 평가한다. 핸들링 과도 응답 속도에 대해 Fig. 11에서 정의하였으며 그 결과 값을 Table 4에 정리하였다.

Fig. 11

Experiment results for yaw responsibility in step input

Table 4

Yaw-rate response time

요 응답 성능 비교를 위해 Yaw-rate gain과 Yaw-rate response time을 도출하였고 Table 3, Table 4에 정리하였다. 이를 통해 요 응답 성능을 살펴보면, 후륜 조향을 하지 않았을 때보다 기존의 방법으로 제어하였을 때 감소한 요 응답 성능 수치에 비해, 제안하는 방법으로 제어하였을 때 각각 43.3 %, 69.8 %의 성능 향상이 있음을 확인하였다.

제안하는 후륜 조향 제어 방법의 유효성 입증을 위해 기존의 방법과의 차량 안정성 및 요 응답성 지표를 비교하였다. 차량 안정성 지표로는 Side-slip angle과 Cornering balance의 RMSE 수치를 비교하였고 요 응답성 지표로는 Yaw-rate gain과 Yaw-rate response time을 비교하였다. 제안하는 방법을 통해 기존의 방법 대비 안정성 측면에서 각각 1.7 %, 3.7 %의 성능 감소가 있었지만 요 응답성 측면에서 43.3 % 69.8 % 성능 증가가 있었다. Trade-off 관계에 있는 차량 안정성과 요 응답성 관계에서, RWS 단일 구동기만을 이용하여 기존 제어 방법에서 얻을 수 있는 차량 안정성을 최대한 유지한 채 요 응답 성능을 향상시킬 수 있음을 확인하였다.

5. 결 론

본 논문에서는 고속상황시 RWS를 이용할 때, 전 후륜 동상제어로 인한 요 응답성이 떨어지는 단점을 해결하기 위해 새로운 제어 전략을 제안하였다. 차량 안정성을 모니터링 하기위해 Side-slip angle을 추정하였다. 추정 성능을 향상시키기 위해 추정 과정에서 발생할 수 있는 Disturbance들을 차량 모델과 통합하였다. 통합 모델을 Kalman filter 알고리즘에 적용하여 Side-slip angle을 추정하였다. 또한 안정성 Index를 정의하고 Weighting function을 도입하여 차량 안정도에 따른 후륜 조향각 제어 가중치를 결정하였다. 최종적으로 차량이 안정하다고 판단될 때 후륜 조향 제어량을 거의 생성하지 않다가 점점 불안정한 상태가 됨에 따라 급격히 제어량을 증가시키는 제어 전략을 통해 안정성은 유지한 채 요 응답성을 향상시켰다.

제안하는 알고리즘의 성능 검증을 위하여 실차 실험을 수행하였다. 차량 안정성 및 요 응답성에 대해 기존의 방법과 제안하는 방법을 비교하였으며 이를 수치화 하여 나타내었다. 수치 비교를 통해 제안하는 알고리즘의 우수성을 확인하였다.

References

• A. T. van Zanten, R. Erhardt, G. Pfaff, F. Kost, U. Hartmann and T. Ehret, “Control Aspects of the Bosch-VDC,” Proceedings of International Symposium on Advanced Vehicle Control, pp.573-608, 1996.
• W. Klier, G. Reimann and W. Reinelt, “Concept and Functionality of the Active Front Steering System,” SAE 2004-21-0073, 2004.
• J. Song, “A Study on Lateral Stability Enhancement of 4WS Vehicle with Active Front Wheel Steer System,” Transactions of KSAE, Vol.20, No.2, pp.15-20, 2012. [https://doi.org/10.7467/KSAE.2012.20.2.015]
• J. Ackermann and W. Sienel, “Robust Yaw Damping of Cars with Front and Rear Wheel Steering,” IEEE Transactions on Control Systems Technology, Vol.1, No.1, pp.15-20, 1993. [https://doi.org/10.1109/87.221348]
• S. Sano, Y. Furukawa and S. Shiraishi, “Four Wheel Steering System with Rear Wheel Steer Angle Controlled as a Function of Sterring Wheel Angle,” SAE Transactions, pp.880-893, 1986. [https://doi.org/10.4271/860625]
• Y. Ko and C. Song, “Stability Control of Four-Wheel Steering Vehicles,” Transactions of KSAE, Vol.16, No.3, pp.127-136, 2008.
• Y. Hirano and K. Fukatani, “Development of Robust Active Rear Steering Control for Automobile,” JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, Vol.40, No.2, pp.231-238, 1997. [https://doi.org/10.1299/jsmec.40.231]
• M. Ariff, H. Zamzuri, M. Nordin, W. Yahua, S. Mazlan and M. Rahman, “Optimal Control Strategy for Low Speed and High Speed Four-wheel-active Steering Vehicle,” Journal of Mechanical Engineering and Sciences, Vol.8, pp.1516-1528, 2015. [https://doi.org/10.15282/jmes.8.2015.26.0148]
• M. Li and Y. Jia, “Decoupling and Robust Control of Velocity-varying Four-wheel Steering Vehicles with Uncertainties via Solving Attenuating Diagonal Decoupling Problem,” Journal of the Franklin Institute, Vol.354, No.1, pp.105-122, 2017. [https://doi.org/10.1016/j.jfranklin.2016.09.029]
• M. Nagai, Y. Hirano and S. Yamanaka, “Integrated Control of Active Rear Wheel Steering and Direct Yaw Moment Control,” Vehicle System Dynamics, Vol.27, Nos.5-6, pp.357-370, 1997. [https://doi.org/10.1080/00423119708969336]
• J. Lu and T. Brown, Rollover Stability Control for an Automotive Vehicle Using Rear Wheel Steering and Brake Control, U.S. Patent No 6,799,092, 2004.
• C. Chatzikomis and K. Spentzas, “Comparison of a Vehicle Equipped with Electronic Stability Control (ESC) to a Vehicle with Four Wheel Steering (4WS),” Forschung im Ingenieurwesen, Vol.78, Nos.1-2, pp.13-25, 2014. [https://doi.org/10.1007/s10010-014-0172-z]
• W. Cho, J. Yoon, J. Kim, J. Hur and K. Yi, “An Investigation into Unified Chassis Control Scheme for Optimised Vehicle Stability and Manoeuvrability,” Vehicle System Dynamics, Vol.46, No.Sup1, pp.87-105, 2008. [https://doi.org/10.1080/00423110701882330]
• ISO 7401, Road Vehicles–lateral Transient Response Test Methods–open-loop Test Methods, 2011.