전동기 파라미터 가변을 통한 변속기용 전동식 오일 펌프의 센서리스 극저온 저속 구동 성능 개선

1. 서 론

엔진변속기에 직접 체결되는 기계식 오일펌프를 영구자석 동기전동기와 제어기에 의해 펌프를 구동하는 전동식 오일펌프로 대체하여 친환경자동차의 연비향상을 도모하고 있다.¹⁾

가격 절감 및 시스템 크기 축소를 위한 영구자석 동기전동기의 구동의 필수적인 회전자 위치정보를 센서를 대신하여 모델 기반의 위치 추정 기법을 사용하는 센서리스 구동 기법이 널리 적용되고 있다.²⁾

모델 기반 센서리스 기법은 전동기 모델로부터 역기전력을 추정하여 회전자 위치 정보를 얻는 방법으로 정확한 전동기 파라미터가 요구되며, 파라미터의 오차는 위치 추정 오차 및 성능저하를 야기한다.³⁾

역기전력은 속도에 비례하는 성분으로 그 크기가 작은 저속일수록 역기전력 추정에 있어 상전압 오차나 전동기의 상저항 및 인덕턴스 오차에 큰 영향을 받는다.³⁾

전동기의 상저항은 코일의 온도 변화에 의해 변화하고, 인덕턴스는 고전류 인가 시의 자기 포화에 의해 변화하게 된다.⁴⁾

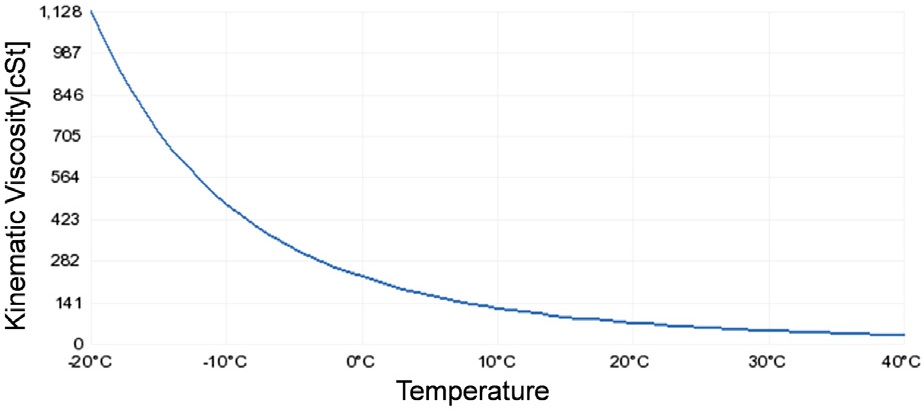
변속기용 전동식 오일펌프의 경우 -40 °C ~ 120 °C의 오일 온도에서의 운전이 필요하고, Fig. 1과 같이 영하 이하 극저온 상황에서는 오일 점도가 기하급수적으로 증가하여 요구 유압도 500 rpm 이하 저속에서 형성될 뿐만 아니라, 정격토크의 5배 이상의 부하로 큰 전류 소모가 요구된다.^5,6) 이러한 정격 이상의 운전 시 요구되는 고전류는 자기포화에 따른 인덕턴스 변화 및 코일 온도 상승에 따른 상저항 변화를 초래한다.

Fig. 1

Kinematic viscosity of ATF(Auto-Transmission Fluid) oil (GM DEXRON-VI)

저자의 기존 연구에서 상전압 측정 및 보상을 통한 센서리스 저속 성능을 향상할 수 있음을 보였다.⁷⁾

또한 센서리스 저속 성능을 확보하기 위하여 위치 추정기의 전동기 파라미터의 가변 적용에 대한 여러 연구가 있었다. 회귀적 최소자승법(Recursive Least Square) 기반의 상저항 및 인덕턴스 추정 기법, d축 전류에 추가적인 DC 및 AC 성분을 인가하여 상저항을 추정하는 기법 등이 대표적인 방법이다.^8,9)

d축 전류에 직류 및 저주파 인가 방법은 비교적 정확한 상저항 추정이 가능하지만, 불필요한 전류 인가에 따른 효율 저하 및 소음 발생을 야기하여 자동차 시스템 적용에 있어 단점이 있다. RLS을 이용하여 상저항과 인덕턴스를 동시에 추정하는 기법이 소개되었지만, 복잡한 파라미터 매트릭스 연산이 필요하여 저가의 마이크로 컨트롤러에서는 구현이 힘든 점이 있다.

본 논문은 센서리스 구동에 널리 적용중인 확장 역기전력 기반 위치 추정 기법을 통해 회전자의 위치를 추정할 때 사용되는 전동기 파라미터인 상저항과 인덕턴스의 정확도를 높여 위치를 정밀하게 추정하는 방법을 제안한다.

확장역기전력 기반 위치 추정기의 파라미터 가변을 위해 RLS에 의해 상저항을 추정하고, 인덕턴스는 실험적으로 오프라인으로 측정된 값을 사용하는 방법이 기존 연구에서 소개되었다.⁴⁾ 기존 연구에서는 RLS에 의한 상저항 추정 시 쇄교자속은 일정하다는 가정하에 진행되었다. 하지만 영구자석의 온도변화에 의해 쇄교자속도 변화하며, -40도의 극저온에서의 고전류 운전이 필요한 변속기용 전동식 오일펌프에서는 쇄교자속의 변화에 대한 영향을 무시할 수 없다.

이를 극복하기 위해 본 논문에서는 확장 역기전력 추정으로부터 획득한 쇄교자속 크기 변화를 고려한 RLS 기반 상저항 추정 기법에 적용하여 보다 정확한 추정 방법을 제안한다.

또한 극저온 시 요구되는 정격의 5배 이상 부하 상황에서 실험적인 인덕턴스 측정 방법의 제약사양을 극복하기 위해 본 논문에서는 유한요소해석 기법을 통한 인덕턴스 계산 값을 이용을 제안한다.

제안된 방법을 270V 1 kW 급의 변속기용 전동식 오일펌프에 적용하여 저속 구동 성능을 개선 결과를 실험적으로 제시한다.

2. 영구자석 동기 전동기의 센서리스 구동

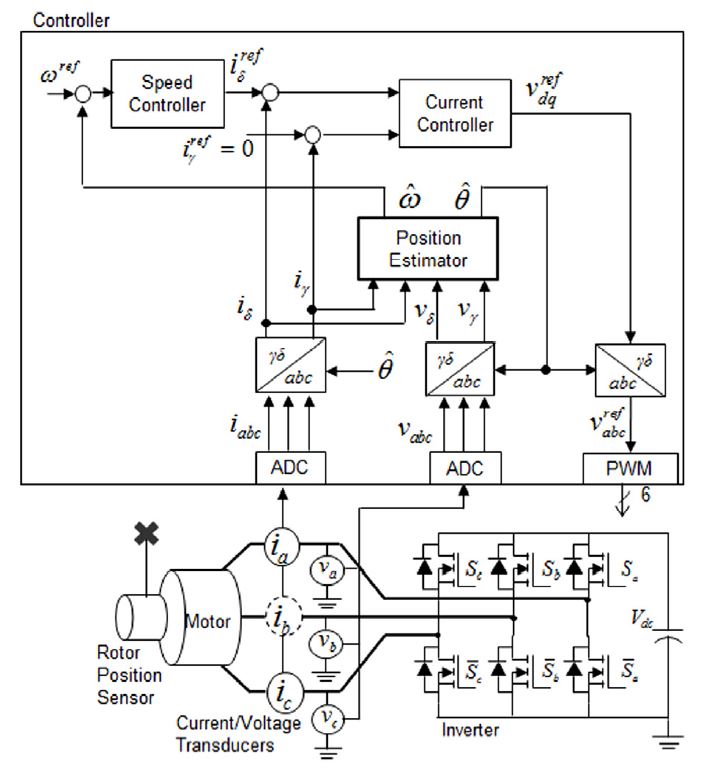
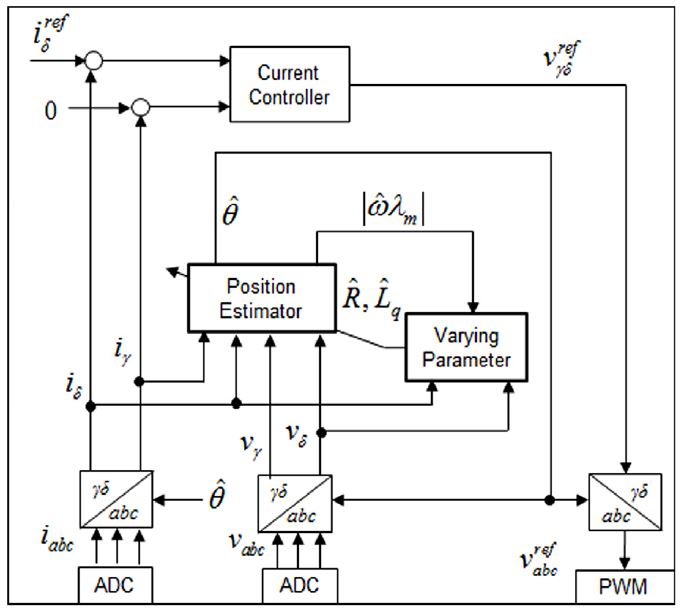
Fig. 2는 영구자석 동기 전동기의 센서리스 구동을 위한 블록다이어그램을 보여준다.

Fig. 2

Block diagram for sensorless drives

3상(abc)의 상전압 및 상전류 측정값을 2상의 동기좌표계(γδ 또는 dq)로 변환하여 직류 성분과 같이 제어할 수 있다. 이 때 q축 전류는 토크 생성에 관여하고 d축 전류는 자속 생성을 담당한다. 일반적으로 최대 토크 제어를 위해 d축 전류는 0를 유지하도록 제어한다.

비례적분 제어기의 의해 속도 및 전류제어를 직렬로 수행하여 얻은 전압 지령치를 역변환 하여 3상 인버터로 출력하여 제어한다.

이 변환을 위해 회전자 위치정보가 필요하다. 센서 대신 전압 및 전류를 입력 받아 역기전력 기반 위치 추정기를 이용하여 위치 및 속도 정보를 얻는 기법이 널리 적용되고 있다.

2.1 확장 역기전력 기반 위치 추정기

영구자석 동기 전동기의 dq축 동기좌표계에서 표현된 전압방정식 모델은 식 (1)과 같다.

$\[ \left[\begin{array}{c}{\nu }_d\\ {\nu }_q\end{array}\right]=\left[\begin{array}{cc}R+p{L}_d& -\omega L_q\\ \omega L_d& R+p{L}_q\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}0\\ \omega {\lambda }_m\end{array}\right] \]$

(1)

행렬식을 대칭행렬로 표현하기 위해 확장 역기전력을 추정된 γδ축 동기좌표계에서 표현하면 식 (2)와 식 (3)과 같다. 식 (4)는 확장 역기전력을 나타낸다.⁴⁾

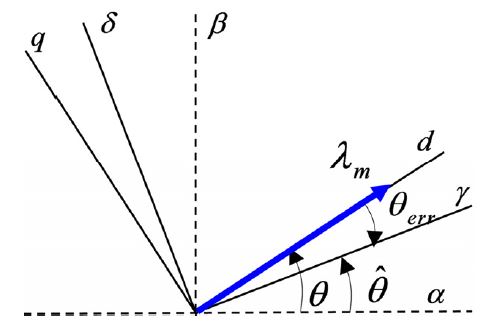
Fig. 3은 실제 dq축 동기좌표계에 비해 위치추정오차 θ_e 만큼 지연된 추정 γδ 축 동기좌표계를 나타내고, 위치 추정 오차는 식 (5)와 같이 계산된다. 이 오차를 0으로 수렴하기 위한 비례적분 필터를 적용하여 위치 및 속도를 추정한다.

Fig. 3

Definition of axes

$\[ \left[\begin{array}{c}{\nu }_{\gamma }\\ {\nu }_{\delta }\end{array}\right]=\left[\begin{array}{cc}R+p{L}_d& -\omega L_q\\ \omega L_q& R+p{L}_d\end{array}\right]\left[\begin{array}{c}{i}_{\gamma }\\ i_{\delta }\end{array}\right]+\left[\begin{array}{c}{e}_{\gamma }\\ e_{\delta }\end{array}\right] \]$

(2)

$\[ \left[\begin{array}{c}{e}_{\gamma }\\ e_{\delta }\end{array}\right]=E_{ex}\left[\begin{array}{c}-\sin {\theta }_e\\ \cos {\theta }_e\end{array}\right]+\left(\widehat{\omega }-\omega \right)L_d\left[\begin{array}{c}-i_{\delta }\\ i_{\gamma }\end{array}\right] \]$

(3)

$\[ E_{ex}= \omega \left\{\left(L_d-L_q\right)i_d+{\lambda }_m\right\}-\left(L_d-L_q\right)\left(p{i}_q\right) \]$

(4)

$\[ {\widehat{\theta }}_e={\tan }^{-1}\left(-{\widehat{e}}_{\gamma }/{\widehat{e}}_{\delta }\right) \]$

(5)

3. 전동기 파라미터 추정 및 가변 적용

삼각함수 계산 시 쇄교자속의 크기는 상쇄되어 그 영향이 없다는 것을 알 수 있다. 또한 상전압 지령치 대신 상전압을 직접 측정 및 보상하여 상전압 오차에 대한 영향을 최소화할 수 있다.⁷⁾

따라서 식 (2)에서 알 수 있듯이 위치 추정 오차는 상저항(R) 및 q축 인덕턴스(Lq)의 전동기 파라미터 변화에 영향을 받는다.

전동기 상저항은 코일 온도에 의해 변화한다. 또한 인덕턴스는 전류의 크기가 커짐에 따라 자기포화에 의해 그 값이 줄어든다. 이러한 온도 변화 및 자기 포화에 의한 파라미터 변화를 추정하는 기법을 다음과 같이 제안한다.

3.1 RLS 기반 상저항 추정

파라미터 추정을 위한 일반적인 RLS 기법은 식 (6)~(8)와 같이 소개되어 널리 적용 중이다.¹⁰⁾ 여기서 Y는 출력, Θ는 파라미터 벡터, Z는 입력 벡터 그리고 P는 공분산(Covariance) 벡터이다. λ는 망각인자(Forgetting Factor)로 1보다 작은 값을 가지고 일반적으로 0.96~0.98의 값을 가진다.

$\[ Y\left(k\right)={\mathbf{\Theta }}^{\mathbf{T}}\left(k\right)\mathbf{Z}\left(k\right) \]$

(6)

$\[ \widehat{\mathbf{\Theta }}\left(k\right)=\begin{array}{l}\widehat{\mathbf{\Theta }}\left(k-1\right)+\frac{\mathbf{P}\left(k-1\right)\mathbf{Z}\left(k\right)}{\lambda +{\mathbf{Z}}^T\left(k\right)\mathbf{P}\left(k-1\right)\mathbf{Z}\left(k\right)}\\ \times \left(Y\left(k\right)-{\mathbf{Z}}^T\left(k\right)\widehat{\mathbf{\Theta }}\left(k-1\right)\right)\end{array} \]$

(7)

$\[ \mathbf{P}\left(k\right)=\frac{1}{\lambda }\left(\mathbf{P}\left(k-1\right)-\frac{\mathbf{P}\left(k-1\right)\mathbf{Z}\left(k\right){\mathbf{Z}}^T\left(k\right)\mathbf{P}\left(k-1\right)}{\lambda +{\mathbf{Z}}^T\left(k\right)\mathbf{P}\left(k-1\right)\mathbf{Z}\left(k\right)}\right) \]$

(8)

이 RLS 기법을 적용하기 위해 식 (1)에서는 미분항을 무시한 정상상태로 표현하면 식 (9)와 같다. 또한 d축 전류 0 제어를 고려하면 상저항 파라미터 추정을 위한 입력 및 출력을 식 (10)과 같이 인덕턴스의 영향을 배제하여 간단히 정의할 수 있다.

$\[ \left[\begin{array}{c}{\nu }_d\\ {\nu }_q\end{array}\right]=\left[\begin{array}{cc}R& -\omega L_q\\ \omega L_d& R\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}0\\ \omega {\lambda }_m\end{array}\right] \]$

(9)

$\[ \left\{\begin{array}{l}Y\left(k\right)={\nu }_q\left(k-1\right)-L_d\omega \left(k-1\right)i_d\left(k-1\right)-{\lambda }_m\omega \left(k-1\right)\\ Z\left(k\right)=i_q\left(k-1\right)\\ \mathrm{\Theta }\left(k\right)=R\end{array}\right. \]$

(10)

인덕턴스의 영향은 배제하였으나 출력 계산을 위해서 쇄교자속 정보가 필요하다. 쇄교자속 또한 영구자석 온도 변화에 따라 변화하는 값이므로 정확한 상저항 추정을 위해서는 가변적으로 적용되어야 한다.

d축 전류가 0으로 제어되고, q축 전류의 변화가 비교적 완만하다면 식 (4)의 확장 역기전력은 일반 역기전력으로 가정될 수 있고 식 (11)으로부터 그 크기를 얻을 수 있다.

$\[ \left|\omega {\lambda }_m\right|=\sqrt{{\widehat{e}}_{\gamma }^2+{\widehat{e}}_{\delta }^2} \]$

(11)

최종적으로 식 (10)을 식 (7) 및 식 (8)에 대입하여 정리하면 식 (12) 및 식 (13)을 얻을 수 있고 복잡한 파라미터 벡터 연산 없이 상저항을 계산할 수 있다.

$\[ P\left(k\right)=\frac{1}{\lambda }\left(P\left(k-1\right)-\frac{P^2\left(k-1\right)i_q^2\left(k\right)}{\lambda +P\left(k-1\right)i_q^2\left(k\right)}\right) \]$

(12)

$\[ \widehat{R}\left(k\right)=\begin{array}{l}\widehat{R}\left(k-1\right)+\frac{P\left(k-1\right)i_q\left(k\right)}{\lambda +P\left(k-1\right)i_q^2\left(k\right)}\\ \times \left(Y\left(k\right)-\widehat{R}\left(k-1\right)i_q\left(k\right)\right)\end{array} \]$

(13)

0의 d축 전류의 가정은 과도응답 상태를 지난 정상응답상태에서 성립될 수 있다. 비교적 느린 응답성이 필요한 극저온 구동에서는 적용 가능하나 빠른 응답성이 요구되는 온도에서는 추가적인 고려가 필요하다.

3.2 유한요소해석을 통한 인덕턴스 계산

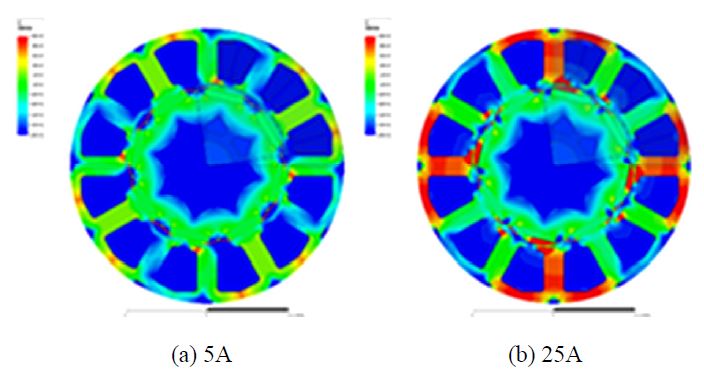
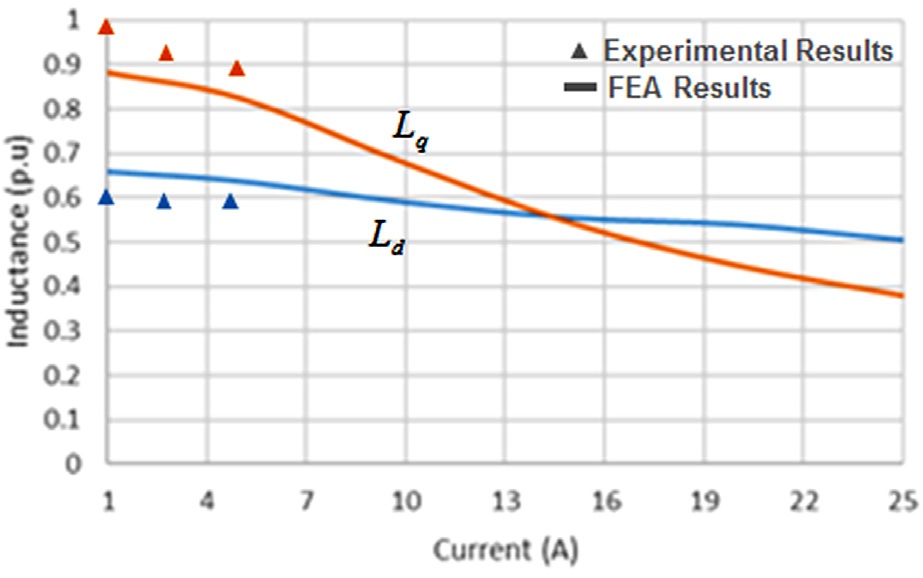
Fig. 4는 유한요소해석을 통해 확인한 전류크기에 따른 영구자석 동기 전동기의 자기포화 상태를 보여준다. 자계강도가 증가할 때 자속밀도가 선형적으로 증가하지 못하고 포화되는 현상에 의해 d축 및 q축 인덕턴스는 인가되는 전류 크기에 따라 Fig. 5와 같이 그 크기가 감소하게 된다.

Fig. 4

FEA results

Fig. 5

Inductance variation due to magnitude of current

Fig. 5에 볼 수 있듯이 실험적으로 측정된 실험치 또한 전류크기에 따라 감소하고 그 변화 양상이 해석치와 유사함을 확인 할 수 있다. 실험적 측정 방법은 저자의 기존 연구에서 제안된 오프라인 측정 방법을 사용하였다.¹¹⁾ 하지만, 극저온에서는 오실로스코프 등의 계측 기기의 허용온도 제약으로 측정이 어렵고, 상온에서는 정격 이상의 큰 전류 인가 시 전동기 발열이 과도하여 측정 오차가 클 뿐만 아니라 전동기 소손 우려도 있기 때문에 실험적 측정 가능한 전류는 정격전류 5 ~ 6 A 수준으로 한계를 가진다.

이런 실험적 한계를 극복하고 극저온에서 요구되는 정격 이상의 전류에서는 유한요소해석 기법을 통해 획득한 인덕턴스 변화 양상을 위치 추정에 가변 적용하여 사용하였다.

5 A 정격전류 범위에서는 그 크기 변화가 10 % 정도 이지만, 극저온 구동 시에는 정격의 5배 이상의 전류가 필요하고, 이에 따른 자기포화에 의해 50 ~ 60 % 이상의 q축 인덕턴스 변화를 야기하게 됨을 알 수 있다. 확장역기전력 추정을 위한 식 (2)에서도 알 수 있듯이 위치 추정 오차는 q축 인덕턴스(Lq)의 영향을 크게 받는다.

유한요소해석 얻은 q축 인덕턴스 값을 전류 크기에 대한 테이블 형태로 구현하여 적용할 수 있고, 보다 간단한 구현을 위해 식 (14)와 같이 선형화하여 적용할 수 있다.

$\[ {\widehat{L}}_q=L_{q_0}-\alpha \cdot \left|i_q\right| \]$

(14)

Fig. 6은 계산된 상저항 및 인덕턴스를 위치 추정기에 가변적으로 적용한 최종 결과를 보여준다.

Fig. 6

Position estimator with varying parameters

q축 전압과 전류를 대신하여 추정된 동기좌표계 상의 δ축 전압과 전류를 사용하여 식 (12)와 식 (13)에 의해서 계산된다. 상저항 계산을 위한 식 (13)을 계산하기 위해서 위치 추정기의 출력으로부터 식 (11)와 같이 쇄교자속의 변화를 피드백 받아 계산한다.

4. 실험 결과

실제 전동식 오일펌프의 센서리스 구동 시 상저항 및 인덕턴스를 가변 적용 전후의 저속 구동 성능을 실험적으로 비교하였다.

Photo. 1은 전동식 오일펌프와 오일탱크로 구성된 시험 벤치이다. 시험 벤치 전체를 온습도 환경 챔버 내 -40 °C에서 방치한 후 시험을 수행하였다. 전동식 오일펌프는 하이브리드 자동차의 자동변속기용으로 8극을 가지며 270 V 1 kW급의 전력 및 3500 rpm의 정격을 가진다. 실제 권선의 온도를 측정하기 위한 온도센서를 부착하였다. 모니터링을 위한 회전자 위치 센서를 장착하여 실제 위치와 추정 위치의 차이를 측정하여 위치 추정기의 성능을 평가하였다.

Photo. 1

Test bench with an electric oil pump and oil tank

상저항 및 인덕턴스의 변화는 권선수가 작은 12 V 기반 저전압 전동기에 비해 10배 이상의 권선수를 가지는 하이브리드 자동차용 270 V 이상의 고전압 전동기일수록 제안된 가변 파라미터의 필요성이 높아진다.

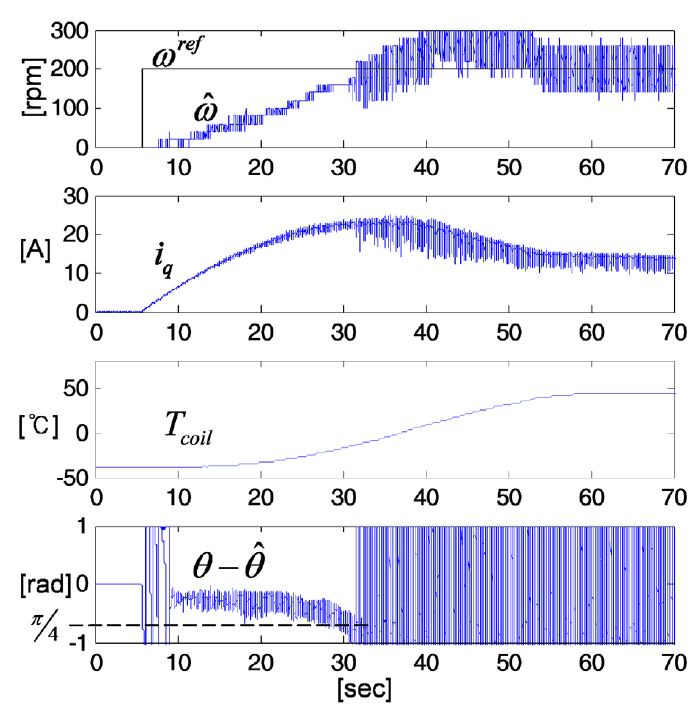
Fig. 7은 고정된 상저항 및 인덕턴스를 가지는 위치 추정기를 가지고 200 rpm 지령에 대한 센서리스구동 결과이다. 구동 초기 6~9초 대의 구동을 보면 초기 회전자의 위치를 알지 못하므로 큰 위치 오차를 가지고 구동을 시작하게 된다. 여기서 위치 오차는 회전자 위치 센서에의 측정된 실측 치와 위치추정기에 의해 추정된 추정치의 차이이다. 위치 추정기가 실행되면서 위치 오차는 줄어들게 되지만 전류의 크기 및 온도가 증가함에 따라 위치 오차가 점점 커짐을 알 수 있다. 오차가 π/4 이상 커지게 되면 전동기는 더 이상 정상 구동을 하지 못하고 안정성을 잃게 된다.

Fig. 7

Test Results with constant resistance and inductance

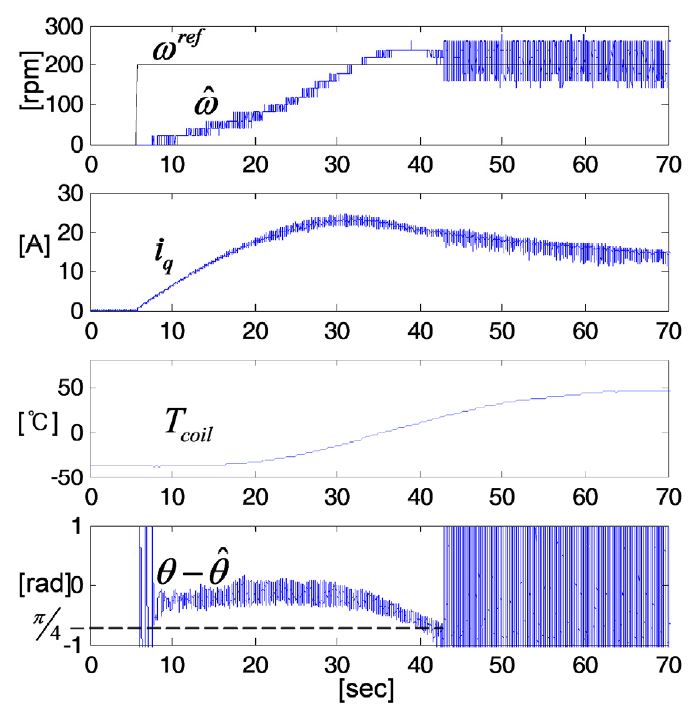
Fig. 8은 상저항은 고정하고, 인덕턴스는 전류 크기에 따라 유한요소해석으로 얻은 식 (14)에 따라 가변 적용한 결과이다. Fig. 7의 경우 보다 전류 크기에 따라 위치 오차가 작지만 코일 온도가 상승함에 따라 위치 오차가 커짐을 알 수 있다. -40 °C의 극저온에서 구동을 시작하였지만 온도 센서에 의해 측정된 코일 온도는 약 1분 이내에 60 °C 이상으로 증가하여 그 온도 변화가 100 °C 이상이 된다.

Fig. 8

Test Results with constant resistance and varying inductance

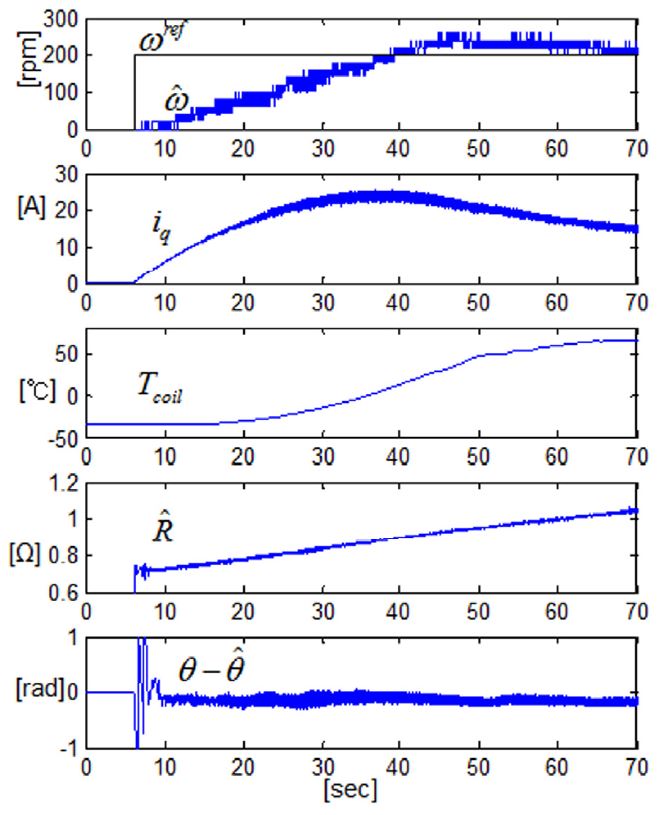
Fig. 9는 인덕턴스 뿐만 아니라 식 (12)와 (13)에 의해 RLS에 의해 온라인으로 추정된 값을 보여준다. 추정된 상저항을 가변 적용한 결과이다. Fig. 7과 8과 비교하여 안정적인 제어 결과를 얻을 수 있음을 확인할 수 있다.

Fig. 9

Test Results with varying resistance and inductance for 200 rpm

Fig. 9를 보면 추정된 상저항은 지속적으로 증가하는 데 비해 온도센서에 의해 측정된 코일 온도는 어느 정도 시간 이후 증가하는 양상을 가짐을 확인할 수 있다. 이는 코일 외곽에 장착된 온도 센서와 코일 중심부 실제 온도의 차이 때문이라고 유추할 수 있다. 코일 외곽은 모터 회전 및 외기 온도에 따른 방열 효과가 코일 중심부 보다는 뛰어나기 때문이다.

실제 상저항에 지배적인 영향을 주는 코일 중심부의 온도는 온도 센서 장착이 어려워 측정이 어렵기 때문에 전류에 따른 코일 온도 변화를 실험적으로 예측하기는 어려움이 있다. 또한 실차 조건의 다양한 방열 조건을 고려하기는 더더욱 어렵다.

제안된 RLS 기반 상저항 추정 방법은 다양한 방열 환경에서 코일 중심부 온도에 의한 상저항을 변화를 직접적으로 추정할 수 있는 유용한 방법임을 확인할 수 있다.

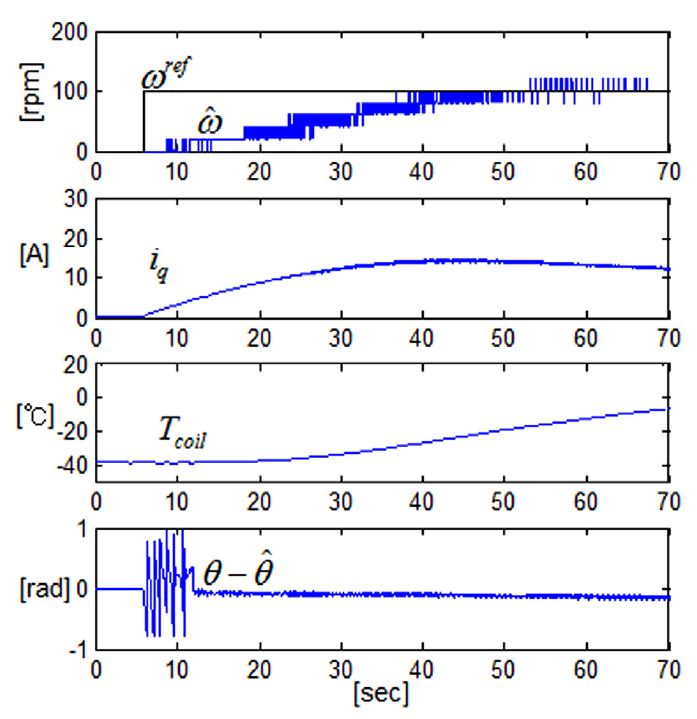
100rpm 지령에 대해서도 Fig. 10과 같이 구동 성능을 확보할 수 있었다.

Fig. 10

Test Results with varying resistance and inductance for 100 rpm

5. 결 론

이 논문은 전동식 오일펌프의 센서리스 구동을 위한 위치 추정기의 상저항 및 인덕턴스 파라미터를 가변 적용함으로써 극저온 시 요구되는 저속 고부하의 구동 성능을 개선할 수 있음을 보였다.

상저항은 일반적인 RLS 기법을 기반으로 쇄교자속 변화를 추가적으로 고려하여 보다 정확한 계산을 온라인으로 수행하여 얻을 수 있었다. 극저온에서 시작하여 고전류에 의한 온도 상승에 따른 상저항 변화를 가변적으로 적용하여 위치 추정 오차를 줄일 수 있었다. d축 전류는 0으로 제어되고, q축 전류의 변화가 비교적 느리게 변화한다는 가정하에 상저항 계산 시 인덕턴스의 영향을 배제할 수 있었다.

인덕턴스는 유한요소해석 결과로부터 오프라인으로 얻은 결과를 이용하여 고전류 인가에 따른 자기포화 현상에 따른 인덕턴스 변화를 가변 하여 위치 추정 오차를 줄일 수 있었다.

270 V 1 kW급 영구자석 동기 전동기를 가지는 실제 전동식 오일펌프에서 제안된 가변 파라미터 기법을 적용하여 영하 40 °C의 온도 조건에서 정격속도(3500 rpm)의 5 % 이하(100 rpm)의 저속에서 구동 성능을 확보할 수 있음을 보였다.

제안된 방법을 이용한 최저 속도 구동으로 극저온에서 변속기 내의 불필요한 유압생성으로 인한 효율 저하 및 기계적 마모를 방지할 수 있다.

제안된 방법은 전동식 오일펌프 이외에 저속 고부하의 운전이 필요한 자동차용 전동 시스템에 적용될 수 있을 것이다.

Acknowledgments

이 논문은 2019~2020년도 창원대학교 자율연구과제연구비 지원으로 수행된 연구결과임.

References

• J. W. Chang and D. Y. Yoon, “Sensorless Starting Method and Fuel Pressure Control of BLDC Motor for Fuel Pump of Vehicle,” Transactions of KSAE, Vol.21, No.2, pp.114-121, 2013. [https://doi.org/10.7467/KSAE.2013.21.2.114]
• J. Y. Yoo, J. H. Lee and H. T. Moon, “Current Sensorless Drive Method for Electric Power Steering,” Int. J. Automotive Technology, Vol.13, No.7, pp.1141-1147, 2012. [https://doi.org/10.1007/s12239-012-0117-1]
• J. S. Kim and S. K. Sul, “Influence of Resistance Error to the Bandwidth of Back-EMF Estimation based SMPMSM Sensorless Drives,” Transactions of the Korean Institute of Power Electronics, Vol.21, No.5, pp.418-426, 2016. [https://doi.org/10.6113/TKPE.2016.21.5.418]
• Y. Inoue, Y. Kawaguchi, S. Morimoto and M. Sanada, “Performance Improvement of Sensorless IPMSM Drives in a Low-Speed Region Using Online Parameter Identification,” IEEE Transactions on Industrial Application, Vol.47, No.2, pp.798-804, 2011. [https://doi.org/10.1109/TIA.2010.2101994]
• H. S. Seok, S. J. Bae and J. Y. Lee, “Development of a Single-suction Double-discharge Automatic Transmission Oil Pump for Power Consumption Reduction,” Int. J. Automotive Technology, Vol.20, No.4, pp.845-854, 2019. [https://doi.org/10.1007/s12239-019-0079-7]
• S. Kim, W. S. Choi, M. Kim, H. Kim and W. Lim, “Analysis of Fuel Economy of Mild Hybrid Vehicle by the Backward Simulation with Considering Power Loss of Oil Pump,” Transactions of KSAE, Vol.26, No.4, pp.533-539, 2018. [https://doi.org/10.7467/KSAE.2018.26.4.533]
• C. Choi and W. Lee, “Improvement of Low Speed Sensorless Drive with Gain Attenuation and Delay Compensation of Measured Phase Voltage for Transmission Electric Oil Pump,” Transactions of KSAE, Vol.27, No.10, pp.819-826, 2019. [https://doi.org/10.7467/KSAE.2019.27.10.819]
• S. J. Underwood and I. Husain, “Online Parameter Estimation and Adaptive Control of Permanent-Magnet Synchronous Machines,” IEEE Transactions of Industrial Electronics, Vol.57, No.7, pp.2435-2443, 2010. [https://doi.org/10.1109/TIE.2009.2036029]
• K. Liu, Z. Q. Zhu and D. A. Stone, “Parameter Estimation for Condition Monitoring of PMSM Stator Winding and Rotor Permanent Magnets,” IEEE Transactions of Industrial Electronics, Vol.60, No.12, pp.5902-5913, 2013. [https://doi.org/10.1109/TIE.2013.2238874]
• E. Ikonen and K. Najim, Advanced Process Identification and Control, Marcel Dekker, New York, pp.28-37, 2001. [https://doi.org/10.1201/9781482294699]
• C. Choi, W. Lee, S. O. Kwon and J. P. Hong, “Experimental Estimation of Inductance for Interior Permanent Magnet Synchronous Machine Considering Temperature Distribution,” IEEE Transactions on Magnetics, Vol.49, No.6, pp.2990-2996, 2013. [https://doi.org/10.1109/TMAG.2013.2238550]