[ Article ]
Transactions of the Korean Society of Automotive Engineers - Vol. 27, No. 12, pp.919-924
ISSN: 1225-6382
(Print)
2234-0149
(Online)
Print publication date 01 Dec 2019
Received 09 Aug 2019
Revised 16 Sep 2019
Accepted 17 Sep 2019
모래지 노면에서의 바퀴 주행 실험과 시뮬레이션 비교
정성헌1)
;
전철웅2)
;
신정훈3)
;
손정현*, 4)
|
1)부경대학교 대학원 기계설계공학과
|
|
2)부경대학교 산업과학기술연구소
|
|
3)부경대학교 대학원 기계설계공학과
|
|
4)부경대학교 기계설계공학과
|
Comparison of a Wheel Running Simulation on the Sandy Road with Experiments
Sung Heon Jung1)
;
Chul Woong Jun2)
;
Jeong Hoon Shin3)
;
Jeong Hyun Sohn*, 4)
1)Graduate School of Mechanical Design Engineering, Pukyong National University, Busan 48513, Korea
|
|
2)Institute of Industrial Science Technology, Pukyong National University, Busan 48513, Korea
|
|
3)Graduate School of Mechanical Design Engineering, Pukyong National University, Busan 48513, Korea
|
|
4)Department of Mechanical Design Engineering, Pukyong National University, Busan 48513, Korea
|
|
Copyright Ⓒ 2019 KSAE / 168-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(
http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In this study, a wheel test bed experimental setup is established in order to investigate the contact phenomenon between a wheel and a sandy road. Meanwhile, the discrete element method(DEM) is used to analyze the dynamic behavior of a rigid wheel driving on a sandy road. A contact method is developed between a rigid wheel and numerous particles. The longitudinal force and vertical force acting on the wheel are measured by using a 6-component load cell, and the wheel sinkage is measured by using a high-speed camera. The results of the simulation showed a good agreement with the experiments.
Keywords:
Discrete element method, Sandy road, Wheel test bed, Dynamic simulation
키워드:
이산요소법, 모래지 노면, 휠 테스트 베드, 동역학 해석
1. 서 론
우주 탐사 및 무인 차량의 발달로 인해 야지 노면을 주행하는 무인 차량 및 로봇의 연구개발이 중요해지고 있다. 무인 차량이 예측이 어렵고 변형되는 노면을 주행 할 경우 실시간으로 노면에 의한 휠의 슬립율 및 작용력을 측정하고 효율적인 주행 성능을 유지하는 것이 무엇보다 중요하다 할 수 있다. 이러한 주행성능, 안정성, 효율성을 확보하기 위해서는 야지 노면에 대한 데이터베이스의 구축이 필요하다. 데이터베이스의 구축은 실험과 시뮬레이션 두 방법으로 구축된다.1) 데이터베이스 구축의 가속화를 위해 가상의 야지 노면 모델링 기법과 휠과 모래지 노면 간 접촉 해석 프로그램 개발을 통해 가상 노면 구축 및 가상/시험분석에 적용할 수 있는 시뮬레이션 모델 구현이 필요하다. 휠과 모래지 노면 간 접촉 시뮬레이션 모델 구현방법은 퍼거슨 곡면 방정식으로 표현하는 방식과 이산요소법(Discrete Element Method)을 통해 입자를 모델링 하는 방식이 있다.2,3) 현재까지 이산요소법을 통한 야지노면 모델링이 가장 좋은 방법으로 알려져 있다. 이산요소법은 1979년에 Cundall에 의해 제안되었다.3) 이후 정형화된 수치방법을 이용하여 상호 입자간의 접촉 판별법 및 충돌 시 상호 침투량에 따른 접촉력 계산에 관심을 둔 연구와 실험을 통해 이산요소법 시뮬레이션의 결과를 검증하는 연구가 이루어졌다.4) 우주 탐사 및 무인 차량의 발달로 인해 모래지 노면 주행이 중요해짐에 따라 패턴이 없는 휠에 대한 모래지 주행 실험과 이산요소법, Bekker method, Dynamic Bekker method 시뮬레이션의 결과를 비교하는 연구가 이루어졌다.5)
본 연구에서는 패턴이 있는 휠의 주행 시뮬레이션 수행을 위해 입자는 이산요소법을 기반으로 모델링 하였으며 삼각요소 모델링 기법을 통해 휠의 형상을 모델링 하였다. 휠 테스트 베드를 다물체 동역학으로 모델링 하고 이산요소법과의 연성해석을 통해 모래지에서 작용하는 수직력, 견인력, 및 휠의 침하량을 계산하였다. 계산된 시뮬레이션 결과는 휠 테스트 베드 실험을 통해 비교 검증하였다.
2. 모래지 모델링
모래지 노면을 모델링하기 위해서 구형의 입자로 모래의 알갱이를 표현하고 이산요소법(DEM)을 이용하여 입자간의 접촉 거동을 시뮬레이션한다. 이산요소법에서 입자들의 운동은 뉴턴 제2 법칙으로 힘과 토크는 식 (1)과 (2)와 같이 계산된다.
2.1 DEM 접촉력 모델
이산요소법을 이용한 모래지 노면의 입자들의 거동은 상호간의 법선, 접선 접촉력, 점성력이 작용하여 결정된다. 본 연구에서는 1882년에 헤르츠(Hertz)에 의해 처음으로 제안된 헤르츠 접촉 모델을 이용하였다.6) 법선 접촉력은 헤르츠 스프링력, 감쇠(Viscous)력, 점성력으로 이루어지며 식 (3)과 같이 표현된다. 법선 스프링력은 식 (4)와 같으며 영률, 반경, 침투량으로 표현된다.
입자의 반경으로 구해지는 R*과 영률과 포아송비로 구해지는 E*는 식 (5)와 (6)으로 표현된다. 침투량은 δij = Ri + Rj - |rij|로 표현되며 rij = ri - rj는 두 입자 사이의 거리를 나타낸다. n = rij/|rij|은 법선 단위 벡터를 나타낸다. 법선방향의 감쇠력은 식 (7)로 나타내어지며 감쇠 계수와 상대속도로 표현된다. 식 (8)은 입자 사이의 상대속도를 나타내는 식이다. 점착력 모델은 가상의 점착 면적에 대해 힘을 계산하는 방식이며 식 (9)와 같다. 가상의 점착 면적은 접촉 반경에 의해 결정이 되며 식 (10)으로 표현된다. 접촉 반경은 식 (11)과 같이 수직력과 입자 반경, 영률에 의해 결정된다. 접선 접촉력은 Tangential sliding friction contact 모델을 사용하였다. 접선력은 계산된 스프링 감쇠 값과 μs × |Fn|을 비교하여 작은 값을 비교하여 계산되며 계산식은 식 (12)와 같다.
접선 속도는 상대속도로 계산되며 식 (13)과 같다. 접선 방향의 유닛 벡터는 식 (14)와 같이 나타낸다. 접선 방향의 침투량은 입자의 접촉 시간부터 접촉이 끝날 때까지의 거리를 계산하며 식 (15)와 같다.
2.2 모래지 노면 모델링
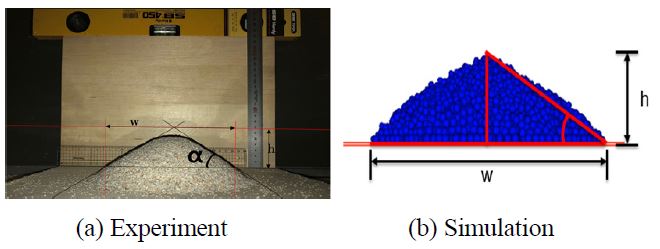
모래는 많은 입자로 이루어져 있어 모래 입자 개개의 물성보다 입자들이 모였을 때의 물성이 필요하다. 이러한 입자들이 모여있을 때 가지는 물성치를 벌크 물성치라 한다. 벌크 물성치는 벌크 밀도와 안식각 실험을 통한 접촉 계수가 있다. 벌크 밀도는 입자 개개의 밀도가 아닌 입자가 모였을 때의 밀도를 나타내는 밀도이며 식 (16)으로 표현된다. 벌크 밀도는 입자의 질량과 입자가 담긴 실린더의 부피를 통해 계산된다. 본 연구에서 사용된 입자의 벌크 밀도는 1426 kg/m3이다. 안식각 측정 실험은 흙이나 모래 같은 분체들을 쌓았을 때 자연 상태로 생기는 경사면이 수평면과 이루는 각을 측정하는 실험이다. 안식각 측정은 Fig. 1(a)와 같이 수행되었으며 폭(w)과 높이(h)를 측정하여 식 (17)과 같이 안식각을 계산하였다. 계산된 안식각은 31°이다.
Experiment and simulation for repose angle
접촉파라미터 계산을 위한 안식각 시뮬레이션은 8천개의 입자가 사용되었으며 입자의 반지름은 1 mm로 안식각 시뮬레이션을 수행하였다. 수행된 시뮬레이션은 시행착오법(Trial and error)법을 사용하였으며 변수는 마찰 계수로 설정하였다. Table1은 마찰 계수에 따른 안신각 결과를 나타내었으며 Fig. 1(b)에 30.4°인 안식각 시뮬레이션을 나타내었다. Table 2는 안식각 시뮬레이션에 사용된 입자의 물성치와 접촉 계수 및 입자 수를 나타내었다.
Repose angle according to friction coefficient
Contact parameters of particles
2.3 3D 형상 대 입자접촉
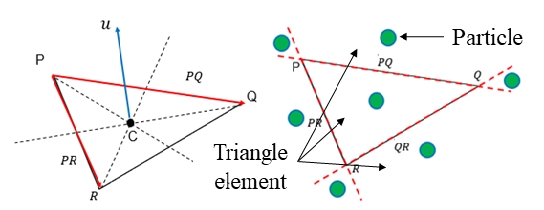
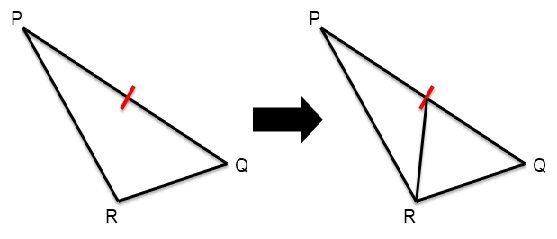
임의의 형상을 가지는 강체와 입자의 접촉을 정의하기 위해 강체를 STL파일형상을 사용하여 통해 삼각형 요소로 모델링 하였다. 입자와 삼각형 요소의 접촉 판별은 Fig. 2와 같이 결정하였다.7) 삼각형 요소의 7개 구역에 대해 입자의 위치를 결정하고 투영 점을 결정하였다. 삼각형의 법선 단위 벡터는 두 변의 외적으로 u = PR × QR 로 계산하였다. STL파일을 통해 얻어진 삼각요소의 크기는 제각각 일 수 있으며 입자의 크기보다 삼각요소의 크기가 클 경우 접촉 판별 과정에서 비효율적 일 수 있다. 삼각요소의 크기를 입자의 크기와 유사하게 만들어 주기 위해 Fig. 3과 같이 삼각형의 가장 긴 변을 결정하고 긴 변의 중심점과 긴 변에 포함되지 않는 점과 연결하여 삼각형을 분할하였으며 삼각형의 크기가 입자의 크기보다 작아질 때까지 반복하였다.
Normal vector and contact detection between particles and triangle element
Segmentation of triangle element
3. 휠 테스트 베드 실험
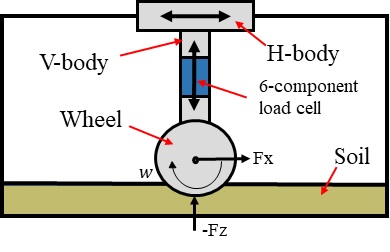
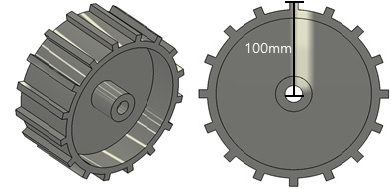
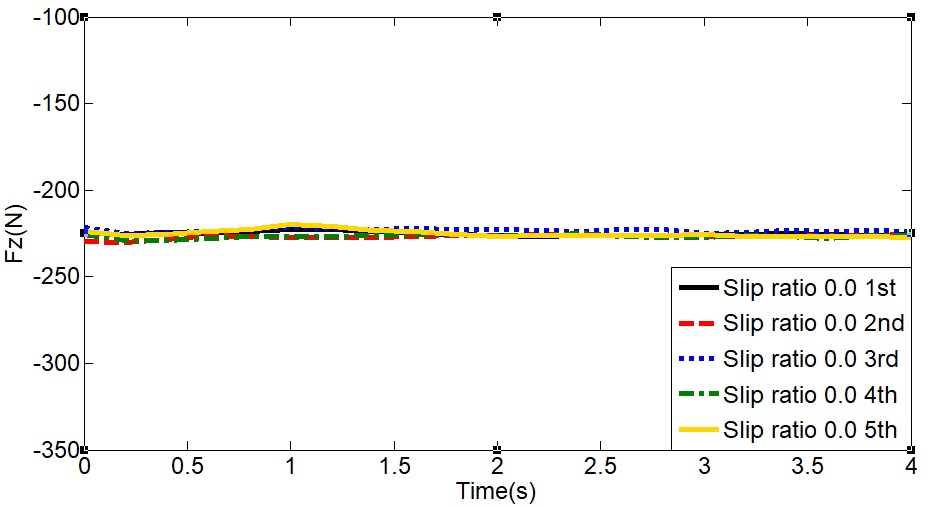
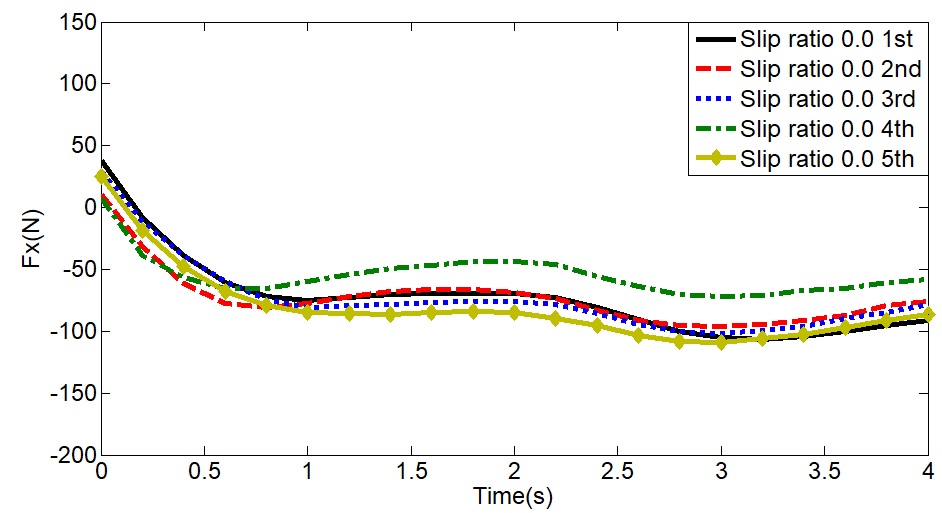
휠 테스트 베드 실험장치의 계략도는 Fig. 4와 같이 나타내었다. 휠 테스트 베드는 주행 시 힘과 토크를 계측할 수 있도록 6분력계를 사용하였으며 6분력계의 좌표계는 +X가 진행방향 -Z는 수직 방향의 좌표계를 가진다. 모래지 위를 주행하는 바퀴의 거동을 분석하기 위해 진행 방향, 수직 방향, 바퀴의 회전이 가능할 수 있게 고려되었다.8) 모래지 위를 주행하는 휠은 초기 침하상태를 기준으로 침하량이 발생하게 된다. 휠의 침하량과 휠의 주행거리를 계측하기 위해 고속카메라를 사용하였다. 휠의 V-body에 추적점(Tracking marker)를 부착하여 점(Marker)의 위치변화를 통해 모래지 위를 주행하는 휠의 침하량과 주행거리를 계측하였다. 실험에서 사용된 휠의 형태와 반경은 Fig. 5에 나타내었다. 휠의 형태는 Spur 기어 형태이며, 반경은 100 mm이다. Fig. 6은 실험에서 사용된 휠 테스트 베드 실험장치를 나타낸 것이다. 본 연구에서 휠 테스트 베드 실험은 슬립율 0의 조건을 재현하기 위해, H-body의 진행방향 속도 10(mm/s), 휠의 회전속도 0.1(rad/s)로 하였으며 강체 휠에 작용하는 수직력, 견인력, 침하량, 진행 거리를 측정하였다. 휠의 주행시간은 약 4.5(s) 주행하였으며 실험의 재연성을 위해 5번의 실험을 수행하였다. Fig. 7, 8은 6분력계로 계측된 시간에 따른 수직력, 견인력을 보여준다. 6분력계로 측정된 수직력은 4초 동안 약 -230(N)의 수직력이 측정되었으며 5번의 실험의 재연성도 확인할 수 있다. 견인력은 약 -70(N) 발생하는 것을 알 수 있으며 수직 방향의 힘에 비해 실험간의 작은 차이가 발생하는 것은 모래지 노면 내부 입자 상태를 전부 동일하게 재연하는 것이 어렵기 때문이다.
Conceptual diagram of wheel test bed
Vertical force without slip
Drawbar pull without slip
4. 시뮬레이션과 실험의 비교
4.1 모래지 위 주행 시뮬레이션
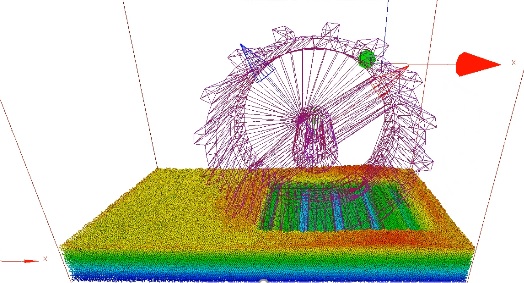
이산요소법을 기반으로 입자 모델링을 하였으며 강체 휠은 3D 형상을 삼각요소로 구성하여 모델링 하였다. 휠의 반경은 실험과 동일하게 100 mm의 반경을 가지며 알루미늄 재질을 적용하였다. 휠은 삼각요소 분할을 통해 약 53만 개로 구성된다. 휠 테스트 베드 시뮬레이션을 위한 입자 수는 약 100만개가 사용되었으며 입자의 지름은 1 mm의 지름을 가진다. 모델링된 입자와 강체 휠은 Fig. 9에 나타내었다. 휠 테스트 베드 주행 시뮬레이션을 위해 H-body, V-body, Wheel이 모델링 되었으며 Table 3은 각 바디의 질량과 관성 모멘트를 나타낸다. 입자와 입자, 입자와 경계면의 접촉 파라미터는 Table 4에 나타내었다. 입자와 휠 접촉은 점착력을 제외한 파라미터를 모두 동일하게 하였으며 점착력은 0으로 하였다. 본 연구에서 사용된 프로그램은 GPGPU 기반의 병렬 프로그래밍의 한 방법인 CUDA를 사용하여 개발된 프로그램이며 다물체 동역학과 대량 입자 간의 연성해석이 가능한 프로그램이다.9)
Simulation of wheel test bed
Properties of wheel test bed
4.2 시뮬레이션 결과 비교
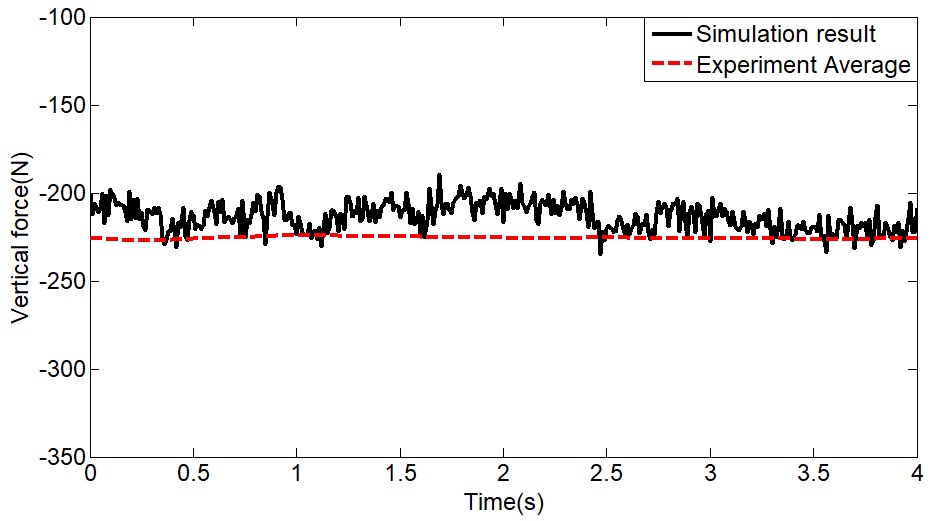
휠 테스트 베드 시뮬레이션은 진행방향(-X)으로 10 mm/s의 속도와 휠의 회전속도 0.1(rad/s)를 적용하여 슬립율 0일 때의 주행 시뮬레이션을 수행하였다. 시뮬레이션 시간은 4.5(s)로 0.5초 동안 휠을 낙하 후 안정화하여 실험과 동일하게 4초간 주행하였다. 실험에서 계측된 수직력과 견인력은 5번의 실험에서 동일한 시간에 측정된 힘들의 평균으로 나타내었다. Fig. 10과 Fig. 11은 실험에서 계측된 평균 수직력과 견인력 시뮬레이션에서 계산된 수직력과 견인력을 비교한 그래프이다. 실험과 시뮬레이션에서 도출된 수직력과 견인력은 시뮬레이션에서 계측된 힘의 정밀도를 표현하기에 적합한 RMSE(Root Mean Square Error)값으로 비교하였다. 수직력의 RMSE값은 16.8 N의 값이 도출되었으며 실험에서 측정된 수직력과 편차가 작은 것을 확인하였다. 견인력의 RMSE값은 26.5 N의 값으로 수직력의 RMS값보다 큰 편차를 가지는 것을 확인하였다.
Comparison of vertical force
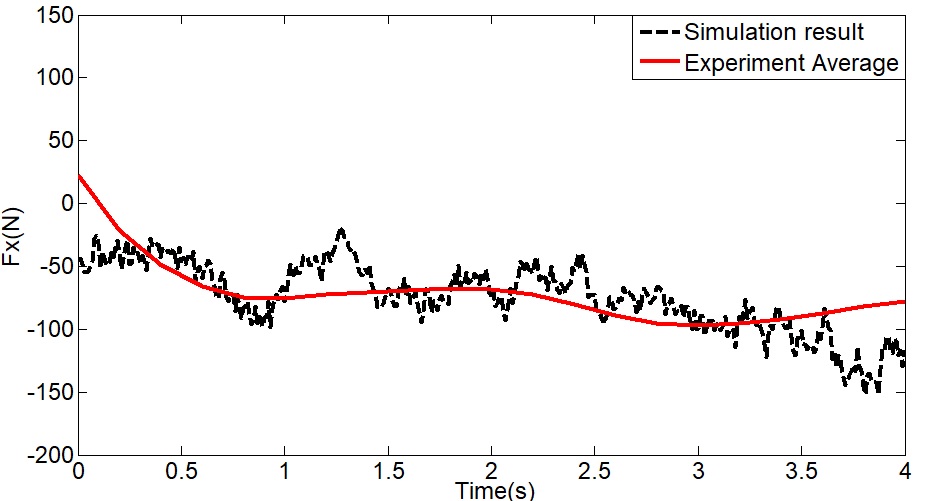
Comparison of drawbar pull
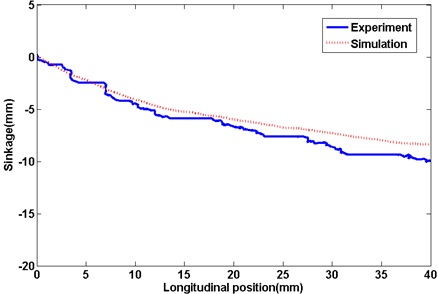
실제 발생되는 견인력은 모래지 노면을 이루는 입자의 내부 배열, 노면의 다짐 정도에 따라 견인력에 큰 영향을 준다. 시뮬레이션에서 실제와 동일한 모래지를 구현하지 못하여 오차가 크게 발생하였다. 이러한 오차를 줄이기 위해서는 입자의 배열과 구 형상으로 표현된 입자를 실제 모래알갱이와 유사한 형태를 통한 입자의 표현이 필요하다고 판단된다. 입자가 구 형상이 아닌 실제 모래 알갱이와 같은 형상을 가지게 된다면 기하학적인 형태로 발생되는 힘을 묘사할 수 있다고 판단되기 때문이다. 주행거리에 따른 평균 침하량의 비교 그래프는 Fig. 12에 나타내었다. 실험에서는 40 mm 진행거리를 이동함에 따라 약 7 mm의 침하량을 보여줬으며 시뮬레이션에서는 약 9 mm의 침하량을 보여줬다. 휠이 주행함에 따라 실험과의 침하량 차이가 점점 발생하는 것을 볼 수 있는데 이 차이는 진행 방향의 힘의 오차가 발생하게 되면서 침하량의 차이가 발생한 것으로 판단된다.
5. 결 론
본 연구에서는 야지노면을 주행하는 무인 자동차의 연구개발이 중요해 짐에 따라 야지노면에 대한 데이터베이스 구축을 위하여 모래지 노면에서의 바퀴 주행 실험과 시뮬레이션을 수행하였다. 시뮬레이션은 이산요소법을 기반으로 모래지를 모델링하고, 입자와 강체와의 접촉 정의를 통해 휠 테스트 베드 주행 시뮬레이션을 수행하였다. 실험과 시뮬레이션 결과를 검증하기 위해 휠 테스트 베드 실험을 수행하였으며 휠에 작용하는 수직력, 견인력, 휠 침하량을 실험과 비교하였다. 시뮬레이션에서계산 된 수직 방향의 힘과 견인력은 16.8 N과 26.5 N으로 견인력에서 더 큰 편차가 발생 하였다. 견인력은 모래지 노면을 구성하는 입자들의 내부 배열과 다짐 정도에 영향을 크게 받기 때문에 RMSE의 편차가 더 크게 발생한 것으로 판단된다. 시뮬레이션에서 실험과 유사한 모래지 노면을 만들기 위해서는 입자의 배열과 구 형상으로 표현된 입자가 실제 모래 알갱이의 형태를 표현하여 기하학적인 형상으로 인한 힘을 묘사하면 실제와 가까운 힘이 발생 할 것으로 판단된다. 실험과 시뮬레이션의 침하량은 견인력에 의해 실험과의 차이가 지속적으로 발생하는 것으로 판단된다.
Nomenclature1)
| |
| M : |
mass, kg |
| : |
acceleration, m/s2 |
| υ : |
velocity, m/s |
| F, f : |
force, N |
| I : |
moment of inertia, kg ⋅m2 |
| : |
angular acceleration, rad/s2 |
| T : |
torque, N ・m |
| E : |
Young’s modulus, Pa |
| R : |
radius, m |
| δ : |
penetration, m |
| c : |
damping coefficient |
| n : |
normal unit vector |
| s : |
tangential unit vector |
| ν : |
poisson’s ratio |
| k : |
stiffness, N/m |
| ξ : |
cohesion coefficient |
| r : |
distance, m |
| μ : |
friction coefficient |
| A : |
area, m2 |
| ρ : |
density, kg/m3 |
| V : |
volume, m3 |
| α : |
repose angle, ° |
| u : |
normal unit vector of triangle element |
Subscripts
| |
| i, j : |
body |
| n : |
normal |
| t : |
tangential |
| sn : |
normal spring |
| sd : |
normal damping |
| c/a : |
cohesion |
| c
: |
relative |
| b : |
bulk |
Acknowledgments
본 논문은 2019년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No.2018R1D1A1B07050817).
References
-
Y. S. Pyoun, Y. D. Jang, J. H. Park, I. H. Cho and Y. C. Lee, “A Study on Development of Test Methodology and Test of No Spin Differential for Off-road Vehicle,” Transactions of KSAE, Vol.13 No.4, pp.32-38, 2005.
-
J. H. Lee and W. S. Yoo, “Study on the 3D Virtual Ground Modeling and Application for Real-time Vehicle Driving Simulation on Off-road,” Transactions of KSAE, Vol.18 No.4, pp.92-98, 2010.
-
P. A. Cundall and O. D. L. Strack, “A Discrete Numerical Model for Granular Assemblies,” Geotechnique, Vol.29, No.1, pp.47-65, 1979.
[https://doi.org/10.1680/geot.1979.29.1.47]

-
A. Datta, B. K. Mishra, S. P. Das and A. Sahu, “A DEM Analysis of Flow Characteristics of Noncohesive Particles in Hopper,” Matrerials and Manufacturing Processes, Vol.23, No.2, pp.195-202, 2008.
[https://doi.org/10.1080/10426910701774742]

-
W. Smith, D. Melanz, C. Senatore, K. Iagnemma and H. Peng, “Comparison of Discrete Element Method and Traditional Medeling Methods for Steady-state Wheel-terrain Interaction of Small Vehicles,” Journal of Terramechanics, Vol.56, pp.61-75, 2014.
[https://doi.org/10.1016/j.jterra.2014.08.004]

-
H. D. Nguyen, Modeling the Dynamics of Toothbrush Using Discrete Element Method, M. S. Thesis, Kumoh National Institute of Technology, Kumi, 2011.
-
C. Ericson, Real-Time Collision Detection, Morgan Kaufmann Publishers, San Francisco, pp.50-52, 2005.
[https://doi.org/10.1201/b14581]

-
A. Recuero, R. Serban, B. Peterson, H. Sugiyama, P. Jayakumar and D. Negrut, “A High-fidelity Approach for Vehicle Mobility Simulation: Nonlinear Finite Element Tires Operating on Granular Material,” Journal of Terramechanics, Vol.72, pp.39-54, 2017.
[https://doi.org/10.1016/j.jterra.2017.04.002]

-
C. W. Jun, Study on Contact Analysis between Spatial Multibody System and Many Particles using GPGPU, M. S. Thesis, Pukyong National University, Busan, 2013.