가중치를 적용한 Variable Look Ahead Distance 모델 개발 및 성능비교
Copyright Ⓒ 2019 KSAE / 168-05
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In most cases, drivers operate the steering and speed control based on curvature, lane, or relative vehicle information. Self-driving cars normally use error distance and error angle to lateral control in order to follow the reference path, and the error parameters are calculated based on the look ahead distance(LAD). For an efficient lateral control, the LAD must vary according to the road and the driving environment. In this paper, a LAD model was proposed by using lateral error, road curvature, and vehicle speed. In order to check the performance of the proposed model, we compared our own with the static and conventional LAD model. Computer simulations and experiments were performed in order to verify the advantages of the proposed LAD model.
Keywords:
LAD(Look ahead distance), Curvature, Weight, Variable LAD, Static LAD, Lateral vehicle, Lateral error키워드:
전방주시거리, 곡률, 가중치, 가변하는 전방주시거리, 고정된 전방주시거리, 자차와의 횡방향오차, 전방주시거리와의 횡방향오차1. 서 론
최근 자율주행 기술 및 관련된 운전자 보조시스템(ADAS)에 관한 연구가 진행1-5)되면서 운전자들의 횡방향 조향 제어에 관한 연구 범위가 점차 확대되고 있다.6-9) 일반적으로 자동차를 운전하는 운전자들은 곡률이나 차선 또는 상대 차량 정보를 기반으로 조향 제어를 수행한다. 자율주행 자동차 또한 스스로 주행하기 위해 차선이나 곡률 등의 정보가 필요하며,10) 효율적인 횡방향 제어를 위해 전방 주시거리인 LAD(Look Ahead Distance)가 도로 및 자차 주행환경에 따라 가변되어야 한다.11-13) 횡방향 이탈거리, 이탈각 등 중요한 제어 파라미터가 LAD에 따라 변화하기 때문이다.
고속도로나 일반국도 등 많은 도로에서 운전 시 대부분의 운전자들은 직선 도로와 곡선 도로에서의 전방주시거리가 달라진다. 직선 도로에서는 멀리보고 운전하며 곡선 도로에서는 가깝게 보며 운전하는 것이 일반적이다. 따라서 자율주행 자동차의 LAD는 도로 환경에 따라 가변하는 값이어야 한다. 또한 운전자들은 대부분 전방 상황에 따라 고속, 저속 주행하므로 속도에 따라 전방 주시거리가 달라진다. 예들 들어 차량 앞에 장애물이 없거나 차량이 적은 도로에서는 멀리주시하며 고속 주행하고, 전방에 장애물이 있거나 차량이 많은 도로에서는 가깝게 주시하며 저속 주행하게 된다. 즉, 도로환경의 변화에만 LAD가 가변되는 것이 아니라 전방에 장애물이나 선행차량의 존재에 따른 속도변화에도 LAD가 가변되어야 한다. Wang 등의 Variable LAD14)모델은 차량과 레퍼런스 경로사이의 수직거리와 자차속도를 반영하여 구성하였으며 실차기반으로 Static LAD모델과 비교하여 Variable LAD모델 기반의 제어성능이 우수함을 보였다. 그러나 Variable LAD모델에서는 도로의 곡률대신 차량과 경로사이의 수직거리와 속도를 제어 파라미터로 사용했기에 도로환경이 급격히 변할 때 LAD가 빠르게 반응하지 못하는 단점이 존재한다. 경로추적에서 곡률은 널리 사용되는 제어 파라미터이며 효율적이라는 연구사례가 있다.15) 따라서 본 논문에서의 LAD모델은 횡방향 오차(Lateral error)와 도로 곡률, 자차의 속도 데이터를 이용하여 신규 LAD모델(Proposed LAD)을 제안하였다. 그리고 Proposed LAD모델의 성능 확인을 위해 곡률, Lateral error 와 속도 데이터에 각각 가중치를 적용하여 Variable LAD모델과 Proposed LAD모델의 성능을 비교하였다. 2장에서는 Variable LAD 모델과 Proposed LAD모델을 설명하고 3장에서는 CarSim SW 기반으로 Static LAD, Variable LAD, Proposed LAD의 성능을 비교한다. 4장에서는 실차기반으로 세 가지 LAD모델의 성능을 비교, 분석하고 5장에서는 결론을 맺는다.
2.1 기존의 Variable LAD 수학적 모델
2.1 기존의 Variable LAD 수학적 모델
Variable LAD모델은 2차 다항식 함수를 적용한 LAD를 출력하는 방법이다. 알고리즘을 나타내는 식은 다음과 같다.
| (1) |
L은 LAD이고 v는 차량의 속도이며, N은 차량과 경로사이의 수직거리이다. A, B, C, 그리고 D는 모두 설계자의 파라미터로 일정한 상수 값으로 정의한다. 2차식 LAD에서 정의한 식 (1)에서의 차량과 경로사이의 수직거리 N은 우회전이나 좌회전 시 부호가 변화하게 된다. CarSim에서는 N의 부호가 좌회전 시 (+)로 나타나고 우회전 시 (-)로 나타난다. 즉, D의 부호가 (-)이므로 우회전하는 곡률이 생겼을 시 LAD는 오히려 길어진다. 따라서 본 논문에서의 비교 성능평가에서는 N값에 절댓값을 적용하여 사용하였다.
2.2 Proposed LAD의 수학적 모델
본 논문에서 제안한 Proposed LAD는 횡방향 오차(Latertal error)와 곡률데이터에 의한 수학적 모델과 속도데이터에 대한 수학적 모델을 이용하여 LAD를 출력한다.
| (2) |
| (3) |
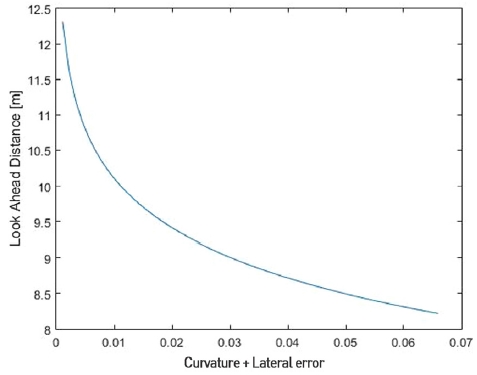
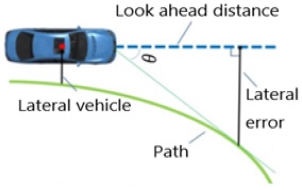
식 (2)에서 yLc(t)는 LAD와 경로사이의 수직거리인 xLat 횡방향오차(Lateral error)데이터와 xCur 곡률(Curvature) 데이터를 이용하여 LAD의 값을 출력해주는 수식이다. 해당 LAD의 특성은 Fig. 1과 같이 곡률과 Lateral error가 커질수록 LAD 길이가 짧아진다. 같은 논리로 직선 도로에서는 LAD 길이가 길어지게 된다. 하지만 곡률이 0이 된다면 LAD는 무한대로 길어질 것이기에 무한대로 길어지지 못하게 제한하는 설정이 필요하다. α는 설계자의 파라미터로 일정한 상수이다.
Properties of LAD by curvature and lateral error data
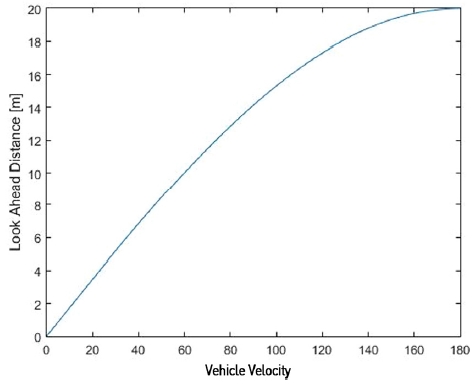
식 (3)에서 yLv(t)는 자차의 속도인 Vx 데이터를 이용한 LAD의 값을 계산하여 출력해주는 수식이다. 속도와 관련된 LAD의 성질은 속도가 빨라질수록 LAD 길이가 길어져야한다. 같은 논리로 속도가 느려질 때는 LAD 길이가 짧아져야한다. β는 설계자의 파라미터로 일정한 상수이다. 이 식의 성질은 Fig. 2와 같이 나타난다.
The property of LAD by vehicle speed
2.3 가중치를 적용한 Proposed LAD
2.2 Proposed LAD의 수학적 모델에서 제시한 식 (2), (3)에서 LAD를 계산할 때 Lateral error와 곡률, 속도데이터를 이용하여 출력한다. 이때 이 두 개의 LAD를 동시에 출력하고 둘 중 최소가 되는 값을 우선순위로 결정하여 조향 제어를 한다면, 곡선 주행 시 곡률데이터에 의해 LAD가 너무 짧게 출력되어 속도 데이터에 의한 LAD 영향을 무시하는 경우가 발생한다. 예를 들어 고속으로 주행해도 될 정도의 곡률이 큰 곡선도로에서 일반적으로 운전자들은 멀리 보며 운전한다. 즉, 이와 같은 경우에는 속도데이터가 LAD에 영향을 미쳐야 한다.
따라서 본 논문에서는 두 식의 LAD 출력 값 중 최소가 되는 값을 사용하여 둘 중 하나의 데이터가 무시되는 상황을 방지하기위해 가중치를 적용했다. 가중치를 적용하게 되면 Lateral error와 곡률, 속도 데이터를 모두 활용가능하기에 위와 같은 문제점을 보완할 수 있다.
| (4) |
식 (4)에서 W1와 W2는 yLc(t) (Lateral error와 곡률데이터에 의한 LAD) 와 yLv(t) (속도데이터에 의한 LAD)의 각 가중치이다. 이때 W1와 W2는 설계자에 따라 다르게 설계될 수 있으며 W1+W2 = 1로 설정한다.
3. CarSim and Matlab Simulink
3.1 CarSim과 Matlab Simulink 환경 구축
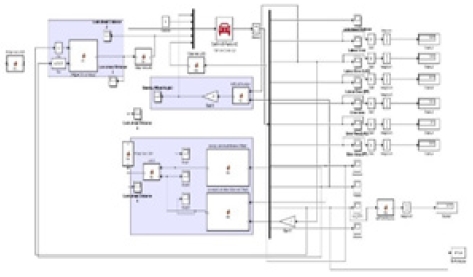
본 논문에서는 CarSim과 Matlab Simulink를 통해 다양한 데이터들을 활용하여 Simulation을 진행하였다. CarSim에서는 차량정보와 Path 정보를 출력한다. 차량정보의 속도데이터, Path 정보인 곡률데이터, 차량과 Path 정보인 횡방향오차(Lateral error와 Lateral vehicle)를 활용한다. Matlab Simulink에서는 제어기정보를 생성하여 CarSim에서 제공해주는 인터페이스에 입력한다. 가감속제어기, 조향제어기, LAD를 계산하는 제어기를 설계하여 차량에 입력한다. 조향제어는 Stanley16) 조향제어기로 설계하였다.
| (5) |
δ(t)는 Steering wheel angle, θe(t)는 기준 Path와 차량헤딩각 오차인 Error angle , vx(t)는 자차의 속도, efa(t)는 횡방향오차(Lateral error), k는 설계자의 파라미터로 상수이다.
Interface between CarSim and Matlab Simulink
3.2 Static, Variable, Proposed LAD 모델 비교
Static LAD모델에서는 LAD가 변하지 않고 일정한 값을 출력한다. 본 시뮬레이션에서는 Static LAD의 길이를 8 m로 설정하였다. 그리고 Variable LAD모델에서는 식 (1)을 적용시키고 Proposed LAD 모델에서는 식 (2), (3)을 적용하여 각 LAD모델을 Matlab Simulink에 설계하였다.
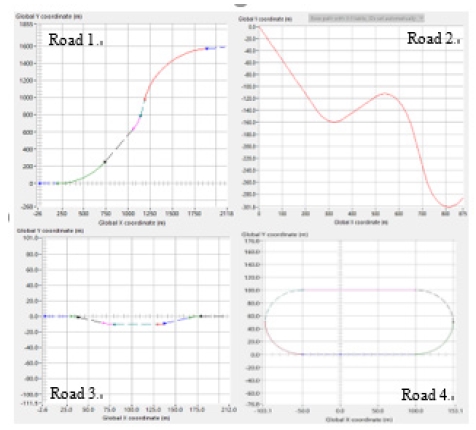
식 (4)에서의 가중치설정은 Fig. 4의 Road 1, Road 2, Road 3와 같이 여러도로 환경에서 다양한 가중치 조합으로 수행한 시뮬레이션 결과를 반영하였다. Table 1의 결과를 참조하여, W1=0.8, W2=0.2로 설정함으로써 속도데이터보다 횡방향오차(Lateral error)와 곡률데이터에 더 큰 가중치를 설정하였다.
Path information provided by CarSim
Error values on different roads according to various weight setting values
Table 1에서의 결과를 보면 다양한 도로에 각 다른 속도로 주행했을 시 W1=0.8, W2=0.2로 설정한 가중치가 Lateral vehicle이 가장 작게 나타난 것을 확인할 수 있다. W1의 가중치가 더 큰 이유는 곡률과 Lateral error 발생 시 LAD의 변화가 더 중요하기 때문이다. 또한 직선경로에서 속도의 작은 영향으로 인해 LAD가 짧아지는 경우를 예방하기 위함이다. 이에 대한 결과는 실차 실험에서도 검증하였다. 실차로 시험할 경일대학교도로를 Road 4에 형상화했으며 시뮬레이션을 통해 Variable LAD 모델과 Proposed LAD 모델을 비교 평가하였다. 차량의 속도는 16 ~ 25 kph로 가변하는 속도로 설정한다.
CarSim에서 제공해주는 LAD와 Lateral error(xLat), Lateral vehicle(N)의 설명은 Fig. 5와 같다.
LAD and lateral error, lateral vehicle
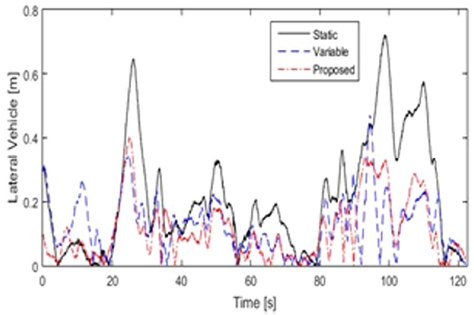
시뮬레이션에서 조향 제어는 Lateral error를 활용하여 stanley 조향제어기로 실험하였다. 비교 항목은 Lateral vehicle의 절대 값을 적용한 적분 값이다. 즉 Path 주행 시 차량 중심점과 경로와의 에러 값을 적분하였다. 세 모델의 비교 결과는 Table 2와 Fig. 6에서 확인할 수 있다.
Lateral vehicle comparison between Static LAD and Proposed LAD
Lateral vehicle comparison of three model
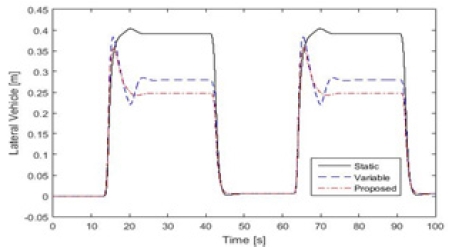
먼저 Static LAD 모델과 Proposed LAD모델을 비교분석해보았다. Table 2에서 Static LAD모델보다 Proposed LAD모델의 Lateral vehicle 적분 값이 더 작게 나타난다. 전체경로에 대한 Lateral Vehicle 적분 값의 차이가 7.13m로 Proposed LAD모델의 오차(Lateral vehicle)가 더 작게 나타난다. Fig. 6을 보면 10~20초 근방과 65~70초 근방에서 Lateral vehicle 값의 차이가 크게 나는 것을 확인가능하다. 이렇게 Lateral vehicle차이가 크게 발생하는 이유는 Proposed LAD모델이 곡률과 횡방향오차(Lateral error)를 사용하여 급격한 도로환경 변화에 더 빠르게 대응하기 때문이다.
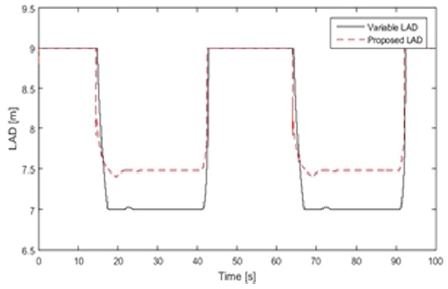
이와 동일하게 Variable LAD모델과 Proposed LAD모델을 비교 분석해 보았다. Table 2에서Variable LAD모델보다 Proposed LAD모델의 Lateral vehicle 적분 값이 더 작게 나타난다. 전체경로에 대한 Lateral Vehicle 적분 값의 차이가 1.34m차이로 Proposed LAD모델의 오차가 더 작게 나타난다. 그리고 Fig. 6에서 10초에서 50초, 60초에서 100초 사이에 Lateral vehicle값이 작게 출력된다. 또한 20초 부근에서 Variable LAD모델은 급격한 Perturbation으로 오차를 유발시키는 반면 Proposed LAD모델은 완만한 perturbation으로 오차를 줄였다. Fig. 7에서 15초, 42초, 65초, 92초 부근을 보면 Variable LAD모델보다 Proposed LAD모델반응이 더 빠르게 나타난다. 그 이유로 Variable LAD모델에서는 차량의 속도와 차량중심과 경로사이의 수직 거리 이 두 가지의 성분만 활용하지만 Proposed LAD모델은 차량속도, 곡률, Lateral error 까지 세 가지의 성분을 활용하기 때문이다. 그 결과로 Fig. 6에서 15초와 65초 부근에 Proposed LAD모델이 Variable LAD모델보다 Lateral vehicle값이 더 작게 나타난다.
LAD Comparison between Variable LAD and Proposed LAD
4. D2 기반의 실차 시험
4.1 D2(실차) 소개 및 환경 구축
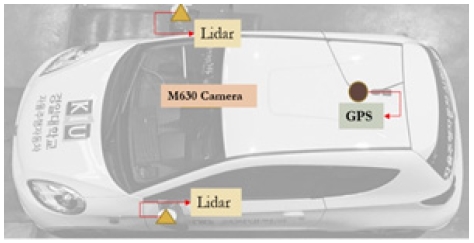
앞서 시뮬레이션을 통해 실험한 결과를 바탕으로 2.2에서 정의한 Proposed LAD모델과 3.2와 2.1에서 정의한 Static LAD, Variable LAD모델을 실차 실험에 적용하기 위해 초소형전기차 D2를 활용하였다. D2는 라이다센서 2개와 카메라센서 1개, 고정밀GPS(RT-2002)가 장착된 자율주행 차량이다. 아래의 Fig. 8은 D2차량과 D2에 장착된 센서 구성 모습이다.
D2 Photograph and specification
4.2 Static, Variable, Proposed LAD 모델 비교
D2 기반으로 실시한 실차 실험은 경일대학교 순환로에서 진행하였다. 아래의 Fig. 9는 경일대학교 위성사진과 자율주행으로 운행한 경로를 나타낸다. 화살표가 출발선이고 각 점들이 자율주행 경로를 나타낸다. 그리고 과속방지턱이 7개 존재하기 때문에 자율주행 차량이 그 앞에서 속도를 급격하게 줄여 자차의 속도가 지속적으로 변경된다. Static LAD모델은 3.2에서와 같이 변하지 않는 값이기 때문에 LAD 길이를 8 m로 설정한다. 그리고 Variable LAD모델에서는 식 (1)을 적용시킨다. Proposed LAD모델에서는 식 (2), (3)을 이용하여 Proposed LAD모델을 설계한다. 식 (4)에서의 가중치는 시뮬레이션과 마찬가지로, W1=0.8, W2=0.2로 설정한다. 교내에서 주행하므로 차량의 속도는 0 ~ 30 kph범위에서만 가 감속 되도록 설정되어 있다. 실차에서 조향 제어는 Lateral error와 Error angle를 활용하여 Stanley 제어기로 시험한다.
Map of Kyungil University and auto driving route
시뮬레이션에서는 Sampling time이 5 ms로 매우 빠르고 경로 오차 값이 매우 작게 발생하기 때문에 LAD 모델 별 비교를 위해 Lateral vehicle의 절대 값을 적용한 적분 값을 사용하였다. 그에 비해 실차실험에서는 경로오차 값이 비교적 크게 나타나고 Sampling time을 40 ms로 비교적 느려 LAD 모델 비교를 위해 Lateral vehicle의 평균 제곱근 오차를 사용하였다. 또한, 직선 경로와 곡선 경로에서의 차이를 각각 비교하기 위하여 두 가지 환경을 나누어서 경로 오차 값을 산출하였다. 세 모델을 비교한 결과는 Table 3, 4와 Fig. 10, 12에서 확인할 수 있다.
Lateral vehicle comparison between Static LAD and Proposed LAD according to the section of road
Maximum lateral vehicle comparison of three model
Lateral vehicle comparison of three model
먼저 Static LAD 모델과 Proposed LAD모델을 분석해보았다. Table 3에서 Static LAD모델과 Proposed LAD모델의 Lateral vehicle의 값은 확연하게 차이가 발생하는 것을 볼 수 있다. Lateral vehicle의 평균 제곱근 오차 값이 직선 길에서는 0.37 m, 커브 길에서는 3.21 m의 차이로 Proposed LAD모델의 성능이 Static LAD모델보다 더 우수하다. Fig. 10은 직선 경로에서 세 가지 LAD 모델의 Lateral vehicle 값을 시간에 따라 나타낸 것이다. 대부분의 구간에서 Proposed LAD모델이 Static LAD모델에 비해 우수한 특성을 보인다. 따라서 3.2에서의 Simulation 실험 결과와 동일하게 Proposed LAD모델이 해당 환경에서 제어에 더 적합한 모델이라는 것을 확인할 수 있다.
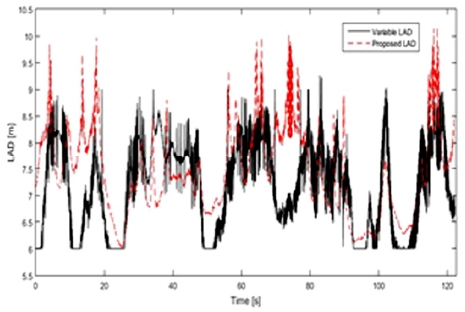
이와 동일하게 Variable LAD모델과 Proposed LAD모델을 비교분석해보았다. Fig. 10에서 Proposed LAD모델이 대부분의 구간에서 Variable LAD모델에 비해 우수한 성능을 보여준다. Fig. 11은 시간에 따른 Variable LAD모델과 Proposed LAD모델의 값을 보여준다.
LAD comparison between Variable LAD and Proposed LAD
전체적으로 Variable LAD모델의 값이 매우 급격하게 변화하는 것을 볼 수 있고, Variable LAD모델은 최소 LAD값으로 설정한 6 m 값을 출력하는 경우가 매우 빈번했다. 이것은 주행 중 과속방지턱 앞에서 자율주행차량이 급격히 속도를 줄였을 때에 Variable LAD모델의 값이 급격히 줄어들었기 때문으로 분석된다. 이러한 급격한 파라미터 변동은 제어에 좋지 않은 영향을 미칠 수 있다. 하지만 Proposed LAD모델은 Variable LAD모델에 비해 보다 연속적인 값을 보여준다. 그 이유로 2.2에서 식 (4)에 의해 식 (2)과 식 (3)에 가중치를 주어 필터링이 되었기 때문이다.
Table 3의 결과를 보면 직선도로에서 Variable LAD모델과 0.29 m 차이로 Proposed LAD모델이 더 우수하다. 반면에 커브구간으로 한정하면 Variable LAD 모델이 0.07 m만큼 더 우수한 특성을 보였다. 그러나 Table 4를 참조하면 최대경로이탈오차(Max Lateral vehicle)에서는 Proposed LAD모델이 가장 우수한 성능을 보여주었다.
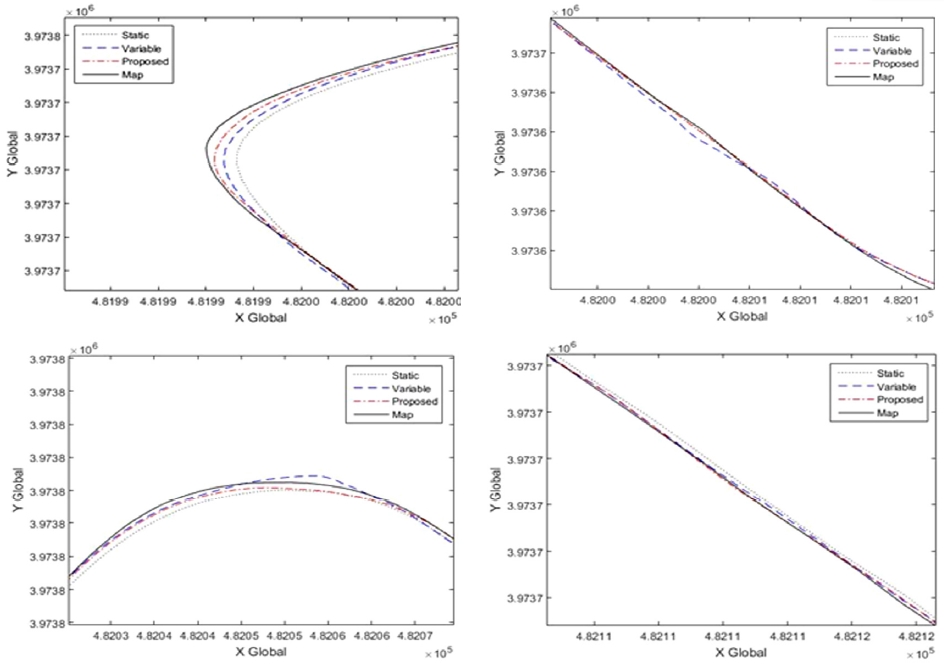
Fig. 12의 첫 번째 그래프는 급커브 구간의 주행 좌표를 표시한 것이다. 두 번째 그래프는 커브가 시작되기 전 과속방지턱이 있는 직선 도로의 주행 좌표를 표시한 것이다. 세 번째 그래프는 일정한 곡률로 유지되는 커브 도로의 경우이다. 네 번째 그래프는 두 번째 그래프 경로의 반대편 직선 도로의 주행 좌표를 표시한 것이다. 네 경우 모두 Proposed LAD모델을 사용하였을 때에 추종해야 할 Map 경로와 가장 유사하게 주행하였음을 확인가능하다.
X, Y Coordinate comparison of three model
Fig. 11에서 Variable LAD 모델을 보면 15초, 70초 부근에 급격한 Perturbation현상을 보인다. 그 이유는 Variable LAD 모델이 속도에 의해 큰 영향을 받기 때문이다. 도로 주행 환경에서 급격한 커브가 존재하여 자율주행 차량이 자차의 속도를 급격히 감소하거나 직선 도로에서 과속방지턱이 존재하여 급격한 감속이 발생 할 경우에 Variable LAD 모델은 LAD 값이 급격하게 감소하게 된다. Fig. 12 그래프들을 보면 Variable LAD모델의 경로가 Proposed LAD모델보다 기준 경로에서 한번씩 크게 벗어나는 것을 보여준다. 이처럼 급격히 감소한 LAD 값에의해 Lateral vehicle과 같은 경로오차 값이 증가 하게 된다.
반면에 Fig. 11에서 Proposed LAD모델은 2.2에서 식 (3)에 의해 곡률과 Lateral error에 더 큰 가중치를 줌으로서 자차의 속도가 급격히 변하여도 LAD가 연속적인 값으로 변화하기 때문에 Lateral vehicle가 크게 증가하지 않는 결과를 보였다. 해당 현상은 Fig. 10에서 0 ~ 20초 부근과 60 ~ 70초 부근에 잘 나타나 있다.
Fig. 12의 세 번째 그림을 보면 Variable LAD모델을 사용한 자율주행 차량의 이동 경로가 매우 불안정한 것을 볼 수 있다. 그 이유는 커브 길에 과속방지턱과 같은 Disturbance가 있기 때문이다. Variable LAD모델에서는 커브와 과속방지턱에 의해서 갑작스러운 감속 때문에 매우 불안정한 LAD 값을 출력하게 되어 최종 자차의 주행경로가 매우 불안정한 모습을 보인 것이다. 반면에 Proposed LAD의 경우에는 속도와 곡률, Lateral error에 따라 가중치를 주어 LAD를 출력하기 때문에 급격하게 속도가 변화하더라도 연속적인 LAD 값을 출력할 수 있었다. 따라서 Proposed LAD 모델을 사용 시 과속방지턱과 같은 Disturbance 환경에서도 우수한 제어 결과를 도출할 수 있었다.
5. 결 론
본 논문에서는 자율주행 자동차의 경로 추종 제어를 위해 가중치를 사용한 LAD 모델을 제안하였다. Proposed LAD모델의 성능을 검증하기 위해 Static LAD와 Variable LAD모델과 비교를 통해 Proposed LAD의 우수성을 확인하였다.
Proposed LAD모델에서 차량의 속도, 곡률, Lateral error 세 가지의 파라미터를 활용하여 Static LAD모델에 비해 경로추종오차인 Lateral vehicle이 감소하였다. 또한 Proposed LAD 모델에 차량의 속도와 곡률, Lateral error에 가중치를 적용하여 Variable LAD모델에 비해 연속적인 LAD 출력 값을 도출했으며 그 결과 경로추종오차 및 최대경로추종오차가 감소함을 확인하였다.
향후 연구 방향으로 LAD의 가변에 따라 스티어링 휠 변동에 의해 운전자에게 끼치는 승차감과 심리적 영향에 관한 연구 개발이 필요하며 Fuzzy Logic 기반의 LAD모델의 가중치를 주행 환경과 에러 파라미터에 따라 자동 업데이트하는 방법을 고려 중에 있다. 또한 운전자의 LAD를 내부 카메라 등으로 분석하여 실제사람의 LAD와 유사한 LAD 모델을 만들어 적용해 볼 계획이다.
Acknowledgments
본 논문은 산업통상자원부 산업기술혁신사업(10079730, 자동차전용도로 / 도심로 자율주행 시스템개발 및 성능평가)의 지원을 받아 수행하였습니다.
References
-
C. Park and S. Kee, “Implementation of Autonomous Driving System in the Intersection Area Equipped with Traffic Lights,” Transactions of KSAE, Vol.27, No.5, pp.379-387, 2019.
[https://doi.org/10.7467/KSAE.2019.27.5.379]
-
H. Lee and S. Kee, “Development of an Autonomous Driving Open Platform Using an Micro Electric Vehicle,” Transactions of KSAE, Vol.26, No.4, pp.449-456, 2018.
[https://doi.org/10.7467/KSAE.2018.26.4.449]
-
M. Kang, S. Hur, I. Park and Y. Park, “Map Building Based on Sensor Fusion for Autonomous Vehicle,” Transactions of KSAE, Vol.22, No.6, pp. 14-22, 2014.
[https://doi.org/10.7467/KSAE.2014.22.6.014]
-
W. Na, J. Kim and H. Lee, “Study on TTC-based Optimal Lane Change Algorithm in Adaptive Cruise Control,” Transactions of KSAE, Vol.27, No.8, pp.627-636, 2019.
[https://doi.org/10.7467/KSAE.2019.27.8.627]
-
H. Kang, D. Lee and K. Huh, “Development of Lane Change System considering Acceleration for Collision Avoidance,” Transactions of KSAE, Vol.21, No.2, pp.81-86, 2013.
[https://doi.org/10.7467/KSAE.2013.21.2.081]
-
M . Kim, S. Shin and J. Park, “Study on Vehicle Lateral Control for Backward Driving,” 13th International Conference on Ubiquitous Robots and Ambient Intelligence(URAI), pp.191-193, 2016.
[https://doi.org/10.1109/URAI.2016.7625734]
-
D. Kim, C. Han and J. Lee, “Sensor-based Motion Planning for Path Tracking and Obstacle Avoidance of Robotic Vehicles with Nonholonomic Constraints,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol.227, No.1, pp.178-191, 2013.
[https://doi.org/10.1177/0954406212446900]
-
P. Brian, C. Michal, Z. Sze, Y. Dmitry and F. Emilio, “A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles,” IEEE Transactions on Intelligent Vehicles, Vol.1, No.1, pp.33-55, 2016.
[https://doi.org/10.1109/TIV.2016.2578706]
-
K. Lee, J. Bak and C. Lee, “A Study on DGPS/GIS-based Vehicle Control for Safe Driving,” Transactions of KSAE, Vol.21, No.5, pp.54-58, 2013.
[https://doi.org/10.7467/KSAE.2013.21.5.054]
-
H. Woo, B. Yong, K. Kim and J. Lim, “Road Test Scenario and Performance Assessments of Lane Keeping Assistance System for Passenger Vehicles,” Transactions of KSAE, Vol.24, No.2, pp.255-263, 2016.
[https://doi.org/10.7467/KSAE.2016.24.2.255]
-
J. Park, S. Bae, B. Koo and J. Kim, “When Path Tracking Using Look-ahead Distance about the Lateral Error Method and the Velocity Change Method Tracking Comparison,” Control, Automation and Systems (ICCAS), pp.1643-1647, 2014.
[https://doi.org/10.1109/ICCAS.2014.6987822]
-
P. Hingwe and M. Tomizuka, “A Variable Look-ahead Controller for Lateral Guidance of Four Wheeled Vehicles,” Proceedings of the 1998 American Control Conference, pp.31-35, 1998.
[https://doi.org/10.1109/ACC.1998.694619]
-
J. Park and P. Nikravesh, “A Look-Ahead Driver Model for Autonomous Cruising on Highways,” SAE 961686, 1996.
[https://doi.org/10.4271/961686]
-
W. Wang, T. Wu and T. Hus, “The Improved Pure Pursuit Algorithm for Autonomous Driving Advanced System,” 2017 IEEE 10th International Workshop on Computational Intelligence and Applications (IWCIA), pp.33-38, 2017.
[https://doi.org/10.1109/IWCIA.2017.8203557]
-
G. Heredia and A. Ollero, “Stability of Autonomous Vehicle Path Tracking with Pure Delays in the Control Loop,” Advanced Robotics : the International Journal of the Robotics Society of Japan, Vol.21, Issues 1-2, pp.23-50, 2007.
[https://doi.org/10.1163/156855307779293715]
-
S. Thrun, M. Montemerlo, H. Dahlkamp, D. Stavens, A. Aron, J. Diebel, P. Fong, J. Gale, M. Halpenny, G. Hoffmann, K. Lau, C. Oakley, M. Palatucci, V. Pratt, P. Stang, S. Strohband, C. Dupont, L. Jendrossek, C. Koelen, C. Markey, C. Rummel, J. Niekerk, E. Jensen, P. Alessandrini, G. Bradski, B. Davies, S. Ettinger, A. Kaehler, A. Nefian and P. Mahoney, “Stanley: The robot that won the DARPA Grand Challenge,” Journal of Field Robotics, Vol.23, No.9, pp.661-692, 2006.
[https://doi.org/10.1002/rob.20147]