동적 계획법을 이용한 도심 주행 연비 최적화

1. 서 론

지난 수년간 전 세계 자동차의 수는 기하급수적으로 늘면서 그에 따른 교통 분야의 에너지 소비가 증가하였다. 그 결과 배기가스로 인한 대기 오염과 지구 온난화는 사회적 이슈가 되었고, 이를 예방하기 위해 정부는 완성차의 연비와 배기가스 배출을 규제하고 있다. 차량에 의한 대기 오염을 줄이기 위해서는 차량이 소비하는 에너지를 효율적으로 사용하여야 한다. 자동차의 에너지 효율을 증가하는 방법으로는 제작 단계에서 차량의 부품 및 디자인 개발 그리고 하이브리드 자동차(HEV), 전기자동차(EV)와 같이 파워트레인 구조변화, 효율적으로 연료를 소비하도록 주행을 개선하는 방법이 있다.¹⁾ 본 논문에서는 마지막 방법인 에너지 효율 주행에 초점을 맞추어, 연료소모를 최소한으로 사용하여 도심 도로의 일정 거리를 주행하는 방법에 대한 연구를 진행한다.

차량은 출발해서 목적지에 도착하기까지 수많은 가, 감속을 통해 주행한다. 불필요한가, 감속은 차량 파워트레인 전반의 손실을 초래하고, 연료를 추가적으로 소모하게 된다. 따라서 도로의 여러 가지 특성들을 반영한 효율적인 주행이 요구 된다. 도심에서는 특히 교통신호로 인해 차량의 이동이 통제되고 신호 구간에서 발생 되는 미세먼지가 상대적으로 높게 측정되기 때문에 더욱 주행방식의 중요성이 커진다.²⁾ 실제 상황에서 효율적인 주행을 위해서 차량 및 운전자는 도로의 상황을 미리 파악하여야 한다. 본 연구에서는 차량과 인프라의 정보를 주고받는 방식(V2I)에 의해서 차량이 목적지까지의 도로 상황 데이터와 접근이 가능하다고 가정한다. 시간 기반의 교통 신호 시스템과 도로의 지리적 특성들을 고려하고, 전역 최적화 방법 중 하나인 동적 계획법(Dynamic programming)을 이용해서 전체 주행에서의 최적 주행 방법을 찾는다. 또한 신호에 의해 차량이 정차하면 엔진이 아이들링 상태로 불필요한 에너지를 소비하기 때문에 패널티를 주어 정지하는 구간을 최소화한다.

2. 차량 모델링

시뮬레이션 주행 상에서 연비 최적화를 진행하기 위해서는 실차의 주행과 크게 벗어나지 않도록 적절한 모델링이 필요하다. 본 연구에서는 차량 모델을 5단 자동변속기가 탑재 된 내연 기관 차량으로 선정한다. 개략적인 차량의 제원은 Table 1과 같다. 차량의 엔진과 변속기 등과 같은 부품들은 상용 프로그램인 Autonomie의 모델을 이용하였다.³⁾ 각 부품들의 특성을 적용하여 후방향 시뮬레이션을 위한 모델링을 진행하였고, 각 스텝에 따른 요구 파워가 정해지면 역으로 계산하여, 에너지 소비량을 계산하였다.

Table 1

Specification of vehicle

2.1 종방향 차량 동역학 기반 차량 모델링

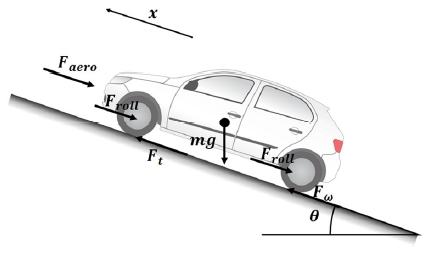
차량이 감가속시 요구되는 견인력과 제동력을 계산하기 위해서 Fig. 1과 같은 차량의 종방향 운동방정식을 이용하고, 식 (1)으로 표현된다.

Fig. 1

Longitudinal vehicle dynamics

$\[ M\frac{dv\left(t\right)}{dt}=F_t\left(t\right)-F_{loss}\left(t\right)-F_{brake}\left(t\right) \]$

(1)

여기서, M은 차량의 전체 질량(kg), v은 차량의 속도(m/s), F_t은 견인력(N), F_loss은 저항에 의한 손실(N), F_brake은 기계적 제동력(N)을 나타낸다. F_loss는 식 (2), (3)과 같이 계산된다.⁴⁾

$\[ F_{loss}=F_{aero}+F_{roll}+F_g \]$

(2)

$\[ \left\{\begin{array}{c}{F}_{aero}=\frac{1}{2}\rho A_f{C}_d{\left\{v\left(t\right)-v_{air}\left(t\right)\right\}}^2\hfill \\ F_{roll}=mg{f}_r\cos \theta \hfill \\ F_g=mgsin\theta \hfill \end{array}\right. \]$

(3)

여기서, F_aero,F_roll,F_g는 각각 공기역학적 저항, 구름저항, 중력에 대한 저항이고, ρ는 공기 밀도, A_f는 차량의 전면적, C_d는 공기 역학 항력 계수, v_air는 공기의 속도, g는 중력, f_r는 구름 저항 계수, θ는 경사각을 나타낸다. 계수들과 공기의 속도가 일정하다고 가정하면, 저항에 의한 손실은 v(t)의 2차식으로 표현 할 수 있다.

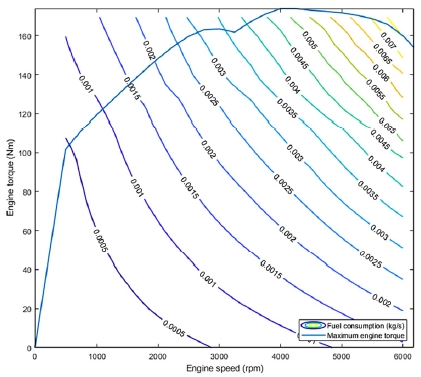
엔진 모델은 Fig. 2와 같이 맵 기반의 준정적 모델로 구성된다. 연료 소비는 엔진의 토크와 각속도의 함수로서 식 (4)와 같이 표현 되고, 단위 시간 당 연료 소비를 결정한다. 요구 되는 가속도를 만족하는 파워가 정해지면, 견인력과 제동력이 결정된다. 후방향 시뮬레이션에 의해, 종감속 기어와 변속기, 클러치의 특성들을 반영하여 견인력과 차량의 속도는 엔진의 토크와 각속도로 역으로 계산되고 식 (5)와 같이 나타낸다.⁵⁾ 계산 된 엔진의 토크와 각속도는 앞서 언급된 엔진의 연료 소비 모델에 이용하여 단위 시간 당 연료 소비량이 결정된다.

Fig. 2

Engine fuel consumption map

$\[ \dot{m}=f\left(T_{eng},{\omega }_{eng}\right) \]$

(4)

$\[ \left\{\begin{array}{c}\begin{array}{c}{T}_{eng}=\frac{F_w{R}_{wheel}}{r_{tm}{r}_{fd}}\hfill \\ {\omega }_{eng}=\frac{v\left(t\right)r_{tm}{r}_{fd}}{R_{wheel}}\hfill \end{array}\hfill \end{array}\right. \]$

(5)

여기서, T_eng,ω_eng은 각각 엔진의 토크와 각속도, R_wheel은 차량 바퀴의 반지름, r_tm,r_jd은 각각 변속비와 종감속비를 나타낸다.

3. 최적 연비 주행 시뮬레이션

2장에서의 차량 모델링을 토대로 실제 도심 도로의 특성을 반영한 주행 시뮬레이션을 진행 한다. 정해진 루트의 고도와 각각 교차로에서의 신호데이터를 최적화에 적용한다. 적절한 목적함수를 설정하고, 신호에서 차량이 멈추는 것을 방지하기 위해 목적함수에 패널티를 부여하여 불필요한 차량의 정지를 피한다. 동적 계획법을 이용하기 위해 각 스테이트를 이산화 하고, 속도와 컨트롤을 최적화한다.

3.1 도심 도로 선정 및 특성

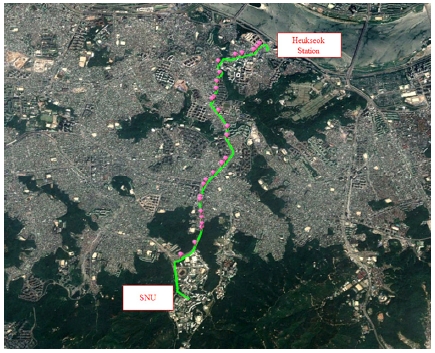
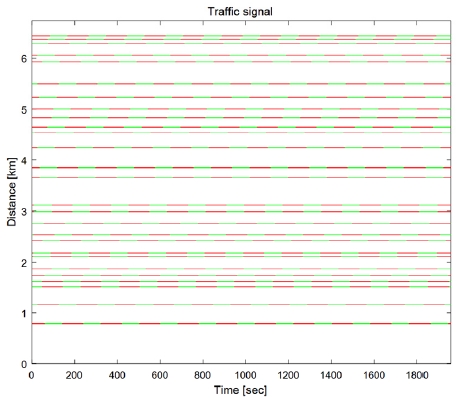
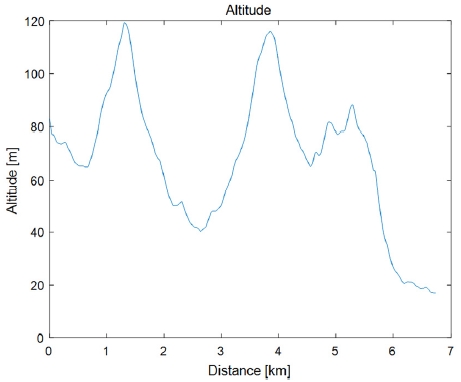
도심에서의 최적 주행을 위하여 실제 도심 도로를 선정하고 특성을 반영한다. Fig. 3과 같이 서울대 정문에서 흑석 역까지의 도로를 타겟 루트로 선정한다.⁶⁾ 선정된 루트에서 교통 신호 시스템을 고려하며 도로의 고도, 속도 제한을 제한 조건으로 정하고, 차량은 주행 중 각각의 데이터와 접근이 가능하다고 가정한다. 시간과 위치에 따른 신호 시스템은 관악경찰서에서 제공 받은 신호체계 리포트를 기반으로 구성하였으며, Fig. 4와 같이 루트 상에서 총 27구간이 존재한다. 도로의 고도는 거리에 따라 Fig. 5와 같고, 구글어스(Google Earth)에서 제공 된 데이터를 이용하였다. 최적화는 위 3가지 조건들을 고려하여 진행한다.

Fig. 3

Route from Seoul National University (SNU) to Heukseok station

Fig. 4

Traffic signal

Fig. 5

Road altitude

3.2 동적 계획법을 이용한 최적 주행 최적화

본 장에서는 3장 1절에서 언급 된 도로의 특성들을 고려하여, 연료가 최소로 사용 되도록 차량의 주행 속도 프로파일을 최적화 한다. 최적화 문제를 해결하기 위해서, 동적 계획법을 이용한다.

3.2.1 스테이트(State) 이산화

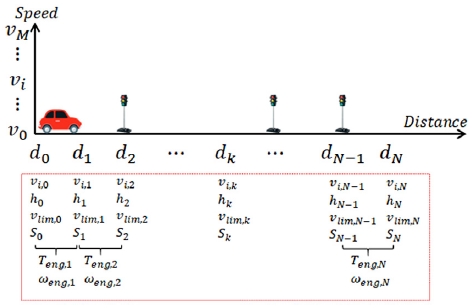
동적 계획법을 이용한 최적화를 진행하기 위해서 먼저 스테이트(State) 이산화를 하여야 한다. 본 연구에서는 거리 기반의 최적화를 위해 총 거리를 단위 거리에 따라 이산화를 한다. 또한 Fig. 6과 같이 차량의 속도에 초점을 맞춰, 차량의 가동범위 내에서 속도를 이산화 하고, 각각의 속도 변화에 따라 엔진의 컨트롤을 역으로 계산한다. 즉, 차량의 위치에 따른 속도가 결정되면, 해당 위치와 시간에 따른 신호상황과 도로의 고도를 고려하여 엔진의 작동점이 정해진다. 이산화 과정은 스텝에 따른 크기를 작게 하면 최적 값에 대한 정확도는 증가하지만, 계산 시간이 길어진다. 반대로 스텝 크기가 커지면, 정확도는 감소하고, 계산 시간은 짧아지게 된다. 본 연구에서는 반복시뮬레이션을 통해 거리의 스텝 크기는 0.01 km, 속도의 스텝 크기는 1 km/h로 정하였다. Table 2에서는 파라미터들의 정의가 나타나 있다.

Fig. 6

Discretization and parameters for dynamic programming

Table 2

Defined parameters for dynamic programming

3.2.2 신호 시스템

도심 도로의 신호 시스템을 최적화에 적용하기 위해서 알고리즘을 구성한다. 차량이 주행 중 정지 신호로 인해 정지하게 되면, 엔진은 아이들링 상태로 작동하게 된다. 차량은 더 이상 주행하지 않지만, 엔진은 아이들링을 유지하기 위해 연료는 계속 소모하게 된다. 불필요한 연료 소비를 막기 위해 본 연구에서는 정지 신호에 차량이 정지하는 것을 최소화하는 알고리즘을 추가한다.

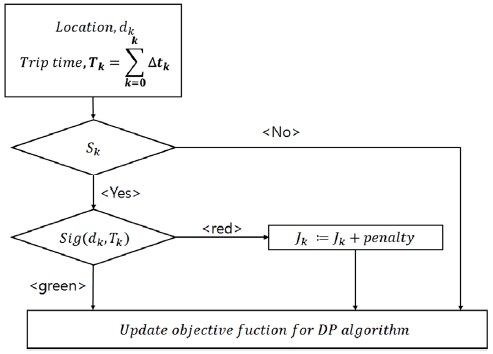
알고리즘은 Fig. 7과 같이 구성 된다. 차량이 신호등이 존재하는 위치에 도달하게 되면, 미리 확보한 신호 시스템의 테이블에 따라 알고리즘을 적용한다. 최적화를 진행하며 매 스텝 거리마다 신호등의 유무를 판단한다. 시뮬레이션 상 현재 위치에 신호등이 존재하고, 빨간 불에 차량이 정지를 해야만 하는 경우, 목적함수에 패널티를 추가 적으로 부여하여 차량이 신호로 인해 정지하는 것을 최소한으로 줄이며 주행하도록 한다.

Fig. 7

Penalty algorithm of traffic signal system

3.2.3 동적 계획법

동적 계획법은 제한 조건을 고려해서 전역 최적 값을 구할 수 있는 방법이다.⁷⁾ 일반적인 동적 계획법의 표현식은 식 (6)과 같이 표현 되며, 각 경로에서 목적 함수의 최적 값은 다음 스텝부터 최종까지의 최적 값을 참조하여 계산되고, 최적의 경로를 도출할 수 있다. 스텝별로 전에 계산된 최적 값들을 계속 참조하기 때문에 중복 계산을 피할 수 있다.

$\[ J_{k,N}^{*}\left(x_k\right)=\min \left[J_{k,k+1}\left(x_k,u_k\right)+J_{k+1,N}^{*}\left(x_{k+1}\right)\right] \]$

(6)

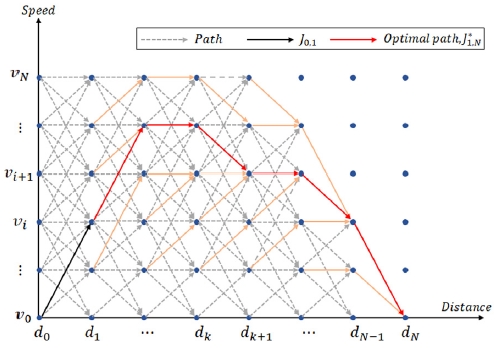
본 연구에서는 Fig. 8과 같이 운전 경로와 거리가 정해지면, 동적 계획법을 이용하여 정해진 목적함수 값을 최소로 하도록 최적화를 진행한다.

Fig. 8

Structure of dynamic programming on speed-distance 2D graph

3.2.4 목적 함수

최적화를 진행하기에 앞서 최소의 값을 갖는 목적 함수를 설정 해주어야 한다. 위에서 언급했듯이, 차량은 엔진의 맵 기반 모델을 기반으로 식 (7)과 같이 엔진의 토크와 속도의 함수를 이용해 결정 된다.

$\[ m_k={\int }_{k-1}^k\frac{f\left(T_{eng,k},{\omega }_{eng,k}\right)}{\overline{v_k}}ds \]$

(7)

하지만 연료 소모량만을 설정하면, 연료 소모만을 최소화하기 위해 차량이 가속을 거의 하지 않고, 저속으로만 운행하게 되어 주행시간이 매우 긴 결과 값이 나오게 된다. 따라서 본 연구에서는 목적 함수에 주행 시간을 추가하여 이를 보정한다. 또한 주행 시간에 가중치를 두어 최적화 과정에서 총 주행 시간과 연료 소모량의 비중 조절이 가능하도록 한다. 목적 함수는 식 (8)과 같이 나타난다.

$\[ J_k=m_k+\alpha \cdot \frac{ds}{\overline{v_k}} \]$

(8)

여기서, α는 가중치 계수를 의미한다.

도로의 특성과 차량의 부품의 한계성에 의해 최적화 알고리즘에 제한 조건을 설정한다. 먼저, 주행 조건으로 출발과 도착은 정지 상태를 유지한다. 엔진의 토크와 각속도는 엔진의 스펙에 맞게 설정한다. 차량의 제한 속도는 단위 거리에 따른 함수로서 도로의 실제 교통법규를 반영하여 설정한다. 전체 제한 조건은 식 (9)와 같다.

$\[ \left\{\begin{array}{c}{T}_{eng,min}\left({\omega }_{eng}\left(k\right)\right)\le T_{eng}\left(k\right)\le T_{eng,max}\left({\omega }_{eng}\left(k\right)\right)\hfill \\ {\omega }_{eng,min}\left(k\right)\le {\omega }_{eng}\left(k\right)\le {\omega }_{eng,max}\left(k\right)\hfill \\ v_{min}\left(k\right)\le v\left(k\right)\le v_{max}\left(k\right)\hfill \\ v\left(0\right)=v\left(N\right)=0\hfill \end{array}\right. \]$

(9)

여기서, T_eng은 엔진의 토크, ω_eng은 엔진의 속도, v는 차량의 속도를 의미한다.

4. 주행 연비 최적화 결과

도로의 고도와 속도 제한, 교통 신호 시스템을 고려한 최적화 알고리즘의 결과를 분석한다. 전체 주행 거리에 따른 주행 시간과 연비를 도출하고, 여러 조건들에 따른 차량의 주행 양상을 파악한다. 또한 목적함수 내 가중치 계수에 따라 연비와 주행시간의 변화를 분석하고, 적절한 가중치 계수를 선정한다.

4.1 대표 케이스 결과 분석

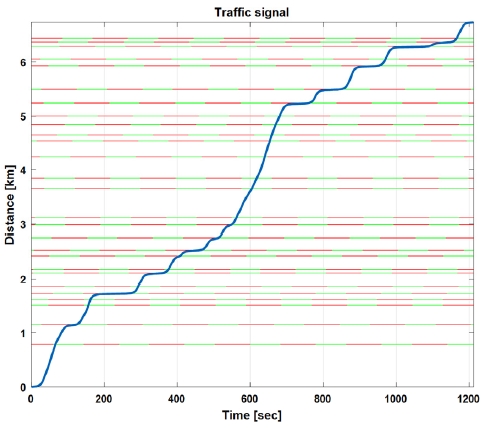
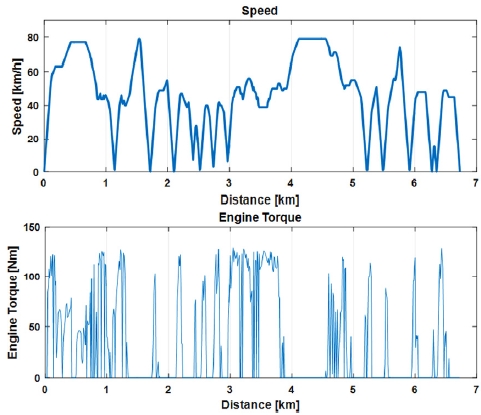
목적 함수의 가중치 계수에 따라 차량의 주행 프로파일과 연비, 주행 시간은 다른 결과를 나타낸다. 차량 컨트롤에 초점을 맞춰 분석하기 위하여 본 절에서는 한 가지 대표 케이스를 선정해서 분석을 진행한다. 대표 케이스의 가중치 계수와 연비, 주행 시간, 총 주행거리는 Table 3과 같다. Fig. 9는 교통 신호 시스템과 시간에 따른 차량의 주행을 보여준다. 정지 신호시, 목적 함수에 패널티를 부과함으로써 차량이 신호에 이르기 전에 감속 및 가속을 통해 대부분의 신호에서 정지 없이 주행하고 있다. 하지만, 차량의 스펙과 속도 제한의 한계에 의해 9구간에서는 차량이 정지 후 주행을 하는 결과를 나타내었다. Fig. 10은 거리에 따른 차량의 최적 속도와 그에 따른 엔진의 토크를 보여준다. 도로의 오르막 경사가 있는 경우에 엔진의 최적지점을 맞추기 위해 차량의 속도가 변화되고 있지만 상대적으로 변화 폭이 적은 주행을 하고 있다. 내리막 경사에서는 속도를 높여서 목적함수의 주행시간을 최소화하며 연료 소모를 줄이는 결과를 나타낸다. 고속으로 주행하고 있지만 엔진의 토크는 낮은 토크를 발생하거나 추가적인 연료 공급 없이 속도를 유지하고 있다. 연비 최적화를 통해 구해진 엔진 토크는 차량 주행에 상위제어를 위한 값으로 실제 주행 시 레퍼런스로 사용하여 차량을 컨트롤 할 수 있다.

Table 3

Weight factor and simulation results

Fig. 9

Vehicle driving and traffic signal for a representative case

Fig. 10

Distance-based vehicle speed and engine torque

5. 결 론

본 연구에서 최적 연비를 갖는 차량의 도심주행프로파일을 도출하였다. 내연 기관 차량을 타겟으로 하여 차량의 종방향 운동방정식을 기반으로 차량 모델링을 하였다. 각 차량 부품은 상용 프로그램 Autonomie의 데이터를 이용하여 모델링 하였다. 최적화 방법으로는 전역 최적화 방법 중 하나인 동적 계획법을 이용하였으며 차량의 부품의 한계점에 따라 제한 조건을 설정하고, 도심 도로들의 지리적 특성들을 반영하여 최적화를 진행하였다. 추가로 교통 신호 시스템을 이용하여 차량이 정지에 의한 엔진의 아이들링 상태를 최소화하도록 패널티를 주었다. 위 방법을 적용한 시뮬레이션 결과는 아래와 같다.

• 1) 목적 함수의 시간 항에 가중치 계수를 곱함으로써 주행 시간과 연비의 비중을 조절할 수 있는 최적화 방법을 고안하였다.
• 2) 차량이 접근 가능한 교통 신호 데이터에 의해 미리 가, 감속하여 신호에 따른 정지를 최소화하여 엔진 아이들링에 따른 불필요한 연료소비를 줄였다.
• 3) 목적함수의 가중치에 따라 연료 소비와 주행 시간은 트레이드오프 관계를 갖는 데, 가중치 계수를 변화해가며 반복 시뮬레이션을 진행한 결과로 특정 계수 이상에 주행의 이점이 크게 줄어 가중치 계수의 경계를 설정하였다.

본 연구는 타겟이 되는 루트의 지리적 특성과 교통 신호를 고려하여 진행하였다. 하지만 실제 주행에서는 고려된 사항 외에 다양한 제한 조건들이 존재한다. 향후 연구에는 V2V기반으로 대상 차량과 앞 차량 간의 차속, 가속, 상대거리 등 데이터를 참조하여 효율적인 연비를 갖는 속도프로파일을 도출할 예정이다. 또한, 다수 차량에 개발 된 주행 시스템을 적용했을 경우의 전체 적인 교통의 주행 결과를 비교 분석할 예정이다.

Acknowledgments

본 연구는 과학기술정보통신부의 재원으로 한국연구재단-미래소재디스커버리사업의 지원을 받아 수행한 과제이다(No. 2017M3D1A1040688).

References

• A. Sciarretta, G. De Nunzio, and L. L. Ojeda, “Optimal Ecodriving Control: Energy-Efficient Driving of Road Vehicles as an Optimal Control Problem”, IEEE Control Systems, 35(5), p71-90, (2015).
• A. Goel, and P. Kumar, “Characterisation of Nanoparticle Emissions and Exposure at Traffic Intersections through Fast-response Mobile and Sequential Measurements”, Atmospheric Environment, 107, p374-390, (2015). [https://doi.org/10.1016/j.atmosenv.2015.02.002]
• Argonne National Lab, Autonomie, https://www.autonomie.net/ (2019).
• H. Y. Lee, C. B. Kang, J. S. Kim, S. W. Cha, and Y. -I. Park, “Component Sizing for Development of Novel PHEV System”, Transactions of KSAE, 24(3), p330-337, (2016). [https://doi.org/10.7467/ksae.2016.24.3.330]
• D. H. Lee, J. R. Jeong, Y. -I. Park, and S. W. Cha, “The Component Sizing Process and Performance Analysis of Extended-Range Electric Vehicles (E-REV) Considering Required Vehicle Performance”, Transactions of KSAE, 21(2), p136-145, (2013). [https://doi.org/10.7467/ksae.2013.21.2.136]
• Google, Google Earth, https://www.google.com/earth/ (2019).
• J. R. Jeong, D. H. Lee, C. W. Shin, D. B. Jeong, K. D. Min, S. W. Cha, and Y. -I. Park, “Comparison of the Fuel Economy of Series and Parallel Hybrid Bus System Using Dynamic Programming”, Transactions of KSAE, 21(1), p92-98, (2013). [https://doi.org/10.7467/ksae.2013.21.1.092]