가솔린엔진제어기 공기량결정함수의 시뮬레이션 환경 구축 및 파라미터 매핑 자동최적화
Copyright Ⓒ 2019 KSAE / 165-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The purpose of the air charge for a gasoline engine ECU is to predict the relative air charge load in a cylinder by using MAP or MAF sensors. Numerous parameters in the ECU function have to be calibrated in order to convert the sensor value to air charge load. Manual calibration is time consuming or even impossible due to the high number of correlated parameters. Tiers supplying an ECU make use of internal parameter optimizers not only for the air charge function, but also for some other functions. However, these optimizers are not generally opened to third parties so as to protect intellectual property. In this study, a generic parameter optimizer, MOCA, has been utilized in order to simulate the air charge function and to optimize the calibration parameters for minimizing the deviation between the measured actual output and the model output. Optimum results by MOCA were almost the same as the results of the Tier internal optimizer. This automated calibration performed offline on a PC by MOCA instead of the manual calibration at a test bench would be able to replace the Tier internal optimizers, as well as save time and costs, throughout the entire calibration process.
Keywords:
MOCA, Parameter optimizer, Simulation environment, Gasoline engine ECU, Air charge키워드:
모카, 파라미터최적화도구, 시뮬레이션환경, 가솔린엔진제어기, 흡입공기량1. 서 론
최근 개발되고 있는 엔진은 성능, 연비 및 강화되는 배출가스 규제 등의 조건을 만족하기 위한 목표를 갖고 있다. 이를 위해 직분사, 가변밸브, 과급, 배기가스재순환 등과 같은 기술들이 도입되면서 다수의 액추에이터를 엔진에 장착하고 있다. 이로 인해 시스템의 복잡성 및 자유도가 증대되었고, 각 액추에이터의 최적 운전점을 결정해야 하는 파라미터 개수가 급격히 증가되었다.1)
다수의 파라미터를 여러 운전점에서 동시에 수작업으로 캘리브레이션 하는 것은 제어로직의 복잡성 및 파라미터간 상호작용 때문에 쉽지 않거나 불가능 한 경우가 많다. ECU를 제공하는 공급자(Tier)는 일부 캘리브레이션 항목에 대해 다수의 파라미터를 동시에 자동최적화 매핑할 수 있는 내부용 툴을 보유하고 있으나, 기술보안 때문에 자동차제조사를 비롯한 제 3기관에 이 툴을 제공하는 경우는 드물다.
본 연구에서는 가솔린엔진제어기(ECU) 공기량결정함수 캘리브레이션을 위하여 ECU 제어사양서와 동일한 몇 가지 형태의 모델을 작성한 후, 이 모델을 이타스 MOCA를 이용하여 ECU 공기량결정함수를 시뮬레이션하고, 다수의 캘리브레이션 파라미터를 자동최적화 매핑할 수 있는 환경을 만들고자 한다. 이와 같은 방법으로 수행된 결과를 공급자 내부용 자동최적화 툴 결과와 비교/검증하여 실사용 및 양산적용 가능성과 그 효용성 등을 평가하고자 한다.
2. 본 론
2.1 실험 엔진 및 파라미터 자동최적화 매핑 툴
공기량결정함수 시뮬레이션 및 자동최적화 매핑 수행을 위해 입･출력값으로 사용한 실험데이터는 A 자동차제조사(OEM)에서 개발한 직렬4기통 터보차저가 장착된 가솔린 엔진의 실험데이터이며, 이 엔진의 대략적인 사양은 Table 1에 나타냈다.
Specification of an engine
공급자는 일부 캘리브레이션 항목에 대해 내부 사용 목적의 파라미터 자동최적화 매핑 툴을 보유하고 있다.
이 툴은 캘리브레이션 엔지니어가 해당 캘리브레이션 항목에 대한 자동최적화 매핑을 수행할 수 있도록 보조하여, 수동으로 매핑해야 하거나 심지어 불가능할 수 있는 다수 파라미터를 동시에 매핑할 수 있도록 지원한다. 보쉬(Bosch)사 MAPxxx, C사 COMxxx 및 H사 ENxxx 등이 이러한 툴의 예로 알려져 있다.
자동최적화 툴은 캘리브레이션 효율성 개선 및 원형(Prototype) 수요 감소를 통한 개발비용 절감 효과 때문에 공급자로부터 ECU 및 제어 소프트웨어를 공급받아 캘리브레이션을 수행해야 하는 자동차제조사는 이와 같은 자동최적화 툴에 대한 수요가 많다.
하지만 공급자가 개발한 자동최적화 툴은 ECU 내부 핵심 제어로직 노출, 최적화 알고리즘 기술노출 및 캘리브레이션 노하우 노출 등을 우려한 공급자의 기술보안 목적 때문에 자동차제조사를 비롯한 제 3기관에 배포되는 경우가 제한적이다.
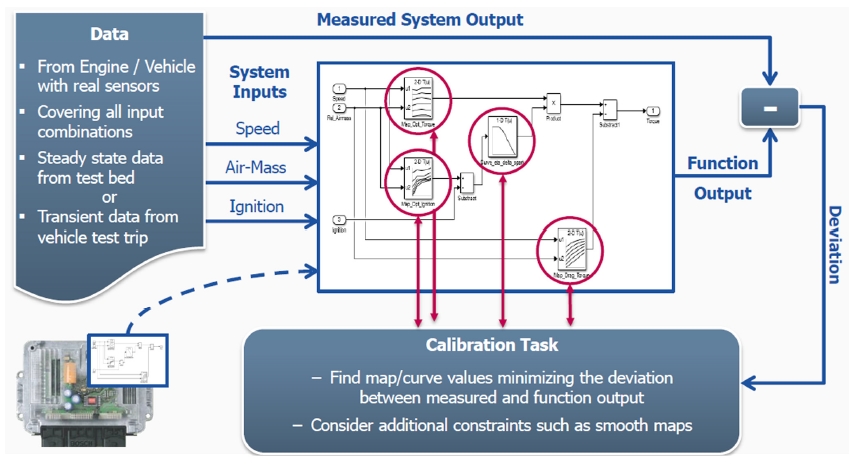
이타스에서 개발한 상용 툴 MOCA는 Fig. 1과 같이 측정데이터와 변경 가능한 파라미터를 포함하는 ECU 제어로직을 불러와서, 제어로직에 의한 모델 출력값을 연산하고, 모델 출력값과 실측에 의한 측정데이터를 일치시키도록 제어로직 내 파라미터를 자동으로 최적화 하는 툴이다. 추가적으로 데이터 및 파라미터에 대한 시각화 기능 및 최종 결과물을 엑셀 및 DCM 형태로 추출해주는 기능이 있다.
Main function of MOCA
이 툴의 장점은 공급자가 제공하지 않는 자동최적화 툴에 대한 대안으로서 제어로직에 따른 모델 출력값을 시뮬레이션 할 수 있을 뿐만 아니라, 툴 내부 기울기 기법(Gradient Method)에 기반한 최적화 알고리즘을 통해서, 제어로직 내 파라미터 매핑을 자동으로 수행할 수 있다는 점이다. 또한 사용자가 로직을 수정, 변경할 수 있는 자유도를 가지고 있기 때문에 변경된 제어로직에 의한 시뮬레이션 결과를 미리 확인해 볼 수 있는 환경을 구축할 수 있다. 이렇게 함으로써 제어로직 변경에 따른 개선효과 여부를 미리 파악할 수 있는 장점이 있다.2)
2.2 보쉬 플랫폼 공기량결정함수
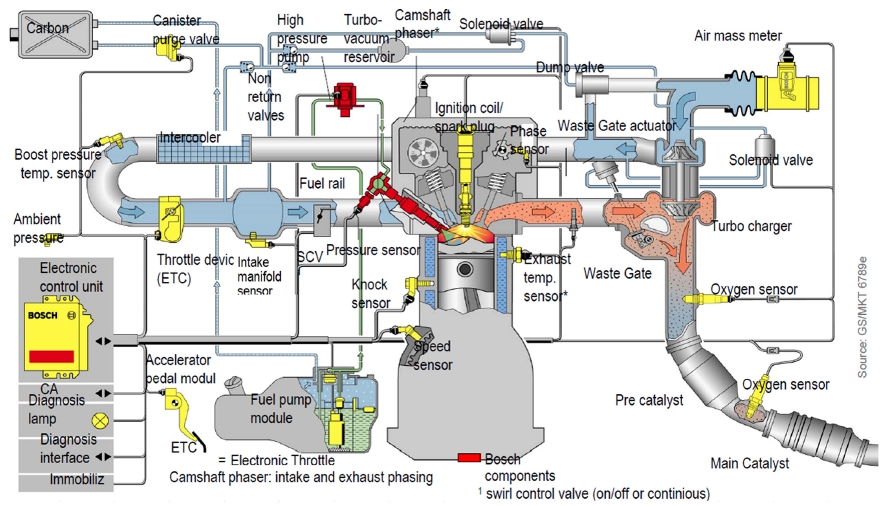
보쉬 플랫폼에 기반한 가솔린 엔진 매니지먼트 시스템(EMS)을 Fig. 2에 도식화하였다.3) 공기량결정함수는 공기유량(MAF) 센서를 이용하여 실린더에 충진되는 공기량을 직접적으로 계산하는 방법과, 흡기압(MAP) 센서를 이용하여 간접적으로 계산하는 방법이 있다. 배기가스재순환(EGR) 등과 같은 복잡한 흡기시스템을 사용하지 않는 엔진은 생산원가 등을 고려, 흡기압센서만을 이용하여 공기량을 모델링하는 경우가 다수다.
Bosch engine management system schematic3)
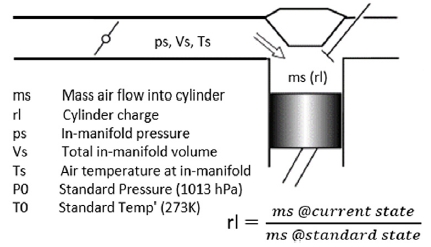
MEx17 플랫폼 기반의 공기량결정함수는 실린더에 충진되는 공기량을 rl(Relative Load)이라는 값으로 공기 충진율을 정의한다. Fig. 3과 같이 rl은 0 °C, 1기압 표준상태에서 실린더에 완충되는 공기량에 대한 현재 운전상태의 공기량 충진 비율로, rl이 크다는 것은 실린더 내부의 충진 공기가 많다는 것 또는 엔진부하가 크다는 것을 의미한다. 자연흡기 엔진의 경우 rl은 통상 100 % 이하이고, 터보차저가 장착된 경우 100 % 이상의 값을 나타낼 수 있다.
Basic concept of cylinder air charge model for MEx174)
물리적 현상에 기반한 공기량결정함수는 흡기압력에 영향을 미치는 모든 인자를 고려하는데, 연료증발가스에 의한 퍼지, 내/외부 배기가스재순환, 공기량 제어 액추에이터(SCV, VIS) 등이 이에 해당된다.4,5)
보쉬 MEx17 플랫폼에 의한 공기량결정함수는 아래와 같은 형태로 공기 충진율을 표현한다.
rl=F(충진율기울기,흡기압력,잔류가스압력)
여기서 흡기압력 항은 흡기압센서에 의한 흡기매니폴드 압력이고, 충진율기울기와 잔류가스압력 항은 엔진회전수, CVVT 캠 위치, 흡기온도, 배기온도, 배기압력 등에 의해 결정되는 값이다. 이러한 입력값을 바탕으로 엔진의 현재 운전상태에 해당하는 충진율기울기와 잔류가스압력 항에 관련된 파라미터를 매핑하는 것이 공기량결정함수 캘리브레이션이다.
MOCA에서 제어로직을 불러올 수 있는 모델 타입은 크게 다섯 가지다. ASCMO 모델, 시뮬링크 모델, ASCET 모델, FMU 모델, 그리고 MOCA에서 직접 핸드코딩 방식을 통해 구현하는 모델 타입이다. 본 연구에서는 MEx17 플랫폼 ECU 제어사양서를 참고하여 제어로직과 동일한 구조를 갖는 세 가지 타입의 공기량결정함수 모델을 작성하였다. 첫 번째는 시뮬링크 모델(Fig. 4) 타입이고, 두 번째는 시뮬링크 모델을 기반으로 변환한 FMU 모델 타입이다.
Simulink model of MEx17 air charge function (Blur effect is applied for intellectual property)
FMU(Functional Mockup Unit)는 모델교환과 동시시뮬레이션을 목적으로 만들어진 파일 형태이며, xml형태의 기술파일과 소스코드를 포함하는 압축파일 형태의 dll 실행파일로 구성된다. FMU 모델의 장점은 제어로직의 공개 없이 dll 파일 형태로 제어로직 모델을 추출하여 교환할 수 있다는 점과, MOCA에서 자동최적화 시 시뮬링크 모델을 사용하는 경우보다 계산시간을 단축할 수 있다는 점이다.
마지막 세 번째 모델 타입은 MOCA에 있는 “Function” 메뉴의 공식편집(Formula Editor) 기능을 이용하여 제어로직에 표현된 연산을 직접 핸드코딩 하는 방식의 모델 타입이다. 본 논문에서는 이 모델 타입을 “공식코딩(Formula Coding)”이라고 칭하겠다. 공식코딩은 앞선 두 가지 방법 대비 MOCA에서 자동최적화 시 계산시간을 획기적으로 줄일 수 있는 장점이 있지만, 현재 피드백 제어나 적분연산 등과 같이 복잡한 형태의 연산은 구현할 수 없다. 공기량결정함수는 이와 같은 제약조건 모델에 해당되지 않기 때문에 Fig. 5와 같이 공식코딩을 이용하여 세 번째 타입의 모델을 생성하였다.
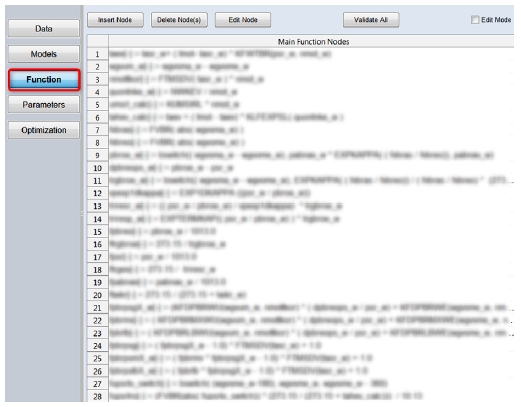
Formula Coding by Function menu in MOCA for air charge function (Blur effect is applied for intellectual property)
동일한 제어로직을 세 가지 타입으로 구현한 이유는 첫째, 모델의 구성이 동일하면 MOCA에서 모델 타입과 무관하게 동일한 모델 출력값을 연산한다는 것을 확인하기 위함이고, 둘째, 모델 타입간 자동최적화 속도를 상대적으로 비교하기 위함이다.
해당 엔진의 공기량결정함수 캘리브레이션을 위해 입력변수로 엔진회전수(rpm), 흡기압력(hPa), CVVT 캠의 배기밸브닫힘시점, 흡기밸브열림시점을 설정하였다. 데이터 측정은 A 자동차제조사의 엔진테스트벤치에서 엔진이 운전 가능한 전체 운전영역에서 추출된 2300여 개의 측정점에서 ECU 데이터 및 가스분석기에 의한 실측 공기량 등을 측정하였고, 이 데이터를 MOCA의 입력 데이터로 사용하였다.
2.3 공기량결정함수 자동최적화 매핑
공기량결정함수를 캘리브레이션 한다는 것은 ECU 제어로직에 의한 모델 공기량과(rlmodel) 엔진테스트벤치에서 가스분석기로 측정한 실측 공기량의(rlmeasured)차이를 최소화 하도록 하는 ECU 제어로직 내 파라미터를 매핑하는 것을 의미한다.6) 보쉬 MEx17 플랫폼 공기량결정함수는 이를 캘리브레이션 하기 위한 파라미터 개수가 30여개에 달하며, 엔진시스템이 복잡해질수록 장착된 액추에이터 수가 늘어나기 때문에 파라미터 개수는 늘어난다. 여러 파라미터를 동시에 수작업으로 매핑하는 것은 현실적으로 불가능하기 때문에 자동최적화 툴이 요구된다.
보쉬는 공기량결정함수 제어로직 내 다수 파라미터를 자동최적화 하기 위해 MAPxxx 이라는 내부용 최적화 툴을 보유하고 있으며, 이 툴을 이용하여 공기량결정함수 캘리브레이션을 효율적으로 수행할 수 있다. ECU와 가스분석기에 의한 측정데이터로부터 제어로직 입력값에 해당하는 데이터를 서로 매칭시키고, 자동최적화를 수행하고자 하는 파라미터에 대해 활성/비활성 설정을 하면, MAPxxx는 ECU 제어로직에 의한 모델 공기량 rlmodel과 가스분석기를 통해 측정한 실측 공기량 rlmeasured이 일치하도록 하는 최적 파라미터를 툴 내부 알고리즘에 의해 자동으로 도출해준다. 이와 함께 최적화 파라미터에 의해 연산된 모델 출력 rl도 함께 도출해 준다. 사용자는 도출된 최적화 파라미터를 ECU에 적용하여 검증을 거친 후 공기량결정함수 캘리브레이션 수행을 완료한다.
본 연구에서는 보쉬 내부용 툴 MAPxxx을 사용하여 그 결과를 도출하고, 이 결과를 MOCA 툴을 통해 도출된 결과와 비교/분석하기 위해 사용하였다. MAPxxx를 통해 자동최적화에 소요된 시간은 대략 500여 초를 기록하였다.
보쉬 플랫폼 공기량결정함수 자동최적화 매핑을 위한 내부용 MAPxxx을 대체하고자, 상용 MOCA를 이용하여 아래와 같은 최적화 단계를 수행하였다.
- 1) Fig. 5에 보이는 MOCA “Data” 메뉴에서 ECU 및 가스분석기에서 측정한 데이터를 불러온다.
- 2) “Parameters”메뉴에서 매핑하고자 하는 제어로직 내부의 파라미터를 정의하고 설정한다. 또는 DCM을 불러와서 DCM 내의 파라미터를 MOCA “Parameter” 메뉴의 파라미터로 설정할 수 있다.
- 3) “Models” 메뉴에서 Fig. 4의 시뮬링크 모델과 FMU 변환 모델을 각각 불러온다. 불러온 시뮬링크 모델, FMU 모델 내부의 입력변수는 1)항에 의해 정의된 데이터로, 모델 내부 파라미터는 2)항에 의해 정의된 파라미터로 각각 서로 매칭시킨다.
- 4) “Function” 메뉴에서 시뮬링크 모델, FMU 모델과 동일한 공기량결정함수 모델을 MOCA에서 순차적인 교점 정의 방식의 핸드코딩 기법을 통해 Fig. 5와 같이 공식코딩 모델을 작성한다.
- 5) “Optimization” 메뉴에서 공기량 매핑을 위한 판정기준(Criteria)을 정의한다. ‘제어로직 모델 출력값에 의한 모델 rl(rlmodel)과 실측 rl(rlmeasured)이 같다’는 조건을 판정기준으로 설정한다.
- 6) 제어로직에 있는 30여개의 파라미터 중에서 엔진의 기하구조(Geometry)에 따른 고정 파라미터, 시스템 관련 상수 등과 같이 매핑이 불필요한 파라미터를 제외 후, 자동최적화 매핑이 필요한 9개 파라미터를 활성화하여 자동최적화를 수행한다. 이 파라미터 활성화 설정은 보쉬 내부용 툴 MAPxxx에 의한 자동최적화 수행에도 동일하게 적용하였다.
- 7) 자동최적화 수행을 위한 반복계산의 멈춤 조건은 반복횟수와 허용오차 조건이 있으며, 허용오차는 이전 단계의 RMSE와 현재 단계의 RMSE 차이다. 본 연구에서는 반복계산 멈춤 조건으로 반복횟수 3000회, 허용오차 10-7 조건을 설정하였고, 두 조건 중 어느 한 가지 조건을 우선적으로 만족하면 반복(Iteration)에 의한 반복계산은 종료된다.
- 8) “Optimization” 메뉴에 추가로 “Sequence” 옵션이 있다. 이 항목은 최적화 시 여러 파라미터의 최적화 순서를 정하거나, 여러 최적화 판정기준이 있는 경우에 판정기준 적용 활성화 여부 및 이에 대한 가중치 등을 설정할 수 있다. 본 연구에서는 MOCA의 Sequence 옵션을 사용하여 일부 파라미터에 대해 우선적인 최적화를 수행한 후, 잔여 파라미터에 대해 단계적인 최적화를 순차적으로 수행하였다.
3. 결 과
3.1 시뮬레이션 및 자동최적화 매핑 환경 구축
공기량결정함수 자동최적화를 위해 작성한 세 가지 타입의 모델 즉, 시뮬링크 모델, FMU 모델, 공식코딩 모델이 MOCA에서 내부 연산을 통해 각각의 모델 rlmodel을 도출함으로써 MOCA를 이용한 공기량결정함수의 PC 시뮬레이션이 가능하게 되었고, 자동최적화 매핑을 위한 환경을 구축하게 되었다. 해당 제어로직 모델과 제어로직의 입력 데이터가 존재하면, 최종 출력값인 모델 rlmodel 뿐만 아니라, 충진율기울기, 잔류가스압력 등과 같이 MOCA에서 교점으로 설정한 제어로직 내부의 중간 연산 과정 항에 대한 시뮬레이션 값을 확인할 수 있었다. 또한 임의의 가상데이터를 입력 받거나 파라미터를 조정하게 되면 MOCA에 의해 연산된 모델 출력 rlmodel을 시뮬레이션 할 수 있게 됨으로써, 모델기반 공기량결정함수 가상 캘리브레이션이 가능하게 되었다.
3.2 작성한 모델 타입에 따른 결과 비교
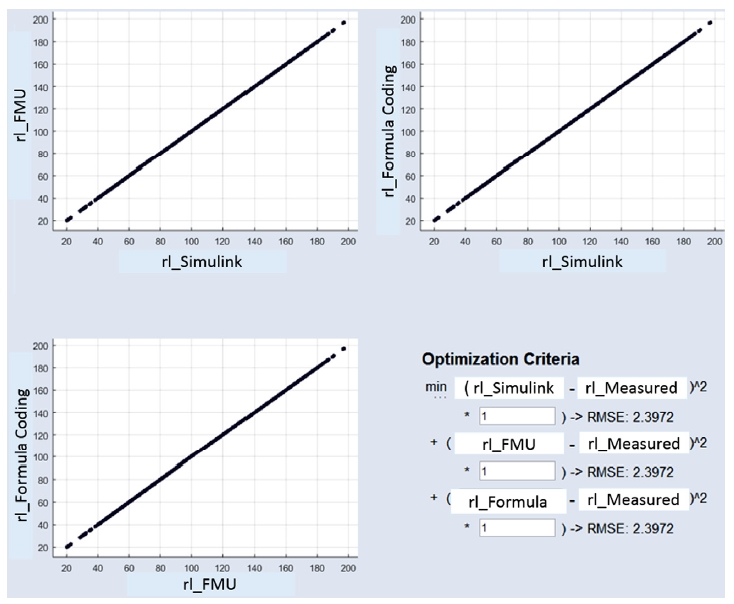
공기량결정함수 자동최적화 매핑을 위해 작성한 시뮬링크 모델, FMU 모델, 공식코딩 모델을 하나의 MOCA 파일에 모두 불러온 후, 그 결과를 동시에 비교하였다. MOCA에 불러온 세 가지 모델 타입에서 추출한 각각의 모델 rlmodel 즉, rl_시뮬링크, rl_FMU, rl_공식코딩의 모델 출력값 결과를 2차원 그래프 X/Y축에 할당하여 Fig. 6과 같이 나타냈다. 좌측상단, 우측상단, 좌측하단 그래프는 각각 rl_시뮬링크 = rl_FMU, rl_시뮬링크 = rl_공식코딩, rl_FMU = rl_공식코딩로서, 각각의 모델 출력이 서로 일대일 선형관계를 나타냈으며, 이는 3가지 모델이 서로 정확히 일치한다(rl_시뮬링크 = rl_FMU = rl_공식코딩)는 것을 의미한다.
Comparison of results about three types of models
한편 Fig. 6 우측 하단에 표현된 것처럼 세 가지 모델 타입에 동일한 임의의 파라미터 데이터 값을 적용하면, 각각의 모델 타입에 대한 전체 2300여 측정데이터의 모델 rlmodel과 실측 rlmeasured의 평균제곱근오차 RMSE(rlmodel_(시뮬링크, FMU, 공식코딩) - rlmeasured)가 2.3972로 모델 타입과 무관하게 모두 동일하였다. 이는 MOCA에서 연산된 세 가지 타입의 모델 rlmodel이 모델 타입과 무관하게 모두 동일한 연산 결과를 나타낸다는 것을 함축하며, 이를 모든 측정 점에서 데이터를 추출하여 확인하였다.
MOCA에서 핸드코딩으로 작성한 공식코딩 모델이 외부 모델을 불러와서 연산한 결과와 동일하다는 것은 MOCA의 핸드코딩 방식을 통해서도 ECU 제어로직을 동일하게 구현할 수 있다는 것을 의미한다.
i7 2.9GHz CPU PC 기준으로 MOCA에서 반복계산에 따른 컴퓨터 계산속도를 비교하면 시뮬링크 모델 약 15분/1회, FMU 모델 약 5분/1회, 공식코딩 약 2초/1회를 기록했다. MOCA에서 시뮬링크 모델을 사용한 경우, 모델과 연동하여 연산을 수행하기 때문에 계산속도가 현저하게 늦고 수렴에 상당한 시간이 소요되었다. FMU 모델은 MOCA에서 시뮬링크 모델을 사용할 경우 계산속도의 단점을 해결하기 위해 지원된 모델 타입이다. 기존 시뮬링크 모델 사용 대비 계산시간을 1/3로 단축하였으나, FMU 모델을 도입하더라도 복잡한 모델이나 입력 데이터 및 파라미터 개수가 많은 경우는 계산시간을 현저하게 줄이는데 한계가 있었다. 하지만 MOCA의 공식코딩을 사용한 경우 계산시간이 현저하게 감소 되었다. 이는 외부 모델과의 연동 없이 MOCA 상에서 공식코딩에 의한 연산을 직접 수행하기 때문에 가능하게 된다.
세 가지 모델 타입에 따른 결과의 동일성 및 PC 계산속도 비교 결과를 고려, 이후 진행될 MOCA를 이용한 공기량결정함수 자동최적화 매핑은 공식코딩 모델만으로 최적화 수행하여 그 결과를 도출하였다.
3.3 MAPxxx에 의한 모델 검증 및 자동최적화
MOCA를 이용한 자동최적화의 선행단계로 MAPxxx를 이용한 자동최적화를 수행하였다. 그 이유는 첫째, 본 연구를 목적으로 ECU 제어사양서를 참고하여 작성한 공기량결정함수 모델이 실제 ECU 제어로직과 일치하는지 여부를 판단하기 위한 목적과 둘째, MAPxxx에 의한 최적화 결과를 MOCA를 이용한 자동최적화 결과와 비교/분석하기 위한 기준으로 설정하기 위함이다.
MAPxxx은 ECU 제어사양서와 일치한 제어로직이 툴 내부에 반영되어 있기 때문에, MAPxxx에 의한 모델 출력 rl_MAPXXX은 ECU에 의한 출력 rl_ECU와 동일하다. 따라서 MAPxxx에 의해 최적화된 파라미터 결과를 MOCA에 적용한 모델의 파라미터 초기값으로 설정하여, MAPxxx에 의한 모델 출력과 MOCA에 의해 연산된 모델 출력이 동일하다면 작성한 모델은 ECU 제어로직과 일치한다고 할 수 있다. MAPxxx과 MOCA로부터 도출된 각각의 모델 rl(rl_MAPXXX, rl_MOCA)로 MOCA에 적용한 공기량결정함수 모델과 ECU 제어로직의 일치성을 검증하였다.
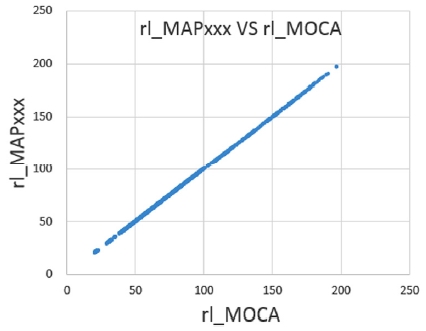
MAPxxx에 의해 최적화된 파라미터 결과값을 MOCA의“Parameter”항목 초기값 데이터로 설정하면, Fig. 7에서 보는 바와 같이 rl_MAPXXX과 rl_MOCA가 서로 일대일 선형관계를 갖는 그래프를 나타내게 된다. 여기서 rl_MOCA는 rlmodel_(공식코딩)이 치환된 값이다. 이 그래프 결과는 MOCA에 적용된 공기량결정함수 모델이 MAPxxx 내부에 반영된 ECU 제어로직과 동일하게 작동하고 있다는 것을 의미한다.
Comparison of results by MAPxxx and MOCA
RMSE 기준으로 MAPxxx에 의한 전체 측정데이터의 RMSE(rl_MAPXXX - rlmeasured)는 2.3921, MOCA에 의한 RMSE(rl_MOCA - rlmeasured)는 2.3972로 거의 동일했다. 소수점 셋째 자리 이후 차이는 제어로직 내부에서 0으로 나누는 연산 항을 방지하도록 처리하는 툴 간 알고리즘 차이와, 연산 과정에서 소수점 이하 자릿수를 처리하는 툴 간의 해상도 차이에 기인한 오차로 확인하였다. 이 과정을 통해 MOCA에 적용한 공기량결정함수 모델이 실제 ECU 제어로직과 동일하게 작동하고 있다고 판단하였다.
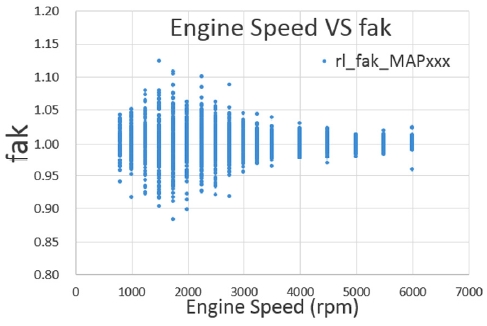
최적화에 의해 연산된 모델 rlmodel과 실측 rlmeasured의 차이를 비교하기 위해 fak 이라는 용어를 정의하였다. fak은 실측 rlmeasured에 대한 모델 rlmodel의 비율이다. Fig. 8과 같이 MAPxxx에 의한 자동최적화 결과는 전체 2300여개 측정데이터 중 5 % 오차 범위(fak: 1±0.05) 내에 97 %에 해당하는 측정데이터 개수가 분포하였고, 이는 자동차제조사의 공기량결정함수 캘리브레이션 목표를 만족하는 수준이다.
Optimum result by MAPxxx
본 연구에서는 MAPxxx에 의한 결과를 기준으로, 다음 절에서 MOCA에 의한 자동최적화 결과를 MAPxxx에 의한 최적화 결과와 비교/분석하였다.
3.4 MOCA에 의한 자동최적화
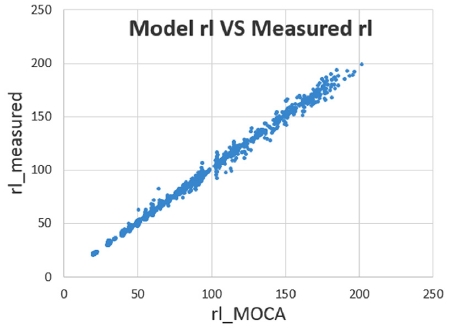
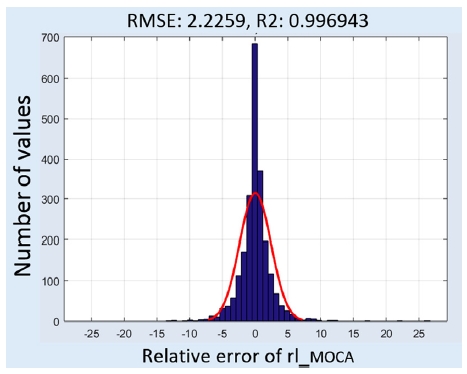
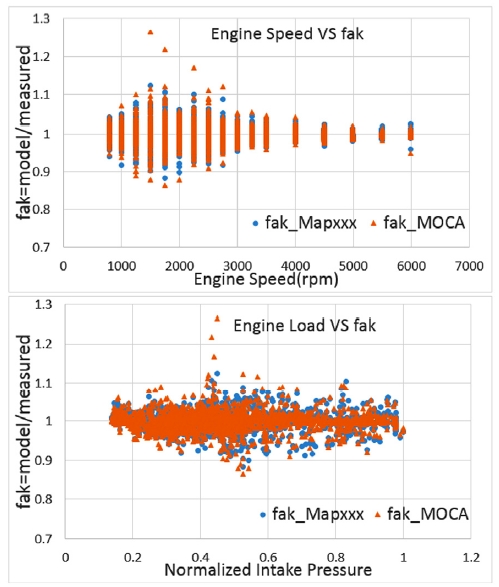
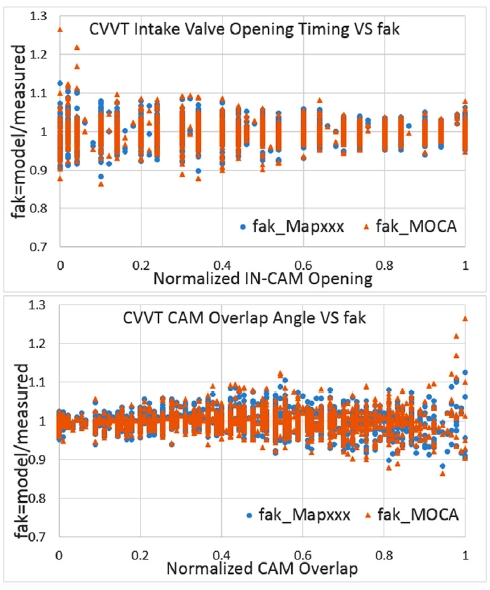
앞서 언급한 바와 같이 MOCA에 의한 자동최적화는 모델 타입에 따른 결과의 동일성 및 PC 계산시간을 고려, 공식코딩 모델로 최적화 수행하여 결과를 도출하였다. Fig. 9(a),(b)를 보면 실측 rlmeasured 대비 모델 rlmodel 결과는 5 % 오차 범위 내에 97 %에 해당하는 측정데이터 개수가 분포하고, 전체 데이터에 대한 RMSE 2.2259, R2 0.9969로서 MAPxxx에 의한 자동최적화 결과와 유사하거나 더 나은 결과를 얻을 수 있었다. Fig. 10(a)는 엔진회전수 및 엔진부하, Fig. 10(b)는 CVVT 캠 작동 영역에 대한 툴 간 오차 비교 그래프이다. 전체 운전영역에서 MOCA에 의한 자동최적화 결과가 보쉬 내부용 툴 MAPxxx에 의한 자동최적화 결과와 대동소이함을 나타냈다.
Optimum result by MOCA - modeled VS measured
Optimum result by MOCA - error histogram
Error comparison over engine speed and load
Error comparison over CVVT CAM (IVO, Overlap)
하지만 일부 영역에서는 MAPxxx 결과 대비, MOCA에 의한 모델 rl_MOCA과 실측 rlmeasured이 다소 큰 오차를 보였다. 캠 오버랩이 많은 중속의 스로틀 천이 영역에서 오차가 크게 발생하였는데, 파라미터의 평활인자(Smoothness factor)에 기인하였다.
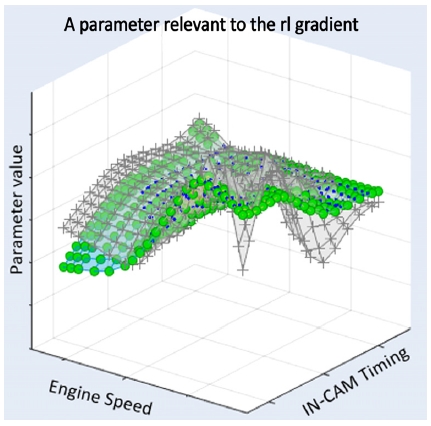
MOCA에서는 파라미터의 교점 간 곡률 정도를 나타내는 평활인자를 정의하여 각 파라미터마다 이를 조절할 수 있는 옵션이 있다. 오차가 큰 영역의 파라미터 평활인자가 완만하게 설정되어 교점간 곡률을 급격하게 조절하여 오차를 줄이는 방향으로의 최적화 제한조건이 있었기 때문에 오차가 다소 발생하였다. 이를 개선하기 위해 MOCA에서 2차원 커브 및 3차원 테이블 형태의 파라미터에 대한 평활인자를 급격하게 조정할 수 있도록 설정 변경하여 해당 영역의 오차를 줄일 수 있었으나, 이와 같이 설정하면 파라미터 형상 왜도가 나빠지게 된다. 왜도가 좋지 못한 최적화 파라미터는 엔진간 편차를 고려하였을 때 양산 ECU에 쉽게 적용하기 어렵기 때문에, 최종 최적화 결과는 Fig. 11과 같이 rl 오차와 도출된 파라미터의 왜도 및 형상을 고려하여 결정하였다.
Feature of an optimized parameter by MOCA and MAPxxx; green circle by MOCA, gray cross by MAPxxx
4. 결 론
- 1) 가솔린엔진제어기 공기량결정함수 제어로직을 시뮬링크, FMU, MOCA의 공식코딩 모델 타입으로 각각 작성하였으며, 세 가지 모델 타입간 모델 출력의 동일성 검증 및 ECU 제어로직과의 일치성을 검증하였다.
- 2) MOCA를 통해 가솔린엔진제어기 공기량결정함수에 대한 시뮬레이션 환경을 구축함으로써, ECU가 없는 PC 환경에서 다양한 운전 조건의 입력 데이터 및 파라미터 데이터 변경을 통해 ECU에 의해 연산되는 공기량결정함수의 모델 rlmodel을 시뮬레이션 할 수 있었다.
- 3) MOCA를 이용한 가솔린엔진제어기 공기량결정함수 자동최적화 매핑을 수행하여, 공급자 내부용 자동최적화 매핑 툴을 사용하여 도출한 결과와 유사한 수준의 최적화 결과를 얻을 수 있었다.
- 4) 자동최적화 과정에서 경계조건, 평활인자와 같은 옵션 및 파라미터 최적화 순서 설정 등에 따라 결과가 달라질 수 있으므로, 최적화 수행 시 이에 대한 고려가 수반되어야 수준 높은 자동최적화 매핑이 가능하다.
- 5) MOCA를 통한 공기량결정함수 자동최적화가 가능하게 되어, 자동차제조사는 공급자가 제공하지 않는 내부용 파라미터 자동최적화 툴을 대체함으로써 외부 용역비용 절감 및 기술 자립화가 가능하게 되었다.
- 6) 자동차제조사는 엔진 및 차량개발 과정에서 MOCA에 의한 시뮬레이션을 통해 ECU에 적용되는 데이터를 검증함으로써 신뢰성을 확보하고, 자동최적화를 통해 기존 수작업 매핑 대비 개발시간을 단축하여 캘리브레이션 효율성을 증대시킬 수 있게 되었다.
Nomenclature
| ECU : | engine control unit |
| rl : | relative air-charge load, % |
Subscripts
| model : | modeled output |
| measured : | measured output by experiment |
Acknowledgments
본 연구가 진행될 수 있도록 도움을 주신 A 자동차 연구소 관계자 분들께 감사를 드립니다.
References
- C. H. Jo, and K. J. Yoon, “Mapping Optimization of PCV Diesel Engine using DoE Method”, KSAE Fall Conference Proceedings, p362-370, (2005).
- T. Gutjahr, H. Kleinegraeber, and T. Kruse, “Automated Optimization of Physics Based Sensor Models for Embedded Control Systems”, Proceedings of the 2018 Ground Vehicle Systems Engineering and Technology Symposium, Novi, Michigan, (2018).
- D. Woldring, T. Landenfeld, and M. J. Christie, “DI Boost: Application of a High Performance Gasoline Direct Injection Concept”, SAE 2007-01-1410, (2007).
- J. Gerhardt, H. Honninger, and H. Bischof, “A New Approach to Functional and Software Structure for Engine Management Systems - BOSCH ME7”, SAE 980801, (1998).
- Y. H. Kang, and D. H. Choi, “Simulation-based Intake Manifold Runner Length Optimization for Improving Performance, Fuel Consumption and Emission of a Gasoline Engine”, Transactions of KSAE, 18(5), p62-67, (2010).
-
H. Joshua, J. Kelly, H. Hoetzendorfer, N. Keuth, H. Pflueg, T. Winsel, and S. Roeck, “Industrialization of Base Calibration Methods for ECU-functions Exemplary for Air Charge Determination”, SAE 2010-01-0331, (2010).
[https://doi.org/10.4271/2010-01-0331]
