적응형 순항제어 상황에서의 위험도 기반 차선 변경 최적제어 알고리즘에 대한 연구

1. 서 론

최근 세계적으로 자율 주행 자동차에 대한 관심이 높아지면서 ADAS(Advanced Driver Assistance System) 기능에 대한 연구가 활발히 진행 중 이다. 자율주행의 핵심 기능으로 종방향 제어 시스템인 ACC(Adaptive Cruise Control), AEB (Autonomous Emergency Braking control)가 있으며, 횡방향 제어 시스템으로 LKA(Lane Keeping Assistance), LCS(Lane Change System) 같은 기능에 대한 연구가 진행 중이다.^1-12)

또한 국내외 자동차 연구자들은 운전자의 안전과 편의성 향상을 위한 다양한 연구를 진행하고 있다. 특히 주행 중 운전자와 보행자에게 큰 상해로 이어지는 교통사고를 줄이기 위한 센서와 알고리즘들이 개발되어 상용화 되었고, 유럽 연합에서는 2021년 이후 유럽에서 출시되는 모든 신차에 AEB기능을 필수로 지정하기도 할 만큼 그 중요성이 갈수록 높아지고 있다.

통계에 따르면 교통사고 발생건수의 94 %는 운전자의 부주의로 인한 사고이다. 그 중 사고 심각도가 높은 39 % 이상의 사고는 차선변경으로 발생하였고, 대부분의 경우 운전자의 거리판단 미숙으로 발생한 사고라 조사되었다.¹³⁾

차선 변경 시 발생하는 사고를 줄이기 위해 교통 사고율 감소를 위한 LDW(Lane Departure Warning) 시스템 연구가 이루어 졌다. 또한 차선변경을 위한 시스템인 LCS(Lane Change System)와 차선 변경 경로 생성에 대한 연구를 통해 차선을 변경하고자 하는 운전자의 편의성과 안전성 향상을 위한 연구가 진행 되었다.^14-22) 본 연구의 목표 또한 운전자의 편의성과 안전성의 향상이지만 안전도와 위험도를 직접적으로 고려한 제어전략을 제시하고자 한다. 더 나아가 제어 차량만의 안전성뿐 아니라, 주변 차량들과의 영향을 고려한 전략을 제안하고자 한다.

본 연구는 ADAS 의 핵심 기능 중 하나인 차선 변경 시스템(Lane Change System)에 위험도 지표인 TTC(Time To Collision)를 고려한 최적 제어기를 설계, 안정성 향상을 검증하고자 한다. 이를 위해 차량 동역학을 이용한 종 방향 모델과 횡 방향 모델을 적용하였고, 이 모델을 기반으로 최적제어기인 LQR(Linear Quadratic Regulator) 제어기를 설계하였다.^23-26) 설계한 LQR 종방향 제어기(적응형 순항 제어)의 제어요구거리에 종방향 TTC를, 차선 변경을 위한 LQR 제어기의 가중치에는 횡방향 TTC를 반영하였다. 제어 알고리즘을 검증하기 위한 시뮬레이션 환경은 Mathlab/Simulink와 Carsim으로 구성되었다. 본 논문에서 제안하는 최적 차선 변경 알고리즘의 안정성 향상을 확인하기 위해, 동일한 차선 변경 시나리오에서 LQR 제어기를 사용한 경우와 TTC가 반영된 LQR 제어기를 적용한 결과를 비교하였다.

2. 차량 모델

2.1 종방향 동역학 모델링

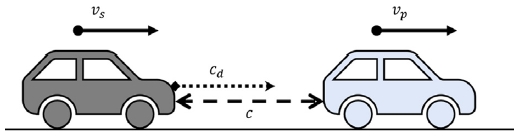
차선 변경 최적 제어기 설계를 위해 적응형 순항 제어에 적용된 종방향 동역학 모델링을 사용하였다.²¹⁾ Fig. 1의 적응형 순항 제어 시스템은 식 (1)의 상태 방정식으로 표현 가능하다. a는 제어차량의 가속도이며, a_p는 전방차량의 가속도이다.^27,28)

Fig. 1

Vehicle longitudinal scheme at ACC situation

$\[ \begin{array}{c}{\dot{x}}_{long}=A_{long}{x}_{long}+B_{long,1}a+B_{long,2}{a}_p\hfill \\ =\left[\begin{array}{cc}0& -1\\ 0& 0\end{array}\right]x+\left[\begin{array}{c}0\\ -1\end{array}\right]u+\left[\begin{array}{c}\tau \\ 1\end{array}\right]a_p\hfill \end{array} \]$

(1)

이때, 상태 변수 x_long는 식 (2) 로, c는 제어차량의 레이더를 통해 측정한 전방차량과의 상대거리이며 v_s는 제어차량의 속도, v_p는 전방차량의 속도이다.

$\[ x_{long}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}{c}_d-c\\ v_p-v_s\end{array}\right] \]$

(2)

식 (3)의 c_d 는 전방차량의 추종을 위한 종방향 요구 상대거리로 안전 제동거리인 c₀와 Time gap τ, v_p로 구성된다.

$\[ c_d=c_0+\tau v_p \]$

(3)

2.2 횡방향 동역학 모델링

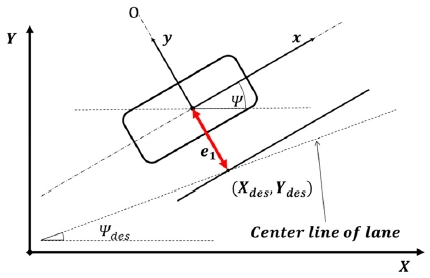
식 (4)의 횡방향 상태 방정식 모델링을 위해 Fig. 2의 자전거 모델을 사용하였고, 식 (5)의 상태변수 x_lat로 구성하였다. 상태 변수의 y_e는 횡방향 거리 오차, $$ {\dot{y}}_e$$는 횡방향 속도 오차, ψ_e는 요각 오차, $$ {\dot{\psi }}_e$$는 요레이트 오차이다.^27,29)

Fig. 2

Vehicle lateral scheme with bicycle model

$\[ {\dot{x}}_{lat}=A_{lat}{x}_{lat}+B_{lat,1}\delta +B_{lat,2}{\dot{\psi }}_{des} \]$

(4)

$\[ x_{lat}={\left[x_3{x}_4{x}_5{x}_6\right]}^T={\left[y_e{\dot{y}}_e{\psi }_e{\dot{\psi }}_e\right]}^T \]$

(5)

$\[ \begin{array}{c}{A}_{lat}=\hfill \\ \left[\begin{array}{cccc}0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & -\frac{2C_{\alpha f}+2C_{\alpha r}}{m{v}_s}\hfill & \frac{2C_{\alpha f}+2C_{\alpha r}}{m}\hfill & \frac{-2l_f{C}_{\alpha f}+2{l_{r}C}_{\alpha r}}{m{v}_s}\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & -\frac{2{l_{f}C}_{\alpha f}-2l_r{C}_{\alpha r}}{I_z{v}_s}\hfill & \frac{2{l_{f}C}_{\alpha f}-2l_r{C}_{\alpha r}}{I_z}\hfill & -\frac{2{l_f^{2}C}_{\alpha f}+2l_r^2{C}_{\alpha r}}{I_z{v}_s}\hfill \end{array}\right]\hfill \end{array} \]$

$\[ B_{lat,1}=\left[\begin{array}{c}0\\ \frac{2C_{\alpha f}}{m}\\ 0\\ \frac{2l_f{C}_{\alpha f}}{I_z}\end{array}\right] \]$

$\[ B_{lat,2}=\left[\begin{array}{c}0\\ -v_s-\frac{2C_{\alpha f}{l}_f-2C_{\alpha r}{l}_r}{m{v}_s}\\ 0\\ -\frac{2C_{\alpha f}{l}_f^2-2C_{\alpha r}{l}_r^2}{I_z{v}_s}\end{array}\right] \]$

상태방정식에서 C_αf와 C_αr은 각각 전륜과 후륜 타이어의 코너링 강성이고, l_f와 l_r은 차량 무게 중심으로부터 전륜과 후륜의 휠베이스까지의 길이, δ는 조향각이며 m은 차량 무게, I_z는 차량 관성 모멘트이다.

3. 차선 변경 알고리즘

3.1 차선 변경 경로

현재까지 진행된 차선 변경 시스템 연구에서 차선 변경 경로 생성을 위한 연구가 활발해왔고, 다양한 방법을 적용한 차선 변경 경로가 제안되어 왔다. 하지만 본 연구는 목적은 효율적이고 안정적인 차선 변경 경로 생성이 아닌 차선 변경 시 위험도를 고려한 상위 제어 알고리즘의 개발이므로, 결과 비교의 편리를 위해 단순화된 차선 변경 경로를 적용하고자 하였다.

$\[ y_{des}\left(t\right)=Road Width\times \frac{2}{\pi }arctan\left(t\right) \]$

(6)

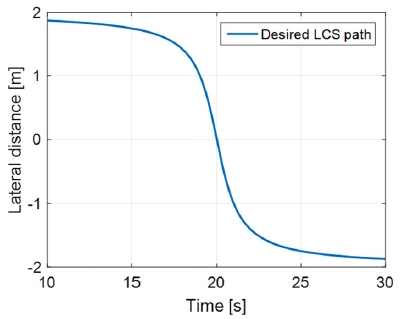
Fig. 3은 제어차량의 LCS 제어기에 입력되는 차선 변경 지령을 보여준다. 이는 식 (6)의 삼각함수와 도로 폭 파라미터를 사용하여 생성한 단순화된 차선 변경 경로이다.

Fig. 3

Simplified lane change path

3.3 TTC를 고려한 차선 변경 LQR 제어기

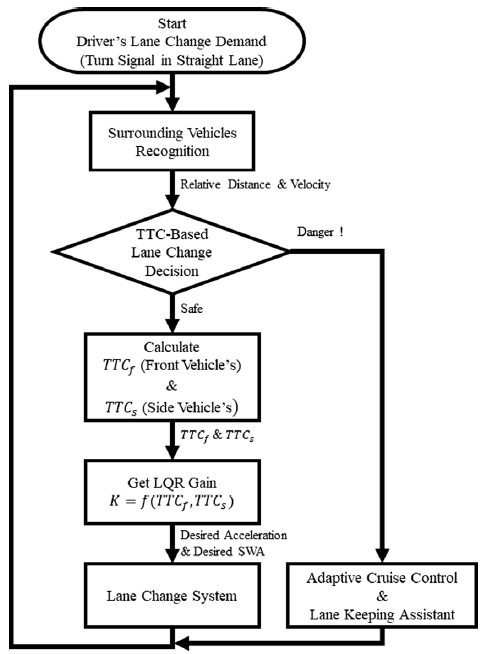
Fig. 4의 그림은 본 논문에서 제안하는 TTC를 고려한 차선 변경 제어 시스템의 순서도를 보여준다. 운전자 혹은 자율 주행자동차의 차선 변경 요구를 시작으로 주변차량(전방차량, 측방차량)을 인지, 위치와 속도 데이터를 취득한다. 취득한 데이터를 사용, 주변차량들과의 TTC를 계산하여, 차선 변경이 가능한 상황인지 판단한다. 차선변경이 가능한 경우, TTC를 적용한 LQR 제어를 통해 전방차량과 측방차량으로부터 더욱 안전하게 차선을 변경하게 된다.

$\[ TTC=\frac{d_r}{v_r} \]$

(18)

Fig. 4

TTC-based lane change system flowchart

이때, 식 (18)에 사용된 d_r과 v_r은 각각 식 (19), (20)이다. d_{r, i}는 i 방향의 상대거리, v_{r, i}는 i 방향의 상대속도이다.

$\[ d_r=\sqrt{{d_{r,x}}^2+{d_{r,y}}^2} \]$

(19)

$\[ v_r=\sqrt{{v_{r,x}}^2+{v_{r,y}}^2} \]$

(20)

3.3.1 종방향 위험도 제어

위험도 기반 차선 변경 제어에서는 3.2에서 설명했던 종방향 LQR 제어기의 상태변수를 변형하여 전방차량과의 위험도를 고려하고자 하였다. 이를 위해 식 (3)의 종방향 요구 상대거리 대신 종방향 위험도(TTC_f)가 고려된 식 (21)을 적용하였다.

$\[ c_{lcs}=c_0+{\tau }_{lcs}{ v}_p \]$

(21)

$\[ {\tau }_{lcs}=\tau \left(1+1/TT{C}_f\right) \]$

(22)

식 (21)에서 τ대신 사용된 식 (22)의 τ_lcs는 종방향의 위험도가 증가할수록 TTC_f가 감소하고, 결과적으로, 차선 변경 제어 시 종방향 요구 상대거리 c_lcs가 증가하게 된다. 이를 통해 차선 변경 시 전방 차량과의 안전성을 향상 시킬 수 있게 된다.

3.3.2 횡방향 위험도 제어

반면, 횡방향의 위험도를 고려한 차선 변경 최적 제어기의 설계를 위해서 3.2에서 사용한 식 (7)의 상태방정식을 사용하되, 위험도를 고려한 가치함수를 사용하였다. 위험도 인자인 TTC를 고려하여 더욱 안전한 최적제어기를 설계하기 위해, 식 (10)의 가중치 Q 대신 횡방향 위험도 (TTC_s)가 고려된 식 (23)의 Q_lcs를 적용하였다.

$\[ Q_{lcs}=\left[\begin{array}{cc}{Q}_{2\times 2}& 0\\ 0& Q_{4\times 4}TT{C}_s\end{array}\right] \]$

(23)

따라서 식 (12)의 가치함수 대신 식 (24)의 TTC가 고려된 가치함수를 횡방향 제어기에 반영하였다.

$\[ \begin{array}{c}{J}_{lcs}=\hfill \\ {\int }_0^{\infty }\left(x_{lat}{\left(t\right)}^T\left(Q_{4\times 4}TT{C}_s\right)x_{lat}\left(t\right)+\cdots \right)dt\hfill \end{array} \]$

(24)

측방차량과의 위험도가 커질수록 TTC_s는 0에 가깝게 감소한다. 이에 따라 가치함수에 적용되는 Q_lcs의 횡방향 제어 가중치(Q_4×4TTC_s) 또한 줄어들게 된다. 즉, 측방차량과의 위험도가 높아질수록, 차선변경 제어의 가중치가 감소한다. 따라서 Fig. 3의 차선 변경 경로를 비교적 느리게 추종하여 차선 변경을 수행하고 종방향 제어 성능에 더욱 가중치를 주어 제어를 한다.

3.3.1과 3.3.2에서 설명한 τ_lcs와 Q_lcs를 적용, 3.1의 최적제어기 설계 과정을 거쳐 만들어진 TTC를 고려한 차선 변경 LQR 제어기는 식 (25)으로 정리, 적용된다.

$\[ \left\{\begin{array}{l}{a}_{lcs}=-K_1\left(c_{lcs}-c\right)-K_2\begin{array}{l}\left(v_p-v_s\right)\\ \left(using Q_{lcs}\right)\end{array}\\ \begin{array}{cc}{\delta }_{lcs}=-\sum _{j=3}^6{K}_j{x}_j& \left(using Q_{lcs}\right)\end{array}\end{array}\right. \]$

(25)

본 논문에서 고려한 위험도는 제어차량과 주변차량들의 거동에 따라 실시간으로 변하는 값이다. 위험도에 따라 달라지는 LQR 제어 이득을 제어기에 적용하기 위해서 제어이득 K는 실시간으로 연산되어야 한다. 하지만 LQR 제어기는 역방향 연산을 통해 계산되므로 제어기 적용의 편리를 위해 제어기 이득을 오프라인으로 미리 계산하여 적용하였다.

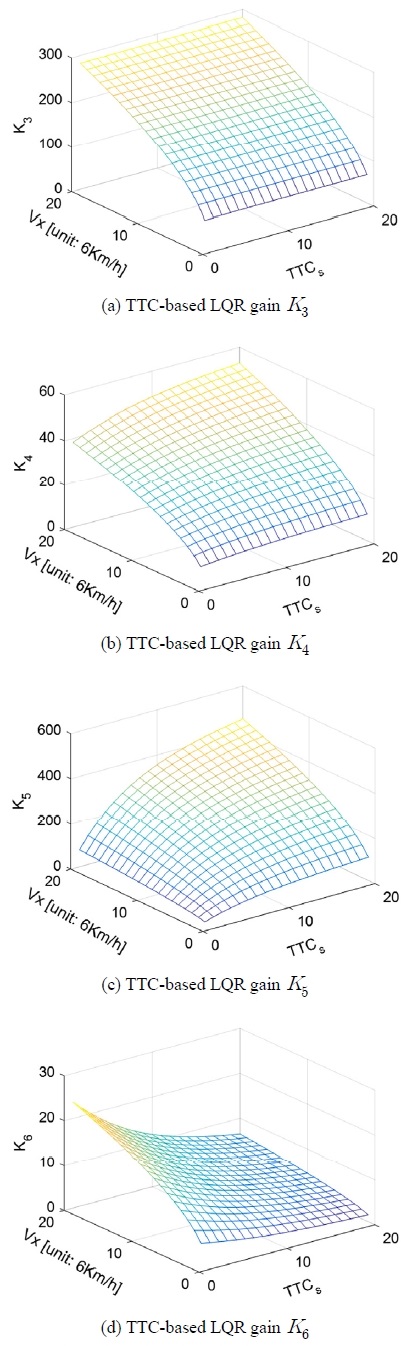
위험도의 변화에 영향을 받지 않는 종방향 제어 이득 K₁과 K₂은 상수로 계산되므로, 이를 제어기에 직접 반영하였다. 반면, 횡방향 위험도와 제어 차량의 속도에 영향을 받는 횡방향 제어기 이득 K₃∼K₆은 Fig. 5(a) ~ (d)의 3-D Map으로 구성, 시뮬레이션 검증에서는 Matlab/Simulink의 Look-up table을 사용하여 제어기에 적용하였다.

Fig. 5

TTC-based LQR controller gain map

4. 주행 시나리오 및 시뮬레이션 결과

4.1 주행 시나리오 및 시뮬레이션 구성

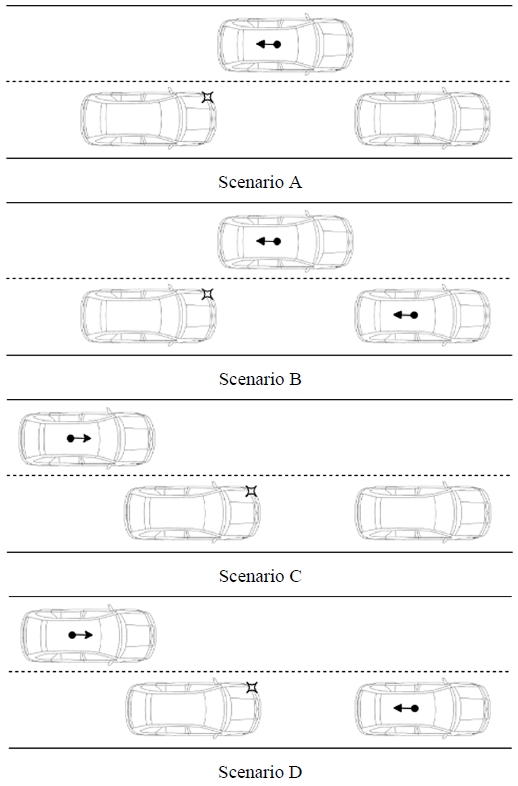
위험도 기반 차선 변경 최적 제어기를 검증하기 위해 직선 도로위에서 Fig. 6의 네 가지 차선 변경 시나리오를 고려하였다. 시나리오 모두 제어차량의 관점에서 위험도를 높이는 주행을 하는 경우이다. 즉, 제어차량의 위치를 기준으로 가까워지는 주행을 하는 경우들이다. 시나리오A는 주행 중 측방차량이 전방에서 감속하면서 제어차량에 접근하고, 시나리오B는 전방차량과 함께 측방 차량이 감속하며 제어차량에 접근하는 경우이다. 시나리오C는 후방에서 측방차량이 가속하며 접근하는 경우, 시나리오D는 C의 상황에서 전방차량이 감속하며 접근하는 경우를 보여준다. Fig. 6의 네가지 상황 모두 차선변경 시 위험한 상황을 모의하고 있으나, 시나리오B는 전방 거리와 측방 거리 모두 여유를 주고 있지 않으므로 차선변경을 하지 않는 것이 합리적인 판단이 될 것이다. 반면 시나리오D는 시나리오B와 마찬가지로 종방향, 횡방향 위험도가 모두 높아지겠으나, 빠른 차선변경을 통해 위험도를 낮출 수 있을 것이다. 따라서 일반적인 상황에서의 위험도를 모의하는 시나리오A와 C를 사용하여 시뮬레이션을 진행하였다. 또한 종, 횡방향 위험도가 모두 높은 시나리오D는 악의 주행 시나리오로 간주하여 추가 검증하였다.

Fig. 6

Vehicle driving scenarios for lane change

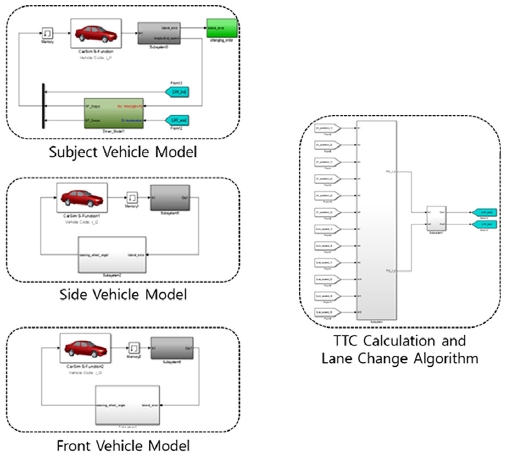
시뮬레이션 검증을 위해 Fig. 7과 같이 제어차량과 주변 차량을 차량 동역학 프로그램인 Carsim을 사용하여 구성하였고, 결과 검증의 편의를 위해 측방 차량 모델과 전방 차량 모델은 차선과 시나리오의 속도 프로파일을 추종하도록 제어기를 구성하였다. 또한 TTC 계산 및 차선 변경 판단을 위한 알고리즘, 차선 변경 제어기를 Matlab/Simulink로 구성하였다. 높은 위험도에서의 시뮬레이션 결과 비교를 위해 Fig. 4의 위험도 기반 차선 변경 판단 과정(TTC-based lane change decision)은 본 논문의 시뮬레이션에서 고려하지 않도록 하였다.

Fig. 7

Simulation configuration (Simulink & Carsim)

시뮬레이션 구현을 위해 Mathworks社의 Matlab 2015b 32bit 버전과 Mechanical Simulation社의 Carsim 8.0 버전을 사용하였다.

본 논문에서 제안하는 위험도 기반 최적 제어기를 사용하였을 때, 제어기에서 고려하고자 한 지표인 위험도가 감소되는지 시뮬레이션을 통해 확인하고자 하였다. 동일한 차선 변경 경로를 인가할 때, 차선 변경 경로를 추종하는 일반적인 LQR 제어기의 결과와 논문에서 제시한 위험도 기반 LQR 제어기의 시뮬레이션 결과를 비교하기 위해 각 차량의 속도와 횡방향 이동 거리, 종방향 위험도, 횡방향 위험도를 비교 하였다. 각각의 위험도는 효과적인 분석을 위해 위험도의 역수인 TTC^-1 (inversed TTC)로 계산, 분석하였다.

4.2 시뮬레이션 결과

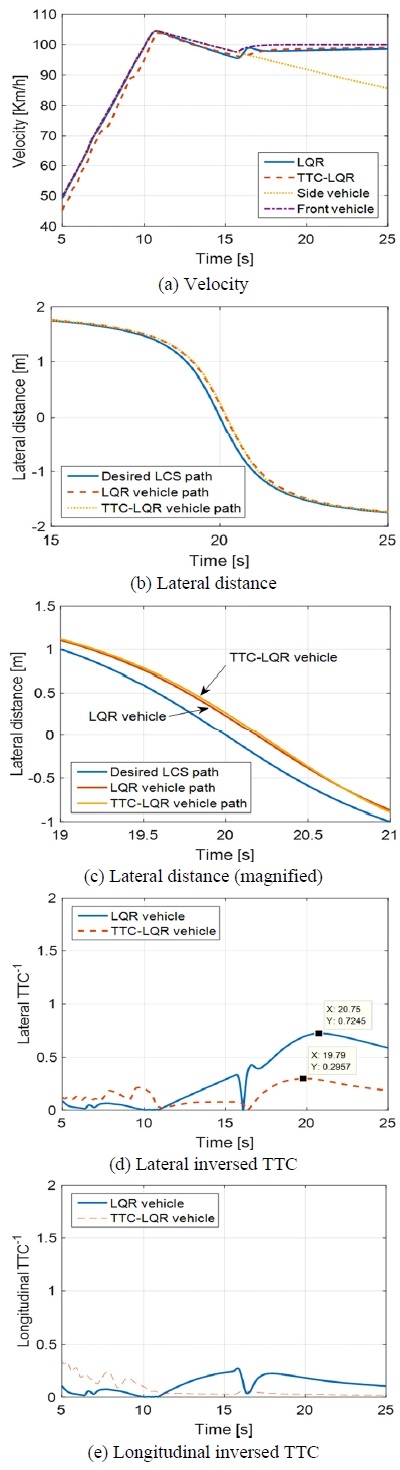
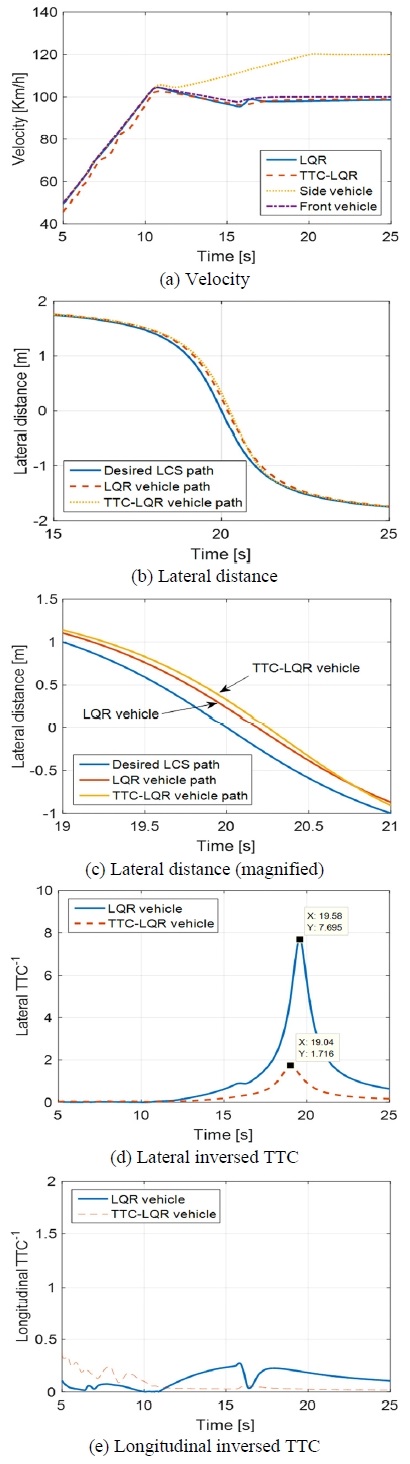
Fig. 8 ~ Fig. 10의 결과에서 (a)는 차량 속도, (b)는 횡방향 이동거리, (d)는 횡방향 위험도, (e)는 종방향 위험도를 보여준다. 시뮬레이션 결과 중 횡방향 이동거리는 근소한 차이를 보기 쉽도록 (c)에 확대하여 추가하였다.

Fig. 8

Simulation result of scenario A

Fig. 8(a)는 측방 차량이 전방에서 감속하여 접근하는 시나리오A의 차량 속도이다. 이때 (b)와 (c)에서 확인할 수 있듯, LQR 제어 차량과 TTC 기반 LQR 제어 차량 모두 성공적으로 차선을 변경했지만 횡방향 이동거리는 큰 차이가 없었다. 이는 (d), (e)의 TTC^-1에서 볼 수 있듯, 시나리오의 종방향, 횡방향 위험도가 1 이하의 수치로 매우 낮았기 때문이다. 특히 종방향 위험도의 경우, 0에 가까운 수준인데, 이것은, 차량 모델링 및 제어기 설계에서 적응형 순항 제어가 고려되었기 때문이다. 또한 16 s에서 종, 횡방향 위험도가 매우 낮아지는 경향을 보였다. 이 또한 적응형 순항 제어의 영향으로 전방차량과의 거리 유지를 위해 제어 차량이 감속하였기 때문이다.

시나리오C의 횡방향 위험도는 시나리오A보다 높았다. 이는 앞서 설명하였듯, 종방향 제어를 통해 제어차량이 감속하였고, 후방에서 가속하는 측방차량에 대한 위험도가 높아졌기 때문이다. 이러한 이유로 시나리오C의 시뮬레이션 결과는 Fig. 9(c) 횡방향 이동거리에서 Fig. 8와는 조금 다른 차이를 보였다. 위험도 기반 최적 제어기를 적용 한 경우, 차선 변경 지령을 20.76 s 전까지 따라가지 못하고, 20.76 s가 돼서야 LQR 제어 차량을 따라잡고, 그 이후 지령을 더 잘 추종함을 확인하였다. 이는 매우 근소한 차이 이지만 제어차량이 100 Km/h로 주행하고 있음을 고려 할 때, 이 차이가 위험도에 미치는 영향은 결코 무시할 수 없을 것이다. 이 결과는 위험도 기반 최적제어기가 횡방향 위험도를 반영하여 위험도가 클 때 차선 변경의 속도를 늦추었고, 마찬가지로 위험도가 낮아졌을 때 차선 변경을 서둘렀음을 보여준다. 결과적으로 위험도 기반 최적 차선 변경 제어기를 통해 차선 변경 수행과 동시에 (d)의 횡방향 위험도가 77.70 % 감소됨을 확인하였다.

Fig. 9

Simulation result of scenario C

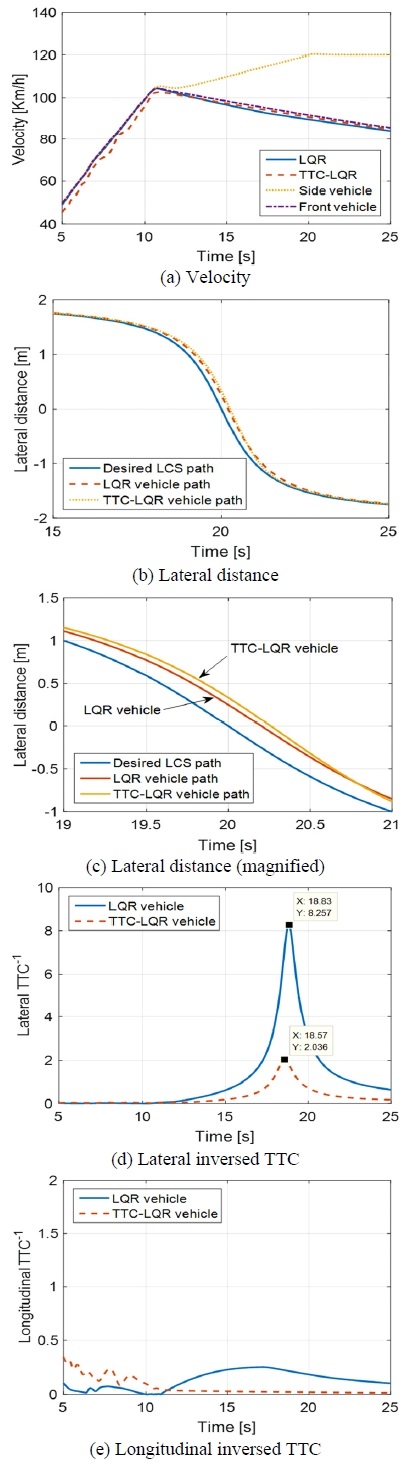
본 논문의 시뮬레이션에서 악의 주행 시나리오로 고려된 시나리오D의 결과는 Fig. 10이다. 시나리오D는 시나리오C 처럼 측방 차량이 후방에서 가속하며 접근하지만, 전방차량이 등속주행이 아닌 감속한다는 차이가 있다. 횡방향 위험도는 시나리오C보다 조금 더 높은 경향을 보였는데, 전방차량과의 거리를 유지하는 적응형 순항 제어의 영향으로 제어차량이 감속하게 되면서 반대로 측방차량과의 위험도가 상승하였기 때문이다.

Fig. 10

Simulation result of scenario D

Fig. 10(d)의 결과를 통해 위험도가 가장 높은 악의 주행 시나리오에서 또한 위험도 기반 최적 차선 변경 제어를 통해 위험도를 큰 폭으로 감소시킬 수 있음을 확인하였다.

위험도 기반 최적 제어기를 시뮬레이션을 통해 검증하였고, Fig. 8 ~ Fig.10의 결과를 확인하였다. 시뮬레이션 검증에서는 Fig. 6에서 고려한 4개의 시나리오 중 3개의 시나리오를 사용하였다. 최적 제어기 설계 시 고려한 종방향 동역학 모델링에서 적응형 순항 제어의 요구거리가 고려되었기 때문에 시나리오에서 위험도가 높지 않았지만, TTC 기반 최적 차선 변경 제어기를 적용하여 종방향 위험도가 더욱 감소되는 경향을 보였다. 위험도 기반 최적 차선 변경 제어기는 횡방향 위험도 감소에 더욱 효과적이었다. 위험도 기반 최적 차선 변경 제어기를 사용한 결과, 각각의 시나리오에서 위험도를 고려한 제어전략을 통해 차선 변경 시 Table 1과 같이 제어차량의 횡방향 위험도의 최대값이 큰 폭으로 감소됨을 확인하였다.

Table 1

Comparison of maximum inversed lateral TTC

5. 결 론

본 논문에서는 자율 주행 기능과 ADAS의 핵심 기능인 차선 변경 제어 시스템에 위험도를 고려한 최적제어 전략을 제안하였다. 차선 변경 경로가 주어졌을 때, 최적제어의 가치함수로 위험도 지표인 TTC를 고려한 LQR제어기를 설계하였다. 이를 위해 주변차량을 고려한 종방향, 횡방향 상태방정식 모델을 사용하여 TTC를 고려하지 않은 LQR 차선 변경 제어기와 TTC를 고려한 위험도 기반 LQR 제어기를 설계하였고, Matlab/Simulink와 차량 동역학 시뮬레이터 Carsim을 사용하여 차량 모델과 제어기를 구성하였다. 위험도를 고려한 최적 제어기의 성능을 검증하기 위해 논문에서 제시한 4개의 시나리오 중 3개의 차선변경 시나리오에서 시뮬레이션을 수행, 그 결과를 분석하였다. 횡방향 위험도가 급격하게 높아지는 시나리오에서 위험도를 고려한 제어차량은 종방향, 횡방향의 위험도를 최소화 하는 방향으로 차선변경을 수행하였고, 높은 수준의 안전도 향상을 확인할 수 있었다.

Acknowledgments

본 연구는 산업 통상 자원부 산업핵심기술개발 사업 “ADAS의 시험 평가를 위한 실차 시험용 가상 주행 환경구현 및 차량 주행 동기화 장치 개발기술 개발 (10052501)” 과제의 지원으로 수행되었음.

References

• G. Marsden, M. Mcdonald, and M. Brackstone, “Towards an Understanding of Adaptive Cruise Control”, Transportation Research Part C: Emerging Technologies, 9(1), p33-51, (2001). [https://doi.org/10.1016/s0968-090x(00)00022-x]
• S. Kim, M. Tomizuka, and K. Cheng, “Smooth Motion Control of the Adaptive Cruise Control System by a Virtual Lead Vehicle”, Int. J. Automotive Technology, 13(1), p77-85, (2012). [https://doi.org/10.1007/s12239-012-0007-6]
• H. Kim, K. Shin, I. Chang, and K. Huh, “Autonomous Emergency Braking Considering Road Slope and Friction Coefficient”, Int. J. Automotive Technology, 19(6), p1013-1022, (2018). [https://doi.org/10.1007/s12239-018-0098-9]
• J. B. Cicchino, “Effectiveness of Forward Collision Warning and Autonomous Emergency Braking Systems in Reducing Front-To-Rear Crash Rates”, Accident Analysis and Prevention, 99(Part A), p142-152, (2017). [https://doi.org/10.1016/j.aap.2016.11.009]
• N. Kim, J. Lee, M. Soh, J. Kwon, T. Hong, and K. Park, “Improvement of Longitudinal Safety System’s Performance on Near Cut-In Situation by Using the V2V”, KSAE Annual Conference Proceedings, p747-755, (2013).
• C. Moon, Y. Lee, C. Jeong, and S. Choi, “Investigation of Objective Parameters for Acceptance Evaluation of Automatic Lane Change System”, Int. J. Automotive Technology, 19(1), p179-190, (2018). [https://doi.org/10.1007/s12239-018-0017-0]
• J. Ryu, and J. Kim, “A Lane-change Collision Avoidance Algorithm for Autonomous Vehicles and HILS (Hardware-In-the-Loop Simulation) Test”, Trans actions of KSAE, 7(5), p240-248, (1999).
• T. Jeong, and K. Yi, “Lane Change Algorithm for Collision Avoidance for Vehicle Intelligent Cruise Control Systems”, KSME Annual Conference Proceedings, p865-870, (2002).
• K. I. Ahmed, Modeling Drivers’ Acceleration and Lane Changing Behavior, Ph. D. Dissertation, Bangladesh University of Eng. and Technology, Dhaka, (1999).
• O. Mokhiamar, and M. Abe, “Combined Lateral Force and Yaw Moment Control to Maximize Stability as well as Vehicle Responsiveness during Evasive Maneuvering for Active Vehicle Handling Safety”, Vehicle System Dynamics, 37, p246-256, (2002). [https://doi.org/10.1080/00423114.2002.11666236]
• S. Ulbrich, and M. Maurer, “Towards Tactical Lane Change Behavior Planning for Automated Vehicles”, 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, p989-995, (2015). [https://doi.org/10.1109/itsc.2015.165]
• V. Butakov, and P. Ioannou, “Personalized Driver/Vehicle Lane Change Models for ADAS”, IEEE Transactions on Vehicular Technology, 64(10), p4422-4431, (2015). [https://doi.org/10.1109/tvt.2014.2369522]
• S. You, J. Kim, J. Park, and K. Jhang, “Design of a Longitudinal and Lateral Integrated Lane Change Controller considering Traffic Conditions”, KSAE Annual Conference, p709-710, (2015).
• L. Guo, P. S. Ge, M. Yue, and Y. B. Zhao, “Lane Changing Trajectory Planning and Tracking Controller Design for Intelligent Vehicle Running on Curved Road”, Mathematical Problems in Engineering, 2014, p1-9, (2014). [https://doi.org/10.1155/2014/478573]
• W. Chee, and M. Tomizuka, “Lane Change Maneuver of Automobiles for the Intelligent Vehicle and Highway System (IVHS)”, American Control Conference, p3586-3587, (1994).
• W. Chee, and M. Tomizuka, Vehicle Lane Change Maneuver in Automated Highway Systems Vehicle Lane Change Maneuver in Automated Highway Systems, California Partners for Advanced Transportation Technology, (1994).
• H. Jula, E. B. Kosmatopoulos, and P. A. Ioannou, “Collision Avoidance Analysis for Lane Changing and Merging”, IEEE Transactions on Vehicular Technology, 49(6), p2295-2308, (2000). [https://doi.org/10.1109/25.901899]
• J. Feng, J. Ruan, and Y. Li, “Study on Intelligent Vehicle Lane Change Path Planning and Control Simulation”, 2006 International Conference on Information Acuisition, p683-688, (2006). [https://doi.org/10.1109/icia.2006.305809]
• J. Nilsson, M. Brannstrom, E. Coelingh, and J. Fredriksson, “Lane Change Maneuvers for Automated Vehicles”, IEEE Transactions on Intelligent Transportation Systems, 18(5), p1087-1096, (2017). [https://doi.org/10.1109/tits.2016.2597966]
• J. Lee, C. Kang, W. Kim, and C. Chung, “Risk Assessment for Autonomous Lane Change Systems”, KSAE Spring Conference Proceedings, p527-529, (2015).
• H. Kang, D. Lee, and K. Huh, “Development of Lane Change System considering Acceleration for Collision Avoidance”, Transactions of KSAE, 21(2), p81-86, (2013). [https://doi.org/10.7467/ksae.2013.21.2.081]
• K. Kim, D. Kim, and K. Yi, “Development of Lateral Collision Risk Index”, KSAE Annual Conference Proceedings, p1376-1381, (2012).
• D. Soudbakhsh, and A. Eskandarian, “A Collision Avoidance Steering Controller using Linear Quadratic Regulator”, SAE 2010-01-0459, (2010). [https://doi.org/10.4271/2010-01-0459]
• M. Gidlewski, and D. Żardecki, “Automatic Control of Vehicle Steering System During Lane Change”, 24th International Technical Conference on the Enhanced Safety of Vehicles (ESV), National High-way Traffic Safety Administration, No.15-0106, (2015).
• A. W. Divelbiss, and J. T. Wen, “Trajectory Tracking Control of a Car-trailer System”, IEEE Transactions on Control Systems Technology, 5(3), p269-278, (1997). [https://doi.org/10.1109/87.572125]
• G. A. Dukerman, “Profile-Following Entry Guidance Using Linear Quadratic Regulator Thory”, AIAA Guidance, Navigation, and Control Conference and Exhibit, No.2002-4457, (2002). [https://doi.org/10.2514/6.2002-4457]
• R. Rajamani, Vehicle Dynamics and Control, 2nd Edn., Springer, New York, (2012).
• S. Moon, I. Moon, and K. Yi, “Design, Tuning and Evaluation of a Full-range Adaptive Cuise Control System with Collision Avoidance”, Control Engineering Practice, 17(4), p442-455, (2009). [https://doi.org/10.1016/j.conengprac.2008.09.006]
• M. S. Netto, S. Chaib, and S. Mammar, “Lateral Adaptive Control for Vehicle Lane Keeping”, Proceedings of the 2004 American Control Conference, 3, p2693-2698, (2004).