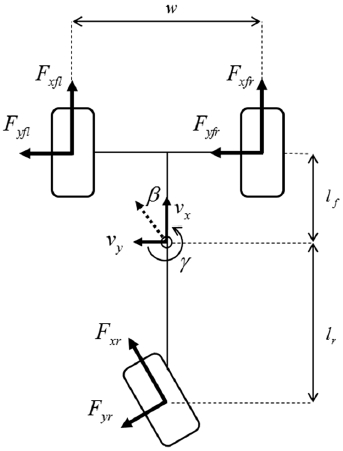
삼륜 전기자동차의 전구간 조향 및 속도 영역 통합 제어 전략

1. 서 론

에너지 및 환경 문제로 인하여 전 세계적으로 자동차 배기가스 및 연비 규제가 강화되고 있다. 이에 따라 친환경 자동차에 대한 연구가 활발히 이루어지고 있다. 다양한 형태의 친환경차량 중 개인용 전기 자동차는 작고 가볍기 때문에 에너지 효율이 좋으며 주차 용이성을 장점으로 갖는다. 이러한 개인용 전기 자동차의 조향 시스템과 바퀴 수 등에 변화를 주어 에너지 효율이 높은 차량 구조에 대한 연구를 수행하여 후륜 조향 및 스키드 조향을 갖는 삼륜 전기 자동차가 제안되었다.¹⁾

Fig. 1

Three-wheeled vehicle model

제안된 삼륜 전기 자동차는 앞바퀴는 독립된 두 개의 인휠 모터로 구성되고 뒷바퀴는 좌 우 90도 회전 가능한 한 개의 조향 모터로 이루어져 있다. 따라서 제안된 삼륜 전기 자동차는 운전자 입력(엑셀/브레이크, 조향 핸들)에 따라 차량의 두 개의 앞바퀴 토크와 뒷바퀴 조향을 결정하기 위한 제어 전략이 필요하다.

제안된 삼륜 전기 자동차의 제어 입력을 결정하기 위한 기존 연구로 두 가지 형태의 제어기가 연구되었다.^2,3) 그 중 하나는 저속에서 Tight turn이 가능한 Kinematic model 기반 제어기이고, 다른 하나는 일반적인 형태인 사륜 차량과의 동특성 차이에 의해 발생하는 운전자 이질감을 줄이기 위한 기준 모델 추종 제어기이다. 하지만, 각각의 제어기는 조향 및 속도 영역이 다르고 서로 다른 구조로 이루어져 있어 두 제어 목표를 이루기 위한 새로운 제어 전략이 요구된다.

본 논문에서는 각 제어기가 기반으로 하는 차량 모델을 상호작용 다중 모델 알고리즘에 적용하여 기존 두 제어 입력의 가중치를 선정하고, 이를 통해 차량의 전 구간 조향 및 속도 범위에서 제어 입력을 결정하였다.

본 논문의 구성은 다음과 같다. 2장에서는 기존 연구를 통해 제안된 Kinematic model 기반 제어기와 기준 모델 추종 제어기를 소개하고, 3장에서는 상호작용 다중 모델을 기반으로 한 제어 전략을 설명한다. 4장에서는 제안한 제어 전략을 상용 소프트웨어 Carsim을 사용한 모의실험 결과를 확인하였다. 마지막으로 5장에서 결론 및 요약을 통해 정리한다.

2. 삼륜 전기자동차의 기존 제어기

2.2 기준 모델 추종 제어기³⁾

제안된 후륜 조향 삼륜 전기자동차의 경우 일반적인 전륜 조향 사륜 자동차와 다르게 후륜 조향에 의한 영향, 뒷바퀴가 하나이기 때문에 발생하는 선회 시 좌 우 바퀴에 인가되는 하중 이동 변화의 의한 영향 등으로 다른 동적 특성을 지닌다. 이러한 동적 특성 차이를 확인하고자 1/5 축소 모형자동차를 이용한 연구가 수행되었다.⁴⁾

동적 특성 차이는 기존의 운전자가 제안된 삼륜 전기자동차를 주행할 경우 이질감을 느낄 수 있다. 이러한 이질감을 고려했을 때, 고속에서 운전자의 불편함을 야기할 수 있다. 따라서 이러한 고속에서의 제안된 후륜 조향 삼륜 전기자동차의 특성이 기존 사륜 자동차를 추종하도록 기준 모델 추종 제어기가 제안되었다.

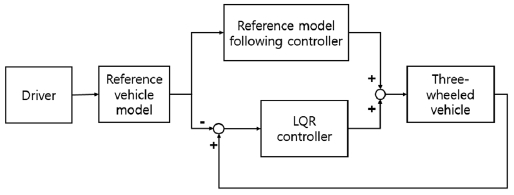
제안된 기준 모델 추종 제어기는 Fig. 2와 같은 구조로 이루어졌다. 기준 모델에 해당하는 사륜 자동차를 Reference로 선정하여 차량의 Body side slip angle과 요 속도(Yaw rate)를 추종하도록 한다. 이 때, 제어기는 Feedforward와 Feedback 으로 구성되고 Feedforward 제어기는 선형화된 타이어 모델을 이용한 삼륜 자동차의 Dynamic model을 사용하여 식 (9), (10)과 같이 차량의 조향 및 토크 분배를 결정한다.

Fig. 2

Reference model following controller

$\[ {\delta }_r=\frac{2C_f+C_r}{C_r}{\beta }_d+\frac{m{V}_x^2+2C_f{l}_f-C_r{l}_r}{C_r{V}_x}{\gamma }_d \]$

(9)

$\[ \Delta T=\frac{2C_{f}l{r}_e}{w}{\beta }_d+\frac{\left(ml{V}_x^2+2C_f{l}_{f}l\right)r_e}{w{V}_x}{\gamma }_d \]$

(10)

Feedback 제어기는 차량의 Body side slip angle과 요 속도(Yaw rate)를 제어 변수로 정하고 이를 LQR controller 를 통해 구성하였다.

3. 통합 제어 전략

기존에 연구된 두 제어기는 서로 다른 목적으로 제안되었기 때문에 제어 입력의 특징 및 구조가 다르다. Kinematic model 기반 제어기는 뒷바퀴가 큰 조향 각도가질 때 적절한 제어 입력을 결정할 수 있지만 기존 사륜 자동차와 다른 동특성 차이로 인한 운전자 이질감을 줄일 수 없다. 반대로 기준 모델 추종 제어기의 경우 기준 모델에 해당하는 사륜 자동차의 상태 변수를 추종하기 때문에 운전자 이질감을 줄일 수 있다. 하지만 조향 범위의 경우 사륜 자동차가 제안된 삼륜 자동차보다 작기 때문에 타이트 턴을 위한 제어 입력을 포함하지 않는다. 따라서 본 논문에서는 두 제어기의 장점과 단점을 상호 보완하는 하나의 통합된 제어 전략을 제안하고자 한다.

3.1 가중치를 이용한 통합 제어 전략

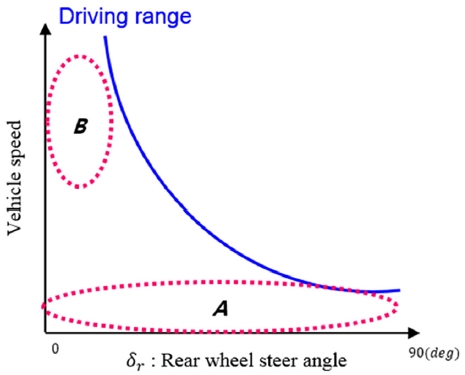
두 제어기를 구성하는 각각의 차량 모델은 Kinematic model과 선형화된 타이어 모델을 적용한 Dynamic model이다. Kinematic model은 저속에서 적합한 차량 모델이고 반대로 Dynamic model은 고속에서 타이어 슬립을 고려했을 때 적합한 차량 모델이다. 그렇기 때문에 제안된 두 제어기가 적합한 차량의 조향 및 속도 영역을 Fig. 3과 같이 나타낼 수 있다. A 영역은 저속영역으로 Kinematic model 기반 제어기가 적합하며, B영역은 Dynamic model을 기반으로 한 기준 모델 추종 제어기가 적합하다.

Fig. 3

Range of steering angle and vehicle speed

기존 두 제어기의 제어 입력은 2장에서와 같이 서로 다른 차량 모델 및 제어 구조로 이루어져 있기 때문에 하나의 제어기를 확장하여 구성하기는 어렵다. 따라서 본 논문에서는 두 제어기에 가중치를 이용하여 다음과 같은 하나의 통합된 제어 입력을 구성하고자 한다.

$\[ u=\mu u_1+\left(1-\mu \right)u_2 \]$

(11)

제어 입력 u은 Kinematic model 기반 제어기의 제어 입력 u₁과 기준 모델 추종 제어기의 제어 입력 u₂에 각각의 가중치 μ, (1-μ)을 곱하여 구성한다. 이 때 가중치를 속도 및 조향에 대한 함수로 구성한다. 예를 들어 차량의 속도가 저속으로 갈수록 Kinematic model 기반 제어기의 가중치를 1이 되도록 구성하면 기준 모델 추종 제어기의 가중치는 0이 되고 제어 입력은 Kinematic model 기반 제어기의 제어 입력이 된다. 반대로 고속에서 Kinematic model 기반 제어기의 가중치를 0이 되도록 구성하면 기준 모델 추종 제어기의 가중치는 1이 되고 제어 입력은 기준 모델 추종 제어기의 제어 입력이 된다. 이와 같이 속도 및 조향에 따른 가중치를 선정하고 이로부터 전 구잔 조향 및 속도 영역에서 통합된 제어 입력을 결정한다.

3.2 제어 입력의 가중치

3.2.1 상호작용 다중 모델

두 제어기의 기반이 되었던 횡방향 차량 모델을 통해 제어 입력의 가중치를 정하고자 하였다. 이를 위해 본 연구에서는 상호작용 다중 모델 방법을 사용하여 차량의 속도 및 조향 상태에 따른 두 모델의 확률을 계산하고 이를 가중치로 사용하고자 한다.

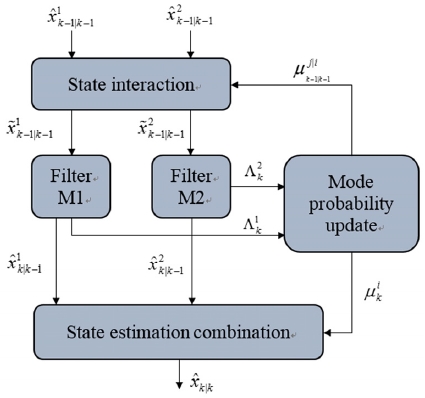
상호작용 다중 모델 방법은 차량 분야에서 위치 정보를 위해 사용되는 GPS, IMU와 같은 측정 장비에서 얻는 측정값의 왜곡을 보상하기 위한 목적으로 사용되었다.^5,6) 상호작용 다중 모델은 크게 Interacting, Filter, Mode probability update로 구분할 수 있다. Fig. 4와 같은 구조로 Interacting을 통해 다중 모델의 이전 State와 Covariance를 예측한다. 그리고 예측된 값을 통해 Mode probability update에서 각 모델의 확률을 계산하고 최종적인 State를 추종한다.⁷⁾ 이 과정에서 각 모델의 확률인 Mode probability를 기반으로 하여 가중치를 결정한다.

Fig. 4

A block diagram of the IMM algorithm

3.2.2 가중치 선정

상호작용 다중 모델의 Mode probability를 통해 가중치를 결정하기 위해 상용 소프트웨어인 Carsim을 사용하여 모의실험을 하였다. 모의실험을 통해 얻은 Mode probability를 기반으로 차량의 속도 및 조향에 따른 가중치를 결정하고자 하였다.

상호작용 다중 모델의 Mode probability는 모델 불확실성을 포함하는 Process noise 크기에 영향을 받는다.⁷⁾ 적절한 크기의 Process noise를 정하는 기준은 Measurement residual로 이용되는 상태 변수인 Body side slip angle이 아닌 오로지 모델을 통해 예측되는 요 속도를 통해 결정한다. 만약 적절한 Process noise 값이 결정되면 모의실험을 통해 출력되는 차량 모델 값과 상호 작용 다중 모델을 통해 추정되는 요 속도 차이가 작게 나타날 것이다.

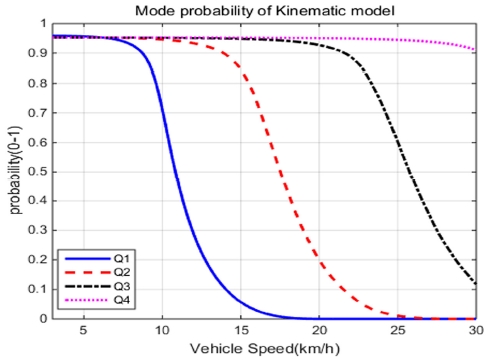
Fig. 5는 뒷바퀴 조향각이 15도로 고정된 상태에서 4개의 서로 다른 Process noise일 때 차량의 속도에 따른 Kinematic model의 Mode probability를 나타낸 그래프이다. Process noise에 따라 Mode probability의 형태가 매우 크게 달라지는 것을 확인할 수 있다.

Fig. 5

Mode probability

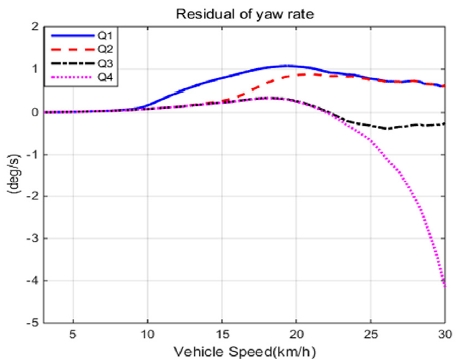
적절한 Process noise를 선정하기 위해 요 속도의 시뮬레이터 차량 모델 값과 상호 작용 다중 모델 값의 차이인 Residual을 비교를 하였다. Fig. 6을 통해 Process noise에 따른 요 속도의 Residual 차이를 확인할 수 있고 이를 평균과 표준편차를 Table 1으로 정리할 수 있다. 따라서 가장 작은 요 속도의 Residual을 갖는 것은 Q₃이기 때문에 Process noise가 Q₃일 때 얻은 Mode probability를 통해 가중치를 결정한다.

Fig. 6

Residual

Table 1

Residual of yaw rate (Mean and Std.)

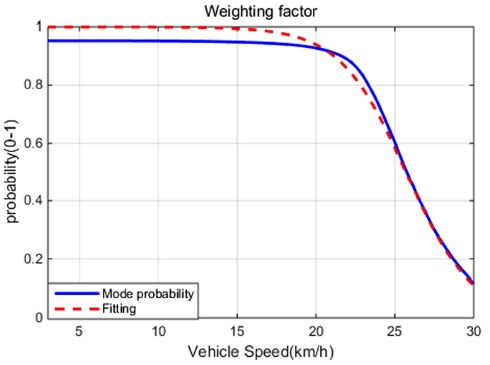
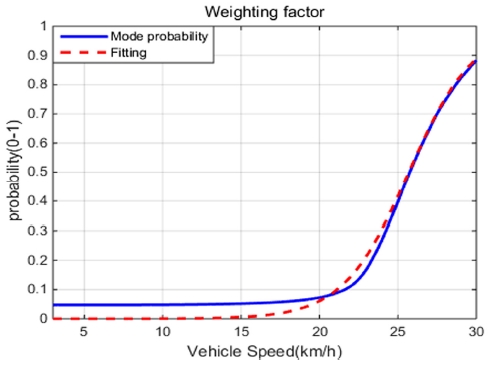
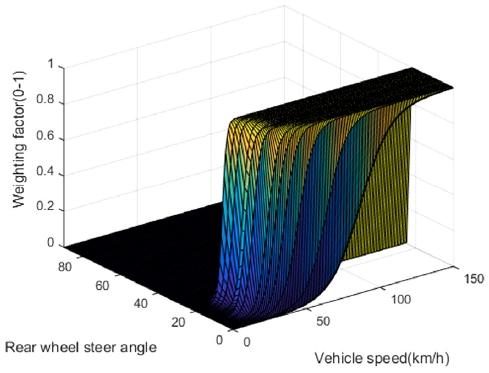
위와 같은 방법을 통해 구한 Mode probability는 그대로 제어 입력의 가중치로 사용할 수 없다. 실제 차량 모델은 모델 불확실성을 포함하기 때문에 속도가 0에 가까운 저속에서 Kinematic model의 Mode probability가 1이 되지 않는다. Fig. 5를 보면 5 km/h이하에서 약 0.95의 크기를 나타낸다. 이러한 차이는 제어 입력의 가중치로 사용하기 때문에 문제를 야기할 수 있다. 본 연구에서 가중치를 적용하는 두 제어기 중 기준 모델 추종 제어기의 경우 Feedback 제어기를 포함하기 때문에 저속에서 작은 크기의 가중치로 인하여 전체 제어 입력이 발산할 수 있다. 그렇기 때문에 Fig. 7~8과 같은 형태로 Curve fitting을 하여 가중치를 결정한다. 이와 같은 방법으로 조향 각에 따른 가중치를 구하여 Fig. 9와 같은 Look-up table로 가중치를 구성하였다.

Fig. 7

Weighting factor of u1 (Fixed rear wheel angle)

Fig. 8

Weighting factor of u2 (Fixed rear wheel angle)

Fig. 9

Weighting factor of u2 (Full range)

4. 모의실험 결과

모의실험은 정속 주행과 가속 주행으로 나누어 진행하였다. 먼저 정속 주행은 저속과 고속 상황을 가정하여 기존 제어기가 목표로 하였던 저속에서 타이트 턴과 고속에서 기준 모델인 사륜 자동차의 거동을 추종하는 것을 확인하고자 한다. 그리고 가속 주행을 통해 속도 및 뒷바퀴 조향이 시간에 따라 변화할 때 가중치를 적용한 제어 입력의 변화를 확인하고자 한다. 이는 상용소프트웨어 시뮬레이터인 Carsim를 사용하여 진행하였다.

4.1 정속 주행 시 기존 제어기와 비교

4.1.1 저속 주행

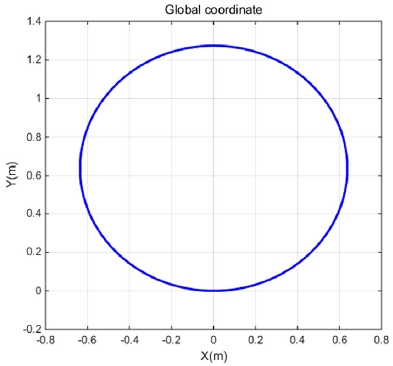
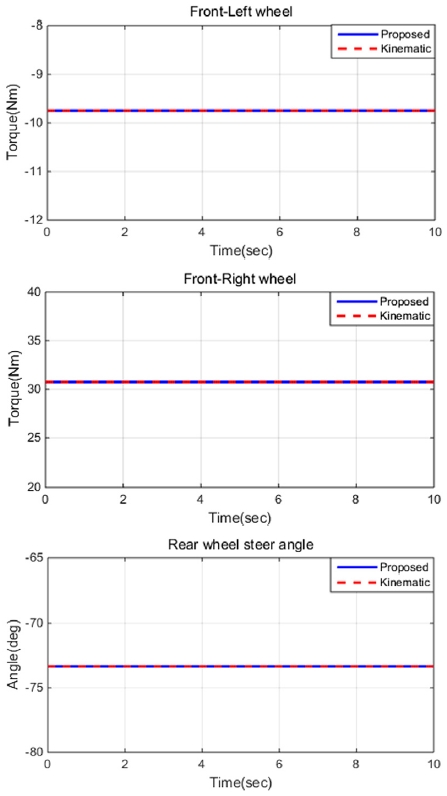
Fig. 10~11은 차량 속도 6 km/h , 조향비 1:1, 스티어링 휠 80도로 일정하게 유지하는 상황에서 차량의 주행 궤적 및 제어 입력 비교 그래프이다.

Fig. 10

Trajectory of vehicle at low speeds (Tight turn)

Fig. 11

Control inputs at low speeds

차량의 주행궤적은 선회 반경이 매우 작은 타이트 턴이 가능함을 확인할 수 있다. 또한, 제어 입력의 경우 기존 Kinematic model 기반 제어기와 동일하게 결정되는 것을 확인할 수 있다.

4.1.2 고속 주행

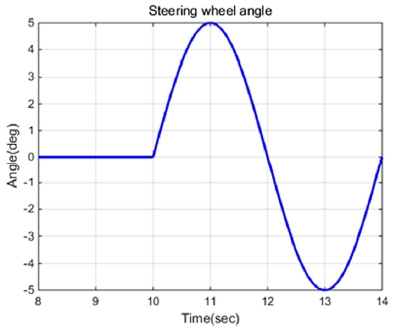
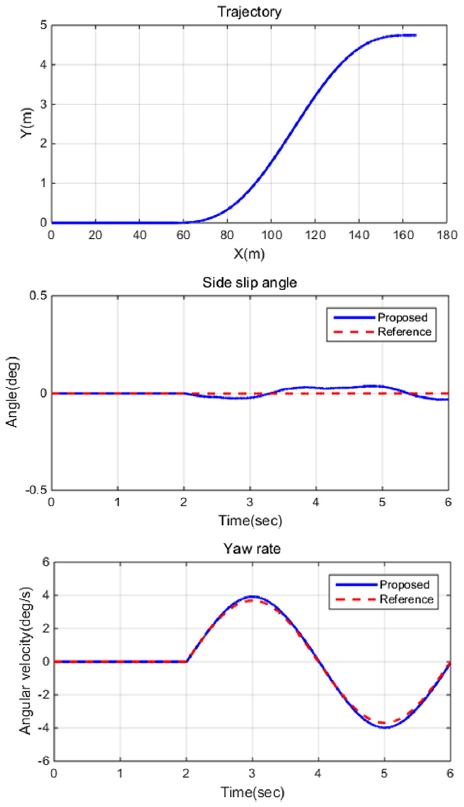
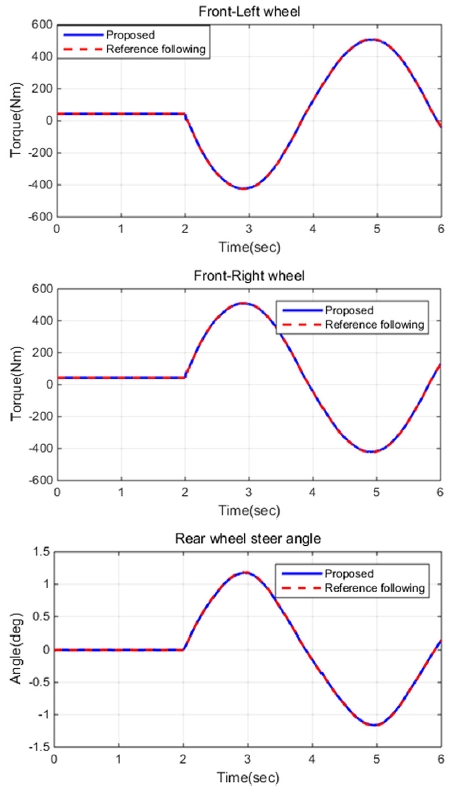
Fig. 13~14는 차량 속도 100 km/h , 조향비 16:1, 스티어링 휠은 Fig. 12와 같이 입력되는 차선 변경 상황에서 차량의 주행 궤적, 상태 변수 및 제어 입력 비교 그래프이다.

Fig. 12

Steering wheel angle

Fig. 13

Trajectory and states (Side slip angle and yaw rate)

Fig. 14

Control inputs at high speeds

제안한 방법을 통해 기준 모델의 상태 변수인 Body side slip angle과 요 속도를 추종하는 것을 확인할 수 있다. 이 때, 완벽한 제어 성능이 나타나지 않는 이유는 삼륜 전기자동차의 하중 이동에 의한 타이어 접지력 한계 때문이다. 기존 기준 모델 추종 제어기와의 제어 입력을 비교하면 동일한 값으로 나타나는 것을 확인할 수 있다.

4.2 가속 주행 시 제어 입력 변화

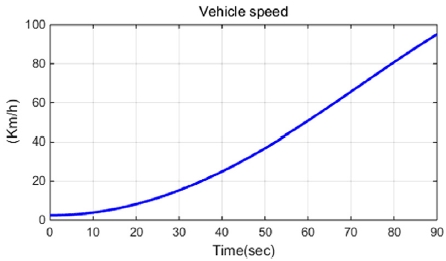
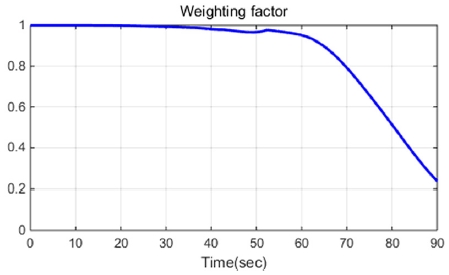
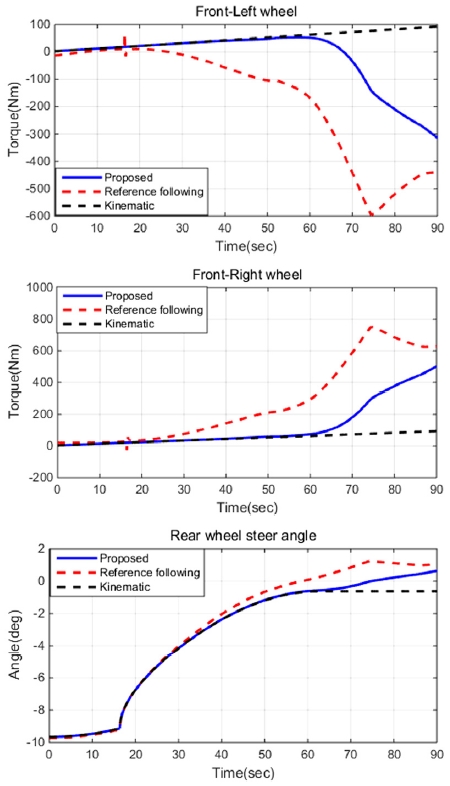
Fig. 16~17은 Fig. 15와 같이 시간에 따라 속도가 증가하고, 스티어링 휠은 10도로 고정됨에 따라 시간에 따른 가중치 변화 및 제어 입력을 나타낸 그래프이다.

Fig. 15

Vehicle speeds

Fig. 16

Weighting factor

Fig. 17

Control inputs

모의실험 결과 속도가 증가함에 따라 제어 입력의 가중치는 Fig. 16과 같이 변화하고 이에 따라 제안된 방법의 제어 입력(Proposed)은 Fig. 17과 같은 형태로 저속 구간에서는 Kinematic 기반 제어기의 입력(Kinematic)을 추종하고 고속으로 갈수록 기준 모델 추종 제어기의 입력(Reference following)을 추종하게 된다. 따라서 가속 주행 시 연속되고 발산되지 않는 결과를 확인할 수 있다.

5. 결 론

본 논문에서는 전 구간 조향 및 속도 영역에서 후륜 조향 및 스키드 조향 시스템을 가진 삼륜 전기자동차의 제어 전략을 제안하고자 하였다.

이를 위해 일반적으로 Estimation을 위해 사용되는 상호 작용 다중 모델(IMM) 방법을 제어 입력에 적용하였다. 상호 작용 다중 모델 방법으로부터 기존 제어기들의 기반이 된 Kinematic model과 Dynamic model의 속도 및 조향 각도에 따른 확률을 구하여 기존 제어기 사이의 가중치로 사용하였다.

상용 소프트웨어인 Carsim을 사용하여 제안한 방법이 정속 주행 시 저속과 고속에서 기존 제어기와 동일한 제어 입력이 갖는지 확인하였다. 또한, 시간에 따라 차량 속력이 변화할 때 제어 입력이 연속적으로 부드럽게 연결되는 것을 확인하였다.

결과적으로 본 연구를 통해 상호작용 다중 모델 방법을 제어 입력 사이의 가중치를 결정하는 방법으로 활용하여 기존에 제안된 두 제어기의 서로 다른 목표인 저속에서 타이트 턴이 가능하고 고속에서 운전자 이질감 감소 및 동일한 거동을 갖는 것을 통시에 만족하는 통합된 제어 전략을 제안하였다.

Acknowledgments

본 연구는 정부의 재원으로 한국연구재단의 지원 (No. 2010-0028680) 및 (No. NRF-2017R1A2B4 006520)을 통해 수행된 연구임.

References

• J. You, Y. Park, and Y. Park, Comparison of Steering and Driving System for a Personal Urban Electric Vehicle: about Power Consumption and Rollover Stability, M. S. Thesis, KAIST, Daejeon, (2012).
• Y. Park, Y. Park, J. Sim, and M. Ryu, Control Method of the Three-wheel Electric Vehicle, KR Patent 10-1597702, Feb., 19), (2016.
• M. Ryu, and Y. Park, Implementation of Reference Model Following Control to the Scale-down Three-wheeled Urban Electric Vehicle, M. S. Thesis, KAIST, Daejeon, (2015).
• M. Ryu, and Y. Park, “1/5 Scale Model of Three-wheeled Urban Electric Vehicle”, KSAE Annual Conference Proceedings, p1267, (2014).
• K. Jo, K. Chu, K. Lee, and M. Sunwoo, “Integration of Multiple Vehicle Models with an IMM Filter for Vehicle Localization”, IEEE Intelligent Vehicles Symposium, p746-751, (2010). [https://doi.org/10.1109/ivs.2010.5548118]
• K. Jo, K. Chu, J. Kim, and M. Sunwoo, “Distributed Vehicle State Estimation System using Information Fusion of GPS and In-vehicle Sensors for Vehicle Localization”, 14th International IEEE Conference on Intelligent Transportation Systems, p2009-2014, (2011). [https://doi.org/10.1109/itsc.2011.6083010]
• A. F. Genovese, “The Interacting Multiple Model Algorithm for Accurate State Estimation of Maneuvering Targets”, Johns Hopkins APL Technical Digest, 22(4), p614-623, (2001).