다구찌 기법을 적용한 Stone Chipping에 의한 변형량 최소화를 위한 환경 요인 분석

1. 서 론

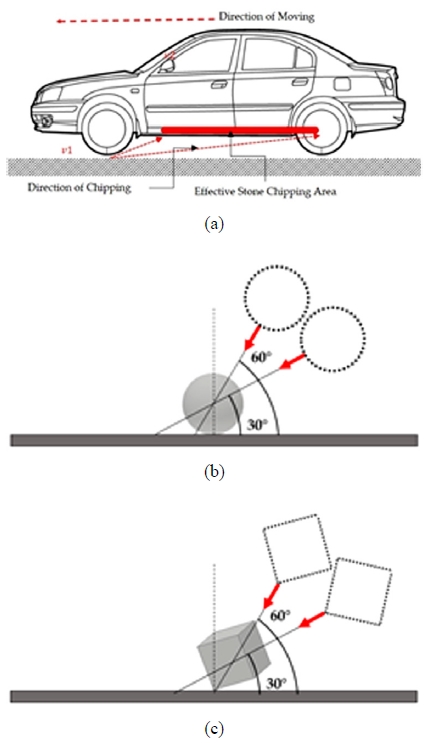
일반적으로 차량 주행 시, 노면의 작은 낙하물 또는 Stone은 타이어의 슬립에 의해서 차량 후륜으로 튀어 언더바디 및 하부 부품에 충격을 가한다. 이와 같이 수많은 작은 충격들에 의해 발생하는 마멸 현상을 ‘Stone Chipping’이라 한다.

Stone Chipping에 의해 발생한 작은 마멸현상으로 인해 외부로 노출된 부품은 부식이 야기할 수 있다. 또한 Stone의 질량이 큰 경우, 충격 시간은 비교적 짧은 시간에 언더바디의 파손의 원인이 되기도 한다. 이와 같은 파괴 현상은 극단적으로 언더바디 부품의 외형 변형뿐만 아니라, 차량 하부에 위치한 파워트레인 부품의 기능의 상실을 초래할 수 있다. 따라서 자동차제조사에서는 차량 정비 시, Checking List 항목으로 지정하여, 유지보수 및 관리하고 있다.

현재 자동차제조사는 Stone Chipping에 대한 차량 파손을 최소화하기 위해서, 차축 후륜 및 외관에는 보호 필름을 부착하고 있으며, 차량 하부에는 세라믹 코트와 같은 보호 피막 또는 노출 부분은 Electroplating을 시공함으로써 수동적으로 문제를 해결하고 있다.^1,2)

그러나 일반적으로 기존 내연기관 차량과 달리, 전기 기반의 파워트레인을 장착하는 친환경차량의 Layout은 차축 후륜에 배터리를 포함한 파워팩이 장착되기 때문에, Chipping 현상 또는 교통사고로 인한 기능 상실 또는 화재의 위험이 따른다. 따라서 이와 같은 사고를 예방하기 위한 언더바디 부품의 보호 기능을 극대화할 할 수 있는 강건 설계를 필요로 한다.³⁾

언더바디 부품의 강건 설계 요소 인자를 분석 및 도출하기 전에 주행 환경 및 충격 환경 인자를 분석할 필요가 있다.

종래의 연구에서 타이어의 횡력 특성과 타이어 공기압, 차량의 높이의 조건에 따라 차속 60kph, 80kph, 110 kph에 대한 Stone Chipping 현상과 충격 집중 영역 및 포텐셜에너지에 대한 예측을 했다.⁴⁾ 이와 같이, Stone Chipping으로 인해 발생할 수 있는 위험영역에 가해지는 충격에너지에 영향을 미치는 인자를 고려한 분석이 필요하다. Roberto⁵⁾는 Stone Chipping에 대한 수학적 모델을 제안했고, 이 모델을 기반으로 하는 시뮬레이션을 통해 언더바디 부품에 대한 영향도를 분석하였다. 또한 차량 주행 속도, 타이어의 마찰 및 공기압과 같은 수학적 모델 변수는 실제 주행 환경과 동일하게 재현되지 않는다. 따라서 Stone Chipping 위험지점에 가해지는 충격에 영향을 미치는 인자를 고려한 분석이 필요하다. Oka 등⁶⁾은 외부 입자의 속도와 충격 각도의 영향을 분석하기 위해, 다양한 재료에 대한 Erosion시험을 통해 분석하였다.

Lonyuk 등⁷⁾은 Single-Impact Stone Chip Tester를 사용하여 코팅 기법, 발사 속도 및 온도에 따른 피복 탈착 및 파손 저항성을 관찰하고 통계적 기법을 사용하여 Critical 조건과 요인의 영향도를 분석하였다. 마찬가지로 Erosion은 복잡적인 과정이며, 모든 실험 환경을 포함하기 어렵게 만드는 많은 요소에 의해 지배된다. 각각 인자의 주요 영향도를 분석하기 위해 제어된 조건을 따르는 것이 합리적이나, 수치적 방법은 충격으로 인한 Erosion의 전체 세부 사항을 설명하기에는 적절하지 않을 수 있다.

Kumar 등⁸⁾은 Multiple Particles의 입사각, 입사속도 및 Plate소재모델(Ti Alloy, Stainless Steel)에 따른 Plate erosion 손상을 Explicit Finite Element Analysis를 이용하여 분석하였다.⁸⁾

앞서 언급한 바와 같이 Impact Erosion에 의한 변형량 최소화를 위해 고려해야 할 인자 수는 많다. 이때 다양한 인자에 대해 실험 횟수를 최소로 하며 실험계획을 수립할 수 있도록 만들어 놓은 표가 직교배열표이다.⁸⁾ 다구찌 직교배열표를 활용한 실험계획법은 구조설계 뿐 아니라 전반적인 영향도 분석 및 최적화 분야에 효율적으로 활용되고 있으며, 최근 Ilangovan 등은 다구찌 직교배열표 실험계획법을 이용하여 구리-니켈 주석 합금 경도와 마모의 최적화 연구가 진행되었다.^9-12)

본 논문에서 유한요소해석과 다구찌 실험계획법을 활용하여 Stone Chipping에 의한 언더바디부품의 변형량을 최소화할 수 있는 인자를 도출하였다. 이 때, Stone Chipping의한 포텐셜 에너지는 약 40 J ~ 50 J 대비 100배에서 소성변형이 일어나는 순간에 대한 분석을 진행하였다.⁴⁾

일반적으로 기존 논문은 차량 부품의 강건 설계 인자 도출 및 형상 분석에 초점을 맞추고 있으나, 본 논문에서는 Stone Chipping에 의한 환경 요인에 대해서 분석하였다. 즉, 차량 언더바디 부품 설계 시, 주행 환경, 사용 조건, 주변 환경을 고려하여 부품 설계에 대한 환경 인자를 도출하였다. 따라서 언더바디 부품의 강건 설계 시, 환경 요인을 우선 고려 대상으로 적용할 수 있고, 설계 변수 분석 및 범위 설정에 대한 객관적인 근거를 제시할 수 있는 방안으로 사용될 수 있다.

2. Stone Chipping 실험을 위한 시험계획법

본 논문에서 충격에 따른 언더바디 부품의 변형량을 예측하기 위해서, 대상 시료를 일반적인 HEV, EV 차량으로 선정하였다. 언더바디 부품의 소재는 현재 가장 널리 사용되고 있는 알루미늄 또는 주철로 고려되었다.

본 논문에서는 언더바디 부품에 충격이 발생할 수 있는 영역을 차축 후륜으로 가정하였으며, Plate는 가장 넓은 면적으로 정사각형 500×500mm에 Chipping 현상이 일어나는 것으로 설정하였다.

Stone의 충돌 속도, 입사각, 질량 및 언더바디 부품의 소재, 두께에 따른 최대 변형량 및 충격 거동을 분석하였으며, 차량 주행 속도가 60kph에서 110kph의 범위에서 10g의 질량을 가지는 Stone에 의한 충돌로 발생하는 Stone Chipping현상으로 생성되는 포텐셜에너지는 약 40~50J이다.⁴⁾

일반적으로 Stone의 충돌 속도가 낮고, 입사각은 대상과의 접선에 가까우며, 질량은 작을수록 포텐셜에너지가 낮을 것으로 예상되나, 각각의 다양한 변수 및 상관 관계로 인해 최대변형량에 영향을 주기 때문에, 교호작용에 의한 영향도를 분석해야 한다.

본 논문은 Stone Chipping에 의한 환경 및 영향도 분석을 위한 것으로써, Stone Chipping에 의한 강건 설계 요소 인자 도출 및 선정하기 전에, 환경 요인에 의한 영향도를 분석하기 위한 Stone 속도, 입사각, 질량 간의 교호 작용을 우선 분석해야 한다. 따라서 본 논문에서는 다구찌 직교배열표를 하기와 같이 구성하였다.

다구찌 직교배열표 구성을 위해서 낙하 충격 실험을 위한 Stone의 질량을 2kg, 낙하 속도는 6m/s (약 20kph)로 2수준의 Inner Array에 대입될 제어 인자들과의 교호작용과 잡음 인자, 잡음 인자를 제외한 상수인자를 Table 1과 같이 정리하였다.

Table 1

Control, Noise and Constant factors with interaction formulation

또한 본 논문에서 최대변형율에 영향을 주고 있으나, 제어 불가능한 잡음 인자는 Stone의 형상과 언더 바디 부품의 변형 경화 모델로 한정했다.

실제 도로에 존재하는 Stone은 임의의 다양한 형상이지만, 분석의 정확도를 위해서 구 또는 특정할 수 있는 임의의 형태로 가정하였다.¹²⁾ 또한 언더바디 부품으로 가정한 정육면체 시편 대상의 형태도 잡음 인자로 포함하여, Stone의 형태에 따른 영향도를 확인하였다.

하기의 Table 1에 제어 인자와 잡음 인자, 그리고 불변상수를 나타내고 있다. Table 1에서 선정한 제어 인자는 5개, 교호작용은 2개이므로 이에 따라 자유도는 5(2-1)+2(2-1)(2-1) = 7이다.

L₈(2⁷)직교배열표의 자유도가 7이므로 이를 사용할 수 있고, L₈(2⁷)직교배열표의 Standard Linear Graph를 참고하여 직교배열표 Inner Array각 열에 해당하는 요소와 교호작용을 선정하여 직교배열표를 작성하였다. Outer Array는 2수준 잡음 인자 M₁, M₂ × N₁, N₂에 따라 각 시행에 따른 4회 실험으로 구성하였다.

3. Single Stone Impact Finite Element 해석 모델

3.1 물성치 모델

일반적으로 소재의 소성 거동을 유동 응력에 대한 수학적 모델에 관한 다양한 연구가 진행되고 있다. 또한 유한요소해석 및 검증을 수행할 때, 인장시험 결과를 바탕으로 한 Multi linear Isotropic Hardening Model을 사용한다. 그리고 Johnson Cook Plasticity Model은 고속 충돌 모델 해석을 위해 변형부의 고온으로 인한 급격한 항복응력 거동까지 모사할 수 있는 소재 모델로 금속소재의 Constitutive Behavior가 잘 나타나기 때문에, 비선형 접촉 및 충격에 관한 문제를 수학 모델로 해결하고자 할 때 유용하게 쓰이고 있다.^13-15)

Johnson Cook Model은 Hardening 법칙과 Rate Dependence를 포함한 Analytic 수식으로, 식 (1)과 같이 표현할 수 있다.

이때 상수 A, B, n, C, m 은 실험을 통해 획득할 수 있는 상수이다. 여기에서 σ^Y는 Von-mises Flow Stress, A는 소재의 Yield Stress, B는 Strain Hardening Parameter, n은 Strain Hardening Exponent, C는 Strain Rate Sensitivity Parameter, 그리고 m은 Temperature Exponent를 의미한다.

$$ \dot{ϵ}$$은 유효소성 변형률이고 , $$ {\dot{ϵ}}^{\mathrm{*}}=\dot{ϵ}/{\dot{ϵ}}_0$$ 은 무차원 소성 변형률 속도로 $$ {\dot{ϵ}}_0=1.0s^{-1}$$이다. T^*는 Non dimensional 온도로 식 (2)과 같이 정의되며 T_melt는 소재의 녹는점, T_transition은 항복 스트레스에 대한 온도 의존도가 없는 온도 또는 그 이하에서 Transition 온도로 정의된다. 이전 연구에서 실험을 통해 구한 Al6061-T6와 Steel 4340의 Johnson-cook parameters는 Table 2와 같다.¹⁶⁾ 본 논문에서는 두 가지 소재모델을 수치해석 과정에서의 잡음 인자로 설정하였다.

$\[ {\sigma }_Y=\left[A+B_{\epsilon }^n\right]\left(1+Cln{\epsilon }^{*}\right)\left(1-T^{*m}\right) \]$

(1)

$\[ T^{*}=\frac{T-T_{transition}}{T_{melt}-T_{Tramsition}} \]$

(2)

Table 2

Input parameters for the Johnson-cook plasticity model

3.2 Finite element analysis model

본 논문에서는 제어 인자에 따른 Stone Chipping에 최대 변형량에 대한 영향도를 상용 해석 소프트웨어를 사용하여 분석하였다. 상용 해석 소프트웨어인 Matlab 을 이용하여 Stone과 Plate의 형상에 대한 정의와 Stone 입사 속도 및 입사각을 설정하여 실험계획법을 적용하였다.¹⁷⁾ 다구찌 실험계획법을 적용하기 위해, 외란에 따른 환경변화를 고려하고 실험 순서를 무작위 임의의 선정이다.

그러나 본 논문에서는 상용 유한요소해석 소프트웨어를 사용하여 진행하기 때문에 무작위 추출을 진행하지는 않았다.

본 논문에서 Stone과 Plate 사이의 접촉에 따른 최대 변형량을 분석하기 위해서, Fig. 1과 같이 Stone의 형상과 입사각에 따라 3차원 모델링으로 구성하였다.¹⁸⁾ 충돌 해석관점에서 Contact 조건은 비선형 문제임으로 Explicit Dynamics를 적용하였다. 또한 경계조건은 Plate의 네 모서리를 모든 방향에 대해서 Fixed하고, Stone의 속도만 제어한다. Plate의 소재에 대한 모델로 각각 Al6061-T6와 Steel 4340에 대해 Multi linear Hardening 모델과 Johnson-Cook Plasticity 모델 두 가지 모두 설정하였고, Plate는 Plane Mesh로 지정하여 두께를 제어하였다.

Fig. 1

Impact analysis model by collison stone: (a) Underbody geometry and effective stone chipping area due to the code angle of tire belt, (b) Collison depiction of sphere stone, (c) Collison direction of cubic stone

4. 실험계획법에 따른 해석 결과

4.1 저속 충격 조건에 따른 해석 결과

본 논문에서는 Stone Chipping에 대한 유한요소해석 조건은 Stone의 속도를 저속과 고속으로 나누어 분석하였다. 저속 충격에서는 Explicit Dynamics 해석을 시행하는 경우, 탄성영역구간에서 수렴하게 되고 소성변형이 일어나지 않는다. 그러나 고속 충격이 일어나는 경우, 충격에 의한 에너지 전달 및 소성변형이 발생된다. 따라서 소재 모델은 고속 충격 조건에 한정하여 잡음 인자로 고려될 수 있다.

4.1.1 저속 충격 조건에서 S/N Ratio 분석

신호 대 잡음 분석은 제어 인자의 적정 조건을 찾을 수 있을 뿐만 아니라, 잡음 인자의 영향을 고려하여 가장 바람직한 결과를 도출할 수 있다.

본 논문의 목적은 외부충격에 대한 Plate의 최대 변형량이 최소가 되도록 하는 것이므로 망소특성 신호 대 잡음 비(S/N ratio for smaller-the-better) 는 식 (3)과 같이 계산될 수 있다.

식 (3)에서 n은 잡음 인자에 대한 실험결과 총 수를 의미하며, yi는 i번째 잡음 인자에 대한 값을 의미한다.

$\[ \frac{S}{N}=-\log \frac{\sum _{i=1}^n{y}_i^2}{n} \]$

(3)

Table 3과 같이 5개 제어인자에 대한 2수준 직교배열표 L₈(2⁷)에 해석 결과를 구성하였다. Table 3의 외측배열은 4 회 반복에 대해 측정된 Plate의 변형량이며, 식 (3)을 이용하여 S/N Ratio를 정리하였다.

Table 3

Impact analysis results at low stone velocity

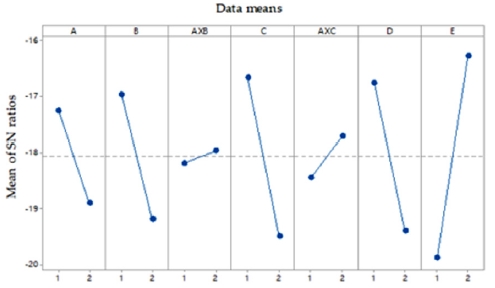
이를 바탕으로 계산한 S/N Ratio에 대한 수준별 반응 그래프는 Fig. 2로 표현될 수 있다. Fig. 2에서 확인할 수 있듯이, Plate의 두께(E), Plate의 소재(D), Stone의 속도(A), Stone의 입사각(B), Stone의 질량(C) 순서로 Plate의 최대 변형량에 강한 영향을 주며 Interaction Effect는 미비함을 알 수 있다.

Fig. 2

Signal to noise response graphs at low stone velocity. Smaller is better

따라서 큰 S/N Ratio를 갖기 위해 선정할 수 있는 요인과 수준은 5가지(A1, B1, C1, D1, E2)이다.

전반적인 실험 S/N Ratio 평균($$ \widehat{T}$$) 은 -18.077dB이다. 위의 최적 요인과 수준을 고려하여 예상할 수 있는 S/N비는 식 (4)~(7)으로 다음과 같이 계산할 수 있다.

$\[ \begin{array}{l}\widehat{u}=\overline{T}+\left(\overline{A_1}-\overline{T}\right)+\left(\overline{B_1}-\overline{T}\right)+\left(\overline{C_1}-\overline{T}\right)\\ +\left(\overline{D_1}-\overline{T}\right)+\left(\overline{E_2}-\overline{T}\right)\end{array} \]$

(4)

$\[ \widehat{u}=\left(\overline{A_1}+\overline{B_1}+\overline{C_1}+\overline{D_1}+\overline{E_2}-4\overline{T}\right) \]$

(5)

$\[ \begin{array}{l}\widehat{u}=-17.248-16.964-16.660-16.750\\ -19.874+4\times 8.077\end{array} \]$

(6)

$\[ \widehat{u}=-15.188\left(dB\right) \]$

(7)

추가적으로 잡음 인자 열의 평균 분석을 통해 각 잡음의 영향을 파악할 수 있다. 잡음의 반응표는 Table 4와 같다. 이를 통해서 Stone의 모양에 의한 잡음 영향은 큰 반면 소재 모델에 의한 잡음의 효과는 0이다.

Table 4

Response table of noise factors

소재모델은 소성영역의 해석에서 차이를 보일 수 있는데 유한요소해석에서는 소성변형을 일으킬 수 있는 에너지가 충분치 않아, 소재모델이 탄성영역에서 거동하기 때문에 잡음 효과는 0이다. 따라서 Stone의 형상은 Inner Array에 추가하여 영향을 파악하고, 고속 충격 환경과 같이 Stone의 운동에너지를 높여 소재 소성영역에서의 잡음의 영향을 파악해 볼 필요가 있다.

4.1.2 저속 충격에서 변수조건에 따른 분석

분산 분석은 측정데이터 전체 분산을 몇 개의 요인 효과에 대응하는 분산과 나머지 오차 분산으로 나누어 검정이나 추정을 실시하는 것이다. 유의수준(α)과 유의 확률(Significance probability, P value)를 비교함으로써 수준을 변경하더라도 결과에 영향을 미치지 않는 인자를 구별할 수 있다.

본 본문에서 통계적으로 유의한 영향을 미치는 인자를 확인하기 위해 제어 인자에 대한 P value 를 유의 수준과 비교하여 제어 인자와 반응 사이의 연관성이 없음으로 설정하는 귀무 가설(Null Hypothesis)을 평가한다.

이때 유의수준(α)은 0.05로 설정하였다. 즉, 현실에서는 연관성이 없으나, 오차로 인해서 연관성이 존재한다는 결론을 내릴 위험이 5 %임을 의미한다.

F value는 분산분석의 F-test statistic으로, Mean square for treatments와 Mean square for error의 비로 정의한다. Test statistic이 1보다 매우 크다면 귀무가설(Null hypothesis)를 기각할 수 있고 제어 인자의 효과가 존재한다는 것을 뜻한다.¹⁹⁾

제어 인자의 연관성을 확인하는 검정이므로 Fixed Effect Model을 사용하였으며 분산분석 결과는 Table 5와 같다. Stone Mass, Plate Material, Plate Thickness의 F-value와 P-value의 결과로 통계적으로 유의함을 알 수 있다.

Table 5

ANOVA result: F-value & P-value of control factors at low stone velocity

4.1.3 Stone의 형상인자를 포함한 저속 충격 분석

잡음 인자인 Stone의 모양은 저속 충돌 실험에서 유의한 영향을 미치므로 Table 3의 3번째 열인 A×B 대신 Stone의 모양(F)을 제어요인으로 대체하여 분석이 가능하다. 본 실험에서 A×B, A×C의 교호작용 효과는 미비하므로 A×C를 오차항으로 풀링하고, 잡음인자는 제거하여 변형량에 대한 직교배열 결과표를 작성하면 Table 6과 같다.

Table 6

Modified impact analysis results at low stone velocity including stone shape

본 결과를 토대로 평균 수준 분석을 진행한 반응 그래프 Fig. 3을 도출할 수 있다. 수정된 반응 그래프에서 Stone Chipping에 따른 변형량에 가장 큰 영향을 주는 인자는 Stone의 질량(C)이고, Stone의 모양(F)은 Stone과 관련된 제어인자 중 입사각보다 큰 영향을 주는 인자임을 알 수 있다.

Fig. 3

Signal to noise response graphs of high velocity impact analysis. Smaller is better

4.2 Stone의 형상을 고려한 고속 충격 조건에 따른 해석 결과

4.2.1 고속 충격 조건에서 S/N Ratio 분석

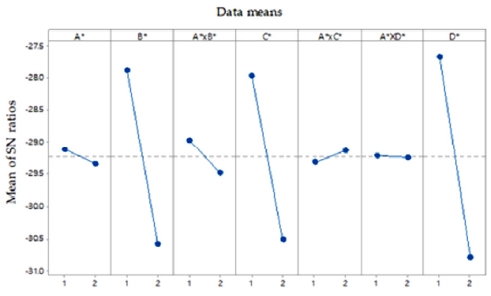
분산 분석에 따라 Stone의 모양을 Inner Array에 추가하여 영향을 파악하고 운동에너지를 높여 소재 소성영역에서의 소재 모델 영향을 분석한다. Plate는 분산 분석에서 구한 최적의 요인으로 두께 2mm, 소재는 SS 4340으로 선정하였다. 이에 따라 Table 1의 Plate Material(D)와 Plate Thickness(E)는 고정값이고 하기의 Table 7과 같이 Stone Shape(A^*)를 새로운 제어 인자로 설정하였다. Table 1의 잡음인자(M)과 동일하게 Sphere 형상과 Cube 형상을 비교하였으며 고속 충돌의 변형량을 확인하기 위해 Stone Velocity(B^*)는 30m/s, 60m/s로 설정하였다. 본 논문에서 실험 자유도는 8이므로 선형적인 그래프 선정 방법에 따라 각 요인을 L₈(2⁷) 직교배열표에 배치하였다. 새롭게 선정한 직교배열표는 Table 8과 같고 소재 모델을 잡음 인자로 선정하여 유한요소 해석을 진행하여, Fig. 3과 같음을 확인하였다.

Table 7

Modified analysis control factor formulation

Table 8

Impact Analysis results at high stone velocity

신호 대 잡음비 분석과 분산 분석에 따라 Stone의 모양(A^*)을 Inner array에 추가하여 영향을 파악하였으나 고속 충돌의 경우 Stone의 모양은 Plate의 최대 변형량에 큰 영향을 미치지 못하는 것을 Table 8과 하기의 Fig. 3을 통해 확인할 수 있다. 여전히 Stone의 속도(B^*), 입사각(C^*), 질량(D^*)가 Plate의 최대 변형량을 결정하는 주요 요인으로 판단할 수 있다.

고속 충돌의 결과는 저속 충돌 변형과 달리 소성 변형이 이뤄졌으므로, 소재 모델에 따른 최대 변형량의 차이가 있었다. 잡음 인자인 소재 모델에 의한 응답 평균은 1수준에서 29.897, 2수준에서 30.316이고 이 차이는 0.419이다. 이는 다른 인자에 비해 현저히 낮은 값으로 고속 충돌의 해석 시, 소재 모델은 특별한 고려를 할 필요가 없다.

4.2.2 고속 충격에서 변수조건에 따른 분석

4.1.2절의 분석과 같이 고속 충돌 해석 시 분산분석을 진행하였으며, 0.05의 유의수준에서 분산분석 결과는 Table 9와 같다. Stone shape(A^*)을 제외한 모든 제어인자들은 F-value는 1보다 매우 큰 값을 가지고, P-value는 유의수준 0.05보다 작은 값으로 통계적으로 유의함을 알 수 있다.

Table 9

ANOVA result: F-value & P-value of control factors at high stone velocity

즉, 고속 충돌 해석의 경우 판의 변형량에 크게 관련된 제어인자는 Stone Velocity, Incidence Angle, Mass이다. 고속 충돌의 경우 재료 소성영역에서 변형이 일어나므로 Stone의 입사에너지가 Stone의 형상보다 훨씬 유의미한 차이를 야기함을 알 수 있다.

5. 결 론

본 논문은 Stone Chipping에 의한 환경 및 영향도 분석를 분석하였다. 즉, Stone Chipping에 의한 언더바디 설계 형상 변수 인자 도출 및 선정하기 전에, Chipping에 의한 환경 요인 영향도를 분석하였다.

• 1) 저속 충돌 분산 분석 결과, 통계적으로 Stone보다 Plate에 관련된 소재, 두께 등과 같은 인자들이 변형량에 영향을 주는 인자임을 알 수 있다. 저속충돌, 고속충돌 모두 Stone의 인자 교호작용은 모두 무시할 수 있음을 알 수 있다. 즉, Stone 속도, 질량, 입사각을 독립적 제어인자로 설정하여 실험하는 것이 타당하다.
• 2) 저속 충돌의 경우 잡음인자로 선정한 Stone의 형상이 유의미한 고려대상임을 알 수 있으나 고속 충돌 시, Stone 형상은 상대적으로 다른 Stone 제어인자에 비해 변형량에 대한 효과가 미비하다. 따라서 현실적으로 가혹 환경 조건의 Stone Chipping을 고려할 경우 Stone의 형상 보다는 다른 인자가 충격 변형량에 영향을 주는 것으로 판단된다.
• 3) 향후 두께의 변화는 차체 중량과 직결되는 요인이므로 Stone Chipping 변형량을 최소활 수 있는 최소의 두께를 선정할 필요가 있다. 따라서 전기자동차 언더바디 부품 설계 시, 다구찌 실험계획법을 이용하여 다른 주요인과의 영향을 분석한 뒤, 제한 조건과 목적함수 상보관계를 고려하여 최적의 두께를 도출할 수 있다.

Acknowledgments

본 논문은 중소벤처기업부 산학협력 기술개발사업(소형차량 엔진(KAPPA)용 Damper Pully 공정 기술 및 신뢰성 평가 기술 개발(S2635634))과제와 2018년 과학기술정보통신부의 재원으로 한국연구재단 원자력연구개발사업(No. NRF-2018M2A8A4083765)의 지원을 받아 수행되었습니다.

References

• C. S. Lin, H. B. Lee, and S. H. Hsieh, “Microstructure and Formability of ZnNi Alloy Electrodeposited Sheet Steel”, Metallurgical Mat. Trans A, 31, p475-485, (2000). [https://doi.org/10.1007/s11661-000-0283-z]
• O. Kaji, and S. Matsumura, “Study of a Method for Evaluating Stone Chipping Resistance of Vehicle Films”, JSAE Review, 15, p341-365, (1994).
• S. U. Jung, Y. J. Chu, H. S. Kim, K. S. Kim, and B. H. Lee, “A Study of Impact Reliability Evaluation by Using 3D Scan in Automotive Undersed Parts”, KSAE Spring Conference Proceedings, p306, (2017).
• Y. J. Chu, H. J. Eun, and S. Y. Lee, “Prediction of Damage to the Underbody due to Stone Chipping”, Appled Science, 8, p1805-1813, (2018).
• V. Roberto, “On the Simulation of the Effects of the “Stone Chipping,” on the Car Underbody-An Application of Monte Carlo Methods, SAE 2010-01-0731, (2010).
• Y. I. Oka, T. Ohnogi, and M Matusumra, “The Impact Dependence of Erosion Damage Caused by Solid Particle Impact”, Wear, 203, p573-579, (1997).
• M. Lonyuk, M. Bosma, A. C. Riemslag, J. Zuidema, A. Bakker, and M. Janssen, “Stone-impact Damage of Automotive Coatings: A Laboratory Single-impact Tester”, Progress in Organic Coating, 58, p241-247, (2006).
• N. Kumar, and M. Shukla, “Finite Element Analysis of Multi-particle Impact on Erosion in Abrasive Water Jet Machining of Titanium Alloy”, Journal of Computational and Applied Mathematic, 236, p4600-4610, (2012). [https://doi.org/10.1016/j.cam.2012.04.022]
• Glen Stuart Peace, Taguchi Method: A hand-on approach, University of Michigan, Addison-Wesley, p246-291, (1992).
• S. Selvakumar, K. P. Arulshri, K. P Padmanaban, and K. S. K Sasikumar, “Design and Optimization of Machining Fixture Layout Using ANN and DOE”, The International Journal of Advanced Manufacturing Technology, 65, p1573-1586, (2013). [https://doi.org/10.1007/s00170-012-4281-2]
• S. Ilangovan, J. Sreejith, M. Manideep, and S. Harish, “An Experimental Investigation of Cu-Ni-Sn Alloy on Microstructure, Hardness and Wear Parameters Optimization Using Doe”, Tribology in Industry, 40(1), p156-163, (2018). [https://doi.org/10.24874/ti.2018.40.01.15]
• M. K. Shin, K. T. Park, K. B. Lee, H. I. Bae, and G. J. Park, “Design of the Active Hood Lift System Using Orthogonal Arrays”, Transactions of KSAE, 14(4), p123-131, (2006).
• G. R. Johnson, and T. J. Holmquist, Test Data Computational Strength and Fracture Model Constants for 23 Materials Subjected to Large Strains, High Rates, and High Temperatures, LANL Technical Report, (1989).
• E. S. Leonard, “Aluminum Plate Perforation: a Comparative Case Study using Lagrange with Erosion, Multi Material Ale, and Smooth Particle Hydrodynamics”, 7th European LS-DYNA Conference, 14th May, Salzberg, Austria, (2009).
• J. Y. Youn, S. H. Kim, and Y. S. Jin, “A Study on the Impact Resistance of Plastic Underbody Parts”, SAE International Journal of Materials and Manufacturing, 9(3), p776-780, (2016). [https://doi.org/10.4271/2016-01-0515]
• D. H. Woo, Y. S. Lee, and T. W. Kim, “A Study on the Rectangular Plate Under High Velocity Impact”, KSME Conference Proceedings, p3701-3704, (2013).
• A. Y. Ben, and A. Levy, “Absorbed Shear Energy during Solid Particle Impact on Ductile Surface”, Wear, 368, p162-172, (2016).
• C. H. Shiuh, and C. L. Yu, “The Finite Element Analysis of Composite Laminates and Shell Structures Subjected to Low Velocity Impact”, Composite Structures, 66(1-4), p277-285, (2004).
• D. C. Montgomery, Applied Statistics ad Probability for Engineers, 6th Edn., Wiley, Hoboken, (2007).