[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 27, No. 7, pp.509-519

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jul 2019

Received 26 Feb 2019 Revised 06 Apr 2019 Accepted 09 Apr 2019

DOI: https://doi.org/10.7467/KSAE.2019.27.7.509

최적운전계획법에 의한 전기차의 고전압 배터리셀 온도 관리

김재웅^*^{, 1)}

; 신영기²⁾

1)현대자동차 통합열관리리서치랩
2)세종대학교 기계공학과

Temperature Management of EV Battery Cell by Optimal Operation Scheduling

Jaewoong Kim^*^{, 1)}

; Younggy Shin²⁾

1)Thermal Management Research Lab., Hyundai Motor Company, 150 Hyundaiyeonguso-ro, Namyang-eup, Hwaseong-si, Gyeonggi 18280, Korea
2)Department of Mechanical Engineering, Sejong University, Seoul 05006, Korea

Correspondence to: ^*E-mail: neo@hyundai.com

Copyright Ⓒ 2019 KSAE / 164-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

This paper proposes a model-based thermal load predictive optimal control that can be more efficiently managed in the future of mobility. Due to environmental concerns, heat management has become an integral part of battery performance and durability in regard to the fast-growing electric vehicles. A thermal management simulator of the battery system has been constructed in Simulink and verified against vehicle test data to be used as a virtual plant for the development of optimal scheduling of battery cooling devices. An optimal operation scheduling based on linear programming and model has been developed and compared with the existing rule-based control. Based on the comparison, it is concluded that the optimal scheduler saves more energy and improves battery durability with significant margins in two extreme test cases.

Keywords:

Thermal management, Optimal operation scheduling, Model predictive control, Linear programming, EV

키워드:

열관리, 최적운전계획법, 모델예측제어, 선형계획법, 전기자동차

1. 서 론

화석연료의 고갈과 환경문제에 대한 해결 방안으로 자동차는 에너지사용의 효율화를 추구하고 있다. 특히 하드웨어와 소프트웨어의 발전에 힘입어 앞으로의 자동차의 발전 방향은 외부와 차량의 양방향통신(Connectivity or V2X)와 전동화(Electrification or hybridization)에 의한 에너지사용의 효율화이다.

Farrington¹⁾의 연구에 의하면 환경차와 같은 고효율의 차량은 구동장치 외의 보기류의 부하에 따른 연비효과가 크게 나타난다. 보기류 중에 큰 동력을 사용하는 열관리 장치의 소모에너지 최적화는 고효율을 추구하는 미래자동차에서는 필수적인 영역이라고 할 수 있다.

기존에는 차량레벨에서의 차량정보로써 속도, 각 부위 온도, 압력 등 현 시점의 내부 상태 정보만 활용하였다. 하지만 차량간 정보가 연결되어 교통/사회망 레벨까지 확장된 환경에서 볼 때, 차량레벨의 정보뿐만 아니라 미래시점의 차량 정보와 외부 환경까지 예측이 가능해지면서 보다 효율적으로 열을 관리할 수 있게 된다. 그리고 구동부의 전동화에 따른 배터리셀전지의 사용은 필연적이며 자동차의 성능은 이 배터리셀전지로 이루어진 배터리팩의 성능에 지배적인 영향을 받는다. 자동차에서 요구되는 배터리팩의 성능은 출력, 에너지용량, 급속충전, 내구 등인 데 이 모든 것이 배터리셀의 온도에 좌우된다. 따라서 배터리의 열관리는 미래자동차에서 중요한 영역이다.

Lopez-Sanz 등²⁾은 HEV 차량의 열관리에서 비선형 모델을 사용하여 예측제어알고리즘을 구현하였다. 이는 차량내에서 구현하기 힘든 단점을 지니고 있다. 그리고 Tao와 Wagner³⁾은 칼만필터를 적용하여 배터리 코어온도를 추정하고 최적제어이론에 의해 이상적인 냉각 유체온도를 결정하였다. 하지만 유량을 고정시킴으로써 유량과 유체온도사이의 에너지 최적화가 고려되어 있지 않았다.

본 논문은 전기자동차의 핵심이 되는 배터리열관리에 있어 열부하 예측제어 이론을 적용하여 배터리셀온도를 목표온도로 관리하면서 이에 따른 냉각 소모에너지를 최소화하는 것이다. 배터리 열관리 모델링과 실차 검증을 통하여 가상 플랜트를 구축하고, 선형모델기반으로 열부하 예측 최적제어(MPC)를 설계하고 시뮬레이션함으로써 기존 룰기반 제어와의 성능 비교한 결과를 보여준다.

2. 전기차의 동력전달계 구성 및 열관리 회로

본 장에서는 전기차의 동력 전달계를 살펴보고 이에 대한 차량 구동력 모델을 구성하며, 구동부품의 발열특성을 고려하여 열관리 회로를 설정한다.

2.1 전기차 동력전달계 구성

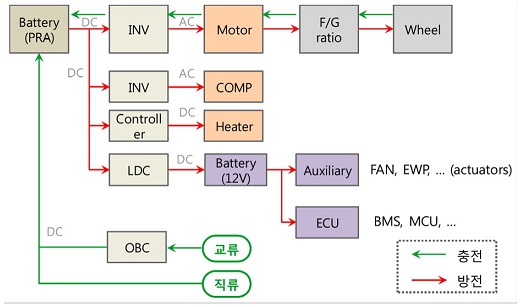
화석연료를 에너지원으로 사용하는 내연기관과는 달리, 전기차는 배터리의 전기에너지로 전기모터를 구동함으로써 구동력을 얻는 차량이다. Fig. 1은 전기차의 에너지 흐름을 개략적으로 보여준다. 전기차 배터리팩에서 발생되는 전기에너지는 고전압의 직류 성분으로, 구동부품의 특성에 맞게 저전압 또는 교류로 변환하여 해당 구동부품을 작동하게 된다.

Fig. 1

Energy flow of electric vehicle

차량에 사용하는 구동모터는 교류모터인 영구자석형 동기모터(PMSM) 또는 유도모터(IM)를 주로 사용하며, 운전자의 페달조작 시그널에 따라 인버터에서 모터의 목표 토크와 회전속도 구현을 위해 모터에 인가할 3상 전기를 생성하고, 최종적으로 차량이 원하는 속도로 움직이게 된다. 그리고 구동모터는 운동에너지를 전기에너지로 바꾸는 발전기 역할도 할 수 있으므로 회생제동의 기능도 가진다.

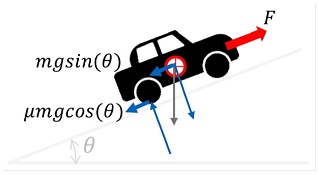
Fig. 2에서 보여주는 것처럼 차량이 임의의 속도로 달리기 위해 필요한 구동력은 식 (1)과 같다. 그리고 구동모터에서 요구되는 출력토크와 회전속도는 식 (2)와 같이 표현된다.

Fig. 2

Vehicle free body diagram

P v e h = F V F = m d V d t + μ m g ⋅ cos ⁡ θ + m g ⋅ sin ⁡ θ + 12 ρ a i r A C d V 2

(1)

T m o t = P v e h / ω ω = V / R t i r e ⋅ F G R

(2)

그리고 배터리 전기에너지에서 각 부품으로 전달되는 에너지가 변환될 때 손실이 동반되며 이 손실에너지는 대부분 열의 형태로 나타나는 데, 발생된 열은 부품의 열화 등 내구를 저하하거나 부품의 열손상으로 시스템이 제 기능을 못하게 될 수도 있으므로 반드시 적절한 냉각시스템을 갖추어야 한다.

2.2 전기차 열관리 회로

차량의 열관리는 차량구동장치에 해당하는 파워트레인 열관리와 캐빈에 거주하는 인체 열관리가 적절히 이루어져야 하는 데, 자동차의 구동장치가 내연기관에서 전기전자화로 바뀜에 따라 열관리 대상이 변화되고 이에 따른 요구조건도 달라지게 되었다. 전기차에서 요구되는 열관리 회로는 각 시스템의 냉각성능을 충족시킴과 동시에 냉각에 있어 적은 에너지로 효율적으로 운영되어야 하며 캐빈에 있는 승객에게도 열적 쾌적한 환경을 제공할 수 있도록 설계되어야 한다.

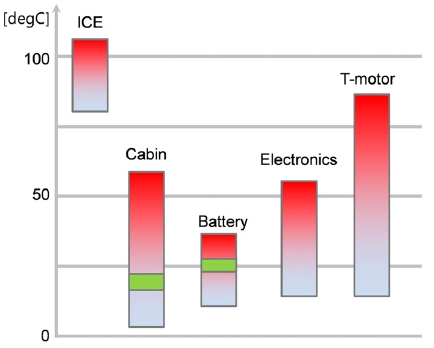
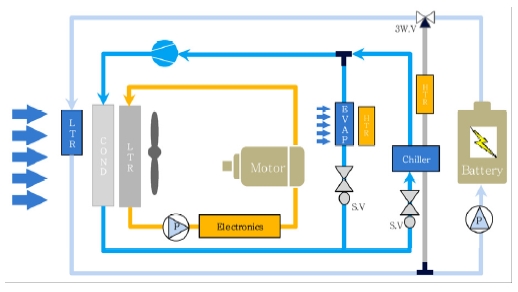
전기차에서 열관리가 필요한 부위는 배터리, 구동모터 및 전장품, 그리고 캐빈 등으로 분류할 수 있으며, Fig. 3에서 나타낸 각 시스템별로 요구되는 유체온도를 고려하여 시스템별 열교환기를 독립적으로 또는 통합적으로 배열할 수 있다. 본 논문에서는 적은 에너지로 배터리를 냉각할 수 있도록, 열교환기 맨 앞단에 별도의 배터리 전용라디에이터를 배치하고 외기온이 높을 때 컴프레서 작동을 통한 저온의 냉매를 이용하여 냉각이 이루어질 수 있도록 Fig. 4와 같이 열관리 회로를 구성한다.

Fig. 3

System-specific thermal management fluid temperature

Fig. 4

Thermal circuit for electric vehicle

3. 배터리시스템 열관리 모델

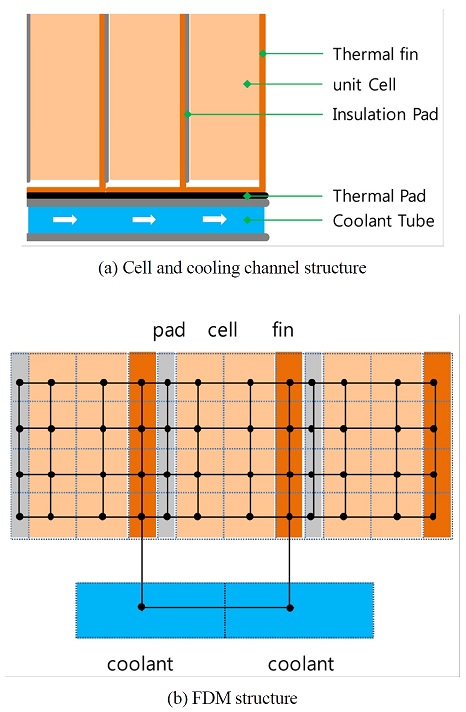
리튬이온배터러의 셀 전압은 3.2~4.2 V 수준이며 다수의 파우치형 리튬이온 셀(Cell)이 전기회로상 병렬로 연결되어 스택(Stack) 전압을 형성하고, 이 스택들이 전기회로상 직렬로 연결되어 모듈(Module) 전압을 이루게 되며, 최종적으로 모듈들이 전기회로상 직렬로 연결되어 고전압을 형성하게 된다. 배터리시스템 관리 제어기와 보호장치가 추가되어 고전압의 배터리팩(Pack) 또는 배터리시스템을 완성하게 된다. 특히 배터리시스템은 각 셀의 출입 전류에 따른 발열을 처리하고 셀온도를 관리하기 위해 배터리모듈 아래에 냉각채널로 이루어진 냉각시스템을 포함하게 된다.^8,9)

본 장에서는 배터리 요구 출입전력에 따른 SOC를 기반으로 셀전압과 셀전류를 산출하고, 셀내부의 전자 이동시 동반되는 발열량과 배터리셀로부터 냉각수로의 열전달현상을 모델링하고 모델을 검증한 결과를 보여준다.

3.1 배터리의 전기모델

배터리셀의 전기적 거동은 내부의 전기에너지 충전량 또는 SOC(State Of Charge)와 부하의 크기에 따라 달라진다. 기전력인 Open circuit 전압은 SOC와 SOH(State Of Health)에 따라 다르게 나타나는데, 열화에 따른 SOH를 무시하고 기전력은 식 (3)과 같이 SOC에 비례한다고 가정할 수 있다. 부하 P에 따른 전류 i는 식 (4)으로 표현되며, 내부저항과 부하에 따른 전압(Close circuit)은 식 (5)와 같이 나타낼 수 있다. 그리고 부하에 따른 전력을 소모한 후의 SOC는 식 (6)과 같이 표현할 수 있다.

ε = a × S O C + b

(3)

i = ε 2 - 4 r P 2 r

(4)

V = ε - i r

(5)

S O C t = S O C t - 1 - ∫ t - 1 t I c e l l d t C c e l l

(6)

3.2 배터리의 열모델

배터리시스템의 온도 거동을 파악하는 데 있어 확장성을 고려하여 모듈단위로 열모델링을 수행하는 것이 유리하며, 셀내부의 온도편차를 시뮬레이션하기 위해 셀과 냉각수 등의 각 구성품을 Fig. 5와 같이 유한차분법(FDM)으로 접근하여 다수의 노드로 분리하여 열모델링을 수행한다.

Fig. 5

Thermal structure of battery system

내부에너지 변화량은 배터리셀의 온도 증감으로 나타나는데, 배터리셀의 입출력 전류에 따른 발열량과 근접한 노드와의 열교환량의 합에 의해 구해진다. 이를 단위 체적에 대하여 수식으로 나타내면 식 (7)과 같이 편미분방정식으로 표현되며, 차분형태로 나타내면 식 (8)과 같이 된다.

ρ C p d T d t = q ˙ + k x ∂ 2 T ∂ x 2 + k y ∂ 2 T ∂ y 2 + k z ∂ 2 T ∂ z 2

(7)

ρ C p ∆ V d T d t = q ˙ ∆ V + k x T i + 1 - T i - T i - T i - 1 ∆ x / A y z + k y T j + 1 - T j - T j - T j - 1 ∆ y / A z x + k z T k + 1 - T k - T k - T k - 1 ∆ z / A x y

(8)

그리고 배터리셀의 온도를 관리하기 위해 냉각수를 이용하는데, 안전상의 문제로 간접 열교환방식을 사용한다. 구조적으로 배터리셀은 전도판에 접촉되며 그 전도판은 냉각채널까지 열적으로 연결된다. 그리고 배터리셀 온도는 냉각채널에 흐르는 냉각수의 온도와 유량 조절로 관리된다. 이를 유한요소형태로 표현한 것이 식 (9)이다.

ρ C p A ∆ x d T c o o l, i d t = Q ˙ c e l l 2 c o o l + m ˙ C p T c o o l, i + 1 - T c o o l, i

(9)

3.3 배터리의 발열모델

배터리셀 방열량은 SOC, 셀 온도, 셀의 충방전 전류 및 배터리 열화도(SOH)에 따라 달라지는데, 여기서는 배터리 열화에 의한 발열특성변화는 무시한다.

셀 발열량은 거시적으로 전기적 저항에 의한 비가역 발열량과 산화 환원반응에 따른 가역 발열량의 합으로 나타낼 수 있으며 이를 식으로 표현하면 식 (10)과 같다. 여기서 T는 절대온도이며 n은 화학양론적 계수로 1이며 F는 패러데이 상수로 96485 C/mol이다.

Q ˙ = r I 2 + ∆ s n F T I

(10)

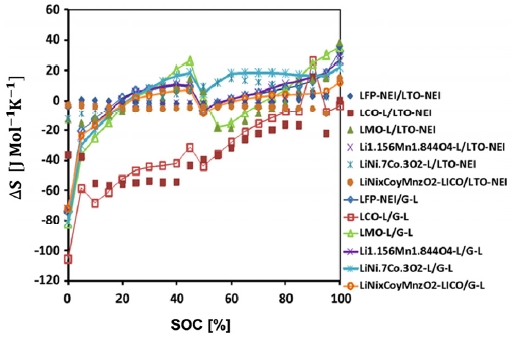
비가역 발열 현상은 충방전에 따른 리튬양이온이 셀 내부 전해질을 이동할 때 이동 저항에 의해 나타나는 현상이며, 기본적으로 이동 저항의 크기는 셀 내부의 온도가 높을수록 낮은 경향을 보인다. 그리고 충방전에 따른 가역 발열은 셀 온도와 충전상태량을 표현하는 SOC에 따른 엔트로피 변화량에 의해 결정되며 비가역 발열현상과 달리 상태에 따라 발열뿐만 아니라 흡열현상도 나타나게 된다. 이는 식 (10)의 가열 발열량항에서 보면 충전과 방전이 전류의 부호가 다르므로 서로 상반된 현상을 나타남을 알 수 있다. 배터리 셀의 전극을 형성하는 물질의 성분에 따른 엔트로피 변화 특성 곡선을 Fig. 6에서 보여준다.

Fig. 6

Entropy change curve of Li-ion cell4)

3.4 배터리 열해석 모델 검증

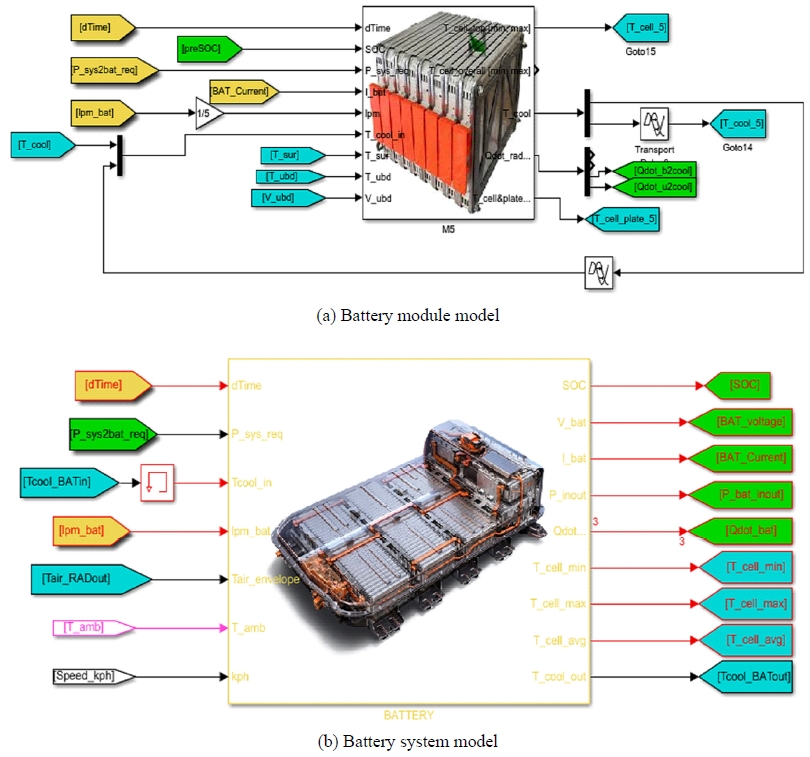
배터리 출입 전력에 따라 셀전압과 셀전류를 계산하고 셀내부의 전자의 이동시 동반되는 엔트로피 변화열과 저항에 의한 발열량을 계산한다. 그리고 앞에서 정의한 배터리 온도 해석모델에 의해 배터리셀 온도와 배터리셀로부터 냉각수로의 전열이 열전달되는 모델을 Matlab/simulink로 구현한 결과가 Fig. 7과 같다.

Fig. 7

Thermal analysis model of battery system

Matlab/simulink로 구현된 모델을 검증하기 위해 배터리에 요구하는 출입전력, 냉각수 입구온과 유량, 외기온 및 초기값을 실차 측정데이터에서 추출하여 입력조건으로 주고, 배터리셀온과 냉각수 출구온 거동을 저부하와 고부하조건에서 각각 수행한 시뮬레이션 결과와 비교함으로써 발열모델과 열저항모델을 검증한다.

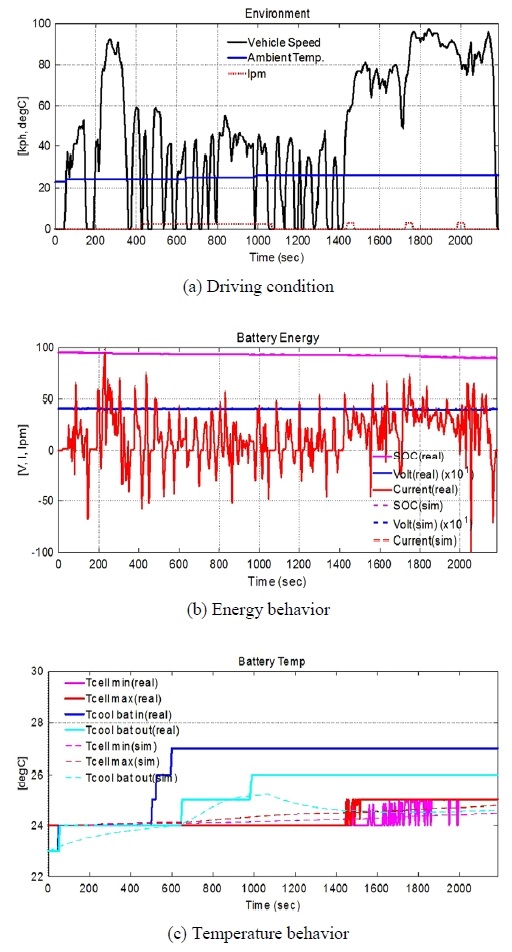
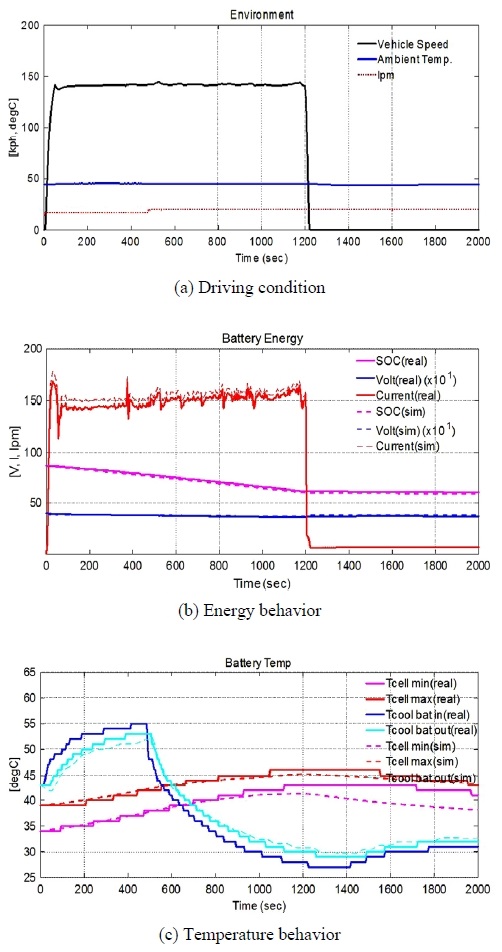
저부하조건으로 UDDS와 HWY모드를 연속으로 수행한 결과와 고부하조건으로 고속모드를 수행한 결과가 각각 Fig. 8과 Fig. 9이다. 그림 (a)는 주행속도 및 외기온을 보여주며, (b)는 SOC, 전류, 전압의 거동을 보여주며 (c)는 배터리온도과 냉각수 출구온 거동을 보여주고 있다. 여기서 실차 센서의 측정 정밀도는 1 °C이며 배터리셀의 측정 위치는 셀 상단의 표면에 위치한다. 저부하 조건에서는 배터리셀 온도와 냉각수 출구온의 시뮬레이션 거동이 실차 평가결과와 유사하게 추종됨을 볼 수 있으나, 1100초 이후 유동 작동이 간헐적으로 이루어져서 냉각수 출구온이 다소 차이를 보인다. 그리고 고부하 조건에서도 배터리셀 온도와 냉각수온 출구온의 시뮬레이션 거동이 실차 평가결과와 유사하게 추종됨을 볼 수 있다. 1200초 이후의 저방전인 idle구간에서는 다소 오차를 보이고 있는 데, 측정 센서가 셀 표면에 접촉되어 측정하는 방식으로 온도가 상승할 때보다 식힐 때는 실제 온도보다 더 높게 측정된 것으로 예상된다. 전반적으로 실차평가결과와 비교했을 때 전기모델, 발열모델과 열저항모델이 적절하게 구현되었음을 확인하였고 이를 바탕으로 다음 장에서 제어로직 변경에 따른 효과를 검증하고자 한다.

Fig. 8

Simulation result of mild load

Fig. 9

Simulation result of heavy load

4. 배터리열부하 예측 최적제어 알고리즘

기존의 냉각 제어알고리즘은 온도, 압력 등이 설정 상태에 도달했을 때의 작동조건을 미리 설정한 룰기반(Rule-based) 제어 또는 PID제어로 이루어진다. 이들은 직관적으로 간단하게 구성될 수 있는 장점이 있는 반면 현재의 상태값에 따른 일괄적이고 획일적인 제어로서 배터리 열관리와 같이 복잡한 시스템에서 부하 예측이나 시나리오기반의 제어 등 전략적인 제어를 반영하기에는 한계가 있다. 또한 냉각 안전율(Safety factor)까지 반영한 기존의 룰기반 냉각 설정제어에서는 성능을 맞추기 위해 냉각전력이 과다하게 소비되는 경우가 종종 있다.

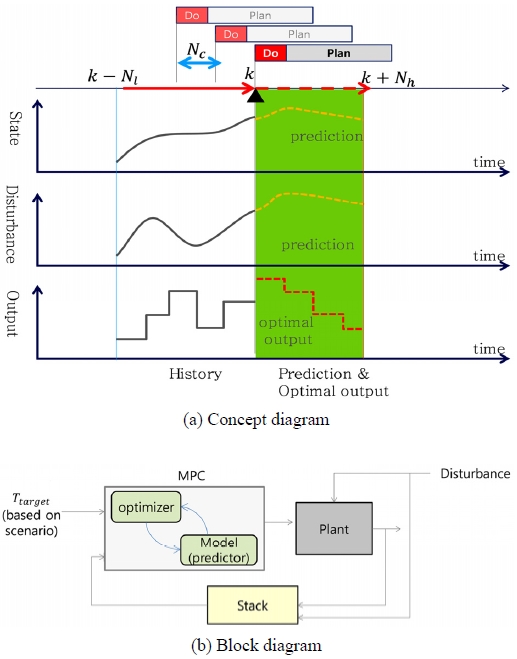
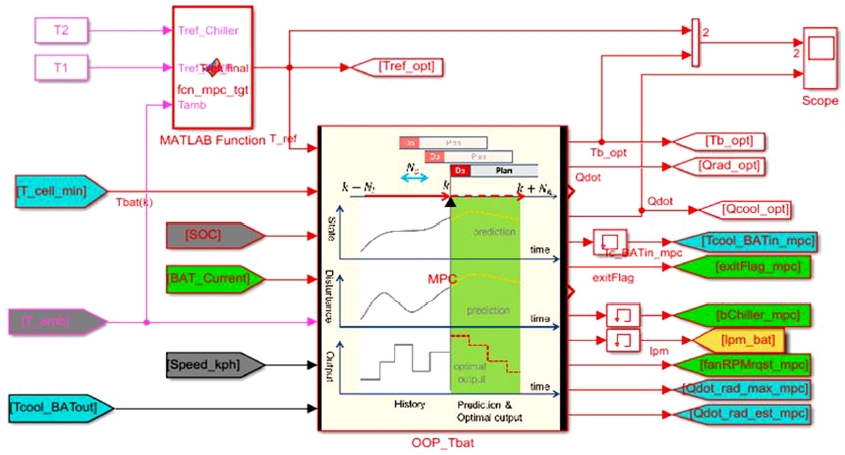
본 연구에서는 시스템의 열부하 예측을 통해 상충관계가 있는 냉각 성능과 소비전력을 최적화할 수 있는 최적운전계획법(Optimal operation scheduling)을 적용하고자 한다. 최적운전계획법은 모델기반 열부하예측 최적제어(MPC, Model Predictive Control)로 Fig. 10(a)에서 나타낸 것처럼, 일정시간간격(N_c)마다 현 시점(k)에서 외란을 포함한 과거이력(k-N_l,...,k-1) 상태값을 활용하여 일정기간(N_h)의 시스템 상태값을 예측하고 성능과 소비전력에 대한 비용함수를 고려하여 최적의 제어값을 출력하는 것이다. 최적운전계획법에 대한 전체 블록선도는 Fig. 10(b)와 같으며 미래 부하를 예측하기 위해서는 미래의 외란 및 상태값을 예측할 수 있는 모델식이 있어야 한다.

Fig. 10

Introduction to optimal operation scheduling

본 장에서는 배터리열관리에 있어 선형모델이론식을 만들고 성능과 냉각전력에 대하여 최적제어알고리즘 이론식을 수립한다. 이를 Matlab 코드로 구현하여 기존 룰기반 제어와의 성능차이를 보여준다.

4.1 상태 예측 동적 선형 모델

본 연구에서는 선형계획법(Linear programming)을 최적운전계획법으로 적용할 것이므로 제어대상인 플랜트의 동적 거동을 선형모델로 모사해야 한다. 그리고 미래 온도변화를 예측하기 위해서는 외란예측모델도 필요하다.

배터리온에 영향을 주는 중요한 외란으로 SOC, 배터리 출입전류, 외기온 그리고 차속을 선정하였고 이들이 제어변수인 배터리온 T_b에 미치는 영향을 식 (11)의 이산형 미분 방정식으로 표현하였고 실험결과와의 비교를 통해 계수를 구하였다. 여기서 k는 현재 시점을 나타내고 k+i는 현재 시점에서 i만큼 떨어진 미래시점을 나타낸다. 그리고 과거데이터의 크기인 N_l은 반응 시상수 정도의 크기를 갖는다. 배터리온도의 과거 이력을 반영하기 위해 시상수 크기인 N_l 시점과 N_l/2시점만을 적용한 이유는 온도 변화가 완만하여 과거의 모든 데이터를 적용할 필요가 없다는 점 그리고 식 (11)의 구조상 현재시점에서 과거 데이터를 이용하여 예측할 수 있는 미래의 최대 크기는 N_h=0.5N_l이기 때문이다.

정리하면 미래의 배터리온도 T_b[k+i]는 우항의 첫 번째와 두 번째 항인 배터리온도의 과거값, 세 번째에서 여섯 번째 항인 미래 외란, 그리고 일곱 번째 항인 미래 조작변수인 냉각수로의 전열량으로 표현된다. 본 논문에서 사용된 설정값은 N_l=10min이다.

T b k + i = a 1 T b k + i - N l + a 2 T b k + i - 0.5 N l + a 3 S O C k + i + a 4 I b k + i + a 5 T a m b k + i + a 6 V k p h k + i + a 7 Q ˙ c o o l k + i

(11)

배터리온에 영향을 주는 외란은 차량 주행 환경 또는 운행상태에 따라 수시로 변화한다. 자율 주행 또는 차량간 통신(V2X)환경에서는 보다 정확한 외란 예측이 가능하나 이런 환경이 갖추어지지 않은 경우, 차량 시스템내의 과거 이력에 의존하여 추정할 수 있다. 일반적으로 과거이력의 평균값을 사용하는데, 식 (12)과 같이 이동평균필터식(Moving Average Filter)으로 나타낼 수 있다.⁵⁾ 여기서 N_d는 외란 학습용 데이터의 크기를 나타낸다.

D j k + i = ∑ a = 1 N d D j k - a / N d

(12)

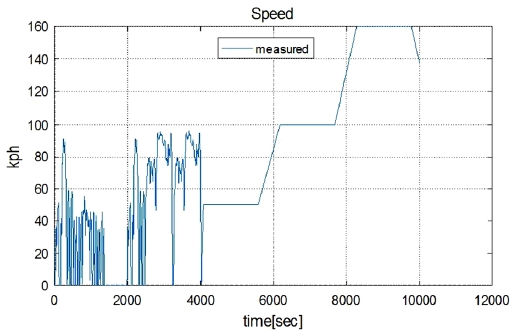
학습용 차량 데이터를 획득하기 위해 Fig. 11과 같이 FTP, HWY모드 및 정속모드 등 다양한 차속 조건으로 구성된 프로파일로 주행하였다.

Fig. 11

Driving mode for learning

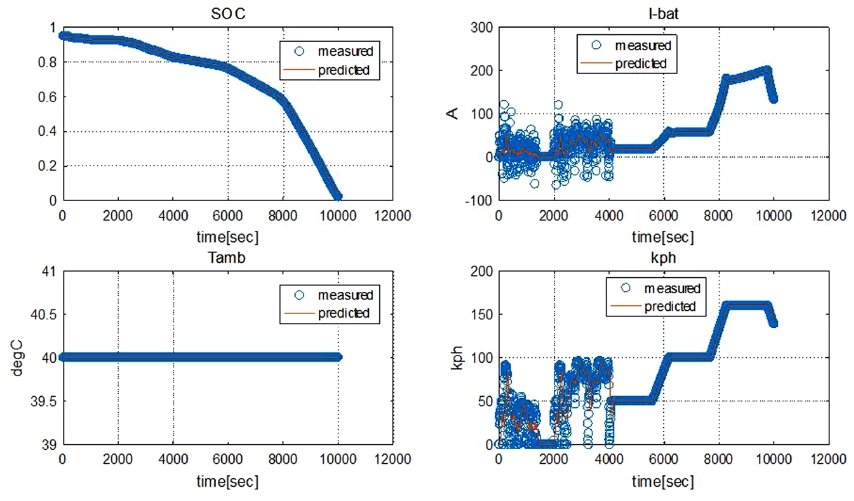
이 평가를 통해 획득한 배터리 출입전류, 차속, 외기온 그리고 SOC의 외란의 실측값 대비 예측한 결과를 Fig. 12에서 보여준다. 이동평균필터를 이용한 외란 예측이 실측값을 추종함을 볼 수 있다.

Fig. 12

Disturbance prediction result

시스템 상태예측 모델을 구한다는 것은 결국 식 (11)에서 각 계수에 해당하는 시스템 변수를 구하는 것이다. 이는 전기차량의 주행패턴에 따른 실험데이터를 활용하여 시스템의 학습에 의해서 구할 수 있다. 식 (11)은 선형식이므로 식 (13)와 같이 일반화할 수 있고 계수값은 다변수에 대한 다중선형회귀법(Multiple Linear Regression)에 의해 식 (14)과 같이 구할 수 있다. 여기서 주의할 것은 학습하기 위해 시계열 데이터(Time sequence data)가 필요하다는 것이다.

y t = ∑ i = 1 n a i x i t

(13)

e 2 = ∑ i = 1 n a i x i t - y t 2 → ∂ e 2 ∂ a i = 0 P t = x 1 t x 2 t … x n t T A = a 1 a 2 … a n T ∑ i = 1 n P t P t T A = ∑ i = 1 n P t y t ∴ A = ∑ i = 1 n P t P t T - 1 ∑ i = 1 n P t y t

(14)

차량 실험데이터를 식 (14)에 의해 구한 각 계수값은 Table 1과 같다. SOC, 전류, 외기온의 계수와 같이 양수값은 배터리온도에 대하여 양의 효과를 나타내며, 차속과 냉각수로의 전열량의 계수와 같이 음수값은 배터리온도에 대하여 음의 효과를 나타낸다.

Table 1

Result of system parameter

4.2 최적제어알고리즘 설계

시스템의 열부하 예측을 통해 상충관계가 있는 냉각 성능과 소비전력을 최적화하기 위한 제어식을 수립한다. 본 연구에서는 산업 활용이 가능하고 비용함수에 대한 확장성이 좋은 선형계획법(LP)를 적용한 모델예측제어(MPC) 알고리즘에 대하여 전개한다.

제어변수는 배터리온과 그와 관련된 열량처리에 있어 중요한 역할을 수행하는 라디에이터와 에어컨의 처리열량을 고려하여 다음과 같이 정의한다.

x k = x k = x k, 1 x k, 2 x k, 3 x k, 4 = Q ˙ r a d k Q ˙ a c k Q ˙ c o o l k T b k - T r e f T

(15)

그리고 비용함수와 이에 대한 제한조건은 다음과 같이 정의한다.

j k = β 1 β 2 β 3 β 4 x k

(16)

s . t E q . 10 0 ≤ Q ˙ c o o l k ≤ Q ˙ m a x - Q ˙ r a d k - Q ˙ a c k + Q ˙ c o o l k ≤ Q ˙ e r r Q ˙ r a d k + Q ˙ a c k - Q ˙ c o o l k ≤ Q ˙ e r r 0 ≤ Q ˙ r a d k ≤ Q ˙ r a d m a x 0 ≤ Q ˙ a c k ≤ Q ˙ a c m a x … T b m i n ≤ T b k ≤ T b m a x

각 데이터들이 시계열인 점을 고려하여 다음과 같이 확장할 수 있다.

X = X k + 1 : k + N p = x k + 1,1 x k + 1,2 x k + 1,3 x k + 1,4 ⋯ x k + N h, n - 1 x k + N h, n T

(17)

m i n x J = f T X s . t A e q X = b e q A i q X ≤ b i q X l ≤ X ≤ X u

(18)

식 (18)에서 각 행렬은 다음과 같이 정의된다.

f = β 1 β 2 β 3 β 4 ⋯ β 1 β 2 β 3 β 4 T A e q = 00 a 7 10000 ⋯ 00 000000 a 7 1 ⋯ 00 ⋯ ⋯ 00 00000000 ⋯ a 7 1 b e q = ∑ j = 1 m a j T b k + 1 - s j + ∑ j = 1 n b j D j k + 1 ⋯ ∑ j = 1 m a j T b k + N h - s j + ∑ j = 1 n b j D j k + N h A i q = - 1 - 1 10 ⋯ 0000 11 - 1 0 ⋯ 0000 ⋯ ⋯ ⋯ 0000 ⋯ - 1 - 1 10 0000 ⋯ 11 - 1 0 b i q = Q ˙ e r r Q ˙ e r r ⋯ Q ˙ e r r Q ˙ e r r T

최종적으로 식 (18)에 대한 해를 구하면, 미래시점의 1~N_h까지의 최적의 값인 X_opt를 구할 수 있으며 첫 번째 값이 다음 시점의 제어기에서 처리해야 할 최적 제어량이다. 즉 최적의 냉각수로의 전열량인 $Q ˙ o p t$ 를 결정하고 이 때의 최적 배터리온인 T_opt를 추정할 수 있다.

4.3 시뮬레이션 결과

배터리온 관리에 있어 적은 에너지로 최적제어를 수행하기 위해 식 (11)을 활용하여 미래의 최적해를 구하는 비용함수를 적용한 식 (18)를 Matlab/simulnk로 구현한 것이 Fig. 13과 같다.

Fig. 13

MPC algorithm implementation block in simulink

배터리온, 외란, 냉각수온, 그리고 배터리온 목표값을 입력으로 주고 MPC 알고리즘에 의해 최적 냉각열량 및 냉각모드를 결정한다. 그리고 냉각모드에서 라디에이터 냉각 모드시 최적 방열량을 만족시키는 최소소모동력의 냉각수 유량펌프 작동속도와 팬작동속도를 결정하며, 칠러 냉각 모드시 시스템 성능에 해당하는 최대 냉력에서의 최대 유량을 기준으로 최적 방열량에 해당되는 유량을 결정하고 이에 따른 목표 냉각수온을 기준으로 컴프레서 작동속도를 자동으로 결정하게 된다.

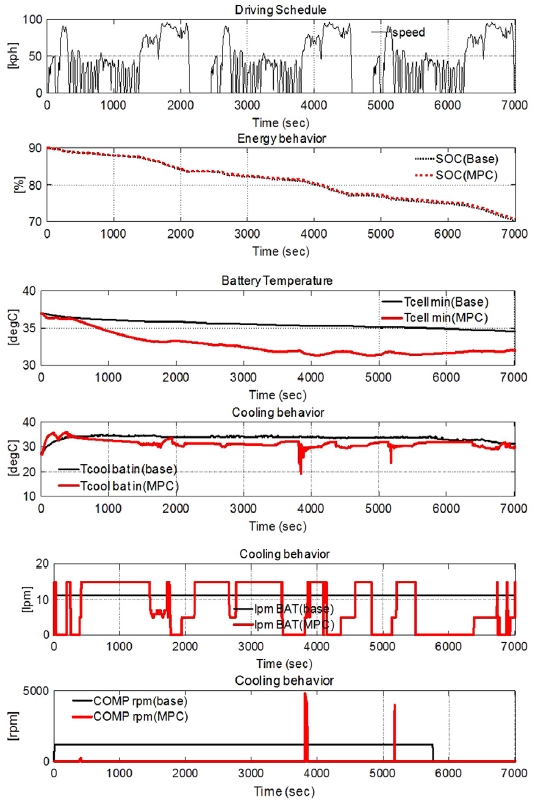
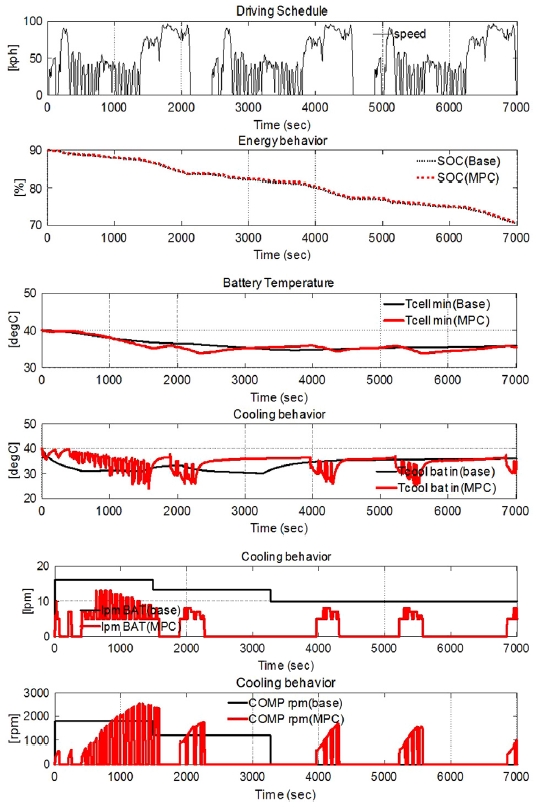
비용함수 가중치 [β₁β₂β₃β₄]는 튜닝요소에 해당되는데, 여기서는 [1 10 0 0]로 설정하였다. 평가주행 모드는 UDDS, HWY모드 그리고 IDLE로 이루어진 사이클을 3세트 반복하였고, 배터리셀 온도 대비 외기온이 낮아 배터리 라디에이터를 통한 냉각이 가능한 경우와 외기온이 높아 에어컨 칠러를 이용해야하는 경우에 대하여 시뮬레이션한 결과를 Fig. 14와 Fig. 15에서 보여준다.

Fig. 14

Simulation result @ ambient 27 °C, initial Temp. of battery cell 37 °C

Fig. 15

Simulation result @ ambient 40 °C, initial Temp. of battery cell 40 °C

Fig. 14와 같이 외기온이 충분히 낮은 경우, 배터리전용 라디에이터를 이용할 수 있는 경우이다. 기존의 룰기반 제어는 배터리셀 온도에 따라 미리 설정된 값의 컴프레서 작동속도와 냉각수유량에 의해 제어되는 반면 MPC는 미래 냉각 부하를 예측하여 소모에너지가 적은 최적의 유량 및 컴프레서 회전속도로 작동시킨다. MPC제어의 경우 룰기반 제어 대비 차량소모에너지는 2.4 % 낮은 수준이면서도 배터리셀 온도가 3 °C 낮게 제어될 수 있음을 알 수 있다. 이는 MPC제어로 적은 냉각에너지로 배터리 내구성 향상에 기여할 수 있고 이로 인해 주행거리 증대가 가능함을 보여준다.

그리고 Fig. 15와 같이 외기온이 높은 경우는 배터리전용 라디에이터를 활용하지 못하고 에어컨 시스템을 활용해서 냉각해야 하는 경우이다. 룰기반 제어 대비 배터리 열모델을 가진 MPC제어의 차량소모에너지는 1.7 % 낮으며 목표온도를 약 1000초 빨리 도달함을 볼 수 있고, 전반적으로 배터리셀 온도는 동등이하로 제어됨을 알 수 있다. 배터리셀 온도가 유지되지 못하고 간헐적으로 하강하는 경우가 발생되는 데, 이는 부하예측모델 또는 배터리 열모델의 부정확성에 기인한다.

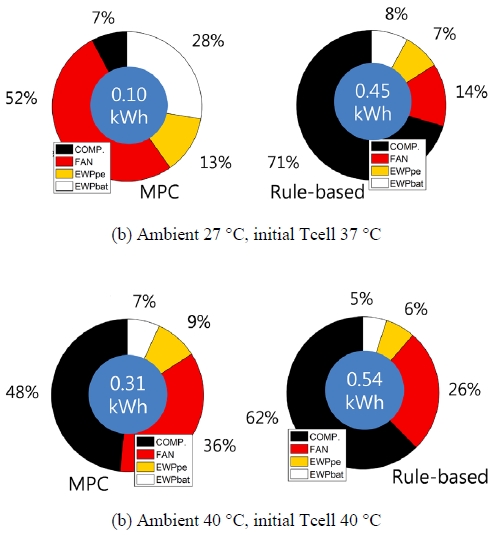
상기 평가에서 냉각 장치만의 소모에너지를 비교하면, Fig. 16에서 볼 수 있듯이 MPC제어가 라디에이터 냉각을 하는 경우 78 %, 칠러 냉각을 하는 경우 43 % 저감되었음을 알 수 있다.

Fig. 16

Energy consumption of auxiliary

5. 결 론

배터리 시스템 열관리 모델을 만들고 검증함으로써 다양한 제어이론에 대한 가상 플랜트로 활용할 수 있도록 하였으며, 열부하 예측 최적제어가 룰기반 제어보다 적은 냉각에너지로 배터리셀 온도를 관리할 수 있으며 배터리 열내구 향상에도 도움이 됨을 확인하였다.

1) 차량 구동 모델과 배터리 시스템 열관리 모델을 Matlab/simulink로 꾸미고, 실차평가결과와 모델 검증을 수행하여 배터리 발열모델, 전기모델과 열전달모델이 타당함을 보였다. 이를 다양한 제어이론에 대한 가상 플랜트로 활용할 수 있다.
2) 배터리 열제어에 있어 열부하 예측 최적제어 이론을 수립하고 시뮬레이션을 통해 룰기반 제어 대비 MPC제어가 냉각에너지를 적게 사용하면서도 배터리온도를 더 낮게 관리함을 확인하였다.
　 - 현재의 배터리셀 온도에 따라 미리 설정된 값으로 컴프레서 작동속도, 냉각수 유량 등을 제어하는 룰기반 제어에 비해 미래의 열부하에 기반한 MPC제어가 적은 에너지로 배터리셀 온도를 관리함을 확인하였다.
　 - 외기온이 셀온도보다 충분히 낮아 배터리 전용 라디에이터를 이용할 수 있는 경우에는 MPC제어가 2.4 %의 차량소모에너지를 저감하면서도 배터리셀 온도도 3 °C 낮게 제어함으로써 배터리 셀 내구향상에 기여하고 냉각에너지는 78 % 저감하였다.
　 - 외기온이 높아 에어컨 칠러를 사용해야 하는 경우에는 MPC제어가 1.7 %의 차량소모에너지를 저감하였고, 목표온도에 1000초 가량 빨리 도달하여 배터리 셀 내구성 향상에 기여하였으며 이 때의 냉각에너지는 43 % 저감되었다.

Nomenclature


m :	mass, kg
g :	gravitational acceleration, m/s²
V :	velocity, m/s or Voltage, V
T :	torque, Nm or temperature, K
F :	force, N
P :	power, W
μ :	rolling resistance coefficient, -
ω :	angular velocity, rad/s
I :	electric current, A
C :	coulomb, C=A*sec
r :	electrical resistance, Ω
N :	number of data, EA
θ :	road inclination, rad
k :	thermal conductivity, W/m-K
x :	control variable, AU
j :	cost function, AU
X :	control variable in time series, AU
J :	cost function in time series, AU

Subscripts


l :	length of past data for learning
h :	length of prediction data (horizon)
b :	battery
lb :	lower bound
ub :	upper bound

Acknowledgments

본 논문은 현대자동차 산학과제 지원을 받아 수행한 연구입니다.

References

R. Farrington, Impact of Vehicle Air Conditioning on Fuel Economy, Tailpipe Emissions, and Electric Vehicle Range, NREL, (2000).
J. Lopez-Sanz, C. Ocampo-Martinez, J. Alvarez-Florez, M. Moreno-Eguilaz, R. Ruiz-Mansilla, J. Kalmus, M. Graeber, and G. Lux, “Nonlinear Model Predictive Control for Thermal Management in Plug-in Hybrid Electric Vehicles”, IEEE Transactions of Vehicular Technology, 66(5), p3632-3644, (2017).
X. Tao, and J. Wagner, “A Thermal Management System for the Battery Pack of a Hybrid Electric Vehicle : Modeling and Control”, Journal of Automobile Engineering, 230(2), p190-201, (2015). [https://doi.org/10.1177/0954407015582323]
V. V. Viswanathan, D. Choi, D. Wang, W. Xu, S. Towne, R. E. Williford, J. G. Zang, J. Liu, and Z. Yang, “Effect of Entropy Change of Lithium Intercalation in Cathodes and Anodes on Li-ion Battery Thermal Management”, Journal of Power Sources, 195(11), p3720-3729, (2010). [https://doi.org/10.1016/j.jpowsour.2009.11.103]
P. Kim, Kalman Filter for Beginners with Matlab Examples, Ajin, (2010).
F. P. Incropera, and D. P. DeWitt, Fundamentals of Heat and Mass Transfer, 3rd Edn., John Wiley & Sons, New York, (2011).
J. S. Arora, Introduction to Optimum Design, Elsevier Korea LLC, (2012).
S. K. Baek, and S. J. Park, “Thermal Analysis of a Battery Cooling System with Aluminum Cooling Plates for Hybrid Electric Vehicles and Electric Vehicles”, Transactions of KSAE, 22(3), p60-67, (2014). [https://doi.org/10.7467/ksae.2014.22.3.060]
M. Y. Ryu, T. W. Kim, S. S. Park, J. S. Lee, and S. J. Park, “A Study on the Characteristics of the Indirect Air Cooling System of a Lithium-ion Battery Module for Vehicle”, 26(5), p663-675, (2018). [https://doi.org/10.7467/ksae.2018.26.5.663]