리튬 폴리머 배터리의 SOC 추정을 위한 확장 칼만 필터의 LSTM 기반 보정방법
1)한국기술교육대학교 기계공학과2)한국기술교육대학교 메카트로닉스공학과
2)Department of Mechatronics, Korea University of Technology and Education, Chungnam 31253, Korea
Copyright Ⓒ 2019 KSAE / 164-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
State of charge(SOC) and open circuit voltage(OCV) are essential for maintaining the performance and preventing battery malfunction in an electric vehicle(EV). Estimation methods about battery have been studied for decades; however, it is still difficult to estimate precise SOC immediately after the discharge. The extended Kalman filter(EKF) is generally used for diagnosis, but its accuracy can be reduced based on the parameter of the battery equivalent model. EKF, which is compensated by the long short-term memory(LSTM) network, is proposed in this paper. LSTM trains the tendency of the battery’s state and proceeds in a way that corrects the result of the EKF according to the load profile after discharging. This proposed method is verified through a comparison with the actual OCV and SOC. The findings of this experiment show the decrease in the margin of error when compared with normal EKF based on different load profiles.
Keywords:
Electric vehicle, Neural network, Long short-term memory, Extended kalman filter, SOC키워드:
전기자동차, 인공신경망, 장단기 기억, 확장칼만필터, 충전량1. 서 론
최근 지구온난화에 의해 급격한 기후변화 및 자연재해가 증가하면서 그 원인에 적지 않은 비중을 차지하는 기존 석유 에너지 차량들의 친환경화에 대한 중요성이 더욱 커지고 있다. 그 중 전기 에너지 기반의 EV는 현재 시판중인 친환경 자동차 중 가장 많은 비중을 차지하고 있다. 또한 현재 EV에 장착되고 있는 리튬 계열 배터리의 발전뿐만 아니라 그래핀 배터리 등 새로운 배터리의 지속적인 개발로 그 시장이 더욱 커질 것으로 기대되고 있다. 이러한 상황에서 성능에 중요한 영향을 미치는 배터리의 SOC를 추정하고자 하는 연구1,2)가 지속적으로 시행되고 있다. SOC는 배터리의 성능유지를 위해 필요한 요소 중 하나로 배터리 관리 시스템(Battery Management System, BMS)이 배터리를 제어하는데 필요한 기준 역할을 수행3)한다.
SOC를 추정하기 위해 크게 2가지 방법이 사용되는데, 첫 번째는 전류적산법(Coulomb count- ing)으로 식 (1)과 같이 계산한다.
| SOCt=SOC0-ηC0∫t0I dt | (1) |
여기서 SOC0 및 C0는 각각 배터리의 초기 충전량 및 최대 전하량을 나타내며 I 는 부하에 인가된 전류이다. η는 전하 효율 계수로써 방전 시 η=1로 가정4)한다. 전류적산법은 식 (1)과 같이 계산이 간단하나 SOC0를 알 수 없고 시간이 지날수록 오차가 누적되는 단점이 존재하여 일반적으로 두 번째 방법인 확장 칼만 필터를 사용한다. 이 방법은 등가모델을 이용해 OCV를 추정하고 OCV-SOC 선도로 SOC를 찾는 방법으로써 노이즈에 강하고 실시간 추정이 가능하다는 장점이 있으나 배터리가 방전 될 때의 온도 및 화학적 변화를 모두 포함하는 모델을 구현하기가 어렵다는 단점이 있어 아직 관련 연구5,6)가 계속 되고 있다.
한편, 2017년 한국에너지공단의 조사에 따르면 전기자동차의 주 사용처는 출퇴근 및 단거리 주행 이며 SOC 70 % 이하일 때 바로 충전을 하는 운전자가 다수였다. 배터리는 화학적 불안정에 의하여 방전 직후 OCV와 휴지 시간 이후 실제 OCV간에 오차가 발생하는데, 위와 같이 자주 충・방전하는 환경에서 전류 적산법과 OCV-SOC 선도를 사용하는 BMS는 방전 직후 정확한 OCV, 즉 SOC의 측정이 어렵기에 과 충전 및 방전으로 인한 영구적인 성능 하락의 가능성이 높다.
따라서 본 논문에서는 EKF가 OCV를 추정할 때 발생하는 모델에 의한 오차를 감소시키고, 다양한 방전 환경에서 정확하게 최종의 SOC를 찾는 것을 목표로 한다. 이를 위해 EKF로 OCV를 추정한 뒤, 추정값과 실측값의 오차를 Recurrent Neural Network(RNN) 중 하나인 RNN-LSTM 기반의 인공신경망으로 보정하는 방법을 제안하고 실제로 측정된 OCV 및 SOC와 제안한 방법의 추정값을 비교하여 이를 검증한다.
2. 확장 칼만 필터
2.1 배터리 모델 및 파라미터 설정
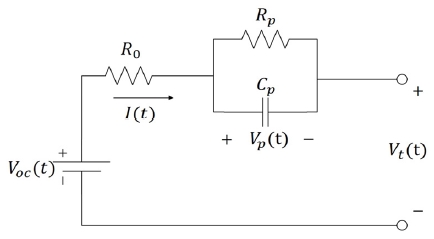
확장 칼만 필터는 비선형 모델의 상태를 추정하기 위하여 널리 사용되는 방법으로 등가 모델의 정확도에 크게 영향을 받는다. 본 연구에서는 모델 자체의 복잡함을 줄이고 신뢰성을 보장할 수 있도록 Fig. 1과 같은 1차 RC 모델을 등가회로7)로 채택하였다.
1차 RC회로는 내부저항 R0 및 분극 저항 Rp, 분극 커패시터Cp로 이루어져 있다. Voc는 개방전압, Vt는 부하 전압이며 Vp는 분극 현상에 의한 과도응답을 나타내는 Rp및 Cp에 대한 분극 전압이다. 여기서 내부저항 R0은 펄스형태의 부하를 인가한 뒤에 식 (2)를 이용하여 구할 수 있다.
| R0=Voc-VinitIinit | (2) |
여기서 Vinit, Iinit는 각각 부하를 건 직후 배터리의 전압과 전류이고 Voc는 배터리의 초기 전압을 나타낸다. 분극저항 Rp, 분극 커패시턴스 Cp는 방전 종료 직후 전압이 상승할 때 시정수(τ = RpCp)로 나타나며 이를 통해 Rp 및 Cp를 구할 수 있다. 다만 이를 위해서는 시스템의 빠른 측정 속도를 요구하므로 본 논문의 실험에서는 Curve fitting으로 값을 설정하였다.
Fig. 1의 1차 RC 등가 회로에서 아래의 식 (3), (4)을 구할 수 있으며, 이를 정리하여 개방전압 Voc, 분극전압 Vp를 상태 벡터, 그리고 전류 I(t)를 입력으로 하는 상태방정식을 식 (5), (6)과 같이 구성할 수 있다.8)
| ˙Voc(t)=I(t)/C0 | (3) |
| Vp(t)=RpI(t-1)(1-e-ΔtRpCp) | (4) |
| [Voc(t+1)Vp(t+1)]=[100e-ΔtRpCp][Voc(t)Vp(t)]+[-1/C0Rp(1-e-ΔtRpCp)]I(t) | (5) |
| Vt=Voc-Vp-IR0 | (6) |
2.2 칼만 필터의 수행
앞서 구해진 1차 RC 모델의 상태방정식을 토대로 칼만 필터를 수행한다. 예측단계는 다음의 식 (7), (8), (9)의 과정을 거친다. 이를 통해 각 시간의 칼만 게인 Kt를 구하게 되며, 식 (10), (11)에서는 계산된 칼만 게인 Kt를 사용하여 상태벡터 xt의 업데이트 과정을 수행한다.
| ˆx-t=Aˆx+t-1+But | (7) |
| P-t=AP+t-1AT+Qt | (8) |
| Kt=P-tCT(CP+t-1CT+Rt)-1 | (9) |
| ˆx+t=ˆx-t+Kt(yt-(Cˆx+t-1+Dut)) | (10) |
| P+t=(I-KtC)P-t | (11) |
여기서 Qt는 모델 오차에 의한 공분산, Pt는 측정 오차에 대한 공분산을 나타낸다. 상태방정식의 A 및 B항은 식 (5) 그리고 C 및 D항은 식 (6)과 같다. 칼만 필터로 추정된 OCV는 OCV-SOC 선도를 통해 SOC로 변환될 수 있는데, 본 논문의 실험에서는 Curve fitting을 통해 아래의 식 (12)와 Table 1의 상수 a1 ... a6를 가지는 5차 다항식으로 OCV와 SOC의 관계를 정의하였다.
| SOC(t)=a1Voc(t)5+a2Voc(t)4+a3Voc(t)3+a4Voc(t)2+a5Voc(t)+a6 | (12) |
일반적으로 칼만 필터를 사용할 때 Rp, Cp 등 등가회로의 내부 파라미터들은 부하 전류, SOC 그리고 온도 등 다양한 환경요소에 의해 변화되며 이는 모델에 기인한 오차로 나타나게 된다. 본 연구에서는 이러한 오차를 RNN-LSTM 인공신경망을 통하여 보정하는 방법을 제안한다.
3. RNN - LSTM
3.1 Recurrent Neural Network
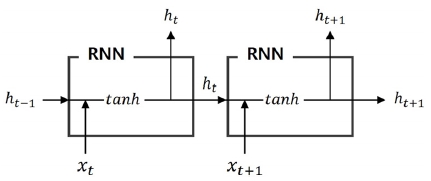
Recurrent Neural Network(RNN)은 다른 인공 신경망들과 다르게 출력된 데이터가 다음 단계의 입력으로 가는 재귀형태로 이루어져 있다. 이러한 특성으로 인하여 하나의 RNN 셀(Cell)을 시간에 따라 연속적으로 붙여 놓은 형태로 표현할 수 있고 시간 t에서의 입력 패턴 뿐 아니라 이전에 입력 받은 데이터의 경향성도 함께 판단한다. 이러한 특성으로 인해 자연어 처리에 응용9)되는 경우가 많지만 최근에는 경향성 있는 데이터의 처리가 필요한 다양한 분야10,11)에 응용되고 있다. 배터리에서도 부하 전류의 변화, 온도 등 주변 환경이 지속적으로 영향을 미치므로 일반적인 형태의 인공 신경망에 비해 좋은 결과를 기대할 수 있다. RNN의 구조는 Fig. 2와 같으며 히든 스테이트 ht의 계산은 식 (13)과 같이 이루어진다.
| ht=σh(Whxt+Uhht-1+bh) | (13) |
여기서 W 및 U는 각각 입력 xt와 히든 스테이트 ht에 대한 가중치를 뜻하며 b는 편향치를 뜻한다. 하지만 RNN에는 단점이 존재하는데 히든 스테이트 ht가 활성화 함수 Tanh를 통해 다음 단계로 전달되므로 신경망이 진행 될수록 ht가 0에 수렴하는 문제가 발생한다. 이 문제를 기울기 소실(Gradient Vanishing)에 의한 장기 의존성(Long Term Dependency)문제라고 하며, 이 때문에 본 논문에서는 해당 문제를 개선한 LSTM 인공 신경망을 사용한다.
3.2 Long Short Term Memory
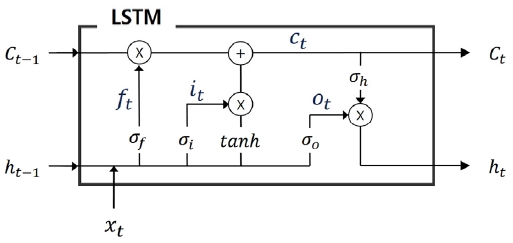
LSTM은 RNN을 기반으로 한 인공 신경망으로써 신경망은 히든 스테이트 ht뿐 아니라 덧셈 연산을 통해 출력되는 셀 스테이트 ct를 다음 스텝의 입력으로 사용함으로써 장기 의존성 문제를 해결한 신경망구조이다. LSTM의 전체적인 구조는 Fig. 3과 같으며 히든 스테이트 ht 및 셀 스테이트 ct는 식 (14), (15), (17)의 망각 게이트, 입력 게이트, 출력 게이트를 결합하여 생성한다.
| ft=σf(Wfxt+Ufht-1+bf) | (14) |
망각 게이트 ft는 이전 시간에서 들어온 셀 스테이트 ct-1를 현재 시간 t에서 어느 정도 반영할지 결정한다. 활성화 함수 σf는 시그모이드 함수를 사용하기 때문에 결과 값이 0에서 1로 갈수록 이전의 데이터를 잊지 않음을 뜻한다.
| it=σi(Wixt+Uiht-1+bi) | (15) |
입력 게이트 it는 셀 스테이트 ct에 반영될 LSTM 셀의 입력을 조정한다. 이때 셀의 입력은 이전 히든 스테이트 ht-1 및 현재 시간의 입력 xt이다. tanh를 활성화 함수로 하는 σi와의 연산을 통해 입력게이트는 -1과 1사이의 값을 갖게 된다.
| ct=ft∘ct-1+it∘σc(Wcxt+Ucht-1+bc) | (16) |
식 (16)을 통해 현재시간 t의 셀 스테이트 ct를 결정한다. 여기서∘는 행렬의 요소를 각각 곱하는 Hadamard product를 나타내며 망각 게이트 ft와 이전 시간의 셀 스테이트 ct-1, 그리고 입력 게이트 it와 σc(Wcxt+Ucht-1+bc)의 Hadamard 연산을 통해 계산한다.
| ot=σo(Woxt+Uoht-1+bo) | (17) |
| ht=ot∘σh(ct) | (18) |
| yt=Wyht+by | (19) |
출력 게이트 ot는 tanh를 활성화 함수 σo로 사용한다. 현재 시간의 히든 스테이트 ht는 식 (18)과 같이 셀 스테이트 ct를 활성화 함수 σh에 대입한 뒤 출력 게이트 ot와 Hardamard 연산을 통해 구한다. yt는 LSTM 셀의 출력으로써 식 (19)와 같이 구할 수 있다.
이러한 방식으로 신경망이 진행되기 때문에 LSTM은 셀 스테이트 ct와 히든 스테이트 ht를 각 게이트를 통해 필요한 값만 선별적으로 취함으로써 장기의존성 문제를 해결하고 이전의 경향성을 계속해서 가져 갈 수 있다.
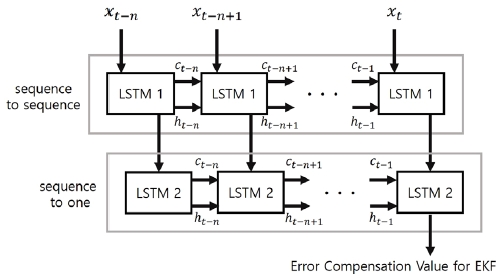
본 논문에서는 위의 Fig. 4와 같이 25개 뉴런을 가진 Sequence to sequence 구조의 LSTM, 그리고 15개 뉴런을 가진 Sequence to one 구조의 LSTM을 2개의 레이어로 구성한 인공 신경망을 제안한다. 신경망 내의 가중치 초기값은 평균 0, 표준편차 0.01을 가지는 가우시안 분포를 따르며 편향치의 초기값은 0이다. 방전 시작 후 부터 방전 종료 직전까지의 전압Vt, 전류It, 셀의 온도 Tavg의 시계열 데이터를 입력으로 사용하며 목표는 방전 종료 후 3시간이 지났을 때의 배터리 전압과 확장 칼만 필터를 이용해 추정된 OCV의 오차이다. 입력 데이터는 시계열 데이터, 출력은 하나이기 때문에 Sequence to one의 입출력을 가지는 LSTM 레이어를 마지막에 두고 그 앞에 Sequence to sequence 형태의 LSTM 레이어를 결합하여 더 깊은 교육을 할 수 있게 구성 하였으며 교육은 경사 하강법(Gradient Descent)을 이용한다.
4. 실 험
4.1 시스템 구성
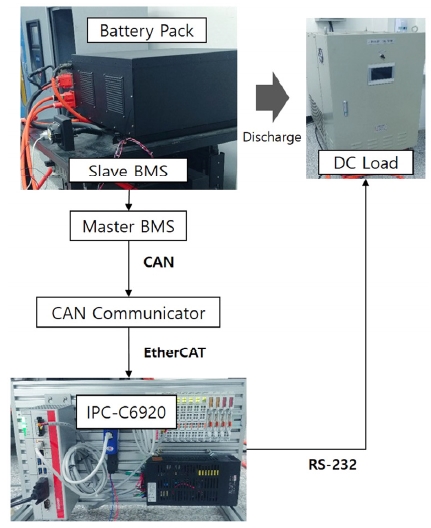
실험을 위하여 Beckhoff사의 IPC-C6920 PC와 Anybus사의 CAN Communicator를 사용하여 배터리 측정 시스템을 구성하였다. PC와 BMS는 CAN과 EtherCAT 통신을 통해 데이터를 주고 받으며, PC는 이를 시각화한다. DC Load는 PC와 RS-232 시리얼 통신으로 연결되어 전류 프로파일을 받아 배터리에 부하를 인가한다.
배터리 팩은 10개의 슬레이브 BMS와 마스터 BMS가 전압, 전류 그리고 온도를 측정하며 시스템의 전체적인 구성은 Fig. 5에 나타내었다. 실험에 사용된 배터리는 LG Chemical사의 셀이 사용되었으며 배터리팩의 스펙은 Table 2에 나타내었다.
실험의 진행은 초기 배터리의 SOC 75 % 이하의 범위에서 시작하며 최대 65 %까지 방전을 수행한다. 방전을 위한 전류 프로파일은 임의로 설정하였으며 인공 신경망의 교육에 사용된 데이터는 총 9개의 데이터 세트로 이 중에서 방전 시작부터 종료 시까지 약 500초간의 전압, 전류, 온도에 대한 시계열 데이터를 사용한다. 그리고 이를 학습데이터 7개, 테스트 데이터 2개로 나누고 LSTM 인공 신경망에 교육하였다. 이후 교육이 완료된 LSTM에 대해 테스트 데이터를 이용하여 결과를 도출해낸다. 그리고 정확도 비교를 위해 일반적인 EKF의 OCV 추정값과 LSTM을 이용해 보정된 OCV값을 비교하며 이를 방전 후 3시간이 지나 안정적인 상태의 OCV 실측값과 비교하였다.
4.2 확장 칼만 필터에 의한 OCV 추정 결과
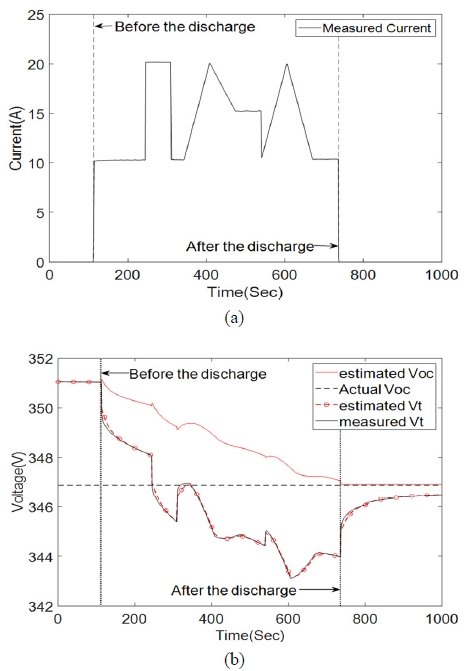
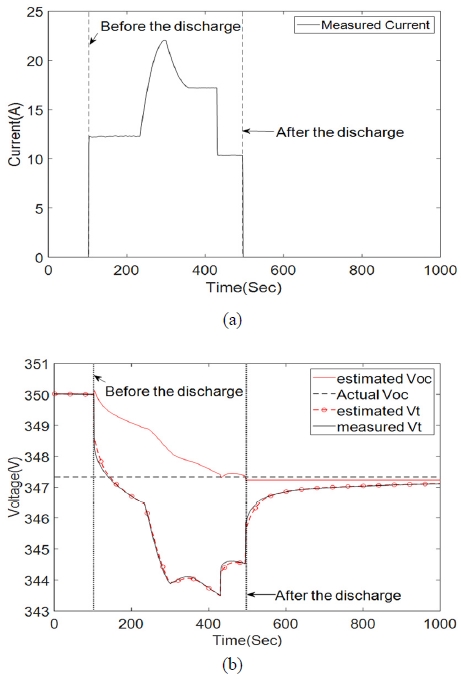
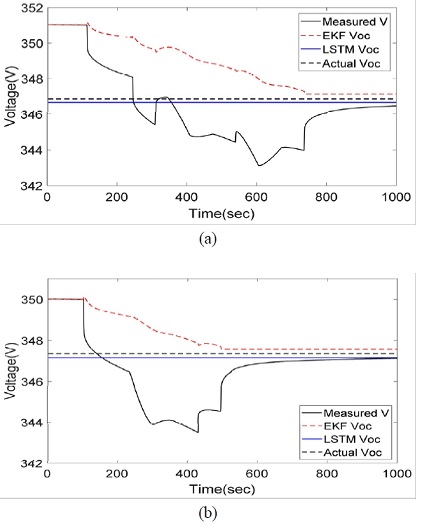
앞 절에서 언급된 1차 RC 회로를 기반으로 한 상태방정식 모델에 EKF를 적용하여 OCV를 추정한다. 본 논문의 실험에서는 실험을 통해 얻은 Table 3의 R0, Rp, Cp 평균값을 사용하였으며 2개의 테스트 데이터 세트에 대하여 EKF를 수행한다. 각각의 테스트는 Test-1, Test-2라고 지칭하며 부하 전류 프로파일 및 칼만 필터에 의한 OCV 추정 결과를 관측기인 부하 전압 Vt와 같이 Fig. 6 및 Fig. 7에 나타내었다.
Fig. 6의 (b) 그리고 Fig. 7의 (b)에서 Actual Voc는 방전이 종료된 뒤 3시간이 지난 후의 배터리 팩의 전압을 나타낸다. EKF는 방전이 종료됨과 동시에 추정 과정을 정지하여 OCV의 추정값이 RC회로의 영향으로 시간에 따라 변화하는 것을 방지한다. Test-1과 Test-2의 초기 OCV는 각각 351.04 V, 350.01 V이며 위 실험의 결과는 Table 4에 정리하였다.
EKF를 사용하였을 때 Test-1 및 Test-2 프로파일에서 추정된 OCV 값과 실제 OCV 값은 위와 같이 각각 RMS(Root Mean Square)오차 0.27 및 0.21의 결과를 보였다.
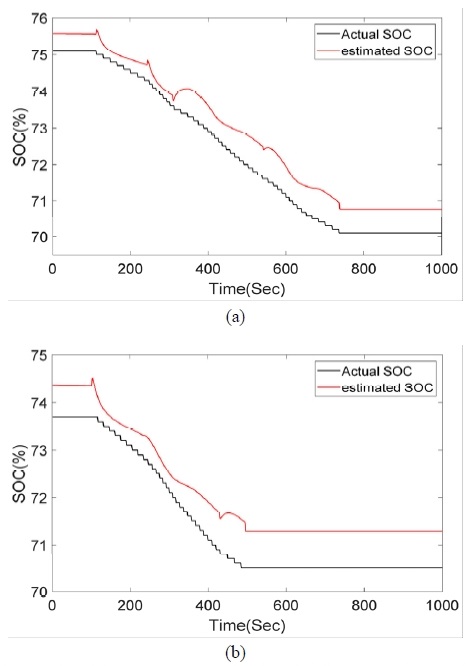
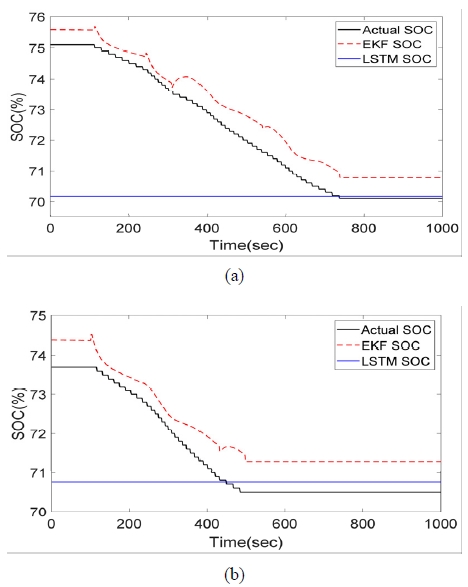
SOC의 추정값은 EKF를 통해 추정된 OCV를 이용하여 구할 수 있으며 Fig. 8에 나타내었다.
위 그래프에서 기준이 되는 Actual SOC는 전류적산법을 기반으로 측정된 결과이다. EKF에 의한 OCV 추정값을 OCV-SOC 선도를 사용해 SOC로 변환하여 도식화하였으며 추정된 SOC와 실제 SOC는 Test-1과 Test-2에서 각각 RMS 오차 0.67 및 0.7을 기록하였다. 실측 값 및 추정값은 아래의 Table 5에 그 결과를 나타내었다.
EKF에 의하여 추정된 OCV 및 SOC에서 발생하는 오차는 1차 RC 회로를 배터리의 등가 회로 모델로 사용함으로써 발생하는 오차, 그리고 상태 방정식에서 Rp, Cp의 값이 고정되어 있기 때문에 발생하는 오차에서 기인했다고 할 수 있다.
4.3 LSTM에 의한 OCV 추정 결과
EKF를 사용하여 OCV를 추정하였을 때 발생하는 오차를 보정하기 위하여 LSTM 인공 신경망을 사용한다. 본 논문에서 제안된 LSTM의 결과 값은 방전 종료 직후 상수 형태로 출력되며 이를 EKF의 OCV 추정 값과 더하여 업데이트 된 OCV를 구할 수 있다. LSTM을 이용해 업데이트 된 추정 결과를 Fig. 9와 Table 6에 정리하였다.
LSTM에 의하여 보정된 OCV값을 기반으로 하여 방전 직후 배터리의 최종적인 SOC를 추정한다. 그 결과를 Fig. 10 및 Table 7에 나타내었으며, 또한 EKF를 사용하여 추정한 OCV 및 SOC의 RMS 오차와 LSTM 인공 신경망을 사용해 보정한 후의 RMS 오차는 Table 8에 나타내고 비교하였다.
5. 결 론
본 연구에서는 전기자동차가 주행 후 정차하였을 때, 즉 배터리의 방전 직후를 가정하여 안정적인 상태의 OCV를 EKF를 이용해 추정하고 발생하는 오차를 LSTM을 통해 보정하는 방법을 제안하였다. 정확한 비교를 위해 SOC 70~65 %의 한정적인 환경에서 실험을 진행하였으며, 고전압 배터리 및 DC Load를 이용하여 방전 실험을 진행하고 방전 후 3시간이 지난 뒤 안정된 상태의 전압과 비교하였다. 확장 칼만 필터는 OCV 및 분극 전압Vp를 상태 벡터로 하는 1차 RC 모델을 사용하였으며 LSTM은 Sequence to sequence 및 Sequence to one 레이어를 결합하여 구성하였다. 실험을 통해 EKF만 적용했을 때에 비하여 LSTM으로 보정하였을 때 RMS 오차가 감소함을 보였다.
현재는 방전 종료 후 안정적인 상태의 OCV를 정확하게 추정하는 것에 초점을 두었으며 실험을 통해 그 가능성을 확인하였으나, 향후 실시간 보정 및 보다 넓은 방전 전류에서의 적용을 위하여 다양한 방전 전류 프로파일에 대한 방전 실험이 선행되어야 할 것이다.
Acknowledgments
이 논문은 2017년도 한국기술교육대학교 교수 교육연구진흥과제 지원에 의하여 연구되었음.
References
- H. He, R. Xiong, X. Zhang, F. Sun, and J. X. Fan, “State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model”, IEEE Transactions on Vehicular Technology, 60(4), p1461-1469, (2011).
-
X. Hu, S. E. Li, and Y. Yang, “Advanced Machince Learning Approach for Lithium-Ion Battery State Estimation in Electric Vehicles”, IEEE Transactions on Transportation Electrification, 2(2), p140-149, (2016).
[https://doi.org/10.1109/tte.2015.2512237]

- E. Meissner, and G. Richter, “Battery Monitoring and Electrical Energy Management Precondition for Future Vehicle Electric Power Systems”, Journal of Power Sources, 116(1-2), p79-98, (2003).
-
S. C. Huang, K. H. Tseng, J. W. Liang, C. L. Chang, and M. G. Pecht, “An Online SOC and SOH Estimation Model for Lithium-Ion Batteries”, Energies, 10, p512-529, (2017).
[https://doi.org/10.3390/en10040512]

- H. G. Kim, S. J. Heo, and G. B. Gang, “Modeling and Characteristic Analysis of HEV Li-ion Battery Using Recursive Least Square Estimation”, Transactions of KSAE, 17(1), p130-136, (2009).
-
K. W. Jang, and G. B. Chung, “A SOC Estimation Using Kalman Filter for Lithium-Polymer Battery”, Transactions of the Korean Institute of Power Electronics, 17(3), p222-229, (2012).
[https://doi.org/10.6113/tkpe.2012.17.3.222]

-
X. Hu, S. Li, and H. Peng, “A Comparative Study of Equivalent Circuit Models for Li-ion Batteries”, Journal of Power Sources, 198, p359-367, (2012).
[https://doi.org/10.1016/j.jpowsour.2011.10.013]

-
H. Dai, X. Wei, Z. Sun, J. Wang, and W. Gu, “Online Cell SOC Estimation of Li-ion Battery Packs Using a Dual Time-scale Kalman Filtering for EV Applications”, Applied Energy, 95, p227-237, (2012).
[https://doi.org/10.1016/j.apenergy.2012.02.044]

- M. Sundermeyer, R. Schlüter, and H. Ney, “LSTM Neural Networks for Language Modeling”, INTERSPEECH Annual Conference Proceedings, p194-197, (2012).
-
H. W. Kim, and S. H. Park, “LSTM Based LKAS Yaw Rate Prediction Model Using Lane Information and Steering Angle”, Transactions of KSAE, 26(2), p279-287, (2018).
[https://doi.org/10.7467/ksae.2018.26.2.279]

- M. Cornia, L. Baraldi, G. Serra, and R. Cucchiara, “Predicting Human Eye Fixations via an LSTM-Based Saliency Attentive Model”, IEEE Transactions on Image Processing, 27(10), p5142-5154, (2018).