[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 27, No. 6, pp.427-433

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jun 2019

Received 05 Oct 2018 Revised 31 Oct 2018 Accepted 04 Mar 2019

DOI: https://doi.org/10.7467/KSAE.2019.27.6.427

프레스 도어 임팩트 빔 경사각이 굽힘 강도에 미치는 영향

이상민¹⁾ ; 강성종^*^{, 2)}

1)대구가톨릭대학교 대학원 자동차공학과
2)대구가톨릭대학교 기계자동차공학부

The Effect of Press Door Impact Beam Inclination Angle on Bending Strength

Sangmin Lee¹⁾ ; Sungjong Kang^*^{, 2)}

1)Graduate Schoot of Automotive Engineering, Daegu Catholic University, Gyeongbuk 38430, Korea
2)Department of Mechanical & Automotive Engineering, Daegu Catholic University, Gyeongbuk 38430, Korea

Correspondence to: ^*E-mail: sjkang@cu.ac.kr

Copyright Ⓒ 2019 KSAE / 163-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

The bending strength of the inclined press door impact beam was numerically evaluated. First, three-point bending analyses were carried out with a changing beam inclination angle. Next, using the system model, including spring elements, which represent the body stiffnesses at the door mounting areas, the modeling simplification was discussed, and the effects of the impact beam inclination was examined. Finally, the structure reinforcement methods required for achieving the strain energy of the horizontal impact beam were inspected. The beam thickness and body mounting stiffness increases were separately considered. Prior to optimizing the beam section shape and increasing the material strength, it is critical to minimize the inclination angle of the door impact beam at the initial design stage.

Keywords:

Bending strength, Press impact beam, Inclination angle, Three point bending analysis, Body stiffness at mounting area, System model

키워드:

굽힘강도, 프레스 임팩트 빔, 경사각, 3점 굽힘해석, 차체 마운팅부 강성, 시스템 모델

1. 서 론

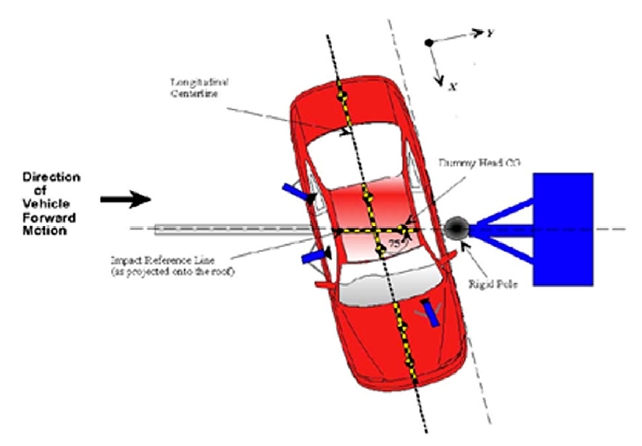
측면충돌 시 승객 상해를 최소화하기 위해 도어 내부에 장착되는 도어 임팩트 빔은 변형가능 영역에서 높은 굽힘강도(Bending strength)가 요구되며 FMVSS 측면충돌 폴 시험은 더 높은 굽힘강도를 요구하고 있다(Fig. 1). 도어 임팩트 빔에는 강관이 적용된 강관 임팩트 빔과 프레스 제작되는 프레스 임팩트 빔(Press impact beam) 두 가지 종류가 있다(Fig. 2).^1,2) 열처리된 강관과 양끝의 브라켓들로 구성된 강관 임팩트 빔에 비해 프레스 임팩트 빔은 일체형으로 압연 강판을 프레스 성형하므로 생산비용이 저렴하나 개단면 형상으로 인해 굽힘강도 확보가 어려워 SUV와 같이 사이드 실 위치가 높은 차종이나 작은 차에 주로 적용되고 있다.

Fig. 1

FMVSS side impact pole test

Fig. 2

Door impact beam type

자동차 부품업체에서는 도어 임팩트 빔 개발을 위해 임의의 지지부간 거리를 설정한 후 경사지지 않은 빔의 3점 굽힘시험을 통해 최대굽힘강도와 변형에너지 등을 상대 비교하고 있다. 그러나 임팩트 빔은 도어 내부의 패키징과 장착위치 선정에 따라 일반적으로 경사지게 위치하므로 굽힘강도 저하가 발생되어 경사각(Inclination angle)을 고려하지 않은 임팩트 빔 굽힘강도 평가는 완성차 수준의 강도와 상이한 결과를 산출하게 된다. 반면 지금까지 프레스 도어 임팩트 빔의 연구는 단면 형상 최적화와 핫 프레스 성형에 의한 고강도화에 연구가 집중되어 왔으며 도어 내 임팩트 빔 마운팅 방법과 경사각이 미치는 영향에 대한 연구는 미미하다.^3-6) 따라서 도어 임팩트 빔 경사각이 굽힘강도에 미치는 영향 정도를 파악함으로써 경사각을 고려한 강도평가의 중요성과 차체 경량화를 위한 임팩트 빔 설계 프로세스 개선 방안에 대해 연구할 필요가 있다.

본 연구에서는 프레스 도어 임팩트 빔의 경사각에 따른 굽힘강도 변화를 파악하고 빔 경사각 존재에 따라 요구되는 구조 보강 수준에 대해 검토하였다. 먼저 3점 굽힘해석(Three point bending analysis)을 통해 경사각 변화에 따른 굽힘강도 저하 경향을 살펴보았다. 다음으로 도어의 차체 마운팅부 강성(Body stiffness at mounting area)을 고려한 시스템 모델(System model)을 구성하여 모델 단순화 타당성을 확인한 후에 경사각에 따른 시스템 모델의 변형에너지 변화를 고찰하였다. 또한 경사각이 없는 임팩트 빔수준의 변형에너지를 확보하기 위해 요구되는 빔 두께 증가와 차체 마운팅부 강성 증가 정도를 검토하였다. 해석에는 LS/Dyna를 사용하였다.⁷⁾

2. 본 론

2.1 경사각에 따른 3점 굽힘 모델 해석

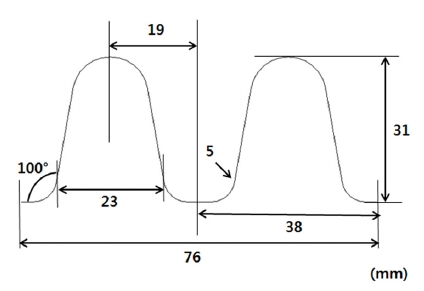
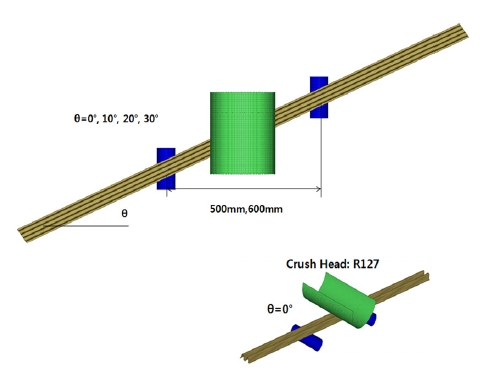
빔 단면형상은 Fig. 3과 같으며 두께는 1.2 mm, 소재는 SPFC 1180을 적용하였다. Fig. 4는 경사진 빔의 3점 굽힘해석 모델을 나타내며 지지부 거리 L_tb=500 mm와 600 mm에 대해 해석하였고 경사각 θ는 0°, 10°, 20°, 30°로 변화시켰다. 요소 평균 사이즈는 3 mm이며 모든 접촉부의 마찰계수는 0.1로 정의하였으며 측면층돌 폴 시험에 적용되는 폴 반경과 동일한 반경 127 mm의 강체헤드에 0.127 m/s의 수직방향 변위 하중을 가해 준정적 해석하였다.

Fig. 3

Press impact beam section

Fig. 4

Three point bending analysis model

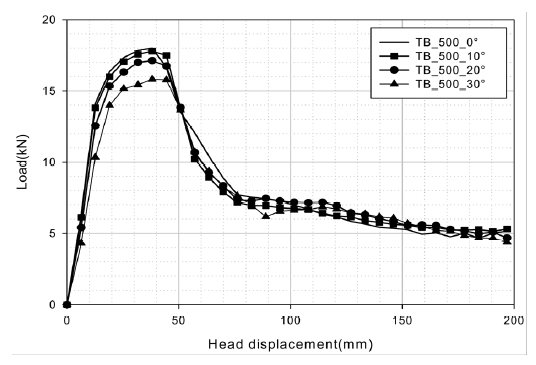
모델명은 TB_지지부거리_경사각으로 정의하였으며 Fig. 5에 지지부 거리 500 mm에 대한 하중-변위 선도를 대표적으로 나타냈다.

Fig. 5

Load-displacement curve from three point bending analysis of Ltb=500 mm

최대굽힘강도 F_{tb_max}와 헤드변위 0~80 mm의 변형에너지 E_tb로 해석결과를 평가하였으며 Table 1에 나타냈다. 경사각 증가함에 따라 최대굽힘강도가 저하하면서 변형에너지도 함께 저하되며 경사각이 20° 이상이 되면 그 저하 정도가 심하게 나타나 지지부 거리 600 mm,경사각 30°인 경우 경사각이 없는 경우에 비해 최대강도 12.9 %, 변형에너지 11.9 %가 각각 감소되었다. Table 2는 F_{tb_max}와 E_tb룰 지지부 사이 빔 중량 W_b로 나눈 단위 중량에 대한 성능을 나타내며 경사각 θ가 커질수록 지지부 사이 빔 중량이 cosθ에 반비례하여 증가함에 따라 단위중량 당 굽힘성능은 더 크게 저하되어 지지부 거리 500 mm, 경사각 30°일 때 경사각이 없는 경우에 비해 단위중량 당 최대강도는 24.2 % 변형에너지는 23.4 % 각각 크게 감소되었다.

Table 1

Maximum load and strain energy from three point bending analysis

Table 2

Maximum load and strain energy per weight from three point bending analysis

2.2 경사각에 따른 시스템 모델 해석

2.2.1 시스템 모델 구성

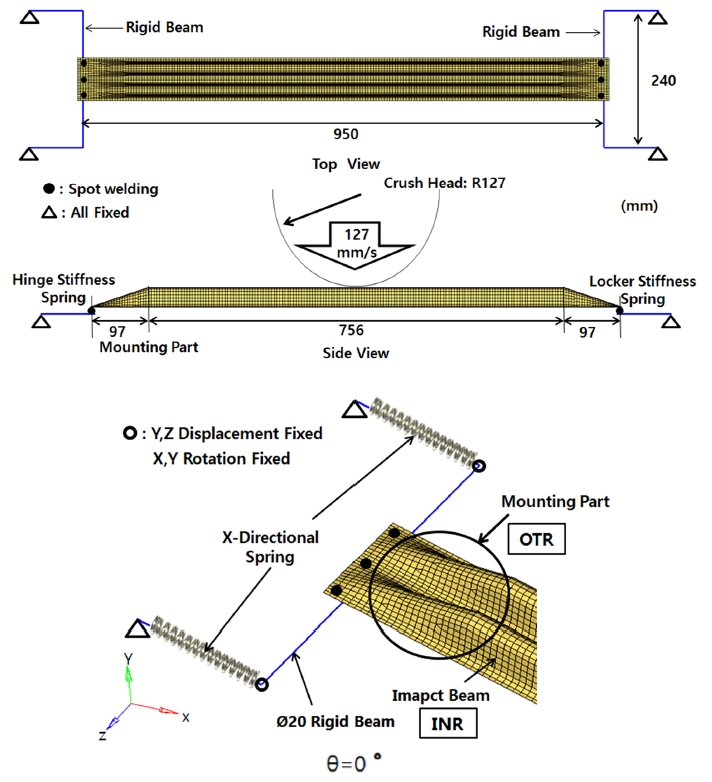
Fig. 6은 경사지지 않은 프레스 빔의 시스템 해석 모델과 하중 및 경계조건을 나타낸다.^6,8)

Fig. 6

System analysis model

강체 빔 사이의 길이는 950 mm로 하였으며 도어 내 안쪽(Inner, INR) 쪽에 마운팅 됨을 가정하여 양끝 97 mm를 마운팅부로 형상화하였다.

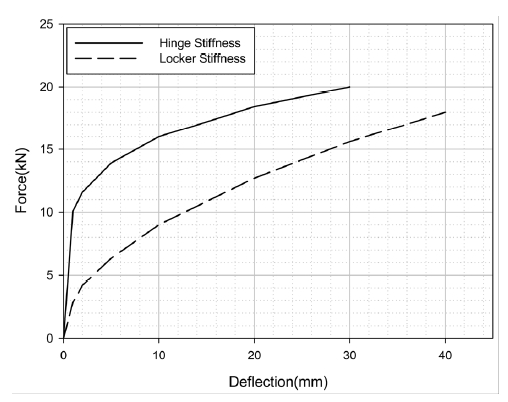
임팩트 빔 양 끝에 직경 20 mm, 길이 240 mm의 강체 빔 두개를 점용접을 가정하여 직각방향으로 결합하였으며 도어의 차체 마운팅부 강성을 나타내는 스프링들을 강체 빔 끝 4곳에 연결시켜 시스템 모델을 구성하였다. 앞의 스프링 2개는 상하 힌지 마운팅부의 차체강성을 그리고 뒤의 스프링 2개는 록커 마운팅부의 차체강성을 각각 나타내며 스프링 끝 4곳을 모두 완전 구속하였다. 강체 빔 끝 모두에 빔 길이 방향의 이동과 빔 폭 방향의 회전 만 가능하도록 구속조건을 정의하였으며 3점 굽힘해석과 같은 동일한 변위하중을 빔 중앙에 수직방향으로 가하였다. 실차에서 도출된 마운팅부 강성을 이용하여 앞 2개 스프링에는 Fig. 7의 힌지 강성을 그리고 뒤 2개 스프링에는 Fig. 7의 록커 강성을 각각 정의하였다.

Fig. 7

Spring stiffness

2.2.2 경사진 빔 시스템 모델링 단순화 타당성 검토

설계초기 다양한 장착위치와 경사각을 갖는 임팩트빔의 굽힘강도 평가가 필요하며 모델링 시간 단축을 위해 모델링 단순화 기법이 요구된다.

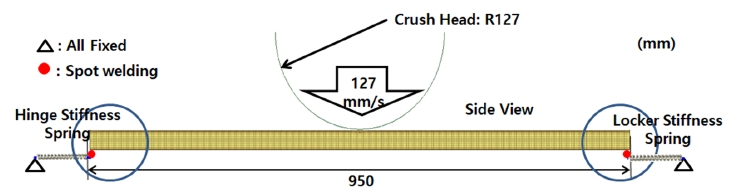
먼저, 경사각이 없는 경우에 대해 양 끝 마운팅부를 형상화하지 않은 일정단면 빔 모델에 대해 해석을 수행하여 빔 형상 단순화의 타당성을 검토하였다. 양끝의 빔 마운팅부를 형상화한 Fig. 6과 달리 Fig. 8은 빔 전체에 일정단면을 적용하고 강체 빔을 연결시킨 모델 SS_US_0°이며 하중 경계조건은 Fig. 6과 동일하게 적용하였다.

Fig. 8

System analysis model of uniform section beam

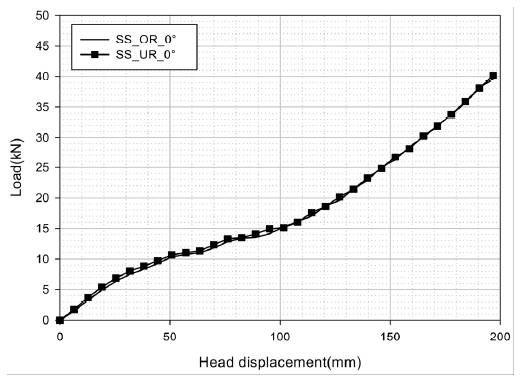
Fig. 6 모델인 SS_OR_0° 해석결과와 함께 Fig. 9에 하중-변위 곡선을 나타냈으며 빔 끝단부 형상이 영향을 주는 초기 변위 60~80 mm 구간에 미소한 차이를 나타낼 뿐 두 모델의 하중 곡선이 전체적으로 유사하게 나타났다. 따라서 경사진 빔의 실차 적용을 고려한 빔 마운팅부의 상세 형상화는 시스템 모델 굽힘강도에 영향이 없음을 알 수 있다.⁶⁾

Fig. 9

Load-displacement curve from system analysis of uniform section beam

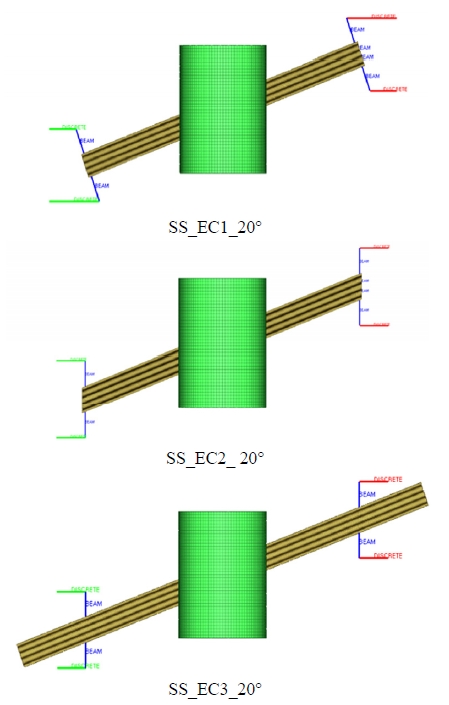
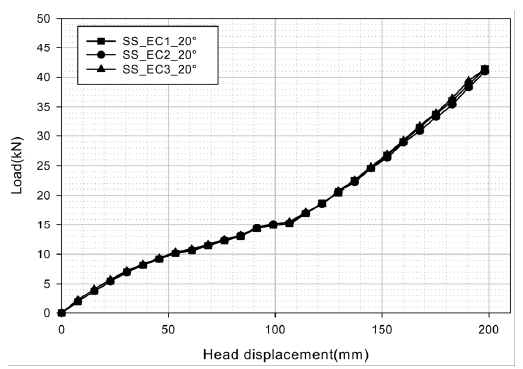
다음으로 빔 경사각 변화에 따른 시스템 모델링 방법의 단순화 타당성을 검토하기 위해 20° 경사진 일정단면 빔에 대해 모델링 방법을 3가지로 변경하여 해석을 수행하였다. Fig. 10에서 모델 SS_EC1_20°는 경사각 20° 만큼 회전된 빔에 빔 길이방향에 직각을 유지하도록 강체 빔을 연결시킨 모델이며 모델 SS_EC2_20°는 충분한 길이의 빔을 모델링하여 20° 만큼 회전시키고 강체 빔 장착위치의 빔 바깥부분을 잘라내고 국부적으로 요소를 다시 메싱(Meshing)한 후에 강체 빔을 도어 상하방향으로 장착시킨 모델이다. 또한 모델 SS_EC3_20°는 충분한 길이의 빔을 모델링하여 경사각 만큼 회전시킨 후 도어 상하방향으로 위치시킨 강체 빔 용접부의 절점들과 인근 임팩트 빔 절점들을 연결시킨 모델이다. 경계 및 하중조건은 Fig. 6과 동일하며 하중-변위 선도는 Fig. 11과 같다. 3가지 모델 모두 전체적으로 유사하게 산출되어 임팩트 빔 개발 시 도어 내 장착위치 변화와 경사각 변화에 따라 순발력 있게 굽힘해석을 수행하기 위한 시스템 모델링 기법으로 SS_EC3가 가장 적합하다고 판단된다.

Fig. 10

Different modeling method for system analysis

Fig. 11

Load-displacement curve from system analysis using different modeling method

2.2.3 경사진 빔의 시스템 해석

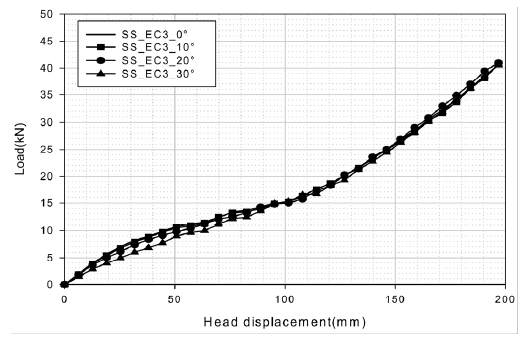
SS_ESC3의 모델링 기법을 적용하여 10°와 30° 모델을 추가 구성하여 해석을 수행하였다. 모델명은 SS_EC3_경사각으로 정의하였으며 Fig. 12는 경사각 20° 모델의 변형형상을 그리고 Fig. 13은 하중-변위 선도를 나타낸다. Table 3에 빔 자체 굽힘강도의 영향이 큰 변위 0~100 mm에서의 변형에너지 E_{s_100}과 차체 마운팅부 강성이 영향을 크게 미치는 변위영역을 일부 포함하는 변위 0~150 mm에서의 변형에너지 E_{s_150}을 비교하였으며 아울러 변형에너지 E_{s_100}을 강체 빔 사이의 빔 중량 W_s로 나눈 E_{s_100}/W_s를 나타냈다.

Fig. 12

Deformed shape from system analysis of SS_EC3_ 20°

Fig. 13

Load-displacement curve from system analysis

Table 3

Strain energy from system analysis

앞서의 3점 굽힘해석과 마찬가지로 경사각이 증가할수록 변형에너지가 감소하여 20° 이상이 되면 변형에너지 저하가 크게 나타났으며 빔 자체 굽힘강도의 영향이 큰 E_{s_100}의 경우 보다 뚜렷한 저하가 나타나 경사각 30°의 경우 13.9 % 감소되었다. 경사각 증가에 따른 빔 중량 증가로 인해 단위중량에 대한 변형에너지는 더 큰 비율로 감소하여 30°의 경우 단위중량에 대한 E_{s_100} 감소율은 25.1 %에 달하였다.

2.3 경사각이 없는 빔 수준의 변형에너지 확보를 위해 요구되는 구조 보강 정도

경사각 20°와 30°의 시스템 모델 SS_EC3를 대상으로 경사각이 없는 임팩트 빔의 변형에너지를 목표로 했을 때 요구되는 빔의 두께증가와 도어의 차체 마운팅부 강성증가 정도를 검토하였다.

2.3.1 빔 두께 증가

기존 두께 1.2 mm에서 0.05 mm 씩 증가시켜가면서 검토한 결과 Table 4와 같으며 경사각이 없는 빔과 대등한 성능을 갖는 최소 요구 두께는 20°의 경우 1.25 mm 그리고 30°의 경우 1.40 mm로 추정되며 이때 각각 4.2 %와 16.7 %의 중량 증가가 초래된다.

Table 4

Strain energy of thickness increased system model

2.3.2 도어 차체 마운팅 강성 증가

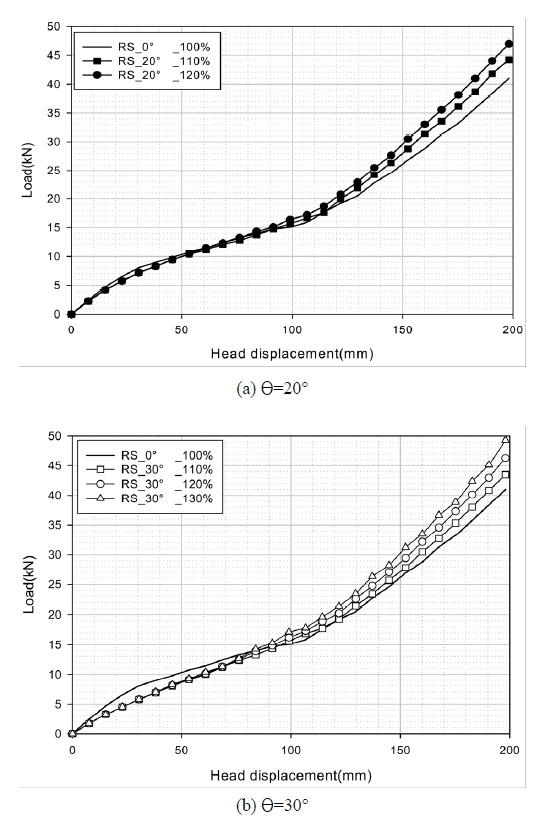
도어 차체 마운팅부 강성을 나타내는 시스템 모델의 스프링 강성을 어느 정도 증가시켜야하는지 검토하였다. SS_EC3 모델에 대해 스프링 강성을 기존 대비 110 %, 120 %, 130 %로 하여 해석하였으며 차체 마운팅부 강성이 충분한 영향을 미치는 변위 0~200 mm의 변형에너지 E_{s_200}를 포함하여 결과를 비교하였다. 모델명은 RS_경사각_강성(%)로 정의하였으며 하중-변위 곡선은 Fig. 14와 같으며 변형에너지 결과는 Table 5와 같다.

Fig. 14

Load-displacement curve of system model with increased body mounting stiffness

Table 5

Strain energy of system model with increased body mounting stiffness

경사각 20° 빔의 경우 경사각이 없는 빔의 변형에너지수준을 확보하기 위해서는 약 20 %의 도어 차체 마운팅부강성 증가가 요구된다. 한편 경사각 30° 빔의 경우 E_{s_150}과 E_{s_200} 목표 달성을 위해서는 약 30 %의 차체 마운팅부 강성 증가가 요구되나 그럼에도 불구하고 빔 자체의 굽힘강도가 지배적인 역할을 하는 0~100 mm까지의 변형에너지 E_{s_100}은 뚜렷한 증가를 나타내지 않으므로 이 영역에서도 목표를 달성하기 위해서는 마운팅부 강성중가와 함께 빔 두께증가가 함께 요구된다. 도어가 마운팅되는 부위의 차체강성을 20~30 % 정도 증가시키기 위해서는 차체 필라부 보강이 필요하고 그에 따른 큰 중량 증가가 초래된다. 이상의 결과에서 도어 임팩트 빔의 형상 최적화나 소재 고강도화에 앞서 도어 초기설계 단계에서 빔 경사각을 최소화하는 것이 매우 중요함을 알 수 있다.

3. 결 론

프레스 도어 임팩트 빔의 경사각이 굽힘강도에 미치는 영향을 연구한 결과 다음과 같은 결론들이 산출되었다.

1) 경사진 3점 굽힘해석 결과 경사각이 증가함에 따라 최대강도가 저하하면서 변형에너지도 함께 저하되며 경사각이 20° 이상이 되면 저하 정도가 크게 나타난다. 지지부 거리가 600 mm이고 경사각이 30°인 경우 경사각이 없는 경우에 비해 최대굽힘강도가 12.9 %, 변위 0~80 mm까지의 변형에너지가 11.9 % 각각 감소되었다. 빔 경사각이 클수록 빔 중량이 증가되어 지지부 거리 500 mm, 경사각 30°일 때 경사각이 없는 경우에 비해 단위중량 당 최대굽힘강도는 24.2 %, 변형에너지는 23.4 % 각각 크게 감소되었다.
2) 설계초기 다양한 사이즈와 경사각을 갖는 임팩트 빔의 신속한 굽힘해석을 위한 시스템 모델링 기법의 타당성을 확인하였다.
3) 도어 차체 마운팅부 강성을 고려한 시스템 모델 해석을 수행하였다. 해석결과 3점 굽힘해석과 마찬가지로 경사각 증가에 따라 빔 변형에너지가 감소되었으며 경사각이 20° 이상이 되면 그 감소 정도가 크게 나타났다. 경사각 30°인 경우 경사각이 없는 경우에 비해 빔 자체의 굽힘강도 영향이 큰 변위 0~100 mm 영역에서의 변형에너지가 13.9 % 감소되었고 빔 단위 중량당 변형에너지는 25.1 %나 감소되었다.
4) 경사각이 없는 빔과 대등한 변형에너지를 확보하기 위해 요구되는 빔 두께증가 정도와 차체 마운팅부 강성 증가 정도를 각각 검토한 결과 두께의 경우 경사각 20° 빔은 0.05 mm 그리고 경사각 30° 빔은 0.20 mm 이상의 두께 증가가 요구되어 각각 4.2 %와 16.7 %의 중량 증가가 초래된다. 한편 차체 마운팅부 강성의 경우는 경사각 20° 빔은 약 20 %의 차체 마운팅부 강성 증가가 요구되나 경사각 30° 빔은 약 30 %의 강성 증가에도 0~100 mm까지의 변형에너지에 큰 변화가 없어 빔 두께증가 등이 함께 적용되어야 한다. 도어 임팩트 빔 경사각 증가에 따라 중량이 증가하는 반면 굽힘강도가 저하되며 강도 확보를 위한 두께 증가와 차체 마운팅부 보강 등에 의해서 큰 중량증가가 초래될 수 있다.
5) 차체 경량화 설계를 위해서는 도어 초기 설계단계에서 임팩트 빔의 경사각을 최소화하는 것이 중요하며 경사진 빔에 대한 강도해석을 통해 단면형상 최적화나 소재 고강도화 방법을 고찰하여야 한다.

References

S. H. Lim, K. W. Lee, and D. S. Kim, “Design Concept Study of Body Structure According to Euro and North America Side Impact Tests”, KSAE Fall Conference Proceeding, p1275-1280, (2003).
S. J. Kang, “Strength of Pipe Type Door Impact Beam with Changed Bracket Mounting Method and TRP Application”, Transactions of KSAE, 24(4), p379-385, (2016). [https://doi.org/10.7467/ksae.2016.24.4.379]
H. Lim, S. Y. Lim, and Y. B. Chun, “Study on Optimal Design of Cold Forming Door Impact Member”, KSAE Annual Conference Proceedings, p980-990, (2014).
S. B. So, J. H. Kim, H. T. Choi, and C. Ha, “Shape Development of Door Mounting Integrated Impact Beam”, KSAE12-G0005 p25-32, (2012).
K. R. Jo, and S. J. Kang, “The Section Design of Press Door Impact Beam for Improving Bending Strength”, Transactions of KSAE, 25(1), p74-81, (2017). [https://doi.org/10.7467/ksae.2017.25.1.074]
K. R. Jo, and S. J. Kang, “The Effect of Mounting Location in Door and Body Stiffness on Press Door Impact Beam Bending Strength”, Transactions of KSAE, 25(2), p272-278, (2018). [https://doi.org/10.7467/ksae.2018.26.2.272]
LS-DYNA User’s Manual, Nonlinear Dynamic Analysis of Structures, Version 971, LSTC, (2006).
B. K. Chun, and S. J. Kang, “Development of Side Door Intrusion Analysis Technique Using Simple Concept Model”, KSAE Spring Conference Proceedings, p517-524, (1994).