[ Article ]

Transactions of The Korean Society of Automotive Engineers - Vol. 27, No. 4, pp.301-308

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Apr 2019

Received 30 Jul 2018 Revised 01 Nov 2018 Accepted 18 Dec 2018

DOI: https://doi.org/10.7467/KSAE.2019.27.4.301

전륜 듀얼 모터 토크 벡터링 시스템의 제어 알고리즘 개발 및 조종 안정성 평가에 관한 연구

박재영¹⁾ ; 이재우¹⁾ ; 허승진^*^{, 2)}

1)국민대학교 자동차공학전문대학원
2)국민대학교 자동차공학과

Study on Control Algorithm Development of Front Wheel Driven Dual Motor Torque Vectoring System and Handling Performance Evaluation

Jae-Young Park¹⁾ ; Jae-Woo Lee¹⁾ ; Seung-Jin Heo^*^{, 2)}

1)Graduate school of Automotive Engineering, Kookmin University, Seoul 02707, Korea
2)School of Automotive Engineering, Kookmin University, Seoul 02707, Korea

Correspondence to: ^*E-mail: sjheo@kookmin.ac.kr

Copyright Ⓒ 2019 KSAE / 161-07
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

This study developed a torque vectoring control algorithm to improve the handling performance of an electric vehicle and to evaluate the performance of the vehicle dynamics for enhanced controllability and stability. First, this study configured the control algorithm with a supervisory controller that decides the control mode by checking the current driving status of the vehicle and a target yaw rate calculator that reflects the steady-state and transient-state response characteristics according to the control mode, as well as the reference yaw rate calculation, desired yaw moment calculation, and transferred torque calculation. The control mode consists of the agile mode that controls the torque vectoring to improve controllability, and the safe mode that controls the torque vectoring to improve stability. Second, this study performed the modeling of the dual motor type torque vectoring system and an EV AWD vehicle. Finally, this study defined the driving test scenario and evaluation method, as well as the quantitative performance index for each vehicle test, and established a co-simulation environment for the handling test evaluation. It was found that when a vehicle is controlled by applying the torque vectoring system, the handling performance improved according to controllability and safe mode by verifying the simulation.

Keywords:

Torque vectoring, Electric vehicle, Vehicle dynamics, Handling test, Dual motor system

키워드:

토크벡터링, 전기차, 차량동역학, 핸들링 시험, 듀얼 모터 시스템

1. 서 론

1.1 연구 배경

자동차는 더욱 빠르고, 쾌적하고, 안전하게 운전자를 목적지까지 도달하게 함으로써 우리 삶에 꼭 필요한 이동수단이지만, 미세먼지 증가, 지구 온난화 가속, 화석에너지 고갈 등의 사회 문제들이 야기되고 있다. 자동차 업계에서는 이런 문제를 해결하기 위해 기존 화석연료의 사용을 최소화하고 연비향상을 위한 EV, HEV, PHEV, FCEV 등 다양한 방식의 환경차를 출시하고 있다. 최근 소비자들은 환경차를 접하게 되면서 기존 고성능 내연기관 차량과 마찬가지의 구동 및 제동, 승차감 및 조종 안정성, 안전, 소음진동, 내구 성능 등을 요구하고 있고, 자동차 업계에서는 소비자들의 요구사항을 만족시키기 위하여 고성능 환경차의 요소 기술 개발에 관한 많은 연구를 진행하고 있다. 대표적으로 모터를 보조 동력원으로 사용하여 가속성능을 향상하거나, 전･후륜 구동력 분배 또는 토크 벡터링 기술을 적용하여 핸들링 성능을 향상하는 등 환경차의 차량동역학적 성능 향상에 관한 연구가 수행되고 있다.

1.2 연구 동향

차량의 안정성 향상을 위한 제어 기술은 오랜 시간 동안 연구됐다. ABS(Anti-lock Braking System)는 제동 시휠 잠김 현상을 방지하고, TCS(Traction Control System)는 가속 시 휠 슬립 현상을 방지한다. 선회 상황에서 ESC(Electronic Stability Control)는 엔진의 동력을 제한하거나, 바퀴 중 하나 이상에 브레이크를 적용하여 차량의 안정성을 유지하도록 도와준다. 이 시스템들은 차량의 안정성을 향상하는 관점에서는 매우 유리하지만, 엔진 동력 제한 및 브레이크를 사용함으로써 차량의 종방향 속도를 감소시키기 때문에 운전자의 의도와는 별개로 구동 성능 관점에서는 불리하다. 이런 단점을 개선하기 위해 구동 토크 전달 기반의 토크 벡터링 시스템에 관한 연구가 수행되기 시작하였다. 센터 커플링을 사용하여 구동력을 전륜에서 후륜으로 전달함으로써 종방향 속도를 유지하면서 후륜 횡력을 줄여 차량의 언더스티어 발생을 억제해 선회 안정성을 향상했다. 그리고 e-LSD(Electronic Limited-Slip Differential) 및 토르센 차동장치(Torsen Differential)를 사용하여 고속 선회 시 선회 내측 바퀴에 슬립이 발생하는 상황에서 슬립이 작은 선회 외측에 구동 토크를 전달하여 오버스티어 발생을 억제해선회 안정성을 향상했다. 선회 속도를 유지하면서 안정성을 향상하는 관점에서는 매우 유용한 시스템이지만, 구동 토크를 단방향으로 전달하기 때문에 센터 커플링은 오버스티어 발생을 e-LSD 및 Torsen Differential은 언더스티어 발생을 제어할 수 없는 한계가 존재한다. 이런 시스템의 한계를 극복하기 위해 구동 토크를 선회 내측에서 외측으로 또는 외측에서 내측으로 바퀴에 토크 전달 방향 및 양을 제어하여 상황에 따라 언더스티어 및 오버스티어 발생을 억제할 수 있도록 클러치를 사용한 능동형 차동장치(Active Differential) 토크 벡터링 시스템이 개발되었다.

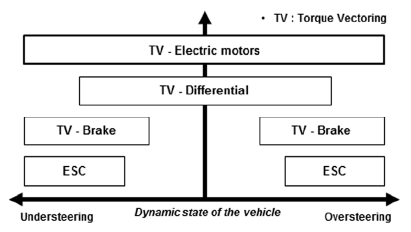
최근에는 모터를 사용하여 회생 제동이 가능하고 좌우 토크를 독립적으로 제어 가능한 토크 벡터링 시스템에 관한 연구가 활발하게 진행되고 있다. 모터를 사용할 경우 모터의 빠른 응답 특성과 넓은 제어영역을 활용하여 토크 벡터링 기술을 적용하기에 유리하다. Fig. 1처럼 능동식 차동장치(Active Differential)보다 넓은 제어 범위 및 100 % 좌우 독립제어가 가능하고, 브레이크나 ESC를 사용하는 제동 시스템 방식보다 미세한 언더스티어 및 오버스티어 영역에서 제어할 수 있는 장점이 있다.^2,11)

Fig. 1

Range of action of various torque vectoring system

본 논문에서는 전기차의 조종 안정성(Handling) 향상을 위한 전륜 듀얼 모터 방식의 토크 벡터링 시스템에 토크 벡터링 제어 알고리즘을 설계하여 적용한다. 그리고 토크 벡터링 성능평가를 하기 위한 시뮬레이션 환경을 구성하고, 차량의 조종 안정성 관점에서 성능을 분석하는 것을 목표로 한다.

2. Torque Vectoring 시스템

2.1 Torque Vectoring 개요

2.1.1 Torque Vectoring 원리

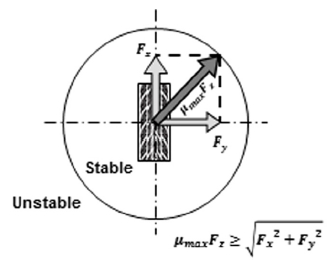
토크 벡터링(Torque Vectoring), 또는 ATD(Active Torque Distribution)은 각각의 바퀴 토크를 가변적으로 제어하는 시스템이다. 바퀴 토크의 변화는 종방향 타이어 힘을 변화시키고, 캄의 마찰원의 원리로 인해 횡방향 타이어 힘도 변화시킨다. 여기서 캄의 마찰원의 원리는 Fig. 2처럼 타이어에 발생하는 총 마찰력의 크기는 횡방향 힘과 종방향 힘의 합 벡터 크기를 초과하지 않는다는 원리이고, 토크 벡터링에서 타이어 힘들과의 관계를 설명하기 위해 사용된다.¹⁾

Fig. 2

Kamm’s friction circle principle

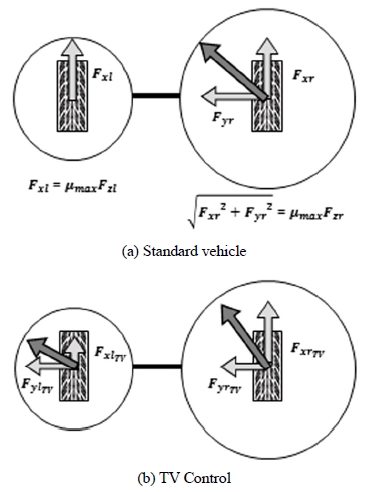
토크 벡터링의 개념은 작동 원리를 통해 설명할 수 있다. 예를 들어 좌 선회 시, 하중 이동으로 인해 선회 외측 바퀴의 마찰원 크기는 증가하고 선회 내측 바퀴의 마찰원 크기는 감소한다. Fig. 3(a)을 보면, 마찰원 크기의 감소로 인해 선회 내측 바퀴의 종방향 타이어 힘은 마찰 한계에 도달하는 상황이 발생된다. 이때 횡방향 타이어 힘은 존재할 수 없게 되기 때문에 차량은 불안정한 거동을 보인다. 이러한 불안정한 차량 거동을 피하기 위해 Fig. 3(b)처럼 토크 벡터링을 사용하여 선회 내측 바퀴의 토크를 감소시키고 외측 바퀴의 토크를 증가시키면, 선회 내측 바퀴의 종방향 타이어힘은 감소하고 캄의 마찰원의 원리로 인해 선회 내측 바퀴의 횡방향 타이어 힘이 존재한다. 따라서 차량은 불안정한 거동을 피할 수 있게 되고 토크 벡터링을 했을 때와 하지 않았을 때의 종방향 및 횡방향 타이어 힘의 관계는 수식 (1)~(2)처럼 정리가 가능하다.³⁾ 이 수식의 기본적인 아이디어는 선회 시 차량의 구동 성능과 안정성을 유지하기 위해 토크를 분배하는 것이다.

Fig. 3

Effect of torque vectoring

F y l T V + F y r T V = F y r

(1)

F x l T V + F x r T V = F x l + F x r

(2)

2.1.2 Torque Vectoring 목적

차량의 조종 안정성(Handling)은 조종성과 안정성을 종합적으로 표현하는 차량동역학 용어이다. 조종성은 주어진 주행코스 이탈범위에 대한 운전자의 신속한 조향제어 가능성(Controllability, Agility, Maneuverability)이고, 안정성은 외란 요소에 대한 차량의 자체적인 코스 안정성(Course Stability)을 의미한다. 조종성과 안정성은 상반되는 특성이 있다.

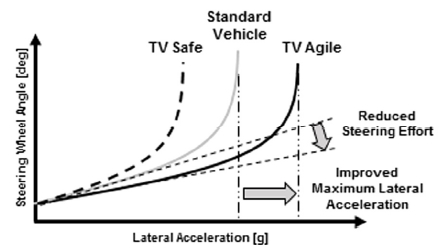
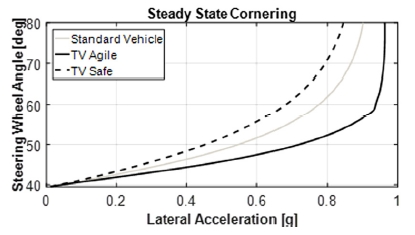
고유조향특성(Self-steering Characteristics)은 정상원선회(Steady State Cornering) 시험을 통해 원형 궤적을 유지하기 위한 횡가속도에 따른 조향 핸들 각의 변화율을 비교하여 Fig. 4처럼 확인할 수 있다. 횡가속도에 따른 조향핸들 각의 변화율은 횡가속도 약 0.4~0.5 g 내에서 선형구간을 유지하며, 이선형 구간의 변화율을 고유조향계수(Understeer Coefficient)라 한다.

Fig. 4

Purpose of torque vectoring

토크 벡터링은 조종성 또는 안정성 향상 목적에 따라 차량의 고유조향특성을 변경할 수 있는 장점이 있다.⁴⁾ Fig. 4에서 TV Agile은 조종성 향상을 목적으로 TV Safe는 안정성 향상을 목적으로 제어함을 의미한다. 토크 벡터링을 조종성 향상을 목적으로 TV Agile 제어하면, 차량의 고유조향계수는 감소하고 최대 횡가속도는 증가한다.⁶⁾ 고유조향계수의 감소는 주어진 코스를 유지하기 위한 운전자의 조향 입력을 감소시킬 수 있음을 의미하고, 최대 횡가속도의 증가는 차량의 횡방향 안정성 한계를 증가시킬 수 있음을 의미한다. 그리고 안정성 향상을 목적으로 TV Safe 제어하여 차량의 고유조향계수를 증가시키면, 외란 요소에 대한 차량의 자체적인 코스 안정성을 증가시킬 수 있다.

2.2 Torque Vectoring 제어 알고리즘

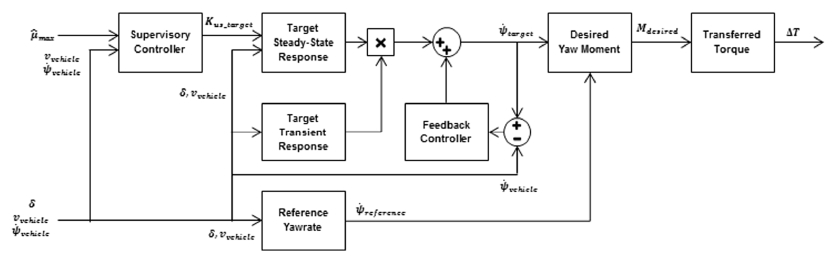
토크 벡터링 제어 알고리즘은 현재 차량의 주행상태를 판별하고, 조종성 또는 안정성 향상 목적에 따라 목표 요레이트를 계산한다. 그리고 기준 요레이트와 목표 요레이트의 차이를 기반으로 요구되는 보상 요모멘트를 계산하고, 좌우 바퀴의 구동 토크를 발생시켜 요모멘트의 방향과 양을 제어하는 방식으로 Fig. 5처럼 구성되어 있다.

Fig. 5

Block diagram of torque vectoring algorithm

2.2.1 통합 제어기

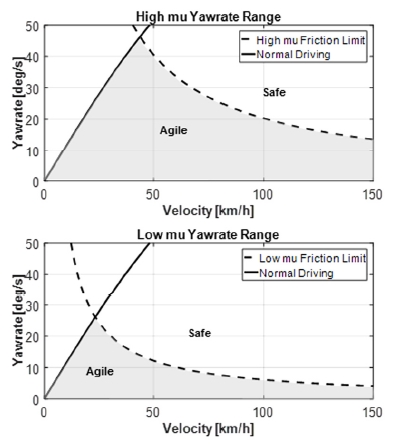
현재 차량의 주행상태를 판별하는 통합 제어기(Supervisory Controller)에서는 정상 주행 영역(Normal Driving Range) 및 마찰 한계 영역(Friction Limit Range)의 최대 요레이트와 주행속도에 따른 실제 차량의 요레이트의 크기를 비교하여 토크 벡터링 제어 모드를 결정한다. 통합 제어기의 주요 역할은 차량의 정상 주행상태에서 안정성을 향상하기보다는 조종성을 향상할 수 있도록 토크 벡터링 제어 목적에 맞게 보다 효율적으로 사용하기 위함이다. 그리고 도로 노면 상태와는 상관없이 차량의 주행상태가 정상 주행상태이면 조종성, 불안정상태이면 안정성 향상이 토크 벡터링 제어 목적이다.

정상 주행 영역은 차량의 최대 조향각을 고려한 속도에 따른 정상상태 요레이트 값 $ψ ̇ N o r m a l D r i v i n g$ 을 의미하며, 요증폭률(Steady -State Yaw Magnitude Ratio) 공식을 응용한 수식 (3)과 같다. 실제 차량의 요레이트 값이 정상 주행 영역 안에 존재하지 않으면, 차량은 불안정상태라고 판단할 수 있다.

ψ ̇ N o r m a l D r i v i n g ≤ υ l + K u s υ 2 δ m a x

(3)

마찰 한계 영역은 횡방향 안정성을 고려한 속도에 따른 요레이트 값 $ψ ̇ F r i c t i o n L i m i t$ 을 의미하며, 최대 횡력과 마찰력의 관계를 정리한 수식 (4)~(5)와 같다. 또한, 마찰 한계 영역에서도 마찬가지로 실제 차량의 요레이트 값이 마찰 한계 영역 안에 존재하지 않으면, 차량은 불안정상태라고 판단할 수 있다. 본 논문에서는 마른 아스팔트와 같은 고마찰 노면과 눈길과 같은 저마찰 노면의 두 가지 상태만 고려한 예를 제시하였고, 마찰계수는 추정된 값을 사용하도록 설계하였다.

m a y ≤ μ ̂ m g

(4)

ψ ̇ F r i c t i o n L i m i t ≤ μ ̂ g υ

(5)

제어 모드는 조종성 모드(Agile Mode)와 안정성 모드(Safe Mode)로 구분되고, 각 모드에 따라서 목표하는 차량의 고유조향계수는 다르게 산출한다. 만약 실제 차량의 요레이트 값이 정상 주행 영역과 마찰 한계 영역의 교집합 영역에 존재하게 되면 차량은 안정적인 거동이 가능하므로 Fig. 6의 색칠된 부분처럼 조종성 모드로 판단한다. 교집합 영역에 존재하지 않게 되면, 차량은 불안정적인 거동이라고 판단하여 안정성 모드로 결정하게 된다.

Fig. 6

Yawrate range of supervisory controller

2.2.2 Torque Vectoring 제어기

조종성 또는 안정성 제어 모드에 따른 차량의 목표 고유조향계수가 산출되면, 토크 벡터링을 위한 목표 요레이트(Target Yawrate)를 계산한다. 목표 요레이트는 차량의 정상상태 및 과도상태 응답특성을 반영하여 계산되도록 설계하였다.⁷⁾

정상상태 응답 특성을 반영한 목표 정상상태 요레이트는 정속 원형주행 시의 조향 입력에 대한 차량의 정상상태 요증폭률을 응용한 수식 (6)을 이용해 계산한다. 이 수식에 포함된 목표 고유조향계수는 목표 요레이트를 계산하는데 매우 중요한 파라미터이고, 통합 제어기에서 산출된 값이다.⁹⁾

ψ ̇ t a r g e t - s = υ l + K u s - t a r g e t υ 2 δ

(6)

요운동 응답속도 및 증폭률에 관련된 차량의 과도상태 응답 특성은 요레이트 필터로 구성하여 반영하였다. 요레이트 필터는 몇 가지 단계로 구성된다. One-track model의 운동방정식을 라플라스 변환해 수식 (7)처럼 전달함수로 구성한다. 이 수식에서 T_z는 시간 상수, ω_n는 비감쇠 요 고유진동수, ζ는 요 감쇠비를 나타낸다. 그리고 목표하는 과도상태 응답 특성을 설정하기 위해 세 가지(⋋_D, ⋋_S, ⋋_Z) 튜닝 파라미터를 추가하여 수식 (8)처럼 전달함수를 변형한다. ⋋_D는 증폭률에 해당하는 감쇠비(Damping ratio), ⋋_S는 응답시간(Response time), ⋋_Z는 입력에 대한 동적 응답(Dynamic response)과 관련된 튜닝 파라미터이다. 수식 (8)에서 $ψ ̇ / δ s . s$ 는 정상상태 응답 값을 의미한다. 따라서 이 정상상태 응답 값이 상쇄되도록 수식 (9)처럼 선형 필터를 구성하면, 과도상태 응답특성만 반영할 수 있다.

G δ f → ψ ̇ s = ψ ̇ δ s . s 1 + T z s 1 + 2 ζ ω n s + 1 ω n 2 s 2 δ

(7)

G δ f → ψ ̇ t a r g e t - t s = ψ ̇ δ s . s 1 + T z ⋋ Z ⋋ S s 1 + 2 1 - ⋋ D (1 - ζ) ⋋ s ω n s + 1 ⋋ s 2 ω n 2 s 2

(8)

Γ δ f → ψ ̇ t a r g e t - t s = G δ f → ψ ̇ t a r g e t - t s G δ f → ψ ̇ t a r g e t - t 0

(9)

목표 요레이트 $ψ ̇ t a r g e t$ 는 정상상태 응답 특성을 반영한 요레이트 값과 과도상태 응답 특성을 반영한 필터 값의 곱으로 계산한다. 그리고 실제 차량의 요레이트 값과 비교하여 목표 요레이트 값을 보상해줄 수 있도록 PID 피드백 제어기를 설계하였다. 기준 요레이트 $ψ ̇ r e f e r e n c e$ 는 One-track model을 이용하여 제어하지 않은 차량의 요레이트를 계산하였다. 요구되는 보상 요모멘트는 M_desired는 목표 요레이트와의 차이를 기반으로 Two-track model의 운동방정식과 Sliding mode control을 사용하여 수식 (10)처럼 정리하였다. 요구되는 보상 요모멘트를 발생시킬 수 있는 좌우 바퀴의 구동 토크 ∆T 는 수식 (13)처럼 계산하여 좌우 모터에서 생성하였다.

M d e s i r e d = I Z cos ⁡ δ ψ ̈ t a r g e t + ψ ̇ t a r g e t - ψ ̇ r e f e r e n c e + I r cos ⁡ δ F y r r + F y r l - l f F y f r + F y f l - I w cos ⁡ δ F x r r + F x r l

(10)

T r = 12 T m o t + Δ Τ

(11)

T l = 12 T m o t - Δ Τ

(12)

Δ Τ = I W ω ̇ f r - ω ̇ f l + s r d y n l w M d e s i r e d

(13)

본 논문에서는 조종성 및 안정성 모드에 따른 토크 벡터링 시스템의 성능을 검증하기 위해 제어 목표를 다음과 같이 설정하였다. 목표 고유조향계수는 최대 횡가속도 구간에서 차량의 횡방향 안정성이 오래 유지될 수 있도록 조종성 모드일 때는 30 % 감소, 안정성 모드일 때는 30 % 증가하도록 설정하였다. 그리고 제어 모드에 상관없이 요운동 응답속도 및 증폭률에 관련된 차량의 과도상태 응답 특성은 모두 향상하는 것을 목표로 설정하였다.

3. Torque Vectoring 시스템의 조종 안정성 성능평가

3.1 통합시뮬레이션 환경구축

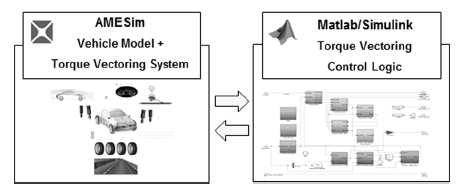
토크 벡터링 시스템의 조종 안정성 평가를 위한 통합 시뮬레이션 환경을 구축하였다. 차량 및 토크 벡터링 시스템은 SIEMENS사의 Amesim을 사용하여 모델링 하였고, 토크 벡터링 제어 알고리즘은 Matlab/Simulink를 사용하여 설계하였다.

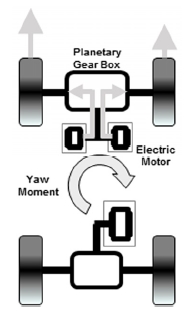
차량 모델은 EV AWD 차량으로 Fig. 8과 같이 파워트레인을 구성하였다. 전륜에는 구동 및 토크 벡터링을 위한 듀얼모터 시스템을 선정하였다. 좌우 모터에서 발생한 토크는 유성기어를 통해 각 바퀴에 전달하도록 구성하였고, 좌우 바퀴에 독립적으로 토크를 발생시켜 차량의 요구되는 요모멘트를 생성하도록 하였다.^8,10) 후륜에는 구동을 위한 모터를 모델링하였고, 전후륜 구동력은 4:6의 고정 배분비를 갖도록 하였다.

Fig. 7

Simulation environment

Fig. 8

Dual motor type torque vectoring system

3.2 시뮬레이션 성능평가

토크 벡터링 조종 안정성 성능을 평가하기 위해 ISO 규정을 참조하여 주행시험 시나리오 및 평가방법과 시험항목별 정량적 성능지수를 정의하였다. 본 논문에서는 통합 제어기의 성능을 평가하기보다는 조종성과 안정성 모드에서 토크 벡터링 제어를 통해 차량의 조종 안정성 성능이 얼마나 향상되는지에 대한 평가를 하였다. 모든 결과 그래프에서 토크 벡터링을 하지 않았을 때를 Standard Vehicle, 토크 벡터링 조종성 제어는 TV Agile, 토크 벡터링 안정성 제어는 TV Safe로 나타내었다.

3.2.1 정상원선회 시뮬레이션

정상원선회(Steady-State Cornering)는 ISO4138 기준에 따른 차량의 고유조향 특성을 규명하기 위한 주행시험 방법이다. 차량의 주행속도를 점차 증가시키면서 선회반경 50 m를 유지하기 위한 추가 조향 핸들 각을 입력하는 조건으로 시뮬레이션을 하였다. 횡가속도 약 0.4 g에서의 횡가속도에 따른 조향 핸들 각의 변화율인 고유조향계수와 최대 횡가속도 값을 성능지수로 선정하였다.

정상원선회 시뮬레이션 결과는 Fig. 9와 같다. 조종성 향상을 목적으로 제어했을 때는 고유조향계수가 감소하여 약 언더스티어 특성이 강화되었다. 이는 운전자의 Steering effort가 감소하여 선회 시 적은 조향 핸들 조작을 요구한다고 판단할 수 있으므로 차량의 조종성(Controllability)이 향상되었음을 의미한다. 그리고 차량의 한계 횡가속도가 증가하였다. 이는 극한 주행상황에 대한 차량의 안정성 한계(Stability Margin)가 향상되었음을 의미한다. 안정성 향상을 목적으로 제어했을 때는 고유조향 계수가 증가하여 차량의 강 언더스티어 특성이 강화되었다. 이는 외란 요소에 대한 차량의 자체적인 코스 안정성(Course Stability)이 증가하였음을 의미한다.

Fig. 9

Steady-State cornering simulation result

3.2.2 J-turn 시뮬레이션

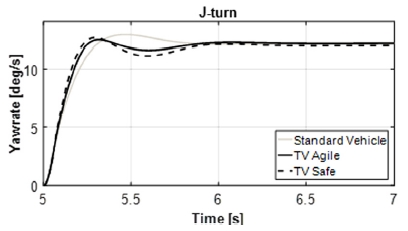
J-turn(Step Steering Input)은 ISO7401 기준에 따른 차량의 과도상태 응답특성을 규명하기 위한 주행시험 방법이다. 차량의 주행속도는 100 km/h로 일정하게 유지하고, 정상상태 횡가속도 0.6 g에 해당되는 조향 핸들 각속도 500 deg/s를 입력하는 조건으로 시뮬레이션을 하였다. 요레이트 응답시간 및 오버슈트 비율과 TB Factor를 성능지수로 선정하였다. TB Factor는 조향 핸들 각의 50 %에 해당하는 요레이트시간 부터 요레이트 오버슈트 도달할 때까지의 시간 값과 정상상태 차체미끄럼각의 곲으로 이루어 지며, J-turn 시험 결과의 주요 평가치로 사용된다.

J-turn 시뮬레이션 결과는 Fig. 10과 같다. 조종성과 안정성 향상을 목적으로 제어했을 때는 차량의 요레이트 응답시간 및 오버슈트 비율이 모두 감소하였다. 이는 작은 차체 요운동으로 빠르게 안정주행궤도에 도달 가능하다고 판단할 수 있으므로 차량의 기동성(Maneuverability)이 향상되었음을 의미한다. 그리고 TB Factor도 감소하였다. 이는 작은 차체미끄럼각으로 빠른 요레이트 응답특성을 가진다고 판단할 수 있다.

Fig. 10

J-turn simulation result

3.2.3 이중 차선 변경 시뮬레이션

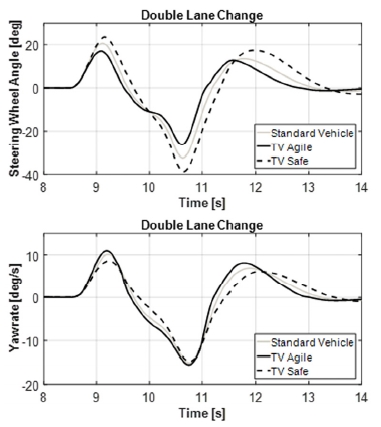
이중 차선 변경(Double Lane Change)은 ISO3888 기준에 따른 차량의 주행코스 추종 성능 및 민첩성 등 과도상태 응답 특성을 규명하기 위한 주행시험 방법이다. 차량의 주행속도는 120 km/h로 일정하게 유지하고, 주행코스를 유지하기 위한 추가 조향 핸들 각을 입력하는 조건으로 시뮬레이션을 하였다. 조향 핸들 각의 전체 RMS 값, 조향 핸들 각의 시간 대비 차량의 요레이트 발생 지연 시간, 요레이트 Peak to Peak 값, 두 번째 차선 변경구간의 통과시간 등을 성능지수로 선정하였다.

이중 차선 변경 시뮬레이션 결과는 Fig. 11과 같다. 조종성 향상을 목적으로 제어했을 때는 조향 핸들 각의 RMS 값이 감소하였다. 이는 주행코스를 유지하기 위한 운전자의 조향 핸들 조작이 감소하였으므로 차량의 조종성(Controllability)이 향상되었음을 의미한다. 그리고 차량의 요레이트 발생 지연 시간은 감소하였고, 요레이트 Peak to Peak 값은 증가하였다. 요레이트 발생 지연 시간의 감소는 운전자의 조향 핸들 조작에 따른 차량의 반응이 빨라졌으므로 민첩성(Agility)이 향상되었음을 의미한다. Peak to Peak 값의 증가는 차량의 안정성(Stability)은 저하되었지만, 값의 차이가 크지 않으므로 비슷한 수준으로 유지되었음을 의미한다. 주행코스 통과시간 또한 감소하였는데 이는 주어진 코스를 민첩하게 통과하였음을 의미한다. 안정성 향상을 목적으로 제어했을 때는 조향 핸들 각의 RMS 값은 증가하였고, 차량의 요레이트 Peak to Peak 값은 감소하였다. 이는 주행코스를 유지하기 위한 운전자의 조향 핸들 조작을 많이 하더라도 차량의 안정성은 향상되었음을 의미한다.

Fig. 11

Double lane change simulation result

3.2.4 조종 안정성 성능평가

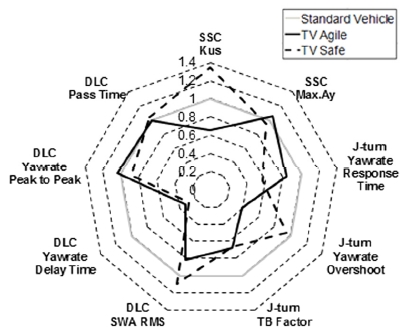
토크 벡터링을 하지 않았을 때를 기준으로 조종성과 안정성 시뮬레이션 결과의 성능지수를 정규화하여 나타내면 Fig. 12와 같다.

Fig. 12

Handling simulation result

조종성 향상을 목적으로 제어했을 때는 조종성, 안정성 한계, 기동성, 민첩성 등의 향상을 확인할 수 있다. 정상원선회 결과에서는 약 언더스티어 경향이 강화되고, 한계 횡가속도가 증가하여 조종성과 안정성 한계 향상을 확인하였다. J-turn 결과에서는 요레이트 응답시간 및 오버슈트 비율, TB Factor 감소로 기동성 향상을 확인하였다. DLC 결과에서는 조향 입력, 요레이트 발생 지연시간, 주행코스 통과시간 감소로 민첩성이 향상되었음을 확인하였다. 따라서 운전자가 조향 핸들 조작을 적게 하더라도 주행코스를 신속하게 통과할 수 있으므로 토크 벡터링 조종성 목표에 부합한다고 할 수 있다.

안정성 향상을 목적으로 제어했을 때는 안정성 향상을 확인할 수 있다. 정상원선회 결과에서는 강 언더스티어 경향이 강화되어 코스 안정성이 증가하였음을 알 수 있다. DLC 결과에서는 조향 입력이 증가하였지만, 요레이트 값이 감소하여 안정성이 향상되었음을 확인하였다. 따라서 운전자가 조향 핸들 조작을 많이 하고, 주행코스를 느리게 통과하더라도 차량은 안정적으로 거동할 수 있음을 의미하기 때문에 토크 벡터링 안정성 목표에 부합한다고 할 수 있다.

4. 결 론

본 논문에서는 전기차의 조종 안정성(Handling) 향상을 위한 전륜 듀얼 모터 방식의 토크 벡터링 시스템에 관한 연구를 진행하였다. 토크 벡터링 제어 알고리즘을 설계하여 차량 및 토크 벡터링 시스템에 적용하였다. 또한, 통합시뮬레이션 환경을 구축하여 조종 안정성 시뮬레이션을 진행하였고, 조종성 및 안정성 모드에 따른 토크 벡터링 성능을 검증하였다. 위의 주요 연구 추진 내용과 관련하여 얻어진 결론은 다음과 같다.

1) 현재 차량의 주행상태를 판별하여 토크 벡터링 제어모드를 결정하는 통합 제어기와 정상상태 및 과도상태 응답 특성을 반영한 토크 벡터링 제어 알고리즘을 설계하였다.
2) 듀얼 모터 방식의 전륜 토크 벡터링 시스템을 적용한 EV AWD 차량을 모델링 하였다.
3) 토크 벡터링 성능을 검증하기 위한 주행시험 시나리오 및 평가방법과 시험항목별 정량적 성능지수를 정의하였다.
4) 세 가지 시뮬레이션 평가를 통해 조종성 및 안정성 모드에 따른 차량의 조종 안정성이 향상되었음을 검증하였다.

Nomenclature


F_x :	longitudinal tire force, N
F_y :	lateral tire force, N
F_z :	vertical tire force, N
a_y :	lateral acceleration, m/s²
υ :	vehicle velocity, m/s
K_us :	understeer gradient, deg/g
δ :	steering wheel angle, deg
$ψ ̇$ :	yawrate, deg/s
Τ :	torque, N･m
M :	yaw moment, Nm

References

S. J. Heo, Vehicle Dynamics and Introduction, Moonwoondang, Seoul, (2001).
P. van Vliet, “Torque Vectoring for Improved Vehicle Dynamics”, Vehicle Dynamics Expo, (2010).
V. Ivanov, K. Augsburg, and D. Savitski, “Torque Vectoring for Improving the Mobility of All-terrain Electric Vehicles”, 12th European Regional Conference of the International Society for Terrain-Vehicle Systems, (2012).
R. Folke, R. Böker, A. Thomys and L. König, “Torque Vectoring - a New Level of Freedom for Electric Vehicles”, ATZ Worldwide Magazine, 112(6), p8-12, (2010).
S. Kaspar, R. Stroph, T. Bunte, and S. Hohmann, “Optimisation of Vehicle Dynamics via Torque Vectoring for Space Optimised Electric Vehicle”, ATZ Worldwide Magazine, 116(2), p54-60, (2014). [https://doi.org/10.1007/s38311-014-0026-1]
D. Crolla, Encyclopedia of Automotive Engineering, Int. Edn., John Wiley & Sons, Chichester, (2015).
T. Bunte, S. Kaspar, S. Hohmann, and J. Brembeck, “Inverse Model Based Torque Vectoring Control For a Rear Wheel Driven Battery Electric Vehicle”, IFAC Proceedings Volumes, 47(3), p12016-12022, (2014).
C. Chatzikomis, A. Sorniotti, P. Gruber, M. Bastin, R. M. Shah, and Y. Orlv, “Torque-Vectoring Control for an Autonomous and Driverless Electric Racing Vehicle with Multiple Motors”, SAE International Journal of Vehicle Dynamics, Stability, and NVH, 1(2), p338-351, (2017). [https://doi.org/10.4271/2017-01-1597]
M. Canale, L. Fagiano, M. Milanese, P. Borodani, “Robust Vhicle Yaw Control Using an Active Differential and IMC Techniques”, Control Engineering Practice, 15(8), p923-941, (2007). [https://doi.org/10.1016/j.conengprac.2006.11.012]
K. Sawase, and Y. Ushiroda, “Improvement of Vehicle Dynamics by Right-and-Left Torque Vectoring System in Various Drivetrains”, Mitsubishi Motors Technical Review, 20, p14-20, (2008).
J. H. Yi, K. H. Lee, I. H. Kim, D. W. Jang, and S. J. Heo, “A Study of Torque Vectoring Application in Electric Vehicle for Driving Stability Performance Evaluation”, Transactions of KSAE, 22(3), p250-256, (2014). [https://doi.org/10.7467/ksae.2014.22.3.250]