포신의 고각과 방위각 오차 최소화를 위한 차륜형 전투차량의 최적설계

1. 서 론

무장 체계를 탑재한 전투차량의 포신 오차는 서로 다른 오차 인자들의 조합으로 발생하고, 오차의 형태는 발생 조건에 따라 고정 오차, 가변 오차, 임의 오차로 분류할 수 있다.¹⁾ 고정 오차는 포 점프, 시차(視差)와 같이 무장 체계에 따라 일정한 규칙을 가지고 발생하는 오차로서 실험 데이터를 통해 보정이 가능한 반면,²⁾ 임의 오차의 경우 사수의 조준 오차, 탄의 불량과 같이 예측 불가능한 조건에서 발생한다. 가변 오차는 임무 환경에 따라 달라지는 주행 환경 가운데 나타나며 지형의 변화, 풍향, 포신의 편각, 반동력 등이 해당된다. 따라서 전투차량 설계 시 포신의 오차를 최소화할 수 있는 최적 모델을 도출하기 위해서는 가변 오차 인자가 차량에 미치는 영향을 분석하고, 이를 최소화하기 위한 최적의 설계 변수 값을 찾는 것이 효과적이다.

가변 오차의 크기를 예측하기 위한 방법으로 오차 근사식을 도출하기 위한 연구가 진행되어 왔다.^3,4) 근사식을 활용할 경우 포신 오차에 미치는 각 포신 오차 인자들의 영향도를 비교할 수 있고, 오차를 보상하기 위한 고각과 방위각을 미리 계산할 수 있는 장점이 있다. 그러나 정확한 근사식을 도출하기 위해서는 시험 데이터 확보가 중요할 뿐만 아니라, 새로운 무장 체계를 개발할 경우 물질적으로, 시간적으로 비용이 많이 요구되는 한계를 가진다. 이러한 단점을 극복하기 위해 가상의 해석 모델을 개발하여 시뮬레이션을 수행하는 연구가 다양한 형태로 진행되어 왔고,^5-7) 서로 다른 오차 인자들에 의한 오차 발생량을 예측하였다.^8,9) 해석 정확도를 높이기 위해 무장체계의 유한 요소 모델을 개발한 사례가 있으며 반차(Half car) 모델을 활용하여 현가 특성을 고려한 오차 해석이 수행된 바 있다.^10-12) 그러나 유한 요소 모델의 경우 3차원 모델로 확장할 경우 해석을 위한 시간 비용이 증가할 뿐만 아니라, 기동 체계의 특성을 모두 고려한 연구는 진행이 많이 이루어지지 않았다. 그리고 반차 모델의 경우 3차원 모델에서 나타날 수 있는 오차 인자를 반영하지 못하는 한계를 가진다.

따라서 본 연구에서는 모델 기반 설계기법을 통해 기동 성능과 화력 성능을 동시에 고려할 수 있는 3차원 가상 시제 모델을 개발하고, 이를 활용하여 포신의 오차를 분석하고자 한다. 그리고 포신의 포구 지향 오차를 최소화하기 위한 전투차량 서스펜션 부품의 최적설계 프로세스를 정립한다. 서로 다른 오차 인자들을 고려하여 시뮬레이션을 수행하였고, 포신의 고각 오차와 방위각 오차를 분석하였다. 기동 성능으로는 차량의 주행 속도를, 화력 성능으로는 사격 시 발생하는 반동력을 오차 인자로서 고려하였으며 외부 노면의 형상 변화도 동시에 고려하였다. 오차 분석 결과를 토대로 포신의 고각 오차와 방위각 오차를 최소화하기 위한 다목적 최적설계를 수행하였고 두 가지 목적함수의 파레토 최적 설계안을 도출하였다.

2. 전투차량 모델

2.1 전투차량 모델링

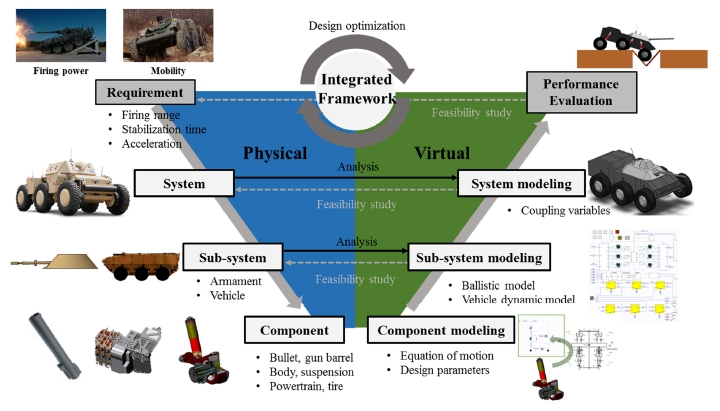
본 연구에서는 6륜형 전투차량인 Autonomous platform demonstrator(APD)의 가상시제 모델을 활용하여 포신 오차를 분석하였다.¹³⁾ 모델기반 체계공학을 활용하여 전투차량의 성능을 예측하기 위한 가상시제 모델을 Fig. 1과 같이 V-process를 이용하여 구축하였다. 모델링에 앞서 성능을 살펴보기 위한 전투차량 모델을 체계 수준에서 분석하였고, 하나의 체계를 화력 부체계와 기동 부체계로 분류하였다. 각 부체계는 성능을 정확히 예측하기 위해 필요한 주요 컴포넌트들로 구성된다.

Fig. 1

V-Process for model-based system engineering

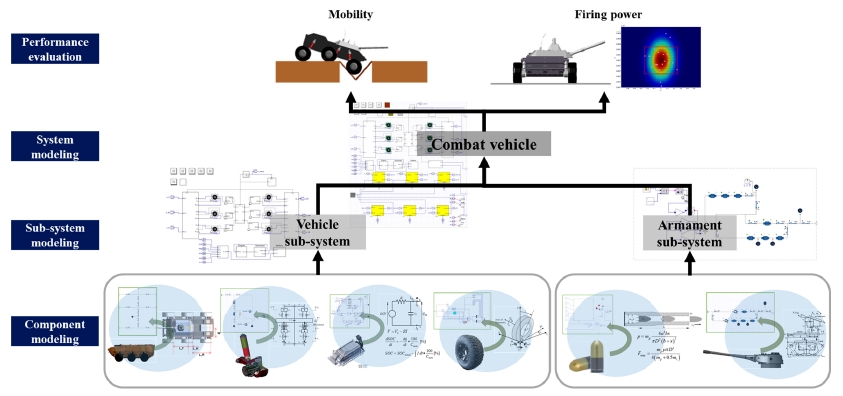
모델링은 Fig. 2와 같이 컴포넌트 수준부터 수행하였고 이를 활용하여 부체계, 체계 수준으로 가상시제 모델을 확장하였다. 기동 부체계는 6륜형 전투차량의 차체와 구동계, 현가계, 타이어로 구성하였고, 화력 부체계는 포탑과 강내탄도 해석 모델로 구성하였다.

Fig. 2

Development of wheeled military vehicle model

2.2 주행 시나리오

사격 정확도에 영향을 미치는 가변 오차인자로는 주행 속도, 노면 형상, 사격 반동력을 고려하였다. 서로 다른 오차 인자들이 복합적으로 작용하는 주행 시나리오에서 발생하는 포신의 고각과 방위각 오차를 살펴보기 위하여 오차 인자들을 각각 세 가지 수준으로 Table 1과 같이 구성하였다.

Table 1

Type of error sources

동일한 노면 주행 시 주행 속도의 변화에 따른 오차를 살펴볼 수 있도록 저속, 중속, 고속 주행으로 분류하여 시뮬레이션을 수행하였다. 노면 형상은 고각 오차와 방위각 오차를 모두 살펴보기 위해 평지뿐만 아니라 대칭형 범프, 비대칭형 범프 조건에서 주행하였고, 사격 형태는 단발 사격, 연속 사격, 점사로 분류하였다. 서로 다른 오차 인자들의 조합으로 나타날 수 있는 27 가지의 주행 시나리오를 구성하였고 포신의 고각 오차와 방위각 오차 결과를 정리하여 분석하였다.

3. 포신 오차 측정

3.1 오차 측정 절차

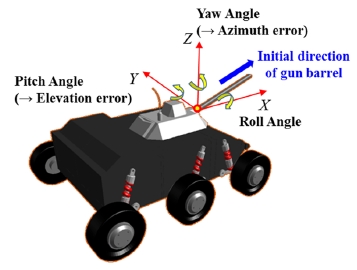
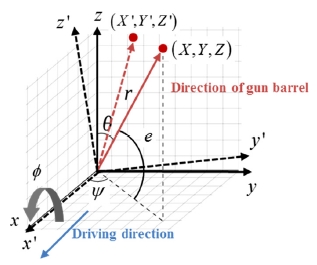
Fig. 3은 포신 오차가 발생하지 않은 전투차량 모델의 초기 모습을 나타낸다. 포신의 오차는 포신의 시작부에서 측정하였고, 초기 포신의 지향 방향으로부터 주행 시 발생하는 피치각과 요각을 각각 고각 오차와 방위각 오차로 활용하였다. 차량이 기울어짐에 따라 발생하는 오차를 함께 고려하기 위해 롤각에 의한 영향도 함께 반영하여 최종 고각 오차와 방위각 오차를 예측하였다. Fig. 4에서 길이 r인 포신의 지향 방향이 [X, Y, Z]^T이고 차량이 기울어져 롤각(ϕ)이 발생한 경우, 회전한 포신의 지향 방향인 [X^′, Y^′, Z^′]^T는 다음과 같이 구할 수 있다.

Fig. 3

Measuring point of gun error

Fig. 4

Rotation of gun barrel due to roll angle

$\[ \left[\begin{array}{c}{X}^{\text{'}}\hfill \\ Y^{\text{'}}\hfill \\ Z^{\text{'}}\hfill \end{array}\right]=\left[\begin{array}{c}1 0 0 \hfill \\ 0 \cos \varphi -\sin \varphi \hfill \\ 0 \sin \varphi \cos \varphi \hfill \end{array}\right]\left[\begin{array}{c}X\hfill \\ Y\hfill \\ Z\hfill \end{array}\right]=\left[\begin{array}{c}X\\ Y\cos \varphi -Z\sin \varphi \hfill \\ Y\sin \varphi +Z\cos \varphi \hfill \end{array}\right] \]$

(1)

그리고 회전좌표계를 이용하여 [X, Y, Z]^T를 표현하면 아래 식과 같다.

$\[ X=r\sin \theta \cos \psi \]$

(2)

$\[ Y=r\sin \theta \sin \psi \]$

(3)

$\[ Z=r\cos \theta \]$

(4)

이 때, [r, θ, ψ]^T는 아래와 같이 정의된다.

$\[ r={\left(X^2+Y^2+Z^2\right)}^{1/2} \]$

(5)

$\[ \theta ={\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left(\frac{Z}{r}\right) \]$

(6)

$\[ \psi ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{Y}{X}\right) \]$

(7)

회전 후 얻어지는 θ^′는 식 (1)~ (7)을 통해 아래 식을 만족한다.

$\[ \cos \left({\theta }^{\text{'}}\right)=\frac{Z^{\text{'}}}{r^{\text{'}}}=\frac{Y\sin \varphi +Z\cos \varphi }{r}=\sin \theta \sin \psi \sin \varphi +\cos \theta \cos \varphi \]$

(8)

그리고 고각 오차(e)와 θ의 관계를 이용하여

$\[ \theta =\frac{\pi }{2}-e \]$

(9)

롤각(ϕ)을 반영한 고각 오차(e^′)는 다음과 같이 구할 수 있다.

$\[ {\theta }^{\text{'}}=\frac{\pi }{2}-e^{\text{'}} \]$

(10)

$\[ \sin \left(e^{\text{'}}\right)=\cos e\sin \psi \cos \varphi -\sin e\cos \varphi \]$

(11)

$\[ e^{\text{'}}={\mathrm{s}\mathrm{i}\mathrm{n}}^{-1}\left(\cos e\sin \psi \cos \varphi -\sin e\cos \varphi \right) \]$

(12)

같은 방법으로 롤각을 고려하여 계산한 방위각 오차(ψ^′)는 아래 식과 같다.

$\[ {\psi }^{\text{'}}={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\cos e\sin \psi \cos \varphi -\sin e\sin \varphi }{\cos e\cos \psi }\right) \]$

(13)

3.2 오차 측정 결과

전체 27가지의 주행 시나리오 중 고각 오차가 가장 크게 나타난 경우는 저속 주행, 비대칭형 범프 통과, 점사인 반면, 방위각 오차의 경우 고속 주행, 비대칭형 범프 통과, 점사 시에 가장 큰 오차가 발생하였다. 고각 오차의 경우 저속으로 주행하며 범프를 통과할 때 범프에 의해 영향을 받는 시간이 길어지게 된다는 점과 범프 통과 시 수직방향으로 나타나는 포신의 움직임이 큰 점에 기인하여 큰 오차 값이 얻어진 것으로 판단된다. 반면, 고속 주행 시에는 범프의 영향을 받는 시간이 상대적으로 짧아질 뿐만 아니라, 범프 통과 후 현가장치에 의해 고각 오차를 줄이는 시간이 앞당겨지므로 상대적으로 적은 오차가 발생하였다. 방위각 오차의 경우 이와 반대로 주행 속도가 빠른 경우 더 큰 오차가 발생하였는데, 이는 고속으로 비대칭 범프를 통과할 경우 기존 주행 경로를 이탈하는 정도가 높아짐에 따라 포신이 지향하고 있는 방위각도 함께 높아진 것으로 확인된다.

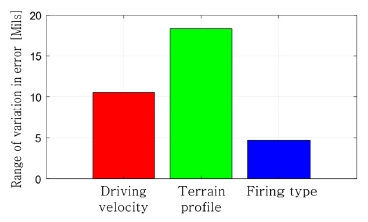
Fig. 5는 오차 인자와 오차의 변화 범위 간의 관계를 나타낸다. 먼저 주행 속도의 영향을 살펴보기 위해, 노면 형상(평지, 대칭형 범프, 비대칭형 범프)과 사격 형태(단발, 연속, 점사)의 조합으로 발생 가능한 아홉 가지 주행 시나리오를 구성하였다. 이 후, 주행 속도의 변화에 따른 최대 오차를 각 시나리오 별로 비교한 결과, 주행 속도의 영향으로 최대 약 10.5 Mils 가량의 오차 변화가 나타나는 것을 확인할 수 있었다. 같은 방법으로 노면 형상과 사격 형태의 변화가 오차 발생에 미치는 영향을 살펴보았고, Fig. 5에 나타낸 바와 같이 노면 형상에 의한 오차 변화가 가장 높은 것을 확인할 수 있었다. 다음으로 주행 속도와 사격 형태 순으로 오차 발생에 높은 영향을 미치는 것을 알 수 있다.

Fig. 5

Effect of error sources

노면 형상의 영향은 배제한 채, 사격 형태의 영향을 독립적으로 살펴보기 위해 평지 노면 주행 시의 고각 오차를 비교하였다. 단발 사격 대비 연속 사격 시 최대 고각 오차는 약 1.5배 증가하였고, 점사 시의 최대 고각 오차는 약 2.9배 증가하는 것을 확인 할 수 있었다. 이는 사격 후 포신의 고각 오차가 안정화되지 않은 채 사격이 지속적으로 이루어져 나타난 결과로 판단된다. 한편, 평지에서 주행 간 사격 시 속도 변화로 인한 고각 오차의 변화는 상대적으로 매우 낮게 나타나는 것을 확인할 수 있었다.

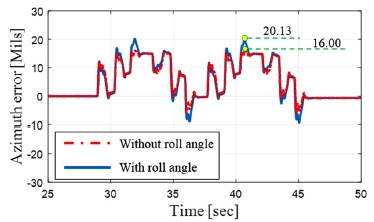
Fig. 6은 차량의 롤각을 고려한 방위각 오차 그래프를 나타낸다. 롤각을 반영한 결과 방위각 오차는 최대 약 4 Mils, 고각 오차의 경우 최대 약 0.9 Mils가량의 차이가 나타남을 확인할 수 있었다. 따라서 포신의 오차를 정확히 예측하기 위해서는 3차원 가상시제모델을 이용하여 피치각과 요각뿐만 아니라 롤각에 의한 영향도 함께 고려하는 것이 중요한 것을 확인할 수 있다.

Fig. 6

Effect of roll angle on azimuth error

4. 최적설계

4.1 최적설계문제 정식화

포신의 고각과 방위각 오차를 줄이기 위한 다목적 최적설계를 수행하였다. 주행 속도는 두 오차의 특성을 모두 고려하기 위해 중속으로 사용하였고, 사격 형태는 점사 조건으로 설정하였다. 노면 형상은 차량의 주행 안정성 평가에 사용하는 RRC 9를 채택하였고, 이는 대칭형 범프와 비대칭형 범프를 모두 포함한다.¹⁴⁾ 두 개의 오차를 동시에 목적함수로 사용하는 다목적 최적설계 문제 정식화는 다음과 같다.

$\[ \begin{array}{c}\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{ }\mathrm{ }\mathrm{ }{\left\{{\left(w_1{f}_1\right)}^p+{\left(w_2{f}_2\right)}^p\right\}}^{\frac{1}{p}}\hfill \\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{ }\mathrm{ }{\mathit{x}}_{\mathrm{l}\mathrm{b}}\le \mathit{x}\le {\mathit{x}}_{\mathrm{u}\mathrm{b}}\hfill \\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }{f}_1=\sqrt{\frac{1}{T_2-T_1}{\int }_{T_1}^{T_2}{e}_E^{2}dt}, { f}_2=\sqrt{\frac{1}{T_2-T_1}{\int }_{T_1}^{T_2}{e}_A^{2}dt}\hfill \end{array} \]$

(14)

설계변수(x)는 서스펜션에 사용되는 스프링 상수와 댐핑 계수이고 목적함수(f₁,f₂)의 형태는 특정 구간이 아닌 주행 중의 전반적인 오차를 최소화하기 위해 고각오차(e_E)와 방위각 오차(e_A)의 제곱평균제곱근(Root mean square) 값을 사용하였다. T₁과 T₂는 주행 시작 시간과 종료 시간을 나타낸다. 두 가지 오차를 모두 목적함수로 사용하는 다목적 최적화이므로 목적함수는 가중치 합 형태로 변경하였고, 각 오차 항에 작용하는 가중치(w₁,w₂)를 갱신하여 목적함수 공간에 존재하는 파레토 최적설계안을 도출하였다. 목적함수에 사용한 파라미터 p는 파레토 최적해를 탐색할 때 목적함수의 형태를 비선형으로 변경하기 위해 사용하였고 설계안 도출 시 적응적으로 갱신하였다. 설계변수는 Table 2와 같이 전륜, 중륜, 후륜으로 구분하여 전체 6개를 사용하였고, 설계변수의 범위는 하한(x_lb)과 상한(x_ub)을 갖도록 제한조건을 추가하였다. 또한 최적화 과정 동안 가상시제모델의 시뮬레이션으로 인한 시간 비용을 최소화하기 위해 시뮬레이션 응답을 효율적으로 예측할 수 있는 크리깅 대체모델을 제작하여 최적화에 사용하였다.

Table 2

Design variables

4.2 최적설계 결과

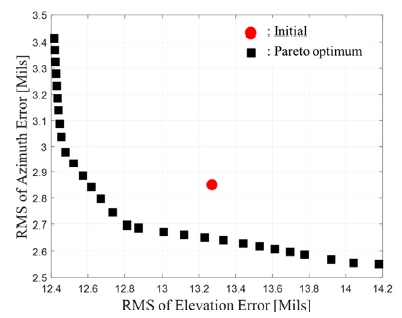
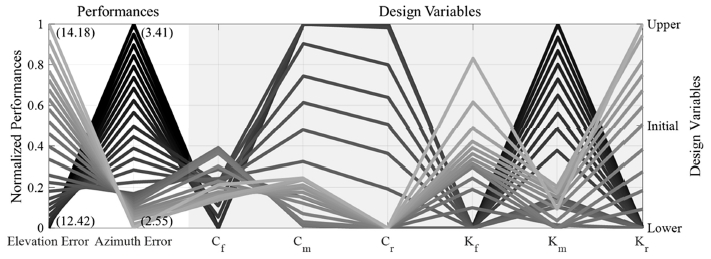
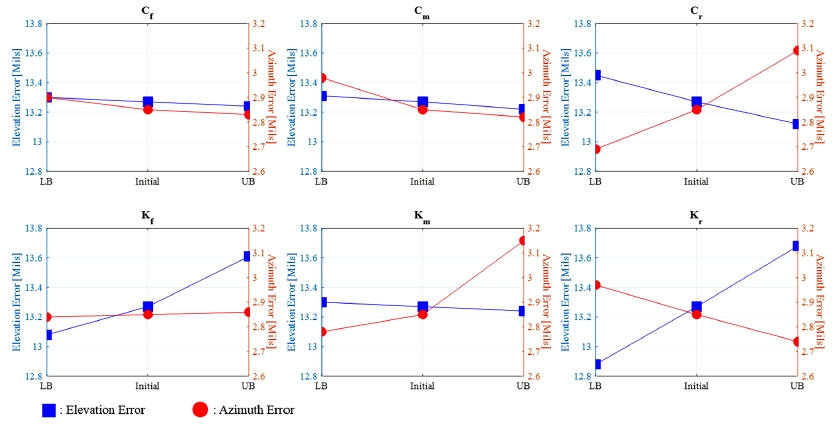
최적설계를 통해 Fig. 7과 같이 목적함수 공간에 존재하는 29개의 파레토 최적 설계안을 도출하였고, 기존 모델 대비 고각 오차는 최대 6 %, 방위각 오차는 최대 11 % 낮출 수 있는 것을 확인하였다. 각 설계안들의 정보를 나타내는 평행좌표그림(Parallel coordinate plot)은 Fig. 8과 같다. 평행좌표그림에 표시된 각각의 선은 Fig. 7에 나타낸 29개의 설계안에 대응되어 최적 설계안에서 발생하는 포신 오차와 해당 설계안의 설계변수 정보를 함께 제공한다. 목적함수인 고각과 방위각 오차는 0부터 1사이의 값을 가지도록 정규화하였고, 설계변수는 하한과 상한 범위 내에서 표현된다. 전륜에 비해 상대적으로 중륜과 후륜에서 최적 설계변수의 범위가 넓게 나타나는 것을 확인할 수 있고, 이는 Fig. 9에서 알 수 있듯이 각 설계변수의 하한(LB), 초기(Initial), 상한(UB) 값에서의 오차 변화가 상대적으로 중륜과 후륜의 스프링 상수와 댐핑 계수의 변화에 따라 크게 발생한 점에 기인한 것으로 판단된다.

Fig. 7

Pareto optimum solutions

Fig. 8

Parallel coordinate plot of Pareto optimum solutions

Fig. 9

Effect of design variables on elevation error and azimuth error

도출한 파레토 최적 설계안은 오차를 최소화할 수 있는 최적 모델의 범위를 목적함수 공간에서 나타내며, 각 설계변수의 최적 값이 가지는 변동 폭을 제시한다. 이는 전투차량 설계 시 최종 모델을 결정하기 위한 의사결정에 활용할 수 있을 것으로 판단된다.

5. 결 론

본 연구에서는 차륜형 전투차량의 3차원 가상시제모델을 사용하여 포신 오차를 분석하였고, 고각과 방위각 오차를 최소화하기 위한 최적설계를 수행하였다. 기동과 화력 성능을 고려한 3차원 모델을 사용하여 비대칭 범프통과 시 발생하는 차량의 기울어짐을 고려하였고, 서로 다른 오차인자들이 복합적으로 작용할 때 발생하는 포신의 고각과 방위각 오차를 예측하였다. 현수장치의 스프링 상수와 댐핑 계수를 설계변수로 활용하여 포신 오차를 최소화하기 위한 파레토 최적해를 도출하였고, 고각 오차는 최대 6 %, 방위각 오차는 최대 11 % 낮출 수 있었다. 본 연구결과는 포탑 안정화 장치 설계의 사양 결정에 활용할 수 있고 안정화 장치 설계 시 오차 발생에 영향을 주는 설계 파라미터의 최적화를 수행할 경우 성능 개선에 효과적인 최적 설계안을 도출 할 수 있을 것으로 예상된다.

Acknowledgments

본 연구는 한국 국방과학연구소의 지상체계분석특화 연구실 과제의 지원을 받았으며, 이에 감사드립니다.

References

• L. S. Strohm, An Introduction to the Sources of Delivery Error for Direct-Fire Ballistic Projectiles, No.ARL-TR-6494, Army Research Lab Aberdeen Proving Ground MD Weapons and Materials Research Directorate, p8-21, (2013).
• E. J. Kim, and T. I. Suh, “Study on Analyzing and Correction of Dynamic Battery Alignment Error in Naval Gun Fire Control System by using Image of Boresight Telescope”, Journal of the Korea Institute of Military Science and Technology, 16(6), p745-751, (2013). [https://doi.org/10.9766/kimst.2013.16.6.745]
• S. H. Yoo, D. Y. Chung, M. H. Oh, N. H. Shin, and S. H. Nam, “Analysis of the Estimation of the Deflection and Hit Probability of a Gun Barrel of Next Infantry Fighting Vehicle”, Journal of the Korea Institute of Military Science and Technology, 9(3), p12-19, (2006).
• N. D. Devine, Standardizing Methods for Weapons Accuracy and Effectiveness Evaluation, M. S. Thesis, Naval Postgraduate School, Monterey, (2014).
• J. Balla, “Dynamics of Mounted Automatic Cannon on Track Vehicle”, International Journal of Mathematical Models and Methods in Applied Sciences, 5(3), p423-432, (2011).
• J. H. Hong, J. Y. Kim, K. S. Huh, K. Y. Jhang, and J. E. Oh, “Dynamic Performance Analysis for 6WD/6WS Armored Vehicles”, Transactions of KSAE, 5(6), p155-166, (1997).
• Y. I. Sohn, J. H. Lee, and B. S. Song, “Development of a Tracked Vehicle Model for Real-time Simulation of Semi-active Suspension System”, Transactions of KSAE, 11(4), p135-143, (2003).
• S. H. Lim, W. C. Lim, S. J. Min, T. H. Lee, J. B. Ryoo, and J. J. Pyun, “Model-Driven Design Framework for Future Combat Vehicle Development based on Firepower and Mobility: (1) Integrated Performance Modeling”, Korean Journal of Computational Design and Engineering, 19(4), p316-323, (2014). [https://doi.org/10.7315/cadcam.2014.316]
• W. C. Lim, S. H. Lim, S. Y. Kim, S. J. Min, T. H. Lee, J. B. Ryoo, and J. J. Pyun, “Model-Driven Design Framework for Future Combat Vehicle Development based on Firepower and Mobility: (2) Integrated Design Optimization”, Korean Journal of Computational Design and Engineering, 19(4), p324-331, (2014). [https://doi.org/10.7315/cadcam.2014.324]
• N. Ahmed, R. D. Brown, and A. Hameed, “Finite Element Modelling and Simulation of Gun Dynamics Using ANSYS”, Tenth International Conference on Computer Modeling and Simulation, p18-22-22, (2008). [https://doi.org/10.1109/uksim.2008.22]
• J. B. Song, S. Y. Choi, and K. Park, “Aiming Error Analysis of Guns in Ground Combat Vehicles Operating on Bumpy Roads”, Journal of Mechanical Science and Technology, 29(12), p5145-5150, (2015). [https://doi.org/10.1007/s12206-015-1114-x]
• I. J. Youn, J. P. Im, H. B. Shin, J. K. Lee, and M. J. Shin, “Performance Evaluation of Control Algorithms for 1/2 Tracked Vehicle with Semi-Active Suspension System”, Transactions of KSAE, 9(4), p139-147, (2001).
• S. Y. Kim, W. C. Lim, H. S. Kim, N. H. Ryu, K. H. Kwon, S. H. Lim, S. J. Min, and T. H. Lee, “Robust Target Cascading for Improving Firing Accuracy of Combat Vehicle”, Journal of Mechanical Science and Technology, 30(12), p5577-5586, (2016). [https://doi.org/10.1007/s12206-016-1126-1]
• T. O. Procedure, Vehicle Test Facilities at Aberdeen Test Center and Yuma Test Center, Automotive Directorate (TEDT-AT-AD). US Army Aberdeen Test Center, p72-76, (2012).