
카메라 캘리브레이션을 위한 영상의 주파수 특성 기반 스테레오 카메라의 상대적인 회전값 추정


Copyright Ⓒ 2019 KSAE / 159-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper proposes an approach to the estimation of a relative rotation of stereo images. To this end, it endeavors to achieve the self-calibration of a depth camera. In the past few years, the depth camera system has been embedded in mobile devices, and this trend requires an acquisition of camera parameters in real time and in an efficient manner. In contrast to conventional methods using a checkerboard or a set of known pattern objects(or planes), or employing the properties of epipolar geometry, this study presents a simple and novel approach to the estimation of the rotation of stereo cameras in the frequency domain, based on the analysis of the magnitude response of images.
Keywords:
Stereo vision, Camera calibration, Camera geometry, Frequency domain, Extrinsic parameters키워드:
스테레오 비전, 카메라 캘리브레이션, 카메라 기하, 주파수 영역, 외부 파라미터1. 서 론
카메라 캘리브레이션(Camera calibration)은 컴퓨터 비전의 영역 중 깊이 값 추출을 위해 활용되는 스테레오 방식에서 반드시 선행되어야 할 절차이다.1) 스테레오 방식과 더불어 수동방식을 활용한 3차원 복원을 위한 깊이정보 추출에 관한 연구는 지난 수 십 년 동안 컴퓨터 비전, 패턴인식, 영상 처리 등의 기술을 기반으로 활발히 연구가 진행되어 왔다. 또한 자율주행 자동차, 공장 자동화, 로봇 등 인공지능 기술, 에 대한 필요성이 커짐에 따라 인간의 시각을 보조 또는 대신할 수 있는 컴퓨터 비전 기술에 대한 수요가 증가함에 따라 카메라 캘리브레이션에 대한 연구의 중요도는 앞으로 더욱 높아질 것이다.2-4) 3차원 복원의 방법은 크게 두 가지, 수동방식과 능동방식으로 나누어 볼 수 있다.5-7) 두 개 이상의 카메라(주로 두 개)를 활용하는 스테레오 방식은 여전히 깊이 값 및 3차원 좌표를 측정하기 위해 널리 사용되고 있다. 그 이유는 지난 수 십 년 동안 활용되면서 알고리즘이 안정화 및 최적화 되어 있는 경우가 많으며, 테스트를 위한 환경구축이 비교적 간단하기 때문이다. 이러한 장점에도 불구하고 스테레오 방식은 몇 가지의 한계점 또는 단점을 내재하고 있다. 첫째, 카메라 캘리브레이션 결과의 의존성이다. 카메라 캘리브레이션은 스테레오 방식에서 사용되는 두 개의 카메라들에 대한 특성 및 기하학적 관계를 정량적으로 제공한다. 이 값들을 활용하여 카메라가 획득한 2차원 이미지로부터 실제의 3차원 영상에의 좌표를 계산할 수 있다. 가장 잘 알려진 카메라 캘리브레이션 알고리즘은 특정 패턴을 가진 물체를 카메라로 여러 번 촬영하여 카메라의 특성값(Camera parameters)을 계산한다.8,9) 스테레오 방식을 적용한 깊이 카메라 시스템에서는 정확한 캘리브레이션 결과를 얻기 위해 Zhang8)의 알고리즘이 많이 사용되어 왔다. 위의 방법에서 체커보드(Checkerboard)가 사용되며, 약 10회 이상 카메라의 방향과 위치를 바꾸어 가며 체커보드를 촬영한다(단, 카메라와 체커보드간의 직선 거리는 일정한 값으로 유지한다). 체커보드 외에도 원형패턴 등이 사용되기도 하였다.10) 최적화 과정을 반복하면서 캘리브레이션 결과를 얻기 때문에, 실험환경, 초기에 가정한 변수(Parameter) 값 등이 캘리브레이션 결과에 영향을 준다. 체커보드 등의 패턴의 특이점 추출에 실패하거나 코너 추출의 정확도가 낮아질 경우 캘리브레이션의 결과 정확도는 낮아진다.11) 완벽한 참값을 구하는 것은 불가능 하므로, 최적화된 결과를 카메라의 특성값으로 활용하게 된다. 최적화 과정에서 오류가 발생할 경우 캘리브레이션 이후의 절차인 디스패리티(Disparity)와 깊이(Depth) 계산되는 결과들은 치명적인 오류를 포함하고 있을 확률이 높다. 둘째, 카메라 캘리브레이션이 성공적으로 수행 되었더라도, 스테레오 카메라로 촬영한 두 영상(좌, 우 영상) 사이에서 특징점들을 매칭할 때 에러가 발생할 경우 디스패리티(Disparity) 값에 영향을 줄 수 있다(디스패리티 값은 깊이 값의 역수에 비례한다). 특히 카메라 캘리브레이션 과정에서 수행되는 최적화 절차는 스테레오 방식의 불안정한 결과를 초래 할 수 있으며, 캘리브레이션 자체를 수행하는 데에 걸리는 시간과 계산량 또한 실시간 3차원 복원 또는 실시간 깊이값 추정에 부정적인 결과를 초래할 수 있다. 그러므로 카메라 캘리브레이션은 여전히 컴퓨터 비전 분야에서 풀어야 할 문제점이 많은 분야이며, 이러한 문제점을 해결하고, 불안정성을 개선하기 위하여 다양한 방식의 캘리브레이션에 대한 연구가 진행되어 오고 있다.12,13) 3차원 좌표 정보를 얻는 과정에서 카메라 캘리브레이션 결과의 정확도는 매우 중요하므로 오랜 기간 검증되고 사용되어 온 기존 방식의 캘리브레이션은 여전히 깊이정보 추출에서 많이 사용되고 있다. 카메라 캘리브레이션은 실제 3차원 물체(또는 장면)와 이 실제 물체가 카메라에 투영된 2차원 영상 간의 기하학적인 관계에 대한 정보를 제공한다. 그 정보들은 크게 두가지로 나누어 볼 수 있는데 하나는 카메라의 내부 특성값(Intrinsic parameter)이고 다른 하나는 외부 특성값(Extrinsic parameter)이다. 내부 특성값 행렬의 구성요소는 초점거리, 이미지 중심, 스케일링 비율과 비대칭도(Skewness) 이다. 이 구성요소들은 2차원의 카메라 영역에서 정의되는 영상의 픽셀(Pixel) 좌표와 실제 3차원 영상의 3차원 좌표 사이의 관계를 결정해 준다. 외부 특성값은 카메라들 간의 상대적인 위치 정보를 제공한다. 외부 특성값 행렬은 회전행렬 (R3×3)과 이동 변위 벡터 (T3×1)로 구성되어 있다.14) 기존의 카메라 캘리브레이션은 카메라로 평면을 다른 위치에서 여러 번 촬영한 후 패턴의 실제 사이즈(미리 알려진 값)와 카메라들이 획득한 패턴의 2차원 이미지 영역에서의 크기 사이의 관계를 활용하여 카메라의 내부 및 외부 특성값을 최적화 과정을 통해 계산하여 캘리브레이션을 수행한다.8) 캘리브레이션은 카메라의 특성값들을 반복적으로 계산하는 최적화 과정이므로 촬영횟수, 평면상의 패턴갯수 등이 증가할수록 캘리브레이션의 정확도가 높아질 가능성이 높다. 정확도와 계산량 간의 트레이드 오프(Trade-off)가 존재함과 동시에 과적합(Overfitting)의 부작용이 발생할 수도 있다. 그 외에도, 핀홀 카메라 모델, 렌즈 왜곡 모델링, 초점거리 불변 등 캘리브레이션 과정에서 일반적으로 가정하는 요소들로 인해 깊이 값의 오류 또는 계산한 깊이 값의 편차가 발생할 수 있다. 요약하자면, 카메라의 외부 특성값들은 3차원 물체 또는 장면의 상대적인 원근정보를 제공할 수 있으며, 절대적인 값을 획득하기 위해서는 내부 특성값이 반드시 필요하며, 이 값들의 추정은 최적화 과정을 통해 이루어진다.
최근에는 인공지능에 대한 연구가 활발해 짐과 동시에 자율주행 자동차, 로봇 등의 응용분야에서 컴퓨터 비전 기술에 대한 요구가 증가하고 있다. 그러나, 이러한 응용분야에서 활용되는 비전 시스템에서는 전통적인 방식의 캘리브레이션을 적용하기에 한계가 따른다. 그 이유는 자동차, 로봇 등에서는 실시간으로 깊이정보를 계산해야 하고, 실시간 캘리브레이션이 필요한 상황이 발생할 수 있다. 전통적인 방식의 캘리브레이션 방법은 계산량의 증가를 가져오기 때문에 효율적인 실시간 캘리브레이션을 달성하기 어렵다. 그리하여 지난 몇 년간 전통적인 방법을 대체하는 캘리브레이션 방법들이 소개되었다.15) 그 중 대표적인 예시들은 소실점(Vanishing point) 활용한 캘리브레이션,16) 선 추출을 통한 캘리브레이션,17) 에피폴라 기하를 활용한 영상기반 캘리브레이션13,18) 등이다. 소개되는 방법들은 캘리브레이션 알고리즘의 효율성을 높이기 위해 제안되었다. 그러나 이 방법들 역시 기존의 캘리브레이션이 포함하는 한계점을 내재하고 있거나, 또 다른 한계점을 내재하고 있다. 첫째, 실제 영상을 기반으로 한 새롭게 소개된 캘리브레이션 알고리즘은 에피폴라 기하(Epipolar geomtry) 를 가정하였다. 그러나 실제 3차원 물체 또는 영상 중에 에피폴라 기하 특징을 가지고 있지 않은 경우도 많아서 한계가 있다. 두 영상간의 Epipolar geometry가 정의되지 않을 경우, 또는 Essential matrix 의 분할이 제대로 되지 않을 경우 알고리즘 동작이 제대로 되지 않는다는 단점이 있었다.19) 둘째, 영상기반의 캘리브레이션을 활용하고 있으나, 스테레오 카메라들이 획득한 영상들 간의 특징점 매칭이 여전히 요구되는 점에서 한계가 있다.1,16) 특징점 매칭의 정확도가 낮아질 경우, 캘리브레이션의 결과는 불안정해 진다. 그 외에 소개된 방법들은, 최적화 되어야 할 변수들이 여전히 존재하였으며, 초기값 설정이 필요한 방법이었거나, 실제 영상의 구조에 대해 특수한 가정을 한 경우가 있었기 때문에 여전히 한계가 존재하였다.
본 논문에서는 스테레오 영상을 이용하여 카메라 간의 상대적인 회전행렬을 추정하는 방법을 제안한다. 회전행렬은 스테레오 카메라 간의 상대적인 위치 정보를 제공하는 중요한 요소이며, 모바일 기기 등 소형화된 깊이 카메라에서는 변위벡터보다 더 중요한 역할을 하는 요소이다. 본 논문에서는 기존의 캘리브레이션에서 활용되었던 체커보드, 영상간의 기하학적인 관계, 영상들에 존재하는 특이점 등을 이용하지 않고 획득한 영상 전체를 주파수 영역에서 분석하고 활용한다. 최근에 여러 분야에 비젼 소프트웨어 또는 비젼 시스템이 탑재되고 있으므로, 기존의 캘리브레이션 작업을 위한 환경 구축이 쉽지 않게 되었다. 또한 카메라의 소형화로 인해 카메라 간의 변위 값(Translation vector)는 거의 변동이 없거나 있더라도 매우 작은 양이다. 그러므로 두 카메라 간의 상대적 회전각을 추정하는 것의 중요성이 증대하고 있다. 특히, 내부 특성값 행렬이 카메라의 제조단계에서 제공 될 경우 효율적인 캘리브레이션 시스템을 구축할 수 있다. 획득된 영상의 2차원 디지털 퓨리에 변환을 한 후, 주파수 응답의 특성을 활용하여 회전각을 추정하는 방법을 제안한다. 제 2장에서는 카메라 캘리브레이션에 대한 기본적인 내용을 소개하고, 3장에서는 본 논문이 제안하는 알고리즘에 대해 자세히 설명한다. 4장에서 실험결과 및 분석결과를 제시한 후 5장에서 논문을 끝맺는다.
2. 카메라 캘리브레이션 및 깊이값 복원
전통적인 방식의 카메라 캘리브레이션은 체커보드 같은 일정한 패턴을 가진 평면을 활용한다. 스테레오 카메라가 이 체커보드를 10회 이상 촬영한 후, 촬영된 영상으로부터 패턴의 특징점들을 2차원 상에서 추출하고, 이를 실제 패턴의 사이즈와 비교하여, 캘리브레이션의 결과인 카메라 특성값(내부/외부)를 계산한다. m⊂2와 M⊂3을 각각 2차원 이미지(카메라가 촬영한 이미지)의 픽셀 좌표와 실제 물체의 3차원 좌표로 정의한다. 점 m과 M 사이의 관계는 투영행렬 P (perspective projection matrix)에 의해 다음과 같이 표현된다. 실제로 m과 M은 2차원 점과 3차원 점으로 이루어진 행렬이다.
| (1) |
호모지니어스(homogeneous) 좌표계에서 두 점을 표현하면 m=(u,v,1)이고 M=(x,y,z,1)이다. m=(u,v)과 M=(x,y,z)로 나타내어도 동일한 의미를 가진다. 식 (1)은 캘리브레이션에서 사용된 카메라가 핀홀모델로 가정되었다는 것을 의미하며, “≃”을 사용하고 “=”을 사용하여도 무방하다. P 는 내부특성값 행렬 (K), 외부특성값을 구성하는 회전행렬(R)과 변위벡터(t)로 분해될 수 있다.19)
| (2) |
회전행렬 R과 변위벡터 t의 사이즈는 각각 3×3과 3×1이다. fx와 fy는 카메라의 x방향(또는 가로방향)으로의 초점거리와 y방향(또는 세로방향)의 초점거리를 나타낸다. fx는 fy는 상수이며 같다고 가정한다. 즉, fx=fy=c (상수)이다. 이 가정이 적용되지 않을 경우 캘리브레이션은 더 복잡해진다. 그러나 일반적으로 카메라의 제조단계에서 초점거리의 값은 제공되므로, 위와 같이 가정해도 무방하다. 두 개의 카메라가 획득한 영상들 간에 에피폴라 제한조건이 만족하였을 때 Fundamental 행렬 (F)은 아래와 같이 표현된다.
| (3) |
식 (3)은 스테레오 방식에서 두 카메라와 목표 물체 사이의 기하학적인 관계를 나타냄과 동시에 제한조건을 나타낸다. [∙]T는 행렬의 전치행렬을 나타내며 식 (3)을 활용하여 캘리브레이션의 중간단계인 렉티피케이션(Rectification)의 정확도를 정량적으로 판단할 수 있고, 이는 캘리브레이션의 정확도와 직접적인 연관이 있다. 또한 식 (3)을 캘리브레이션의 정확도를 평가하는데에 사용하기도 한다. 캘리브레이션을 완료한 후 깊이값 z는 아래와 같이 표현할 수 있다.
| (4) |
b,f,d는 각각 두 카메라의 광학중심 간의 거리(baseline), 초점거리, 디스패리티(Disparity)를 나타낸다. b는 카메라의 배치 단계에서 결정되는 것이고, d는 상대적인 깊이 값의 정보를 알려주며 f는 절대적 깊이 값을 제공하는 역할을 한다. 디스패리티는 좌우 영상의 매칭된 영역이 수평방향의 변위차를 나타내며, 이 값은 깊이값과 직접적인 연관이 있다. 디스패리티 값만으로도 3차원 영상의 상대적인 원근 또는 상대적인 깊이를 추정할 수 있다. 그러므로 대략적인 3차원 현실세계의 정보를 제공하기 위해 디스패리티 계산결과의 정확도는 매우 중요하며 렉티피케이션의 정확도에 영향을 준다.
3. 제안 방법
이 장에서는 스테레오 카메라 두 개의 캘리브레이션의 구성요소 중 회전행렬(또는 회전각)을 구하는 방법을 제안한다. 회전행렬 외에도 변위벡터, 내부 특성값 등의 계산이 필요하지만, 본 논문에서는 회전행렬을 구하는 방법을 다룬다. 회전행렬을 구하는 방법에 주안점을 둔 이유는 두가지이다. 첫째, 카메라의 내부 특성값은 제조단계에서 제공되는 경우가 많다. 전통적인 캘리브레이션 방법이 내부 특성값을 계산하지만, 제작단계에서 정해진 내부특성값이 사전에 제공된 경우, 이것을 최적화 과정을 통해 계산하는 것은 시간과 계산량 측면에서 비효율적이라고 할 수 있다. 둘째, 최근 들어서 깊이 카메라는 모바일 기기에 탑재되는 추세를 보이고 있다. 이런 경우 모바일 기기의 특성상 변위벡터의 크기, 즉 베이스라인의 크기는 1 cm 이하인 경우가 많으며, 이 값 역시 제조단계에서 결정이 된다. 카메라 사용 중 변동이 생길 수 있으나 그 값 역시 매우 작기 때문에(mm 단위) 캘리브레이션 결과 및 깊이값 측정의 결과에 주는 영향이 회전행렬보다 작다고 할 수 있다. 그러므로 본 연구에서는 스테레오 카메라 시스템에서 사용되는 두 카메라 간의 회전행렬 추정에 주안점을 두고 있다. 제안하는 회전행렬 추정 연구의 전체 Fig. 1처럼 요약할 수 있다.
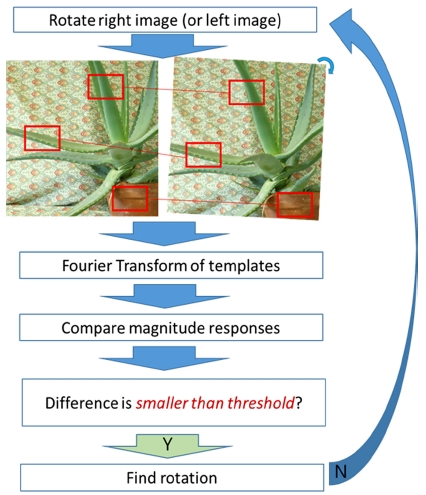
Middlebury dataset is used5), A and C : Rectified left and right. B and D : Magnitude of FT of A and C, respectively. Since A and C are related by horizontal translation (disparity), magnitude responses are same in frequency domain
스테레오 카메라가 영상을 촬영한 후 이 두 영상은 좌우 영상으로 나뉘어진다. 이 두 영상은 현재 각각의 카메라에 의해 상대적인 회전각을 포함하고 있으며, 이 값이 결정되어야 성공적인 렉티피케이션(Rectification)을 할 수 있고, 그 후 디스패리티 값을 구할 수 있다. 두 영상 간의 회전각을 추정하기 위해 기존의 방법들처럼 에피폴라 제한 조건 또는 특징점 매칭 등을 사용하지 않고, 촬영된 이미지를 2차원 주파수 영역에서 분석하였다. 주파수 영역에서의 분석을 위해 2차원 퓨리에 변환(2D DFT)을 수행하였다. 2D DFT를 수행하기 전에 좌우 영상의 공통영역을 분리해야 한다. 두 카메라 사이에 시차(Parallax)가 존재하므로, 주로 가장자리 부분들의 영상은 좌우 영상이 공통적으로 포함하고 있지 않다. 그러므로, 이러한 공통적이지 않은 영역들을 제거해 주는 작업을 한 후 2D DFT를 수행한다. 또한 공통적인 영역끼리의 매칭을 통한 비교를 위해 영상 전체를 활용하는 대신, 영상 내에서 16개의 부분영상(패치, Patch)을 활용한다. 2D DFT 수행 후 각 영상의 주파수 크기응답의 특성을 기반으로 두 영상간의 회전각을 추정한다. 1장에서 언급한 바와 같이, 카메라 내부 특성값들은 이미 구해졌다고 가정하고 본 논문에서는 다루지 않기로 한다. IL(x,y)⊂2와 IR(x,y)⊂2을 각각 좌측과 우측 카메라가 획득한 2차원 영상으로 정의한다. 좌우 영상들은 픽셀들로 이루어진 이산신호로 취급할 수 있고, 2차원 영역에서 정의되므로 2차원 이산 퓨리에 변환(2-Dimensional Discrete Fourier Transform, 2D-DFT)을 계산하며, IL(x,y)와 IR(x,y)의 2D-DFT 결과는 각각 IL(u,v)와 IR(u,v)로 정의한다(본 논문에서 다루는 신호는 모두 2차원이므로 2D를 생략하도록 한다). 스테레오 카메라는 3차원의 공간에 존재하므로, 영상들도 3차원 DFT를 수행하여 회전행렬 추정을 하는 것이 더욱 정확한 결과를 가져온다. 그러나 본 논문에서는 영상이 카메라에 획득된 2차원의 상태만을 놓고 분석하여 두 영상(또는 카메라) 간의 상대적인 회전각을 추정함으로써 향후 진행될 3차원 회전행렬 추정연구로 확대해 나갈 것이다.
| (5) |
| (6) |
여기서 u,v는 주파수 변수이며, 회전각 추정을 위해 사용되는 영상은 M×N 사이즈로 일치시킨다(식 (5)와 (6)에서의 u,v 는 2장에서 언급한 2차원 좌표를 나타내는 u,v와 다름을 주의한다). M과 N은 각각 DFT를 수행할 때 사용된 샘플 개수이다(즉 x축과 y축으로 각각 M-DFT와 N-DFT를 계산하였다). IL(x,y)와 IR(x,y)의 상대적 위치(또는 두 카메라의 상대적 위치)는 카메라의 외부 특성값들, 즉 회전과 변위에 의해 결정된다.
| (7) |
회전행렬 R (R⊂2×2)이 결정되면 두 영상 사이에는 변위벡터 t에 의한 관계만 존재한다. 이러한 경우 두 영상, IR(x,y)와 간의 관계는 위치 영역과 주파수 영역에서 아래와 같이 표현될 수 있다.
| (8) |
| (9) |
IR(x,y)와 의 DFT의 크기응답의 관계는 식 (9)에 의해 아래와 같이 나타난다.
| (10) |
Fig. 2에서 나타난 것처럼 회전각 추정이 완료된 두 영상간의 크기응답은 거의 동일하다.21) 즉 두 영상이 변위벡터에 의해서만 관계되어 있을 경우 퓨리에 변환의 크기응답은 동일하다. 회전각 추정이 완료된 두 영상은 변위벡터에 의해서만 관계되어 있으므로, 변위차를 활용하여 디스패리티를 계산하여 깊이값을 계산할 수 있다.

Middlebury dataset is used5), A and C : Rectified left and right. B and D : Magnitude of DFT of images. Since A and C are only related by translation, magnitude responses are same in frequency domain based on Eq.s (9) and (10)
위의 식들을 모두 고려하여 보아 추정하는 회전행렬()은 다음 식을 만족한다.
| (11) |
|∙|는 절대값을 표현하고, 절대값 대신 놈(Norm)을 계산해도 무방하다.
식 (9)와 (10)로부터 영상들의 퓨리에 변환의 크기 응답은 회전행렬 추정에 중요한 역할 한다. 다시 말해서 회전행렬 추정이 완료된 두 영상 사이에는 변위벡터의 차이만 존재한다. 즉, 주파수 영역에서는 위상 응답의 차이만 가지게 되고, 위상응답은 주파수의 크기응답에서는 영향을 주지 않는다. 그러므로 회전행렬의 추정이 완료된 좌우 영상의 주파수 응답 크기는 동일하다. 기존의 캘리브레이션에서는 특징점 매칭, 호모그라피(Homography) 행렬 추정, 에피폴라 제한조건 기반한 기반행렬(Fundamental matrix) 계산등을 완료한 후 렉티피케이션(Rectification)이 완료되었으나,13,18) 본 연구에서는 좌우 영상의 주파수 영역에서의 크기응답을 비교하는 것만으로 렉티피케이션을 완료할 수 있다. 즉 기존의 캘리브레이션 기술에서 사용되었던 패턴화 평면, 특징점, 소실점 등을 활용하는 절차가 필요 없다는 것이 본 연구의 장점이라고 할 수 있다. 본 연구에서 회전행렬을 추정한 후 변위벡터의 추정이 필요할 경우 이에 대해서만 Fundamental 행렬 또는 Essential 행렬 분해를 활용하여 구할 수 있다.14,18)
4. 실험 결과 및 분석
이 장에서는 스테레오 영상들 사이의 회전각을 추정하기 위해 제안된 방법을 시뮬레이션 하여 나타난 결과를 보여준다. 실험은 매우 간단하고 직관적으로 수행될 수 있으며, 매트랩을 사용하여 구현하였다. 회전각 추정 결과는 참값(Ground-truth)과 추정값의 차이를 구하여 정량적으로 나타낸다. 퓨리에 변환후 렉티피케이션 된 좌우 영상의 크기응답을 비교하는 방법, 또는 회전각 추정 후의 두 영상의 특징점들 간의 수직 좌표를 비교하여 제안한 방법 등을 활용하여 정확도를 정량적으로 나타낼 수 있다. 등 다양한 방법을 활용하여 결과를 평가할 수 있으며, 본 논문에서는 간단히 참값과 추정값의 차이를 구하여 제안된 방법을 평가한다. 본 실험은 두 영상 사이의 회전각이 주어진 상황에서 회전각을 추정하므로 참값이 주어진 실험이다. Fig. 3과 Fig. 4에서 원래 영상과 영상의 퓨리에 변환 결과를 보여준다. 퓨리에 변환 후 크기 응답을 비교한 결과는 Fig. 3과 Fig. 4에 나타나 있다. Fig. 4의 아래에서는 회전각 추정 이전의 두 영상을 2D-DFT 한 후, 크기 응답의 차이를 계산하였고, Fig. 5에서는 회전각 추정 후 두 영상을 2D-DFT 후 크기응답의 차이를 제시하였다. 두 그림에서 나타나듯이, 회전각의 추정값이 참값에 가까워질수록 크기응답의 차이는 줄어든다. 크기응답의 차이는 Root Mean Square Error(RMSE)를 사용하였다. 기존 방식 대비 제안한 방식을 활용한 회전각 추정 결과의 정확도는 유사하거나 약간 증가 하였다. 다만, 두 영상 간의 회전각이 작을수록, 추정의 정확도는 감소하는 경향을 보였다. 비교 대상이 된 기존 알고리즘들16,20)과의 직접적인 비교를 수행하기에는 실험환경들, 실험조건 등이 모두 다르고, 실험 대상이 된 영상들도 다르기 때문에, 본 논문에서는 회전각 추정 결과만을 비교하여 나타내었다.

A and B : Left and right images taken by stereo camera. In this paper, the images are from Middleburry dataset5), and the rotation is applied to the images
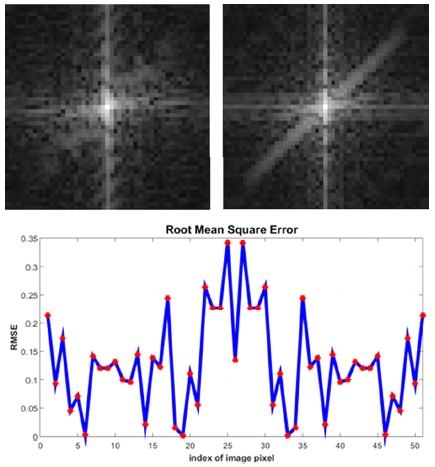
Magnitude responses of the images in Fig. 2, and the root mean square error (RMSE) of the magnitude responses
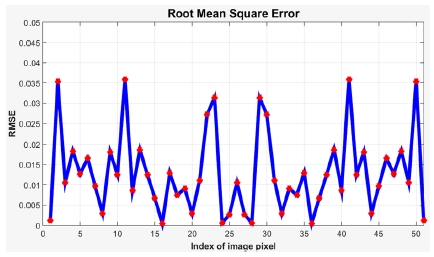
Magnitude responses and RMSE of two images after estimation of rotation is performed. RMSE is much less than the case of the result shown in Fig. 2
제안한 방식으로 추정한 회전각의 정확도는 아래의 식을 활용하여 평가한다.
| (11) |
본 논문에서는 두 영상간의 회전각을 1도에서 15도까지 무작위로 변화시키면서 제안하는 방법을 활용하여 회전각을 추정하였다. 그리고, 영상 전체를 한꺼번에 이용하지 않고, Fig. 1과 Fig. 5에서 나타내었듯이 영상의 일부분을 활용하여 회전각을 추정하였다. 제안한 방법을 적용한 결과의 오차율은 Rgt(회전각의 참값)에 따라 조금씩 차이를 보였다. 최대 정확도를 보이는 영상에서는 오차율이 5 % (Rgt = 3도일 때 약 0.1도 오차) 미만이었으나 정확도가 낮은 영상에서는 15 %(Rgt = 5도일 때 약 0.8도 오차)정도의 오차율을 보였다. Table 1에서는 오차율의 평균값을 나타내고 있다.
Golban and Nedevschi20)의 논문에서는 추정한 회전각의 오차는 평균적으로 0.1382도였으며(최대 0.2도 이상, 최소 약 0.05도이며 오차율이 제시되지 않았음), 본 논문에서 제시한 방식을 활용할 경우 기존 결과들과 비교하였을 때 본 연구는 별도의 제한조건이나 매칭 등의 계산을 활용하지 않고, 영상만을 활용하였다는 점에서, 알고리즘의 효율성, 계산의 간편성 등을 고려한다면 본 연구에서 제시하는 방법이 경쟁력이 있다는 것을 알 수 있다.
5. 결 론
본 논문에서는 두 영상간의 상대적인 회전각을 추정하는 방법을 제안하였다. 제안한 방법은 기존의 캘리브레이션 방법과 다르게 촬영된 영상을 직접적으로 활용하였으며, 특징점 추출, 패턴화 물체 등을 활용하지 않았다. 그리하여 회전각 추정의 효율성을 달성할 수 있었고, 향후 카메라 캘리브레이션의 효율화를 달성할 수 있을 것으로 기대할 수 있다. 또한 본 연구의 내용은 현재 많은 관심을 얻고 있는 자율 주행 또는 무인 자동차, 로봇, 생산 자동화 시스템 등 인간의 시각능력을 활용한 업무를 보조하거나 대체할 수 있는 분야에 다양하게 응용될 수 있다. 제안된 방법은 매우 간단하다는 장점이 있으며 향후 변위 벡터 및 카메라의 내부 변수(Intrinsic parameter)들 까지 추정할 수 있는 연구가 추가적으로 수행되어야 할 것이다. 3차원 정보 및 깊이정보 획득 기술은 향후 자동차, 로봇 등 다양한 분야에서 활용될 것이므로 본 논문에서 제안한 방법이 이러한 분야들에서 상당부분 기여할 것으로 기대한다.
References
-
J. Salvi, X. Aramangue, and J. Battle, “A Comparative Review of Camera Calibrating Methods with Accuracy Evaluation”, Pattern Recognition, 35(7), p1617-1635, (2002).
[https://doi.org/10.1016/s0031-3203(01)00126-1]

-
M. S. Kang, S. J. Hur, I. H. Park, and Y. W. Park, “Map Building Based on Sensor Fusion for Autonomous Vehicle”, Transactions of the KSAE, 22(6), p14-22, (2014).
[https://doi.org/10.7467/ksae.2014.22.6.014]

-
K. S. Sharma, S. R. Sahoo, and P. V. Manivannan, “A Hybrid Vision System for Dynamic Obstacle Detection”, International Conference on Robotics and Samrt Manufacturing, p153-160, (2018).
[https://doi.org/10.1016/j.procs.2018.07.019]

-
J. Zbontar, and Y. LeCun, “Computing the Stereo Matching Cost with a Convolutional Neural Network”, Conference on Computer Vision and Pattern Recognition, (2015).
[https://doi.org/10.1109/cvpr.2015.7298767]

-
S. M. Seitz, B. Curless, J. Diebel, D. Scharstein, and R. Szeliski, “A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms”, Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (2006).
[https://doi.org/10.1109/cvpr.2006.19]

-
H. Sarbolandi, D. Lefloch, and A. Kolb, “Kinect Range Sensing: Structured-light versus Time-of-Flight Kinect”, Computer Vision and Image Understanding, 139, p1-20, (2015).
[https://doi.org/10.1016/j.cviu.2015.05.006]

- J. Y. Hwang, D. G. Hong, and K. S. Huh, “Development of a Vision Sensor-based Vehicle Detection System”, Transactions of KSAE, 16(6), p134-140, (2008).
-
Z. Zhang, “A Flexible New Technique for Camera Calibration”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(11), p1330-1334, (2000).
[https://doi.org/10.1109/34.888718]

-
R. Y. Tsai, “A Versatile Camera Calibration Techniaue for High-Accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses”, Journal of Robotics and Automation, 3(4), p323-344, (1987).
[https://doi.org/10.1109/jra.1987.1087109]

-
J. Heikkila, “Geometric Camera Calibration Using Circular Control Points”, Transactions on Pattern Analysis and Machine Intelligence, 22(10), p1066-1077, (2003).
[https://doi.org/10.1109/34.879788]

-
J. Heikkila, and O. Silven, “A Four-step Camera Calibration Procedure with Implicit Image Correction”, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), (1997).
[https://doi.org/10.1109/cvpr.1997.609468]

- M. Pollefeys, R. Koch, and L. Van Gool, “Self-Calibration and Metric Reconstruction Inspite of Varying and Unknown Intrinsic Camera Parameters”, International Journal of Computer Vision, 32(1), p7-25, (1999).
- T. Dang, C. Hoffmann, and C. Stiller, “Continuous Stereo Self-Calibration by Camera Parameter Tracking”, IEEE Transactions on Image Processing, 18(7), p1536-1550, (2009).
-
O. Faugeras, The Geometry of Multiple Images, The MIT Press, Cambridge, (2004).
[https://doi.org/10.7551/mitpress/3259.001.0001]

-
F. Li, H. Sekkati, J. Deglint, C. Scharfenberger, M. Lamm, D. Clausi, J. Zelek, and A. Wong, “Simultaneous Projector-Camera Self-Calibration for Three-Dimensional Reconstruction and Projection Mapping”, IEEE Transactions on Computational Imaging, 3(1), p74-83, (2017).
[https://doi.org/10.1109/tci.2017.2652844]

-
J. -K. Lee, and K. -J. Yoon, “Real-Time Joint Estimation of Camera Orientation and Vanishing Points”, The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), p1866-1874, (2015).
[https://doi.org/10.1109/cvpr.2015.7298796]

-
A. F. Habib, M. Morgan, and Y. -R. Lee, “Bundle Adjustment with Self–Calibration Using Straight Lines”, The Photometric Record, 17(100), p635-650, (2002).
[https://doi.org/10.1111/j.1477-9730.2002.tb01908.x]

-
O. D. Faugeras, Q. -T. Luong, and S. J. Maybank, “Camera self-calibration: Theory and Experiments”, European Conference on Computer Vision, p321-334, (1992).
[https://doi.org/10.1007/3-540-55426-2_37]

-
E. E. Hemayed, “A Survey of Camera Self-calibration”, IEEE Conference on Advanced Video and Signal Based Surveillance, (2003).
[https://doi.org/10.1109/avss.2003.1217942]

-
C. Golban, and S. Nedevschi, “An Experiment on Relative Rotation Estimation from Distant Points with Monocular Vision”, IEEE International Conference on Intelligent Computer Communication and Processing (ICCP), (2013).
[https://doi.org/10.1109/iccp.2013.6646115]

- D. W. Lee, and J. H. Na, “Estimation of a Relative Rotation between a Pair of Images in Frequency Domain”, KSAE Fall Conference Proceedings, p634-640, (2017).
