HRV40강의 크리프 거동 평가 및 수명 예측

2.1 Monkman-Grant 식

크리프 시험에서는 재료에 일정 온도와 하중을 부가하여 시간에 따른 변형량을 측정하고, 최종 파단 시간을 기록하여 분석한다. 그러나 실제 가동조건에서의 크리프 시험은 많은 시간이 요구되며 그에 따른 시험 비용이 증가하기 때문에 많은 연구자들은 단시간의 크리프 시험 결과로부터 장시간 영역에서의 크리프 거동을 예측할 수 있는 연구를 수행하고 있다.^4-6) 그 중 장시간 크리프 거동을 예측하기 위해 널리 사용되는 Monkman-Grant관계식은 시험에서 측정된 최소 크리프 속도(또는 정상상태 크리프 속도)와 크리프 파단시간 사이에 식 (1)과 같은 관계가 있음을 보여준다.^7-11)

여기서 m과 C 는 Monkman-Grant 상수이며, 최소 크리프 속도 $$ {\dot{ϵ}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$와 파단시간 t_r을 log-log scale의 대수좌표에 도시하였을 때 반비례 선형관계를 나타내므로, 상수 m과 C를 알면 단시간 파단시간 데이터로부터 장시간 예측 데이터를 얻을 수 있다.

2.2 보정 Monkman-grant 식

그러나 소재의 손상 메커니즘이 다른 경우에는 같은 소재에 대하여도 다른 m값을 보이므로 이를 보정하기 위한 보정 Monkman-Grant 관계식이 Dobes와 Milicka에 의하여 제안되었다.⁸⁾ 보정 Monkman-Grant 관계식 (2)는 $$ {\dot{ϵ}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$ 과 t_r외에 크리프 파단 변형률 ϵ_r를 포함하여 많은 경우에 대하여 향상된 정확성을 보이는 것으로 알려져 있다. ϵ′과 C′은 보정 Monkman-Grant식의 상수이다.

2.3 Larson-Miller Parameter

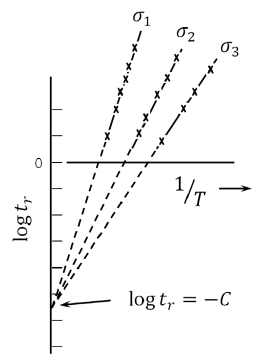
크리프가 진행된 온도와 파단시간을 인자로 한 시간 - 온도 파라미터도 수명예측을 위한 기법으로 사용된다. 1952년에 Larson과 Miller는 크리프 파단시간 t_r와 온도 T (Kelvin)를 이용하여 식 (3)과 같은 Larson-Miller 파라미터 관계식을 제안하였다. 여기서 C_LM 은 같은 응력 조건에서 수행된 다수의 크리프 데이터를 Fig. 1과 같이 ln (t_r)와 절대온도의 역수로 도시하여 피팅하였을 때의 세로축 절편의 값이며, 소재가 갖는 특성이다.

Fig. 1

Stess-rupture data at various stresses for identifying Larson-Miller constant, CLM

또한 P_LM 는 응력에 대한 함수로 표현될 수 있으므로 실험적으로 얻은 P_LM-응력 데이터를 통하여 원하는 온도와 응력에 대한 수명 예측이 가능하다.

3.1 시험편

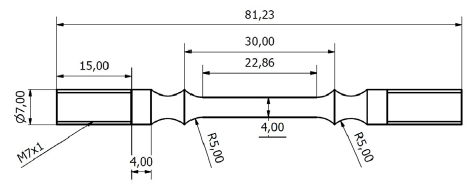
본 시험에 사용된 HRV40강은 750 °C 이상의 온도에서 가동되는 자동차 엔진밸브의 재료로 사용되며 주요 화학성분은 Table 1과 같다. ASTM E139 ‘Standard Test Methods for Conducting Creep, Creep-Rupture, and Stressrupture Tests of Metallic Materials’에 명시된 규격을 따라 시험편을 제작하였으며, 평행부의 직경과 표점거리를 각각 4 mm와 30 mm로 가공하였다. 시험편의 형상과 주요 치수는 Fig. 2와 같다.

Table 1

The main chemical composition of HRV40 steel

Fig. 2

HRV40 creep specimen geometry

3.2 시험방법

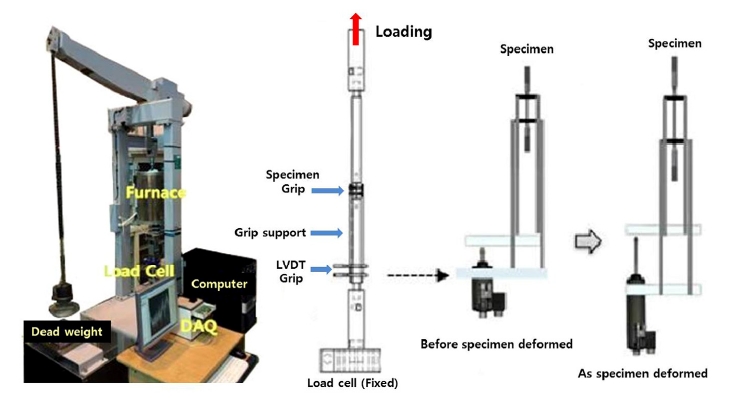
크리프 시험을 수행하기 위한 시험장치는 30 kN 용량의 하중 인가 장치, 전기로, 변위 측정장치로 구성하였으며, 시험기의 모습과 변형률 측정장치의 작동원리를 Fig. 3에 나타내었다. 시험편 가열을 위하여 자동 온도제어가 가능한 1,000 °C 용량의 개폐식 전기로를 사용하였으며, 가열시 시험편이 목표온도에 도달한 후 2시간을 유지하여 열평형을 이룬 상태에서 하중을 부가하였다.

Fig. 3

Creep tester and strain measuring device

온도는 K형 열전대의 끝단을 시편의 표점거리 사이 중앙부에 접촉하여 측정하였으며, 시험 중 온도를 시험목표 온도에서 ±1 °C 범위 이내로 유지하였다. 본 연구에서는 자동차 엔진밸브의 가동 환경을 고려하여 750 °C와 800 °C의 온도에서 시험을 수행하였다.

하중은 응력 조건으로 설정한 50~250 MPa에 맞게 계산된 양의 무게추를 사용하여 시험편이 열평형상태에 도달한 후 부가되었으며, Load cell을 이용하여 실제 부가된 하중을 측정, 저장하였다.

Creep 변형률은 표점거리의 변형량을 측정할 수 있도록 시험편에 직접 장착된 장치에 LVDT(Linear variable displacement transformer)를 장착하여 시험편이 파단되어 시험이 종료될 때까지 실시간으로 저장하였으며, Creep strain은 식 (4)에 따라 계산되었다. 여기서 l₀는 열평형 상태에 도달한 뒤 하중을 부가하지 않은 상태에서의 표점거리, l은 시험 중 LVDT로부터 측정한 표점거리이다. 또한 Creep strain rate는 시간에 대한 Creep strain의 순간변화율로서, 식 (5)와 같이 계산하였다.

4.1 Creep strain curves

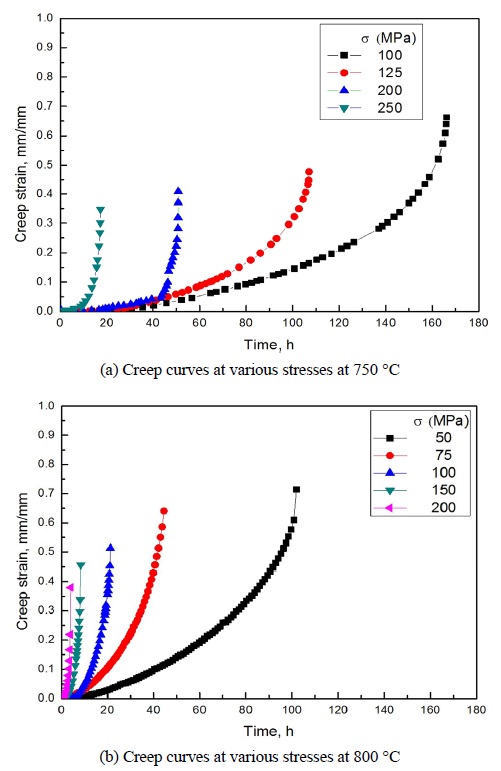
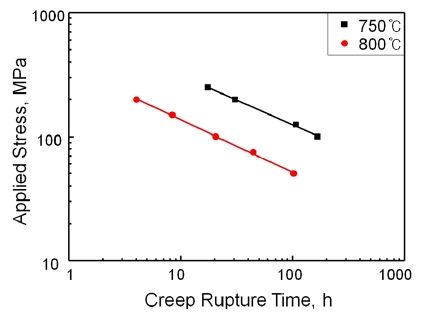
750 °C와 800 °C에서 시험을 통하여 얻은 HRV40강의 크리프 곡선을 각각 Fig. 4(a), (b)에 나타내었다. 전반적으로 1차 크리프 곡선(Primary creep curve)은 두드러지지 않았으며 2차 크리프 곡선(Secondary 혹은 Steady state creep curve)과 3차 크리프 곡선(Tertiary creep curve)이 지배적으로 나타남을 확인하였다. 온도와 응력별로 정리한 시험결과를 Table 2에 나타내었다. Fig. 5에 응력과 크리프 파단 시간과의 관계를 log-log scale의 대수좌표에 나타내었다. 파단시간과 응력의 관계식이 식 (6)과 같이 정의되며, 직선은 식 (6)에 따라 피팅한 것이다.

Fig. 4

Creep curves of HRV40 at temperature of (a) 750°C and (b) 800°C

Table 2

The result data of creep test of HRV40 steel

Fig. 5

Time to rupture vs. applied stresses at each temperature

이 때 상수 k의 값은 피팅된 직선의 기울기로, 재료 내 구조적 변형에 따라 바뀌는 값이다. 예를 들어 입계 및 입내 파괴, 산화, 재결정 등의 변화가 생기면 상수 k의 값이 바뀐다.¹⁾ 본 시험에서는 750 °C와 800 °C에서 k값이 각각 2.51, 2.35로 약 6 % 이내에서 유사하게 나타났으므로 이 온도범위에서 크리프 변형기구가 변형되지 않았음을 알 수 있다.⁹⁾

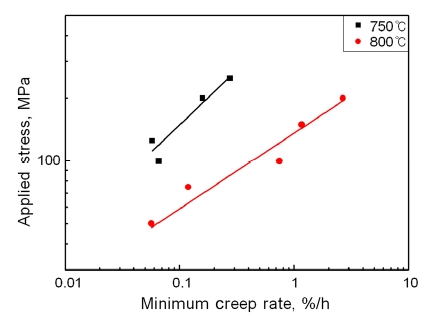
최소 크리프 속도는 식 (7)과 같이 Norton’s Power Law에 의하여 각 온도에 대한 응력의 관계식으로 나타낼 수 있다. HRV40 소재의 750 °C와 850 °C 조건에서의 최소 크리프 속도와 응력의 관계를 Fig. 6과 같이 log-log 스케일 좌표상에 나타내었다.

Fig. 6

Relation between applied stresses and minimum creep rates

여기서 A는 크리프 상수, n은 크리프 지수로서 750 °C와 800 °C에서 각각 4.15×10^-6, 2.00과 6.55×10^-6, 2.43 의 값으로 계산되었다.

4.2 Monkman-Grant and Modified Monkman-Grant relations 와 수명 예측

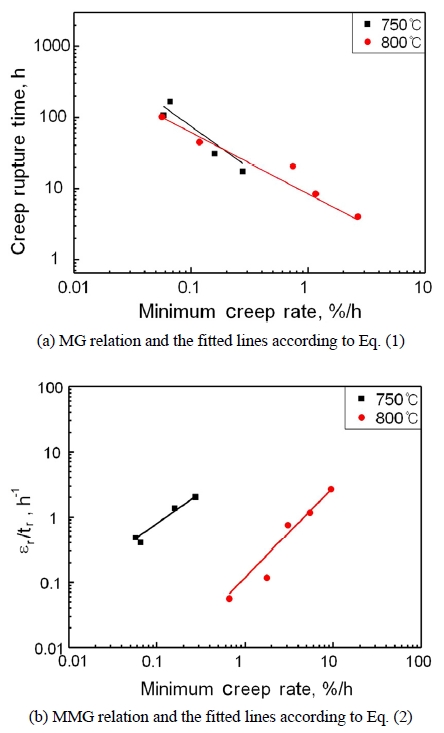
시험으로부터 얻은 최소 크리프 속도와 파단시간을 이용하여 식 (2)와 (3)에 따라 Monkman-Grant(MG)와 Modified Monkman-Grant(MMG)을 Fig. 7(a)와 (b)에 나타내었으며, 온도별로 정리한 MG equation 및 MMG equation의 상수를 Table 3에 나타내었다.

Fig. 7

(a) MG and (b) MMG relations of HRV40 steel

Table 3

Equation constants of MG (1) and MMG (2)

Fig. 7(a)와 Table 3에 나타낸 것과 같이 상수 m 값은 750 °C와 800 °C에서 각각 1.19, 0.86으로, 차이가 존재하였다. 이는 HRV40강에 대하여 서로 다른 온도에서는 다른 MG 관계식을 가지므로 한 온도에 관한 MG 관계식을 이용하여 다른 온도에 대한 수명예측을 하기에 적합하지 않음을 의미한다.

소재의 손상 메커니즘이 달라지는 경우 크리프 파단 변형률을 고려한 MMG 관계식을 통해 수명예측의 정확성을 높이는 경우가 있다. 앞서 구한 MG 관계식의 상수는 온도별로 서로 차이가 있었으므로 MMG기법을 HRV40 강의 경우에 적용하여 보정 가능한 지 확인하였다. Fig. 7 (b)와 Table 3에 나타낸 것과 같이 상수 m′ 값은 750 °C와 800 °C에서 각각 0.952, 1.38로 도출되었으며, MG의 경우와 마찬가지로 온도에 따른 차이를 보였다.

HRV40 강의 경우 한 온도에서의 MG 와 MMG 관계식을 이용하여 다른 온도의 수명예측을 하는 것은 적합하지 않음을 확인하였으나 Fig. 7에 나타난 것과 같이 각 온도 내에서는 일정한 경향성을 보이므로 같은 온도에서의 수명 예측이 가능한 지를 추가 시험을 통하여 확인해 보았다.

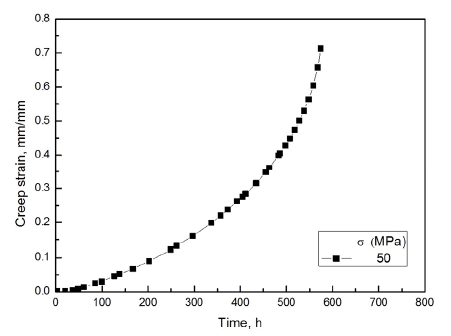
장수명 예측을 위하여 선정한 시험 온도와 응력은 각각 750 °C와 50 MPa이며, 수행한 결과 얻은 크리프 변형률-시간 그래프를 Fig. 8과 같이 나타내었다. 최소 크리프 속도 $$ {\dot{ϵ}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$는 0.02245 h^-1 로 확인되었으며, 파단 시간과 크리프 파단 변형률은 각각 574 h와 71.3 % 으로 확인되었다. 최소 크리프 속도 $$ {\dot{ϵ}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$와 식 (1)과 750 °C에서의 상수 m과 C를 식 (1)에 대입하여 계산된 예상 크리프 파단 시간은 445 h 였으며, 이는 실제 파단시간에 비하여 22.4 %의 오차율을 가진다. 이와 같이 MG 관계식을 이용하면 크리프 초기단계에서 도출 가능한 최소 크리프 속도 $$ {\dot{ϵ}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$를 이용하여 장수명 예측을 할 수 있으며, 이후 추가적인 시험을 통하여 더욱 정확한 MG 관계식을 도출하면 오차율을 낮출 수 있을 것으로 예상된다.

Fig. 8

Creep curve of HRV40 at temperature of 750 °C

4.3 Larson-Miller Parameter와 수명 예측

식 (3)을 이용하여 각 시험에서의 Larson-Miller 파라미터 P_LM과 응력의 관계를 Fig. 9와 같이 좌표상에 나타내었다. 여기서 C_LM 값은 문헌조사를 통해 일반적인 금속이 갖는 C_LM = 47을 사용하였다.¹⁾ Fig. 9의 붉은 선도는 식 (8)과 같이 P_LM를 응력에 관한 함수로 회귀분석하여 나타낸 것이다. 식 (8)을 이용하여 해당 응력에서의 P_LM을 구한 뒤 식 (3)에 온도조건을 대입하면 해당 온도와 응력 조건에서의 파단시간 t_r을 예측할 수 있다.

Fig. 9

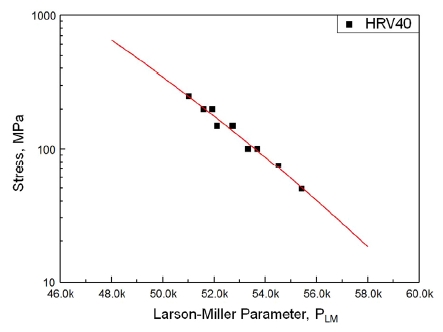
Stress vs. Larson-Miller Parameter relationship of HRV40 with fitting curve defined by the quadratic polynomial model

4.2절에서와 같이 온도 750 °C와 50 MPa의 응력에 대하여 Larson-Miller Parameter를 통한 수명예측을 수행하였으며, 예측된 수명시간은 1,332 h로 나타났다. 이는 실제 크리프 시험을 통하여 측정한 파단시간 574 h에 대하여 약 132 %의 오차를 보였으며, 이는 앞서 MG기법을 통한 수명예측보다 정확성이 떨어지는 수치이다. 이에 대하여서는 추가적인 연구를 통하여 크리프 시험 데이터 확보로써 정확성과 신뢰도를 향상시키거나 Orr-Sherby-Dorn 또는 Manson-Harerd와 같은 다양한 시간-온도 파라미터 기법을 사용한 수명예측과의 비교가 필요하다.