C-MDPS 차량의 응답 성능 최적화 연구

1. 서 론

조향장치는 편의, 연비 및 안전에 대한 중요성이 강조됨에 따라 유압식 파워 스티어링에서 Motor를 이용하여 조타력을 어시스트 하는 전동 파워 스티어링 시스템(Motor Driven Power Steering, 이하 MDPS)을 주로 사용하고 있다.¹⁾ MDPS 시스템은 별도 ECU 및 센서류 등을 이용하여 MDPS 모터를 제어하여 운전자의 조타력을 보조하는데, MDPS 타입 중 가장 보편적으로 사용 하고 있는 컬럼 타입의 MDPS(이하 C-MDPS) 장착 차량에 대해 조타감 뿐 아니라 응답성 또한 주요 성능 중 하나로 요구 되고 있다. 차량 전체적인 관점에서 봤을 때 응답성은 매우 중요한 성능 중 하나로써, 응답 성능이 좋은 차량이라고 하면 스티어링 입력에 대해 차량의 반응이 빠르고 안정적으로 반응한다는 것을 의미한다.^2,8)

좋은 응답 성능을 가진 차량을 개발하기 위해 설계자는 Transition, Weave 와 같은 시험 모드에 대한 차량 반응을 분석하고, 그에 알맞은 부품을 개발 한다. 그리고 평가자는 주관평가 및 계측을 통해서 핸들링 성능을 평가 및 검증을 한다. 따라서 핸들링 성능이 좋은 차량을 개발하기 위해서는 설계 초기 단계에서부터 핸들링 성능 해석이 선행되어야 한다.

현대의 자동차는 중형급 차량 까지 C-MDPS 시스템을 장착하고 있으며 중대형 이상의 차량에 Rack type MDPS(이하 R-MDPS) 시스템을 장착 하고 있다. C-MDPS 시스템은 토크를 측정 할 수 있는 기구인‘토션바’가 스티어링 컬럼에 장착되어 있고 최대 100 Nm 힘이 컬럼을 통해 전달되어 시스템 비틀림이 발생하게 된다. 이런 비틀림 현상은 응답 지연으로 나타나게 되어 차량 전체의 응답성능에 영향을 미치게 된다. 차량 관점에서 응답성능에 큰 영향을 미치는 요소는 전/후륜 서스펜션의 설계인자이다. 서스펜션의 장착 위치를 결정짓는 키네매틱 설계와 외력에 대한 변화를 설계하는 컴플라이언스 설계에 따라 차량의 응답성능이 변화하게 된다. 그리고 시스템을 설계할 때 응답성능 이외 다른 기본성능을 만족하기 위해서 구속 조건이 따르게 된다. 목표로 하는 응답성능을 얻기기 위해서는 이런 구속조건이 만족하는 범위 내에서 이루어 져야 하며 응답성능에 대한 영향도가 높은 주요 인자를 바탕으로 최적화 설계가 필요하다. 본 논문에서는 C-MDPS 시스템이 장착되어 있는 D-seg 차량을 대상으로 하여 스티어링 및 차량 시스템 모델링, 차량 응답성능에 대한 영향인자 분석 방법 및 최적화 프로세스를 제안한다.

2. 시스템 모델링

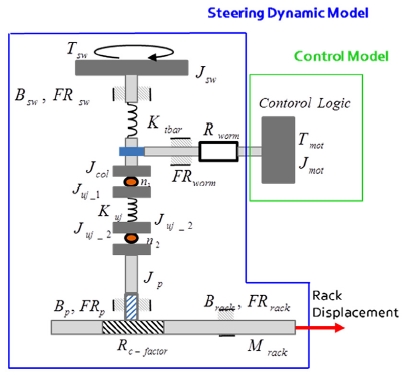
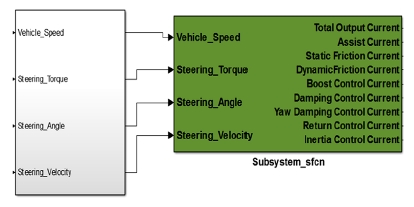
차량의 응답성능을 분석하기 위해 차량 모델과 조향계 모델링을 활용한다. 차량 모델의 경우 상용 S/W 인 CAR-Maker를 활용하였고, 조향계 모델은 상세 모델링을 위해 MATLAB 시뮬링크를 활용하였으며 Fig. 1과 같이 구성 된다.³⁾

Fig. 1

C-MDPS system structure

2.1 스티어링 시스템

2.1.1 운전자 모델

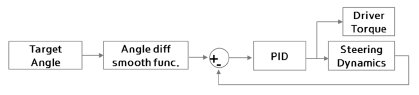
운전자가 느끼는 토크를 모델링하기 위해서 운전자 모델이 필요하다. 운전자가 입력하고자 하는 값은 각도 이지만 실제로 시스템에 입력되어 지는 값은 조향 휠을 회전시키기 위한 토크 값이다. 따라서 Fig. 2와 같이 목표 입력 각도를 회전시키기 위한 Angle Feedback 으로 드라이버 모델을 구현한다.

Fig. 2

Driver model block diagram

2.1.2 스티어링 컬럼 모델

C-MDPS 시스템에서는 스티어링 컬럼에 MDPS 시스템에 의해 생기는 마찰력, 토션바 비틀림 현상이 발생하며, 휠이 가지고 있는 물리적 특성 등이 존재한다. 다음 사항을 고려하여 식 (1)과 같이 운동방정식을 기반으로 하여 스티어링 컬럼을 모델링한다.

$\[ J_{sw}{\ddot{\theta }}_{sw}=T_{sw}-B_{sw}{\dot{\theta }}_{sw}-{FR}_{col}{\dot{\theta }}_{col}-K_{tbar}\left({\theta }_{sw}-{\theta }_{col}\right)+T_{MDPS} \]$

(1)

J_sw : steering wheel inertia

T_sw : driver torque

B_sw : steering wheel damping coefficient

FR_col : steering column friction

K_tbar : torsion bar stiffness

T_MDPS : MDPS assist torque

$$ {\ddot{\theta }}_{sw}$$ : steering wheel angular acceleration

$$ {\dot{\theta }}_{sw}$$ : steering wheel angular velocity

$$ {\theta }_{sw}$$ : steering wheel angle

$$ {\dot{\theta }}_{col}$$ : steering column angular velocity

$$ {\theta }_{col}$$ : steering column angle

2.1.3 랙 - 피니언 모델

조향 컬럼에서 발생되는 회전 운동은 랙-피니언 기구에 의해 병진운동으로 전환된다. 랙-피니언 시스템은 식 (2), (3)과 같이 랙의 질량, 댐핑, 차량으로부터 들어오는 외력에 운동방정식이 결정이 된다.

$\[ J_p{\ddot{\theta }}_p=T_p-B_p{\dot{\theta }}_p-{FR}_p{\theta }_p-R\bullet f\left(t\right) \]$

(2)

$\[ f\left(t\right)=M\ddot{x}+b\dot{x}+{FR}_{rack}+F_{rack} \]$

(3)

where

J_p : pinion inertia

T_p : pinion input torque

B_p : pinion damping coefficient

FR_p : pinion friction

R : gear ratio

$$ {\ddot{\theta }}_p$$ : pinion angular acceleration

$$ {\dot{\theta }}_p$$ : pinion angular velocity

$$ {\theta }_p$$ : pinion angle

M : rack mass

b : rack damping coefficient

F_rack : rack force from vehicle

FR_rack : rack friction

$$ \ddot{x}$$ : rack acceleration

$$ \dot{x}$$ : rack velocity

2.1.4 유니버셜 조인트 모델

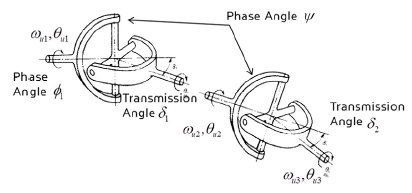
스티어링 시스템은 자동차 구조상 엔진이나 내부 부품에 의해 컬럼과 랙-피니언을 일직선으로 연결하기 어려워 Fig. 3과 같이 유니버셜 조인트를 활용하여 컬럼과 피니언이 연결 된다.

Fig. 3

Universal joint structure

유니버셜 조인트는 꺾임 구조로 인하여 입력 각도와 출력 각도가 상이하게 나타나게 되는데 연결구조에 의한 각도 변화는 식 (4), (5)와 같다.

$\[ {\theta }_2={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\frac{\tan \left({\theta }_1+\varphi \right)}{\cos \delta }-{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\frac{\tan \left(\varphi \right)}{\cos \delta } \]$

(4)

$\[ {\theta }_3={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\frac{\tan \left({\theta }_2+\psi \right)}{\cos \delta }-{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\frac{\tan \left(\psi \right)}{\cos \delta } \]$

(5)

where

θ1 : universal input angle

θ2 : universal 1^st output angle

θ3 : universal 2^nd output angle

δ : universal transmission angle

Φ : universal 1^st phase angle

ψ : universal 2^nd phase angle

유니버셜 조인트의 강성은 시스템 비틀림에 큰 영향을 미치는 인자중 하나로 연결 부품인 스파이더 2개와 샤프트 강성을 하나의 등가 강성으로 식 (6)과 같이 나타낸다.

$\[ J_{univ}{\ddot{\theta }}_2=-B_{univ}{\dot{\theta }}_2-{FR}_{univ}{\dot{\theta }}_2-K_{univ}\left({\theta }_2-{\theta }_{2\mathrm{\text{'}}}\right) \]$

(6)

where

J_univ : eqivalent universal joint inertia

B_univ : eqivalent universal joint damping coefficient

FR_univ : eqivalent universal joint friction

K_univ : eqivalent universal joint stiffness

θ₂ : universal 1^st output angle

θ_2’ : universal 1^st output angle after torsion

2.2 MDPS 제어 시스템

MDPS는 모터에 전류를 인가하여 토크를 발생시켜 운전자 조타력을 보조한다. 따라서 원하는 조타감을 만들어 내기 위해 전류맵을 튜닝하게 되는데 전류맵 튜닝에 따라 차량의 응답성도 변화한다. 이를 모델링하기 위해서 전류맵을 기반으로 한 모터 및 제어 로직 모델이 필요하다.

2.2.1 모터 모델

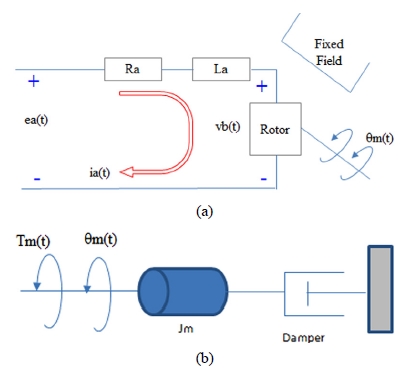
모터 모델은 등가 DC 모터 모델을 사용한다. 모델은 Fig. 4와 같이 모터의 전류 입력에 따른 토크 출력 성능을 결정짓는 루프방정식 식 (7)과 토크에 따른 물리적 움직임을 나타내는 운동방정식 식 (8)로 구성된다.

Fig. 4

(a) Electrical model (b) Dynamic model

$\[ R_a{i}_a\left(t\right)+L_a\frac{{di}_a\left(t\right)}{dt}+{\nu }_b\left(t\right)=e_a\left(t\right) \]$

(7)

$\[ i_a\left(t\right)=\frac{T_m\left(t\right)}{K_t}=\frac{1}{K_t}{J}_m\frac{d^2{\theta }_m\left(t\right)}{{dt}^2}+\frac{1}{K_t}{D}_m\frac{{d\theta }_m\left(t\right)}{dt} \]$

(8)

where

R_a : resistance

i_a : current

L_a : inductance

v_b : back EMF

e_a : voltage

T_m : motor torque

K_t : torque constant

J_m : motor inertia

θ_m : motor angle

D_m : motor damping coefficient

2.2.2 제어 알고리즘

모터 모델은 전류 입력의 크기에 따라 출력토크가 결정이 되며 전류맵을 설정하는 방법에 따라서 어시스트 토크가 변화하게 된다. 여기서 사용되는 제어 알고리즘은 Fig. 5와 같이 조향각, 조향각속도, 조향토크 및 차속을 활용한 Open loop 제어로 이루어져 있다.⁴⁾

Fig. 5

Control algorithm

2.3 차량 시스템

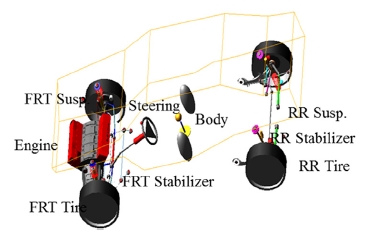
차량 응답성에 대한 스티어링 시스템과 MDPS 제어 시스템의 영향도 분석을 위해 MATLAB 시뮬링크 환경에서 차량 모델 구현이 가능한 CarMaker S/W를 활용하며 그 구성은 Fig. 1과 같다. CarMaker 차량 모델은 운전자 Kinematic 과 Compliance에 대한 정보를 활용하여 차량에 대한 성능을 설계 할 수 있는 장점이 있어 각 시스템 별 영향도를 동시에 분석하기 용이한 모델이다. 또한 저자유도 차량모델 분석결과를 토대로 차량의 부품 설계 단위에서 설계안을 도출하기 위해 Fig. 6의 ADAMS Full Car 모델을 활용한다.

Fig. 6

Adams full car model

3. 응답성 영향도 분석 방법

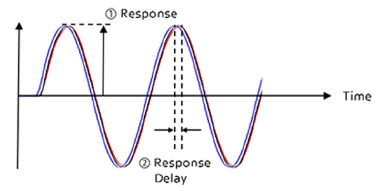
차량의 응답성에 대한 영향도를 분석하기 위해 응답성을 Fig. 7과 같이 스티어링 시스템의 경우 조향 입력에 대한 랙 출력의 크기가 크고 입력에 대한 응답 지연시간이 작을수록 응답성이 빠르다고 정의한다. 서스펜션의 경우에는 동일 입력에 대해 요레이트 반응의 크기와 횡가속도 반응의 크기가 클수록 응답성이 빠르다고 정의한다.

Fig. 7

System response

본 연구에서는 스티어링 시스템 기구 설계 인자를 Table 1과 같이 설정하고 실험계획법을 통해 설계 인자에 대한 영향도 분석을 실시한다. 시스템 설계 인자는 토션바 강성, 마찰력 등을 포함한 15개 인자로 설정하였으며 실험 방법은 인자간 교호작용 관계를 확인할 수 있는 Box-Behnken 실험 계획법을 사용하며 시험 모드는 80 kph 조건에서 0.3 Hz Sine 입력을 사용한다.⁵⁾

Table 1

Steering system design factors

MDPS 제어로직 영향인자 분석을 위해 제어 튜닝 인자를 Table 2와 같이 설정하였으며, 총 7개 제어로직에 대해 분석을 실시한다. 실험 방법은 동일하게 Box-Behnken 실험 계획법을 사용하였고 시험 모드는 80 kph 0.3 Hz Sine 입력 조건이다.

Table 2

MDPS tuning parameters

서스펜션은 전륜과 후륜에 대해 Table 3과 같이 Kinematic 성능과 Compliance 성능 인자를 활용하여 영향도 분석을 실시하였으며 전/후륜 Kinematic 인자 12개, Compliance 인자 96개 총 108개 성능인자에 대한 영향도 분석을 실시한다. 차량의 주요 성능 인자 영향도 분석 결과를 토대로 차량 단위에서의 개선방안을 도출하여 응답성 개선 안을 제시한다.

Table 3

Suspension performance parameters

4. 응답성 영향도 분석 결과

4.1 스티어링 시스템 기구부

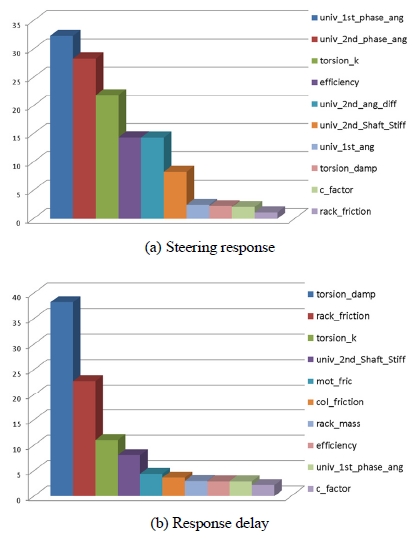
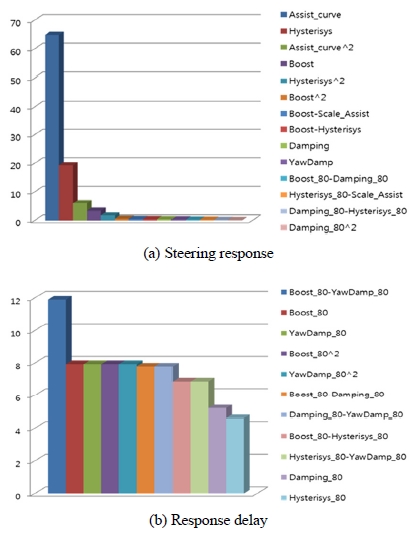
스티어링 시스템에서의 응답성 결과 그래프는 Fig. 8에 나타내었다. Fig. 8(a)는 조향 입력에 대한 랙 출력 반응의 크기에 대한 영향도를 나타내며 주 영향 인자는 유니버셜 조인트의 장착각도 및 꺾임각, 토션바 그리고 기어효율이 있으며, Fig. 8(b)는 응답지연에 영향을 미치는 영향도를 나타내며 주 영향 인자는 토션바 특성, 랙마찰력, 유니버셜 조인트 강성 등이 있다.

Fig. 8

Results of steering system effectiveness

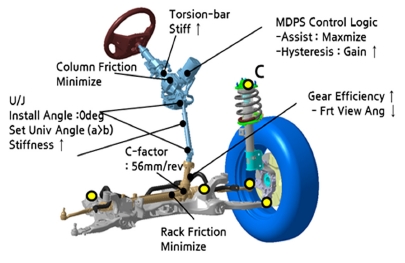
영향도 분석결과를 토대로 응답성 개선을 위한 방안을 정리해 보면 컬럼부에서는 토션바 강성을 가능한 크게 증대 시켜야 하며, 컬럼 마찰력 및 모터 마찰력을 가능한 낮춰야 한다. 또한 유니버셜 조인트는 장착 위상이 0 deg가 되도록 조립 되어야 하며 꺾임 각은 1^st 각도가 2^nd 각도 보다 더 크게 설정이 되어야 한다. 또한 랙-피니언에서는 마찰력 감소 및 기어효율 증대를 위해 장착각도를 직각에 가까운 방향으로 설계를 해야 하며 C-factor를 단순히 증대 시키는 것이 아니라 알맞은 값으로 설정되어야 한다.

4.2 MDPS 제어 시스템

MDPS 제어 인자에 대한 응답성 결과 그래프는 Fig. 9에 나타내었다. Fig. 9(a)는 조향 입력에 대한 랙 출력 반응의 크기에 대한 영향도를 나타내며 주 영향인자는 Assist 제어와 Hysterisys 제어로 나타났다. Fig. 9(b)는 응답지연에 영향을 미치는 영향도를 나타내고 있지만 ANOVA 분석 결과 신뢰도 19 % 수준으로 응답 지연에 대한 제어로직의 영향도는 매우 낮은 것으로 나타났다.

Fig. 9

Results of control parameters effectiveness

영향도 분석 결과를 토대로 제어로직 개선 방향은 응답성을 향상시키기 위해서는 응답 초반에 어시스트 량을 증대시키는 것이 효과가 있으나 이는 조향 감성품질에 영향을 미칠 수 있으므로 어시스트 제어를 높일 수 있는 방안 설정이 필요하다. 또한 히스테리시스 게인을 높이게 되면 리턴 시 차량 반응성을 향상시킬 수 있으나 게인을 높이기 위해서는 기구적으로 낮은 마찰력이 제공되어야 한다. 마찰력을 저감시키는 것 또한 차량 응답성을 향상시키는 방안으로 기구부와 제어가 연계되어 응답성 개선이 필요하다.⁶⁾

4.3 서스펜션 시스템

4.3.1 전륜 서스펜션 성능 인자

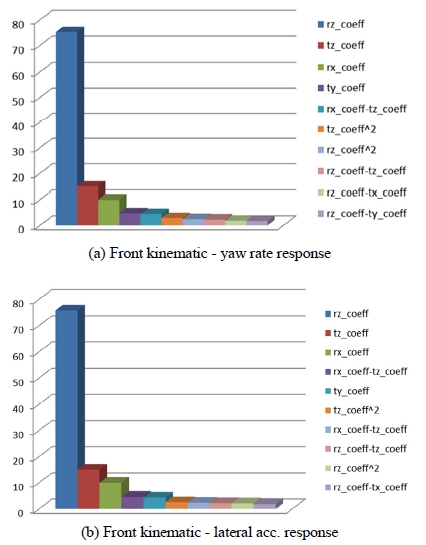
전륜 서스펜션 키네매틱 인자에 대한 응답성 결과 그래프는 Fig. 10에 나타내었다. Fig. 10(a)는 조향 입력에 대한 요레이트 반응의 크기를 나타내고 Fig. 10(b)는 횡 가속도 반응의 크기를 나타낸다. 전륜 서스펜션 키네매틱 주 영향인자는 타이어 toe에 영향을 주는 rz 변화량과 타이어 강성 관련 인자인 tz, 캠버 변화에 영향을 주는 rx 변화량이 차례로 영향을 미친다.

Fig. 10

Results of front suspension kinematic parameters effectiveness

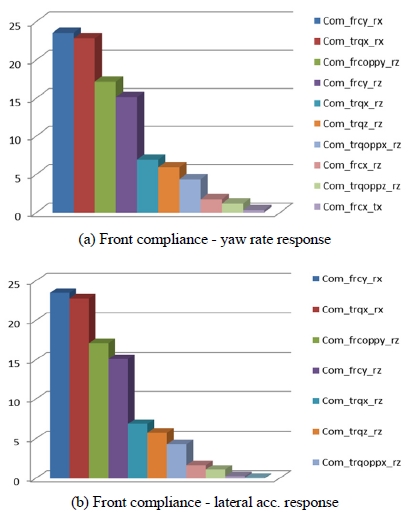
전륜 서스펜션 컴플라이언스 인자에 대한 응답성 결과 그래프는 Fig. 11에 나타내었다. Fig. 11(a)는 조향 입력에 대한 요레이트 반응의 크기를 나타내고 Fig. 11(b)는 횡 가속도 반응의 크기를 나타낸다. 전륜 서스펜션 컴플라이언스에서 주 영향 인자는 캠버 변화에 영향을 주는 횡력에 대한 rx 변화량이 가장 큰 영향 인자이며 토우 변화에 영향을 주는 횡력에 대한 rz 변화량이 그 다음 주 영향 인자이다.

Fig. 11

Results of front suspension compliance parameters effectiveness

응답성을 빠르게 하기 위해 전륜 키네매틱이나 컴플라이언스 특성을 Toe-in으로 설계 할 경우 빠른 응답을 확보할 수 있지만 차량 관점에서는 오버스티어 현상에 의해 차량 안정성에 문제가 될 수 있으므로 안정성이 확보되는 차원에서 Toe-out량을 줄이는 방향으로 설계한다. 또한 캠버 변화량이 커질수록 반응성이 빠르므로 타이어 마모 영향도가 허용하는 범위 내에서 캠버 변화량을 키우는 방향으로 설계한다.

4.3.2 후륜 서스펜션 성능 인자

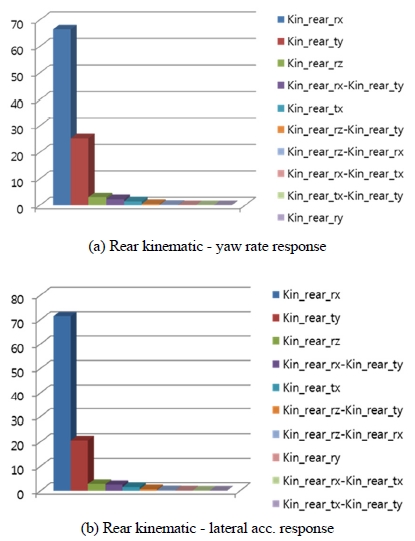
후륜 서스펜션 키네매틱 인자에 대한 응답성 결과 그래프는 Fig. 12에 나타내었다. Fig. 12(a)는 조향 입력에 대한 요레이트 반응의 크기를 나타내고 Fig. 12(b)는 횡 가속도 반응의 크기를 나타낸다. 후륜 서스펜션 키네매틱에서는 타이어 캠버에 영향을 주는 rx 변화량과 범프 스티어에 영향을 주는 ty 변화량이 주 영향인자로 나타나는 것을 볼 수 있다.

Fig. 12

Results of rear suspension kinematic parameters effectiveness

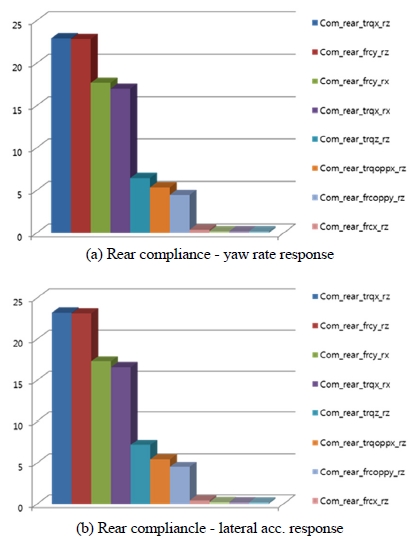
후륜 서스펜션 컴플라이언스 인자에 대한 성능 결과 그래프는 Fig. 13에 나타내었다. Fig. 13(a)는 조향 입력에 대한 요레이트 반응의 크기를 나타내고 Fig. 13(b)는 횡 가속도 반응의 크기를 나타낸다. 후륜 서스펜션 컴플라이언스 특성에서 주 영향 인자는 토우에 영향을 미치는 횡력에 의한 rz 변화량과 캠버에 영항을 미치는 rx 변화량이 주요 인자이다.

Fig. 13

Results of rear suspension compliance parameters effectiveness

응답성을 빠르게 하기 위해 후륜 타이어의 Toe-in 크기를 줄여야 하지만 차량의 안정성 확보에 영향을 주므로 일정한 Toe-in 컴플라이언스 특성을 유지한 상태에서 (-)캠버 컴플라이언스 증대하는 방향으로 설계하여 타이어 횡력을 최대화시켜 차량의 응답성을 개선해야 한다.

차량 관점에서는 전륜에서 횡력이 크게 발생할수록 반응성이 빨라지고 후륜에서 횡력이 크게 발생할수록 안정성이 높아진다고 해석할 수 있다. 따라서 후륜의 Toe-in을 증가시키면 전륜의 Toe-out 량을 줄일 수 있으므로 이를 만족하는 최적 설계가 필요하다.

5. 응답성능 최적화

5.1 스티어링 시스템

스티어링 시스템은 설계 인자간의 교호작용이 거의 없이 설계 값을 최소로 하거나 최대로 하였을 때 좋은 성능이 나오는 망대, 망소 특성을 가진다. 따라서 결과를 바탕으로 Fig. 14와 같이 토션바 강성 증대, 마찰력 감소, 유니버셜 조인트 장착 각도 및 꺾임각 설정, 기어 효율 증대, MDPS 제어 알고리즘 튜닝을 통해 응답성 개선이 가능하다.

Fig. 14

Steering system development strategy

5.2 서스펜션 시스템

서스펜션 시스템의 경우 응답성에 대한 영향도를 성능 인자에 대해서 분석을 실시하였다. 성능 인자는 차량에 외력이 전달될 때의 변화량을 나타내는 지표이기 때문에 실제로 변화량을 원하는 만큼 설계하는 것은 불가능 하다. 따라서 Table 4와 같이 영향도 분석 결과를 실제 설계 인자와 매칭하기 위해 주요 전/후륜 성능인자 20개에 대해 차량 단위에서의 설계 인자를 도출하였다.

Table 4

Correlation of full car design factors with performance parameters

위와 같은 설계인자를 응답성능 관점에서 최적화하기 위해서는 설계를 하고자 하는 목표 값 설정이 필요하며 본 연구에서는 응답성을 향상하기 위한 목표 K&C 성능을 설정 하고 차량 설계 시 필요한 구속조건을 설정하여 조건에 부합하는 최적화 안을 도출한다. 목표 성능과 구속조건을 만족하는 최적화 방안을 도출하기 위해 비선형 시스템의 최적화 프로그래밍 방법 중 하나인 NLPQL 알고리즘을 사용하였으며 이로부터 도출된 전/후륜 서스펜션의 하드포인트 최적화 결과는 Table 5와 같다.⁷⁾

Table 5

Front/rear optimized design factors

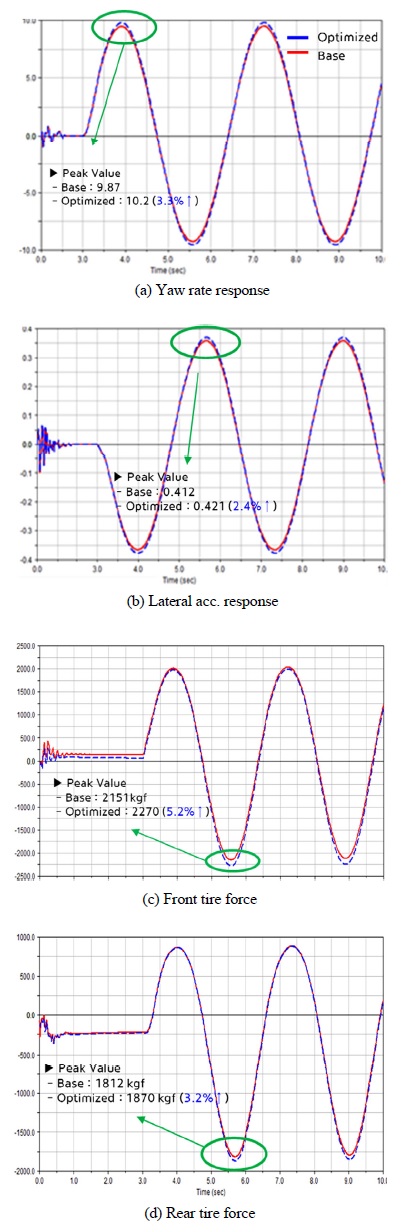
최적화 결과에 대한 차량 응답성 변화를 검증하기 위해 Adams 차량 모델을 활용하여 기존 차량과의 응답 성능 차이에 대한 결과를 Fig. 15에 나타내었다. 먼저 응답성 측면에서 Fig. 15(a), (b)는 응답 크기 변화를 나타내며 요레이트 반응의 크기가 3.3 %, 횡가속도 반응의 크기가 2.4 % 증가하여 응답성이 향상됨을 확인할 수 있다. 차량 안정성 측면에서 Fig. 15(c), (d)는 차량의 전/후륜의 타이어에서 발생하는 횡력 크기 변화를 나타내며 전륜 5.2 % 증가, 후륜 3.2 %가 증가하여 차량의 횡력을 증가시켜 안정성을 확보하면서 응답 성능을 향상시킬 수 있다는 결과를 확인할 수 있다.

Fig. 15

Comparing base and optimized results

6. 결 론

차량의 응답성능을 개선하기 위해서는 분석을 위한 시스템 모델을 구성하고, 영향도 분석 방법론부터 최적 방안을 도출하기 위한 프로세스가 중요하다. 본 논문에서는 일반 상용 S/W에서 제공되는 스티어링 모델이 아닌 실제 설계에 사용되는 파라메터 값을 활용하여 상세 모델링을 하였고 스티어링 모델과 차량 모델에 대해 영향도 분석 및 프로세스를 적용하여 최적화 방안을 제안하고 검증하였으며 주요 결과를 요약하면 다음과 같다.

• 1) 기존 저자유도 차량 S/W에서 제공하지 않는 스티어링 시스템 설계 요소인 토션바 특성, 마찰력 특성, 유니버셜 조인트 특성, 그리고 제어를 위한 모터 특성 및 MDPS 제어로직이 포함되어 있는 응답성 분석을 위한 스티어링 모델을 구성하였으며, 특히 주요 부품인 유니버셜 조인트의 영향도를 확인할 수 있다.
• 2) 반응표면방법론 중 하나인 Box-behnken 실험계획법을 활용하여 스티어링 시스템과 서스펜션 시스템의 설계 인자들의 차량 응답성능에 대한 영향도 분석 결과를 도출하였다.
• 3) 영향도 분석결과를 바탕으로 주요 전/후륜 서스펜션 20개 설계 인자를 도출하고, 목표 값을 달성하기 위한 설계 방안을 실제 변경이 가능한 범위 내에서 최적화 안을 제시하여, 전/후륜의 횡력을 증대시켜 차량의 응답성을 증대시키는 방법을 제시하였다.
• 4) 응답성능이 개선됨을 검증하기 위해 Adams Full car 모델을 활용하였으며, 기존 차량과 최적화 안을 적용한 차량을 비교한 결과 3 % 수준의 응답성능이 개선됨을 확인 하였다.
• 5) 본 연구에서는 기 개발된 차량으로 응답성능 최적화 안을 제안하고 검증을 하였으나 향후에는 설계 초기단계에서부터 차량의 목표성능을 설정하고 제안된 최적화 프로세스를 통해 설계를 진행하면 더 효율적인 차량의 설계가 가능할 것으로 판단된다.

References

• H. S. Cho, B. R. Lee, S. H. Chang, Y. D. Park, and M. J. Kim, “Effects of Vehicle Electric Components on the Steering Input Torque”, Transactions of KSAE, 22(6), p113-119, (2014). [https://doi.org/10.7467/ksae.2014.22.6.113]
• T. D. Gillespie, Fundamentals of Vehicle Dynamics, SAE International, USA, (1992). [https://doi.org/10.4271/r-114]
• M. Harrer, and P. pfeffer, Steering Handbook, Springer, Switzerland, (2017).
• D. W. Lee, S. H. Han, S. W. Cheon, and W. J. Oh, “An Experimental Study of the Effect on Steering Performance by MDPS Logic Parameters”, KSAE Spring Conference Proceedings, p1020-1029, (2011).
• S. H. Park, and J. W. Kim, Modern Design of Experiment, Minyoungsa, (2011).
• S. J. Ko, S. W. Oh, E. K. Gu, and K. S. Nam, “Development of MDPS Control Algorithm for Steering Maneuverability Improvement”, KSAE Annual Conference Proceedings, p1257-1262, (2009).
• K. Schittkowski, “NLPQL: A Fortran Subroutine for Solving Constrained Nonlinear Programming Problems”, Annals of Operations Research, 5(2), p485-500, (1985).
• T. Uno, “車輛運動性能とシャシ-メカニズム”, Grand Prix, (1994).