유한요소해석 기반 공차해석을 활용한 차체 조립 공정의 로케이터 위치 최적설계

1. 서 론

자동차 차체 조립 공정은, 조립 중 부품의 변형이 많이 발생하는 대표적 판금조립 공정이다. 스탬핑(Stamping)으로 제작되는 차체 부품들은 많은 경우 편차를 가지고 있는데, 이로 인해 조립 중에 고정구(Fixture)와 용접건(Weld gun)에 의해 변형된다. 그 결과, 용접 후 조립체는 형상 편차를 갖게 되고 이러한 편차의 누적으로 완성 차체의 품질이 저하된다.

차체 조립 공정의 대부분은 용접로봇을 이용한 자동 공정이다. 즉, 차체를 다수의 스테이션(Station)에 걸쳐 이동시키면서, 부품들을 고정구로 고정한 채 정해진 위치에 점용접한다. 따라서 조립 공정의 설계자는 용접점의 위치, 개수, 순서와 함께 부품별 고정구의 위치와 개수를 결정해야 한다. 고정구에는 두 가지가 있는데, 부품의 자유도를 제약하여 위치와 자세를 결정하는 로케이터(Locator)와 용접 중에 부품이 움직이지 않도록 고정해 주는 클램프(Clamp)가 있다. 차체와 같이 유연한 부품의 조립에서는 고정구의 위치가 조립체 품질에 상당한 영향을 미치므로 중요하다. 그러나 많은 공정 설계자가 체계적인 방법을 사용하지 않고 경험에만 의존함으로써 차체 품질이 저하되는 경우가 많다.

이 문제와 관련하여 다양한 연구가 이루어져 왔다. 예를 들면, Liao¹⁾는 판금 부재의 로케이터와 클램프 개수 및 위치를 최적화하는 유전알고리즘을 개발하였다. 그러나 이 연구에서는 부품 하나만을 고려하여 부품의 편차 및 자중에 의한 처짐을 최소화하는 것을 목표로 하였으므로, 조립체의 품질 개선과는 거리가 있다. Xie와 Hsieh의 연구²⁾에서는 조립 공정의 사이클 타임을 최소화하는 클램핑 및 용접 순서 결정 기법을 개발하였으나, 이는 생산성 향상을 목적으로 하는 연구이다. 또한, 최원혁³⁾은 유전알고리즘을 적용하여 차체 조립 공정의 점용접 순서를 최적화하는 기법을 개발한 바 있다. 한재희 등의 연구⁴⁾에서는 유전알고리즘을 활용하여 이종재 점용접부의 인장전단강도, 너깃사이즈, 압흔 깊이가 적정 범위에 있게 되는 최적의 용접 조건을 도출했다. 이 분야의 최적화 기법으로서 인공신경망 알고리즘(ANN)⁵⁾ 또는 사회방사 알고리즘(SRA)⁶⁾등을 이용한 경우도 있으나, 일반적으로 유전알고리즘이 유용한 것으로 알려져 있다.

상기한 연구들은 모두 변형되는 차체 부품의 점용접에 관한 연구이지만, 이 중 조립품의 품질 개선을 위해 고정구의 위치를 최적화하는 기법을 다룬 것은 없다. 본 논문에서는 조립품질 개선을 위한 로케이터 위치 최적화 기법을 연구하며, 부품의 조립 중 변형을 고려하는 공차해석을 위해서는 2장의 영향계수법^7,8)을 사용한다. 참고로, 고정구의 위치 최적화로서 강체 공작물을 대상으로 한 연구는 다수 있지만,^9,10) 변형체 부품을 대상으로 한 연구는 찾아보기 어렵다.

2. 변형체 공차해석

차체 조립과 같이 조립 중 부품의 변형이 많이 발생하는 경우, 변형을 고려하는 공차해석이 필요하다. 몬테카를로(Monte Carlo) 시뮬레이션으로 변형체 공차해석을 하려면, 시뮬레이션 각 횟수마다 달라지는 부품의 편차를 입력하여 유한요소해석을 실행해야하므로 지나치게 많은 시간이 소요된다. 이 문제를 극복하기 위해 개발된 기법이 영향계수법⁶⁾이며, 본 논문에서도 이 방법을 사용한다. 영향계수법은, 단순화된 조립공정 모델에 대해 2회의 유한요소해석을 수행함으로써 부품 편차와 조립체 편차 사이의 선형관계를 도출하는 방법이다.

2.1 차체 조립 공정

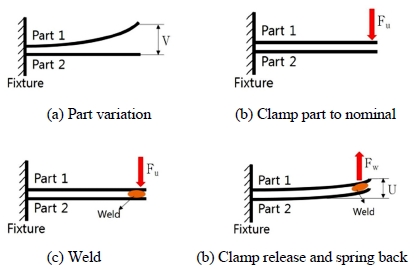
먼저 점용접(Spot welding)으로 이루어지는 차체 조립 공정의 단계를 개념적으로 설명하기 위해 Fig. 1의 외팔보 조립 모델을 고려한다.

Fig. 1

Conceptual model for sheet metal assembly process considering part variations

Fig. 1(a)의 1단계에서는 조립될 두 개의 부품(Part 1과 Part 2)이 고정된다. 그림에 보인 고정구는 각 부품의 위치와 자세를 결정하는 로케이터이다. 이 그림에서는 간단한 설명을 위해 Part 1만 편차 V를 갖고 Part 2는 완벽한 형상인 것으로 나타내었지만, 두 부품 모두 편차를 가져도 무방하다.

2단계(Fig. 1(b))에서는 용접건이 각 부품에 힘을 주어 용접점을 공칭 위치(Nominal position)까지 변위시켜 부품들이 접촉되도록 한다. 실제 공정에서는 클램프가 이 역할을 하지만, 클램프가 보통 용접점 바로 옆에 있으므로 본 논문에서는 용접건이 직접 부품을 클램핑하는 것으로 간주한다.

3단계(Fig. 1(c))에서는 두 부품이 접촉된 상태에서 점용접이 이루어진다. 4단계(Fig. 1(d))에서는, 2단계에서 이루어진 클램핑이 제거됨에 따라 조립체가 스프링백(Spring-back)하여 조립체 편차 U가 남게 된다.

조립 중에 발생하는 변형을 고려하여 공차해석을 수행하기 위해서는, 부품들의 편차로부터 조립체의 편차를 구할 수 있어야 한다. 이를 구하는 방법이 다음 절의 영향계수법이다.

3. 문제 정의 및 해법

이 장에서는, 본 논문에서 다룰 최적화 문제를 정의하고 그 해법을 설명한다.

3.1 문제 정의

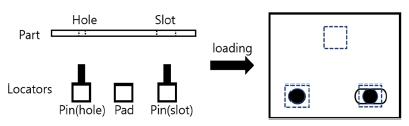
문제 정의에 앞서, 판금 조립 공정의 로케이터에 대해 보다 자세히 설명할 필요가 있다. 로케이터는 부품의 자유도를 제약하여 위치와 자세를 결정하는 장치를 의미하는데, 판금 조립 공정에서는 흔히 두 가지 방식, 즉 3-2-1 방식과 Pad-pin-slot 방식이 사용된다. 본 논문에서는 Pad-pin-slot 방식을 적용하는데, 이 방식에서는 Fig. 2와 같이 구멍과 슬롯이 이미 가공되어 있는 판금 부품을 3개의 패드(Pad)와 2개의 핀으로 제약한다. 본 논문에서는 부품 상에서 이들 제약 위치들을 각각 패드 접촉부, 구멍, 슬롯이라 부르기로 한다.

Fig. 2

Schematic diagram of part and locators

본 논문에서 다루는 문제는, 초기 편차를 가지고 있는 두 개의 차체 부품이 조립될 때 조립체의 중요 위치에서 편차가 최소가 되도록 패드 접촉부, 구멍, 슬롯의 위치를 구하는 것이다.

3.2 로케이터 위치 최적화

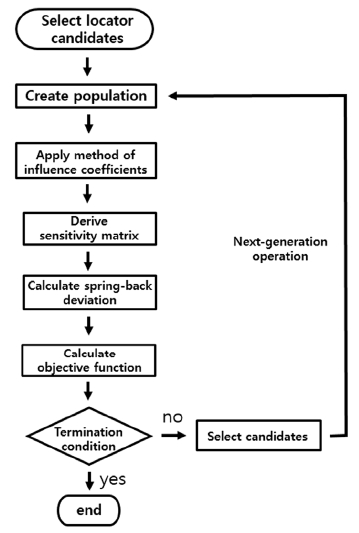
본 논문에서 개발한 로케이터 위치 최적화 기법은 Fig. 3의 흐름도와 같다. 최적화를 위한 알고리즘으로는 이 분야의 기존 연구^1-3)에서 널리 사용되고 있는 유전알고리즘을 채택했다.

Fig. 3

Flowchart of the optimization method for fixture layout design

Fig. 1의 첫 번째 단계로 로케이터 위치의 후보인자를 선정한다. 여기서 ‘후보인자’는 유전알고리즘에서 흔히 크로모솜(Chromosome), 게놈(Genome) 등으로 불리는 것으로서 자식해를 생성하기 위해 사용되는 요소들이다.¹¹⁾

로케이터는 부품 내 임의의 위치에 놓일 수 있지만, 본 연구에서는 최적화 과정에 소요되는 시간을 줄이기 위해 유한한 개수의 후보 위치만 고려하기로 한다.

패드 접촉부, 구멍, 슬롯 각각의 후보 위치가 선정되었으면, 이들의 조합(각 조합을 자식해라 함)으로 1세대 모집단을 구성한다. 각 자식해, 즉 각 로케이터 조합은 상이한 경계조건을 의미하므로, 이들 각각에 대해 2.2절의 영향계수법을 적용해 민감도 행렬을 구한다. 각 자식해에 대해 민감도 행렬이 구해졌으면, 주어진 확률분포를 갖는 부품 편차를 식 (4)에 대입하여 조립체의 편차 분포를 구한다.

이제, 조립체의 편차 분포를 근거로 여러 자식해를 비교, 평가해야 한다. 평가에 사용할 목적함수(Objective function) f는 식 (6)~(8)과 같이 정의한다.

$\[ f=\sum _{k=1}^N\frac{\left|{\mu }_k\right|}{N}+\alpha \bullet \sum _{k=1}^N\frac{{\sigma }_k}{N} \]$

(6)

단,

$\[ {\mu }_k=\sum _{j=1}^M\frac{U_{k, j}}{M} \]$

(7)

$\[ {\sigma }_k=\sqrt{\sum _{j=1}^M\frac{{\left(U_{k, j}-{\mu }_k\right)}^2}{M-1}} \]$

(8)

위의 식에서 측정점은 N개이고 몬테카를로 시뮬레이션은 M회 시행하는 것으로 가정했으며, U_{k, j}는 j번째 시뮬레이션에서 구한 k번째 측정점의 스프링백 변위이다. 따라서 식 (7) 및 (8)은 k번째 측정점에서 구한 스프링백 변위의 평균과 표준편차를 의미한다. 식 (6)의 목적함수 f는 이들 평균과 표준편차를 모든 측정점에걸쳐 평균한 후 더한 값이며, 두 항의 상대적인 크기에 따라 적절한 가중치(Weighting factor) α를 적용할 수 있도록 하였다.

이제 각 자식해(로케이터 조합)에 대해 식 (6)으로 목적함수 f를 구하면, 이들을 정량적으로 비교할 수 있고 f값이 가장 작은 로케이터 조합이 그 세대에서 가장 우수한 자식해라고 볼 수 있다. i번째 세대에서 구한 f의 최소값을 f_min(i)라 하면, Fig. 3의 반복 루프(loop)에 따라 세대를 거듭하면서(i 증가) f_min(i)가 감소하게 된다.

이 반복 작업, 즉 세대를 거듭하는 작업은 f_min(i)가 다음의 수렴 종료조건을 만족할 때까지 계속하는 것으로 한다.

$\[ \frac{f_{\mathrm{m}\mathrm{i}\mathrm{n}\left(i-\gamma \right)}-f_{\mathrm{m}\mathrm{i}\mathrm{n}\left(i\right)}}{f_{\mathrm{m}\mathrm{i}\mathrm{n}\left(i\right)}}\leqq ϵ \]$

(9)

식 (9)에서 γ값과 ε값은 연구자가 문제에 따른 수렴 양상을 관찰하면서 적절히 정해야 하는데, 본 연구에서는 γ=2, ε=0.01로 하였다.

식 (9)의 종료조건을 만족하지 못해 다음 세대 모집단을 생성할 때에는, 현 모집단에서 목적함수 값이 가장 작은 자식해 2개로 다음 모집단 후보인자를 생성하는 순위기반선택¹¹⁾ 방법을 적용한다.

4. 적용 예

3장에서 설명한 최적화 기법을 2개의 문제에 적용하고 그 결과를 보임으로써 개발된 기법의 유용성을 고찰하고자 한다. 유한요소해석을 위해서는 Siemens사의 NX10 Nastran을 사용하였고, 최적화를 위해 Mathworks사의 Matlab R2017a 및 Microsoft사의 Excel 2016을 사용했다.

4.1 평판 조립 문제

먼저 간단한 문제로서 두 개의 얇은 평판이 조립되는 문제(Fig. 4)를 고찰한다. 이 문제에서는 주로 z축 방향의 변위만 발생하므로 1차원 편차 문제라 할 수 있다.

Fig. 4

Assembly of two sheet metal plates

4.1.1 문제 정의

왼쪽 평판을 Part 1, 오른쪽 평판을 Part 2라 하고, 각 평판의 크기는 가로 100 mm, 세로 100 mm이다. Part 1, 2의 두께는 각각 1 mm, 2 mm이고, 재료는 연강으로 물성치는 탄성계수(Young’s modulus) E=207 GPa, 포아송 비(Poisson’s ratio) ν=0.3이다.

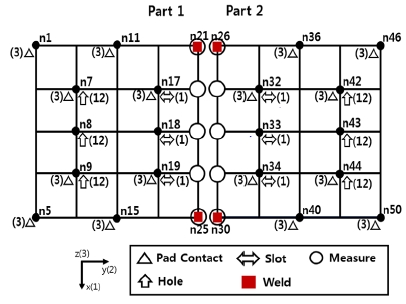
용접점 위치는 Part 1과 Part 2가 만나는 모서리의 양끝 두 점이다. 즉, Fig. 5에서 노드(Node) n21과 n26이 용접되고 n25와 n30이 용접된다. 2장에서 설명한 바와 같이 클램프 위치는 용접점과 동일한 것으로 가정한다. 목적함수의 계산에 사용되는 조립체의 편차 측정점은 두 평판이 맞닿는 모서리를 따라 존재하는 10개 노드(Fig. 5의 O로 표시한 점)이다. 여기서 측정점의 위치는 조립체의 조립품질을 평가하기에 적절한 위치로 선정했다.

Fig. 5

Candidate locators in the two-plate problem

4.1.2 로케이터 후보인자 선정

Fig. 3에 보인 흐름도에 따라, 우선 Part 1, 2의 1세대 로케이터 후보인자를 선정한다. 후보인자는 그 개수가 많을수록 우수한 최적화 결과를 얻을 수 있지만, 계산의 효율성을 고려하여 각 부품별로 패드 접촉부 8개, 구멍 3개, 슬롯 3개를 선정하였다(Fig. 5 및 Table 1 참조). 후보인자들은 가급적 각 부품 내에서 넓게 분포되고 대칭이 되도록 선정했다. Fig. 5에서 괄호 안의 숫자는 그 점에서 제약되는 병진운동의 방향을 의미한다.

Table 1

Candidate locator positions for Generation 1 in the two-plate problem

4.1.3 로케이터 위치 최적화

1세대 모집단을 생성하는데 모집단은 5개의 자식해를 갖는 것으로 하였다. 각 자식해는 부품별로 8개 패드접촉부 후보 중 3개, 3개 구멍 후보 중 1개, 3개 슬롯 후보 중 1개를 무작위로 추출하였다. 그 결과, 도출된 1세대 모집단은 Table 2와 같다.

Table 2

Population of Generation 1 in the two-plate problem

다음으로 영향계수법을 적용하여, 각 자식해를 경계조건으로 하는 유한요소해석을 수행하고 민감도 행렬을 구하였다. 예를 들어, 1번 자식해의 민감도 행렬(10×4)을 보이며 다음과 같다.

$\[ \left[S\right]=\left[\begin{array}{ccc}57.106& -4.657& \begin{array}{cc}449.343& -6.254\end{array}\\ 24.386& -0.186& \begin{array}{cc}192.025& 10.798\end{array}\\ \begin{array}{c}⋮\\ \begin{array}{c}-812.36\\ \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }91.86\end{array}\end{array}& \begin{array}{c}⋮\\ \begin{array}{c}82.472\\ \mathrm{ }\mathrm{ }\mathrm{ }2.134\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}⋮\\ \begin{array}{c}\mathrm{ }\mathrm{ }\mathrm{ }0.113\\ 723.58\end{array}\end{array}& \begin{array}{c}⋮\\ \begin{array}{c}615.967\\ \mathrm{ }\mathrm{ }\mathrm{ }61.880\end{array}\end{array}\end{array}\end{array}\right]\times {10}^{-3} \]$

(10)

계산된 민감도 행렬 [S]를 이용하면, 식 (4)로부터 부품 초기편차 {V}의 정규분포(평균=0, 표준편차=1로 가정)에 따른 조립품 편차 {U}의 분포를 계산할 수 있다. Table 3은 1번 자식해에 대해 100회 몬테카를로 시뮬레이션을 수행하여 구한 편차 값의 예를 보여주고 있다.

Table 3

Assembly deviations at measurement points for offspring 1 of Generation 1 in two-plate problem

Table 4는 이와 같이 구한 편차 값들을 식 (6)~(8)에 대입하여 계산한 각 자식해의 목적함수 값을 오름차순으로 정리한 것이다.

Table 4

Objective function values in ascending order for offsprings in generation 1 in two-plate problem

Table 4로부터, 1세대 모집단에서 2번 자식해의 목적함수 값이 가장 작음을 알 수 있다. 이는 1세대의 5개 자식해 중에서는 2번에 해당하는 로케이터 위치를 사용할 때 조립체의 품질이 가장 좋음을 의미한다.

이제 Fig. 3의 반복 루프(Loop)를 수행하기 위해, 2세대 후보인자를 구성한다(Table 5 참조). 앞에서 설명한 바와 같이 본 논문에서는 순위기반 선택법¹¹⁾을 적용해, 1세대 중 목적함수 값이 가장 작은 2개 자식해(Table 4의 Offsprings 2, 5)의 합집합을 후보인자로 하여 2세대의 3개 자식해(Offsprings 1~3)를 생성했다.

2세대 모집단에서 나머지 2개의 자식해는 두 개의 규칙에 의해 생성된다.¹¹⁾ 먼저 첫 번째 규칙은 1세대 자식해 중 목적함수 값이 가장 작았던 자식해를 그대로 가져오는 것이다(Table 5의 Offspring 4). 이는 세대를 거치면서 목적함수가 발산하지 않고 계속해서 수렴하기 위함이다. 두 번째 규칙으로서, 5개의 자식해 중 1개는 1세대 후보인자로부터 무작위로 생성한다(Table 5의 Offspring 5). 이는 세대를 거치면서 전체 세대가 지역 최적해에 빠져드는 것을 방지하기 위함이다.

Table 5

Population of Generation 2 in the two-plate problem

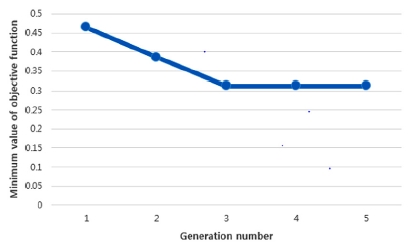
Fig. 3에 보인 바와 같이 위의 과정을 반복 수행한 결과, 5세대에서 종료조건(식 (9))을 만족하여 최적화가 종료되었다. 세대를 거듭함에 따른 목적함수 최소 값의 추이는 Table 6 및 Fig. 6과 같다.

Table 6

Minimum objective function values for succeeding generations in the two-plate problem

Fig. 6

Optimization history in the two-plate problem

5세대에서 목적함수가 최소값을 갖는 최적 로케이터 위치는 Fig. 7과 같이 좌우 대칭임을 알 수 있다. 이는 부품의 두께 외에는 좌우 대칭인 문제의 특징을 고려할 때 합리적인 결과라 볼 수 있다. 또, 패드 접촉부들의 최적 위치가 대체로 측정점 근처에 집중되어 있는데, 이는 이 위치들이 측정점에서의 조립체 편차를 최소화하기에 효과적임을 고려할 때 합리적인 결과로 보인다. 따라서 평판 조립 문제의 결과로부터 본 연구에서 개발된 방법이 신뢰할만한 최적해를 제공함을 알 수 있다.

Fig. 7

Optimal locations of the locators

4.2 휠하우징 조립 문제

본 연구에서 개발한 기법을 실제 차체의 휠하우징 조립 문제에 적용해 본다. 이 문제에서도 4.1절의 평판 조립 문제와 동일한 과정을 거쳤으므로 4.1절과 상이한 부분과 중요 결과만 설명하기로 한다.

4.2.1 문제 정의

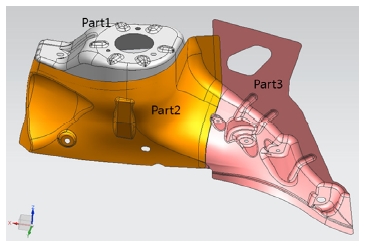
휠하우징은 Fig. 8과 같이 3개의 부품(Part 1, 2, 3)으로 구성되고, Part 1과 Part 2가 조립된 후 Part 2와 Part 3이 조립된다.

Fig. 8

Assembly of wheel housing parts

모든 부품의 두께는 1 mm로 동일하고, 부품의 재료는 연강(E = 207 GPa, ν= 0.3)이다. 용접점은 Fig. 9(a)에서 x로 표시된 5개 점(Part 1의 w1, w2, w3, w4, w5점과 Part 2의 w6, w7, w8, w9, w10점)이다. 측정점은 Fig. 9(b)에 보인 5개인데, 이 점들은 추후 Part 3이 조립될 Part 2 상의 용접점들이다. 즉, Part 1과 Part 2의 조립 공정에서 로케이터를 어디에 배치하면 다음 조립 공정이 원활할 지의 문제를 고찰하는 것이다.

Fig. 9

Weld and measurement points in the wheel housing model: (a) weld points, (b) measurement points

Fig. 8과 9와 같이 부품의 CAD 모델에 이미 구멍과 슬롯이 존재하므로, 이 문제에서는 구멍과 슬롯의 위치가 Fig. 10과 같이 고정된 것으로 가정하고 패드 접촉점의 위치만 최적화하기로 한다.

Fig. 10

Assumed locations of holes and slots in the wheel housing problem

평판 문제와 달리, 3차원 형상을 갖는 휠하우징 문제에서는 용접건의 작용력과 로케이터의 지점반력이 좌표축과 일치하지 않는 방향(즉, 각 점에서 부품에 수직인 방향)으로 작용할 수 있다. 따라서 안정적인 유한요소해석을 위해 패드 접촉부를 한 점이 아닌 원형 면적으로 모델링했다.

4.2.2 로케이터 후보인자 선정

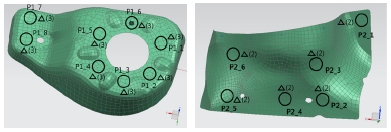
Part 1과 Part 2의 패드 접촉부 위치를 최적화하기 위해, 먼저 1세대 후보인자를 선정한다. 선정 기준은 가급적 국부 수직방향(Local normal)이 유사한 점들 중에서, 부품 전체에 걸쳐 고르게 분포하도록 하였다. 선정된 패드 접촉부의 1세대 후보인자는 Fig. 11에 작은 원으로 표시하였는데 Part 1에서 총 8개, Part 2에서 총 6개이다.

Fig. 11

Candidate pad contacts in the wheel housing problem

4.2.3 로케이터 위치 최적화

Fig. 11의 1세대 후보인자로부터 5개의 자식해를 생성하여 1세대 모집단을 구성하였다. 다음으로는 4.1절의 평판 문제와 마찬가지로, 1세대 자식해 5개 각각에 대해 영향계수법을 적용하여 민감도 행렬을 구하고 몬테카를로 시뮬레이션을 수행하여 각 자식해의 목적함수 값을 계산하였다. 이 값들을 오름차순으로 정리하면 Table 7과 같다.

Table 7

Objective function values in ascending order for offsprings in Generation 1 in the wheel housing problem

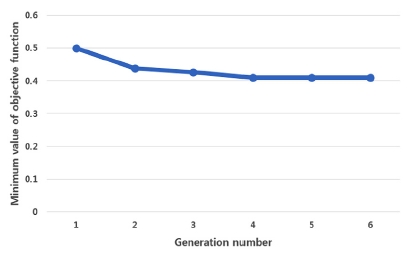
4.1절과 동일한 방법으로 세대를 거듭하며 유전알고리즘을 수행한 결과, 6세대에서 최적화가 종료되었다. 각 세대에서 구한 목적함수의 최소값은 Table 8 또는 Fig. 12와 같다.

Table 8

Minimum objective function values for succeeding generations in the wheel housing problem

Fig. 12

Optimization history in the wheel housing problem

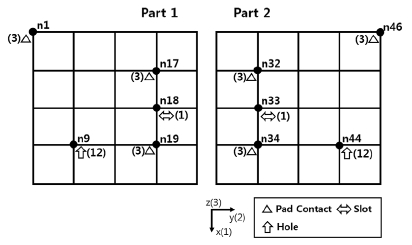
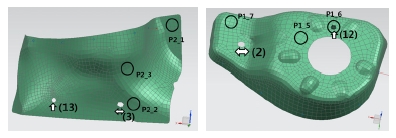
이러한 과정을 거쳐 최종적으로 선정된 최적 패드 접촉부 위치는 Fig. 13과 같다. Part 2의 패드 접촉부가 측정점 근처에 모여 있음을 알 수 있는데, 이는 4.1절 평판 조립 문제의 결과에서와 같은 이유로 그 합리성을 설명할 수 있다. 한편 Part 1의 패드 접촉부는 모두 용접점에서 멀리 위치하고 있는데, 이는 부품의 지지점을 용접부에서 멀리 잡을수록 용접부를 공칭 위치로 변위시키는데 필요한 용접건의 작용력이 작아져서 조립체의 스프링백 변위도 작아지기 때문인 것으로 설명할 수 있다. 이로써 Fig. 13의 결과도 합리적인 것으로 판단되어, 본 연구에서 개발된 방법론이 신뢰성 있는 결과를 제공함을 다시 한 번 확인하였다.

Fig. 13

Optimal locations of the locators in the wheel housing problem

5. 결 론

본 논문에서는, 차체 조립 공정에서 부품의 편차로 인해 발생하는 조립품의 편차를 최소화 하는 로케이터의 최적 위치 선정 기법을 개발하였다. 조립품의 변형을 고려하기 위해 유한요소해석에 기반을 둔 영향계수법(2장)을 사용하였고, 최적화를 위해서는 유전알고리즘(3장)을 활용하였다. 4장에서는 1차원 변형만을 고려하는 평판 조립 문제와 3차원 변형을 고려하는 실제 휠하우징 조립 문제에 최적화 기법을 적용해 최적해를 도출했다. 도출된 결과가 논리적 또는 역학적으로 설명 가능하고 타당함을 보임으로써, 개발된 기법의 효과와 신뢰성을 확인할 수 있었다.

평판 문제와 휠 하우징 문제에서 가능한 모든 로케이터 모집단의 수는 각각 988개와 1120개이다. 모든 경우의 조립체 편차를 직접 구해 비교하는 방법에 비해 본 연구의 기법은 약 95 % 정도의 계산 시간 절감을 의미한다.

본 논문에서는 로케이터의 위치만 변수로 고려했지만, 일반적인 고정구 설계를 위해서는 로케이터와 클램프의 개수, 위치, 순서를 모두 동시에 고려해야 한다. 또한 실제에서는 부품의 간섭이나 접촉도 발생할 수 있으므로, 이를 고려하려면 비선형 해석도 포함되어야 한다. 본 연구를 시발점으로 이러한 향후 연구가 이루어진다면, 조립 차체의 품질을 제고할 수 있는 실용적이고 유용한 고정구 설계 방법론이 개발될 것으로 기대한다.

Acknowledgments

본 연구는 2015년도 홍익대학교 학술연구진흥비의 지원으로 수행되었음.

References

• Y. G. Liao, “A Genetic Algorithm-based Fixture Locating Positions and Clamping Schemes Optimization”, Proceedings of the Institution of Mechanical Engineers, p1075-1083, (2003).
• L. Shelley Xie, and Ching Hsieh, “Clamping and Welding Sequence Optimization for Minimizing Cycle Time and Assembly Deformation”, International Journal of Materials & Product Technology, 17(5-6), p389-399, (2002).
• W. H. Choi, “Tolerance Analysis for Deformation Body Using Method of Tolerance Influence Coefficients and Deformation of Optimal Weld Sequence”, M. S. Thesis, Seoul National University, Seoul, (2005).
• J. H. Han, S. M. Yang, H. S Yu, and T. J Kim, “Optimal Condition for Spot Weldment of Dissimilar Steel Sheet in Automotive”, Transactions of KSAE, 18(4), p68-73, (2010).
• S. Selvakumar, K. P. Arulshri, K. P. Padmanaban, and K. S. K. Sasikumar, “Design and Optimization of Machining Fixture Layout Using ANN and DOE”, The International Journal of Advanced Manufacturing Technology, 65(9-12), p1573-1586, (2013). [https://doi.org/10.1007/s00170-012-4281-2]
• Y. Xing, “Fixture Layout Design of Sheet Metal Parts Based on Global Optimization Algorithms”, Journal of Manufacturing Science and Engineering, 139(10), (2017). [https://doi.org/10.1115/1.4037106]
• H. C. So, K. S. Kim, H. J. Yim, H. S. Jee, B. J. Park, and I. S. Yoo, “A Tolerance Analysis Method for Spot-welded Deformable Auto Body Parts”, Transactions of KSAE, 14(2), p23-31, (2006).
• S. C. Liu, and S. J. Hu, “Variation Simulation for Deformable Sheet Metal Assemblies Using Finite Element Methods”, Journal of Manufacturing Science and Engineering, 119(3), p368-374, (1997). [https://doi.org/10.1115/1.2831115]
• W. Chen, L. Ni, and J. Xue, “Deformation Control through Fixture Layout Design and Clamping Force Optimization”, The International Journal Advanced Manufacturing Technology, 38, p860, (2008). [https://doi.org/10.1007/s00170-007-1153-2]
• K. Krishnakumar, and S. N. Melkote, “Machining Fixture Layout Optimization Using the Genetic Algorithm”, International Journal of Machine Tools and Manufacture, 40(4), p579-598, (2000). [https://doi.org/10.1016/s0890-6955(99)00072-3]
• B. R. Moon, Genetic Algorithm, Da-Sung, Seoul, p39-42, (2001).