GDL 변형거동에 영향을 미치는 설계인자에 대한 연구

1. 서 론

고분자 전해질 연료전지(Proton exchange membrane fuel cell)는 연료로 공급된 수소와 대기 중의 산소가 전해질 막(Membrane)을 사이에 두고 공급되어 전해질 막의 표면의 촉매 층에서 화학반응으로 발생한 화학에너지를 전기에너지로 변환시키는 장치이다.¹⁾ 화석연료를 사용하는 내연기관과 비교하였을 때 연료전지는 에너지 효율이 높으며 소음이 없을 뿐만 아니라 유해가스 배출이 거의 없는 친환경적인 동력원이다.

연료전지의 주요 구성요소 중 하나인 기체확산층(GDL, gas diffusion layer)은 분리판(Bipolar plate)을 통하여 공급된 수소와 산소를 전기화학 반응이 일어나는 막전극접합체(MEA, membrane electrode assembly)로 전달하고, 촉매층에서 수소와 산소의 전기화학반응으로 인해 발생하는 수분을 배출하는 역할을 하고 있다. 기체확산층은 수분을 원활히 배출하기 위해 다공성 구조의 재료를 사용하는데 이는 볼트체결 상태에서 발생하는 압축하중으로 인해 불균일한(Inhomogeneous) 변형과 과도한 변형이 발생할 수 있어 궁극적으로는 공극체적 손실로 인한 물질의 이동을 방해 할 수 있다. 과도한 체결력은 유연한 기체확산층에 손상을 야기하여 채널부에서 층간분리(Delamination)를 발생시킬 수 있으며 멤브레인 막의 손상을 가져올 수 있다.²⁾ 그러므로 연료전지의 설계에 있어서 기체확산층의 정확한 변형거동 예측은 최적의 연료전지를 구현하는데 필요한 요소이다.

기체확산층의 기계적 반응은 제작공정 특성 때문에 하중방향에 많은 영향을 받는다. 기체확산층 내의 탄소섬유는 제작 공정 방향인 수평방향으로 불규칙하게 얽혀있는 다공성 구조이므로 탄소섬유의 방향과 종방향의 물성이 면내(In-plane) 거동 특성에 많은 영향을 미치고 면외(Out-of plane)방향의 거동 특성은 탄소섬유의 굽힘 물성과 횡방향 물성에 의해 나타난다. 이러한 기체확산층 재료 거동의 특성은 거시적 관점에서 연속체 역학의 이론을 이용하여 나타내거나 미시적 모델을 사용할 수 있다.

본 연구에서는 기체확산층의 변형거동을 직교이방성(Orthotropic)으로 가정한 거동모델을 이용하여 압축하중 상태에서 변형특성을 연구하였다. 직교이방성 구성방정식은 상용 유한요소해석 프로그램인 ABAQUS의 사용자재료서브루틴(UMAT)을 사용하여 구현하였고 기체확산층의 변형 거동에 영향을 미치는 설계인자에 대한 연구를 진행하였다. 다구찌 방법을 사용한 실험계획법의 반응값으로 공극률(Porosity)과 채널칩입량(Intrusion)을 설정하였다. 제어인자(Control factor)와 잡음인자(Noise factor)를 선정하여 설계영향 분석에 대한 강건 설계를 하였다. 다구찌 방법은 적은 실험 횟수로도 선정한 인자의 영향을 확인할 수 있을 뿐만 아니라 최적의 인자 값과 인자에 대한 조합을 정량적으로 얻을 수 있다.^3,4)

본 연구의 주요 목적은 설계 반응값인 공극률, 채널침입량에 대한 각 설계인자의 영향 및 최적의 연료전지 성능 구현을 위한 강건한 설계인자 조건을 제시하는데 있다. 전처리 프로그램으로는 HYPERMESH, 유한요소해석을 위한 ABAQUS⁵⁾, 통계 처리를 위한 프로그램인 MINITAB⁶⁾을 사용하여 연구를 수행하였다.

2. GDL 구조해석

2.1 유한요소모델

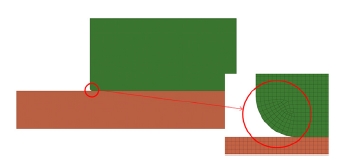
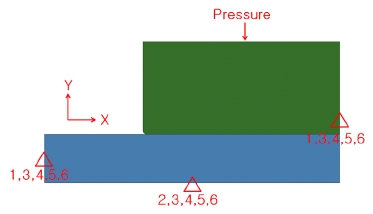
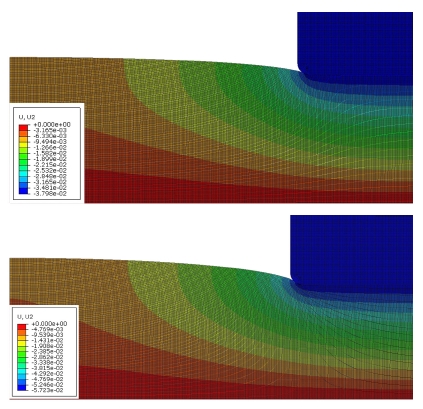
유한요소해석에 사용된 모델은 연료전지의 구성 요소 중 기체확산층과 분리판 으로 구성하였으며, 효율적인 해석을 위하여 2D 평면 변형모델(2D plane strain model)로 이상화하였다. 사용된 유한요소 모델에서는 온도와 습도의 영향을 고려하지 않았고 전해질 막의 강성이 기체확산층에 비해 상대적으로 커서 변형의 정도가 크지 않으므로 모델에서 제외하였다. 또한 해석에 사용된 모델은 연료전지의 중앙부라고 가정하여 볼트 체결력이 균일하게 분포한다고 가정하였고 평면변형을 가정할 수 있도록 채널은 충분히 길다고 가정하였다. 전체모델은 약 224,000여개의 절점과 약 224,500여개의 요소로 구성되었고 모든 모델의 요소의 크기는 2 μm로 모델링하였다. ABAQUS에서 제공하는 평면변형요소인 CPE4 요소를 사용하여 Fig. 1과 같이 모델링 하였다. 반복적인 분리판의 채널 형상과 기체확산층 적층구조 때문에 해석모델은 Fig. 2와 같은 대칭모델을 사용하였다. 그리고 압축하중으로 인한 부품간의 접촉 조건은 기체확산층과 분리판 간의 접촉면에 면대면(Surface to surface) 접촉조건을 부여하였고 체결력에 의한 분리판과 기체확산층의 접선방향의 거동의 경우 미끄러짐 양은 그리 크지 않으므로 0.2의 마찰계수를 가진 소규모 미끄러짐 접촉조건(Small sliding contact)을 사용하였다. 또한 직각을 가진 모서리에서 발생하는 접촉에 의한 수렴 문제로 인해 분리판의 좌측 하단 모서리에 인공적인 반경 20 μm의 필렛을 적용하였다.

Fig. 1

GDL and bipolar plate assembly model

Fig. 2

FEA model of GDL and bipolar plate with BC

2.2 구성방정식

기체확산층은 탄소섬유가 얽혀있는 다공성 재료로서 압축 시 채널/분리판의 반복적인 형상으로 인하여 두께 방향으로 균일하지 않은 공극의 분포를 나타낸다. 몇 몇 연구자들은 이러한 공극의 분포를 실험이나 간단한 분포함수를 이용한 수치적 모델을 이용하여 연구를 진행하였다.^7,8) 이러한 수치적 모델의 응용과 기체확산층의 기계적 물성을 이용한 유한요소 모델은 기체확산층의 형상변화에 대한 연구를 가능하게 하였다. 그러나 기체확산층의 기계적 물성치의 정확한 구현은 기체확산층 자체의 형상 및 구조에 의하여 어려움을 겪어왔다.

대부분의 연구에서 기체확산층의 모델링은 선형 모델(Linear model), 비선형 등방성 모델(Nonlinear isotropic model), 또는 비선형 직교이방성모델(Nonlinear orthotropic model)을 이용하여 구현되었다.^9-11) 기체확산층은 제조공정에 의한 탄소섬유의 배열 때문에 연속체 관점에서 직교이방성으로 구현될 수 있고, 면내 방향으로 탄소섬유의 배열로 인한 면내 강성을 지닌 평면구조물로 가정할 수 있지만 두께 방향으로는 쉽게 변형이 되는 구조이다.

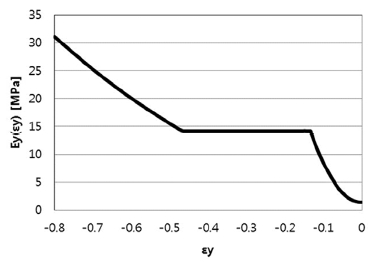
본 연구에서는 Garcia-Salaberri 등¹²⁾이 제안한 거시적 직교이방성모델과 기체확산층의 탄소섬유의 형상을 보 구조물로 모델링한 미시적 모델을 고려하였다. 거시적 직교이방성 모델에서는 실험에 의한 두께 방향 탄성계수를 곡선맞춤(Curve fitting)한 값을 사용하였고 탄성계수의 비선형성은 변형률의 함수로 나타내었다(Table 1, Fig. 3). 미시적 모델에서는 기체확산층 내의 탄소섬유의 분포를 Fig. 4와 같은 간략화된 보 구조물로 가정하여 1차원 응력과 변형율의 관계를 유도하였다.¹³⁾

Table 1

Piecewise polynomial fitting of the through-plane nonlinear behavior12)

Fig. 3

Curve fitted numerical model of Table 1

Fig. 4

Simplified GDL structure13)

직교이방성 모델의 두께 방향 탄성계수 E_y 곡선은 3개의 영역으로 구별되어진다. 즉, 작은 변형에 대한 초기영역, 초기변형과 재 경화 영역사이의 천이 영역, 그리고 재 경화가 발생하는 영역이다.¹²⁾ 다공성 재료의 특성으로 인하여 압축 시 측방향의 변형이 무시할 만큼 작으므로 v_yx는 0으로 가정하였다.

Table 2

Mechanical properties of model 1 and model 212,13)

보가 겹쳐진 형상으로 탄소섬유의 미세 구조를 구현한 기체확산층은 다공성 미세구조 특성을 고려하여 Fig. 4와 같이 서로 직각으로 교대로 배치된 평행한 보로 구성된 간단한 모델로 이상화하였다. 이 모델은 반복성으로 인해 3점 굽힘을 받는 보에 해당하는 단위 셀로 나타내어 압축하중에 대한 응력-변형률 관계를 나타낼 수 있다. 유도된 두께 방향의 탄성계수 식 (1)은 미시적 직교이방성 모델에 적용되었다.

$\[ E_y=\mu \frac{105\pi E}{16}{\left(1-\sqrt{\frac{{⋋p}_0-\epsilon }{1-\epsilon }}\right)}^5 \]$

(1)

위의 식에서 p₀는 초기공극률, μ와⋋는 무차원 보정상수이다.¹³⁾

2.3 유한요소해석결과

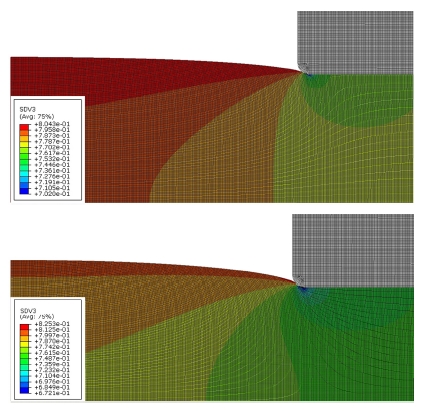
상기한 2종류의 재료모델을 상용유한요소해석 프로그램인 ABAQUS에서 제공되는 사용자 재료서브루틴인 UMAT를 이용하여 구현하였다. 첫 번째로 두께 방향의 탄성계수의 실험치를 이용하여 구성한 비선형 직교이방성 모델에 대한 해석을 수행하였다(Model 1). 재료 모델의 적합성을 평가하기 위하여 실험에 사용한 형상과 같은 유한요소 모델을 생성하여 압축하중을 부여하여 해석을 수행하였다. 1 MPa의 하중을 가한 경우에 Model 1에서의 공극률은 0.7020, 채널침입량의 경우 30.7385 μm이었다. 공극률 식은 다음을 이용하였다.

$\[ \varphi \left(x,y\right)=\frac{V_p}{V}=\frac{{\varphi }_0-1+e^{{\epsilon }_V\left(x,y\right)}}{e^{{\epsilon }_V\left(x,y\right)}} \]$

(2)

여기서 Φ₀는 초기 공극률, V_p는 기공체적, V는 총 체적, ε_V(x,y)은 탄성재료의 각 지점 별 체적변형을 나타낸다.¹²⁾

그리고 기체확산층의 탄소섬유 형상을 보로 모델링한 재료 모델인 Model 2는 Model 1과 같은 1 MPa의 압축하중에서 공극율은 0.6721, 채널침입량은 46.8693 μm를 나타내었다.

Fig. 5

Contour plot of the GDL porosity (top: model 1, bottom: model 2)

Fig. 6

Contour plot of the GDL intrusion (top: model 1, bottom: model 2)

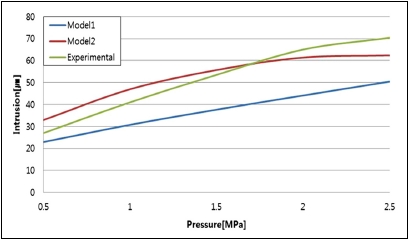
0.5~2.5(MPa)의 압축하중을 가한 경우의 두 모델의 채널침입량 결과값은 실험값과 정확히 일치하지는 않지만 동일하게 하중의 크기에 비례하여 채널침입량이 상승되는 경향을 나타내어 기체확산층의 재료모델이 유한요소해석에 적합하다고 판단하였다(Fig. 7).

Fig. 7

Variation of the GDL intrusion into the channel as a function of the cell assembly pressure12,13)

3. 다구찌 방법

다구찌 방법은 실험계획법 중 하나이며, 직교배열표를 이용한 방법이다. 다구찌 방법은 외부환경을 고려하여 품질과 비용에 대한 최적 설계변수를 구현하는 방법 중의 하나이다. 제품 설계에서 특성치를 반응값으로 설정하여 설계변수의 가능한 수준으로 정의한 직교배열표를 구성하여 가장 안정적이고 신뢰성이 높은 상태를 나타내는 설계변수의 조합을 찾는데 이용된다. 설계 반응값의 분산에 대한 설계 변수의 영향을 고려하여 결과값의 분산을 줄일 수 있는 통제가능한 인자에 대한 조건을 설정하여 강건설계를 가능하게 한다.¹⁴⁾

3.1 설계인자선택

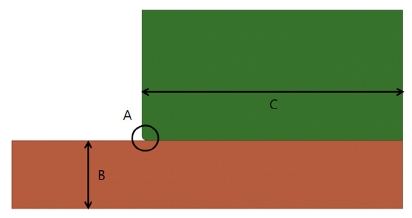
실질적으로 제어가 가능한 필렛 반경 (A), 기체확산층 두께 (B), 분리판 폭 (C)을 선택하여 3종류의 제어인자를 구성하였고(Fig. 8) 정확한 예측이 어려운 y방향 탄성계수(E_y)를 잡음인자로 선택하였다.

Fig. 8

Control factor description for analysis

3.2 직교배열표

강건설계를 통한 기체확산층의 최적화문제에 사용할 제어인자 A, B, C는 Table 3과 같이 3수준으로 설계 범위를 정하였다. 또한, 잡음인자를 2수준으로 정하여 L₉(3³)직교배열표를 구성하였다. 내측배열에는 설계변동을 할 수 있는 제어인자, 외측배열에는 제어가 힘든 잡음인자로 구성하였다.

Table 3

Design factors and levels used in analysis

내측배열의 제어인자들의 수준은 2수준을 기준값으로 하여 설계제한 범위 내에서 1수준과 3수준을 선정하여 설계를 하였고, 외측배열에는 정확한 예측이 어려운 잡음인자를 평균값의 ± 20 %로 수준을 선정하여 2수준으로 Table 3에 나타내었다. 사용된 L₉(3³) 직교배열표는 Table 4에 나타내었으며, 잡음인자를 고려한 반복실험 2번씩을 포함해 총 18번의 해석을 수행하였다.

Table 4

Orthogonal array table for analysis

3.3 해석결과

압축하중에 대한 반응값으로 기체확산층의 공극률과 채널침입량을 설정하였다. 각 설계변수의 조합에 대한 유한요소해석 결과를 사용하여 신호 대 잡음비(Signal to Noise ratio)와 평균을 계산하였다. 공극률의 경우 과도한 압축하중이 가해질 경우 반응물 및 생성물의 이동이 방해 될 수 있으므로 변형 후 적절한 값 이상을 유지하여야 하므로 망대특성을 사용하였고 채널침입량의 경우 압축에 의한 분리판의 기체확산층 침입이 작을수록 좋으므로 망소특성을 사용하였다.

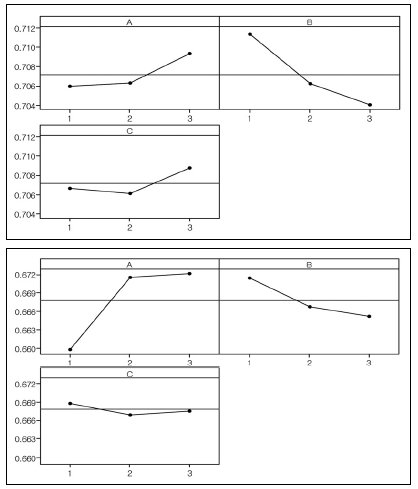
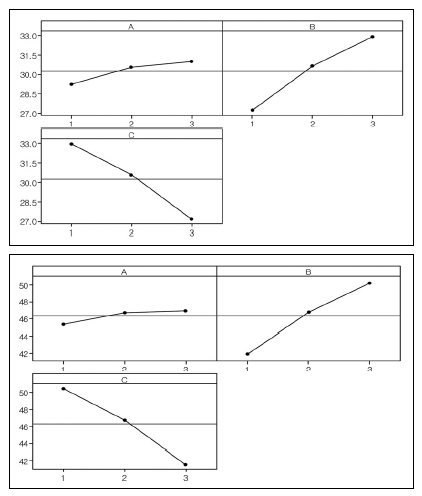
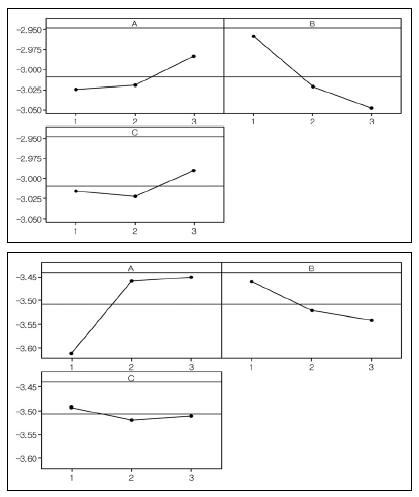
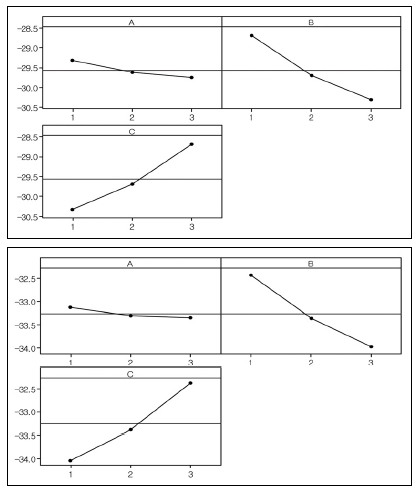
Table 5에는 Model 1과 Model 2에 대한 공극률과 채널침입량에 대한 결과값을 나타내었다. 각각의 설계변수의 변화에 대한 결과값을 도식적으로 나타낸 주 효과도(Main effect plot)를 이용하여 평균에 대해서는 Fig. 9, 10에 나타내었고, S/N비에 대해서는 Fig. 11, 12에 나타내었다. 수준의 변화에 따른 주 효과도 선의 구배가 급격한 경우에는 해당 설계인자가 반응값에 유의함을 나타내고 그렇지 않은 경우에는 상대적으로 유의하지 않음을 나타낸다.

Table 5

Response results by using Taguchi method

Fig. 9

Main effect plots for porosity means (top: model 1, bottom: model 2)

Fig. 10

Main effect plots for intrusion means (top: model 1, bottom: model 2)

Fig. 11

Main effect plots for porosity S/N ratios (top: model 1, bottom: model 2)

Fig. 12

Main effect plots for intrusion S/N ratios (top: model 1, bottom: model 2)

망소특성에서의 S/N비는 데이터 평균과 반비례 관계를 형성한다. 즉, 평균이 낮을수록 채널침입량이 낮다는 것을 나타내고 S/N비의 경우는 평균과는 반대로 높을수록 채널침입량이 낮다는 것을 의미한다. 하지만 망대특성의 경우 망소특성과는 반대로 데이터 평균과 S/N비는 비례관계를 형성한다.

공극률의 경우 평균의 변화에 대해서 Model 1, 2 모두 B인자(기체확산층 두께)가 가장 큰 영향을 나타내었다. 그 다음은 A인자, C인자의 차례로 영향을 주는 것을 확인하였다(Fig. 9). S/N비의 변화에 대해서 Model 1에서는 모든 인자가 민감도에 영향을 주었고 Model 2의 경우는 C인자에 대한 상대적으로 낮은 민감도를 나타내었다(Fig. 11).

채널침입량의 경우는 평균에 대해서는 Model 1에서 B, C인자가 가장 영향을 많이 주었으며 A인자는 상대적으로 유의하지 않았다. Model 2는 Model 1과 거의 유사한 반응을 나타내었다(Fig. 10). S/N비의 변화에 대해서 Model 1, 2에서 모두 B, C 인자가 높은 민감도에 영향을 주었고 A인자는 상대적으로 낮은 민감도를 나타내었다(Fig. 12).

다구찌 방법을 사용한 강건 설계는 반응값에 대한 잡음인자의 영향을 줄임으로써 안정성을 이룰 수 있는 제어인자의 최적조합을 제공하고 설계의 방향성을 제시하는 방법이다. 잡음인자인 두께방향의 탄성계수의 변동에도 불구하고 강건한 반응값(채널침입량, 공극률)의 조건은 설정한 설계인자의 조합이 최대 S/N비를 나타내게 된다. 즉, 잡음인자의 영향을 최소로 하며 반응값(채널침입량, 공극률)의 분산 변화를 최소화 시키며 최소의 채널침입량 또는 최대의 공극률을 얻고자 한다.

공극률은 Model 1에 대해서는 강건 설계의 설계인자 조합이 기준설계보다 약 2.1 %, Model 2에 대해서는 약 0.34 % 향상됨을 나타냈다(Table 6).

Table 6

Comparison of porosity

채널침입량은 Model 1에 대해서는 강건 설계의 설계인자 조합이 기준설계보다 약 19.7 %, Model 2에 대해서는 약 18.4 % 향상됨을 나타냈다(Table 7).

Table 7

Comparison of intrusion

4. 결 론

거시적 직교이방성 모델과 탄소섬유를 보 구조물로 모델링한 미시적 직교이방성 모델을 이용하여 기체확산층의 변형거동을 연구하였다. 모델검증을 통해 재료모델의 적합성을 판단하였으며, 제어 가능한 인자인 제어인자와 정확한 예측이 불가능한 잡음인자를 선정하여 구성한 직교배열표를 사용하는 다구찌 방법을 통해 기체확산층의 강건 설계 방향을 얻고자 하였다. 본 연구에서는 다음과 같은 결과를 도출할 수 있었다.

• 1) Model 1, 2의 강건 설계안은 강건 설계를 만족시키면서 기준모델에 대비하여 향상된 반응값(공극률, 채널침입량)을 나타내었다.
• 2) 공극률 반응에 대한 주요 설계인자는 Model 1과 Model 2에서 모두 기체확산층 두께가 가장 영향을 많이 주었다.
• 3) 채널침입량 반응에 대한 주요 설계인자는 Model 1과 Model 2에서 모두 기체확산층 두께와 분리판 폭이 가장 큰 영향을 주었고 필렛반경의 영향은 미미하였다.
• 4) 기체확산층의 강건한 설계를 위해서는 좀 더 정교한 재료모델의 확립이 필요하다.

Acknowledgments

이 논문은 안동대학교 기본연구지원사업에 의하여 연구되었음.

References

• C. J. Oh, and Y. T. Lee, “Measurement of In-plane Gas Permeability of Gas Diffusion Layers in Proton Exchange Membrane Fuel Cells Under Compressive Strain”, SAREK Summer Conference Proceedings, p934-937, (2016). [https://doi.org/10.6110/kjacr.2016.28.9.367]
• A. R. Jung, K. D. Baik, I. M. Kong, and M. S. Kim, “Effect of Gas Diffusion Layer Structures on Menbrane-shorting Using the Membrane Puncture Stest”, KSAE Annual Confrence Proceedings, p2686-2689, (2011).
• S. Kim, Y. Park, J. Kang, J. Park, and D. Kang, “Optimization of Processing Ship Connecting Rod using Taguchi Method”, KSMPE Spring Conference Proceedings, p113-117, (2007).
• IreTech Minitab Team, New Minitab Workbook, Iretech, Korea, (2009).
• ABAQUS Users Manual, Ver.6.4, HKS, (2003).
• Minitab Users Manual, R14, Minitab Inc., State College, PA, (2010).
• H. S. Chu, C. Yeh, and F. Chen, “Effects of Porosity Change of Gas Diffuser on Performance of Proton Exchange Membrane Fuel Cell”, Journal of Power Sources, 123(1), p1-9, (2003). [https://doi.org/10.1016/s0378-7753(02)00605-5]
• Z. Y. Su, C. T. Liu, H. P. Chang, C. H. Li, K. J. Huang, and P. C. Sui, “A Numerical Investigation of the Effects of Compression Force PEM Fuel Cell Performance”, Journal of Power Sources, 183(1), p182-192, (2008).
• S. G. Kandikar, Z. Lu, T. Y. Lin, D. Cooke, and M. Daino, “Uneven Gas Diffusion Layer Intrusion in Gas Channel Arrays of Proton Exchange Membrane Fuel Cell and Its Effects on Flow Distribution”, Journal of Power Sources, 194(1), p328-337, (2009).
• I. Taymaz, and M. Benli, “Numerical Study of Assembly Pressure Effect on the Performance of Proton Exchange Membrane Fuel Cell”, Energy, 35(5), p2134-2140, (2010). [https://doi.org/10.1016/j.energy.2010.01.032]
• Y. -H. Lai, P. A. Rapapport, C. Ji, and V. Kumar, “Channel Intrusion of Gas Diffusion Media and the Effect on Fuel Cell Performance”, J. Power Sources, 184, p120-128, (2008). [https://doi.org/10.1016/j.jpowsour.2007.12.065]
• P. A. Garcia-Salaberri, M. Vera, and R. Zaera, “Nonlinear Orthotropic Model of the Inhomogeneous Assembly Compression of PEM Fuel Cell Gas Diffusion Layer”, International Journal of Hydrogen Energy, 36(18), p11856-11870, (2011).
• P. A. Gigos, Y. Faydi, and Y. Meyer, “Mechanical Characterization and Analytical Modeling of Gas Diffusion Layers Under Cyclic Compression”, International Journal of Hydrogen Energy, 40(1), p5958-5965, (2015). [https://doi.org/10.1016/j.ijhydene.2015.02.136]
• J. E. Chung, J. K. Ahn, and J. M. Yang, “A Study of Robust Design of FCM Gasket Using Taguchi Method”, KSAE13-J0009, (2013).