자동차 램프용 고분자의 발습 거동에 관한 연구
*This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Under various temperature conditions, the moisture desorption behavior of polymer materials(ASA, ABS, PMMA, PC Optic, PC HT, PC UV) used in automotive lamps was investigated. Differences in the degree of moisture desorption were identified, following the theoretical model of Fick’s second law of diffusion. Next, the parameters of the diffusion process, including diffusion coefficients and activation energy, were determined and modeled through both experimental and numerical approaches. The diffusion coefficients of moisture in the desorption process were then measured, exhibiting a linear relationship with the inverse temperature. Consequently, the results of this study were utilized to predict a change in humidity in the automotive lamps based on the relationship between humidity and diffusion coefficients.
Keywords:
Moisture desorption, Diffusion rate, Automotive lamp, Fick’s 2nd law, Fog키워드:
발습, 확산 속도, 자동차 램프, Fick의 제 2법칙, 김서림1. 서 론
자동차 전조등은 야간 또는 전방 시야 확보가 어려운 상황에서 자동차의 진로를 비추는 가장 중요한 조명이다.1) 기존에는 단순 조명 역할을 했으나, 최근에는 차량 외관의 디자인 중요도가 높아지고, 안전 편의에 대한 요구가 증가됨에 따라 전조등의 기능이 다양해지고 있다. 최근 자동차 전조등용 램프는 할로겐, High-intensity discharge(HID), 발광 다이오드(Light emitting diode, LED) 및 레이저까지 다양한 광원을 사용하고 있으며 그에 따라 램프 내부의 형상도 복잡해지고 있다.2-6) 이로 인해 디자인 자유도가 높은 고분자를 적용한 전조등 부속품 채용이 늘어가고 있는 추세이다.2)
고분자 및 플라스틱은 일반적으로 사출성형을 통해 성형성이 우수하고 복잡한 형상 구현이 가능하다는 장점이 있다.7) 하지만 금속 재료 대비 외부환경에 매우 열악한 특성을 보이는 경우가 있어 적용에 제한이 되고 있다. 자동차의 경우 열악한 온도 및 수분의 조건하에서 장기간 사용되는 경우가 많은데, 고분자는 이러한 조건에서 일반적으로 물성저하가 일어난다고 알려져 있다. 또한, 대부분의 고분자는 수분을 흡수 또는 발습하는 성질을 가지고 있다.8)
전조등의 경우, 밀폐된 공간에서 램프의 점등 및 소등으로 인해 내부 온도가 상승 및 하락하게 되고 이로 인해 플라스틱 부속품 내 함유된 수분을 방출 및 흡습하게 되어 램프 내부의 습도 변화가 일어나게 된다. 이 때 일반적으로 수분의 흡수보다 수분의 발습 과정에서 얻어진 확산계수가 더 큰 값을 보인다.9) 이로 인해 단위 부품에서 방출된 수분이 다시 단위 부품으로 흡습되지 못하고 일부분 표면에 응결되어 김서림 현상이 발생되는 것으로 판단된다. 이렇게 발생된 렌즈 내부 표면의 습기가 전조등 성능 저하 및 미관을 저해하게 된다.2-5)
고분자 소재에 흡수된 물은 고분자 고유의 자유 부피 그리고 수분의 흡착/탈착 과정에서 비가역적으로 생성되는 미세기공 등에 침투하면서 다양한 변화를 야기시킨다. 이 때 온도 변화로 인한 수분의 흡습에 의해 가역적인 변화 또는 비가역적인 변화가 관찰되기도 하며, 소재의 물성 변화를 가져온다.9) 하지만 이러한 온도, 수분에 대한 재료의 영향에 관한 신뢰성 연구는 미약한 실정이고 따라서 고분자 소재인 전조등 구성 부품에서 흡습 및 발습 물성들의 측정과 이해는 수분으로 유발된 고장의 신뢰성 모델링에 필수적이다.
고분자 소재의 수분 흡습 거동에 대한 연구는 다양하게 진행되었다.10-15) Fick의 제 1법칙 및 질량 보존 법칙으로부터 확산 지배 방정식인 Fick의 제 2 법칙을 얻을 수 있으며, 확산 계수 D(식 (1))를 시간의 함수에 따른 샘플 내 물의 누적으로 설명한다.14)
| (1) |
where C : diffusion concentration (kg m-3),
D : diffusion coefficient or diffusivity (m2 s-1),
x : main diffusion direction along sample thickness
이전의 선진 연구를 살펴보면, 확산 지배 방정식에 의해 흡습 거동을 보이고 있으나, 발습 거동에 대한 연구는 미진한 상태로 이에 대한 연구가 필요하다.
본 연구에서는 전조등을 구성하는 부속품용 고분자인 아크릴로나이트릴-스타이렌-아크릴레이트(ASA), 아크릴로나이트릴-부타다이엔-스타이렌(ABS), 폴리메틸메타크릴레이트(PMMA), 광학용 폴리카보네이트(PC Optic), 고내열 폴리카보네이트 공중합체(PC HT), 내UV성 폴리카보네이트(PC UV)의 발습 거동을 분석하였다. 또한 전조등 램프 점등시 각 부속품들은 광원과의 거리 차로 인해 온도 분포에 차이가 발생하기 때문에 온도 조건에 따른 발습 거동을 분석하였다.
2. 실험 내용
2.1 재료
자동차 램프를 구성하는 하우징, 렌즈에 적용되는 고분자를 선택하였으며, 현대모비스를 통해 각 소재사에서 제공되는 소재를 활용하였다. 소재 정보는 Table 1과 같다.
2.2 발습 특성
발습율 측정은 ISO 62 또는 ASTM D570의 시험방법을 참조하였다. 각 소재를 150 × 150 mm로 사출한 후 80 × 50 mm의 사각형 형태로 절단하여 사용하였으며, 이때 시편의 두께는 3 mm이다. 준비된 시편은 발습 실험 전에 80 °C의 오븐에서 약 24시간 건조를 진행하였다. 그리고 수분 흡수 실험은 23 °C, 50 %RH 조건하에서 48시간 방치하였다. 그 후 흡습 중량(WW)을 측정한 후, 적외선 수분 측정기(FD-720, KETT사, Japan)를 통해 40, 55, 70, 85, 100 °C 건조 조건에서 무게 변화(Wd)를 측정하였다. 건조 중량 및 흡수 중량을 이용하여 발습율(Ds)을 식 (2)와 같이 계산하였다.10-15)
| (2) |
where WW : initial weight at the saturation (g),
Wd : weight of sample after t seconds heating (g)
2.3 분석
각 소재의 열적 특성은 DSC(differential scanning calorimetry, PerkinElmer)를 통해 승온 속도 10 °C/분, 질소 분위기하에서 분석하였다.
3. 결과 및 토의
3.1 고분자 소재 분석
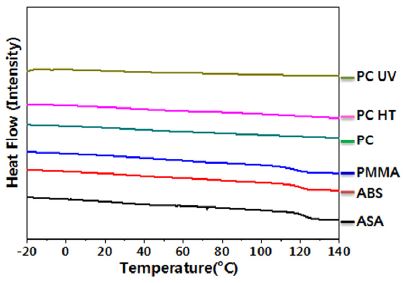
Fig. 1은 자동차 전조등 구성부품에 사용되는 고분자 소재의 DSC 측정 그래프이다. Fig. 1에서 보는 바와 같이 -20 ~ 140 °C 범위 내에서 PC 계열의 고분자를 제외한 3종의 소재에서 유리전이온도가 관찰되었다. 일반적으로 고분자 소재는 유리전이온도 전후로 흡습 및 발습 물성에 다소 급격한 변화를 겪는 것으로 알려져 있다.12) 따라서, 본 연구에서는 발습 온도 분위기를 각 부속품들의 평균 사용온도(100 °C 이하 수준)와 상변화가 발생하지 않는 온도 구간에서 세분화하여 진행하였다.
3.2 확산속도와 발습 특성
전조등용 고분자 소재의 수분 발습에 미치는 온도의 영향을 알아보고자 40, 55, 70, 85, 100 °C의 온도 환경에서 시간에 따른 무게 변화를 측정하였다. 고분자 소재의 수분 흡습 및 발습 속도는 확산계수를 측정하여 정량화할 수 있다.
확산 계수의 계산은 일반적으로 적용된 방법에 지나치게 의존한다. 이에 샘플의 초기 농도가 0이며 주위 분위기가 균일한 농도이고 최종적으로 일정한 농도로 유지되는 것을 고려하면 흡수된 물의 양을 다음 식 (3)과 같이 계산 가능하다.15)
| (3) |
where Mt : water content at time t (%),
MMax : equilibrium water content (%),
l : thickness of the sample (m)
이와 함께, 대부분의 문헌에서는 Mt와 시간과의 그래프를 통해 확산 계수를 구하고 있으며, 흡습 초기 단계에서는 무게 변화와 시간의 제곱근간에 선형적 관계를 보인다.10-14)
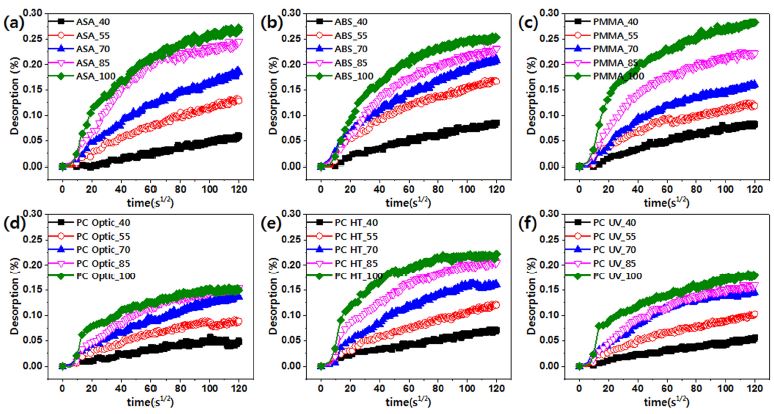
본 연구에서는 흡습과 발습과정이 에너지 활성화 메커니즘의 측면에서 볼 때 동일한 과정임을9) 바탕으로 앞서 설명한 식의 시간에 따른 중량 증가율(Mt)을 시간에 따른 발습율((Ds)t)로 변경 적용하여, 발습 거동도 확산 지배 방정식을 적용하였다. 이에 따라, Fig. 2는 시간의 제곱근에 따른 (Ds)t를 계산하여 도식화한 것이다. 앞서 설명한 바와 같이 초기 발습율과 시간의 제곱근간에 선형적 비례 관계를 갖는 것을 확인하기 위하여 초기 1시간 동안의 발습율과 시간의 제곱근간의 1차 방정식 선형 근사를 통해 도출된 기울기와 결정계수(Adj. R2)를 Table 2에 나타내었다. 결정계수가 1에 가까울수록 우수한 모델근사라 볼 수 있다. Table 2에서 보는 바와 같이 결정계수가 매우 높아 수분 발습의 초기 거동은 시간의 제곱근에 선형적으로 비례함을 알 수 있었다.

Linear slope and adjusted R2 obtained for each condition by the analytical solution of the linear fitting(Y = aX, Y: Desoprtion, X : t1/2) for moisture desorption
식 (3)의 확산 지배 방정식을 활용하여, 실험 결과를 근사한 결과 및 도식화한 것이 Fig. 3부터 Fig. 8이다. Fig. 3부터 Fig. 8의 (a)~(e)에서 보는 바와 같이 온도가 증가함에 따라 발습이 급격하게 이루어지고 있으며, 총 발습량이 증가하는 것을 확인할 수 있다. 흡습에 대한 기존 연구를 살펴보면, 흡수량은 온도에 대하여 비교적 증가하는 경향을 보인다고 알려져 있다.9) 본 연구의 발습 거동 역시 흡습 거동과 동일하게 온도 증가에 따라 발습량이 증가하고 있으며, 확산 지배 방정식인 식 (3)의 근사 결과(Fitting line)와 매우 유사한 경향을 보이고 있어, 발습 거동 역시 흡습 거동과 동일하게 확산 지배 방정식을 따른다는 것을 확인할 수 있었다. 식 (3)으로 근사한 결과를 통해 얻어진 확산 계수를 Fig. 3(f) ~ Fig. 8(f)에 나타내었다. 다양한 온도에서 수분을 발습시킬 때 얻어지는 수분 확산계수는 아레니우스 관계식에 따라 확산계수는 온도의 역수에 비례한다는 것을 확인할 수 있다.
복합소재 내부로의 수분의 확산속도는 기본적으로 에너지 활성화 과정으로 해석하며 따라서 온도에 따른 수분확산 계수는 아레니우스 관계식(식 (4))으로 표현되고 있다.9,10)
| (4) |
where D0 : diffusion constant (m2 s-1),
Ed : activation energy of desorption (J mol-1),
R : ideal gas constant (8.314 J mol-1 K-1),
T : temperature (K)
Fig. 3(f) ~ Fig. 8(f)의 그래프 기울기로부터 각 소재별 활성화 에너지를 구할 수 있다. 이때 활성화 에너지는 흡수된 수분이 일종의 다른 동공(Hole)으로 이동하는데 필요한 에너지를 해석될 수 있다. 측정된 활성화 에너지는 온도 및 습도에 상관없이 일정하였다. 이러한 사실은 일반적으로 문헌9-12)에 알려져 있고 본 논문에서 수행된 실험에서도 동일한 결과를 보였다.
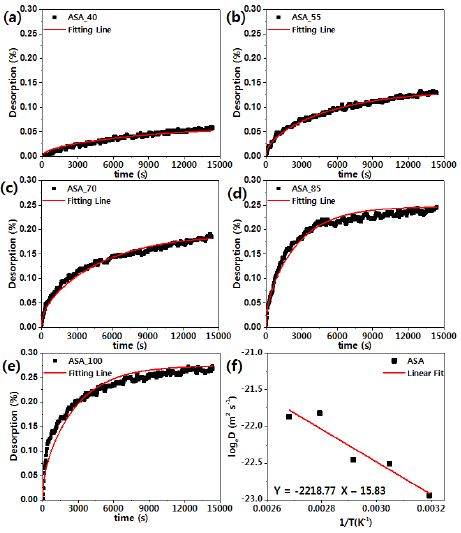
Moisture desorption((Ds)t) of ASA at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
Fig. 3(f) ~ Fig. 8(f)으로부터 구해진 활성화 에너지 및 확산 상수를 Table 3에 정리하였다. Table 2에서 보는 바와 같이 ASA와 ABS의 경우 분자 단위에 동일한 구조가 포함되어 있는데 활성화 에너지 및 확산 상수가 차이를 보이고 있다. 이는 각 단량체간의 조성 차이, 분자량 차이, 그리고 복합소재의 첨가제 종류 및 함량 차이로 인해 서로 다른 특성을 보이고 있는 것으로 판단된다. 따라서 본 연구에서 도출된 확산 계수, 활성화 에너지 등을 각 소재에 일반화하여 적용하면 오차가 발생할 수 있다. 이와 마찬가지로 PC Optic과 PC HT, PC UV의 경우 서로 같은 관능기를 보유하고 있으나, 사슬을 이루는 구조가 다르기 때문에 확산 상수에서 큰 차이를 보이고 있다.
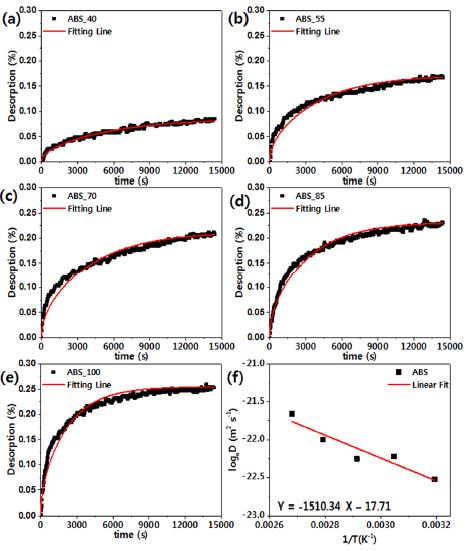
Moisture desorption((Ds)t) of ABS at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
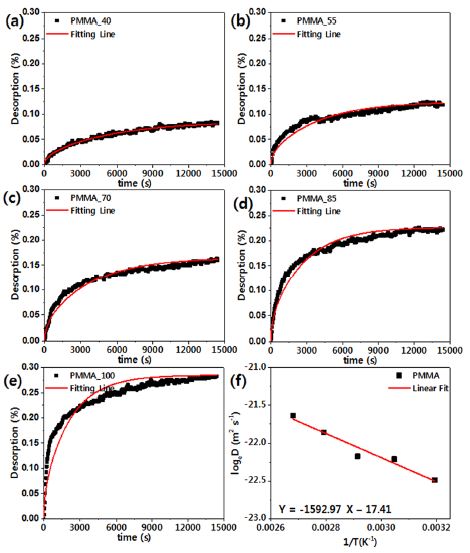
Moisture desorption((Ds)t) of PMMA at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
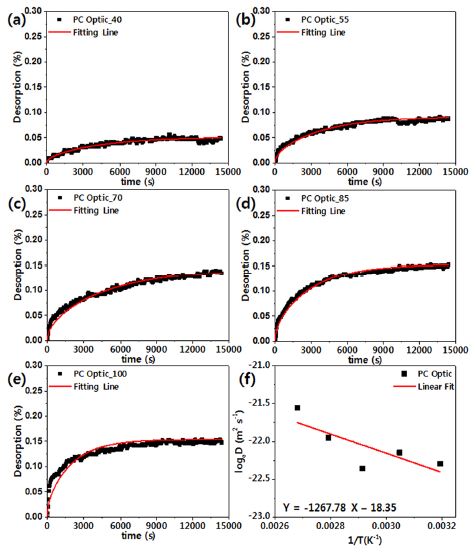
Moisture desorption((Ds)t) of PC Optic at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
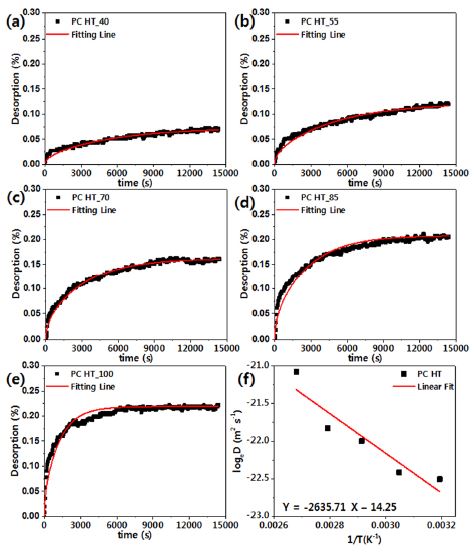
Moisture desorption((Ds)t) of PC HT at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
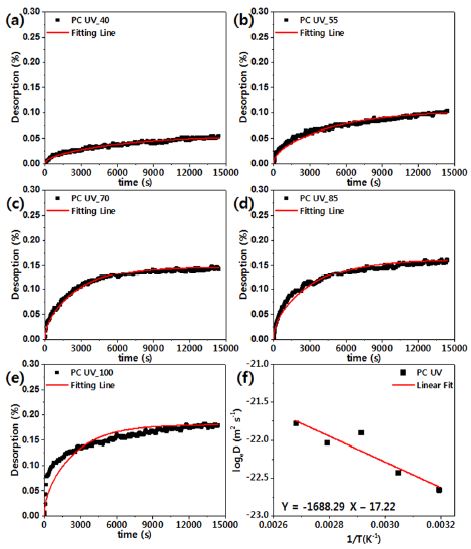
Moisture desorption((Ds)t) of PC UV at various temperatures plotted as a function of t(a~e) and diffusion coefficients(f) in desorption processes complying with Arrhenius equation
앞서 설명한 바와 같이 전조등과 같이 밀폐된 부품에 적용되는 고분자 소재의 흡습 및 발습은 김서림 등 다양한 문제를 야기한다. 고분자 소재로 사출을 통해 단위 부품 성형 후에 평균 2일간 동안 냉각 방치, 부품 적재, 물류 이동, 조립 전 대기, 조립 공정을 거치며 공기 중의 수분을 흡수하게 된다. 부품 조립시 충분한 건조를 진행하면 문제가 없으나, 수분을 전량 제거하는 것은 쉽지 않으며 시간 및 비용 증가로 이어져 실제 작업 라인에서 적용하기는 어려운 문제점이 있다. 따라서 적용 소재의 흡습 및 발습 특성을 충분히 이해하고 부품 설계에 반영함으로써 문제를 해결하고자 하는 연구가 진행되고 있다.
확산 지배 방적식의 초기 단계에서, 샘플의 서로 다른 측면에 대한 확산 전개는 서로 중첩되지 않고 독립적으로 전개되며, 이 구간에서는 식 (3)을 다음과 같이 단순화시킬 수 있다.14)
| (5) |
where At : total area of the sample (m2),
V : volume of the sample (m3)
상기 식 (5)를 활용하면 단위 부품의 총 면적과 부피를 통해 시간에 따른 발습량을 도출할 수 있다. 또한 기존 연구 결과에 따르면 전조등의 경우 습도는 소재의 확산계수 및 열전도도, 부품의 부피 및 두께, 그리고 시간에 따라 변화하는 것으로 알려져 있다.2,3) 이 관계를 통해 시간과 온도의 변화에 따라 단위 부품에서 방출된 수분의 양, 즉 발수량을 근사화할 수 있다.
이와 같이 본 연구 결과는 온도 조건에 따른 발습 거동을 분석하여 향후 전조등 내부의 습기 발생을 예측하는 기초 데이터로 활용하고자 한다.
4. 결 론
본 연구에서는 자동차 전조등을 구성하는 단위 부품에 사용되는 고분자 소재의 온도 조건에 따른 발습 특성을 연구하였다. 또한, 흡습거동과 마찬가지로 발습 거동 역시 확산지배 방정식에 일치하는지를 살펴보았다. 전조등 조립시 단위 부품의 상태 분위기를 고려하여 흡습을 진행하였으며, 흡습된 소재의 분위기 온도에 따른 발습 특성을 진행한 결과, Fickian 모델의 거동과 일치하는 결과를 보였다. 이를 통해 발습 거동 역시 흡습 거동과 마찬가지로 확산 지배 방정식에 따라 거동하는 것을 확인하였다. 또한, 확산 지배 방정식 및 아레니우스 관계식을 이용하여 각 소재의 확산 계수, 활성화 에너지, 확산상수를 도출할 수 있었다. 이는 단위 부품의 면적 및 부피, 부품 온도를 알면 시간에 따른 발습량을 예측하는데 활용할 수 있다.
Nomenclature
| Ds : | diffusion rate, % |
| WW : | initial weight at the saturation, g |
| Wd : | weight of sample after t seconds heating, g |
| D : | diffusion coefficient, m2 s-1 |
| Mt : | water content at time t, % |
| MMax : | equilibrium water content, % |
| l : | thickness of the sample, m |
| At : | total area of the sample, m2 |
| V : | volume of the sample, m3 |
| D0 : | diffusion constant, m2 s-1 |
| Ed : | activation energy of desorption, J mol-1 |
| R : | ideal gas constant, 8.314 J mol-1 K-1 |
Subscripts
| ASA : | acrylonitrile styrene acrylate copolymer |
| ABS : | acrylonitrile butadiene styrene copolymer |
| PMMA : | poly(methyl methacrylate) |
| PC : | polycarbonate |
| PC HT : | high temperature polycarbonate copolymer |
| PC UV : | ultraviolet resistance polycarbonate |
Acknowledgments
본 연구는 산업부에서 지원하는 2014년도 소재부품기술개발사업 내 전략적핵심소재기술개발 사업(과제번호: 10050481)의 연구 수행으로 인한 결과물임을 밝힙니다.
References
- Dictionary Automotive Engineering, The Korean Society of Automotive Engineers, Seoul, (2005).
- C. W. Lee, B. K. Choi, O. Kim, and Y. W. Kim, “Analysis of the Effect of Vapor Release on Fog Generation for Automotive Headlamp”, KSAE Spring Conference Proceedings, p1002-1006, (2014).
-
E. Drapala, “Experimental Study on Water Condensation in Automotive Headlamp”, SAE 2010-01-1326, (2010).
[https://doi.org/10.4271/2010-01-1326]

-
R. Singh, R. Kuzhikkali, N. Shet, S. Natarajan, G. Kizhedath, and M. Arumugam, “Automotive LED Headlamp Defogging: Experimental and Numerical Investigation”, SAE 2016-01-0216, (2016).
[https://doi.org/10.4271/2016-01-0216]

-
J. W. Bielecki, M. Chang, and T. Poorman, “Effect of Moisture Absorption in Plastic on Automotive Lamp Venting”, SAE 2004-01-0663, (2004).
[https://doi.org/10.4271/2004-01-0663]

- M. Stamm, and B. Carlowitz, “Plastics, Properties and Testing,”, Ullmann’s Polymers and Plastics, B. Elvers Editors, Wiley-VCH, Germany, (2016).
-
P. -C. Lee, J. U. Ha, B. -R. Kim, Y. K. Ko, H. U. Lee, S. K. Jeoung, Y. -S. Hwang, J. U. Jung, and Y. Y. Kim, “Study on Efficient Homogeneous Illumination of Automotive Cup Holder”, Transactions of KSAE, 26(1), p113-119, (2018).
[https://doi.org/10.7467/ksae.2018.26.1.113]

-
J. A. Youn, J. H. An, M. D. Yin, J. H. Cho, and D. J. Park, “Safe Adaptive Headlight Controller with Symmetric Angle Sensor Compensator Using Steering-weivel Angle Lookup Table”, Transactions of KSAE, 24(1), p112-121, (2016).
[https://doi.org/10.7467/ksae.2016.24.1.112]

- D. -W. Suh, M. -K. Ku, J. -D. Nam, H. S. Choi, K. -M. Chung, and K. J. Ahn, “Hygrothermal Cycling Studies of Epoxy/Carbon Fiber Composite Laminate”, Polymer, 21(6), p1029-1038, (1997).
-
S. -C. Park, H. -G. Kim, and K. -E. Min, “Effect of MMT on Anti-Water Absorption of Polyamide /MMT Nanocomposites”, Polymer, 37(1), p113-120, (2013).
[https://doi.org/10.7317/pk.2013.37.1.113]

- P. Polyák, D. Szemerszki, H. C. Benke, and B. Pukánszky, “A Novel Method for the Determination of Diffusion Coefficients in Amorphous Poly(3-hydroxybutyrate)”, Polymer Testing, 63, p342-348, (2017).
-
H. Mrad, S. Alix, S. Migneault, A. Koubaa, and P. Perré, “Numerical and Experimental Assessment of Water Absorption of Wood-polymer Composites”, Measurement, 115, p197-203, (2018).
[https://doi.org/10.1016/j.measurement.2017.10.011]

-
A. Launay, F. Thominette, and J. Verdu, “Water Sorption in Amorphous Poly(ethylene terephthalate)”, Journal of Applied Polymer Science, 73(7), p1131-1137, (1999).
[https://doi.org/10.1002/(sici)1097-4628(19990815)73:7<1131::aid-app4>3.0.co;2-u]

-
D. P. N. Vlasveld, J. Groenewold, H. E. N. Bersee, and S. J. Picken, “Moisture Absorption in Polyamide-6 Silicate Nanocomposites and Its Influence on the Mechanical Properties”, Polymer, 46, p12567-12576, (2005).
[https://doi.org/10.1016/j.polymer.2005.10.096]

- S. Joannes, L. Maze, and A. R. Bunsell, “A Simple Method for Modeling the Concentration-dependent Water Sorption in Reinforced Polymeric Materials”, Composites: Part B, 57, p219-227, (2014).