운전자 친화 적응형 순항제어 알고리즘에 관한 연구
*This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Adaptive cruise control is one of the popular features of the advanced driver assistance system(ADAS). It is an extended form of conventional cruise control, and it has been considered as a contributing factor in driving safety and string stability. Recently, human behavior in the automotive industry has become more significant. This paper proposed driver-friendly adaptive cruise control(DF-ACC), and it demonstrated the deduction method control parameter of a current driver. For the design of the DF-ACC algorithm, actual driver behavior data with a driving simulator based on the HIL system were collected and analyzed. Then, driving data were separated in a stable and transient zone. The driver’s desired distance and acceleration as control parameters could be estimated from the driving data in each zone. Lastly, this paper compared real driver driving and DF-ACC simulation data.
Keywords:
Adaptive cruise control, Driver behavior, ADAS, Human driver model, Driver’s parameter estimation키워드:
적응형 순항 제어, 운전자 행태, 첨단 운전자 지원 시스템, 운전자 모델, 운전자 매개변수 추정1. 서 론
최근 자동차 산업은 자율주행자동차를 목표로 단계적인 기술개발이 진행되고 있으며, 현재는 다양한 첨단 운전자 지원 시스템(ADAS)이 차량에 적용되고 있다. 차량의 종 방향 운전자 지원 시스템인 적응형 순항제어시스템(ACC, Adaptive Cruise Control)은 기존의 순항제어시스템(CC, Cruise Control)의 진보된 형태이다. 일반적으로 레이더나 전방차량과의 거리를 측정하여 운전자의 설정 속도와 전방 차량과의 안전거리에 대해 선택적으로 제어한다.1) 이와 관련하여, 선행 연구에서는 전방차량과의 추돌을 방지하기 위한 제어기법, 다수 차량이 존재하는 도로환경에서 String stability를 만족하기 위한 연구와 더불어 연비를 향상시키기 위한 연구들이 진행되어 왔다.2-5)
최근에는 기존연구를 확장하여 시스템의 제어 성능뿐 아니라 운전자의 특성을 제어시스템에 능동 적용하여 운전자 수용성 향상을 돕는 연구들이 수행되고 있다. 문일기와 이경수6)는 개발자에 의해 정해진 상대 거리나 속도를 제어하는 정적이고 고정된 방법을 보완하고자 운전자의 주행 패턴을 분석하여 목표 차간거리(Time-gap)를 도출하였다. Rosenfeld 등7)은 앞선 연구와 유사하게 기존 시스템의 불연속적이고 제한된 파라미터 설정의 문제를 지적하고 실제 운전자의 특성에 최적화된 차간거리 형태와 상대속도를 기계학습(Machine learning) 방법을 이용하여 제안하였다.
다만, 문일기와 이경수의 연구는 오직 차간 거리만 고려하였으며, Rosenfeld는 기존의 운전자 주행정보를 기반으로 운전자 특성을 그룹화하여 새로운 운전자를 성향이 유사한 그룹의 파라미터를 사용하는 간접적인 방법을 택하였다.
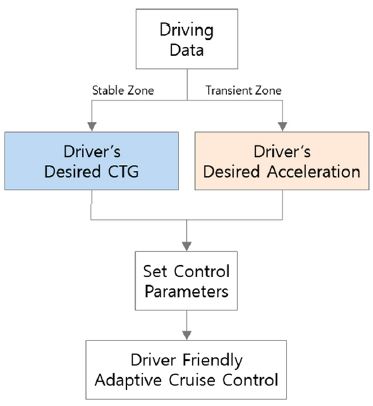
본 연구에서는 운전자의 실시간 주행 데이터를 기반으로 운전자와 유사한 주행 형태로 주행하여 이질감을 개선시킬 수 있는 운전자 친화 적응형 순항제어(DF-ACC) 시스템을 제안한다.
다음 장에서는 드라이빙 시뮬레이터를 통해 취득한 환경을 설명하고, 3장에서 운전자의 주행 특성을 분석하고 개별 운전자의 가・감속 특성을 도출한다. 4장에서는 운전자의 특성을 반영할 수 있는 적응형 순항제어기를 설계한다. 제어기 검증은 도출된 운전자의 특성을 반영하여 시뮬레이션을 진행하고 이를 기존 제어시스템과 실제 운전자의 주행 데이터와 비교한다.
2. 운전자 주행 데이터 취득
2.1 드라이빙 시뮬레이터
dSPACE HILS 기반 드라이빙 시뮬레이터를 이용하여 운전자 DB를 확보하였다. 드라이빙 시뮬레이터는 dSPACE의 ASM Traffic으로 도로환경과 자차량, 주변의 방해차량을 구현하였다. 시나리오는 Model Desk를 통해 모델링 하였다. 실시간 시뮬레이션은 dSPACE Midsize HILS에서 동작하며, 자차량의 제어는 Logitech社의 G27 운전자 조작 장치를 이용하였다. 운전자 조작 장치는 조향 제어를 위한 운전대와, 가・감속 제어를 위한 가속 페달과 브레이크 페달로 구성된다. 차량의 주행 정보와 운전자의 조작 신호는 ControlDesk를 통해 기록한다.
운전자의 현실감을 높이기 위하여 운전자는 MotionDesk를 통한 주행 상황과 ControlDesk를 통해 제공되는 차량의 클러스터를 각 모니터로 시각적 인지가 가능하며, ControlDesk에서 차량의 엔진과 주행 음향을 추가하여 청각적 인지를 동시에 경험하도록 하였다.
차량 동역학 모델은 신뢰도를 위해 dSPACE에서 제공하는 MidSizeCar를 사용하였으며, 이는 24 자유도를 지니고 있다. 본 논문에서는 종방향 제어를 대상으로 하므로 도로는 2차선의 아스팔트 직선 도로를 구성하였으며, 도로 노면의 마찰계수(μ)는 0.9이고 경사로는 존재하지 않는다. 해당 도로에는 전방 1대의 선두차량이 존재한다.
3. 운전자 주행 분석
3.1 운전자 주행 모델
과거 운전자 모델에 대한 연구가 활발히 진행되어 왔으며,8-13) 특히 깁스의 차량 추종 모델은 다수의 연구를 통해 그 합리성을 인정받았다.14,15) 깁스의 운전자 모델은 운전자의 최대 요구 속도와 가속도를 제어 파라미터로 사용하여, 현재속도에서 운전자 지연시간 뒤의 속도를 제시한다. 또한, 선두차량과의 추돌을 방지하는 거리 추종을 위해 선두차량과의 거리와 자차량의 속도 등으로 다음 지연시간 뒤의 감소된 속도를 제시한다.
| (1) |
깁스가 제안한 운전자 모델의 지연시간(τ) 뒤의 속도는 다음과 같다.
| (2) |
| (3) |
위의 식에서 υn(t)와 υn-1(t)는 추종차량과 선두 차량의 t에서의 속도(m/s)이며, anmax는 추종차량이 갖는 최대 가속도(m/s2)이다. τ는 반응 시간(s), Vnmax는 추종차량이 갖는 최대 속도(m/s)이며 선두차량이 존재하지 않을 경우의 설정 속도로 볼 수 있다. bn은 차량 n의 운전자가 행하는 대부분의 극심한 감속값(m/s2)이고, θ는 τ/2로 정의하여 추가적인 편안함을 제공하기 위해 감속하지 않는 시간(s)을 나타낸다. xn(t), xn-1(t)는 시간 t에서 추종차량과 선두차량의 앞 범퍼 위치이다. Sn-1는 Ln-1 + ssafe이며 선두차량의 길이(Ln-1)에서 안전을 위한 최소거리(ssafe)의 합이다. 마지막으로 는 추종차량의 예측하는 전방차량의 최대 감속도(m/s2)이다.
정리하면 깁스의 운전자 모델은 전방 차량에 대한 추종 거리(xn(t), xn-1(t), Sn-1) 항을 포함하고 다음 지연시간의 속도를 가속(υa,n)과 감속(υb,n)으로 분리하였다. 여기에서 지연시간(τ, θ)은 운전자의 반응 속도로 볼 수 있다.
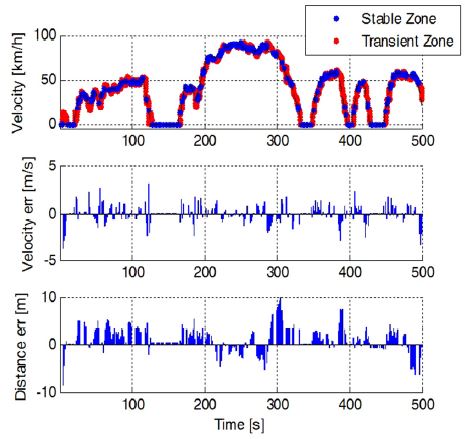
본 연구에서는 깁스모델의 구성을 기반으로 전방 차량과의 추종거리, 운전자의 가・감속 특성을 TTC(Time To Collision)를 이용하여 Fig. 2와 3과 같이 분리 및 분석하였다. 먼저 추종거리는 |TTC-1|< ɛ 인 구간을 정상상태 영역으로 판단하여 운전자의 CTG(Constant Time Gap) 의도를 구하였다.6) 이어서 |TTC-1|> ɛ 인 구간을 과도상태 영역으로 정의하고, 거리와 속도 오차에 대한 운전자의 가속과 감속 특성을 나누어 분석하였다. 여기에서 ɛ는 0.02가 사용되었다.
| (4) |
식 (4)에서 dr는 선두차량과의 상대거리(m)이며 υ와 υp는 자차량과 선두차량의 속도(m/s)이다.
3.2 정상상태 영역
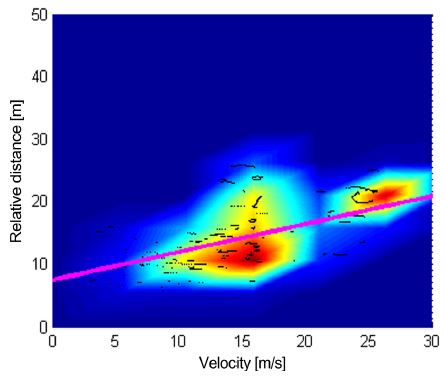
운전자가 의도하는 선두차량과의 요구거리(ddes)는 선행연구에서 제시한 운전자 운전특성파라미터를 고려한 지능화차량의 차간거리 적응제어를 활용한다. 정상상태 영역에서 차량의 속도와 선두차량과의 상대거리를 다항식 회기분석을 이용하여 CTG를 구할 수 있다.6)
| (5) |
2장에서 취득한 운전자의 정상상태 주행데이터를 통해 CTG(h)와 최소 안전거리 (ssafe)를 Fig. 4와 같이 구할 수 있다.
3.3 과도상태 영역
TTC-1 > ɛ 인 구간인 과도상태 영역에서는 전방차량 추종에 대한 속도와 거리오차가 발생하며, 이를 감소시키기 위한 운전자의 요구 가・감속도를 도출할 수 있다. 깁스모델에서는 운전자의 요구 속도에 대한 가속과 선두차량과의 거리에 의한 감속으로 분리하였다. 본 연구에서는 선두차량을 추종할 때 운전자가 가속과 감속을 해야만 하는 상황을 나누어 분리 및 분석하였다.
| (6) |
| (7) |
| (8) |
운전자의 요구 가속도(ades)는 거리와 속도오차에 의해 결정된다. 식 (8)에서 K1과 K2는 각 오차에 대한 제어상수와 가중치를 통해 도출할 수 있다.
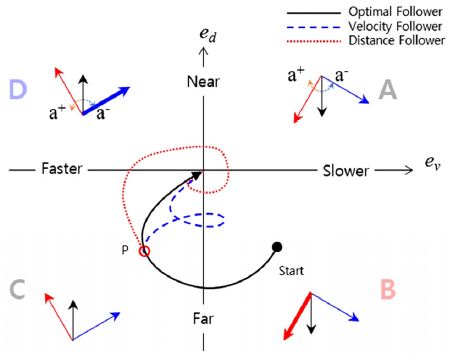
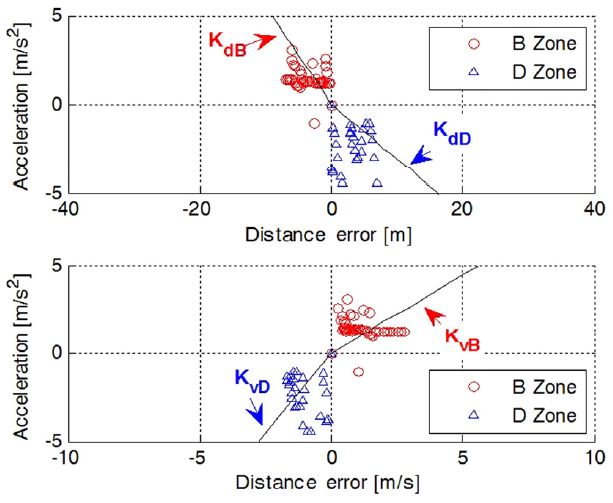
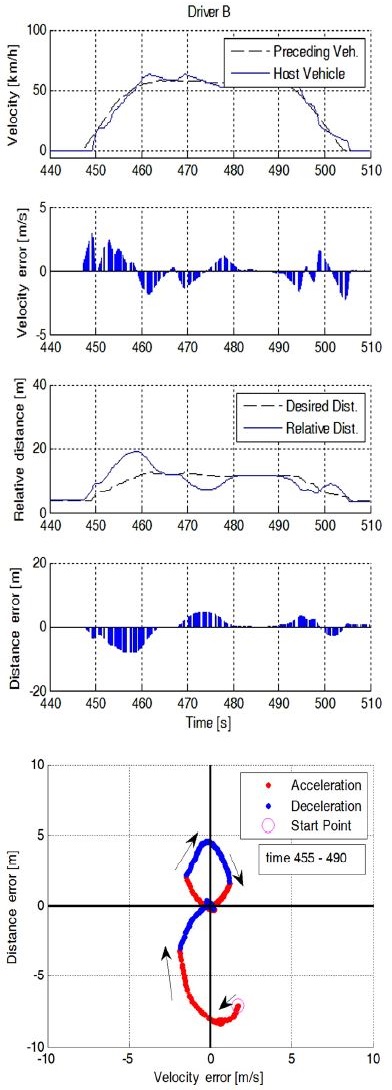
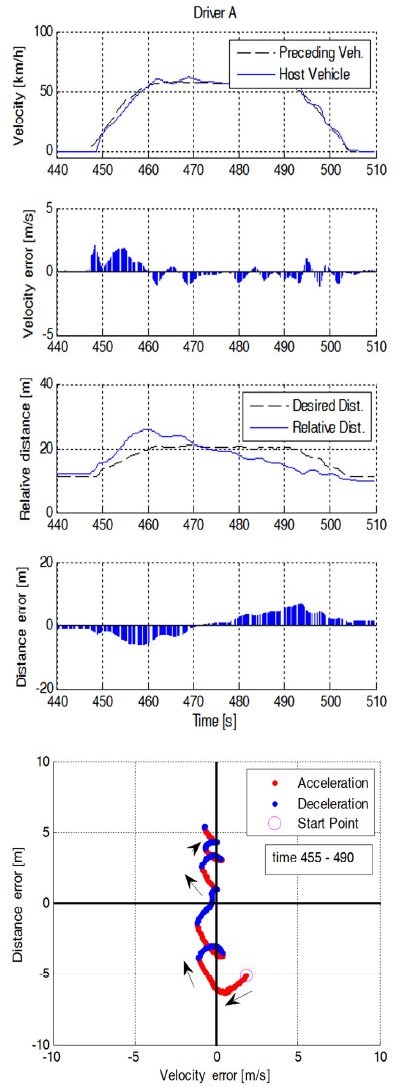
Fig. 5는 식 (6)과 (7)에서 정의한 오차를 각 축으로 거리오차와 속도오차가 모두 0인 정상상태로 수렴하는 제어 전략을 타나내고 있다. A, B, C, D영역은 두 가지 오차의 부호에 따라 나뉘며 각 영역에서의 가・감속에 따른 오차 이동 방향을 표시하였다. 이상적인 운전자(Optimal follower)는 두 오차를 최소의 가・감속 변화로 제거한다. Fig. 5에서 나타낸 것과 같이 오차의 궤적이 0으로 수렴할 수 있는 영역은 A와 C 영역이다. 이상적인 운전자는 해당 영역에 도달하게 되면 적절한 차량의 가속도를 통해 두 오차를 동시에 감소시켜 제거할 수 있다. 하지만 특정 오차에 대해 민감한 운전자의 경우 해당 오차를 우선 제거하는 방향으로 가속도를 제어하게 된다.
운전자의 오차에 대한 요구 가속도는 제어 상수와 가중치로 나누어 생각할 수 있다. 먼저, 각 오차에 대한 제어상수는 영역 B와 D에서 구할 수 있다. 두 영역에서는 오차를 0으로 수렴시키기 위하여 특정 가・감속을 수행하여야만 한다. B영역에서는 차량 간 거리가 요구 거리보다 크며, 전방차량보다 낮은 속도로 주행하는 상태이다. 따라서 정상상태 도달을 위해서는 가속하여 C영역에 진입 후 서서히 감속함으로 정상상태에 도달할 수 있다. D영역은 B영역과 반대되는 상태로 운전자는 차량을 감속하는 방향으로 제어하여 A영역 통과 후 정상상태에 도달한다. 즉, B영역에서는 가속을, D영역에서 감속을 수행하게 된다. 각 오차에 대한 제어상수는 Fig. 5의 B, D영역에서 거리와 속도 오차로 분리된 데이터를 다항식 회기분석을 통해 계산한다.
오차에 대한 가중치는 A와 C영역에서 오차 궤적을 이용하여 판단할 수 있다. Fig. 5를 보면, B영역에서 시작되는 오차 궤적은 C영역으로 진입하게 된다. 이때 속도 오차에 민감한 운전자(Velocity follower)는 거리오차보다 속도 오차를 감소시키기 위해 P지점에서 감속하게 되고, B영역으로 재진입하게 된다. 반대로 거리 오차에 민감한 운전자(Distance follower)는 P지점에서 거리오차를 줄이기 위해 가속하여 D영역으로 진입한다. 즉, A와 C영역에서 오차의 궤적이 eυ = 0인 y축을 지나게 되면 속도 오차에 민감한 운전자로, ed = 0인 x축을 지나게 되면 거리 오차에 민감한 운전자로 판단할 수 있다. 본 논문에서는 각 축을 지나는 궤적의 누적 값으로 운전자의 의도 가중치(W)를 설정하였다.
4. 운전자 친화 적응형 순항 제어 알고리즘
4.1 제어기 설계
적응형 순항제어시스템은 상위제어기와 하위제어기로 구분되어 차량에 적용된다. 상위제어기에서는 운전자의 설정 속도와 레이더 등의 환경센서를 통해 취득한 주변 차량의 주행 정보를 입력으로 자차량의 요구 가속도를 출력한다. 상위제어기의 가속도 명령은 하위제어기에서 차량의 동력계를 제어하여 요구 가속도를 추종하도록 한다.1) 본 논문에서는 상위제어기를 대상으로 하며, 운전자의 주행 특성에 따른 요구 가속도 (ades)를 제안한다.
운전자 친화 적응형 제어기를 설계하고, 제어 파라미터는 3장의 내용으로 적용한다. 운전자는 선두차량과의 상대속도와 요구 상대거리에 대한 오차에 따른 요구 가속도를 운전자의 주행 데이터를 기반으로 도출하고, 각 요소에 대한 가중치를 계산하였다. 계산된 파라미터를 식 (9)의 제어기에 적용함으로써 운전자의 주행을 모사하게 된다.
| (9) |
계산한 요구 가속도는 3.2절의 방법을 이용한다. KdB, KdD, KυB, KυD는 거리와 속도 오차에 대하여 B와 D영역에서 구한 비례제어 상수이다. Wd는 A와 C영역에서 구한 각 거리오차에 대한 가중치이다.
4.2 시뮬레이션 환경
서로 다른 운전자 3명의 드라이빙 시뮬레이터 주행 정보에 대하여, 3장에서 보인 운전자 분석을 수행하였다. 각 운전자 주행의 정상상태 영역에서 구한 CTG(h), 최소 안전거리(ssafe)와 과도상태 영역에서 구한 가속도 제어상수(K), 가중치(W)를 식 (9)의 운전자 친화 적응형 순항제어기에 대입하였다. 시뮬레이션은 운전자가 주행한 환경과 동일하게 dSPACE ASM Traffic 모델을 기반으로 전방 FTP-72로 주행하는 선두차량을 추종하도록 하였다.
4.3 시뮬레이션 결과
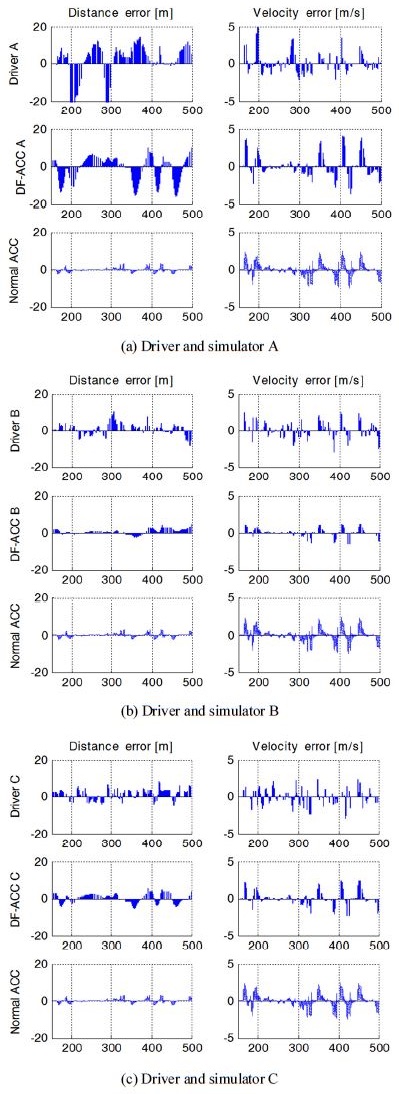
운전자의 주행과 해당 파라미터를 적용한 운전자 친화 적응형 순항제어기의 주행 결과를 비교하였다. Table 2와 Table 3은 운전자 주행 분석으로 구한 각 운전자의 제어 파라미터이며, Fig. 9는 실제 운전자의 주행 데이터, 해당 운전자를 모사한 제어기(DF-ACC) 및 고정된 파라미터를 갖는 일반 제어기(Normal ACC)에 대한 거리와 속도 오차이다. 비교의 신뢰성을 위하여 거리와 속도오차를 모두 포함하는 Rajamani의 제어기 및 제어상수를 설정하였다.1) 운전자 A는 오차에 대한 차량 요구 가속도가 낮아 상대적으로 높은 오차를 가지고 있으며, 운전자 B는 속도오차에 민감하여 해당 오차가 비교적 낮게 나타난다. 운전자 C는 거리오차에 민감함을 확인 할 수 있다. DF-ACC는 각 운전자의 특성을 나타내는 파라미터를 적용하여 유사한 오차 경향성이 있음을 보이는 반면, Normal ACC는 다양한 운전자의 특성을 반영하지 못하고 동일한 형태로 주행하는 것을 볼 수 있다.
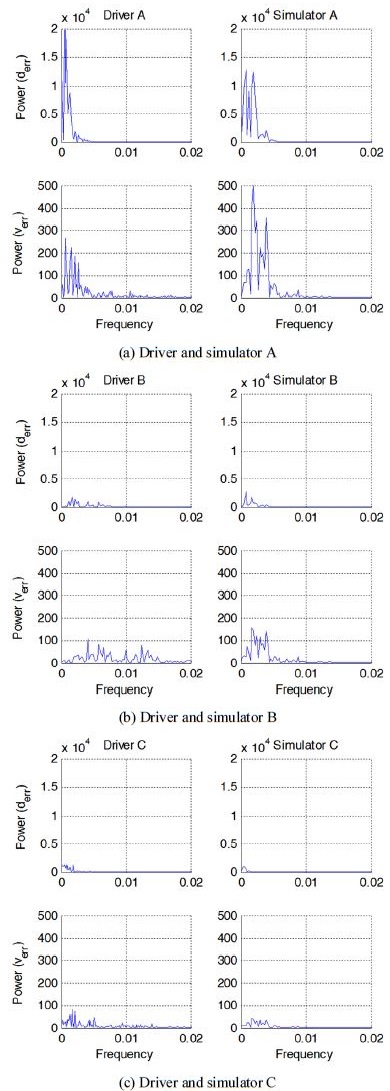
각 운전자의 실제 주행데이터와 운전자 친화 적응형 제어기의 시뮬레이션 결과를 FFT 수행하였다. Fig. 10에서는 운전자(좌)와 제어기(우)의 거리오차와 속도 오차에 대한 FFT를 수행한 결과이다. 앞서 결과를 분석한 것과 동일하게 Fig. 10(a)에서 A운전자는 오차에 대한 민감도가 적어 상대적으로 큰 오차를 수용하고 있으며, Fig. 10(b)와 Fig. 10(c)의 운전자는 비교적 적은 오차를 가지고 있음을 Table 4에서 보이고 있다. 또한, 각 운전자의 파라미터를 적용한 제어기도 해당 운전자의 오차 크기와 유사하게 나타냄을 확인할 수 있다.
5. 결 론
본 연구에서는 선행차량을 추종하는 운전자의 종방향 주행 특성을 분석하기 위하여 검증된 선행연구의 운전자 모델 특성을 사용하였다. 드라이빙 시뮬레이터를 통한 주행데이터는 정상상태 영역에서 추종거리를 취득하고 과도상태 영역에서 가・감속도 특성을 판단할 수 있었다. 각 운전자의 파라미터가 적용된 운전자 친화 적응형 순항제어기는 시뮬레이션 검증을 통해 실제 운전자와 유사한 형태로 주행하는 것을 거리 및 속도 오차를 비교하여 확인하였다.
본 논문에서 제안한 운전자 친화 적응형 순항제어기는 운전자의 특성을 제어기의 파라미터에 직접 적용하여 직관적인 분석이 가능하고 다양한 목적에 따라 변형된 형태로 재사용이 가능할 것으로 기대된다.
다만, 널리 알려진 운전자의 이질감을 대표하는 가속도 변화량(Jerk)은 시뮬레이션의 한계로 모든 경우 실제 운전자에 비하여 작게 나타났다. 따라서 실제 차량의 주행실험을 기반으로 운전자의 수용성을 향상시킬 수 있는 연구가 확장되어야 한다.
Nomenclature
| TTC : | time to collision, s |
| CTG : | constant time gap, s |
Subscripts
| ADAS : | advanced driver assistance system |
| DF-ACC : | driver friendly adaptive cruise control |
| HIL : | hardware in the loop simulator |
| DOF : | degree of freedom |
Acknowledgments
본 연구는 산업통상자원부 산업핵심기술개발사업 “ADAS의 시험 평가를 위한 실차 시험용 가상 주행환경구현 및 차량 주행 동기화 장치 개발 기술 개발(10052501)” 과제의 지원으로 수행되었음.
References
- R. Rajamani, Vehicle Dynamics and Control, 2nd Edn., Springer Science & Business Media, New York, (2011).
- Y. Park, and K. Yi, “A Stop-and-Go Cruise Control Strategy with Guaranteed String Stability”, Transactions of KSAE, 10(6), p227-233, (2002).
-
C. Desjardins, and B. Chaib-draa, “Cooperative Adaptive Cruise Control: A Reinforcement Learning Approach”, IEEE Transactions on Intelligent Transportation Systems, 12(4), p1248-1260, (2011).
[https://doi.org/10.1109/tits.2011.2157145]

- S. E. Shladover, C. Nowakowski, X. Y. Lu, and R. Ferlis, “Cooperative Adaptive Cruise Control: Definitions and Operating Concepts”, Transportation Research Record, (2489), p145-152, (2015).
-
O. Santin, E. Ozatay, J. Michelini, S. Szwabowski, and D. Filev, “Cruise Controller with Fuel Optimization Based on Adaptive Nonlinear Predictive Control”, SAE International Journal of Passenger Cars-Electronic and Electrical Systems, 9(2), p262-274, (2016).
[https://doi.org/10.4271/2016-01-0155]

- I. Moon, and Y. Kyongsu, “Human Drivers' Driving Pattern Analysis and An Adaptive Cruise Conrol Strategy”, Transactions of KSAE, 12(4), p191-197, (2004).
-
A. Rosenfeld, Z. Bareket, C. V. Goldman, D. J. Leblanc, and O. Tsimhoni, “Learning Drivers' Behavior to Improve Adaptive Cruise Control”, Journal of Intelligent Transportation Systems, 19(1), p18-31, (2015).
[https://doi.org/10.1080/15472450.2014.889960]

-
L. A. Pipes, “An Operational Analysis of Traffic Dynamics”, Journal of Applied Physics, 24(3), p274-281, (1953).
[https://doi.org/10.1063/1.1721265]

-
G. F. Newell, “Nonlinear Effects in the Dynamics of Car Following”, Operations Research, 9(2), p209-229, (1961).
[https://doi.org/10.1287/opre.9.2.209]

-
D. C. Gazis, R. Herman, and R. W. Rothery, “Nonlinear Follow-the-leader Models of Traffic Flow”, Operations Research, 9(4), p545-567, (1961).
[https://doi.org/10.1287/opre.9.4.545]

-
J. Tyler, “The Characteristics of Model-following Systems as Synthesized by Optimal Control”, IEEE Transactions on Automatic Control, 9(4), p485-498, (1964).
[https://doi.org/10.1109/tac.1964.1105757]

-
P. G. Gipps, “A Behavioral Car-Following Model for Computer Simulation”, Transportation Research Part B:Methodological, 15(2), p105-111, (1981).
[https://doi.org/10.1016/0191-2615(81)90037-0]

-
M. Bando, K. Hasebe, K. Nakanishi, A. Nakayama, A. Shibata, and Y. Sugiyama, “Phenomenological Study of Dynamical Model of Traffic Flow”, Journal De Physique I, 5(11), p1389-1399, (1995).
[https://doi.org/10.1051/jp1:1995206]

- V. Punzo, B. Ciuffo, and M. Montanino, “Can Results of Car-Following Model Calibration Based on Trajectory Data Be Trusted?”, Transportation Research Record, (2315), p11-24, (2012).
- B. Ciuffo, V. Punzo, and M. Montanino, “Thirty Years of Gipps' Car-Following Model Applications, Developments, and New Features”, Transportation Research Record, (2315), p89-99, (2012).