3.5톤 상용차용 구동축의 구조강도 개선

1. 서 론

상용차용 전륜구동 차축의 구동축(Drive shaft)은 종감속 장치를 거쳐 전달된 구동력을 바퀴에 전달하는 축으로 한 끝은 차동 장치의 사이드 기어에 결합되고 다른 끝은 구동바퀴에 결합된다. 특히, 조향시에도 속도변화 없이 회전력을 원활하게 전달할 수 있도록 축와 등속조인트(CV joint)로 구성되어 있으며, 좁은 공간에서 큰 구동력을 전달하는 제품으로 진동과 소음의 억제, 요구하는 동력을 원활하게 전달할 수 있는 비틀림, 굽힘 강도를 만족하는 경량화 제품을 필요로 하고 있다. 구동축의 개발은 차량이 요구하는 구동력의 크기에 따라 등속조인트의 종류와 핵심 구성 부품의 형상, 축 크기를 고려하여 결정되어야 한다.

부품 경량화, 진동과 소음의 억제 및 구조적 강성을 만족하는 구동 차축에 적용되는 축에 대한 연구는 상용 구조해석 소프트웨어를 이용한 사전 예측 및 검증에 대한 연구가 주로 이루어지고 있다. 국대선 등¹⁾은 일체형 중공 구동축의 구조 안정성 분석을 통하여 구동축에 대한 탄소성 유한요소해석 모델을 생성하고 설계된 제품이 극한 강도에서 파단이 발생되지 않음을 보였으며, 응력-수명 피로해석을 수행하여 요구 수명을 만족함을 보였다. 이호준 등²⁾은 유한요소해석을 통하여 프로펠러 샤프트 요크의 하부 포트 홀(Pot hole) 형상이 비틀림 변형에 영향을 미칠 수 있음을 보이고 강도 개선에 효율적인 하부형상을 제안하였다. 송현석 등³⁾은 프로펠러 샤프트 구성 부품인 R_yoke에 대한 내구성 향상 및 응력 저감을 위하여 설계 변수에 대한 민감도 분석을 바탕으로 개선 설계안을 제시하였다. 한동섭 등⁴⁾은 구동축과 피동 축이 연결되는 프로펠러 샤프트의 교차각이 강도에 미치는 영향을 연구하였다. Avrigean 등⁵⁾은 유니버셜 조인트의 결합 유형 및 빈도에 관한 시장조사 자료를 근거로 스파이더 부품을 주요 결합요소로 선정하여 이에 대한 연구를 수행하였으며, 이외에도 제품의 신뢰성 확보를 위하여 등속조인트에 작용하는 접촉 하중 및 응력을 이론적, 실험적으로 평가하는 연구⁶⁾, 샤프트의 경량화에 따른 강성 및 NVH 특성변화에 관환 연구⁷⁾, 샤프트의 진동 특성이 구동계에 미치는 영향을 평가하고 진동 저감 방안을 제시하는 연구⁸⁾ 등이 활발하게 진행되고 있다.

위와 같이 내구성, 응력저감, 진동 소음 특성 등 다양한 연구가 진행 되었지만 조향구동 차축의 구동 축 개발과 관련된 연구는 아직 미미한 상황이다. 이에 본 논문에서는 3.5톤 상용차에 적용할 구동 축개발을 위하여 유한요소해석 프로그램을 활용한 설계 검증과 취약 부품의 형상을 개선하여 제품의 신뢰성을 높이고자 하였다.

2. 해석모델 생성

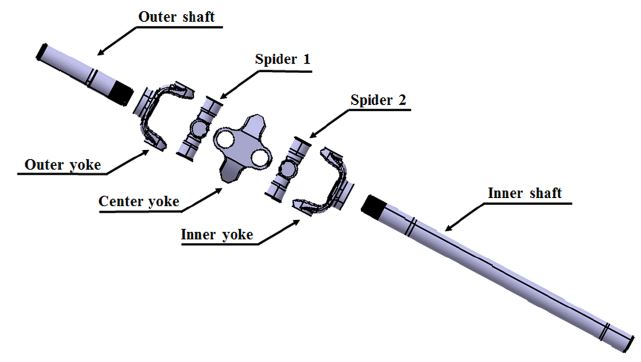
연구의 대상 제품은 3.5톤 상용차의 조향 구동축의 축(Drive shaft)으로 차동장치의 사이드 기어로부터 구동바퀴까지 구동력을 원활하게 전달하는 기능으로 더블카단 형식의 등속조인트와 충분한 비틀림 강성을 갖는 축으로 구성되어 있다. 이에 따라 대상 차종의 차동기어와 구동바퀴간의 거리, 너클의 크기 및 허용각도에 따라 구동축의 치수가 결정되며, 본 연구 개발 적용 차량의 제원을 검토하여 길이 950~960 mm, 넓이 180~200 mm정도에서의 구동 측(Drive shaft)을 개발하고자 한다. 또한 본 제품은 차량의 급격한 가감속, 조향 및 과하중 조건에서도 충분한 비틀림, 굽힘 강도를 필요로 하며, 더블카단 형식의 등속조인트는 센터 요크(Center yoke)에 십자가 형태의 2개의 십자축(Spider)이 결합되고 2개의 십자축은 축에 결합된 Y 자 형태의 요크와 연결되어 조향 시 회전 축심이 임의의 각도로 교차되어도 원활한 동력전달이 가능하도록 구성하였다. Fig. 1은 3.5톤 상용차용 구동축의 구성을 보여주고 있다.

Fig. 1

Drive shaft configuration

2.1 모델 단순화 및 메쉬 생성

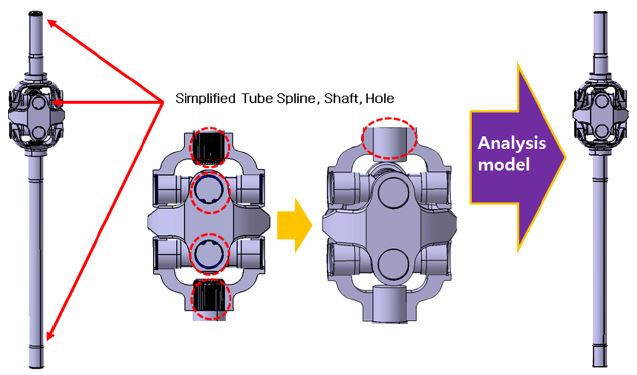
구동축의 구조해석을 위하여 더블카단 조인트의 센터 요크, 스파이더 및 요크 샤프트 부품을 Catia V5를 이용하여 모델링하고 구속조건을 부여하여 조립 제품을 완성하였다. 해석 모델 구성 부품 중 스파이더 고정 핀, 축 및 요크의 미세형상 및 홀 등 초기해석 후 해석 결과에 영향이 미미한 형상은 모델 생성 과정의 오류, 해석 시간 단축을 위하여 단순화하거나 제거하였다. Fig. 2는 간략화 된 모델 형상을 보여주고 있다.

Fig. 2

Simplified model of the drive shaft

해석 모델에 적용된 메쉬는 솔리드 모델링 제품에 주로 사용되는 3D 메쉬 요소인 Tetra 메쉬를 사용하였으며, 스파이더, 요크 등 취약 제품으로 예상되는 부분은 2,3,4 mm 메쉬 크기를 조절하여 수렴성을 검토하였다. 메쉬 크기별 최대 응력 오차값은 약 5 % 내외로 수렴하였으며, 2mm 메쉬 크기를 선정하여 해석을 수행하였다.

Fig. 3에서 조립품, 각 부품에 대한 완성된 해석 모델을 보여주고 있으며, 취약 부품을 검토하기 위하여 탄성해석을 수행하였다. 구동축 각 부품의 물성 데이터는 Table 1에 보여주고 있다.

Fig. 3

Mesh generation of the drive shaft

Table 1

Maximum stress of mesh size

2.2 접촉, 하중 및 구속 조건

구동축은 축 중심이 교차되는 상황에서 조인트부에 원활한 작동이 가능하도록 접촉 조건이 부여되어야 한다. 더블카단 조인트를 구성하는 센터요크, 스파이더, 요크 사이에는 조인트의 원활한 각도 변경이 가능하도록 부쉬(Bush) 형태의 베어링이 삽입되어 있으며, 부쉬 형태의 베어링 내부에는 여러 개의 베어링이 결합되어있어 부쉬베어링 내부에 결합되는 스파이더는 서로 회전이 가능하다. 해석 시 각도 변경이 가능한 조건을 부여하기 위하여 스파이더와 베이링 접촉면에서 회전이 가능하도록 접촉면 슬립을 허용하는 “No separation”, 요크와 베어링 슬립이 발생하지 않으므로, 완전고정이라 가정하여 “Bonded” 접촉 조건을 적용하였다. Fig. 4는 해석모델에 적용된 접촉 조건을 보여주고 있다.

Fig. 4

Contact conditions of analysis model

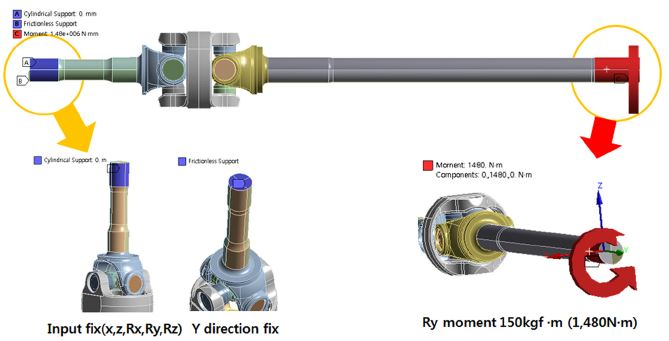
하중 및 구속조건은 Fig. 5와 같이 구동 바퀴와 연결되는 요크 샤프트의 끝 부분은 축 방향 움직임이 미미할 것으로 판단되어 완전 구속하였다.

Fig. 5

Load and boundary conditions of analysis model

구동 샤프트는 차동장치의 사이드 기어를 통하여 구동축에 전달되는 입력토크에 충분한 강도를 가지도록 설계하여야 한다. 본 제품의 적용차량인 3.5 Ton 트럭의 설계 허용 토크는 약 1800 N･m 이상으로 설계 안전강도를 고려하여 2000 N･m 토크를 기준으로 500 N･m 씩 증가시켜 총 5가지 입력 토크에 대한 최대 응력 분포를 검토하였다.

2.3 설계 변수

해석 결과를 바탕으로 개발품의 각 부품별 최대 응력 발생 부분에 대한 검토를 진행하였으며, 취약부 강도 개선을 위한 설계변경 모델(요크, 스파이더부의 반경 및 길이 변경)에 대한 해석을 진행하여 개발 목표에 가장 적합한 구동축 제품을 개발하고자 하였다. Fig. 6은 스파이더 외경 및 길이 변화 등 설계 변경 요소를 보여주고 있으며, 차량제원을 고려하여 총 4가지 케이스에 대하여 해석을 수행하였다.

Fig. 6

Design parameters of the spider

3. 해석 결과 및 개선

3.1 기본 모델(Case 1) 해석

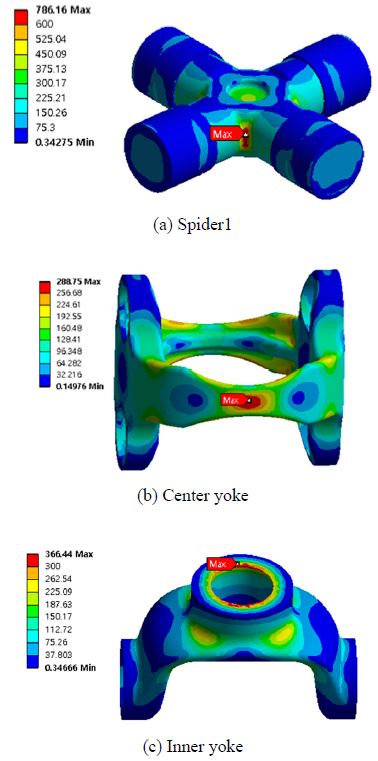
구동축의 최대응력 및 취약부를 알아보기 위하여 입력토크 변화에 따른 유한요소해석을 수행하였다. 각각의 입력토크에서 최대응력은 토크의 증가와 함께 선형적으로 증가하였고 취약부는 동일한 위치에서 나타났다. 또한, 각 부품의 항복응력 대비 최대응력을 검토한 결과 스파이더 1 부품에서 안전율이 1.2로 가장 낮았으며 Inner/Outer yoke shaft, Yoke 순으로 안전율이 낮았다. Fig. 7은 입력토크 2,000 N･m에서 구동축 부품의 해석결과를 보여주고 있다.

Fig. 7

Analysis results of the drive shaft

구동축의 각 구성 부품에 발생하는 최대 응력과 안전계수(항복강도/ 최대응력)를 Table 2에 정리하였다.

Table 2

Material properties of the axle shaft

부품별 최대응력과 취약부를 검토한 결과 출력부와 연결되는 스파이더 1에서 786 MPa 최대응력이 발생하였으며 항복응력에 대한 안전계수는 1.2로 계산되어 가장 취약한 부품이었다. 스파이더 2 또한 비슷한 크기의 최대응력과 안전계수를 보여 설계시 스파이더 부품의 강도를 충분히 고려해야 함을 알 수 있었다. 부품별 안전계수 검토 시 입력축, 출력축, 센터 요크, 출력 요크, 입력 요크 순으로 취약함을 알 수 있었다.

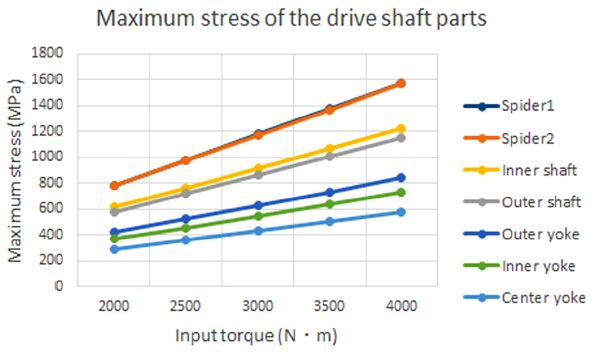
Fig. 8은 Spider, Shaft, Yoke 부품에 대한 입력 토크 별 최대 응력을 보여주고 있으며, 토크의 증가에 따라 최대 응력은 선형적으로 증가하고 있음을 알 수 있었다. Spider 부품은 2,000 N･m 입력 토크 인가 시 최대응력이 786 MPa, 784 MPa로 항복 응력에 근접하였으며, 입력 토크 3,000 N･m 인가 시 항복 응력을 넘는 980 MPa의 최대응력이 발생하였다. 그 외 부품에서는 최대 적용 토크 3,500 N･m까지 항복 응력보다 작은 값으로 충분한 강도를 갖는 것을 알 수 있었다. 설계된 구동축에서 Spider 부품이 차량 사양에 적합한 제품 개발을 위한 핵심 제품으로 입력 토크 3,000 N･m에서 안전한 제품을 개발하기 위하여 스파이더와 요크 연결부의 직경과 길이를 변경하여 추가적인 해석을 진행하였다.

Fig. 8

Maximum stress of the parts according to input torque

Table 3

Maximum stress of the drive shaft parts with torque 2,000 N･m

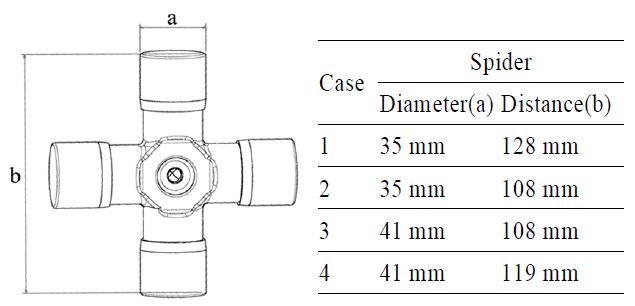
3.2 설계 변경 모델(Case 2, 3, 4) 해석

기본 모델과 비교하여 스파이더 길이를 20 mm 줄인 제품의 입력 토크의 변화에 따른 최대응력과 취약부를 분석하였다. 해석 결과 스파이더의 최대응력은 7 % 정도 작아졌으며 동일한 위치에서 발생하였다. 스파이더 길이가 짧아짐에 따라 스파이더에 발생하는 최대응력은 작아지나 스파이더에 연결되는 입출력 요크의 최대응력은 미세하게 상승하는 것을 알 수 있었다. 길이가 변경된 스파이더 제품은 2,500 N･m 입력 토크 인가 시 최대응력이 959 MPa, 940 MPa로 항복 응력에 근접하였으며, 입력 토크 3,000 N･m 인가 시 최대응력 1,152 MPa로 항복 응력을 초과하였다. 그 외 부품에서는 입력 토크 3,500 N･m까지 제품의 항복응력보다 작은 최대응력 값을 보였다.

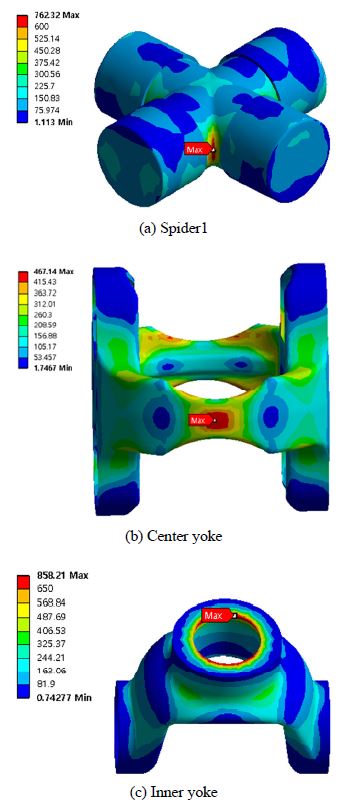
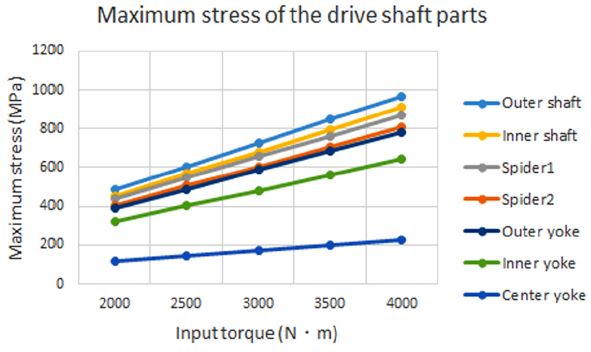
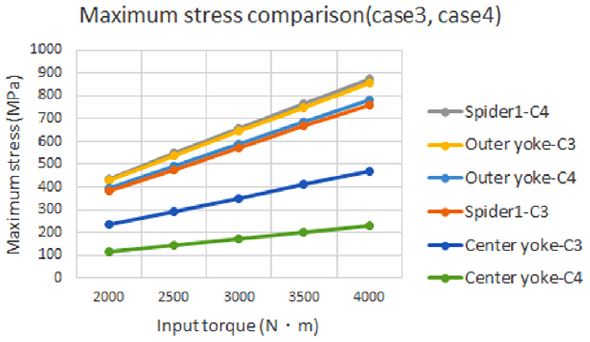
기본 모델 대비 스파이더 길이를 20 mm 줄이고 직경을 6 mm 늘린 제품에 대하여 입력 토크 변화에 따른 최대응력과 취약부를 알아보았다. 기준 모델과 비교하여 스파이더의 최대응력이 대략 51 %(786 MPa -> 381 MPa)정도 크게 감소하였으며 발생 부위는 동일하였다. 스파이더의 직경이 증가함에 따라 입출력 축의 최대응력은 감소하며, 입출력 요크의 최대응력은 증가함을 알 수 있었다. 길이와 직경이 변경된 스파이더 부품은 3,000 N･m 입력토크 인가 시 모든 부품에서 제품의 항복응력보다 작은 최대 응력 값을 보였으며, 최대 4,000 N･m 토크 인가 시 모든 부품에서는 제품의 항복응력을 만족하는 결과를 얻었다. 반면에 스파이더의 취약부의 강도 보강으로 입출력 축의 최대응력이 크게 상승하여 취약부로 나타남을 알 수 있었다. Fig. 9는 주요 부품의 해석결과를 보여주고 있으며, Fig. 10은 입력 토크별 각 부품의 최대응력을 보여주고 있으며 입출력 축의 최대응력이 스파이더 부품보다 큰 것을 알 수 있다.

Fig. 9

Analysis results of the axle shaft (Distance: -20 mm, Dia.: +6 mm)

Fig. 10

Maximum stress of the parts according to input torque (Distance: -20 mm, Dia.: +6 mm)

기본 모델 대비 스파이더 길이를 9 mm 줄이고 직경을 6 mm 늘린 제품에 대하여 입력 토크 변화에 따른 최대응력과 취약부를 분석하였다. 기본 모델과 비교하여 스파이더의 최대응력이 대략 44 %(786 MPa -> 437 MPa)감소하며 최대응력 발생 부위는 동일하였다. 변경된 스파이더 부품은 4,000 N･m 토크 인가 시 항복응력보다 작은 최대응력이 발생하였으며, 입출력 요크, 축의 최대응력은 케이스 3번과 비교하여 작게 증가하여 좀 더 안전함을 알 수 있었다.

이상의 4가지 케이스에 대한 구조해석을 통한 구동축의 검증 결과 길이, 직경 변화에 의한 각 부품별 최대응력의 발생 위치는 동일하게 유지되었으나 취약 부품의 보강 방법에 따라 최대응력 및 취약부의 변화가 발생하였다. 구동축의 가장 취약한 부품인 스파이더는 길이는 작게, 직경은 크게 할수록 제품의 강도가 상승하지만 연결 부품의 최대응력 변화 및 안전율을 고려하여 스파이더 형상을 결정해야 한다. 본 연구에서는 길이는 9 mm 줄이고 직경을 6 mm 늘린 제품이 스파이더의 최대응력 감소와 연결부품의 최대응력 상승을 고려할 때 가장 최적의 제품이었다.

Fig. 11

Maximum stress comparison (Case 3, Case 4)

4. 결 론

본 연구에서는 3.5톤 상용차의 차축 구동축의 강도 향상을 위하여 설계된 제품에 대하여 CAE 방법을 통하여 제품의 응력분포, 취약부를 확인하고 검증하였다. 구동축의 작동 조건을 고려하여 다양한 입력 토크에서 구조해석을 수행하였고 스파이더 부품의 직경, 길이 등 설계 변경된 제품의 검증으로 다음과 같은 결론을 얻었다.

• 1) 5가지 입력 토크에 대한 구동축의 해석 결과 스파이더가 가장 취약 부품이었다. 길이, 직경 변화를 통하여 스파이더 및 주요 부품의 최대응력과 안전율 변화를 검토하였으며, 적용 토크를 만족하는 구동축 제품을 설계 개발하였다.
• 2) 스파이더의 길이가 20 mm 작게 한 제품의 해석 결과 기준 모델 대비 스파이더의 최대응력이 대략 7 % 감소함을 확인하였으며, 스파이더와 연결된 입출력 요크의 최대응력은 미세하게 증가하였다. 입력 토크 2,500 N･m 인가 시 959 MPa의 항복 응력에 근접한 최대응력이 발생하였다.
• 3) 스파이더 길이를 20 mm 줄이고 직경을 6 mm 크게 한 제품의 해석 결과 스파이더의 최대응력은 기본 모델 대비 대략 51 % 감소하였으며, 입출력 요크, 축의 최대응력이 증가하였다. 입력 토크 4,000 N･m 토크 인가 시 스파이더의 최대응력은 762 MPa로 항복 응력 이내 값을 보였지만 입출력 축의 최대응력이 1,025 MPa 로 크게 상승하였다.
• 4) 스파이더 길이를 9 mm 줄이고 직경을 6 mm 크게 한 제품의 해석 결과 최대응력은 기준 모델 대비 대략 44 % 감소하였으며, 입출력 요크, 축의 최대응력은 케이스 3번과 비교하여 작게 증가하였다. 스파이더의 응력 감소와 연결 부품의 응력증가를 고려할 때 가장 적절한 설계 변경 제품으로 판단하였다.

본 연구의 결과는 3.5톤 상용차의 구동축 제품 개발에 도움을 줄 수 있으며, 향후 시제품 제작 및 신뢰성 시험 평가를 통하여 CAE 구조해석을 적용한 제품 개발의 효과성을 확인하고자 한다.

Acknowledgments

본 연구는 산업통상자원부와 한국산업기술진흥원이 지원하는 경제협력권산업 육성사업으로 수행된 연구결과입니다(R0002889).

References

• D. S. Guk, D. G. Ahn, H. J. Lee, and J. H. Jung, “Investigation of Structural Safety of Monobloc Tubular Drive Shaft Subjected to Torque”, Journal of the KSPE, 32(12), p1073-1080, (2015). [https://doi.org/10.7736/kspe.2015.32.12.1073]
• H. J. Lee, M. M. Kang, B. Y. Lee, G. H. Sug, and J. Y. Kim, “Bottom Pot Hole Shape Improvement and Structural Analysis of a Universal Joint Yoke for a Propeller Shaft”, KSAE10-B0105, p37-45, (2010).
• H. S. Song, D. H. Jung, Y. K. Seo, and W. S. Jung, “Durability Assessment and Design Modification of a Propeller Shaft of an Automotive”, KSAE Spring Conference Proceedings, p826-849, (2011).
• D. S. Han, S. H. Lee, and G. J. Han, “Strength Evaluation of a Propeller Shaft According to the Cross Angle”, KSPE Conference Proceedings, p237-238, (2008).
• E. Avrigean, A. M. Pascu, and V. S. Oleksik, “Study of the Cardan Cross Using the Experimental and Analytical Method”, Procedia Engineering, 100, p499-504, (2015). [https://doi.org/10.1016/j.proeng.2015.01.396]
• B. K. Oh, “Strength Analysis of Cross Groove Type Constant Velocity Joint Cage for Propeller Shaft”, Transactions of KSAE, 16(2), p74-79, (2008).
• S. S. Kweon, K. W. Seo, and H. S. An, “Improvement of NVH Performance for Premium Passenger Car Propeller Shaft”, KSAE Annual Conference Proceedings, p1345-1349, (2010).
• E. O. Choi, B. M. Ahn, D. P. Hong, and T. J. Chung, “A Study on the Design of Propeller Shaft for Reduction of Torsional Vibration”, Transactions of KSAE, 7(7), p221-228, (1999).