Deep Neural Network 기반의 차량 주행 경로 예측
* This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In regard to the vehicle safety services, vehicle trajectory prediction is one of the key technologies to estimate when and where the vehicle could be located. The development of the vehicle trajectory prediction algorithms using traditional physics-based models, such as kinematic and dynamic models, often required building a system model with complex equations, as well as gathering sensor noise statistics. In this paper, we proposed a vehicle trajectory prediction algorithm based on a deep neural network(DNN). The input data to the DNN were the driving status information defined in SAE J2735 basic safety message(BSM), while the output layer consisted of longitudinal and lateral trajectory predictions. The adaptive moment estimation(Adam) was used to enhance the learning speed. Through simulations, we compared the performance of the DNN-based approach with that of the traditional approach, and the results showed that the proposed method resulted in improved accuracy and precision of the vehicle trajectory prediction.
Keywords:
Trajectory prediction, Deep neural network, Intelligent vehicles, Driving simulator, V2X communications키워드:
경로 예측, 심층 신경망, 지능형 자동차, 주행 시뮬레이터, 차량사물통신1. 서 론
교통사고 경감을 위해서 최근에 출시되고 있는 차량에는 운전자 운전 보조 시스템(ADAS)으로 전방충돌경고(FCW), 긴급제동(AEB), 적응식 순항제어(ACC), 사각지대감지(BSD), 차선변경보조시스템(LCA) 등 다양한 기능들이 탑재되어 출시되고 있다. 또한, 최근에 발생하였던 영동고속도로 충돌 사고와 같은 운전자 부주의로 인해서 발생하는 사고때문에 ADAS 기능이 필요하다는 인식이 늘어나고 있다. Euro-NCAP에서는 사고를 미연에 방지할 수 있는 ADAS의 성능 평가를 위한 테스트 프로토콜과 지표를 제시하고 있다. 차량의 주행 안전성 평가지표를 만족하는 ADAS 기능을 구현하기 위해서 주변에 존재하는 차량을 인지하는 것이 중요하기 때문에 레이더, 라이다, 카메라 등 다양한 센서를 이용하여 주변 차량을 인지한다.1-3) 센서만을 이용하여 주변 차량을 인지 할 경우 센서의 가시거리 내에 존재하는 차량만 인지를 할 수 있다. 따라서 교차로나 골목길 등의 사각지대에 존재하는 차량에 대한 안전서비스에는 한계가 있다. 이러한 사각지대에 존재하는 위험요소까지 인지하기 위해 IEEE에서는 V2X(Vehicle to everything) 통신을 위한 WAVE(Wireless access in vehicular environment) 표준을 제정하였으며 SAE J2735 BSM(Basic safety message)을 송수신한다. BSM은 안전 메시지 셋 표준으로 차량에 대한 위치(Position), 속도(Velocity), 가속도(Acceleration), 요레이트(Yaw rate), 조향각(Steering angle) 등의 차량 주행 상태 정보를 가지고 있다.4)
FCW나 AEB와 같은 충돌 감지 및 회피 기능들은 주변 차량에 대해서 인지하는 것 뿐만 아니라, 자차의 속도, 조향각 등을 고려하여 미래에 어디에 존재할지에 대한 경로 예측 기반의 기능 구현을 필요로 한다. 경고 알람의 빈번한 작동은 운전자의 집중력을 저하시킬 수 있기 때문에 불필요한 작동을 최소화하기 위해서 신뢰도가 높은 주행 경로 예측을 필요로 한다. 차량의 경로를 예측하기 위해서는 센서로부터 얻을 수 있는 주행 상태 정보를 이용하여 경로 예측을 수행해야하며, 기존에 연구되었던 방법으로는 물리 기반의 등속도(Constant velocity, CV) 모델, 등가속도(Constant acceleration, CA) 모델, 등 선회율 및 등속도(Constant turn rate and velocity, CTRV) 모델, 등선회율 및 등가속도(Constant turn rate and acceleration, CTRA) 모델과 같은 방법들이 연구되어져 왔다.5) 이러한 방법들은 속도, 가속도, 요레이트와 같은 주행 상태 정보를 사용한다. 그러나 주행 도로 환경에 따라 상태 정보가 빠르게 변화할 수 있고, 레이더나 카메라 등의 센서로부터 얻을 수 있는 정보로는 정확한 요레이트 및 조향각 산출이 어렵기 때문에 주변 차량 경로 예측 성능에 한계가 있다. 이를 해결하기 위한 경로 예측 방법으로 몬테카를로 시뮬레이션(Monte Carlo simulation), 은닉 마르코프 모델(Hidden Markov model) 등을 활용하여 주행 가능한 모든 경로에 대한 반복적 시뮬레이션 수행을 통해 가장 높은 확률의 경로를 선택하는 연구가 수행된바 있다.6-8) 하지만 반복적 시뮬레이션 방법의 경로 예측은 모델식이 복잡하며 연산 시간이 오래 걸린다는 단점이 있기 때문에 실시간으로 경로를 예측해야하는 상황에서는 적합하지 않다. 최근에는 학습 기반 알고리즘인 딥러닝이 각광받고 있고 주로 영상 인식에 딥러닝을 적용한 연구가 진행되고 있다. 차량의 경로 예측을 위해 영상의 어떤 부분이 그대로 유지되거나 움직일 것인지, 그리고 어느 방향으로 움직일 것인지 CNN(Convolution neural network)을 활용하여 학습하고 복수의 예측 경로 중 가장 높은 보상을 받는 경로를 선택하는 접근 방식이 있으며9) 그리고 CNN을 이용하여 인식한 차량의 경로 예측을 위해 칼만필터 기반의 알고리즘을 적용한 방법이 있다.10) 본 논문에서는 DNN(Deep neural network)기반의 차량 경로 예측 방법을 제안한다. 경로 예측에 대해 학습된 DNN 모델로 경로 예측을 수행하면 반복적인 시뮬레이션을 하지 않기 때문에 경로 예측에 대한 빠른 연산이 가능하고, 경로 예측 알고리즘 개발 시 차량 동역학 모델과 같은 복잡한 모델식이 필요로 하지 않으며, 새로운 상태변수를 고려할 때에도 기존 모델식을 수정하지 않아도 된다는 장점이 있다.
본 논문에서는 BSM으로부터 얻을 수 있는 정보를 이용한 DNN 기반의 주행 경로 예측 방법에 대하여 다룬다. V2X 통신으로 전송하는 주행 상태 정보는 주행중인 차량 내부 센서로부터 수집된 주행 상태 정보이다. 본 논문에서는 학습 데이터 생성 및 실험 시나리오 구성을 위해 Tass International에서 제공하는 PreScan 시뮬레이터를 사용하였으며 MATLAB/Simulink를 통해 알고리즘 개발 및 검증을 수행하였다.
본 논문의 구성은 다음과 같다. 2장에서 신경망에 대한 이론과 BSM에서 다룰 수 있는 정보를 설명한다. 3장에서는 주행 경로 예측을 위한 DNN 알고리즘 구성 방안에 대하여 설명한다. 4장에서는 DNN 학습 데이터 획득 방안 및 주행 경로 예측 시뮬레이션 결과 제시와 분석을 한다. 마지막으로 5장에서 결론을 맺는다.
2. 이론적 배경
2.1 Neural Network
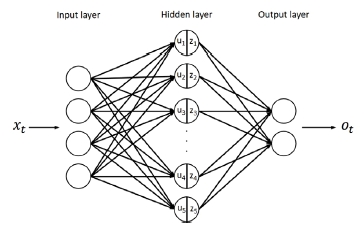
본 논문에서 차량 경로 예측을 수행하기 위해 사용된 모델은 DNN이다. 기본적인 신경망(Neural network)은 Fig. 1처럼 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)이 계층적 배치로 구성되어 있다. 신경망은 입력층으로 들어온 신경망 입력값들을 식 (1)과 같이 가중합 계산을 통해 처리하여 은닉층의 입력값으로 사용하고 이 값을 다음 계층으로 전파시켜줄 때에는 식 (2)와 같이 활성화 함수(Activation function)를 활용한다.
| (1) |
| (2) |
여기서 x는 신경망의 입력값, u는 은닉층의 입력 값, z는 은닉층의 출력 값, o는 출력층의 출력 값, w는 연결가중치이며 출력과 입력의 결합마다 각각 다른 가중치를 가진다. I와 J는 이전 계층과 다음 계층의 노드 수를 나타내고, i와 j는 이전 계층과 다음 계층에 해당하는 노드를 나타낸다. 출력층에서도 은닉층과 동일하게 활성화 함수를 통해 신경망의 최종 출력값을 산출한다.
신경망의 학습 과정은 최종 출력값이 목표 학습값에 근사하도록 연결가중치를 업데이트 하는 과정을 말한다. 최종 출력값과 목표 학습값의 오차는 비용함수(Cost function)를 이용하여 산출한다. 학습 목적에 따라 선형 회귀(Linear regression) 또는 로지스틱회귀(Logistic regression) 등을 사용한다. 오차를 줄이고 신경망의 성능을 높이기 위해서 산출된 오차 정보를 입력층까지 역전파(Backpropagation)11)하여 각각의 가중치를 기울기 하강 기법(Gradient descent algorithm)을 이용하여 업데이트 한다. 여기서 신경망의 은닉층 개수가 2개 이상인 경우 DNN이라고 한다.
2.2 SAE J2735 Basic Safety Message
미국 고속도로 교통안전국(NHTSA)은 모든 신규차량에 대해 차량 통신 기능을 의무화 한다고 발표하였고, WAVE 표준을 채택하고 있다.12) 본 논문에서는 WAVE 통신에서 안전 서비스 목적으로 정의된 BSM을 분석하여 차량 경로 예측에 필요한 주행상태 정보를 선정하여 사용한다.
Table 1은 BSM에 정의되어 있는 정보를 나타내고 있다. BSM Part I에는 주행 경로 예측에 필요한 속도, 가속도, 요레이트, 조향각 등이 정의되어 있다. BSM Part II에는 Path history와 Path prediction 등이 정의되어 있다. Path history에는 차량 주행 시 기록된 위치 정보와 위치 허용 오차, 속도, 방향각이 포함되어 있으며 Path prediction에는 도로 곡선 반경정보가 포함되어 있다. 그러나 Part II는 Part I처럼 지속적으로 송신을 하는 메시지가 아니고 특정 이벤트 발생 시 생성되는 메시지이기 때문에 주기적인 경로 예측에 사용하기에는 적합하지 않다. 본 논문에서는 BSM에서 획득한 차량의 속도, 가속도, 요레이트, 조향각을 활용하여 DNN 기반의 경로 예측 알고리즘을 개발하였다.
3. Deep Neural Network 구성
DNN을 이용하여 차량 주행 경로에 대한 학습을 하고 학습된 모델로 주행 경로 예측이 가능하다는 것을 이전 논문에서 확인하였다.13) 본 논문에서는 경로 예측을 위한 DNN의 입력값으로 차량의 종/횡 방향 속도, 종/횡방향 가속도, 요레이트, 조향각과 각 센서 잡음(Noise)의 표준편차를 이용하였다.
| (3) |
where
υx : vehicle velocity of vehicle body x-axis (m/s)
υy : vehicle velocity of vehicle body x-axis (m/s)
αx : acceleration of vehicle body x-axis (m/s2)
αy : acceleration of vehicle body y-axis (m/s2)
: yaw rate (degree/s)
δ : steering angle (degree)
σ : standard deviation of parameters
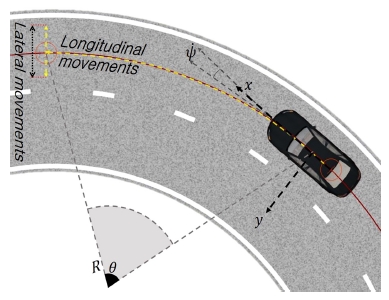
목표 학습값은 1, 2, 3초 후의 종방향 이동거리, 횡방향 이동거리로 선정하였다. Fig. 2는 종/횡방향 이동거리에 대한 도식이다. 종방향 이동거리를 산출하기 위해서 도로 곡률 정보와 차량의 위치 정보를 이용하였다. 도로 곡률은 일정하지 않고 지속적으로 변화하기 때문에 매 Time step마다의 종방향 이동거리를 산출하고 예측하려고 하는 시점까지의 값을 합산하여 설정하였다. 횡방향 이동거리는 Lateral offset의 변화량이며 여기서 Lateral offset은 Fig. 3에서의 Left offset과 Right offset의 차이이다.
종/횡방향 이동거리 산출식은 식 (4), (5)와 같다.
| (4) |
| (5) |
여기서 R은 도로 곡선 반경이며 c는 Lateral offset이다. t는 현재 시점을 나타내며, t+k는 k Time step 후의 시점을 나타낸다.
DNN에서 많이 사용되는 활성화 함수로는 주로 0부터 1까지 표현 할 수 있는 Sigmoid 함수, -1부터 1까지 표현 할 수 있는 Hyperbolic tangent 함수, 모든 음수값은 0으로, 그 외 입력값은 그대로 출력해주는 Rectified linear unit(ReLU) 함수 등을 사용한다. 하지만 최종 출력값으로 산출되는 이동거리값과 입력으로 사용되는 상태변수들의 양수와 음수의 비중이 동일하기 때문에 본 논문에서 사용한 활성화 함수로는 식 (6)과 같은 선형 함수(Linear function)를 사용하였다. DNN 기반의 경로 예측은 신경망의 입력 값과 최종 출력값 사이의 상관관계를 이용한 예측이기 때문에 비용함수로 회귀 방법을 채택하였으며 식 (7)과 같은 평균제곱오차(Mean square error)를 사용하였다.
| (6) |
| (7) |
여기서 on은 n번째 학습 입력값에 대한 DNN 출력값이며, dn은 n번째 학습 입력값에 대응되는 목표 학습값이다. N은 총 학습 데이터 개수이다.
기울기 하강 기법으로는 Adam(Adaptive moment estimation)을 사용하였다.14) Adam은 학습 속도를 높이기 위한 방법 중 하나로 역전파 단계에서 적용되는 기울기 하강 기법의 최적화 알고리즘이다. 이 기울기 하강 최적화 기법의 가장 큰 특징은 학습과정에서 학습률을 변화시키며 적용시키는 것이다.
본 논문에서 사용한 DNN에는 7개의 은닉층, 70개의 노드가 사용되었으며 총 100 epoch 학습을 시켰다. 학습에 사용된 컴퓨터 환경은 Intel i7-6700K 4 GHz CPU, 16 GB RAM, NVIDIA GeForce GTX 750 Ti 그래픽카드이며 MATLAB을 이용하여 학습을 하였다.
4. 주행 시뮬레이션
본 논문에서는 학습 데이터 생성과 실험 시나리오 구축을 위한 소프트웨어로 PreScan 시뮬레이터를 사용하였다.15) PreScan 시뮬레이터는 ADAS 기술개발을 위한 상용 소프트웨어로 레이더, 라이다, 카메라, V2X 통신 등 다양한 센서 및 통신 모듈을 지원한다. 또한 차량의 동역학 모델이 정의되어 있어서 상태 정보 등의 데이터 생성을 할 수 있다.
4.1 학습 데이터 생성 방안
PreScan에서 제공하는 2D Simple Dynamics 모델을 적용하여 경로 예측 알고리즘의 입력으로 사용되는 종/횡 방향 속도 및 가속도와 조향각 정보를 생성하였다.
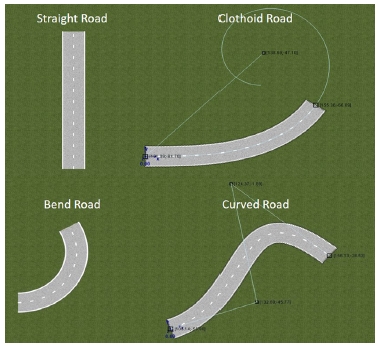
학습 데이터 생성을 위한 주행 시나리오는 Fig. 4와 같은 도로 곡률이 변화하는 클로소이드 도로(Clothoid road), 도로 곡률이 일정한 도로(Bend road) 등을 연결하여 총 100 km의 도로를 설계하였으며 차량의 주행속도는 Table 2와 같이 국토행정부의 도로설계편람을 참고하여 도로 곡선 반경에 따른 설계 속도로 주행 속도를 설정하였다.16) 데이터의 생성 주기는 100 Hz로 설정하였다. 본 논문에서는 차선 변경에 대한 시나리오는 고려하지 않았다. 목표 학습값 산출 시 종/횡방향 이동거리 계산에 사용되는 도로 곡률 정보 획득을 위해서 PreScan에서 제공하는 Lane marker 센서를 차량에 장착시켰다. 위와 같은 설정으로 시뮬레이션 환경에서 차량을 주행하여 총 286,200개의 데이터 셋을 생성하였다. 센서의 잡음은 가우시안 정규분포로 가정하여 Table 3과 같이 잡음 모델을 적용하였다.
4.2 주행 시나리오 구성
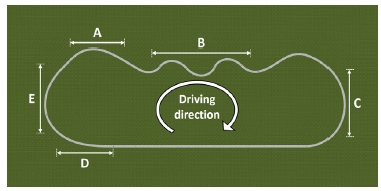
학습이 완료된 경로 예측 DNN 모델의 성능을 검증하기 위한 시뮬레이션 환경에서의 주행 도로는 자율주행 모의 실험 환경을 구축중인 K-City로 선정하였다.17) 주행 도로를 구현하기 위해서 OSM(Open street map)을 이용하여 실제와 동일한 크기의 도로를 PreScan에서 설계하였다. 주행 시나리오는 Fig. 5와 같이 K-City의 외곽순환도로로 선정하였으며 시계방향으로 주행하였다. 한 번 주행하여 생성된 데이터 셋은 16,000개이다.
4.3 시뮬레이션 결과 및 분석
차량 경로 예측 결과는 주행 속도와 조향각에 의한 영향을 크게 받기 때문에 Fig. 5에 나타내었듯 주행 시나리오를 도로 곡률 변화가 다르게 일어나는 5개 구간으로 나누어서 결과를 도출하였다. 각 구간에 대한 주행 거리와 평균 주행 속도 및 도로 곡선 반경은 Table 4에 나타내었다.
DNN 경로 예측 모델을 통하여 산출된 이동거리로부터 차량 좌표계상의 x, y 축 이동량을 산출하는 방법은 다음과 같다.
| (8) |
| (9) |
| (10) |
여기서 θt는 차량의 현재 방향각이며, Xt+k, Yt+k는 Global 좌표계 상의 x, y 이동량이다. 따라서 식 (10)과 같이 차량의 현재 방향각을 사용하여 차량 좌표계 상의 x, y 이동량으로 변환해야 한다.
실험결과는 Table 5에 평균 제곱 오차(Mean absolute error, MAE)와 표준편차(Standard deviation, STD)로 나타내었다. DNN 기반의 경로 예측과 기존 방법과의 비교를 위해서 Kinematic model과 Dynamic model을 통해 산출된 상태 추정값을 사용한 CTRV 모델 기반의 경로 예측 결과와 비교하였다.
실험을 수행한 모든 구간에서 CTRV 모델을 이용했을 때 보다 DNN 모델을 사용한 경우 상대적으로 정확한 주행 경로 예측 결과를 확인하였다. 구간 A, C, E에서의 경로 예측 결과와 비교하여 구간 B, D에서의 결과가 떨어짐을 확인할 수 있는데, 3초 후에 대한 DNN 기반 예측 결과의 경우 구간 A에서 약 0.6 m, 구간 B, D에서 약 3 m 정도의 예측 오차가 발생하였다.
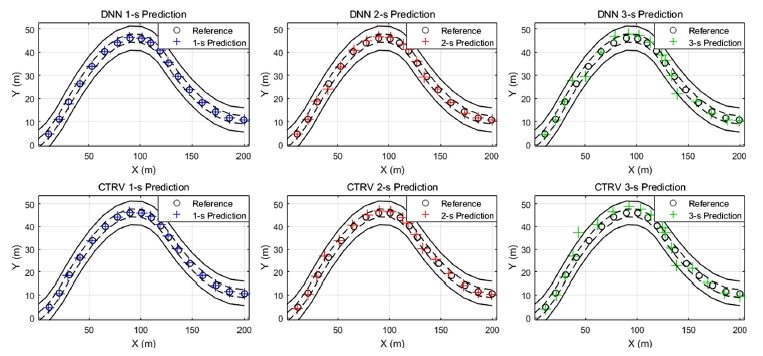
구간 B는 주행 구간 중 곡률 변화가 가장 심하게 발생하는 구간이다. 구간 B의 경로 예측 결과는 Fig. 6을 통해 확인할 수 있으며 차량의 주행 방향은 그림의 왼쪽에서 오른쪽이다. 여기서 CTRV 모델을 이용한 경로 예측은 등선회률 및 등속도를 사용하기 때문에 도로의 곡률 변화에 반응하지 못하여 빈번하게 옆 차선까지 점유하는 형태의 경로예측이 이루어진 반면(3초 후 예측 위치의 경우 약 30 %), DNN 기반의 경로 예측은 도로의 곡률이 급변하는 구간에서 주행 차선을 벗어나기도 하지만(3초 후 예측 위치의 경우 약 15 %) 그 외에는 주행 차선 내에 경로 예측 지점이 존재하는 것을 확인할 수 있다.
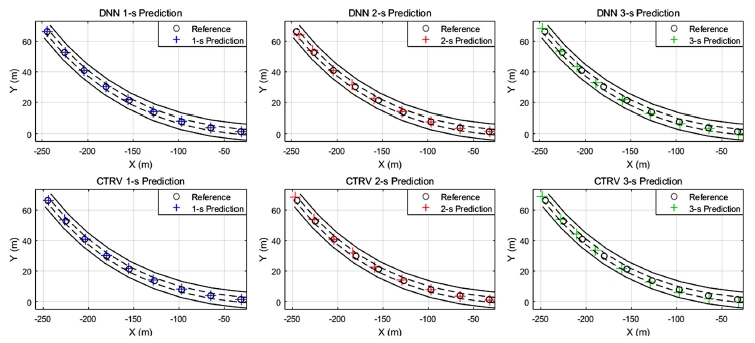
구간 D는 직선로에서의 고속주행 후 곡선 도로로 진입하는 곳이다. 구간 D의 주행 경로 예측 결과는 Fig. 7을 통해 확인할 수 있으며 그림에서 차량의 주행 방향은 오른쪽에서 왼쪽이다. 고속으로 곡선 도로에 진입하기 때문에 모든 주행 구간 중 가장 저조한 경로 예측 결과를 보였지만 3초 후에 대한 예측 위치의 경우 DNN 기반의 결과가 CTRV 기반의 결과 보다 약 0.7 m 적은 오차를 보였다.
5. 결 론
본 논문은 SAE J2735 BSM에 정의되어 있는 V2X 통신으로 수집할 수 있는 차량 주행 정보를 이용하여 DNN 기반의 주행 경로 예측에 대하여 연구하였다. BSM을 분석하여 경로 예측에 사용 가능한 차량의 주행 상태 정보를 제시하고 이를 이용한 경로 예측에 대하여 다루었다. 경로 예측을 위한 DNN 알고리즘의 학습 목표값 설정방안을 제시하였으며, 상용 소프트웨어인 PreScan 주행 시뮬레이터와 MATLAB/Simulink를 이용하여 학습 데이터를 생성하고 알고리즘의 개발 및 검증을 수행하였다.
성능 검증을 위한 주행 시나리오로는 교통안전공단 자동차안전연구원에서 구축하고 있는 자율주행 실험도시인 K-City의 외곽 도로를 PreScan을 이용하여 모사하였으며, BSM에 정의되어 있는 주행 상태 정보를 이용하여 DNN 기반의 경로 예측 결과를 도출하였다. CTRV 모델 기반의 경로 예측 결과와의 비교를 통해 본 논문에서 제안한 DNN 기반의 경로 예측 알고리즘이 다양한 곡선 반경을 가진 도로 주행 상황에서 향상된 경로 예측 정확도와 강인성을 보여주는 것을 확인할 수 있었다.
주행 차량에 대한 경로 예측을 위해 DNN 기반의 접근 방식을 본 논문에서 다루었으나 시뮬레이션 환경에서 실제 차량 및 센서의 특성과 주행 도로 환경을 완벽하게 구현할 수 없기 때문에 개발 알고리즘을 실제 차량에 직접 적용하는 것에는 한계가 있다. 하지만 시뮬레이션 환경에서의 사전 검증을 통해 실제 차량에 구현할 경로 예측 기술 개발에 요구되는 시간적, 물질적 비용을 크게 절감할 수 있다. 그리고 DNN의 입력값으로 제안한 주행 상태 정보가 모두 BSM에서 획득 가능하기 때문에 제안한 알고리즘은 V2X 통신을 활용하여 주변 차량들에 대한 경로 예측을 수행하는 데에 용이하다. 향후 연구방향으로는 학습 데이터로 사용할 차량 주행 정보를 실차로부터 획득하여 제안 경로 예측 기술을 실차에 구현하고 V2X 통신을 활용하여 주변 차량 및 보행자의 경로 예측에 대한 제안 알고리즘의 효용성을 검증할 계획이다.
Acknowledgments
본 연구는 산업통상자원부 및 한국산업기술평가관리원에서 지원하는 산업기술혁신사업(10062375, 환경인식센서 및 V2X 기반 주변 객체(차량, 보행자, 이륜차)의 경로예측 원천기술 개발)의 일환으로 수행하였음.
References
-
S. H. Jeong, J. E. Lee, S. U. Choi, J. N. Oh, and K. H. Lee, “Technology Analysis and Low-Cost Design of Automotive Radar for Adaptive Cruise Control System”, Int. J. Automotive Technology, 13(7), p1133-1140, (2012).
[https://doi.org/10.1007/s12239-012-0116-2]

-
C. H. Jang, C. S. Kim, K. C. Jo, and M. Sunwoo, “Design Factor Optimization of 3D Flash Lidar Sensor Based on Geometrical Model for Automated Vehicle and Advanced Driver Assistance System Applications”, Int. J. Automotive Technology, 18(1), p147-156, (2017).
[https://doi.org/10.1007/s12239-017-0015-7]

- H. -J. Kang, and P. J. Yoon, “Forward Collision Damage Mitigation System”, Auto Journal, KSAE, 33(6), p44-51, (2011).
- SAE International Surface Vehicle Standard, Dedicated Short Range Communications (DSRC) Message Set Dictionary, SAE Standard J2735, (2016).
-
P. Lytrivis, G. Thomaidis, M. Tsogas, and A. Amditis, “An Advanced Cooperative Path Prediction Algorithm for Safety Applications in Vehicular Networks”, IEEE Transactions on Intelligent Transportation Systems, 12(3), p669-679, (2011).
[https://doi.org/10.1109/tits.2011.2123096]

-
H. J. Choi, and B. S. Song, “Path Planning for Static Obstacle Avoidance: ADAM III”, Transactions of KSAE, 22(3), p241-249, (2014).
[https://doi.org/10.7467/ksae.2014.22.3.241]

-
H. K. Kang, D. H. Lee, and K. S. Huh, “Development of Lane Change System Considering Acceleration for Collision Avoidance”, Transactions of KSAE, 21(2), p81-86, (2013).
[https://doi.org/10.7467/ksae.2013.21.2.081]

-
D. Vasquez, T. Fraichard, and C. Lauhier, “Growing Hidden Markov Models: An Incremental Tool for Learning and Predicting Human and Vehicle Motion”, The International Journal of Robotics Research, 28(11-12), p1486-1506, (2009).
[https://doi.org/10.1177/0278364909342118]

-
J. Walker, A. Gupta, and M. Hebert, “Patch to the Future: Unsupervised Visual Prediction”, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, p3302-3309, (2014).
[https://doi.org/10.1109/cvpr.2014.416]

-
D. Yudin, and A. Knysh, “Vehicle Recognition and its Trajectory Registration on the Image Sequence using Deep Convolutional Neural Network”, International Conference on Information and Digital Technologies of IEEE, p435-441, (2017).
[https://doi.org/10.1109/dt.2017.8024333]

-
D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning Representations by Backpropagating Errors”, Nature, 323(9), p533-536, (1986).
[https://doi.org/10.1038/323533a0]

- National Highway Traffic Safety Administration, Vehicle-to-Vehicle Communication Technology for Light Vehicles, Preliminary Regulatory Impact Analysis, FMVSS, (150), (2016).
-
D. Jeong, M. Baek, and S. -S. Lee, “Long-Term Prediction of Vehicle Trajectory Based on a Deep Neural Network”, International Conference on ICT Convergence of KICS, p726-728, (2017).
[https://doi.org/10.1109/ictc.2017.8190764]

- D. Kingma, and J. Ba, “Adam: A Method for Stochastic Optimization”, International Conference on Learning Representations, (2015).
- PreScan: Simulation of ADAS and Active Safety, http://www.tassinternational.com/prescan TASS International, Helmond, (2017).
- Road Design Manual, Ministry of Land, Transport and Maritime Affairs, Korea, (2012).
- 2016 Korea Automobile Testing and Research Institute Annual Report, Korea Transportation Safety Authority, (2017).