고속 제동 시 브레이크 시스템 성능의 영향 인자에 대한 분석

1. 서 론

차량의 운동에너지가 브레이크 시스템을 통해 열에너지로 전환 및 소산되는 과정을 통해 차량은 감속을 하게 된다.¹⁾ 고속 차량일수록 큰 운동에너지 때문에 열에너지 또한 크게 되고, 이는 브레이크 시스템의 높은 온도를 야기 시킨다. 따라서 고속 차량용 브레이크 시스템은 높은 온도에서의 제동 안정성을 보장해야 한다. 특히 서킷 주행시 디스크의 온도는 약 600 °C 이상으로 상승하게 되고, 높은 온도로 인해 디스크-패드간 마찰계수가 낮아지면서 제동력이 약화되는 페이드 현상이 자주 발생한다. 이러한 메커니즘 때문에 패드의 마찰계수의 주 영향인자로서 온도가 중요시 되고 있으나, 이론적으로 보면 제동 압력, 토크, 누적 일률(Accumulated power) 등도 마찰계수에 영향을 준다고 알려져 있다.²⁾ 본 연구에서는 실험적 연구를 통해 브레이크 패드의 마찰계수에 영향을 주는 주요 인자를 분석하고, 통계기법을 이용한 기여도 분석을 통해 각 주요 인자별 영향도를 분석하는 것을 목표로 한다.

2. 고속 제동 성능 평가

본 연구에서는 고온 제동시 마찰계수에 영향을 주는 인자를 분석하기 위하여 브레이크 다이나모미터를 이용하여 시험을 진행하였다. 실차의 경우 고속에서 브레이크 토크를 측정하는데 한계가 있기 때문에 다양한 각도에서의 분석이 어렵다는 단점이 있다.

2.1 주요 영향인자 선정

브레이크 다이나모로부터 얻을 수 있는 계측 데이터는 총 10개로 Table 1과 같다. 이 중, 브레이크 패드의 고온 마찰계수 변화에 영향을 주는 인자로서 제동 토크(Brake torque), 제동 압력(Brake pressure), 디스크온도(Disc temperature), 패드 온도(Pad temperature)의 4개를 선정하였다.

Table 1

Influence parameters of brake pad’s friction coefficient

한편, 제동 가혹도를 대변할 수 있는 값으로 제동 속도 및 제동 시간의 함수로 표현되는 누적 일률(Accumulated power)을 사용할 수 있고, 식 (1) 및 식 (2)를 통해 계산할 수 있다.

$\[ E_B=\frac{1}{2}{m}_{\upsilon }\left({\upsilon }_i^2-{\upsilon }_f^2\right) \]$

(1)

where E_B : braking energy (J)

      m_v : vehicle mass (kg)

      v_i = initial speed (m/s)

      v_f : final speed (m/s)

$\[ P_{Acc}=\sum \frac{\partial E_B}{\partial t} \]$

(2)

where P_Acc : accumulated power (J/s)

      t : braking time (s)

2.2 고속 페이드 모드 생성

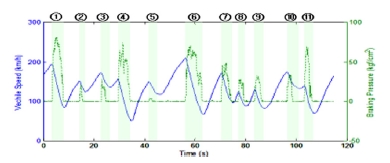
고속 시험 조건 설정을 위해 고성능 차량이 자동차 서킷을 주행하고 있을 때 발생하는 제동에너지를 계산하였다. AUDI R8 V10 coupe 차량을 이용하여 스페인의 Castelloi circuit 1바퀴를 최대 속도로 달릴 때의 속도 및 제동압 데이터를 측정하였고, 결과가 Fig. 1과 같다. 1바퀴의 거리는 4,090 m, 주행시간은 115 s이다. Fig. 1에서 파란색 실선은 차량 속도, 녹색 점선은 제동압을 의미한다. 제동압이 0.5 kgf/cm² 이상인 구간을 제동구간으로 설정하였고, 총 11개 제동구간의 평균 속도는 125 km/h로 산출되었다.

Fig. 1

Vehicle speed and brake pressure result at Castelloi circuit

11개 제동구간의 초기속도, 최종속도 및 제동시간을 바탕으로 계산한 제동에너지 및 누적 일률은 Table 2와 같다. Table 2에서 11번 제동과정동안 발생한 총 제동에너지는 14.57 MJ이고, 1회 제동 평균 1.32 MJ의 제동에너지가 발생했다.

Table 2

Braking energy and accumulated power

차량무게 1,870 kg, 제동구간의 평균 속도 125 km/h, 1회 제동시 평균 제동에너지 1.32 MJ을 식 (1)에 대입하면 식 (3)을 얻을 수 있다.

$\[ 1.32\left[MJ\right]=\frac{1}{2}\times 1870\left[kg\right]\times \left({\left(125\left[km\right]+X\right)}^{ 2}-{\left(125\left[km\right]-X\right)}^{ 2}\right) \]$

(3)

where X : speed variation (km/h)

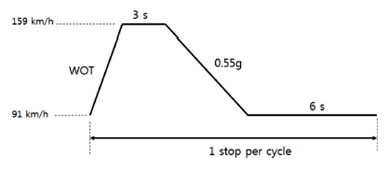
식 (3)으로부터 제동 초기속도와 최종속도의 편차인 X는 34 km/h로 계산되고, 이것은 제동 초기속도는 159 km/h 제동 최종속도는 91 km/h일 때 1.32 MJ의 제동에너지가 발생한다는 것을 의미한다. 한편, 1회 제동시 평균 누적 일률은 0.38 MW와 1회 제동시 평균 제동에너지 1.32 MJ을 식 (2)에 대입하면 1회 제동시 평균 제동시간은 3.48 s로 환산된다. 속도가 159 km/h에서 91 km/h로 3.48 s 동안 줄어든다면 평균 감속도는 0.55 g가 된다. 이상의 계산값을 바탕으로 Fig. 2와 같은 다이나모 시험 모드를 생성하였다. Fig. 2의 조건을 11회 반복했을 때 생성되는 제동에너지의 총합은 서킷 1 바퀴 주행 시 발생되는 제동에너지의 총합과 같다.

Fig. 2

High speed fade test mode using brake dynamometer

2.3 시험 결과 분석

2.2절에서 생성한 시험모드로 AUDI R8 V10 coupe차량의 전륜 브레이크 시스템을 평가한 후 결과를 분석하였다. 초기 갈아맞춤(Bedding)단계로 디스크 표면 온도 100 °C인 상태에서 80 km/h에서 30 km/h로 0.3 g로 감속하는 과정을 50회 반복하였다. 다음 Fig. 2의 시험모드를 총 40회 반복하였고, 이는 서킷을 약 3.4바퀴 주행하는 조건과 같다. Fig. 3, Fig. 4는 브레이크 다이나모미터 시험결과를 보여준다.

Fig. 3

Temperature measurement of disc and pad

Fig. 4

Test result of high speed fade test mode using brake dynamometer

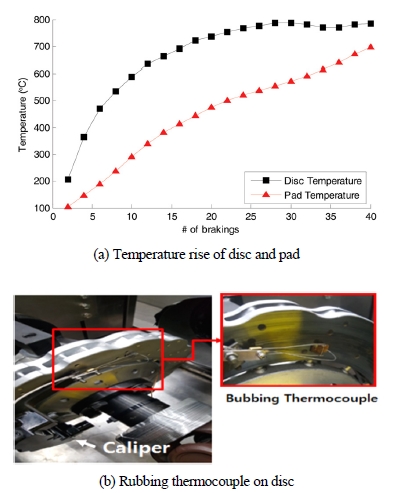
Fig. 3(a)는 반복제동에 따른 디스크와 패드의 온도상승 결과를 보여준다. 디스크 온도는 Fig. 3(b)와 같이 러빙 열전대(Rubbing thermocouple)을 이용하여 표면 온도를 측정하였고, 패드 온도는 열전대를 패드 내부에 삽입하여 측정하였다. Fig. 3(a)에서 디스크 온도는 약 25회 제동 시점이후부터 약 780 °C로 수렴하는 반면, 패드 온도는 계속해서 상승하고 있는 이것은 패드 마모 때문에 패드 내부에 삽입한 열전대가 디스크에 가까워지면서 생기는 현상이다. 패드에 비해 디스크는 상대적으로 마모량이 훨씬 적기 때문에 상대적으로 안정적인 온도 측정 가능하다. 따라서 본 연구에서는 디스크 표면 온도를 제동 온도의 대푯값으로 사용하였다.

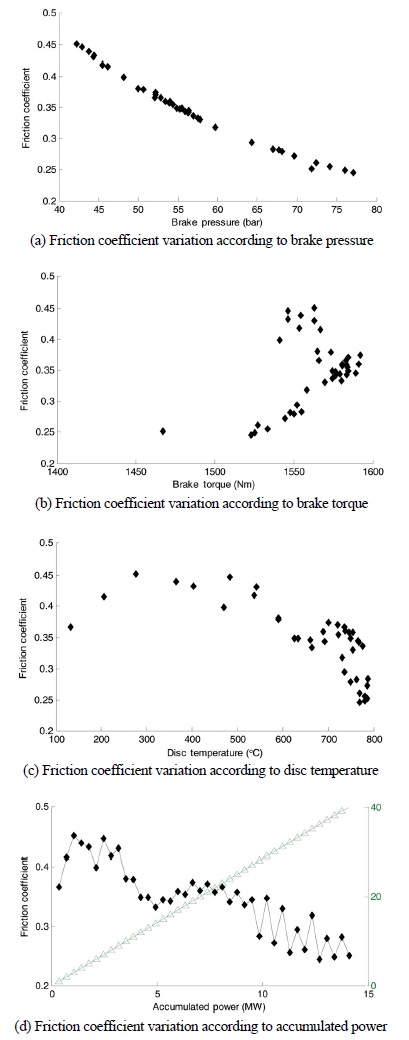
Fig. 4(a)~(c)는 1.1절에서 선정한 주요 영향 인자별 마찰계수 변화 결과이다. 마찰계수는 식 (4)를 이용하여 계산되는 값으로 제동압에 반비례하고 제동토크에 비례하는 특성을 갖는다.

$\[ \mu =\frac{\mathrm{\tau }}{P\times R_{eff}\times A_p} \]$

(4)

where μ : friction coefficient

      τ : brake torque

      P : brake pressure

      R_eff : effective radius

      A_p : equivalent area

Fig. 4(a)는 제동압에 따른 마찰계수 변화를 Fig. 4(b)는 제동 토크에 따른 마찰계수 변화를 보여주고 있다. 감속도 0.55 g를 유지하기 위하여 제동 토크가 일정하도록 장비를 제어하였고, 식 (4)에서 제동 토크, 유효반경 및 등가 면적이 일정했기 때문에 마찰계수는 제동압과 선형 반비례 특성을 갖게 된다. Fig. 4(b)에서 제동토크는 1,500 ~ 1,600 Nm의 영역에서 제어되고 있음을 알 수 있다. Fig. 4(c)는 디스크 온도 변화에 따른 마찰계수 변화를 보여준다. 온도가 약 300 °C일 때 마찰계수는 최대치인 약 0.45에 이르고 550 °C까지 일정한 수준을 유지하고 있다. 이후 마찰계수는 급격히 줄어들어 온도 750 °C 이상 온도 구간에서는 0.35 밑으로 감소하고 있다. 550 °C이상 고온에서 마찰계수가 급격히 낮아지는 구간을 고온 페이드 구간(High temperature fade region)¹⁾이라고 정의하며, 이 구간에서 마찰계수 하강 기울기를 원만하게 유지하고 700 °C 이상 초고온에서도 마찰계수를 0.3 이상으로 유지하는 것이 고성능 브레이크 패드에 요구되는 특성이다. Fig. 4(d)는 누적 일률에 따른 마찰계수 변화이다. Fig. 2의 일정한 제동이 반복됨에 따라 누적 일률은 선형으로 증가하고 이에 따른 마찰계수는 점차 하강하는 양상을 나타내고 있다. 마찰계수는 누적 일률이 약 1 MW에 이르는 지점(3회 제동 지점)까지는 마찰계수가 상승하다가 이후 누적 일률 1 MW(11회 제동 지점)까지는 0.35 이상의 수준을 유지하고 있다. 이후 마찰계수가 하강하고 있으며 누적일률 13 MW 이후에는 마찰계수가 0.25의 수준으로 하강하고 있음을 알 수 있다. 11회 제동이 서킷 1 바퀴 주행시 발생하는 제동에너지와 같으므로 Fig. 4(d) 결과로부터 서킷을 1바퀴 주행한 이후 제동성능이 하강하고 약 3바퀴 주행(누적 일률 13 MW)이후에는 마찰계수가 0.25정도의 낮은 수준이기 때문에 제동력에 문제가 생길 것으로 예상된다. 이상의 결과 분석내용을 바탕으로 마찰계수에 영향을 주는 요소로 디스크 온도, 제동 압력 및 누적 일률을 선정하였다.

3. 주요 인자별 영향도 분석

비선형 관계에 있는 반응변수와 입력변수간의 상호 작용을 수치화 시키는데 통계적 분석 기법이 많이 활용된다.^3,4) 2절에서 선정한 주요 인자 3가지에 대한 영향도를 분석을 위해 식 (5)와 같이 회귀 모델을 선정하였다. 인자의 제곱항 효과는 무시하고 인자간 교호작용은 고려하였다.

where y = friction coefficient

      x₁ = brake pressure

      x₂ = disc temperature

      x₃ = accumulated power

각 변수별 회귀계수 값인 β₀ ~ β₉ 의 값은 최소 자승법(Least squares method)⁵⁾을 이용하여 식 (6)과 같이 계산한다.

여기서 B는 회귀 계수(β)들의 집합, X는 입력변수(x)의 집합, Y는 반응변수(y)의 집합이다. 한편 도출한 회귀 모형함수의 신뢰도를 검증하기위하여 Table 4와 같이 분산분석표(ANOVA table)^5,6)을 이용하였다. 분산분석표에서 실험값을 토대로 계산한 F₀의 값이 자유도 k와 실험횟수 n을 이용하여 F-분포표에서 찾은 F 값보다 클 때 회귀 모형함수는 주어진 유의수준에서 신뢰성을 갖는다.⁵⁾

Table 3

ANOVA(Analysis of Variance) table

Table 4

ANOVA result

브레이크 다이나모미터 실험결과를 바탕으로 식 (6)을 이용하여 유도한 모형함수가 식 (7)과 같다.

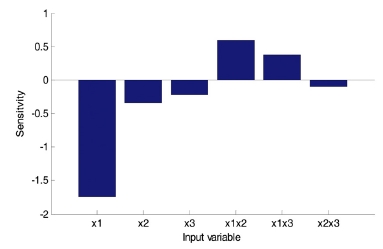
식 (7)에서 x₁의 계수값은 -1.74로 x₂, x₃에 비해 큰 값을 갖고 있고 부호는 음수이다. 이것은 3개의 요인 중 x₁(Brake pressure)가 y(Friction coefficient) 변동에 미치는 영향이 가장 크다는 것을 의미하고 부호가 음수이기 때문에 x₁이 커지면 y는 감소하는 것을 의미한다. x₂와 x₃의 계수값 또한 음수이기 반응변수 y와 음의 상관관계가 있으며 기여도의 크기는 x₂가 x₃보다 다소 큰 것으로 나타나고 있다. 두 가지 인자 간 상호작용을 보면 계수의 절대값의 크기가 x₁x₂ > x₁x₃ > x₂x₃로 나타나고 있으므로 x₁, x₂의 상호 작용효과가 가장 큰 것으로 나타나고 있다. Fig. 5는 식 (7)의 변수별 계수값을 그래프로 도식화한 결과로, 변수별 상대적 기여도 크기를 보여주고 있다.

Fig. 5

Sensitivity analysis results

식 (7)의 신뢰도 검증을 위해 Table 4와 같이 분산분석을 실시하였고, 계산된 F₀의 값이 2,707로, 신뢰수준 95 %의 F value인 2.87보다 크기 때문에 추정된 회귀 모형함수는 95 % 이상의 신뢰도를 갖고 있다고 얘기할 수 있다.

4. 결 론

본 연구에서는 브레이크 다이나모 시험 데이터를 통계적으로 분석하여 고속 제동시 브레이크 패드의 마찰계수에 영향을 주는 주요 인자들의 기여도를 분석하였고, 결과가 아래와 같다.

• 1) 차량을 활용한 서킷 주행 데이터를 바탕으로 브레이크 다이나모미터용 고속 페이드 모드를 생성하였다.
• 2) 제동압력등 5가지의 영향인자중 제동압력, 디스크 온도 및 누적 일률이 마찰계수에 가장 큰 영향을 주고 있는 것을 확인하였다.
• 3) 실험 데이터에 대한 통계 분석 결과 제동압력이 마찰계수에 가장 큰 영향을 주는 것으로 나타났으며, 디스크 온도와 누적 일률의 민감도 크기는 비슷한 수준으로 나타났다.

연구 결과에 대한 종합 분석 결과, 브레이크 패드의 고속 제동성능 향상을 위해서는 제동압력, 디스크 온도 및 누적일률을 설계 요소로 반영하여야 하며 특히 특정 감속도를 내기위한 제동압력의 작동범위가 마찰계수에 큰 영향을 주는 변수임을 확인하였다. 향후 본 연구 결과를 바탕으로, 고속 실차 제동시 나타나는 마찰재 변형/파손등의 특성을 대변할 수 있는 브레이크 다이나모 시험법을 개발할 계획이다.

Acknowledgments

이 연구는 2017년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(10076592, 글로벌 환경규제(Copper) 대응을 위한 멀티피스톤 캘리퍼용 고성능(제동력 0.42이상), 저소음 마찰재 설계 기술 개발).

References

• P. Hwang, X. Wu, and Y. B. Jeon, “Repeated Brake Temperature Analysis of Ventilated Brake Disc on the Downhill Road”, SAE 2008-01-2571, (2008).
• R. Limpert, Brake Design and Safety, SAE International, Warrendale, (1999).
• S. P. Jung, and T. W. Park, “Development of the Optimization Design Module of a Brake System”, Transactions of KSAE, 16(3), p166-171, (2008).
• K. W. Suh, and K. Y. Jung, “The Statistical Evaluation for the Wear Life of Brake Pad Linings in Vehicle Durability Test and Customer Usage Environment”, Transactions of KSAE, 7(5), p213-220, (1999).
• S. P. Jung, K. J. Jun, T. W. Park, and I. C. Ahn, “An Optimum Design of a Gas Circuit Breaker Using Design of Experiments”, Mechanics Based Design of Structures and Machines, 36(4), p346-363, (2008). [https://doi.org/10.1080/15397730802405895]
• S. H. Park, Understanding of Design of Experiments, Minyoungsa, Seoul, (2005).