공기압 실린더 위치 서보계의 강인 제어기 설계

2.1 실험장치

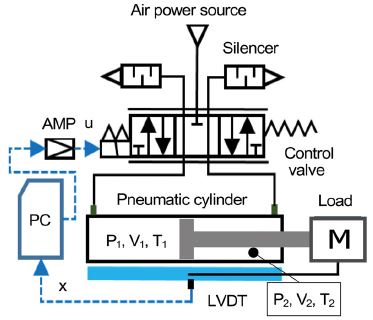
Fig. 1은 공기압 실린더 위치제어계의 개략도이다. 공기압 실린더(DNCI-50-500, FESTO사)는 피스톤 지름 50 mm, 로드 지름 20 mm, 스트로크 500 mm인 편로드 복동형을 사용하였다.

Fig. 1

Position control system in pneumatic cylinder

압축공기의 공급측과 배기측 실린더 내부 챔버 압력은 흡기/배기포트의 매니폴드에 부착된 압력센서(PSE530-M5)로 측정하였다. 또한 피스톤 변위는 LVDT(GYKM600-R, SANTEST사)를 직결하여 측정하였고, 분해능은 0.01 %이다. 비례유량제어밸브는 인가전압 0~10 V, 공급압력 10 bar에서 밸브 통과 최대유량 1,400ℓ/min, 응답시간 4.8 ms인 3위치 5포트 4방향 비례유량제어밸브(MYPE-5-1/4, FESTO사)를 사용하였다.

압력과 피스톤 변위 신호는 AD변환기(CEM - USBIO-01)를 거처 PC에 입력된다. 제어기에서 출력신호는 DA변환기(CEM-USBIO-01)와 증폭기를 거쳐 비례제어밸브에 인가된다. 실험에서 샘플링시간은 0.5 ms로 설정하였다.

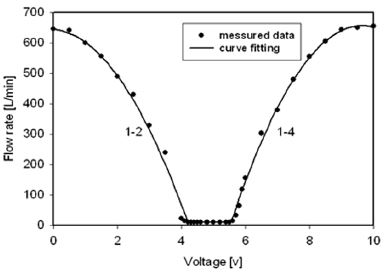
Fig. 2는 공급압력 5 bar에서 인가 전압변화에 따른 밸브를 통과하는 유량 특성을 나타낸다. Fig. 2에서 왼쪽 그래프 1빥2는 인가전압 0~5 V 변화에 대해 공급포트 1에서 실린더 포트 2로의 제어유량, 오른쪽 1빥4는 5~10 V 인가전압에서 공급포트 1에서 실린더 포트 4로 제어되는 유량을 유량계(GFMS- 010018, Aalborg사)로 측정한 것이다. Fig. 2에서 비례제어밸브 스풀의 절환에 따라 밸브를 통과하는 유량은 거의 대칭적으로 제어되지만, 4.2~5.5 V 근방에서 부작동 시간(Dead band)이 나타난다. 이러한 밸브의 비선형요소는 스풀 랜드와 포트 사이의 중합(Overlap), 스풀과 슬리브 사이의 마찰력, 비례솔레노이드의 응답특성 등의 원인으로 발생한다. 공급압력 5 bar에서 최대유량은 640 ℓ/min로 계측되었다.

Fig. 2

Flow characteristics of a control valve

2.2 모델링

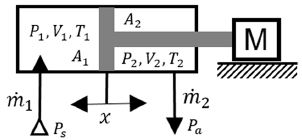
공기압 실린더 구동 시스템은 Fig. 3과 같이 모델링하여 동적 거동을 고찰한다. Fig. 1에서 압축공기가 비례유량제어밸브에서 제어되어 실린더 캡측(Cap)의 압력실(P₁, V₁, T₁)로 질량유량 $$ {\dot{m}}_1$$이 공급되면, 피스톤이 왼쪽에서 오른쪽으로 움직이고, 헤드측(Head) 배기실(P₂, V₂, T₂)의 공기는 $$ {\dot{m}}_2$$로 대기에 배출되는 경우를 고려한다.

Fig. 3

Double acting-single rod pneumatic cylinder

Fig. 3에서 공기압 실린더로 공급되는 질량유량 $$ {\dot{m}}_1$$과 대기로 배출되는 질량유량 $$ {\dot{m}}_2$$는 비례제어밸브의 개구부(Opening area)에서 압축성 유동을 고려하면 다음 식으로 표현된다.^6,7)

식에서 P_s, T_s는 공급압력과 온도, P_a는 대기압, 하첨자 1은 압력실, 2는 배기실을 나타낸다.

공기압 실린더 내부 압력실과 배기실의 압력변화는 질량유량과 공기의 상태방정식에서 다음 식으로 표현된다.

여기서 V_10,20는 실린더 캡측과 헤드측의 간극체적, L은 피스톤의 행정(Stroke)이다.

Fig. 2와 식 (1) ~ (4)에서 보듯이 공기압 실린더를 통과하는 질량유량 식은 압력변화에 강한 비선형성을 나타낸다. 공기압 실린더 위치제어계의 선형시 불변방정식을 얻기 위해, 피스톤의 초기 평형위치 x₀=x_eq, P₁₀A₁=P₂₀A₂, T₁=T₂=T_s에서 선형화하면, 식 (1), (2)는 다음과 같다.

식 (5)에서 x_s는 비례제어밸브의 스풀 변위이고, 각각의 계수는 다음과 같다.

부하를 포함한 피스톤의 운동방정식은 식 (7)과 같고, F_s는 정마찰력, F_L은 부하를 나타낸다.

공기압 실린더와 부하의 동특성에 비교하여 비례제어밸브의 응답이 빠르기 때문에 비례제어밸브의 전달함수는 정수로 취급하여 모델링한다. 식 (1) ~ (7)에서 마찰력과 부하를 무시하고, 비례제어밸브의 인가전압 u에 대한 피스톤의 변위 x사이의 개루프 전달함수를 구하면 다음과 같다.

Table 1의 공기압 실린더 제원과 제어 실험조건 및 식 (1) ~ (7)을 사용하여 파라미터를 구하면, k₁=0.03kg/(s‧m), k₂=0, 감쇠계수 ζ=0.14, 고유진동수 ω_n=274rad/s, 비례제어밸브의 특성을 고려한 밸브정수 K_V=1.286이다. 이 값들을 식 (8)에 대입하면, 공기압 실린더 위치제어계의 개루프 전달함수는 식 (9)와 같다.

Table 1

System parameters used experiment

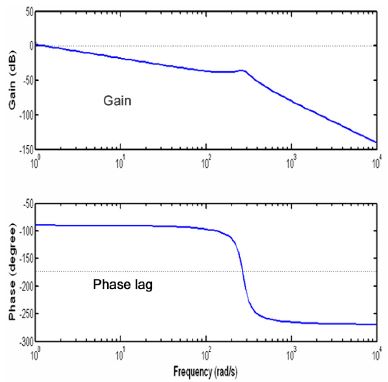
Fig. 4는 식 (9)의 주파수응답 특성이며, 이득(Gain)과 위상지연(Phase lag) 특성에서 보듯이 공진주파수는 약 273 rad/s이다.

Fig. 4

Frequency response of nominal plant P(s)

3.1 혼합감도문제

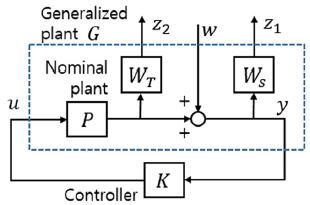
공기압 실린더의 마찰, 비례제어밸브의 부작동 시간, 공기압 관로에서 전달지연, 피스톤 이동에 따른 고유진동수의 변화, 모델 불확실성 등에 따른 응답성의 개선과 강인 안정성을 확보하기 위해, Fig. 5와 같이 혼합감도문제를 적용하였다. u는 제어입력, w는 외부 입력, w는 제어출력, W_S는 감도함수 S에 대한 가중함수(Weighting function),W_T는 상보감도함수 T에 대한 가중함수이다.

Fig. 5

Generalized plant for mixed sensitivity problem

H_∞ 제어이론을 적용하여, Fig. 5에서 P를 공칭모델로 하는 제어기 K를 설계한다.

혼합감도문제의 설계사양은 식 (10)으로 표시된다.

가중함수는 시스템의 파라미터 변동, 부하변동, 외란억제 등에 강인한 응답특성을 고려해야하기 때문에 H_∞ 제어기의 성능을 평가해가면서 가중함수를 조정하여야 하며, 다음과 같이 선정하였다.

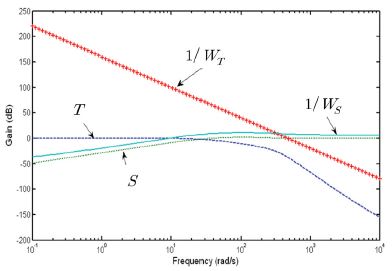
Fig. 6은 주파수 루프정형(Loop sharping)에서 얻어진 감도함수 S와 가중함수 W_S, 상보감도함수T와 가중함수 W_T의 주파수 특성이다. Fig. 6에서 보듯이 감도함수와 상보감도함수의 이득은 가중함수 W_S와 W_T의 역수보다 작아서 식 (10)을 만족한다.

Fig. 6

Frequency response of S , T , WS , WT

3.2 H_∞ 제어기 설계

공기압 실린더 위치제어계는 식 (9)에서 보듯이 원점에 극점을 가지고, 설계조건이 플랜트에 대해 가혹하기 때문에 표준 H_∞ 제어이론을 직접 적용하기는 곤란하다. Fig. 5에서 제어기 K는 폐루프 극점의 극배치 영역 지정 방법 중에서 쌍1차 변환(Bili-near transform)을 적용하고, MATLAB에서 γ 반복법으로 구하였다.⁸⁾ γ가 0.91일 때 가장 작은 값을 가지며, 이 때 제어기의 전달함수는 다음과 같다.

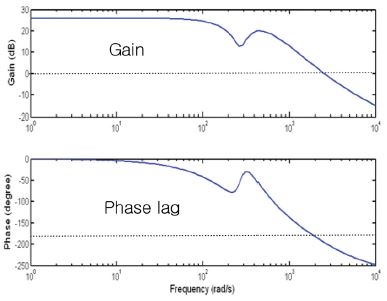
Fig. 7은 식 (13)의 H_∞ 제어기의 주파수 응답이며, Fig. 4의 공기압 실린더 위치제어계 전달함수의 공진주파수에 대응하는 약 273 rad/s 부근에서 이득이 급격하게 감소하다가 증가하는 특성을 나타낸다.

Fig. 7

Frequency response of H∞ controller K (s )

공기압 실린더 구동시스템에 H_∞ 제어기를 적용하여 폐루프 위치제어계를 구성하여 시뮬레이션으로 제어기의 성능을 조사하였다.

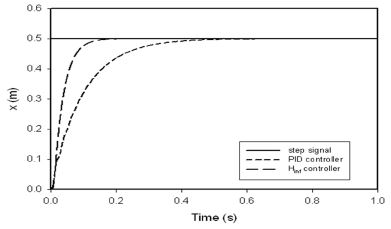
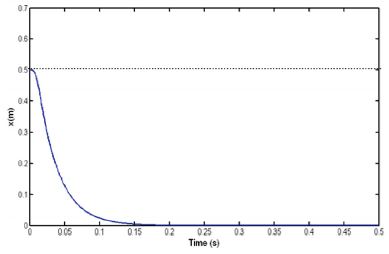
Fig. 8은 스텝입력에 대한 피스톤의 변위의 과도응답 특성을 PID제어와 비교한 것이다. 피스톤의 변위 x=0.5m는 스트로크에 해당하며, H_∞ 제어는 약 0.2초 후에 정상상태에 도달하며, 오버슈트(Over-shoot)나 정상편차가 없이 양호한 응답특성을 나타낸다. PID제어는 Ziegler-Nichols의 이득조정 방법에 따라 비례이득 K_p=8, 미분이득 K_d=0.005, 적분이득 K_i=0.01로 설정하였다.⁹⁾ H_∞ 제어와 PID제어 결과를 비교해 보면, 정상상태에 도달한 후에는 모두 정상편차가 없지만, 과도응답 구간에서 H_∞ 제어가 PID제어 보다 응답 시간이 약 0.4초 정도 빠르다는 것을 알 수 있다.

Fig. 8

Step response of closed loop system

Fig. 9는 계단입력의 외란 w에 대한 피스톤 변위 파형이며, 약 0.15초 이후에는 외란이 제거됨을 볼 수 있다.

Fig. 9

Disturbance rejection characteristics of closed loop system

4.1 개루프 제어

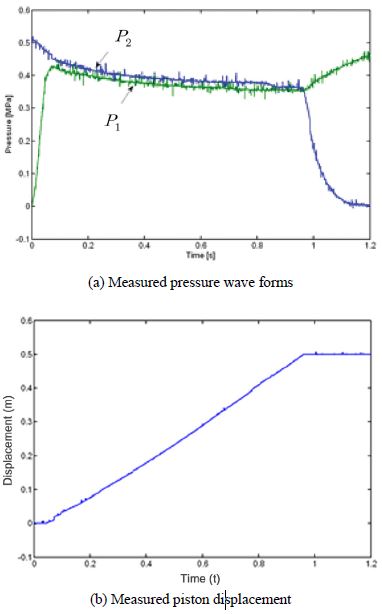
Fig. 10은 공급압력은 0.5 MPa, 부하질량은 7.5 kg에서 피스톤이 전진행정일 때 실린더 내부 압력과 피스톤 변위 파형이다. 압력파형에서 보듯이 비례제어밸브에 제어신호를 인가하면 공급측 실린더 내부 압력 P₁은 초기에 대기압에서 피스톤이 움직이는 순간까지 급격하게 상승하며, 배기측 압력 P₂은 0.5 MPa로부터 점차적으로 낮아진다. 또한 피스톤이 운동하는 동안에 피스톤 전후면의 압력차는 거의 일정하게 유지된다. 피스톤이 스트로크 끝단에 도달한 후 실린더의 공급측 압력은 0.5 MPa까지 상승하고, 배출 압력은 대기압까지 급격하게 떨어지는 것을 볼 수 있다. 피스톤 변위는 약 0.05초 후에 피스톤의 정지마찰력을 극복하여 움직이기 시작하고, 피스톤이 주행하는 동안에 평균속도는 약 0.8 m/s 정도이다. 피스톤이 스트로크 끝단에 도달하였을 때 바운드(Bound) 현상이 나타나지 않는다.

Fig. 10

Measured pressures and piston displacement wave forms of open loop position control (piston extending)

4.2 폐루프 제어

공기압 실린더의 폐루프 위치제어 특성은 H_∞ 제어기를 이용한 실험결과와 2.2에서 구한 모델링 기반 시뮬레이션을 동시에 수행하여 과도응답에 대한 제어성능을 조사하였다. 이 때 비례제어밸브에 인가되는 제어신호는 일정하게 유지되는 것이 아니라 피스톤 변위의 계측 결과에 따라 변하고, 비례제어밸브의 스풀 변위에 따라 밸브 개구면적을 조절하여 실린더로 유입되는 압축공기량과 방출되는 공기유량을 제어하였다.

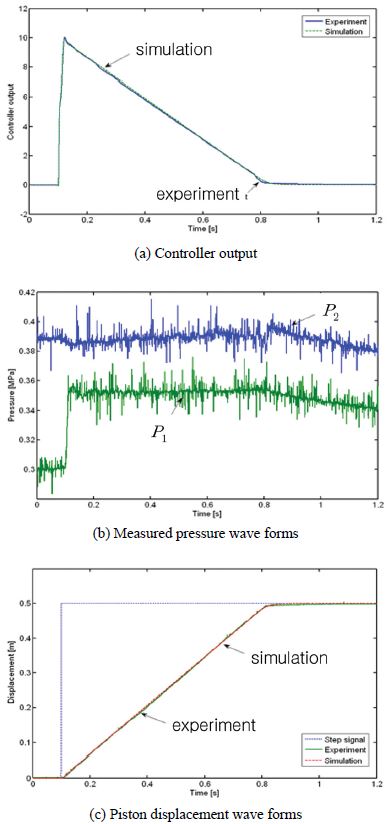
Fig. 11은 폐루프 위치제어계에 피스톤이 전진행정에서 H_∞ 제어기의 출력신호, 공기압 실린더의 내부압력과 피스톤 변위파형이다.

Fig. 11

Comparison of experimental and simulated wave forms for closed loop position control

목표값으로 0.1초 후에 스텝 입력을 인가하였을 때, 실험결과에서 보듯이 H_∞ 제어기의 출력신호는 초기에 급격하게 상승하여 점차적으로 감소하고, 공기압 실린더에 공급된 압력이 순간적으로 상승하여 피스톤이 약 0.11초 후에 빠르게 응답하며, Fig. 10의 개루프 위치제어 결과와 비교하여 응답시간이 현저하게 향상되었다. 또한 피스톤의 평균속도는 전진행정에서 0.7 m/s 정도이며, 피스톤이 스트로크 끝단 부근에 도달하였을 때 H_∞ 제어기의 출력신호가 0으로 수렴하여 비례제어밸브에 인가되는 신호가 거의 없고, 비례제어밸브의 스풀이 포트를 막아 압축공기 공급을 차단한 상태로 된다. 이 때 공기압 실린더의 배기측 챔버의 압력이 증가하여 배압이 형성되고 피스톤에 쿠션이 작용하면서 피스톤의 속도가 낮아지고 스트로크 끝단에 충격 없이 도달하여 양호한 위치제어를 구현한다.

Fig. 10과 Fig. 11에서 보듯이 개루프 제어보다 H_∞ 제어가 응답성과 정상편차 등 제어성능이 우수한 것을 확인하였다. 또한 실험결과와 시뮬레이션 결과가 잘 일치하며, 제안한 공기압 실린더 위치제어계에 대한 모델링의 타당성과 H_∞ 제어의 유효성을 확인하였다.

4.3 외란제거 특성

공기압 실린더의 H_∞ 제어는 목표값 추종성과 더불어 외란제거와 시스템 파라미터 변동에 대한 영향을 효과적으로 제거하여야 한다.

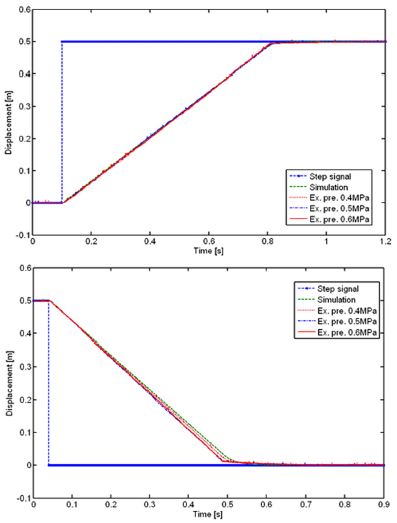
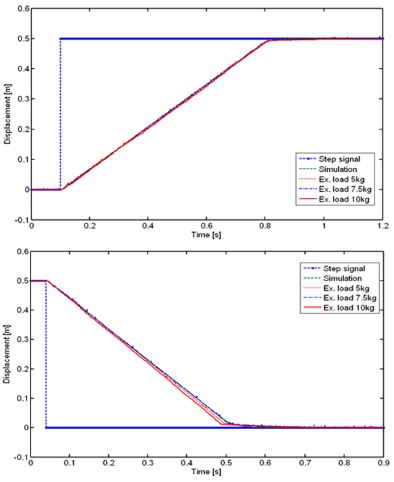
Fig. 12는 부하질량 10 kg에서 공급압력을 0.4 MPa ~ 0.6 MPa까지 변화시켜 외란제거 특성을 비교한 것이다. 피스톤의 전진과 후진행정의 변위파형을 비교해 보면, 전진행정에서는 부하가 일정한 경우 공급압력이 20 % 범위내에서 변동해도 과도응답과 정상상태의 특성에 큰 차이가 없다. 그러나 같은 조건에서 후진행정에서는 피스톤의 운동 초기에는 차이가 없지만 행정 끝단에 도달하는 할 때 약간의 위치편차가 발생하지만 바운드(Bound)현상 없이 목표값에 도달하는 것을 볼 수 있다.

Fig. 12

Comparison of experimental and simulated wave forms with supply pressure variations

Fig. 13은 공급압력 0.6 MPa에서 부하변동(5.0 kg, 7.5 kg, 10.0 kg)에 따른 외란제거 성능을 나타낸 것이다. 피스톤의 전진행정에서는 공급압력이 일정한 상태에서 부하가 변하여도 양호한 위치제어 성능을 얻을 수 있다. 피스톤의 후진행정에서는 공급압력의 변화에 대한 응답특성과 유사한 경향을 나타낸다. 즉 피스톤의 변위가 초기에는 부하변동에 큰 차이를 나타내지 않지만, 행정 끝단에 도달할 무렵에 약간의 편차가 나타난다. 이것은 부하가 변화함에 따라 피스톤 속도가 변하기 때문에 피스톤 속도에 영향을 받는 점성마찰력의 영향으로 생각된다.

Fig. 13

Comparison of experimental and simulated wave forms with load mass variations

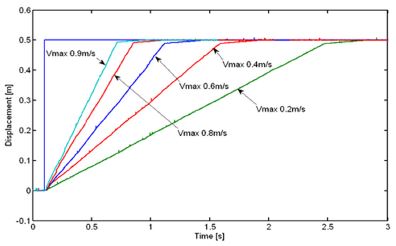
Fig. 14는 공급압력 0.5 MPa, 부하질량 5 kg의 전진행정에서 속도변화에 따른 제어특성을 나타낸다. 피스톤의 구동속도가 증가하여도 오버슈트나 스트로크 끝단에서 바운드 현상이 없이 양호한 제어성능을 나타낸다.

Fig. 14

Comparison of experimental and simulated wave forms with velocity variations