자동차용 휠 베어링 시일의 드래그 토크 예측


Copyright Ⓒ 2017 KSAE
Abstract
The primary function of bearing seals is to prevent lubrication from escaping and foreign materials from entering. The effectiveness of such function is determined by the design of the seal lips. Bearings with low friction rotation are in great demand in the automotive market as a direct result of the regulations stipulating vehicle fuel economy and reduced CO2 emission. Therefore, bearings with a good sealing function and low friction rotation are required. In this paper, estimation of the bearing rotational torque through numerical analysis, based on finite element methods, was investigated. This included calculation of the bearing rotational torque using an axisymmetric model from the commercial software, ANSYS. The seal rubber material properties were performed with three kinds of tension tests and were analyzed using the hyperelastic method for increased accuracy. The results of the analysis were compared with the empirical results and a strong correlation was confirmed.
Keywords:
Drag torque, Seal, Automotive wheel bearing, Rubber, Hyperelastic analysis키워드:
드래그 토크, 시일, 자동차용 휠 베어링, 고무, 초탄성 해석1. 서 론
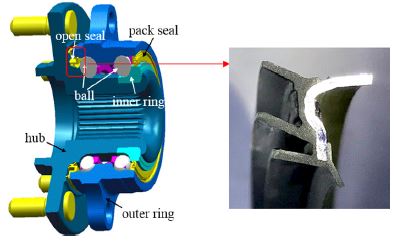
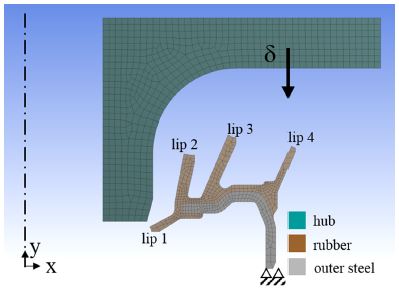
자동차용 휠 베어링은 차량의 무게를 지지하고 회전을 전달하는 부품이며 자동차용 휠 베어링 시일(Seal)은 베어링 외부로부터 이물질 등이 베어링 내부로 침입되는 것을 방지하고 그리스(Grease) 누유를 방지하는 부품이다. Fig. 1은 자동차용 휠 베어링의 구성 및 시일의 형상이다. 휠 베어링은 1960년대 전륜 구동형 자동차의 개발로 인한 경량화 요구로 유닛(Unit)화가 급속히 진행되었다. 휠 베어링 유닛은 속도센서, ABS 센서 등 각종 센서류의 장착으로 컴팩트(Compact)화 되었고, 플랜지(Flange)와 같은 주변 부품과의 조합으로 인하여 더욱 복잡한 형상으로 발전되었다. 또한, 최근 차량의 보증기간이 증가함에 따라 기존의 휠 베어링보다 긴 내구수명을 요구하며 사용기간 중 성능에 대한 신뢰성이 더욱 확실히 요구되고 있다. 휠 베어링의 내구수명은 다른 자동차 부품과는 달리 베어링 밀봉성능 저하에 따른 전동체(Rolling element)와 궤도(Raceway) 사이의 윤활불량에 의한 휠 베어링 손상에 기인하며, 이러한 현상은 베어링의 수명 저하 현상의 대부분을 차지한다. 수명 저하에 가장 영향을 미치는 것이 외부로부터 유입되는 이물질이며, 이물질 유입 방지 역할을 하는 것이 휠 베어링 시일이다.1-4)
최근 전기자동차, 친환경 자동차의 필요성이 대두됨에 따라서 자동차의 연비 저감 및 CO2 배출가스 저감이 자동차 업체들의 가장 중요한 이슈(Issue)가 되고 있다. 휠 베어링은 자동차 전체의 연비 중에서 차지하는 비중이 적지만, 회전부품이므로 그 중요성은 상대적으로 크다고 할 수 있다. 휠 베어링의 연비는 드래그 토크(Drag torque)와 관련이 있으며, 드래그 토크에 핵심적인 역할을 하는 것이 시일이다. 따라서 휠 베어링의 드래그 토크를 줄이기 위해서는 특히 시일에 대한 연구가 반드시 필요하다.
허영민 등5)은 여러 가지 형상설계 변수값들의 변화에 따른 휠 베어링용 시일 립(Lip)의 접촉 수직력과 기동토크를 수치적으로 계산하였다. 계산 결과로부터 기동 토크에 대한 요구 설계기준을 만족시키면서 충분한 밀봉성을 발휘할 수 있는 설계값을 제안하였다. 문형일 등6)은 휠 베어링 시일의 비선형 해석을 수행하여 시일 립의 성능을 예측하고 시험 결과와 비교하여 해석 모델의 신뢰성을 평가하였다. 또한 반응표면법을 이용하여 시일의 형상 최적화를 수행하였다. 김정주7)와 박종직8)은 각각 유한요소 해석을 통하여 자동차용 휠 베어링 시일의 드래그 토크를 예측하였다. 해석으로부터 도출한 접촉력(Contact force)을 이용하여 시일의 드래그 토크를 계산하였다. 계산 값과 측정 값의 오차를 해결하기 위하여 가중치(Weighting factor)를 도입하였다. 그러나 이들 연구들은 베어링 시일에서 가장 기본이 되는 고무의 물성을 하나 또는 두 가지의 시험만으로 예측하였고, 시일 립과 베어링 사이의 마찰계수의 영향을 무시하였다.
본 논문에서는 자동차용 휠 베어링 시일의 드래그 토크 예측에 대하여 고찰하였다. 이를 위하여 유한요소법에 기반한 수치해석을 이용하여 시일의 드래그 토크를 예측하는 기법을 개발하였다. 고무 해석의 신뢰성을 향상시키기 위하여 세 가지 고무 물성시험을 수행하였고, 시일 립의 마찰을 고려하기 위하여 마찰계수 시험을 수행하였다. 이를 이용하여 접촉을 고려한 초탄성 해석(Hyperelastic analysis)을 수행하였다. 해석의 신뢰성을 검증하기 위하여 드래그 토크 시험을 실시하였고, 해석 결과와 시험결과를 비교하였다. 개발된 드래그 토크 예측 기법을 이용하여 고무 물성시험 데이터의 영향과 마찰계수의 영향을 고찰하였다.
2. 고무해석이론 및 고무시험
2.1 고무해석이론
고무와 같이 대변형이 발생하는 재료의 거동을 모사하기 위하여 초탄성 모델이 사용된다. 단위체적당 변형률에너지 포텐셜(Strain energy potential) U의 변화율이 응력에 의한 일률과 같다는 개념을 이용하면 초탄성 재료의 거동은 식 (1)과 같이 표현된다.
| (1) |
where, T : second Piola-Kirchoff stress tensor
ϵ : green-Lagrange strain tensor
고무의 변형은 탄성이며 등방성이라는 가정 하에 변형률에너지 U를 불변량(Invariant) I1,I2,I3의 함수로 표현하면 식 (2)와 같다.
| (2) |
변형률 불변량을 주 신축성(Principal stretch), λ으로 표시하면 다음과 같다.
| (3) |
일반적으로 고무재료는 거의 비압축성(Incompressible)이라고 가정할 수 있다. 따라서 체적 탄성률(Bulk modulus)은 전단계수(Shear modulus)보다 상대적으로 크다. 고무재료의 비압축성을 고려하면 식 (3)의 I3는 1이 되기 때문에 식 (2)는 I1과 I2로 표현할 수 있고 변형률에너지 포텐셜의 변분, ∂U은 식 (4)와 같이 나타낼 수 있다.
| (4) |
초탄성 거동을 모사하기 위한 재료 모델로는 식 (5), (6)과 같이 Moony-Rivlin, Ogden 등 다양한 변형률에너지 포텐셜 식이 있다.9,10)
| (5) |
| (6) |
where,
C10,C01: material constants
D1: material incompressibility parameter
Jel: determinant of the elastic deformation gradient
N,αi,μi,Di: material constants
고무재료의 특성은 식 (5), (6)의 상수, C10,C01,D1,Jel,N,αi,μi,Di에 의하여 결정되며, 이들은 고무의 물성시험, 즉 단축인장시험, 평면인장시험, 이축인장시험으로부터 얻을 수 있다.9,10)
2.2 고무 물성시험
고무재료의 유한요소 해석을 위해서는 고무재료의 물성시험을 통하여 고무의 물성 상수를 결정해야 한다. 고무재료 물성시험의 종류로는 단축인장시험(Uniaxial tension test), 평면인장시험(Planar tension test), 이축인장시험(Biaxial tension test) 등이 있으며, 이 시험결과를 이용하여 해석 시 고무모델의 물성을 모델링할 수 있다. 위의 시험들 중 하나의 시험만으로도 고무재료의 물성계수를 결정할 수 있으나, 실제 해석 적용 시 모델의 변형률 범위 및 변형 거동현상에 따라서 여러 가지 변형 모드를 볼 수 있도록 두 가지 이상의 시험 데이터를 이용하는 것이 바람직하다. 또한, 고무는 반복적인 변형이나 하중이 가해질 때 강성의 감소와 점성으로 인한 히스테리시스(Hysteresis)가 나타나는 Mullins 효과가 존재하므로 재료 시험 시 수 회 반복적인 시험을 수행하여야 한다.
단축인장시험은 고무의 물성을 평가하는 시험 중 가장 기본적인 시험으로 인장변형에 대한 특성을 평가하기 위한 시험이다. 본 논문에서는 ASTM D412-C11)의 규격시편을 이용하여 시험을 수행하였다. 시험은 1 kN의 로드셀(Loadcell)을 사용하여 23 °C에서 20 mm/min의 시험속도, 20 mm의 표점거리의 조건으로 측정하였다. Mullins 효과에 대한 데이터를 얻기 위하여 Loading, Unloading, Reloading의 과정을 4~5회 정도 반복하여 응력-변형률 선도(Stress-strain curve)를 얻었다. 또한, 고무재료는 변형률에 따라 재료의 연성이 달라지는데 이는 고무분자의 가교성의 손실이 변형률에 따라 서로 다르게 나타나기 때문에 발생하는 현상이다. 이를 고려하기 위하여 베어링 시일의 변형하는 변형률에 맞춰서 20 %, 50 %, 80 %, 100 %의 변형률에 대하여 각각 시험을 진행하였다. 시험은 3개의 시편에 대하여 진행하였다.
평면인장시험은 고무의 전단변형에 대한 특성을 평가하기 위한 시험이다. 전단변형의 특성상 시편의 높이 대비 폭을 넓게 하여 양끝단의 변형을 최소화함으로써 재료에 전단변형이 발생하도록 하는 것이 중요하다. 평면인장시험 시편은 일정한 규격이 제시되어 있지는 않으나 순수전단변형을 위해서는 시편의 폭과 높이의 비를 약 10:1 이상으로 제작하는 것이 일반적이다. 본 논문에서는 단축인장시험과 동일하게 3개의 시편에서 20 %, 50 %, 80 %, 100 %의 변형률에 대하여 각각 시험을 진행하였다.
이축인장시험은 고무의 압축변형에 대한 특성을 평가하기 위한 시험이다. 단순압축시험은 지그(Jig)와 고무시편의 접촉면에서 발생하는 마찰로 인하여 순수한 압축모드를 얻기가 어렵다. 등가 이축인장시험(Equal-biaxial tension test)은 단순압축시험과 동일한 변형모드가 발생하며 시험방법이 상대적으로 용이하다는 장점이 있으므로 본 논문에서는 등가 이축인장시험을 수행하였다.12) 평면변형시험과 동일하게 3개의 시편에서 20 %, 50 %, 80 %, 100 %의 변형률에 대하여 각각 시험을 진행하였다.
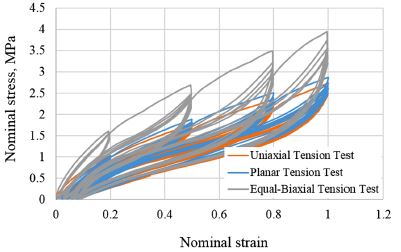
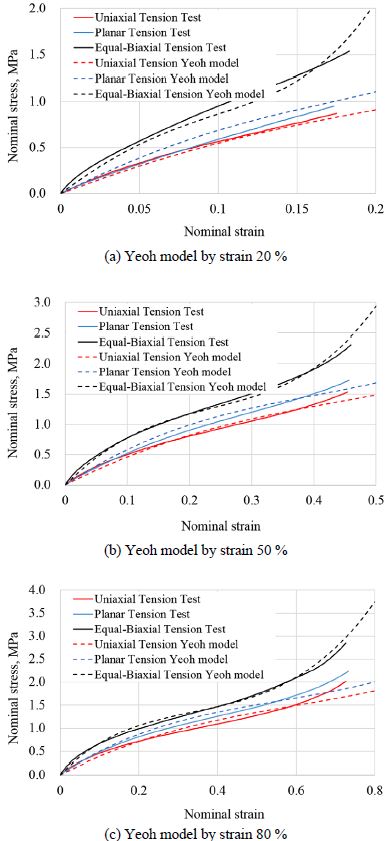
Fig. 2는 각각 단축인장시험기, 평면인장시험기, 등가 이축인장시험기이며, Fig. 3은 단축인장시험, 평면인장시험, 등가 이축인장시험의 결과이다. 시험 시 Loading, Unloading, Reloading의 과정을 4 ~ 5회 반복하였고, 이로 인하여 히스테리시스가 발생하는 Mullins 효과를 Fig. 3에서 확인할 수 있다. 또한, 20 %, 50 %, 80 %, 100 %의 변형률에 대하여 시험을 수행하였고, 각각의 변형률에 따라서 고무 재료의 연성이 달라지는 것을 알 수 있다. 세 가지 시험의 크기순서는 단축인장시험, 평면인장시험, 등가 이축인장시험의 순서로 나타났고, 이는 일반적인 고무 물성시험의 결과와 일치하는 결과이다.
2.3 고무 마찰계수시험
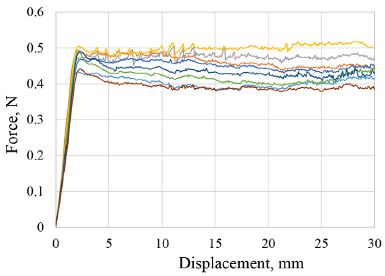
시일의 마찰계수(COF, Coefficient of friction)값을 계측하기 위하여 마찰계수 측정 시험을 UTM을 이용하여 Fig. 4와 같이 수행하였다. 시험에 사용되는 로드셀은 100 N이며, 마찰하중은 2 kg이다. 시험속도는 50 mm/min이며, 이송량(Displacement)은 30 mm이다. 실제 휠 베어링 시일 사용 시 그리스가 도포되어 사용되므로 시험에서도 그리스를 도포하여 측정하였다. 시험은 8회를 측정하였고, 결과는 Fig. 5에 나타내었다. Fig. 5에서 알 수 있듯이 마찰계수는 이송량 위치에 따라서 약간의 차이를 보인다. 즉, 이송량 5 mm에서의 마찰계수가 가장 작으며, 이송량이 증가할수록 마찰계수가 증가하여 이송량이 15 mm 부터는 거의 일정한 마찰계수 값을 갖는다. 본 연구에서는 Fig. 5의 마찰계수 값 중에서 이송량 15 ~ 30 mm 구간에서의 마찰계수인 0.024를 사용하였다. 이 값은 일반적으로 문헌13)에서 얻은 마찰계수와 비교해 볼 때 상당히 작은 값이며, 그 이유는 그리스가 도포되었기 때문이라고 예상된다.
3. 드래그 토크 예측
3.1 드래그 토크 시험
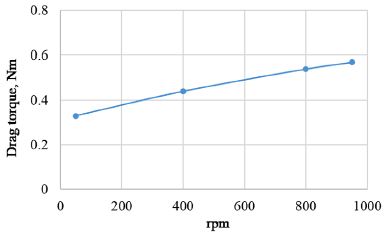
자동차용 휠 베어링 시일의 드래그 토크를 측정하기 위하여 Fig. 6과 같이 드래그 토크 측정 시험을 수행하였다. 드래그 토크 측정은 외륜 지그(Outer ring jig)에 시일을 장착하고, 허브 지그(Hub jig)에 그리스를 도포한 후 실제 조립조건과 동일한 조건으로 외륜 지그와 허브 지그를 장착하고 베어링을 회전하면서 토크 값을 측정하였다. 30분간 시운전 후 1분간 장비를 정지시킨 후 측정 RPM별로 회전하면서 측정하였다. 시험은 총 5회를 측정하였고, 측정 평균값은 Fig. 7과 같다. RPM에 따른 드래그 토크 값을 Excel을 이용하여 추세선을 구하면 식 (7)과 같고 그때의 R2값은 0.9944이다. 즉, RPM에 따른 드래그 토크는 거의 선형으로 변화한다. 식 (7)로부터 0 RPM의 값을 구하면 0.32 Nm이며, 이 값은 정지 시 드래그 토크를 의미한다.
| (7) |
3.2 드래그 토크 해석
자동차용 휠 베어링 시일의 드래그 토크를 예측하기 위하여 시일의 변형해석을 수행하였다. 해석 대상은 허브와 시일이며, 시일은 시일 립와 외철(Outer steel)로 구성된다. 시일의 형상이 축대칭(Axisymmetric)이므로 2차원 축대칭으로 모델링하였다. 해석은 상용소프트웨어인 ANSYS Workbench v.17.214)를 사용하였다. 해석에 사용된 요소(Element)는 각 요소 당 자유도(Degree of freedom)가 Ux,Uy로 2개인 MESH200, 3 node axisymmetric linear triangle 요소와 MESH200, 4 node axisymmetric linear quadrilateral 요소이다. 메쉬(Mesh)는 ANSYS Workbench 내부 명령어를 이용하여 수행하였다. 3 node axisymmetric linear triangle의 요소 수는 24이며, 4 node axisymmetric linear quadrilateral의 요소 수는 1036이다. 전체 절점(Node) 수는 1222이다.
경계조건으로 Fig. 8에서 알 수 있듯이 외철 끝단의 모든 자유도를 고정하였다. 하중조건으로 허브가 아랫방향(y direction)으로 δ 내려가는 조건을 가하였다.
| (8) |
시일의 변형해석을 위하여 대변형(Large deformation)을 고려하였고, 시일 립과 허브의 접촉(Contact)을 고려하였다. 접촉 조건은 침투(Penetration)가 0인 Normal Lagrange로 설정하였고, 마찰계수는 2.3절에서 구한 0.024를 입력하였다. 허브와 외철의 물성치는 Table 1과 같다.
2.2절에서 언급한 고무 물성시험 데이터를 해석에 적용하기 위하여 여러 가지 변형률에너지 포텐셜 식 중 식 (9)에 언급한 Yeoh 3차 모델(Yeoh 3rd order model)14)을 사용하였다.
| (9) |
where,
C10,C20,C30: material constants
D1,D2,D3: material incompressibility parameter
식 (9)에서 C10,C20,C30,D1,D2,D3는 고무의 단축인장시험, 평면인장시험, 등가 이축인장시험 결과로부터 계산된다. Fig. 9는 100 % 변형률에 대한 고무물성시험 결과와 Yeoh 모델에 대한 응력-변형률 선도이다. Fig. 9의 물성시험 결과와 Yeoh 모델의 결과가 유사함으로부터 본 논문에서 제안하는 Yeoh 모델의 변수들이 적절히 선정되었음을 알 수 있다.
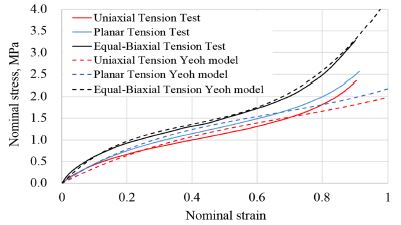
Stress-strain curves by uniaxial tension test, planar tension test, equal-biaxial tension test and their Yeoh models at strain 100 %
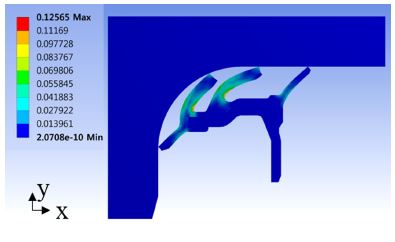
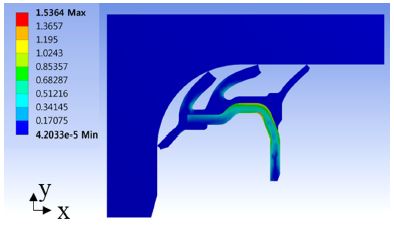
Fig. 8에서 언급한 메쉬, 경계조건, 하중조건과 Table 1에서 언급한 허브와 외철의 물성치, Fig. 9에서 언급한 고무 물성치를 이용하여 시일의 변형해석을 수행하였다. Fig. 10, Fig. 11, Fig. 12는 각각 변형량, 등가 탄성변형률(Equivalent elastic strain), 등가응력(Equivalent von mises stress)을 나타낸다. Fig. 10에서 알 수 있듯이 시일의 최대 변형량은 각 립마다 다르며 각각 0.4 mm, 1.3 mm, 1.9 mm, 0.8 mm이다. Fig. 11, Fig.12에서 각각 알 수 있듯이 최대 변형률이 0.13, 최대 응력이 1.5 MPa이다.
시일의 드래그 토크는 식 (10)과 같이 계산할 수 있다. 위치벡터(Position vector), ri는 립의 초기위치와 변형 후 위치로부터 계산할 수 있고, 하중벡터(Force vector), Fi는 립에서의 접촉 반력(Contact reaction force)으로부터 계산할 수 있다. Table 2는 각 립에서 계산된 위치벡터와 하중벡터, 드래그 토크를 나타낸다.
| (10) |
where, N: total number of lips, ri : position vector, and Fi : force vector
3.1절의 드래그 토크 시험 결과, 0 RPM의 값은 0.32 Nm이며, 이에 해당하는 드래그 토크 해석 결과는 0.30 Nm이다. 이로부터 드래그 토크 해석 결과가 시험을 잘 예측함을 알 수 있다. 따라서 본 논문에서 제안하는 해석 기법을 이용하면 자동차용 휠 베어링 시일의 드래그 토크를 잘 예측할 수 있음을 예상할 수 있다.
4. Case Study
4.1 고무 물성시험 중 변형률의 영향
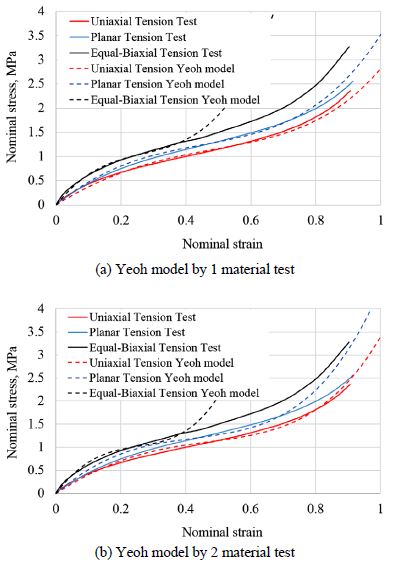
고무 물성시험 중 변형률의 영향을 파악하기 위하여 20 % 변형률 데이터를 이용한 경우, 50 % 변형률 데이터를 이용한 경우, 80 % 변형률 데이터를 이용한 경우, 100 % 변형률 데이터를 이용한 경우에 대하여 각각 식 (9)에 언급한 Yeoh 3차 모델을 이용하여 응력-변형률 선도를 계산하였다. 모델링된 응력-변형률 선도는 Fig. 13에 나타내었고, 이를 이용하여 계산한 드래그 토크는 Table 3에 나타내었다.
Fig. 9와 Fig. 13에서 알 수 있듯이 고무 물성시험 결과와 Yeoh 모델은 그래프 끝 부분에서 상대적으로 큰 차이를 보인다. 이는 이 부분에서 Yeoh 모델이 시험결과를 정확히 반영하지 못하기 때문이다. 3.1절의 드래그 토크 시험결과와 비교한 결과, 100 % 변형률의 경우가 시험결과를 가장 잘 예측함을 알 수 있다.
4.2 고무 물성시험 중 시험 개수의 영향
고무 물성시험 중 시험 개수의 영향을 파악하기 위하여 단축인장시험 데이터만을 이용한 경우, 단축인장시험과 평면인장시험의 두 가지 시험 데이터를 이용한 경우, 단축인장시험, 평면인장시험, 이축인장시험의 세 가지 시험 데이터를 이용한 경우에 대하여 각각 식 (9)에 언급한 Yeoh 3차 모델을 이용하여 응력-변형률 선도를 계산하였다. 모델링된 응력-변형률 선도는 Fig. 14에 나타내었고, 이를 이용하여 계산한 드래그 토크는 Table 4에 나타내었다.
Fig. 14에서 알 수 있듯이 단축인장시험 데이터만을 이용하는 경우, 단축인장시험과 평면인장시험 데이터만을 이용하는 경우, 단축인장시험, 평면인장시험, 이축인장시험 데이터를 모두 이용하는 것을 비교해 볼 때, 단축인장시험 데이터만을 이용하는 경우와 단축인장시험과 평면인장시험 데이터만을 이용하는 경우는 Fig. 9에서와 같이 이축인장 상태를 제대로 모사하지 않음을 알 수 있다. 즉, 100 % 변형률의 경우, 세 가지 시험결과를 모두 이용한 경우의 응력은 4 MPa인데 비하여 한 가지 시험결과만을 이용한 경우의 응력은 26 MPa, 두 가지 시험결과를 이용한 경우의 응력은 17 MPa로서 큰 차이를 보임을 알 수 있다.
Table 4에서 알 수 있듯이 하나의 물성시험 데이터를 이용한 경우와 세 개의 물성시험 데이터를 이용한 경우의 드래그 토크는 0.05 Nm의 차이가 발생한다. 이 차이는 시일의 드래그 토크 0.30 Nm와 비교해 볼 때 무시할 수 없는 값이다. 따라서 하나의 물성시험 데이터를 이용하는 것은 시일의 드래그 토크를 정확히 예측하기 어렵다는 것을 알 수 있다. 이로부터 본 해석의 신뢰도를 위해서는 최소 두 가지 이상의 시험데이터를 이용하여야 함을 예상할 수 있다.
4.3 마찰계수의 영향
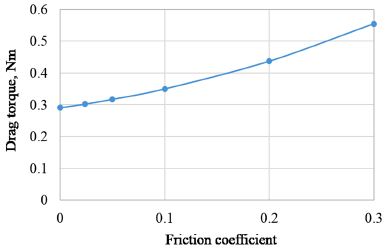
마찰계수는 재료의 물성치가 아니기 때문에 측정을 통하여 구하여야 하며, 본 논문의 경우 그리스 마찰의 마찰계수는 0.024이었다. 일반적으로 그리스가 없는 마찰의 마찰계수는 그보다 큰 값을 가진다. 마찰계수에 따른 드래그 토크의 영향을 알아보기 위하여 마찰계수를 0부터 0.3까지 증가시키면서 드래그 토크를 계산하였고, 그 결과를 Fig. 15에 나타내었다. Fig. 15에서 알 수 있듯이 마찰계수가 증가하면 드래그 토크가 증가한다. 마찰계수에 따른 드래그 토크 값을 3.1절과 유사한 방법으로 Excel을 이용하여 추세선을 구하면 식 (11)과 같고 그때의 R2값은 0.9997이다. 즉, 드래그 토크는 마찰계수의 제곱에 비례하며 드래그 토크를 낮추기 위해서는 마찰계수를 낮추는 것이 중요함을 예상할 수 있다.
| (11) |
5. 결 론
- 1) 본 논문에서는 자동차용 휠 베어링 시일의 드래그 토크를 예측하는 방법에 대하여 연구하였다. 해석의 신뢰성을 향상시키기 위하여 세 가지 고무 물성시험을 수행하였고, 마찰계수 시험을 수행하였다. 이를 이용하여 접촉을 고려한 초탄성 해석을 수행하였다. 해석의 신뢰성을 검증하기 위하여 드래그 토크 시험을 실시하였고, 해석결과와 시험결과를 비교하였다. 드래그 토크 해석 결과가 시험을 잘 예측함을 확인하였고, 이로부터 본 논문에서 제안하는 해석 기법을 이용하면 휠 베어링 시일의 드래그 토크를 잘 예측할 수 있음을 확인하였다.
- 2) 고무 물성시험 중 변형률의 영향을 고려하기 위하여 각각 20 %, 50 %, 80 %, 100 % 변형률 데이터를 이용하여 고무 물성 모델링을 수행하고, 드래그 토크를 계산하였다. 드래그 토크 시험결과와 비교한 결과, 100 % 변형률의 경우가 시험결과를 가장 잘 예측함을 알 수 있다.
- 3) 고무 물성시험 중 시험 개수의 영향을 고려하기 위하여 하나의 물성시험 데이터, 두 개의 물성시험 데이터, 세 개의 물성시험 데이터를 이용한 경우에 대하여 드래그 토크를 계산하였다. 계산된 드래그 토크를 비교한 결과, 본 해석의 신뢰도를 위해서는 최소 두 가지 이상의 시험데이터를 이용하여야 함을 예상할 수 있다.
- 4) 마찰계수에 따른 드래그 토크의 영향을 고려하기 위하여 마찰계수를 0부터 0.3까지 증가시키면서 드래그 토크를 계산하였다. 그 결과 드래그 토크는 마찰계수의 제곱에 비례함을 알 수 있었다.
References
- S. P. Lee, K. N. Kim, B. C. Kim, and I. H. Lee, “Deformation Analysis for Open Seal Mounting Part of Automotive Wheel Bearing”, KSPE Fall Conference Proceedings, p561-562, (2012).
- I. H. Lee, H. S. Jang, and S. P. Lee, “Deformation Analysis by Interference Fit for Inner Ring of Automotive Wheel Bearing Pack-Seal”, KSAE Annual Conference Proceedings, p1336-1338, (2010).
-
S. P. Lee, B. C. Kim, I. H. Lee, Y. G. Cho, and Y. C. Kim, “Distortion Analysis for Outer Ring of Automotive Wheel Bearing”, Transactions of the Korean Society of Mechanical Engineering: A, Vol.36(No.12), p1613-1618, (2012).
[https://doi.org/10.3795/ksme-a.2012.36.12.1613]

-
S. P. Lee, “Bearing Life Evaluation of Automotive Wheel Bearing Considering Operation Loading and Rotation Speed”, Transactions of the Korean Society of Mechanical Engineering: A, Vol.40(No.6), p595-602, (2016).
[https://doi.org/10.3795/ksme-a.2016.40.6.595]

- Y. M. Huh, K. O. Lee, T. Y. Sim, and S. S. Kang, “Study on Geometry Design of Lip-Seal for Automotive Wheel Bearing Considering Drag Torque and Sealing Performance”, Transactions of KSAE, Vol.15(No.4), p10-16, (2007).
- H. I. Moon, J. S. Im, and H. Y. Kim, “Shape Optimization of an Automotive Wheel Bearing Seal Using the Response Surface Method”, Transactions of KSAE, Vol.18(No.6), p84-90, (2010).
- J. J. Kim, A Study of Drag Torque Prediction on Automotive Wheel Bearing Seal, M. S. Thesis, Kangwon National University, Chuncheon, (2016).
- J. Z. Park, Measure to Improve the Accuracy of the Drag Torque Prediction on the Wheel Bearing Seals for Automobiles, M. S. Thesis, Kangwon National University, Chuncheon, (2016).
- R. S. Rivlin, “Large Elastic Deformations of Isotropic IV, Further Developments of the General Theory”, Philosophical Transations of the Royal Society: A, Vol.241, p379-397, (1948).
- R. W. Ogden, “Large Deformation Isotropic Elasticity on the Correlation of Theory and Experiments for Incompressible Rubber-like Solid”, Proceedings of the Royal Society of London, Vol.326, p565-584, (1972).
- ASTM International, ASTM D 412: Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers - Tension, West Conshohocken, (2016).
- K. Miller, Testing Elastomers for Hyperelastic Material Models in Finite Element Analysis, Axel Products, Inc, Ann Arbor, (2016).
-
R. J. Pinnington, “Rubber Frction on Rough and Smooth Surfaces”, Wear, Vol.267(Issues 9-10), p1653-1664, (2009).
[https://doi.org/10.1016/j.wear.2009.06.011]

- SAS IP, Inc, Engineering Data User’s Guide, ANSYS Workbench Documentation, ANSYS Release 17.2, (2016).