원형 광패턴을 활용한 능동방식 3차원 좌표 복원 알고리즘


Copyright Ⓒ 2017 KSAE
Abstract
The measurement of the 3D coordinates of an object surface from a 2D image has been significant in the areas of computer vision, pattern recognition, and machine learning, among others. In particular, it has gained much attention in practical fields, such as 3D camera system, automotive vision system, etc. This paper suggests an approach for the reconstruction of a 3D object surface from a 2D image that was captured by a camera. The camera captures the object overlaid with a set of concentric, circular-shaped light patterns. In the experiment, the geometric information of the light patterns, and the intrinsic and extrinsic parameters provide a mathematical model to achieve a 3D reconstruction result. The reconstruction is carried out on the basis of the relationship between the projected circular patterns and the deformed patterns by a 3D object surface. This paper primarily deals with establishing a mathematical proof of concept for 3D reconstruction by using structured circular light patterns.
Keywords:
3D coordinates reconstruction, Structured light patterns, Concentric circular patterns, 3D camera , 3D object키워드:
3차원 좌표 복원, 구조광 패턴, 동심원 패턴, 3차원 카메라, 3차원 물체1. 서 론
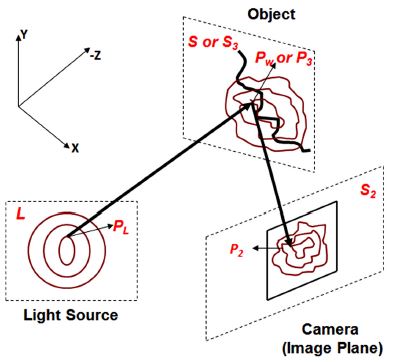
2차원 이미지로부터 실제 세계의 물체 또는 풍경의 3차원 정보를 복원하는 연구는 오랜 기간동안 지속되어 왔다.1,2) 3차원 복원 분야의 응용은 대체로 물체/얼굴 인식, 보안 등의 분야에 국한되어 있었으나, 지난 10여 년간 의료영상, 생산 자동화 시스템 등의 분야로 확대 되었다. 그리고 최근에는 3차원 복원 분야는 위 분야에서 확대되어 게임(가상현실, 증강현실), 자동차 분야 등 타 분야와의 융합에 반드시 필요하게 되었다.3-6) 특히 자동차 분야는 기존의 기계적인 분야에서 벗어나 자율주행, 무인자동차 등의 기술에 필요한 3차원 비전 시스템을 구축하기 위해 3차원 이미징 및 영상처리 분야를 도입하였다.7-10) 2차원 이미지로부터 3차원 좌표를 복원하는 기술은 기본적으로 2차원 이미지와 실제 3차원 물체간의 기하학적인 관계식을 정립 하는 것에서 출발한다. 3차원 복원은 크게 두 가지 방법으로 이루어진다. 한 가지는 수동방식(Passive method)11)이고 다른 한 가지는 능동방식(Active method)12-14)이다. 두 가지 방식을 혼합한 방식(Hybrid method)15,16)도 많이 활용되지만 기본적인 원리로 수동 및 능동 방식이 활용된다. 수동방식은 2개 이상(주로 2개)의 카메라를 활용하여 카메라가 획득한 물체의 이미지로부터 물체의 3차원 좌표를 복원하는 기술이다. 수동방식으로 대표되는 기술은 스테레오 방식이다. 스테레오 방식은 2개의 카메라로 목표물체를 찍은 후 2개의 카메라의 시차(Parallax)를 활용하여 물체의 깊이 정보를 획득하는 것이다. 스테레오 방식으로 3차원 복원을 하기 위해 카메라 캘리브레이션(Camera calibration) 과정은 필수적이다. 카메라 캘리브레이션은 물체의 3차원 정보와 카메라에 찍인 물체 이미지의 2차원 정보 사이의 관계를 정립하기 위해 필요한 파라미터를 제공한다. 이 파라미터는 내부(Intrinsic) 파라미터와 외부(Extrinsic) 파라미터로 구성되어 있다. 외부 파라미터는 2개 카메라들의 상대적인 위치 차이를 나타내며 회전(Rotation)과 이동(Translation) 행렬로 구성되어 있다. 외부 파라미터는 목표 물체의 상대적인 깊이를 계산할 수 있게 해주며 이것을 디스패리티(Disparity)라고 한다. 내부 파라미터는 상대적인(Relative) 깊이정보를 절대(Absolute)깊이 정보로 변환해 주며 초점거리(Focal length), 카메라의 이미지 중심(Principal point) 등으로 구성되어 있다.1,2) 카메라 캘리브레이션은 주로 체커보드 처럼 인위적으로 디자인된 평면 물체를 활용하여 진행된다. 효율적인 캘리브레이션을 위하여 다른 모양의 패턴 또는 다른 모양의 물체가 활용되지만, 상단한 시간과 계산 및 최적화 과정을 요구하는 작업이다.17) 수동방식은 캘리브레이션 등의 정교한 절차를 거쳐 3차원 정보 획득 결과의 정확성을 높이지만, 약점을 지니고 있다. 2개의 카메라로부터 획득된 이미지 간의 특이점 매칭의 과정은 높은 정확도를 요구하지만, 텍스쳐(Texture)가 부족한 물체 또는 반복패턴을 가진 물체, 저조도 환경 등에서 높은 오류를 보인다.18) 이런 약점을 극복하기 위하여 제안된 방식이 능동방식이다. 능동방식은 2개의 카메라 대신 1개의 카메라와 1개의 광원(Light source)을 활용하여 3차원 복원을 하는 기술이다. 광원은 인위적으로 디자인된 광패턴(Light pattern)을 생성하여 목표 물체에 투영(Projection)한다. 투영된 패턴은 물체의 모양에 따라 변형되며, 변형된 광패턴은 1개의 카메라에 의해 획득 및 분석된다. 투영되기 전과 후의 광패턴 정보를 비교 및 분석하여 3차원 복원을 한다. 색깔 패턴, 코드화 패턴 등 다양한 종류의 패턴들이 활용되었다.12,19) Time-of-flight 방식은 물체에 투영된 빛이 반사되는 시간을 측정하여 깊이정보를 획득하는 기술이다.20) 깊이 측정의 정확도는 광패턴 투영방식보다는 높다는 장점이 있으나, 높은 전력과 높은 해상도의 센서가 필요하다는 단점이 있다. 또한 능동방식은 실내에서 활용하기에는 부적합하다는 한계점을 지니고 있다. 그리하여 능동방식과 수동방식의 장점을 조합하여 하이브리드 방식 3차원 복원 방법이 소개되기도 하였다.21,22) 본 논문에서는 원형 광패턴을 활용한 3차원 복원 기술을 소개한다. 원형 광패턴을 생성하는 것은 매우 간단하다. 같은 중심점과 다른 반지름을 가지는 여러 개의 원형 광패턴을 물체에 투영한 후, 물체에 의해 일그러진 원형 광패턴을 분석하여 3차원 복원을 한다(Fig. 1). 카메라와 원형 광패턴의 위치는 고정되어 있다고 가정하며 핀홀(Pinhole) 카메라 모델을 가정한다. 광패턴이 물체에 투영되면 물체의 깊이에 따라 패턴이 일그러진다. 다시 말해서 광패턴이 물체에 투영된 후에는 광패턴이 원형이 아니라 깊이를 가진 3차원 모양의 폐곡선이 되는 것이다. 하지만 광패턴의 (x,y,z) 좌표중 z좌표만 변하고, (x,y) 좌표는 변하지 않는다. 다만 패턴이 평행투영 한다는 가정이 있어야 한다(Fig. 3). 평행투영을 가정하면 (x,y) 좌표가 불변이므로 다음의 식이 성립된다.
| (1) |
| (2) |
(xL,yL), (xw,yw) 는 각각 투영되기 전과 투영된 후의 좌표이다. 식 (1) ~ (2)은 본 논문의 3차원 복원 알고리즘의 수학적 모델 생성에 매우 중요한 역할을 하며, 궁극적으로 물체의 깊이정보 계산을 간단하게 만들어 준다. 이러한 특성은 3차원 복원 알고리즘의 계산 효율성을 높여주며, 다양한 응용분야의 상용화에 필요하다고 할 수 있다. 다음 장(2장)에서는 3차원 복원의 전체 시스템을 간략히 소개하고 3장에서는 본 논문에서 제안하는 알고리즘을 소개한다. 4장에서 실험결과를 제시한 후 5장에서 결론을 맺는다.
2. 3차원 복원 시스템의 구조
구조광 패턴을 활용한 3차원 복원 시스템은 카메라, 광패턴을 생성하는 프로젝터 또는 LED 광원, 목표인 3차원 물체로 구성되어 있다. LED 광원은 저비용으로 광패턴을 생성할 수 있다는 장점이 있으나 해상력의 문제 때문에 3차원 복원 알고리즘의 성능을 저하시킬 수 있으므로 해상력이 높은 일반 프로젝터를 사용하기도 한다(Fig. 1). 특정 패턴을 생성하여 3차원 복원에 활용할 경우 복원 알고리즘에 필요한 수학적 모델을 결정하기가 효율적이다. 3차원 복원의 전체 흐름도는 광 패턴 생성 및 투영, 카메라의 이미지 획득, 2차원 이미지와 3차원 물체의 좌표 간의 관계 분석 및 정립, 복원으로 이루어져 있다(Fig. 2).
서론에서 언급했듯이 본 연구에서 활용되는 광패턴은 중심이 같은 여러 개의 원으로 구성된 원형 패턴이다. 투영된 원형 패턴은 물체의 모양에 따라 변한다. 3차원 복원은 투영되기 전의 원형패턴과 투영된 후 패턴의 모양의 관계로부터 시작한다(Fig. 3).
Fig. 3에서와 같이 원형 패턴의 모양은 반지름과 중심점으로 표현할 수 있으며, 3차원 물체에 투영된 후 변형된 패턴의 모양은 물체의 3차원 좌표 정보를 반영한다. 그러므로 본 논문에서 제안하는 3차원 복원 알고리즘은 원형 패턴의 모양과 투영된 후 변형된 원형 패턴 모양의 관계를 활용한다. 본 논문에서 3차원 복원 알고리즘을 제안하기 위해 실험에서 몇가지 가정을 제시한다. 첫째는 원형 패턴의 평행 투영(Parallel projection) 이다. 둘째는 카메라 렌즈의 왜곡은 이미 해결이 되었거나 무시될 수 있을 정도이다. 셋째는 카메라의 모델은 핀홀 모델이며 마지막으로 카메라의 캘리브레이션은 이미 완료되었다는 가정이다. 이 가정들로부터 원형 패턴은 투영된 후 물체의 깊이 값에만 영향을 받게 되며 이 가정은 3차원 복원의 수학적 모델을 효율적으로 정립할 수 있게 해준다.
3. 3차원 복원 알고리즘 제안 모델
S⊂3은 3차원 물체가 정의된 영역이고, 이 영역에 포함된 점 Pw∈S는 다음과 같이 표현된다.
| (3) |
w는 실제 세계의 좌표(Real world coordinates)를 뜻하는 인덱스(Index)이다(Fig. 3). L⊂3는 원형 광패턴을 생성하는 광원의 위치가 정의된 영역이고, 패턴의 중심점은 원점으로 정한다. 패턴에 위치한 3차원 점 PL은 다음과 같이 표현된다.
| (4) |
| (5) |
i=1,2,......,M-1,M
j=1,2,.......,N-1,N
M,N은 패턴에 위치한 점의 개수와 패턴의 개수를 각각 나타낸다(Fig. 4).
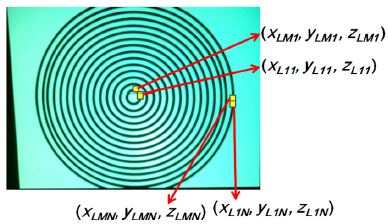
M and N are used to denote the number of points in the pattern and the number of patterns themselves, respectively
S3⊂3는 3차원 물체에 투영된 광패턴의 영역으로 정의되고 3차원 점 P3∈3는 투영된 광패턴에 포함된 점인 동시에 3차원 물체에 포함된 점이기도 하다. P3는 다음과 같이 표현된다.
| (6) |
그리고 P3와 Pw는 다음과 같이 표현될 수 있다.
| (7) |
| (8) |
3차원 물체에 투영된 패턴은 카메라에 의해 이미지로 획득이 되며, 이 이미지는 2차원 이미지이다. 카메라가 획득한 2차원 이미지의 영역은 S2⊂2로 정의되고 이 영역의 점 P2∈2는 다음과 같이 표현된다.
| (9) |
3차원 복원 문제는 P2로부터 P3를 추정하는 것이며, P3∈3,PL∈3,P2∈2 간의 기하학적인 관계를 찾는 것이다(Fig. 3).
f:L→S3,g:S3→S2는 3차원 물체로의 빛 패턴의 투영과 물체에서 카메라 영역으로의 이미지 반사를 각각 나타내는 함수이고, 3차원 복원 문제는 다음의 식으로 간단히 요약될 수 있다.
| (10) |
| (11) |
위에서 언급했듯이 빛 패턴의 평행 투영을 가정하므로 빛이 투영될 때 좌표 (x,y,z) 중에 (x,y)는 변하지 않는다. 또는 스케일링 팩터 (k)만큼만 변한다고 가정할 수 있으나 k=1로 가정하면 (x,y)는 불변한다고 할 수 있다. 특히 카메라 렌즈의 왜곡모델링은 본 논문에서는 고려하지 않기로 한다.
| (12) |
f는 빛의 투영을 나타내는 함수이고, k는 상수이므로 편의상 1로 정한다. 빛은 평행하게 투영되므로 다음의 식이 성립한다.
| (13) |
| (14) |
식 (12) ~ 식 (14)에서와 같이 평행투영은 (x,y)를 유지시키므로, 3차원 물체는 투영된 빛의 z 좌표만 변형시킨다. 그러므로 z는 변형계수 또는 깊이정보로 정의할 수 있다.
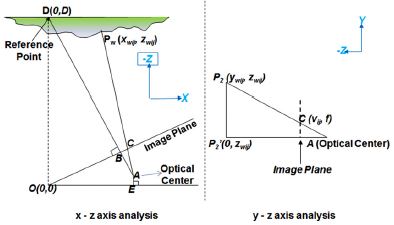
위에서 언급했듯이 본 논문에서 제안하는 3차원 복원 알고리즘은 원형의 빛 패턴을 투영한 후 목표물체의 모양에 따라 변하는 패턴의 모양을 분석함으로서 이루어진다. 이러한 패턴의 변형을 정량적으로 분석하여 3차원 복원을 수행할 수 있을 뿐만 아니라 효율적인 3차원 복원의 응용분야에 적용할 수 있다. 핀홀 모델의 카메라를 가정하였을 때 3차원 복원을 위한 수학적 모델을 제안하기 위해 3차원 (x,y,z) 축을 (x,z)와 (y,z) 축 두 개로 나누어 나타내면 Fig. 5와 같이 나타난다. Fig. 5에 기반하였을 때 다음과 같은 수식들이 성립된다.
| (15) |
| (16) |
| (17) |
| (18) |
f 는 카메라의 초점거리이며 동일 카메라에서의 초점거리는 불변한다고 가정한다. 점 C는 카메라가 획득한 3차원 점 Pw가 2차원으로 투영된 것이다. A,B는 광심(Optical center)와 이미지 중심(Image center)을 각각 나타낸다. θ1=∠AOE, θ1+θ2=θ, d2= 로 두었을 때 점 A,B,C 는 각각 다음과 같이 표현될 수 있다.
A=(-dcosθ1,dsinθ1)
B=(-d1cosθ,d1sinθ)
C=(-d2cosθ,d2sinθ)
식 (15) ~ (18)에 포함된 파라미터들은 카메라 캘리브레이션과 밀접한 연관이 있다. 3차원 복원 과정에서 캘리브레이션은 매우 중요한 과정이다. 그러나 본 논문에서는 자세히 다루지 않는다. 와 가 점 A에서 만나는 특성(핀홀 모델을 가정하였을 때)을 활용하여 3차원 점 Pw=(xw,yw,zw)를 구하는 과정, 즉 3차원 복원의 수학적 모델은 아래와 같이 표현된다.
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
4. 실험 결과
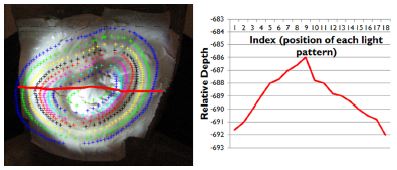
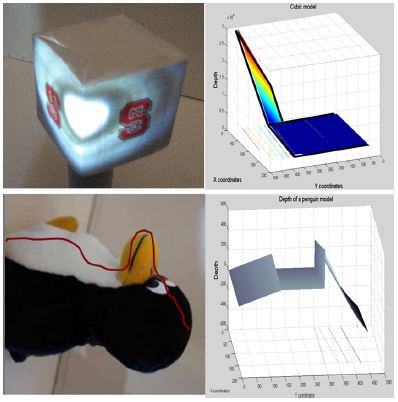
본 장에서는 3장에서 제시한 3차원 복원 알고리즘의 수학적 모델의 시뮬레이션 결과를 제시한다. 실험은 일반 디지털 카메라(Cannon 카메라, 해상도 1280×720) 와 LC2002 Light Modulator(해상도 최대 800×600 pixels)를 활용하였다. 실험 단계에서는 카메라가 획득한 2차원 점 (P2=(u,v) )은 수동 획득 하였다. Fig. 6 에서는 우선 붉은 선을 지나는 부분의 깊이값 (z)을 계산하여 나타내었다.
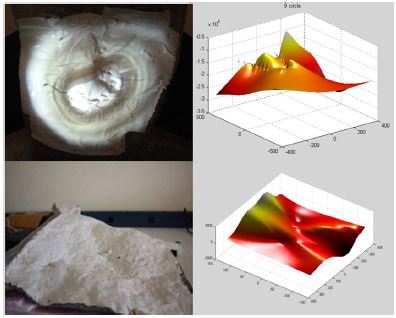
기에 3장에서 제시한 알고리즘을 활용한 3차원 복원 시뮬레이션 결과를 Figs. 7, 8에 나타내었듯이 원형 광패턴을 활용한 3차원 복원은 수학적 모델의 정립의 용이함, 실험의 간결성 등의 장점이 있다. Fig. 7에서는 연속적인 면을 가진 물체의 3차원 복원을 나타내었다. 반면에 Fig. 8에서는 불연속적인 면을 가진 물체의 3차원 복원 결과를 나타내었다.
3차원 복원의 결과를 평가하기 위해서는 참값과의 좌표를 비교하여 볼 수 있으나, 본 논문에서 활용된 물체들은 실제의 일반적인 물체이므로 정확한 참값을 정하기 어려운 점이 있다. 또한 본 논문에서 제시한 알고리즘은 상대적인 깊이값, 즉 상대적인 3차원 좌표를 구하는 수학적 모델을 제시한 것으로서 3차원 복원의 정확한 성능을 표현하기는 어렵다. 상대적인 깊이 값들의 변화량과 실제 물체의 깊이의 변화량 값을 수동으로 측정하여 상관계수를 측정 (0≤correlation≤1)하여 본 연구의 3차원 복원 성능을 아래 Table 1과 같이 타나내었다.
| (24) |
물체 모양의 변화가 크고 다양할수록 광패턴을 활용한 3차원 복원 결과의 유사도가 떨어지는 경향이 있으며, 이론적으로는 광패턴의 밀도를 증가시켜 복원의 정확도를 높일 수 있다. 또한 물체의 변화에 따라 광패턴의 불연속적인 부분이 발생할 경우 복원의 정확도는 떨어지게 된다. 본 연구에서 수행된 실험에서는 얼굴 모델이 타 모델 대비 복원 결과의 정확도가 떨어지는 경향을 보이지만, 광패턴 밀도의 증가 또는 광원의 변화 등을 통하여 성능 향상을 기대할 수 있다. 깊이 값의 정확도는 기존의 연구들에 비하여 모든 물체에 대하여 우세한 것은 아니지만 본 연구에서 제시한 원형 광패턴을 활용한 3차원 복원의 절차 및 수학적 모델은 기존의 연구들 대비 효율성에서 우세하다고 볼 수 있다.
5. 결 론
본 논문에서는 원형 광패턴을 활용한 3차원 복원 알고리즘을 제시하였다. 본 연구에서는 원형 광패턴을 활용한 3차원 복원의 수학적 모델을 제시하였으며, 본 연구를 기반으로 하여 향후 3차원 카메라 시스템, 무인장동차, 가상현실, 증강현실 등 3차원 이미징 기술이 필요한 부분에 다양하게 응용할 수 있을것으로 기대한다. 본 논문에서 제시한 원형 광패턴은 여러 가지의 장점을 보여준다. 첫째는 원형 광패턴의 수학적 표현의 간결성이다. 기존에 활용되었던 광패턴들과는 다르게 원형 광패턴은 수직 및 수평 방향의 정보를 동시에 가지고 있으며, 이 정보들을 하나의 수식으로 간단하게 표현할 수 있다. 둘째는 실험적으로 원형 광패턴의 생성이 간단하다는 점이다. 기존의 패턴들과는 달리 원형 광패턴은 반지름과 중심점만으로 패턴을 표현할 수 있다. 그리하여 광패턴을 생성하는 광원의 위치 고정 및 실험 장비 구축에 많은 시간을 들이지 않아도 된다. 그러나 본 연구와 관련하여 향후 개선해야할 점은 여전히 존재한다. 좀 더 정확한 3차원 복원을 위해 광패턴의 비평행적 투영(Non-parallel projection), 카메라 렌즈 왜곡(Lens distortion)모델링, 카메라 캘리브레이션 등은 앞으로 본 연구 뿐만 아니라 능동방식 3차원 복원 연구에서 지속적으로 연구가 되어야 한다.
References
- O. Faugeras, and Q. T. Luong, The Geometry of Multiple Images, The MIT Press, Cambridge, (2001).
- R. Hartley, and A. Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, 2nd Edn., Cambridge, (2003).
- A. Nigam, G. Chhalotre, and P. Gupta, “Pose and Illumination Invariant Face Recognition Using Binocular Stereo 3D Reconstruction”, Pattern Recognition, Image Processing and Graphics (NCVPRIPG), Fifth National Conference on Computer Vision, p1-4, (2015).
- A. Sinha, and K. Chakravarty, “Pose Based Person Identification Using Kinect”, International Conference on Systems, Man, and Cybernetics, p497-503, (2013).
-
A. Marro, T. Bandukwala, and W. Mak, “Three-Dimensional Printing and Medical Imaging: A Review of the Methods and Applications”, Current Problems in Diagnostic Radiology, Vol.45(No.1), p2-9, (2016).
[https://doi.org/10.1067/j.cpradiol.2015.07.009]

- S. Khattak, B. Cowan, I. Chepurna, and A. Hogue, “A Real-time Reconstructed 3D Environment Augmented with Virtual Objects with Correct Occlusion”, IEEE Games Media Entertainment, p1-8, (2015).
- A. N. Catapang, and M. Ramos, “Obstacle Detection Using a 2D LIDAR System for an Autonomous Vehicle”, 6th IEEE International Conference on Control System, Computing and Engineering, p441-445, (2016).
- H. Zhao, and R. Shibasaki, “A Vehicle-borne Urban 3-D Acquisition System Using Singlerow Range Scanners”, IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol.33(No.4), p658-666, (2003).
- J. Hwang, D. Hong, K. Huh, D. I. Cho, and J. H. Park, “Development of Vision Sensor Based 3D Obstacle Detection System”, KSAE Fall Conference Proceedings, p1169-1174, (2005).
- J. Hwang, D. Hong, and K. Huh, “Development of a Vision Sensor-based Vehicle Detection System”, Transactions of KSAE, Vol.16(No.6), p134-140, (2008).
- S. M. Seitz, B. Curless, J. Diebel, D. Scharstein, and R. Szeliski, “A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms”, IEEE Computer Society Conference on Computer Vision and Pattern Recognition, p519-528, (2006).
- J. Geng, “Structured-light 3D Surface Imaging : a Tutorail”, Advances in Optics and Photonics, Vol.3(No.2), p128-160, (2011).
-
P. Lavoie, D. Ionescu, and E. M. Petriu, “3D Object Model Recovery from 2D Images Using Structured Light”, IEEE Transactions on Instrument and Measurement, Vol.53(No.2), p437-443, (2004).
[https://doi.org/10.1109/tim.2004.823320]

- V. Ganapathi, C. Plagemann, D. Koller, and S. Thrun, “Real Time Motion Capture Using a Single Time-of-flight Camera”, IEEE Computer Society Conference on Computer Vision and Pattern Recognition, p755-762, (2010).
- V. Gandhi, J. Cech, and R. Horaud, “Highresolution Depth Maps based on TOF-stereo Fusion”, IEEE International Conference on Robotics and Automation, p4742-4749, (2012).
- C. Lee, H. Song, B. Choi, and Y. S. Ho, “Multi-view Generation Using High Resolution Stereoscopic Cameras and a Low Resolution Time-of-Flight Camera”, The Journal of Korean Institute of Communication and Information Science, Vol.37A(No.4), p239-249, (2012).
-
Z. Zhang, “A Flexible New Technique for Camera Calibration”, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22(No.11), p1330-1334, (2000).
[https://doi.org/10.1109/34.888718]

-
A. Dipanda, and S. Woo, “Towards a Real-time 3D Shape Reconstruction Using a Structured Light System”, Pattern Recognition, Vol.38(No.10), p1632-1650, (2005).
[https://doi.org/10.1016/j.patcog.2005.01.006]

-
J. Salvi, J. Pages, and J. Batlle, “Pattern Codification Strateges in Structured Light Systems”, Pattern Recognition, Vol.37(No.4), p827-849, (2003).
[https://doi.org/10.1016/j.patcog.2003.10.002]

- M. Hansard, S. Lee, O. Choi, and R. P. Horaud, Time-of-Flight Cameras-Principles, Methods and Applications, Springer Briefs in Computer Science, Springer, London, (2013).
- S. Choi, B. Ham, C. Oh, H. G. Choo, J. Kim, and K. Sohn, “Hybrid Approach for Accurate Depth Acquisition with Structured Light and Stereo Camera”, IEEE International Symposium on Broaband Multimedia Systems and Broadcasting, p1-4, (2012).
- J. Zhu, L. Wang, R. Yang, J. E. Davis, and Z. Pan, “Reliability Fusion of Time-of-Flight Depth and Stereo Geometry for High Quality Depth Maps”, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.33(No.7), p1400-1414, (2011).