해석적 접근을 통한 기어 마찰 동력 손실 예측 및 최소화
Copyright Ⓒ 2017 KSAE
Abstract
A highly efficient parallel-axis gear train is widely used in automobile transmissions. Power losses in a parallel-axis gear train are mainly generated by gears and bearings. In this study, an analytical methodology is introduced to predict the friction-related mechanical power loss of a gear pair in a parallel-axis gear train. The mechanical power loss of a gear under typical operating and lubrication conditions is estimated through a gear contact analysis model and a friction coefficient formulation. A design parameter study is performed to identify the effect of the parameters on gear mechanical power loss. Design optimization is also conducted to minimize the mechanical power loss of the gear pair.
Keywords:
Parallel-axis geartrain, Mechanical power loss, Transmission efficiency, Friction coefficient, Teeth load sharing, Slip loss, Rolling loss키워드:
평행축기어트레인, 기계적동력손실, 전달효율, 마찰계수, 치하중분담, 미끄럼손실, 구름손실1. 서 론
최근 차량의 연비 향상을 위한 기술 개발 노력이 집중되고 있는 개발 환경 하에서 변속기에서는 전달효율 향상을 위한 기술 개발이 절실한 시점이다. 초기 개발 단계인 레이아웃 설계에서부터 부품의 손실 예측까지 전달효율을 정확히 예측하고, 부품의 기여도를 예측하는 것이 중요하다. 전달효율 측면에서 유리한 수동변속기 구조를 개량하고 이를 자동화한 DCT나 AMT를 도입하는 사례가 늘어나고 있다.1) 평행축 구조의 기어트레인에서의 전달효율은 대부분 기어나 베어링에 의한 손실로 나타난다.
국외의 기존 문헌들에서는 기어 마찰에 대한 손실은 1960~80년대에 시험적으로 구한 기어 마찰계수를 이용한 기어 손실 해석방법을 이용하거나, 최근 EHL 해석 기법을 이용하고 시험과 접목시킨 시도까지 다양한 방법으로 연구되어 왔다. 하지만 국내의 경우 오일에 의한 손실 개선에 집중하고 있다. 특히 기어의 마찰 특성을 고려하려는 시도는 박윤경 등2)에 의해서 있었으나, 마찰계수 등에 대한 연구가 부족하고 정확한 기어 물림 손실을 반영한 연구는 부족한 실정이다. 1960년대에 Drozdov and Gavrikov3), O'Donoghue and Cameron4), Misharin5)이나 Benedict and Kelly6)는 각각 특정 시험조건이나 오일조건에서 기어의 마찰 계수를 구하고 수식으로 만들어 사용하였다. 1984년 NASA의 Anderson and Loewenthal7)은 높은 접촉비를 갖는 평치차에서 효율을 접촉해석과 시험적인 마찰계수를 이용하여 계산하는 방법을 수립하였고 이를 적용한 상용 소프트웨어8)도 사용되고 있다. 이러한 실험식들은 시험에서의 제원이나 당시 사용한 오일의 특성에 한정된 경우로 좁은 구간에서의 정확성을 보인다. 최근 Li 등9), Li and Kahraman10)은 시험과 EHL해석을 결합한 새로운 기어 전달효율 해석 기법을 정립하고 시험과의 Correlation 결과를 발표하였고, 이는 가장 최신의 방법으로 알려져 있다.
본 연구에서는 이런 최신 기어 마찰 손실에 대한 해석 기법 이론을 소개한다. 최근의 변속기 기어트레인 설계에서 기어 물림에 의한 기어의 동력손실을 최소화하여 변속기 전달효율을 향상시키는 것은 매우 중요하다. 뿐만 아니라 기어 설계에서는 소음이나 내구 문제의 해결 또한 기초 과정이다. 따라서 기어의 동력손실 최소화를 위한 설계에서 소음이나 내구 문제에 대한 방향성을 알아 볼 수 있는 기어설계 인자 분석에 대한 논의를 수행한다. 또한 설계 인자의 가용 범위 안에서 기어의 마찰 동력 손실을 최소화하면서 굽힘 강도, 마멸성능, 소음 성능을 만족하는 균형있는 기어 설계를 수행하고 토의한다.
2. 기어의 마찰 동력 손실
기어트레인에서 동력 손실 메커니즘을 파악하고 수학적 모델을 통해 기어트레인에서 전달하는 동력의 손실을 계산하여 개선하고 최소화할 수 있다. 변속기에서의 동력 손실은 기어의 슬립, 쳐닝, 베어링, 습식클러치, 씰, 오일펌프 등 다양한 경로를 통하여 나타난다.
기어트레인에서 발생하는 손실은 크게 하중에 의한 손실(Load-dependent power loss)과 속도에만 관계된 하중에 무관한 손실(Load-independent power loss)로 나눌 수 있다.11,12) 하중에 의한 손실은 보통 기어 마찰에 의한 손실로써 마찰손실(Friction loss) 또는 기계적 손실(Mechanical loss)이라고 하고, 하중에 무관한 손실은 오일 드래그에 의한 손실로 회전손실(Spin loss) 또는 교반 손실(Churning loss)이라고 불린다. 기어에서 하중관련 손실은 특정 압력 하에 있는 두 표면이 서로 상대운동을 할 때 발생된다. 하중과 기어의 미끄럼(Slip) 속도, 구름(Rolling) 속도, 오일의 점도(Viscosity), 하중에 의한 오일 특성(Visco- pressure coefficient), 표면조도 등에 의한 오일 유막에 관련된 마찰계수나 구름계수를 구하는 것이 마찰 손실을 계산하는 중요한 요인이다.11,12)
수동변속기와 같이 다수의 외접 물림 기어쌍과 베어링으로 구성된 전형적인 변속기의 기어트레인의 경우, 전체 총 동력손실중에서 기어 물림에 의한 마찰 동력손실이 40 %, 베어링의 동력손실이 50 %, 오일쳐닝 등 회전 동력 손실이 10 %정도된다고 알려져 있다.13) 따라서 기어 물림에 의한 마찰 동력 손실의 연구는 매우 중요하다. 본 연구에서는 기어의 마찰 손실에 관해서만 한정해서 다루고자 한다.
기어에서의 마찰 손실은 기어 제원에 의한 접촉해석 모델과 마찰계수 모델을 이용하여 계산할 수 있다. 기어의 설계제원, Cutter 제원, 기어 구동조건 등으로 구성된 기어 접촉 해석 모델을 이용하여 기어의 모든 접촉점에서 하중이나 접촉압력 분포를 예측한다. 여기서 구해진 하중이나 압력은 마찰계수를 구하는 데 이용된다.
2.1 기어 접촉 해석 모델
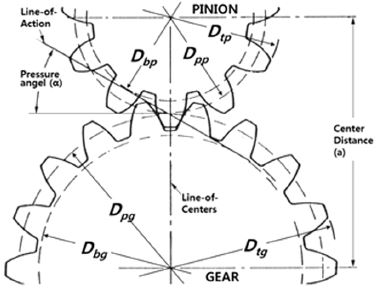
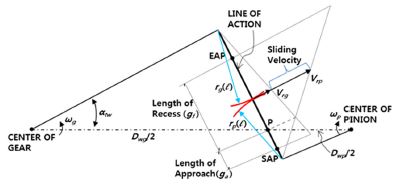
Fig. 1에서처럼 한 쌍의 기어는 접촉선(Line of contact)을 따라 접촉하게 되고, 이때 피치점의 접촉을 사이에 두고 접근길이(Length of approach)와 되물림길이(Length of recession)로 구분된다. 외접기어 쌍의 접촉에서 접근길이와 되물림길이는 Fig. 2와 같이 도식적으로 표현할 수 있고 다음 식과 같이 구할 수 있다.
| (1) |
| (2) |
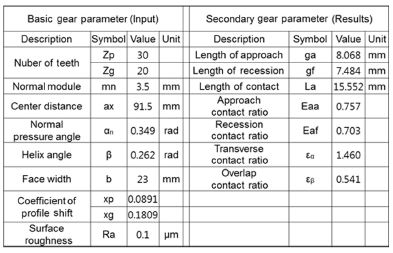
전체 접촉길이는 La=ga+gf로 나타낼 수 있고, 이때 Transverse contact ratio는 ϵα=La/πmtcos(αt)로, Overlap contact ratio는 ϵβ=bsin(β)/πmn로 표현된다.
접촉점에서 각 외접 기어의 곡률반경은 Fig. 2로부터 다음과 같이 구할 수 있다.
| (3) |
| (4) |
접촉점에서의 접선 속도는 접촉위치에 따라 변하게 되고, 이때 기어와 피니언의 구름속도의 차이로 정의되는 미끄럼속도(Sliding velocity)와 기어와 피니언의 평균 구름속도(Rolling velocity)는 다음과 같다.
| (5) |
| (6) |
두 개의 롤러로 구성된 롤링 시험기와 같이 회전축이 고정되어 회전할 때 식 (6)의 구름 속도에 의해 윤활유는 접촉하고 있는 롤러 사이로 끌려 들어오게 되고 이를 Entraining 속도라고 한다.13) 기어의 물림에서도 접촉 기어 치면 사이로 오일을 끌어들이고 유막 두께를 증대시키는 Entraining 속도는 식 (6)과 같이 구름속도로 나타낼 수 있고, 미끄럼 대 구름 계수(Slide-to-roll-ratio)는 다음 식과 같이 도입된다.
| (7) |
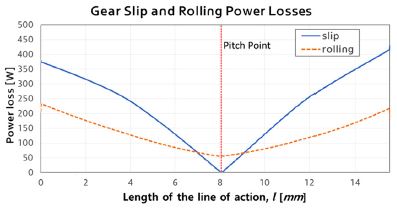
기어와 피니언의 구름속가 같을 때 “순수 구름”상태로 SR=0가 되고, 피니언의 속도가 0일 때 “순수 미끄럼”상태로 SR=2의 값을 갖는다.14) 기어에서는 피치원 근방에서 SR=0로 미끄럼이 없는 “순수 구름”상태를 나타낸다.
기어의 물림 치사이의 접촉압력은 하중과 접촉면적에 달려있고, 접촉면적은 헬리컬 기어에서는 접촉선(Line of contact)의 길이와 헤르쯔 접촉 폭(Hertzian half width)의 반에 달려있다. 여기서는 헤르쯔 접촉 효과는 무시하고 접촉은 접촉선을 따라 발생한다고 가정한다. 마찰력을 무시하면 기어에 의해서 전달되는 토크는 다음과 같다.
| (8) |
여기서 fN(l)은 접촉선을 따라 접촉하는 치표면에 직각으로 작용하는 단위길이당 하중이다. 접촉선의 길이와 작용면 유효부분에 대한 치폭(Face width)의 비는 헬리컬 기어에서 다음과 같이 나타낼 수 있다.15)
| (9) |
여기서, ξ는 접촉 경로를 따르는 무차원 좌표계(Non-dimensional coordinate)로 접촉 경로를 Trans-verse base pitch로 나눈 거리로 표현되고, 이는 접촉선의 길이에 대한 총 물림율과 같다. ψ1=ξ-i, ψ2=ξ-ϵβ-i, ψ3=ξ-ϵα-i, ψ4=ξ-ϵt-i이고, ϵt=ϵα+ϵβ, i는 -Floor(ϵt)에서 Floor(ϵt)까지 1씩 증가하는 값으로 Floor는 Round down을 의미한다. Heaviside function은 H(t)=로 나타내고 해석적 근사치로 k=1000 정도면 이론적 Heaviside function과 잘 일치한다.15)
접촉선을 따라 접촉하는 치표면에 직각으로 작용하는 단위길이당 하중은
| (10) |
이다. 접촉 경로를 따라 하나의 치(Single tooth)에 작용하는 법선 합력은
| (11) |
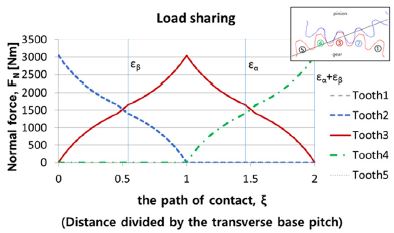
이다. Table 1에 기어 제원과 접촉선(Line of contact)의 길이 및 접촉비(Contact ratio)의 결과를 나타내었다. Fig. 3에 입력토크 50 Nm에 대한 접촉 경로를 따른 Single tooth에 작용하는 법선력을 도시하였다. 한 피치의 치 물림 근방의 5개의 치에 대해서 나타내면 Tooth3은 한 피치내에서 완전히 물리고, Tooth2는 이전 피치에서 반정도 물렸다가 떨어지고, Tooth4는 중간에서 물림을 시작하여 다음 피치로 이동한다. Tooth1은 이전 피치에서 모든 물림을 끝낸 치고, Tooth5는 아직 현 피치에서는 물림이 시작하지 않은 치이다. 따라서 완전물림 1개치와 반 물림 치 2개로 총 물림율 2.0의 결과를 나타낸다.
최대 헤르쯔 압력(Maximum Hertzian Pressure)은 길이당의 하중을 대체하기 위하여 사용된다. 선접촉 문제에 대하여 다음과 같이 나타낼 수 있다.
| (12) |
여기서, Req(l)=rp(l)rg(l)/(rp(l)+rg(l))는 등가 곡률 반경이고, 유효 탄성계수는 E′=2[(1-)/Ep+(1-)/Eg]-1이다. 작용선을 따라 길이당 하중은 W′(l)=fN(ξ(l))이다.
2.2 마찰 계수 모델
많은 참고문헌들을 통해 기어 마찰 계수에 대한 실험적 수식들을 찾을 수 있다. 이들 수식들은 대부분 두개의 디스크 형태의 시험으로부터 구해진 계측 Data를 Curve fitting해서 구해졌다. 일반적인 마찰계수의 형태는 다음과 같다.
| (13) |
여기서 μk, μ0와 μp는 각각 오일의 동점도와 절대점도, 점도압력계수이다. Vs, Vr와 R은 상대 표면의 미끄럼속도, 구름속도의 합과 복합 곡률반경이다. W′와 Pmax는 각각 단위 법선하중과 접촉압력이다. S는 두 접촉면의 초기 표면조도를 나타낸다.
기존의 실험식들은 시험에서의 제원이나 당시 사용한 오일의 특성에 한정된 경우로 좁은 구간에서의 정확성을 보인다. 기어에서 고효율이나 기어 효율의 정확한 효율계산이 필요 없던 과거의 경우에는 상당부분 유용한 모델로 인정을 받았으나, 현재의 기어 개발 상황에서는 보다 더 정확한 기어 마찰 계수 모델이 요구된다. 최근 EHL(Elastohydrodynamic lubrication) 모델을 통한 기어 마찰계수의 계산 방법이 개발되었다.9-12) 하지만 많은 설계변수의 변화에 대해서 EHL 모델을 해석하는 데는 많은 시간이 소요된다. 이러한 단점을 극복하기 위하여 다중 선형 회귀 분석을 통해서 함수화하여 사용하게 된다. 탄성 유체 접촉 전체에 걸쳐 유막의 압력과 두께의 분포는 유막 두께식, 점도-압력-온도 관계식, 밀도-압력-온도 관계식, 에너지 평형과 하중식 등과 Transient Reynolds 식을 동시에 풀어서 구할 수 있다. 순간적인 최소 유막 두께는 다음과 같이 표현된다.
| (14) |
매끄러운 표면의 최소 유막두께와 합성표면의 거칠기 (Sq=)의 비는 λ(l)=hmin/Sq로 나타낼 수 있다. EHL에 기초한 마찰계수 식은 SR, Ph, λ와 Req등의 기어의 주요 인자를 포함하는 다중 선형 회귀 분석에 의해 다음식과 같이 구해진다.
| (15) |
| (16) |
| (17) |
| (18) |
여기서 ai, bi, ci와 di는 상수이다.
기어 접촉 경로를 따른 미끄럼 동력 손실(Slip power loss)을 접촉경로에 대해 적분하여 접촉선의 길이로 나누면 다음과 같은 평균 미끄럼 동력손실을 구할 수 있다.
| (19) |
또한 기어 EHL모델을 이용한 기어 구름 동력손실 밀도는 다음 식과 같이 구할 수 있다.
| (20) |
여기서 ni는 다중회귀분석을 통해 얻어지는 상수 이다.
기어 접촉 경로를 따르는 구름 동력손실을 접촉경로에 대해 적분하여 접촉선의 길이로 나누면 다음과 같은 평균 구름 동력 손실을 구할 수 있다.
| (21) |
기어 쌍에서의 마찰에 의한 기계적 동력 손실은 슬립에 의한 동력손실과 구름에 의한 동력손실의 합으로 다음과 같다.
| (22) |
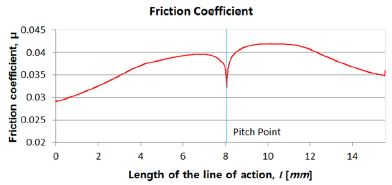
Table 1에 나타나 있는 기어 재원을 이용하고 피니언과 기어의 표면조도를 0.4로 할 때, 85 °C (μ0=10.5cP, μp=10.6GPa-1), 입력 토크 150 Nm, 입력 속도 2000 rpm에서의 마찰계수를 작용선상에서 물림길이에 대해서 Fig. 4에 나타내었다. 마찰계수는 피치점에서 0의 값을 갖고 작용선을 따라서 변화하는 값을 갖는다. 기어 미끄럼 동력손실과 구름 동력손실을 물림율에 대해서 Fig. 5에 나타내었다. SR비가 0인 피치점에서 미끄럼이 발생하지 않으므로 미끄럼 손실은 0이 되는 것을 알 수 있다. 이때, 평균 미끄럼 동력손실은 223.7[W], 평균 구름 동력손실은 126.8[W]로 전체 기계적 동력손실은 350.5[W]가 되고 입력 동력에 대하여 98.88 %의 기어 효율을 갖는다.
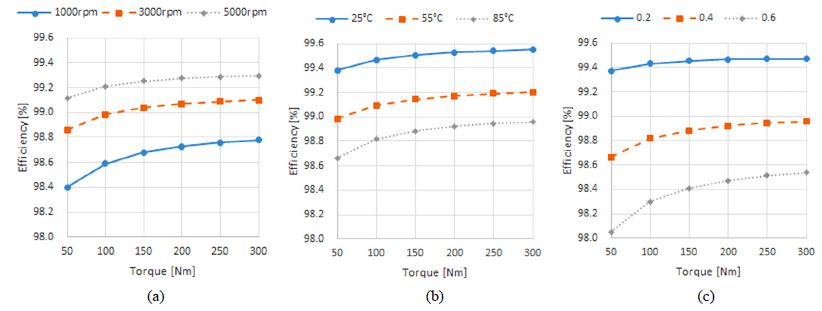
Fig. 6에 입력속도, 오일온도, 표면조도에 대한 기어 효율의 변화를 나타내었다. 입력 토크가 증가하면 입력 동력 증가 대비 손실 동력의 증가가 적어서 상대적으로 효율이 상승한다. 입력 속도와 오일 온도의 감소는 속도와 점도의 영향으로 오일 유막이 발달함으로써 마찰계수를 감소시키므로 효율 증대의 결과를 가져온다. 특히 기어 표면의 조도는 기어 효율에 매우 큰 작용을 하는 것을 알 수 있고, 기어 효율의 증대를 위해서는 표면 조도를 작게 가져가는 것이 필요하다.
3. 기어 동력 손실 저감 설계
변속기의 기어 물림 접점에서 발생하는 동력손실은 전체 구동계 시스템의 손실에서 상당한 비중을 차지한다. 헬리컬 기어쌍의 전달효율이 99 %를 초과하는 등의 매우 높은 경향을 보일지라도, 다단화 등의 영향으로 실제 변속기에서는 여러 개의 기어쌍이 동시에 물리게 되고 전체 전달효율은 각각의 기어쌍의 전달효율의 곱으로 나타나게 된다. 또한 이런 조건 하에서 변속기에서의 동력손실의 최소화 설계는 기어 소음이나 치의 파단, 피팅 등의 내구 등을 함께 고려하는 것이 필요하다. 기어 설계 인자 연구를 통하여, 헬리컬 기어의 기계적 동력손실을 위한 기본 설계 변수의 영향성을 파악하는 것뿐만 아니라 소음이나 내구 등에 대해 전달효율을 따져 보고 균형 있는 설계를 하는 것이 중요하다.
3.1 기어 설계 인자 분석
기어 설계 인자 연구를 위하여, 2장에서 설명한 기어의 기계적 동력손실과 전달효율 모델을 사용하였다. 예측 인자로 소음의 기준을 위하여 Transmission Error(TE)의 1st Harmonics 값을, 기어 피로 수명 기준으로써 최대 접촉응력과 피니언과 기어의 굽힘 응력을 선택하였다. 인자 분석을 위한 해석 조건은 입력 토크 100 Nm, 입력 속도 2000 RPM에서 수행되었다. 기어 설계 인자로 압력각(16°/ 18°/ 20°/ 22°/ 24°), 헬리컬각(13°/ 15°/ 17°/ 19°/ 21°), 기어의 Profile shift(-0.1809 / 0.0 / 0.1809 / 0.3618 / 0.5427)와 모듈(2.2 / 2.5 / 2.9 / 3.5 / 4.4)을 선정하였다. Table 1에 기어쌍의 제원을 나타내었다. 모듈의 변화를 위하여(mn=4.4: Zp=24, Zg=16), (mn=3.5: Zp=30, Zg=20), (mn=2.9: Zp=36, Zg=24), (mn=2.5: Zp=42, Zg=28), (mn=2.2: Zp=48, Zg=32)로 기어 치의 개수를 변경하였다.
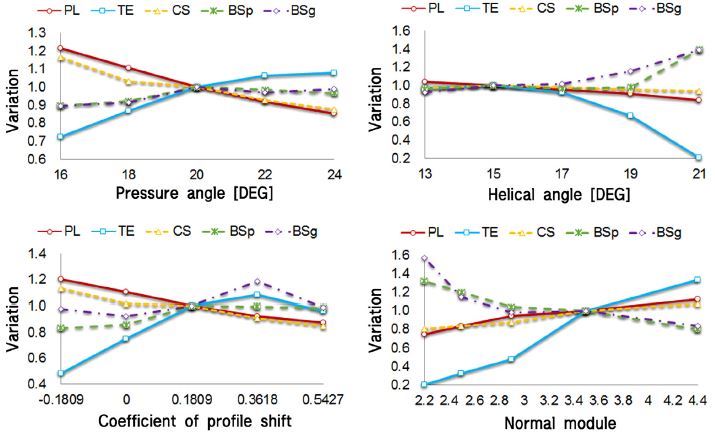
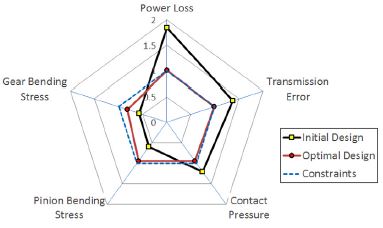
Fig. 7에 압력각, 헬리컬각, 치형수정, 모듈에 대한 인자 분석을 위한 해석 결과를 도시하였다. 그래프의 범례에서 PL은 동력손실, TE는 전달오차의 제1 하모닉 성분, CS는 최대 접촉 응력, BSp는 피니언의 최대 굽힘 응력과 BSg는 기어의 최대 굽힘 응력을 나타낸다. 모든 결과들은 Initial 설계 값을 기준으로 각각의 결과에 대해 정규화하였다.
첫번째로 Fig. 7의 좌측 상단의 그래프에 압력각의 변화에 대한 각 성능들의 변화를 나타내었다. 압력각을 16°에서 24° 변화시킬 때, 압력각의 증가는 동력손실을 감소시키고, 최대 접촉응력을 감소시키며 전달오차를 증가시킨다. 즉 압력각의 증가는 기어 전달효율의 증가(동력손실의 감소), 피팅수명의 감소와 소음의 증가(전달오차의 증가)로 이어질 수 있음을 나타낸다. 전달효율 증대(동력손실의 감소) 설계 관점에서 소음(전달오차)과의 Trade-off 관계가 있음을 알 수 있다. 두번째로 Fig. 7의 우측 상단에 나타낸 것과 같이 헬리컬 기어의 증대는 대상 기어 쌍에서 소음의 감소를 이끌 수 있으나, 나머지 전달효율이나 내구에는 별로 큰 영향이 없는 것으로 나타난다. 다음으로 Fig. 7의 좌측 하단의 그래프에 나타낸 것과 같이 기어의 Profile shift는 압력각의 변화와 매우 유사한 그래프 개형을 갖는 결과를 얻었다. 마지막으로 Fig. 7의 우측하단에 모듈의 증대에 따른 각 성능들의 변화를 나타내었다. 모듈의 증대는 굽힘 응력에 대한 내구 수명은 증대할 수 있지만 소음이나 전달효율, 피팅 수명에는 악영향을 주는 요소라는 것을 알 수 있다. 이러한 인자 분석 결과는 기어의 설계에 있어서 각 설계 변수들을 기어의 성능에 대하여 Trade-off 관계를 명확히 설정하여 선정하는 것이 중요하다는 것을 말해준다.
3.2 기어 성능을 고려한 기어 동력 손실 저감 설계
기어 마찰 동력 손실에 영향을 주는 기어의 설계 인자들은 내구나 소음 등 기어의 다른 성능에도 영향을 미친다. 기어에서의 마찰 동력손실을 저감하기 위한 설계는 반드시 기어의 다른 성능의 저하를 고려하여 이루어져야 한다. 앞 절에서처럼 인자 연구를 통해 기어 마찰 동력 손실, 굽힘 내구 수명, 마멸 내구 성능, 기어 소음 성능에 영향을 주는 인자들을 찾고 이를 각 성능에 대해 최적화하여 균형 있는 기어 설계를 하는 것이 필요하다.16)
Table 1에 나타낸 초기 기어 설계 재원을 바탕으로 앞 절의 인자 분석에서 사용한 설계 재원 및 설계 수준을 이용하여 각각의 성능 해석을 설계 변수 전 조합에 대하여 수행하였다. 이때 기어 동력 손실 저감 설계는 다음 식과 같이 최적설계의 표준식을 이용하여 나타낼 수 있다.
| (23) |
여기서 설계 변수 x는 압력각, 헬리컬각, Gear profile shift와 모듈이다. 동력손실은 현재값으로 정규화되고, 나머지 성능들은 각각의 제한조건으로 정규화되었다. 식 (23)은 설계 변수로 표현되는 기어 마찰 동력손실을 최소화하면서 기어 소음을 나타내는 지표인 Transmission Error의 1st Harmonic 성분이 기준값이하가 되고, 기어 피팅 내구 수명의 지표인 치면에서의 최대 접촉압력이 기준값이하, 기어의 굽힘 피로 내구 수명을 나타내는 지표로 기어와 피니언에서의 굽힘응력이 기준값이하가 되도록 하는 설계변수를 찾는 문제이다.
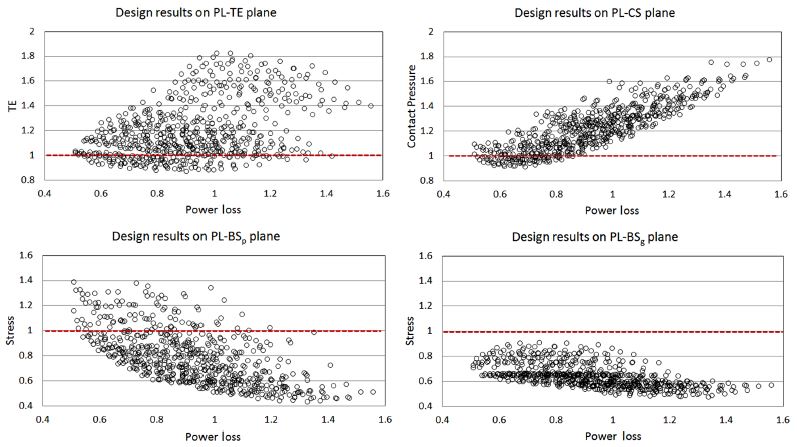
4개의 설계변수가 각각 5개의 수준으로 한정된 공간에서 이산화 되었고, 각각의 성능지표를 구하는 것이 용이하므로 실제 최적설계 알고리즘을 적용하지 않는다. 기어 설계 프로그램인 RMC17)를 통해 전조합 해석을 수행하였다. 전조합 총 54개의 결과를 Fig. 8에 기어 마찰 동력 손실과 각각의 성능 평면에 나타내었다. 각각의 성능의 제한조건을 만족하면서 동력손실이 최소화되는 설계를 찾기위하여, Fig. 8에 나타낸 PL-TE(동력손실-전달오차) 평면에서 전달오차 기준값을 만족하면서 동력손실이 적은 몇 개의 후보군을 선정한다. 두 번째로 후보군 중에서 접촉압력 기준값을 만족하는 설계 중 동력손실이 최소가되는 후보군을 PL-CS(동력손실-접촉압력) 평면에서 압축한다. 이를 굽힘응력에서도 같은 방법으로 수행하면 모든 제한조건을 만족하면서 동력손실이 최소화되는 최적의 결과를 얻을 수 있다.
초기 설계와 최적 설계의 설계변수의 변화를 살펴보면 압력각은 20°에서 24°로, 헬리컬각은 15°에서 17°로, Profile shift는 0.1809에서 0.3618로, 모듈은 3.5 mm에서 2.2 mm로 설계가 변경됨을 알 수 있다. Fig. 9에 각 성능별 설계 결과 변화를 나타내었다. 초기에 기어 굽힘응력을 강화해서 설계되었던 것이 모든 성능에서 제한조건 이내의 균형있는 설계가 이루어졌다. 특히 기어 마찰동력손실은 초기 설계 대비 약 46 %의 향상을 보였다. 이때 초기에 제한조건을 만족하지 못했던 TE와 최대 접촉응력은 제한조건을 만족하면서 향상된 결과를 얻을 수 있었다.
4. 결 론
연비규제가 점점 강화되고 있는 상황에서 전달효율 향상을 위한 변속기 설계는 매우 중요하다. 특히 전달효율의 이점을 갖는 Parallel 기어트레인을 사용하는 수동변속기나 DCT, AMT 등은 기어의 동력 손실을 줄이는 설계가 필요하다.
본 논문에서는 기어의 물림에 의한 동력손실을 계산하는 최신의 방법을 소개하였다. 기어의 물림에 의한 동력손실의 계산은 기어의 접촉 모델과 마찰계수 모델이 중요하다. 또한 소개된 방법을 이용하여 기어의 물림에 의한 동력손실을 계산하는 예를 보이고, 기어의 미끄럼 손실과 구름손실에 대한 전달효율을 계산하였다. 기어의 효율은 기어의 속도, 온도, 표면조도 등에 영향을 많이 받는 것을 볼 수 있었다.
기어의 물림에 의한 동력손실에 영향을 주는 기어 설계 변수들에 대한 인자 분석을 실시하여, 기어의 동력손실 대비 소음에 대한 영향과 내구 수명에 대한 영향을 파악하고 설계 변수의 변경에 따른 기어 성능변화를 살펴보았다. 이산 설계 공간에서 설계변수의 전조합에 따른 기어의 성능 해석을 수행하고 기어의 동력손실을 최소화하면서 다른 성능들의 기준을 만족하는 균형있는 설계를 수행하고 토의하였다.
향후 이러한 이론을 바탕으로 기어의 설계에 있어 기존의 내구 수명 및 소음에 대한 설계뿐만 아니라 기어 효율을 최적화할 수 있는 방법이 마련되어 적용될 수 있을 것으로 생각된다.
Nomenclature
| Dt, Db and Dp : | outer, base and pitch diameter, m |
| α and β : | pressure and helical angle, rad |
| m and Z : | module, mm and no. of teeth |
| ga and gf : | length of approach and recession, mm |
| r : | the radius of curvature, mm |
| w : | rotational speed of gear, rad/sec |
| V : | relative velocity on a contact point, m/sec |
| Mw : | torque applied on gear pair, Nm |
| v and E : | Poisson's ratio, and young's modulus, GPa |
| S : | surface roughness, μm |
| μ0 and μk : | absolute and kinematic viscosity, cP and cSt |
| μp : | visco-press coefficient, 1/GPa |
Subscripts
| g and p : | gear and pinion |
| t, n and w : | transverse, normal and working |
| s, r and e : | sliding, rolling and entering |
References
-
J. C. Cho, W. J. Kim, J. D. Jang, and S. Y. Jang, “Characteristic Dynamics Torque Vibration of Behavior in Wet Clutch Engagement for Dual Clutch Transmission”, Transactions of KSAE, Vol.24(No.2), p183-190, (2016).
[https://doi.org/10.7467/ksae.2016.24.2.183]

- Y. K. Park, G. H. Nam, W. S. Lim, and S. W. Kang, “A Study on the Transmission Efficiency Modeling with Considering of the Friction Characteristics of External Gear”, KSAE Spring Conference Proceedings, p71, (2015).
-
Y. N. Drozdov, and Y. A. Gavrikov, “Friction and Scoring Under the Conditions of Simultaneous Rolling and Sliding of Bodies”, Wear, Vol.11(Issue 4), p291-302, (1967).
[https://doi.org/10.1016/0043-1648(68)90177-4]

- J. P. O’Donoghue, and A. Cameron, “Friction and Temperature in Rolling Sliding Contacts”, ASLE Transactions, Vol.9(Issue 2), p186-194, (1966).
- Y. A. Misharin, “Influence of the Friction Condition on the Magnitude of the Friction Coefficient in the Case of Rollers with Sliding”, Proc. Int. Conf. On Gearing, Inst. Mech. Eng., p159-164, (1958).
- G. H. Benedict, and B. W. Kelly, “Instantaneous Coefficients of Gear Tooth Friction”, Transactions of ASLE, ASLE Lubrication Conference, p57-70, (1960).
-
N. E. Anderson, and S. H. Loewenthal, “Efficiency of Nonstandard and High Contact Ratio Involute Spur Gears”, NASA Technical Memorandum 83725, (1984).
[https://doi.org/10.1115/1.3260774]

- LMS Imagine, Lab AMESim, AMESim Reference Manual, Siemens PLM Software, (2016).
-
S. Li, A. Vaidyanathan, J. Harianto, and A. Kahraman, “Influence of Design Parameters on Mechanical Power Losses of Helical Gear Pair”, JSME J. of Advanced Mechanical Design, System and Manufacturing, Vol.3(No.2), p146-158, (2009).
[https://doi.org/10.1299/jamdsm.3.146]

- S. Li, and A. Kahraman, “Prediction of Spur Gear Mechanical Power Losses Using a Transient Elastohydrodynamic Lubrication Model”, Tribology Transactions, Vol.53(Issue 4), p554-563, (2010).
- H. Xu, Development of a Generalized Mechanical Efficiency Prediction Methodology for Gear Pair, Ph. D. Dissertation, The Ohio State University, Columbus, (2005).
- H. Xu, A. Kahraman, N. E. Anderson, and D. Maddock, “Prediction of Mechanical Efficiency of Parallel-axis Gear Pairs”, J. of Mechanical Design, Vol.129(Issue 1), p58-68, (2007).
- V. Stavytskyy, P. Nosko, P. Fil, A. Karpov, and N. Velychko, “Load-Independent Power Losses of Gear Systems: A Review”, TEKA Kom. Mot. I Energ. Roln. - OL PAN, Vol.10B, p205-213, (2010).
-
H. Spikes, “Basics of EHL for Practical Application”, Lubrication Science, Vol.27(Issue 1), p45-67, (2015).
[https://doi.org/10.1002/ls.1271]

-
P. M. T. Marques, R. C. Martins, and J. H. O. Seabra, “Power Loss and Load Distribution Models Including Frictional Effects for Spur and Helical Gears”, Mechanism and Machine Theory, Vol.96(Part 1), p1-25, (2016).
[https://doi.org/10.1016/j.mechmachtheory.2015.09.005]

- T. H. Chong, and J. H. Baek, “Development of Durability Estimation and Design Systems of Worm Gears”, Transactions of KSAE, Vol.5(No.1), p207-216, (1997).
- Run Many Case (RMC), Gear Design Program, Gear and Power Transmission Research Laboratory, The Ohio State University, (2016).