비절연 OBC의 공통 모드 EMI 문제 개선이 가능한 스위칭 기법

1. 서 론

EV 시장은 탄소 저감과 친환경 에너지 변환에 대한 관심을 힘입어 활황을 맞고 있다. 국내외 여러 완성차 제조업체들은 다양한 차종의 EV를 출시하였으며, 충전 시간 단축, 주행 거리 향상, 상품성 증진, 사용자 경험 향상을 위해 새로운 기술 연구 및 차량 개발에 노력을 기울이고 있다.^1,2)

EV의 충전은 주로 OBC를 통해 이루어진다. 근래에는 11 kW 수준의 OBC 개발과 양산이 이루어졌으며, 실제 시판되는 차량에 적용되었다. 현재는 대용량 OBC 개발과 양산을 목표로 여러 기술 연구들이 이루어지고 있다.^3-6)

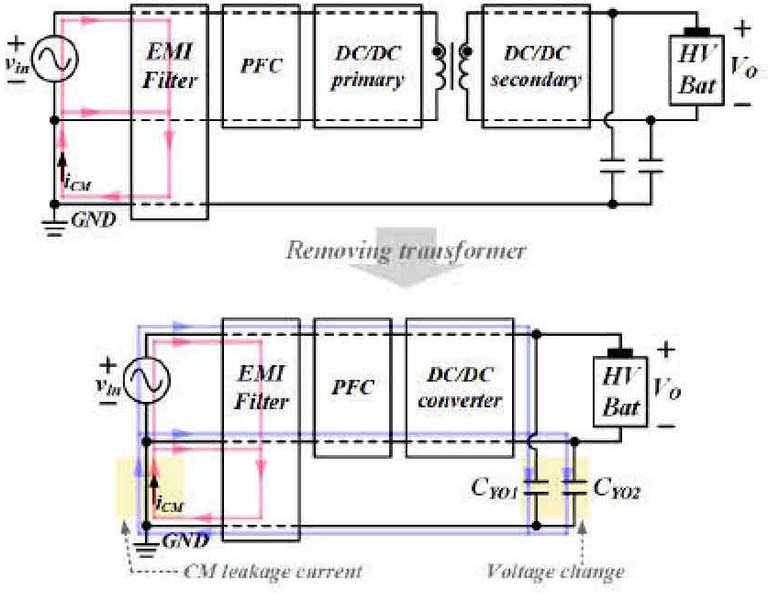
OBC의 대전력화에 뒤따르는 주요 문제점은 회로의 부피가 커진다는 점이다. OBC는 차량 플랫폼의 여분 공간에 배치되는 특성상, 부피 저감 또는 부피 상승 최소화가 필수적이다. 반면, 전력 용량의 상승은 자성체나 커패시터와 같은 수동 소자 부피 증가로 직결된다. 이 때문에 대전력 OBC 개발에 있어서 반드시 고려해야 할 사항은 수동 소자의 부피 저감이며, 이러한 관점에서 최근에는 변압기 제거를 통해 회로 부피를 줄일 수 있는 비절연 OBC에 대한 연구 수요가 있다.^7,8)

비절연 OBC는 DC/DC 컨버터의 변압기를 제거한다는 점에서 부피 저감의 이점이 있는 것은 분명하다. 그러나, DC/DC 컨버터 1차측과 2차측의 절연 성능이 저하되고, PFC단에서 발생하는 CM 전압이 고전압 배터리 측의 Y-커패시터에 인가되어 큰 CM 누설 전류가 발생하는 단점이 있다.^9,10) PFC단에서 발생하는 CM 전압은 PFC 회로 구조와 스위칭 방식에 따라 그 파형이 다르게 나타나나, 일반적으로 주기적으로 변화하는 파형을 갖는다. PFC단의 변화하는 CM 전압은 상술한 바와 같이 비절연 구조로 인해 고전압 배터리 측의 Y-커패시터에 인가되는데, Y-커패시터 양단의 전압 변화는 Y-커패시터를 따라 흐르는 전류를 유발한다. 이 전류는 차량 샤시를 통해 교류 입력 전원측 GND으로 흘러 큰 CM 누설 전류를 형성한다.^11,12)

비절연 OBC에서 발생하는 상기 문제의 원인은 PFC에서 발생한 CM 전압이 지속적으로 변화하는 것이다. 따라서, 비절연 OBC 설계를 위해서는 CM 전압을 제어할 수 있는 PFC 회로를 선정하는 것이 선행되어야 한다. 고효율 달성을 위해 많이 적용되는 BTPFC는 CM 전압이 매 교류 입력의 반주기마다 PFC 출력 전압 또는 0V로 변화한다. 이러한 현상은 BTPFC의 저속 스위칭 소자가 매 교류 입력의 반주기마다 턴온 또는 턴오프되기 때문인데, 이는 BTPFC의 고유한 제어 방식이므로 추가 제어 기법 적용이 불가하다. 따라서, BTPFC는 비절연 OBC의 CM 문제 해소에는 적합하지 않다.

반면, 인버터 PFC의 CM 전압은 정현파 형태의 시비율 제어 지령의 영향을 받아 정현파 형태로 변동하는 파형을 갖는다. 즉, 인버터 PFC의 CM 전압은 적절한 시비율 제어 지령 변경을 통해 제어가 가능하다. 그러므로, 비절연 OBC에는 인버터 PFC가 적합하다고 할 수 있다.^13,14)

본 논문에서는 비절연 OBC의 CM 전압 문제 해소 방안을 제시한다. 단상 풀브리지 인버터 PFC에 일반적인 정현파 시비율 제어 지령이 아닌 개선된 시비율 제어 지령을 적용한다. 이로써, CM 전압 평형을 성취하며 Y-커패시터 전압 변동 문제를 해결하고 CM 누설 전류를 저감한다. 제안 연구의 유효성은 입력 220V_ac 50 Hz / 출력 700V_DC 3.3 kW 실험 결과를 통해 입증한다.

Fig. 1

Major problems of non-isolated OBC

2. 인버터 PFC와 제안하는 스위칭 기법

본 논문의 일반적인 정현파 PWM인버터 PFC와 제안하는 스위칭 기법 및 CM 분석에 있어서, 스위칭 동작에 의해 발생하는 CM 전압의 고주파 성분은 입력 EMI 필터에 인가되며, PFC 출력단과 Y-커패시터에는 저주파 및 DC 성분만 인가된다고 가정한다.

2.1 Unipolar 인버터 PFC와 CM 전압

일반적인 정현파 인버터 PFC는 DC/AC에서 주로 사용하는 인버터 동작의 역방향과 동작과 동일하다. 인버터 스위칭 기법은 Bipolar 방식과 Unipolar 방식으로 나누어 볼 수 있는데, 전류 리플 및 자성체 부피 저감을 위해 Unipolar 방식을 많이 사용한다.

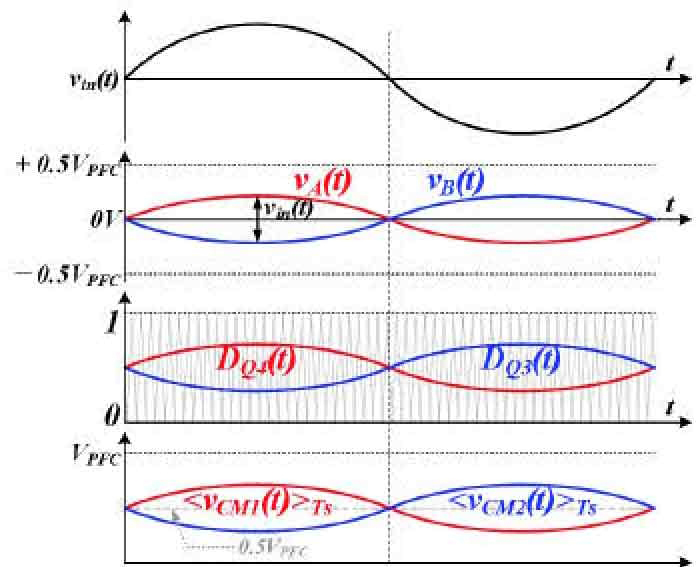
Unipolar 인버터 PFC의 동작 개념, 시비율 지령, PFC 출력단 CM 전압 파형을 Fig. 2에 도시하였다.

Fig. 2

Key waveforms of sinusoidal unipolar inverter PFC

일반적인 정현파 Unipolar PWM의 두 스위칭 레그 지령 전압은 DC 링크 전압 내에서 180° 위상 차이의 정현파 파형을 가지며, 전압 지령의 최댓값과 최솟값은 각각 +0.5V_PFC와 -0.5V_PFC 범위 이내에 위치한다. 단상 풀브리지 인버터 PFC에서 두 스위칭 레그 지령 전압의 차이는 교류 입력 전압과 같다. 이 때, 각 스위칭 레그의 전압 지령 v_A(t), v_B(t)와 스위치 Q_1∼4의 시비율 D_Q1∼4(t)는 각각 다음의 식 (1), (2)와 같이 계산 가능하다.

$\[ \left\{\begin{array}{c}{v}_A\left(t\right)=\frac{1}{2}{v}_{in}\left(t\right)\\ v_B\left(t\right)=-\frac{1}{2}{v}_{in}\left(t\right)\end{array}\right. \]$

(1)

$\[ \left\{\begin{array}{c}{D}_{Q3}\left(t\right)=D_{Q2}\left(t\right)\frac{1}{2}+\frac{1}{2}\frac{v_{in}\left(t\right)}{V_{PFC}}\\ D_{Q4}\left(t\right)=D_{Q1}\left(t\right)=1-D_{Q3}\left(t\right)=\frac{1}{2}-\frac{1}{2}\frac{v_{in}\left(t\right)}{V_{PFC}}\end{array}\right. \]$

(2)

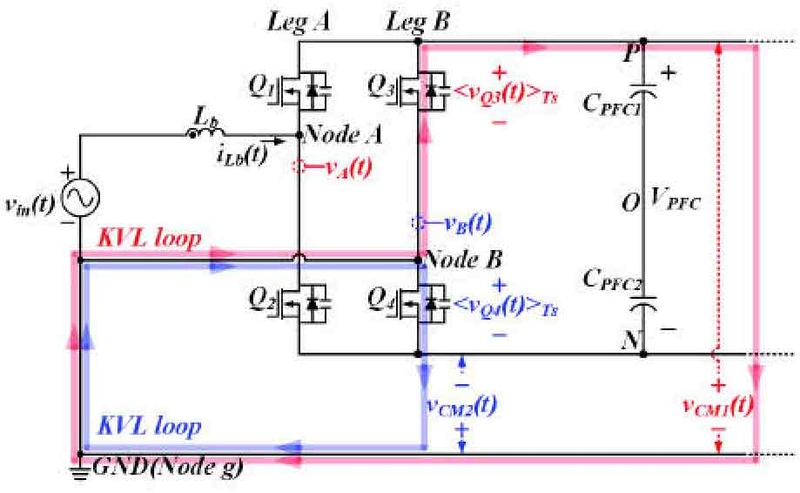
Fig. 3은 일반적인 정현파 Unipolar PWM을 적용한 단상 풀브리지 인버터 PFC에서 PFC 출력단 CM 전압 계산을 위해 간략화된 PFC 회로도를 나타낸다.

Fig. 3

Key waveforms of unipolar inverter PFC

본 2.1절에서 해석하고자 하는 것은 PFC 출력단에 저주파 및 DC 성분으로 나타나는 CM 전압이다. 따라서, 고주파 CM 전압이 인가되는 EMI 필터 회로는 생략해도 무방하다.

Fig. 3을 통해 인버터 PFC 출력단 CM 전압은 각각 Q₃와 Q₄의 스위칭 주기 평균 Drain-to-source 전압과 같음을 알 수 있으며, 이 때, PFC 출력단 CM 전압 v_CM1(t), v_CM2(t)와 Q₃ 및 Q₄의 스위칭 주기 평균 Drain-to-source 전압 <vQ3(t)>_Ts, <vQ4(t)>_Ts는 식 (3)와 같이 계산 가능하다.

$\[ \left\{\begin{array}{c}{v}_{CM1}\left(t\right)={〈v_{Q3}\left(t\right)〉}_{Ts}=V_{PFC}\left(1-D_{Q3}\left(t\right)\right)\\ v_{CM2}\left(t\right)={〈v_{Q4}\left(t\right)〉}_{Ts}=V_{PFC}\left(1-D_{Q4}\left(t\right)\right)\end{array}\right. \]$

(3)

Fig. 3과 식 (3)을 통해, 일반적인 정현파 Unipolar PWM을 적용한 인버터 PFC의 출력단 CM 전압은 Q₃와 Q₄의 시비율 영향을 받아 정현파 형태로 변동함을 알 수 있다.

본 논문에서는 이와 같은 사실을 토대로, PFC 출력 CM 전압의 변동을 제한하고, 비절연 OBC의 교류 입력 전원측 CM 누설 전류를 줄일 수 있는 인버터 PFC의 스위칭 기법을 연구하였다. 제안하는 스위칭 기법의 상세한 사항은 다음의 2.2절에서 자세히 기술한다.

2.2 인버터 PFC의 제안하는 스위칭 기법

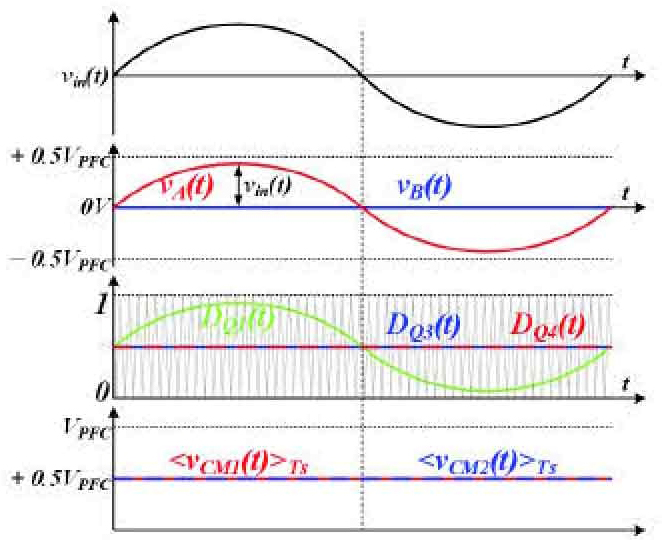
Fig. 4는 제안하는 스위칭 기법을 적용할 때 인버터 PFC의 주요 파형을 나타낸다. 제안하는 스위칭 기법의 Leg B 지령 전압 v_B(t)는 0V로 고정된다. 즉, Leg B를 구성하는 스위칭 소자는 0.5 고정 시비율로 상보 동작한다. 반면, Leg A의 지령 전압 v_A(t)는 정현파 형태로 가변하며 그 크기는 입력 전압 v_in(t)와 동일하다.

Fig. 4

Key waveforms of proposed switching method

위 사항들을 고려하여, 제안하는 스위칭 기법을 적용한 Unipolar 인버터 PFC의 각 스위칭 레그의 전압 지령 v_A(t), v_B(t)와 스위치 Q₃와 Q₄의 시비율 D_Q3(t), D_Q4(t)는 각각 다음의 식 (4), (5)와 같이 계산 가능하다.

$\[ \left\{\begin{array}{c}{v}_A\left(t\right)=v_{in}\left(t\right)\\ v_B\left(t\right)=0V\end{array}\right. \]$

(4)

$\[ \left\{\begin{array}{c}{D}_{Q1}\left(t\right)=\frac{1}{2}+\frac{v_{in}\left(t\right)}{V_{PFC}}\\ D_{Q2}\left(t\right)=\frac{1}{2}-\frac{v_{in}\left(t\right)}{V_{PFC}}\\ D_{Q3}\left(t\right)=D_{Q4}\left(t\right)=0.5\end{array}\right. \]$

(5)

제안하는 스위칭 기법을 적용할 때 인버터 PFC 출력 CM 전압은, 2.1절에서 Fig. 3을 통해 서술한 바와 같이, Q₃와 Q₄의 drain-to-source 전압의 스위칭 주기 평균 전압으로부터 도출 가능하며, 이는 아래의 식 (3)과 (5)를 바탕으로 (6)과 같이 계산된다.

(6)

따라서, 인버터 PFC에 제안하는 스위칭 기법을 적용하면 비절연 OBC 구성 시 주요한 문제가 되는 PFC 출력 CM 전압과 고전압 배터리측 Y-커패시터의 전압을 일정한 값으로 유지할 수 있음을 알 수 있다.

2.3 고주파 CM 전압과 CM 누설 전류 도출

앞선 2.2절의 제안하는 스위칭 기법을 통해 Y-커패시터 전압 변동을 제한하고 동일한 전압을 유지할 수 있음을 확인하였다. 이로써 고전압 배터리의 Y-커패시터를 따라 흐르는 CM 누설 전류를 저감할 수 있다.

그러나, 앞서 분석한 것은 PFC 출력단과 고전압 배터리 Y-커패시터에 나타나는 낮은 주파수 또는 직류 CM 전압이다. 즉, 입력 EMI 필터에 인가되는 고주파 CM 전압은 별도의 해석이 필요하며, 이로 인해 발생하는 CM 누설 전류 또한 추가적인 분석이 진행되어야 한다.

2.3.1 제안하는 스위칭 기법 적용 시 CM 전압 분석

단상 인버터의 CM 전압 분석은 연구 논문을 통해 보고된 바 있으며,¹⁴⁾ 이를 수식으로 표현하면 아래의 식 (7)과 같다.

$\[ v_{CM}\left(t\right)=\frac{v_{Ag}\left(t\right)+v_{Bg}\left(t\right)}{2} \]$

(7)

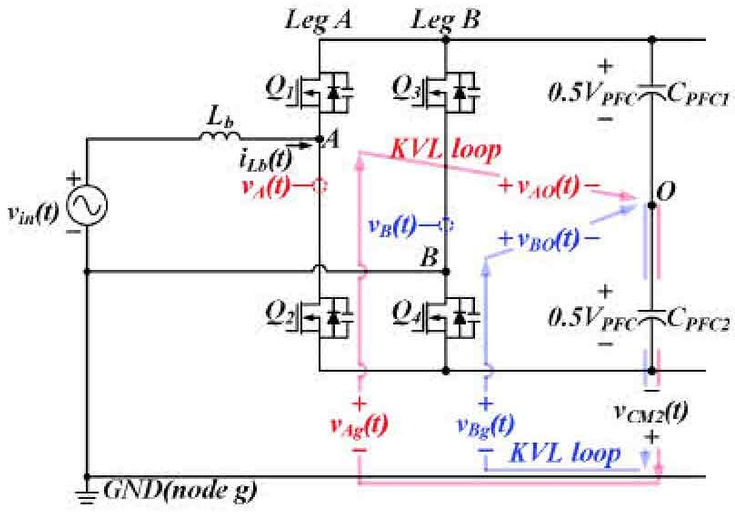
식 (7)의 v_Ag(t)와 v_Bg(t)는 GND로부터 node A와 B까지의 전압을 의미하며, v_CM(t)는 PFC단에서 발생하는 스위칭 CM 전압을 의미한다.

한편, Fig. 5에 도시된 KVL 루프를 통하여 v_Ag(t)와 v_Bg(t)에 대해 식 (8)과 같은 전압 관계를 도출할 수 있다.

Fig. 5

Circuit diagram for CM voltage analysis

$\[ \left\{\begin{array}{c}{v}_{Ag}\left(t\right)=-v_{CM2}\left(t\right)+0.5V_{PFC}+v_{AO}\left(t\right)\\ v_{Bg}\left(t\right)=-v_{CM2}\left(t\right)+0.5V_{PFC}+v_{BO}\left(t\right)\end{array}\right. \]$

(8)

이 때, 제안하는 스위칭 기법을 적용하면, v_CM2(t)는 식 (6)에 의해 0.5V_PFC이다. 따라서, 비절연 OBC의 PFC단에 제안하는 스위칭 기법을 적용할 경우, PFC단 CM 전압 분석은 v_AO(t)와 v_BO(t)로 이루어져도 무방하며, 식 (7)은 식 (9)과 같이 정리될 수 있다.

$\[ v_{CM}\left(t\right)=\frac{v_{AO}\left(t\right)+v_{BO}\left(t\right)}{2} \]$

(9)

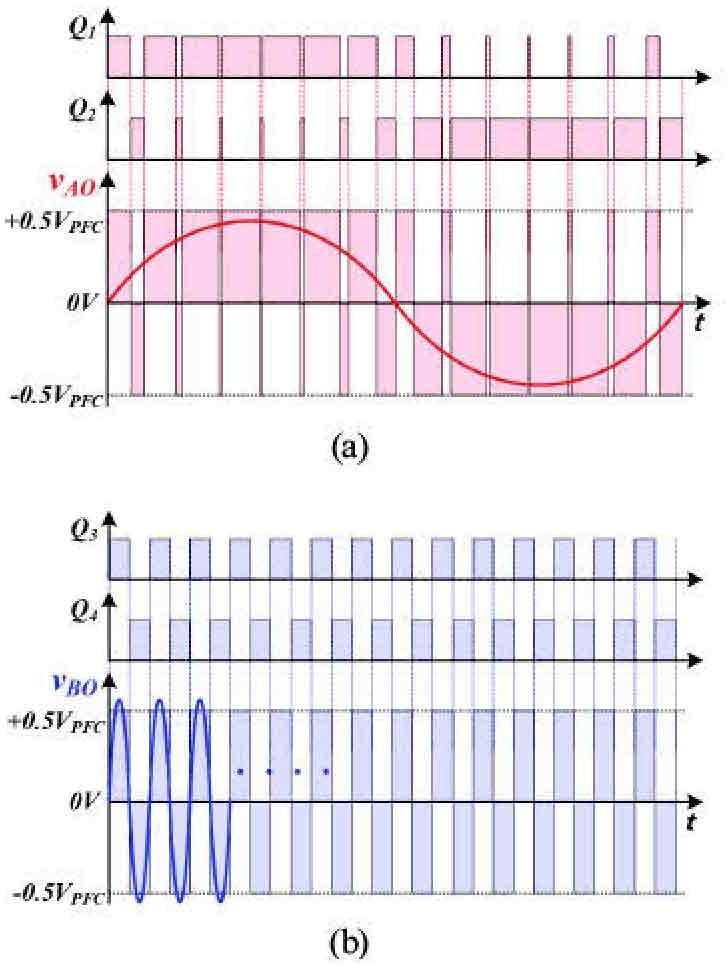
한편, 제안하는 스위칭 기법을 적용하면, Fig. 5의 Leg B는 0.5 고정 시비율로 제어되므로, v_BO(t)는 기본파 주파수가 스위칭 주파수고, 양과 음의 펄스 폭이 서로 같은 구형파 파형을 갖는다. 반면, Fig. 5의 Leg A에는 교류 입력 전압의 전압 지령이 인가되어 가변 PWM으로 제어되므로 v_AO(t)는 기본파 주파수가 교류 입력 주파수와 동일한 정현파 파형을 갖는다. 위 서술한 사항을 토대로, v_AO(t)와 v_BO(t)는 Fig. 6과 같이 그려질 수 있으며, v_AO(t)와 v_BO(t)의 기본파 성분 크기 v_AO.f, v_BO.f는 아래 식 (10)과 같이 계산된다.

Fig. 6

Circuit diagram for CM voltage analysis

$\[ \left\{\begin{array}{c}{v}_{AO.f}=v_{in.max}\\ v_{BO.f}=\frac{2}{\pi }{V}_{PFC}\end{array}\right. \]$

(10)

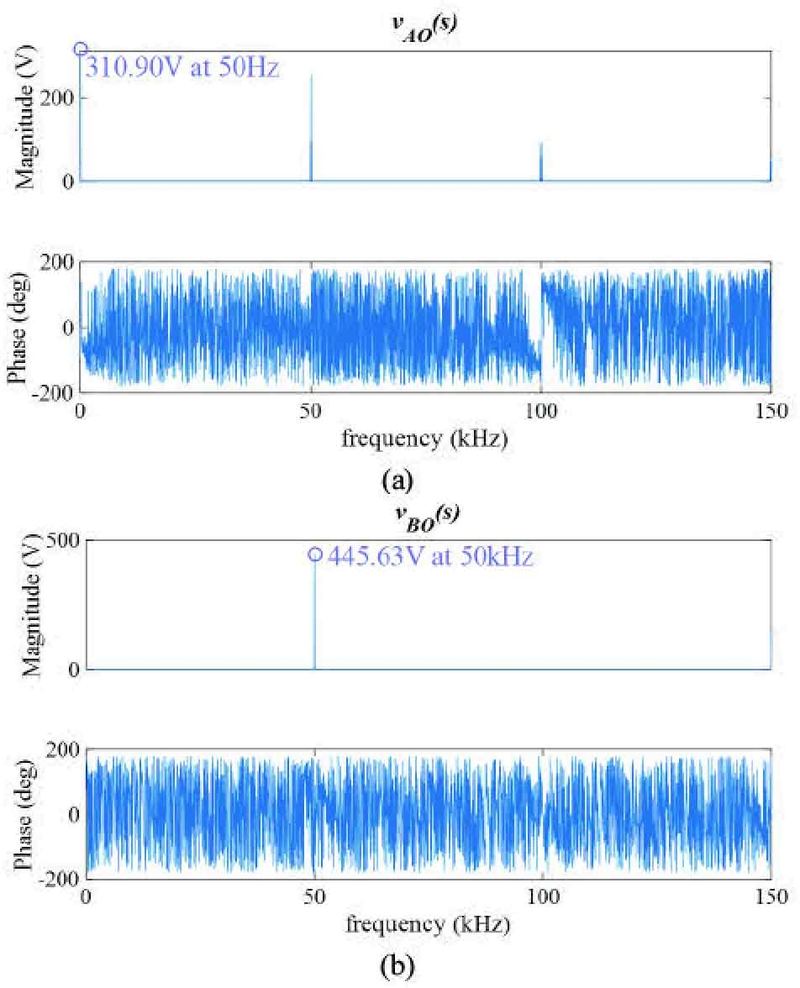
여기서, v_in.max는 입력 교류 전압의 최댓값이다. Fig. 7은 v_AO(t)와 v_BO(t)를 주파수 영역에서 FFT 분석한 결과이다.

Fig. 7

FFT result of vAO(t) and vBO(t)

FFT 분석은 교류 입력 220 V / 50 Hz, 출력 700 V / 3.3 kW, 스위칭 주파수 50 kHz 조건으로 진행되었다. v_AO(s)와 v_BO(s)의 기본파 성분인 50 Hz, 50 kHz 성분의 크기는 각각 310.9 V, 445.63 V로 나타났다. 이는 식 (10)의 결과와 동일하다.

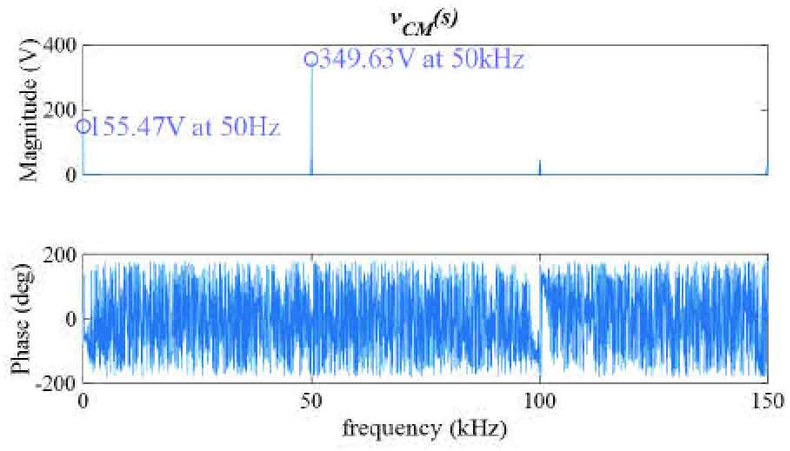
Fig. 8은 식 (9)을 통해 계산된 v_CM(t)의 FFT 분석 결과이다. v_CM(s)의 50 Hz 성분과 50 kHz 성분은 각각 155.47V, 349.63 V로 나타났다. 이는 각각 교류 입력 전압의 크기와 PFC 출력 전압 VPFC의 절반에 해당하는 값이다. 이로써, 제안하는 스위칭 기법을 인버터 PFC에 적용할 때, CM 누설 전류를 유발할 가능성이 높은 성분은 교류 입력 성분 CM 전압과 스위칭 주파수 성분 CM 전압임을 알 수 있다.

Fig. 8

FFT result of vCM(t)

2.3.2 제안하는 스위칭 기법 적용 시 CM 누설 전류

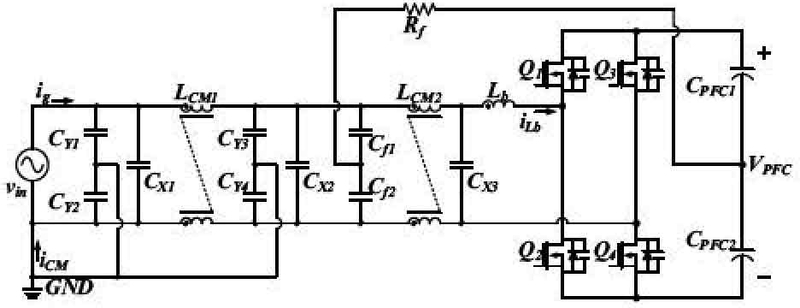
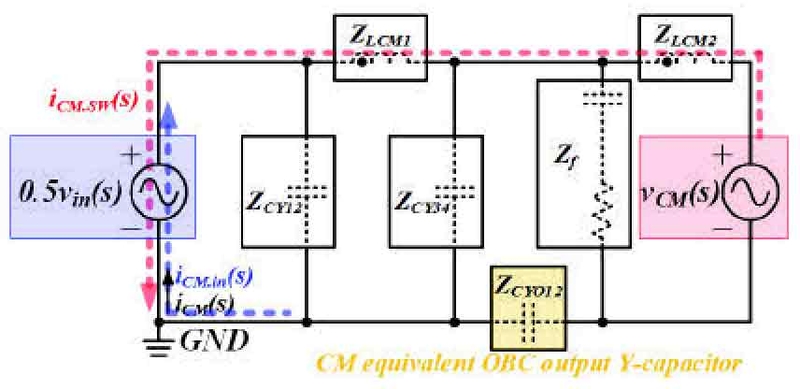
Fig. 9는 입력 EMI 필터를 고려한 인버터 PFC 회로도를 나타낸다. 입력 EMI 필터 회로에는 고주파 CM 노이즈 저감 성능을 확보하기 위해 개선된 EMI 필터 구조를 적용하였다.¹⁵⁾ Fig. 10은 Fig. 9의 EMI 필터를 포함한 비절연 OBC의 CM 등가 회로이며, 일반적인 비절연 DC/DC 컨버터와 OBC 출력 Y-커패시터를 고려하여 CM 등가화하였다.

Fig. 9

Circuit diagram of inverter PFC with input EMI filter

Fig. 10

CM equivalent circuit of non-isolated OBC

Fig. 10에서, 전체 CM 누설 전류는 i_CM(s), 스위칭 동작에 의해 발생하는 CM 누설 전류는 i_CM.SW(s), 교류 입력 전압으로부터 발생하는 CM 누설 전류는 i_CM.in(s)이다.

Fig. 10을 통해 비절연 OBC 전체 CM 누설 전류 i_CM(s)은 중첩의 원리를 바탕으로 i_CM.SW(s)와 i_CM.in(s)에 의해 계산됨을 알 수 있으며, 이를 식으로 표현하면 식 (11)과 같다.

$\[ i_{CM}\left(s\right)=i_{CM in }\left(s\right)-i_{CM.SW}\left(s\right) \]$

(11)

이 때, i_CM.SW(s)와 i_CM.in(s)는 각각 CM 전압 v_CM(s), 0.5vg(s)와 CM 등가 회로상의 소자들이 형성하는 컨덕턴스 G_CM.SW(s), G_CM.in(s)를 통해 계산 가능하다. G_CM.SW(s)와 G_CM.in(s)는 아래의 식 (12) ~ (16)를 통해 도출할 수 있으며, 표현의 편의를 위해 CM 등가 회로상에 존재하는 소자의 임피던스에는 (s)를 생략하였다.

$\[ \left\{\begin{array}{c}{Z}_{CY12}=1/\left(s\left(C_{Y1}+C_{Y2}\right)\right)\\ Z_{CY34}=1/\left(s\left(C_{Y3}+C_{Y4}\right)\right)\\ Z_f=1/\left(s\left(C_{f1}+C_{f2}\right)\right)+R_f\\ Z_{CYO12}=1/\left(s\left(C_{YO1}+C_{YO2}\right)\right)\\ Z_{LCM1}=s{L}_{CM1}\\ Z_{LCM2}=s{L}_{CM2}\end{array}\right. \]$

(12)

$\[ Z_{eq. SW}=\frac{Z_{CY34}\left(Z_f{Z}_{LCM2}+Z_{CY34}{Z}_{CYO12}\left(Z_f+Z_{LCM2}\right)\right)}{Z_f{Z}_{LCM2}+\left(Z_{CYO12}+Z_{CY34}\right)\left(Z_f+Z_{LCM2}\right)} \]$

(13)

$\[ \begin{array}{c}{G}_{CM.SW}\left(s\right)=\frac{i_{CM.SW}\left(s\right)}{v_{CM}\left(s\right)}=\frac{Z_{f12}{Z}_{CY34}}{Z_{eq. SW}+Z_{LCM1}}\\ ̇\frac{1}{Z_f\left(Z_{CYO12}+Z_{CY34}\right)+Z_{LCM2}\left(Z_f+Z_{CYO12}+Z_{CY34}\right)}\end{array} \]$

(14)

$\[ Z_{eq. g}=\frac{Z_f{Z}_{LCM2}+Z_{CYO12 }\left(Z_f+Z_{LCM2}\right)}{Z_f+Z_{LCM2}} \]$

(15)

$\[ \begin{array}{c}{G}_{CM.in}\left(s\right)=\frac{i_{CM,in}\left(s\right)}{0.5v_{in}\left(s\right)}\\ =\frac{Z_{eq.g }{Z}_{CY34}+\left(Z_{LCM1}+Z_{CY12}\right)\left(Z_{eq.g }+Z_{CY34}\right)}{Z_{CY12}\left(Z_{eq. g}{Z}_{CY34}+Z_{LCM1}\left(Z_{eq.g }+Z_{CY34}\right)\right)}\end{array} \]$

(16)

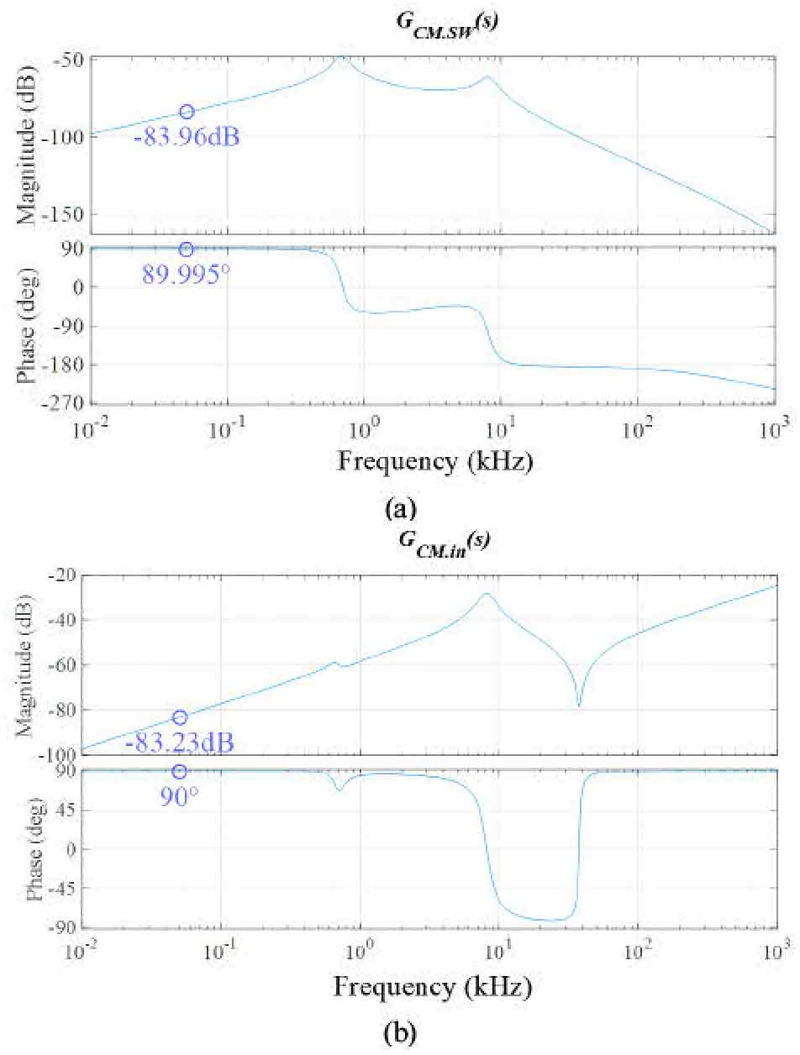
중요한 것은 식 (14)와 (16)의 컨덕턴스 G_CM.SW(s), G_CM.in(s)가 보드 플롯 상에서 어느 정도의 이득을 가지느냐 이다. Fig. 11은 각각 G_CM.SW(s), G_CM.in(s)의 보드 플롯이며, 보드 플롯 도출을 위해 사용한 주요 파라미터는 Table 1과 같다.

Table 1

Key parameter of CM equivalent circuit

Fig. 11

Bode plot of GCM.SW(s) and GCM.in(s)

Fig. 11에서, G_CM.SW(s)의 50Hz 지점 이득과 위상은 각각 –83.96 dB, 89.995도이고, G_CM.in(s)의 50 Hz 지점 이득과 위상은 각각 -83.23dB, 90도로 매우 유사하다. 이는, v_CM(s)의 50 Hz 성분 크기 및 위상과 CM 등가 회로상의 교류 입력 CM 전압 크기 및 위상이 동일하다는 점을 미루어볼 때, 제안하는 스위칭 기법 적용 시, 50 Hz의 두 CM 전압이 근사적으로 상쇄될 수 있음을 의미한다. 다시 말 해, i_CM(s)에 50 Hz 성분이 거의 존재하지 않음을 뜻하며, 비절연 OBC에 제안하는 스위칭 기법을 적용하면 고전압 배터리 Y-커패시터의 전압 변동을 억제함과 더불어 CM 누설 전류를 저감할 수 있다고 말할 수 있다.

한편, 40 kHz 이상 주파수에서 G_CM.SW(s)의 이득은 -100 dB보다 작다. 보편적으로 OBC의 PFC단 스위칭 주파수가 40 ~ 100 kHz 수준임을 고려하면, PFC 스위칭 동작에 의해 발생하는 고주파 CM 누설 전류가 또한 충분히 저감될 수 있음을 짐작할 수 있다.

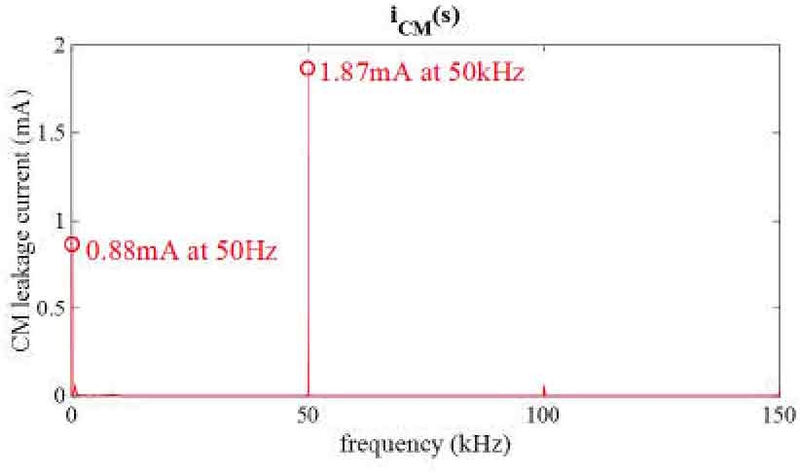
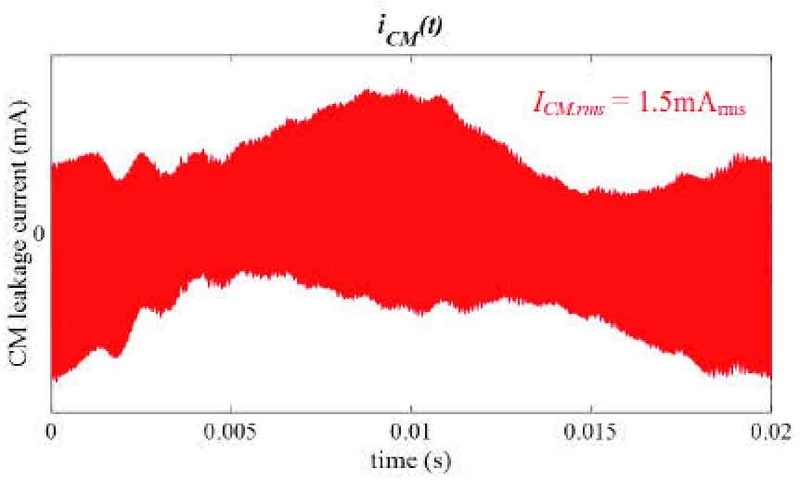
식 (11) ~ (16)을 바탕으로 제안하는 스위칭 기법을 적용한 인버터 PFC의 CM 누설 전류 계산 결과를 Fig. 12와 Fig. 13에 도시하였다. Fig. 12는 주파수 영역 FFT 계산 결과, Fig. 13은 시간 영역 계산 결과이며, CM 누설 전류 계산은 교류 입력 220 V / 50 Hz, 출력 700 V / 3.3 kW, 스위칭 주파수 50 kHz 조건으로 진행되었다.

Fig. 12

Frequency domain FFT result of CM leakage current

Fig. 13

Time domain analysis result of CM leakage current

Fig. 12에서 확인할 수 있듯이, CM 누설 전류는 50 Hz와 50 kHz 성분이 주요하며, 그 크기는 각각 0.88 mA, 1.87 mA로 계산되었다. 이를 시간 영역으로 환한 결과인 Fig. 13을 통해, 제안하는 스위칭 기법을 적용한 인버터 PFC의 CM 누설 전류는 1.5 mA_rms 가량 발생할 것으로 예측할 수 있다.

3. 실험 및 검증

3.1 실험 사양 및 주요 파라미터

제안하는 스위칭 기법의 유효성을 검증하기 위해 PFC단 시제품 회로를 설계하여 실험 검증하였다. DC/DC 출력의 Y-커패시터를 모사하기 위해 PFC단 출력에 Y-커패시터를 직접 연결하여 실험을 진행하였다. 실험에 사용한 시제품 회로의 주요 소자를 Table 2에 정리하였고, Table 3에 주요 입출력 사양을 나열하였다. Fig. 14는 실제 실험 환경 사진이며, CM 누설 전류 측정은 Teledyne LeCroy사의 CP030(30 A_rms, Minimum Sensitivity : 20 mA/div)를 사용하여 진행하였다.

Table 2

Key components of experimental circuit setup

Table 3

I/O specification

Fig. 14

Experimental circuit and condition

3.2 시제품 실험 파형 및 결과 분석

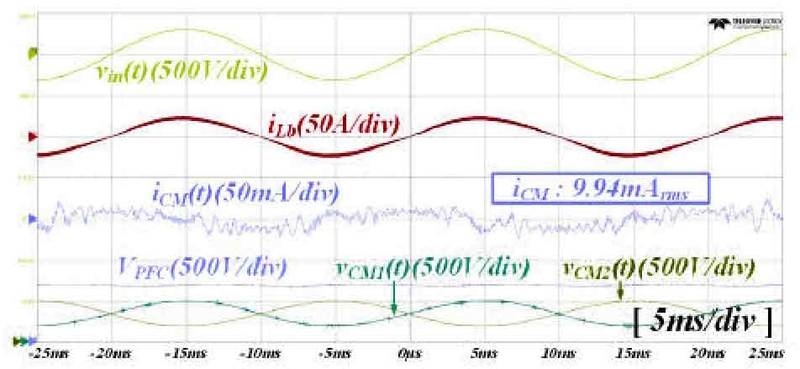
Fig. 15는 일반적인 정현파 Unipolar PWM 방식을 적용한 인버터 PFC의 실험 결과 파형이다. 700V_DC 3.3kW 출력 정상상태에서 Y-커패시터 양단 전압 v_CM1(t)와 v_CM2(t)가 정현파 형태로 변동하고 있음을 확인할 수 있다. 이는 앞서 분석한 2.1절의 식 (3)과 동일하다. 또한 CM 누설 전류 i_CM(t)에 저주파 형태의 변동이 관측되며 실효값은 9.94 mA_rms로 나타났다.

Fig. 15

Experimental waveforms under sinusoidal unipolar PWM

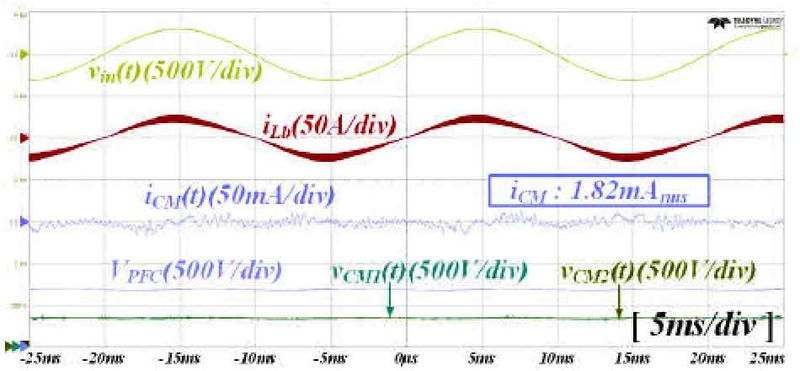
Fig. 16은 제안하는 스위칭 기법을 적용한 인버터 PFC의 실험 결과 파형이다. 700V_DC 3.3 kW 출력 정상상태에서 Y-커패시터 양단 전압 v_CM1(t)와 v_CM2(t)의 전압 변동이 발생하지 않으며 서로 동일한 값을 유지하고 있다. 더불어, CM 누설 전류 i_CM(t)에도 저주파 형태의 변동이 제거되었으며 그 크기는 1.82 mA_rms로 측정되었다.

Fig. 16

Experimental waveforms under proposed switching method

Fig. 13의 CM 누설 전류 분석 결과와 Fig. 16의 실제 측정값 사이에 존재하는 약 320 µA_rms의 편차는 CM 누설 전류 측정 프로브 CP030의 Minimum Sensitivity, 입출력 차단 및 회로 미구동 상황에서 측정될 수 있는 수 백 µA_rms의 작은 CM 누설 전류 offset, CM 등가 회로를 구성하는 수동 소자(특히, 출력단 Y-커패시터)의 소자 값 공산 오차 등에 기인한다고 볼 수 있다. 그러나, 상술한 오차 원인을 고려하더라도 편차의 크기가 약 320 µA_rms 정도라는 점에서 해당 편차는 충분히 작은 값으로 간주되어도 무방하다.

이로써 제안하는 스위칭 기법을 비절연 OBC의 PFC단에 적용하면 고전압 배터리측 Y-커패시터의 전압 변동 문제와 CM 누설 전류 문제를 해결할 수 있음을 알 수 있다.

4. 결 론

본 논문에서는 비절연 OBC의 Y-커패시터 전압 변동 문제와 큰 CM 누설 전류 문제를 개선할 수 있는 PFC단 스위칭 기법을 제안하였다. 일반적인 정현파 기반 PWM 방식에서 벗어나, 한 쪽 스위칭 레그를 0.5 고정 시비율 제어하는 스위칭 기법 연구를 수행하였고, 이로써, 고전압 배터리측 Y-커패시터 양단 전압 변동을 제거하였다. 제안하는 스위칭 기법 적용시 발생하는 CM 전압을 주파수 영역에서 해석하였으며, CM 등가 회로의 컨덕턴스 분석을 통해 CM 누설 전류를 분석하는 방법을 제시하였다. 제안하는 스위칭 기법의 유효성은 3.3 kW 시제품 실험 파형을 통해 검증하였으며, 결과적으로, 제안하는 스위칭 기법을 비절연 OBC의 PFC단에 적용하면 비절연 OBC의 CM 노이즈 문제를 해소할 수 있다.

Acknowledgments

이 논문은 인천대학교 2022년도 자체연구비 지원에 의하여 연구되었음.

References

• J. Park, Y. Jeon, J. Na, S. Cho, Y. Shin, W. Shin and J. Kim, “Development of High Efficiency Power Module for Electric Vehicle Charger,” Transactions of KSAE, Vol.30, No.10, pp.785-792, 2022.
• K. W. Rho and M. S. Noh, “A Study on Methodology to Improve Time-Consuming for Measuring Energy Efficiency and Range of Electric Vehicles,” Transactions of KSAE, Vol.30, No.6, pp.499-509, 2022.
• E. C. Noh, S. M. Park, G. D. Kim, J. W. Son and S. H. Lee, “Machine Learning Based Optimal Design of a 6.6kW Planar Transformer for High Power Density On-Board Chargers,” The Transactions of the Korean Institute of Power Electronics, Vol.29, No.1, pp.24-31, 2024.
• A. Khaligh and M. D’Antonio, “Global Trends in High-Power On-Board Chargers for Electric Vehicles,” IEEE Transactions on Vehicular Technology, Vol.68, No.4, pp.3306-3324, 2019.
• D. Zinchenko, A. Blinov, A. Chub, D. Vinnikov, I. Verbytskyi and S. Bayhan, “High-Efficiency Single- Stage On-Board Charger for Electrical Vehicles,” IEEE Transactions on Vehicular Technology, Vol.70, No.12, pp.12581-12592, 2021.
• H. Wouters and W. Martinez, “Bidirectional Onboard Chargers for Electric Vehicles: State-of-the-Art and Future Trends,” IEEE Transactions on Power Electronics, Vol.39, No.1, pp.693-716, 2024.
• C. Y. Oh, D. H. Kim, D. G. Woo, W. Y. Sung, Y. S. Kim and B. K. Lee, “A High-Efficient Nonisolated Single-Stage On-Board Battery Charger for Electric Vehicles,” IEEE Transactions on Power Electronics, Vol.28, No.12, pp.5746-5757, 2013.
• D. Zhang, D. Cao, J. Huber, J. Everts and J. W. Kolar, “Nonisolated Three-Phase Current DC-Link Buck–Boost EV Charger with Virtual Output Midpoint Grounding and Ground Current Control,” IEEE Transactions on Transportation Electrification, Vol.10, No.1, pp.1398-1413, 2024.
• Y. Zhang, W. Perdikakis, Y. Cong, X. Li, M. Elshaer, Y. Abdullah, J. Wang, K. Zou, Z. Xu and C. Chen, “Leakage Current Mitigation of Non- Isolated Integrated Chargers for Electric Vehicles,” 2019 IEEE Energy Conversion Congress and Exposition (ECCE), pp.1195-1201, 2019.
• Y. Zhang, G. Yang, X. He, M. Elshaer, W. Perdikakis, H. Li, C. Yao, J. Wang, K. Zou, Z. Xu and C. Chen, “Leakage Current Issue of Non-Isolated Integrated Chargers for Electric Vehicles,” 2018 IEEE Energy Conversion Congress and Exposition (ECCE), pp.1221-1227, 2018.
• G. Buticchi, D. Barater, E. Lorenzani and G. Franceschini, “Digital Control of Actual Grid- Connected Converters for Ground Leakage Current Reduction in PV Transformerless Systems,” IEEE Transactions on Industrial Informatics, Vol.8, No.3, pp.563-572, 2012.
• D. Barater, G. Buticchi, E. Lorenzani and C. Concari, “Active Common-Mode Filter for Ground Leakage Current Reduction in Grid-Connected PV Converters Operating with Arbitrary Power Factor,” IEEE Transactions on Industrial Electronics, Vol.61, No.8, pp.3940-3950, 2014.
• C. T. Morris, D. Han and B. Sarlioglu, “Reduction of Common Mode Voltage and Conducted EMI Through Three-Phase Inverter Topology,” IEEE Transactions on Power Electronics, Vol.32, No.3, pp.1720-1724, 2017.
• M. H. Hedayati and V. John, “Filter Configuration and PWM Method for Single-Phase Inverters with Reduced Conducted EMI Noise,” IEEE Transactions on Industry Applications, Vol.51, No.4, pp.3236- 3243, 2015.
• D. I. Lee, Y. J. Hyeon, S. W. J, M. J. Kim and H. S. Youn, “Study on EMI Filter Circuit of 3-Level Boost Converter for Railway Vehicle Based on Hydrogen Fuel Cell,” Journal of the Korean Society for Railway, Vol.26, No.7, pp.463-479, 2023.