자율주행 화물차의 전복 안전성 예측을 위한 머신러닝 기반 연구
Copyright Ⓒ 2025 KSAE / 230-02
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
To enhance the safety of self-driving trucks, a machine learning-based study was conducted to predict rollover risk by utilizing planned path curvature and driving speed. The research involved simulations based on safety tests for truck rollover, facilitating the calculation of the Lateral-Load Transfer Ratio(LTR), a critical metric in evaluating the vehicle’s stability during various maneuvers. In this simulation, the curvature of the planned vehicle path and the lateral acceleration derived from the driving speed were employed as key input data for the machine learning model. Among the various models assessed, the Recurrent Neural Network(RNN) exhibited the highest prediction accuracy, particularly when the lateral acceleration derived from the planned path curvature and speed was utilized as input data. These findings are expected to improve the planning of safe optimal routes and speeds, based on the predicted rollover risk.
Keywords:
Self-driving trucks, Rollover prediction, Lateral-load transfer ratio, Machine learning, Recurrent neural network키워드:
자율주행 화물차, 차량전복 예측, 횡 방향 하중 전달 비율, 기계학습, 순환신경망1. 서 론
레벨 4 수준의 자율주행 화물차의 출현이 주목받는 가운데, 도로 위에서의 안전성 확보는 여전히 중요한 과제로 남아 있다.1) 경찰청 통계2)에 따르면, 2022년 한 해 동안 화물차 사고는 총 24,233건이 발생했으며, 이로 인해 630명이 사망하고 34,922명이 부상당했다. 특별히 차량 단독 전도/전복 사고는 차대차 충돌사고에 비해 적은 비중을 차지하지만 상대적으로 높은 사망률을 보였다.
이러한 화물차의 전복사고로 인한 인적, 물적 손실을 방지하고 도로 운영의 효율성을 높이기 위해서는 차량 속도를 능동적으로 조절하여 사고를 예방하고, 최적의 주행 속도를 예측하여 화물 운송의 효율을 극대화하는 기술이 필요하다. 이와 관련된 전통적인 차량 안전 기술은 ABS와 ESC 같은 실시간 제동 기술을 중심으로 발전해왔지만, 급변하는 상황에 맞춰 위험을 예방할 수 있는 새로운 기술의 필요성이 대두되고 있다.3,4)
차량의 동적 상황에서 전복을 유발하는 요인은 횡방향 가속도, 무게중심 위치 및 높이, 서스펜션 성능, 롤 저항 등이 있으며, 이 중 차량에 작용하는 횡가속도가 가장 큰 요인으로 꼽힌다.5) 횡가속도는 도로의 반경과 차량의 주행 속도를 통해 계산할 수 있으나, 횡가속도만으로는 차량의 안전성을 판단할 수 없고, 다른 요인 중 무게중심 높이 및 서스펜션 성능 등의 차량 성능 요소는 차량의 운용에 따른 노후 및 차량의 관리 상태에 따라 변하며, 화물의 무게 및 위치에 따라 주행 중에도 실시간으로 변화한다. 이러한 이유로 차량의 동역학 모델로서 예측할 수 없는 영역에 대해 최근 기계학습 기반의 자율주행 기술의 발전이 그 해결책으로 주목받고 있다.
선행 연구로 Antonio 등6)은 기계학습을 사용하여 차량의 동적 안전성을 예측하는 방법을 제시한 바 있다. 해당 연구에서는 차량의 속도와 종방향 가속도, 횡방향 가속도, 수직 가속도, Roll rate, Yaw rate, Pitch rate, 조향 각도를 독립변수로 입력하여 Roll 각도와 전·후축의 LTR을 예측하는 기계학습 모델을 구현하였다. Chao 등7)은 신에너지 차량의 전복 방지를 위해 신경망을 이용한 개선된 TTR을 제안하고, 전복에 영향을 미치는 여러 매개변수를 분석하여 예측 정확도와 관련된 다양한 하이퍼파라미터의 영향을 평가하였다. 해당 연구에서 기계학습에서의 은닉층 수, 사이클 수, 학습률, 배치 크기 등 다양한 요소가 예측 정확도에 영향을 미치며, 기계학습 알고리즘이 센서 테스트 기반의 기존 방식보다 더 효율적일 수 있음을 보였다.
본 연구에서는 자율주행 환경에서 계획된 경로의 곡률과 주행 속도를 이용해 도출한 횡가속도를 기반으로 횡 방향 하중 전달 비율(LTR)을 예측하는 기계학습 모델을 구축하고 시뮬레이션을 통해 시험 및 성능 평가를 수행하였다. 차량 전복 안전성 평가를 위해 사용된 LTR은 차량의 양쪽 바퀴에 걸리는 하중의 차이를 나타내는 비율로 1에 가까워질수록, 한쪽 바퀴에 걸리는 하중이 거의 없어지고, 반대쪽 바퀴에 모든 하중이 집중되어 차량이 전복할 수 있음을 의미한다.8) 실험에 사용된 기계학습 모델은 다중 선형 회귀 모델(MLR), Random Forest Regression(이하 Random Forest), 순환 신경망(RNN) 이며, 특별히 순환 신경망 모델의 경우 LTR과 같은 시계열 데이터 예측에 유리하다.
실험 결과는 기계학습 모델의 예측 정확도를 비교하여 보여주며 학습을 위해 입력되는 경로의 곡률과 차량의 속도를 그대로 사용하지 않고 횡가속도로 계산하여 학습을 진행할 경우 더욱 높은 예측 정확도를 지님을 보여준다.
2. 연구 방법
화물차 전복을 평가하는 두 가지 주행 시나리오에 대해 3가지 기계학습 모델을 비교하여 화물차의 주행 전복 안정성 예측하고 학습 데이터 선정에 따른 결과를 비교하였다. 본 연구에서는 TruckSim과 Matlab Simulink를 사용하여 화물차의 주행 데이터를 취득하였다.
2.1 주행 시뮬레이션 시나리오
데이터 취득을 위한 차량 모델은 5축 화물차를 기반으로 작성하였다. 차량의 제원은 전장 12,990 mm, 전고 3,995 mm, 전폭 2,495 mm, 차량 중량 12,800 kg, 무게중심 높이 1,000 mm를 적용하였다. 차량 모델의 각 차축 좌·우측의 타이어에서 수직하중 데이터를 출력하고, 차량 모델의 무게중심 위치에 센서 모델을 설치하여 차량의 이동 경로 좌표 값을 출력하였다.
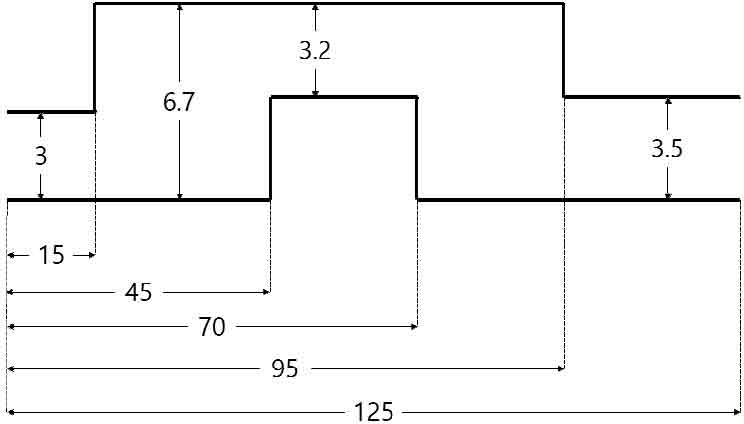
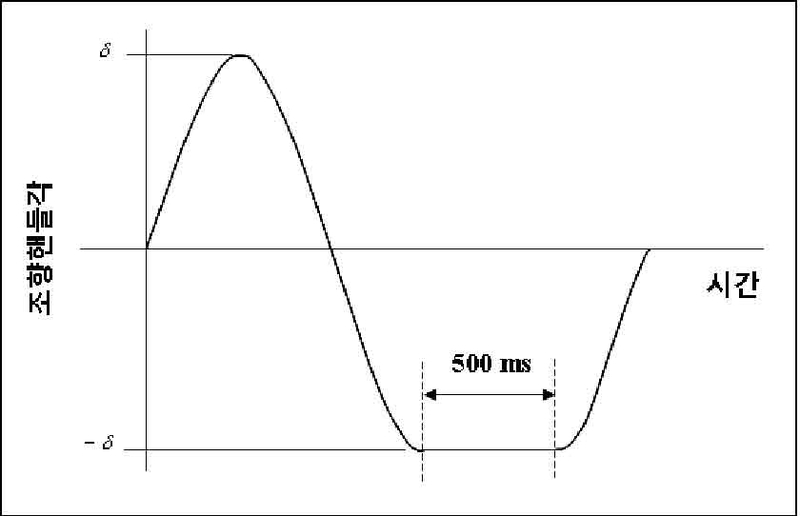
주행 시나리오는 DLC 및 SWD 시험 방법을 기반으로 작성하였다. Fig. 1은 TruckSim에서 DLC 및 SWD 주행 시나리오를 따라 시뮬레이션을 수행하는 모습을 보여준다. DLC 시나리오는 ISO-3888-19) 국제 표준을 기반으로 작성하였다. Fig. 2와 같은 트랙을 구성하고 속도에 따른 전복 안전성을 비교하기 위해 80.5 km/h를 적용하였고, 40 km/h 고정속도와 50 ~ 70 km/h의 변속으로 3가지 속도를 적용하였다. SWD 시나리오는 ‘자동차안정성제어장치 시험’ 규정의 ‘정지시간을 갖는 0.7 HZ 정현파조향시험’10)의 시험 방법을 기반으로 작성하였다. 동일 규정 중 점진증가조향시험을 통해 기준조향핸들각을 구하고, 0.7 Hz의 사인파에 기준조향핸들각에 1.5배를 곱하여 Fig. 3과 같은 조향 모델을 입력하였다. 주행 속도는 규정상의 속도 80 ± 2 km/h에 따라 DLC 시험과 동일하게 최대 속도 80.5 km/h를 적용하였고, 40 km/h 고정속도와 50 ~ 70 km/h의 변속으로 3가지 속도를 적용하였다.
2.2 기계학습 데이터셋 생성
주행로의 곡률 및 차량에 작용하는 횡가속도를 독립 변수로 사용하기 위해 시뮬레이션 데이터 중 차량의 속도와 이동 경로 좌표값을 출력하였다. 주행로의 곡률 k는 다음과 같이 계산한다:
| (1) |
where x : Longitudinal coordinate (m)
wherey : Lateral coordinate (m)
wheret : Time (sec)
계산된 곡률과 차량의 속도 데이터를 이용하여 횡가속도 ay를 다음과 같이 계산한다:
| (2) |
where k : Road curvature
whereVx : Longitudinal speed (m/s)
주행로의 곡률 및 차량에 작용하는 횡가속도를 독립 변수로 사용하고, LTR 지수를 종속 변수로 설정하였다.
LTR 지수는 차량의 좌·우에 작용하는 하중의 비율로 Fig. 4와 같이 차량 좌·우측 타이어의 수직하중을 이용해 다음과 같이 계산하였다.
| (3) |
- where Fzl : Vertical load on left tire (N)
- Fzr : Vertical load on right tire (N)
2.3 기계학습 모델 생성
기계학습 모델을 MLR 모델, Random Forest 모델, RNN 모델을 사용하여 각각의 예측 정확도를 비교하였고, 결과적으로 RNN 모델을 사용하여 차량의 LTR 지수를 예측하는 기계학습 모델을 구현하였다. RNN 모델은 순환신경망으로, 시퀀스 데이터를 처리하는 데 강점을 가진 신경망 구조로서 입력 데이터뿐만 아니라 이전 시점의 데이터를 함께 고려하여 예측을 진행하는 구조로 되어 있어 순차적인 데이터에 더욱 유리하다.11) RNN 파라미터는 Table 1과 같이 설정하였다. 기계학습을 위한 시험 데이터셋은 각 시험 모델별로 나누어 Table 2와 같이 입력하였다.
본 연구에서 사용한 RNN 모델은 입력 레이어, LSTM 레이어, Dropout 레이어, 출력 레이어로 구성하였다. 입력 레이어는 2개의 입력 레이어를 사용하여 곡률과 주행 속도를 사용하는 경우와 곡률과 횡가속도를 사용하는 경우로 분리하였고, 학습을 위한 시간 스텝의 길이는 10으로 적용하였다. LSTM 레이어는 50을 적용하였고, Dropout 레이어는 0.2를 적용하였다. 이는 예측 정확도를 확인하는 과정에서 경험적으로 도출한 수치이다. 출력 레이어는 LTR 만을 예측하여 1개를 적용하였다.
주행로의 곡률 및 차량에 작용하는 횡가속도를 독립 변수로 사용하고, LTR 지수를 종속 변수로 설정하여 학습 및 예측을 진행하였다. 기계학습 데이터셋은 각각의 시뮬레이션 데이터를 시작 시점부터 전반부 70 %를 학습, 이후 종료 시점까지 후반부 30 %를 예측하여 결과를 출력하였고, 예측 성능을 평가하기 위해 Mean Squared Error를 계산하였다. LTR 예측은 속도에 따른 DLC 3종류와 SWD 3종류, 총 6개의 데이터를 각각 학습 및 예측하였다.
3. 연구 결과
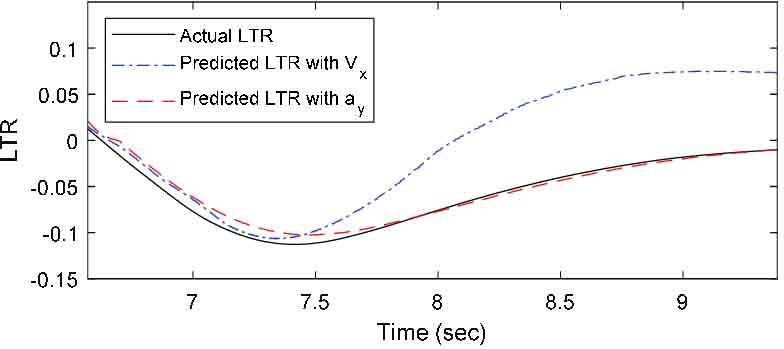
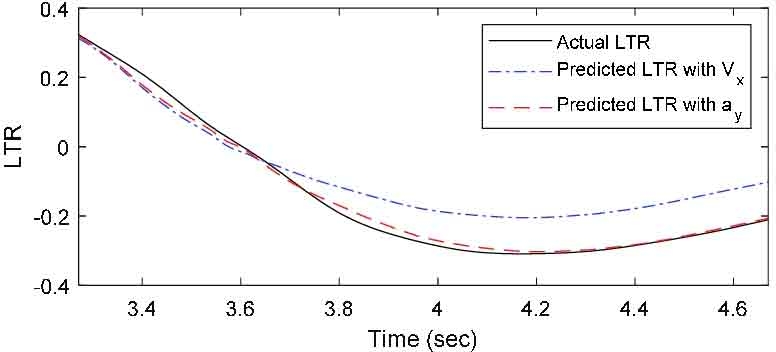
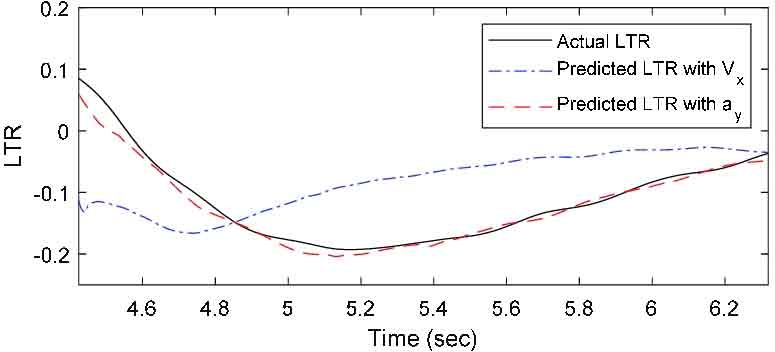
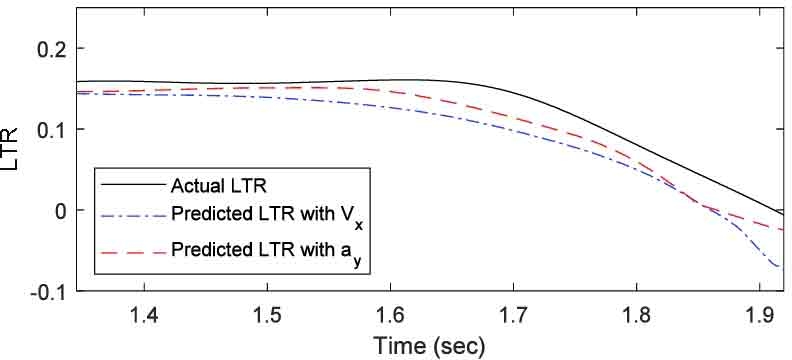
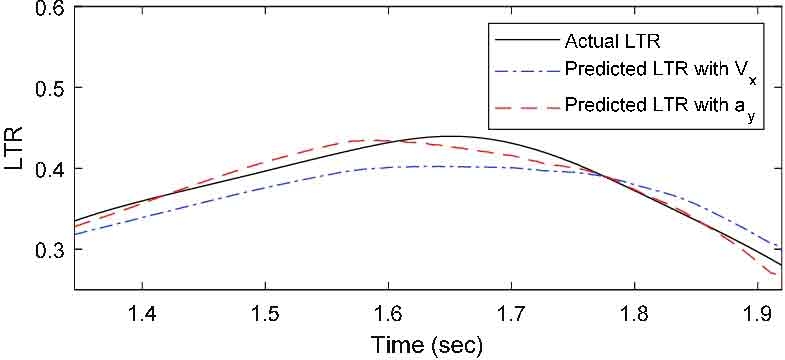
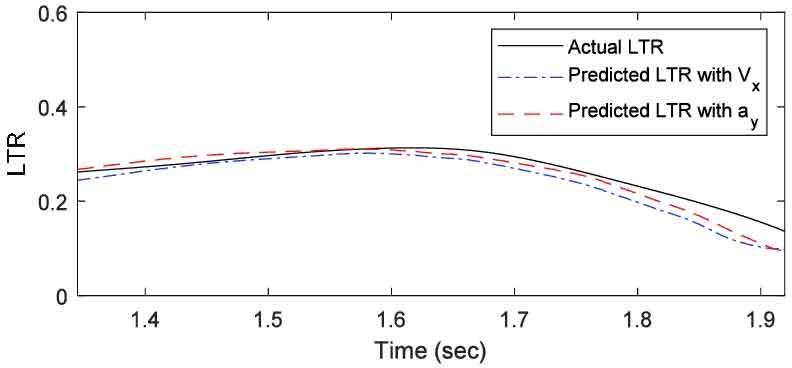
TruckSim과 Matlab Simulink를 사용하여 취득한 주행 데이터를 각각 곡률과 속도, 곡률과 횡가속도로 구분하여 RNN 모델에 입력하여 기계학습을 진행하였다. 총 12개의 LTR 예측 데이터를 출력하였고, 이를 각 시험 방법별 그래프로 나타내었다. Fig. 4부터 Fig. 6은 DLC 시뮬레이션 모델을 각각 40 km/h, 80.5 km/h, 50 ~ 70 km/h 속도로 진행한 후, LTR 지수를 곡률과 속도를 이용하여 예측한 경우와 곡률과 횡가속도를 이용하여 예측한 경우를 실제 데이터와 비교한 그래프이고, Fig. 7부터 Fig. 9는 SWD 시뮬레이션 모델을 동일한 방식으로 비교한 그래프이다. 여기서 Vx는 차량의 주행 속도를, ay는 차량에 작용하는 횡가속도를 의미한다.
3.1 곡률과 속도를 이용한 전복 안전성 예측
주행 경로의 곡률과 차량의 속도를 RNN 모델에 입력하여 학습을 진행한 결과를 Fig. 4부터 Fig. 9에 파란색 1점 쇄선으로 나타내었다.
먼저 차량 속도에 따라 DLC 시뮬레이션 데이터를 기계학습 후 동적 안전성 예측 결과를 분석하였다. Fig. 4의 7.5초 이후 실제 데이터와 평균 0.052, 최대 0.097의 차이를 보인다. Fig. 5의 예측 결과는 3.6초까지 예측 결과가 실제 데이터와 유사한 값을 보이나, 그 후 실제 데이터 보다 평균 0.062, 최대 0.113가량 낮은 예측값을 보인다. Fig. 6의 예측 결과는 앞선 두 케이스와 다르게 예측 데이터가 실제 LTR 데이터와 전혀 다른 값과 양상을 보인다.
다음으로 SWD 시뮬레이션을 통해 예측한 동적 안전성을 분석하였다. Fig. 7의 LTR 예측값과 실제 LTR 데이터가 유사한 경향성을 보이나, 실제 결과값 보다 평균 0.032, 최대 0.068가량 낮은 수치로 예측하였다. Fig. 8의 예측 결과를 보면 실제 LTR 지수 경향과 유사하나, 약 1.65초부터 실제값의 변화와 다른 양상을 보이며. 1.78초부터 예측값이 실제값과 평균 0.014, 최대 0.038의 차이를 보인다. Fig. 9의 예측값은 1.6초부터 실제값보다 평균 0.022, 최대 0.057가량 낮은 수치로 예측하였다.
계획 경로의 곡률과 차량의 주행 속도를 학습 데이터로 사용하는 경우 SWD 시험과 같이 LTR이 완만하게 변하는 상황에서 예측값이 실제값과 유사한 양상을 보인다. 반면 DLC 시험과 같이 차량의 안정성이 급격하게 변화하는 시나리오는 동적 안전성 예측 결과가 실제값과 큰 오차가 발생한다. 이는 기계학습 모델이 도로의 곡률 및 주행 속도와 LTR의 비선형적 관계를 극복하지 못한 것으로 판단된다. 따라서, 각 요소 간의 상관관계를 명확히 하기 위해 곡률과 속도만으로 계산할 수 있는 요소인 횡가속도를 사용하여 예측하는 방법으로 전환하였다.
3.2 곡률과 횡가속도를 이용한 전복 안전성 예측
기계학습에 사용되는 속도 데이터를 식 2를 이용하여 횡가속도로 변환 후 기계학습을 진행한 결과를 Fig. 4부터 Fig. 9에 빨간색 점선으로 나타내었다. 곡률과 속도를 이용한 안전성 예측과 동일하게 DLC 시뮬레이션 데이터를 이용해 속도에 따른 기계학습을 진행하여 예측한 동적 안전성을 분석하였다.
Fig. 4의 예측값과 경향성 모두 동일한 조건에서 실제값과 평균 0.004, 최대 0.016의 차이를 보이며 곡률과 속도를 사용한 케이스에 비해 높은 정확도를 보인다. Fig. 5의 예측값은 실제값과 평균 0.002, 최대 0.033의 차이로 곡률과 속도를 사용한 케이스에 비해 보다 높은 정확도를 보이나, 7.75초 전까지 실제값보다 낮은 값을 예측하는 결과를 보인다. Fig. 6의 예측 결과가 실제 LTR 데이터와 평균 0.008, 최대 0.044의 오차가 발생하였지만, 동일한 조건에서 곡률과 속도를 사용한 케이스에 비해 높은 정확도를 보인다.
동일하게 SWD 시뮬레이션을 통해 예측한 동적 안전성을 분석하였다. Fig. 7의 경우 동일한 조건에서 실제값과 평균 0.019, 최대 0.037의 차이로 곡률과 속도를 사용한 케이스에 비해 오차가 낮아진 결과를 보이고, Mean Squared Error 값 역시 더 낮은 결과가 나타났으나, 1.55초부터 실제 LTR 지수 보다 낮게 예측하는 결과를 보인다. Fig. 8의 예측 결과는 동일한 조건에서 실제값과 평균 0.002, 최대 0.023의 차이로 곡률과 속도를 사용한 케이스에 비해 낮은 오차를 보이며 Mean Squared Error 값 역시 더 낮은 결과가 나타났으나 일부 구간에서 실제 LTR 변화와 다른 경향을 보인다. Fig. 9의 예측 결과는 실제 LTR 지수와 유사한 경향을 보이며, 오차는 평균 0.007, 최대 0.067로 동일한 조건에서 곡률과 속도를 사용한 케이스 보다 더 낮은 오차를 보인다.
모든 속도와 주행 시나리오에 대하여 모두 동일한 조건에서 곡률과 속도를 사용한 케이스에 비해 보다 향상된 예측 결과를 도출하였다.
3.3 속도-횡가속도 예측 정확도 비교
곡률과 속도를 사용한 전복 안전성 예측 결과와 곡률과 횡가속도를 사용한 전복 안전성 예측 결과를 비교하였다. 여기서 횡가속도는 계획된 경로의 곡률과 계획된 주행 속도를 이용하여 계산된 값이다.
Table 3은 곡률과 속도를 사용한 예측 결과와 곡률과 횡가속도를 사용한 예측 결과를 각각 Model A와 Model B라 하고 Mean Squared Error 값을 비교한 결과이다. Mean Squared Error 비교에 따른 성능 비교 결과 모든 시험 방법에서 주행 속도를 그대로 사용하는 것보다 횡가속도로 변환하여 사용하는 것이 보다 향상된 예측 결과를 얻을 수 있음을 볼 수 있다.
3.4 기계학습 모델 성능 비교
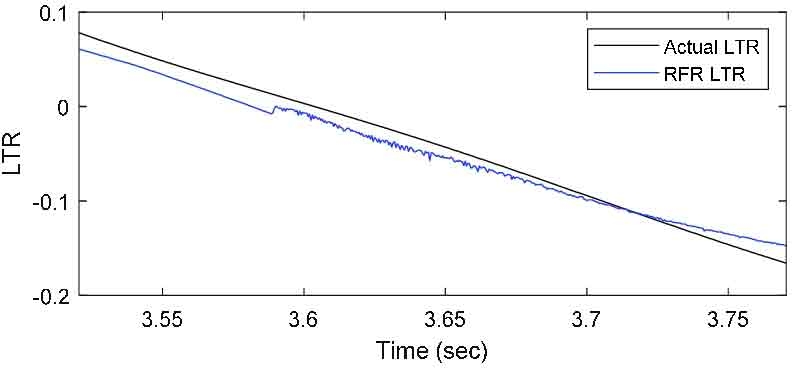
기계학습 모델에 따른 예측 정확도 비교를 위해 MLR, Random forest, RNN을 사용하여 기계학습을 진행하였다. Fig. 10과 11은 80.5 km/h 속도로 진행한 DLC 시뮬레이션과 SWD 시뮬레이션을 통해 생성한 곡률과 횡가속도 데이터를 기계학습을 이용하여 각 시뮬레이션 모델을 학습한 후 실제 데이터와 예측 결과를 비교한 그래프이다.
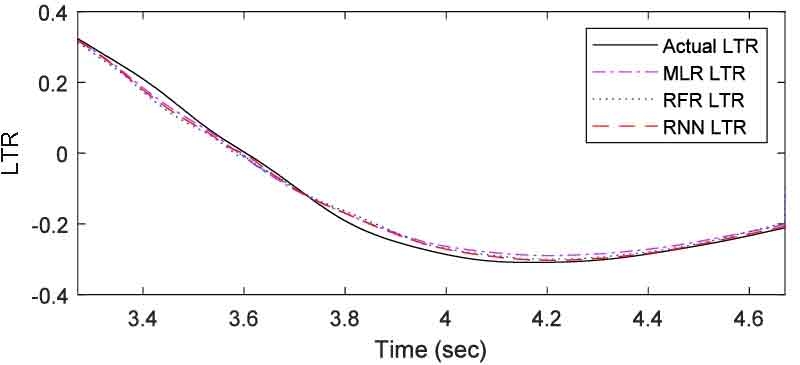
Comparison of LTR prediction results with various machine learning models(Driving Scenario: DLC test)
Table 4는 전복 안전성 예측 결과의 실제 데이터에 대한 Mean squared error 값이다. Mean squared error 값을 비교하였을 때, RNN 모델이 가장 낮은 수치를 나타내었다. 이는 RNN 모델이 전복 안전성을 예측하는 데 있어 가장 높은 정확도를 가짐을 의미한다.
MLR 모델의 경우 RNN 모델 다음으로 낮은 오차를 보인다. Fig. 10과 Fig. 11을 보면, DLC 시나리오의 경우 다른 기계학습 모델과 유사한 값을 보인다. 하지만 SWD 시나리오의 경우, 1.4초 이후 실제값보다 높은 예측값을 보이고, 그 오차 범위가 RNN 보다 큰 값을 보인다. Random forest 모델의 경우 Fig. 12와 같이 DLC 시나리오의 3.59 ~ 3.75초 구간 사이에서 예측 데이터의 미세한 진동을 확인할 수 있고, SWD 시나리오는 예측을 전혀 수행하지 못하는 결과를 확인할 수 있다.
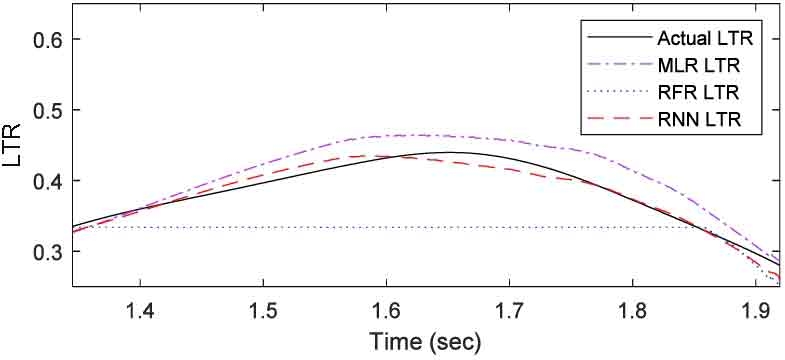
Comparison of LTR prediction results with various machine learning models(Driving Scenario: SWD test)
결과적으로 Mean squared error 값과 예측 데이터 양상을 종합적으로 고려할 때, 화물차의 전복 안전성 예측에 있어 RNN 모델을 사용하는 것이 가장 적합한 것으로 판단된다.
4. 결 론
본 연구에서는 화물차의 전복 안전성을 예측하기 위해 시뮬레이션을 활용한 주행 데이터 생성과 기계 학습 기반의 모델의 성능 검증을 수행하였다. 생성된 주행 시뮬레이션 데이터를 기계학습 데이터셋으로 설정하고, RNN 모델을 이용하여 전복 안전성을 예측하였다. 본 연구를 통해 다음과 같은 결과를 확인하였다.
- 1) 화물차의 주행 과정에서 LTR 지수를 계획된 주행 경로와 차량의 주행 속도 정보를 통해 예측할 수 있었다.
- 2) 차량의 주행 속도와 계획 경로의 곡률을 직접 사용하기 보다 횡가속도를 계산하여 학습 데이터셋으로 사용할 때 기계학습을 통한 전복 안전성 예측 정확도를 높일 수 있었다.
- 3) 기계학습 기반의 LTR 예측 모델을 통해 차량의 주행 과정에서 전복에 대한 안전성을 유지하는 최적의 주행 속도를 역산할 수 있는 가능성을 제시하였다.
본 연구의 한계점은 전복 안전성을 평가하기 위한 주행 시나리오의 구간이 기계학습을 진행할 만큼 충분히 길지 않아 각 시뮬레이션 케이스 간 예측 정확도의 차이가 발생하였다는 점이다. 이를 해결하기 위해서는 충분한 길이의 구간에 대한 주행 데이터를 기반의 해석이 이루어져야 할 것이다. 또한, 전복 안전성 예측 모델을 이용하여 자율주행 화물차의 주행 중 전복 위험 구간에서 사전 계획된 주행 경로 및 예측한 최적 LTR을 기반으로 횡가속도를 역산하여 최적의 주행 속도를 도출하고 주행에 적용하는 방법에 대해 추가적인 연구를 준비 중이며, 시뮬레이션 및 실차 실험을 통한 검증이 필요하다.
Nomenclature
| LTR : | lateral-load transfer ratio |
| TTR : | time to rollover |
| DLC : | double lane change |
| SWD : | sine with dwell |
| MLR : | multiple linear regression |
| CNN : | convolutional neural network |
| RNN : | recurrent neural network |
| LSTM : | long short-term memory |
Subscripts
| x : | longitudinal |
| y : | lateral |
Acknowledgments
본 연구는 국토교통부/국토교통과학기술진흥원의 “자율주행기술개발혁신사업” 지원으로 수행되었음(과제번호 21AMDP-C162388-01).
References
-
D. Wang, L. Gao, Z. Lan, W. Li, J. Ren, J. Zhang, P. Zhou, S. Wang, J. Pan, D. Manocha and R. Yang, “An Intelligent Self-Driving Truck System for Highway Transportation,” Frontiers in Neurorobotics, Vol.16, Paper No.843026, 2022.
[https://doi.org/10.3389/fnbot.2022.843026]

- Korean National Police Agency, “2023 Traffic Accident Statistics,” Report No.132002, Korean National Police Agency, 2023.
- S. S. Kim, “Prediction of ABS Braking Distance Using Simulation Technique,” KSAE Annual Conference Proceedings, pp.573-577, 2017.
-
J. W. Kim and J. H. Cho, “Augmented Forward Collision Warning System Based on Prediction of Vehicle Braking Distance,” Journal of Korean Institute of Information Technology, Vol.16, No.4, pp.21-28, 2018.
[https://doi.org/10.14801/jkiit.2018.16.4.21]

-
R. Rajamani, Vehicle Dynamics and Control, Springer Science & Business Media, 2011.
[https://doi.org/10.1007/978-1-4614-1433-9_2]

-
T. Antonio, L. Dimauro, F. Velardocchia, G. Paciullo and M. Velardocchia, “An Intelligent Predictive Algorithm for the Anti-Rollover Prevention of Heavy Vehicles for Off-Road Applications,” Machines, Vol.10, No.10, Paper No.835, 2022.
[https://doi.org/10.3390/machines10100835]

-
P. P. Chao, R. Y. Zhang, Y. D. Wang, H. Tang and H. L. Dai, “Warning Model of New Energy Vehicle Under Improving Time-to-Rollover with Neural Network,” Measurement and Control, Vol.55, No.9-10, pp.1004-1015, 2022.
[https://doi.org/10.1177/00202940221113588]

- P. A. Kim, S. S. Yoo and H. S. Lee, “Predicting the Dynamic Safety of Heavy Vehicle Using the Lateral Load Transfer Ratio,” Journal of the Korean Society of Mechanical Technology, Vol.24, No.5, pp.936-941, 2022.
- International Organization for Standardization, “ISO 3888-1:2018. Passenger Cars - Test Track for a Severe Lane-Change Manoeuvre - Part 1: Double-Lane Change,” Geneva, Switzerland: ISO, 2018.
- Ministry of Land, Infrastructure and Transport, “Performance and Standards for Automobiles and Automobile Parts Enforcement Regulations,” Appendix 1, No.50, Electronic Stability Control (ESC) Test.
-
S. Hochreiter, “Long Short-Term Memory,” Neural Computation, Vol.9, No.8, pp.1735-1780, 1997.
[https://doi.org/10.1162/neco.1997.9.8.1735]