평균 토크 향상을 위한 단절권 매입형 영구자석 동기전동기의 회전자 배리어 형상 최적 설계
Copyright Ⓒ 2024 KSAE / 227-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The IPMSM is primarily used within industrial fields of mobility, where high output, efficiency, and a wide operational range are crucial, depending on the driving conditions. IPMSM’s electrical characteristics vary based on the winding method. Short-pitch winding exhibits lower torque ripple, a lower total harmonic distortion(THD) of back electromotive force, and reduced leakage inductance at the end-turn than full-pitch winding. However, the average torque is small. Therefore, this study aimed to improve the average torque of IPMSM using short-pitch winding. Specifically, the objective function was to maximize the average torque. The torque ripple, the THD of the back electromotive force, and efficiency were set as constraints. Sensitivity analysis was conducted to select optimal design variables. The experiments were designed using the orthogonal array technique. The metamodel was performed by applying 11 metamodeling techniques and predicted R2, and the optimal point was determined by combining the most accurate metamodel and hybrid metaheuristic algorithm. Finally, finite element analysis(FEA) was conducted on the optimal point to confirm the validity of the metamodel-based optimal design.
Keywords:
Optimization, PMSM, Short-pitch winding, Metamodel, Mobility키워드:
최적화, 매입형 영구자석 동기전동기, 단절권, 메타모델, 모빌리티1. 서 론
최근 환경 오염 및 기후 변화에 따라 온실가스 감축을 위한 환경규제 강화로 인해 자동차, 철도, 전기 추진 선박 및 항공 분야와 같은 모빌리티 분야는 기존의 엔진 기반의 구동 시스템에서 전동기를 이용하는 친환경 전기 구동 시스템으로 전환되고 있다.1)
모빌리티 분야는 환경 및 주행 상황에 따라 저속 또는 고속에서 운전되기 때문에 고출력 및 고효율뿐만 아니라 넓은 운전 영역을 갖는 전동기가 필요하다.2)
매입형 영구자석 전동기(IPMSM)는 회전자 내부에영구자석이 매입된 형태로 표면부착형 영구자석 전동기(SPMSM)와 달리 고속 운전 시 영구자석이 비산될 위험성이 없다.3) 또한 회전자의 구조로 인해 마그네틱 토크뿐만 아니라 릴럭턴스 토크 또한 발생되기 때문에 높은 출력 밀도를 가지게 되며 약계자 제어를 통해 고속에서도 높은 출력을 유지할 수 있다.4) 따라서 고출력, 고효율 및 넓은 운전 영역이 요구되는 모빌리티용 전동기로 많이 사용된다.5)
IPMSM은 사용되는 권선 방식에 따라 전기적인 특성에 차이가 발생한다. 권선 방식은 크게 고정자 하나의 치에 한 상의 권선을 집중되게 감는 방식인 집중권(Concentrated winding)과 한 상의 권선을 여러 슬롯에 분포되게 감는 방식인 분포권(Distributed winding)이 있다. 분포권은 권선 작업이 집중권에 비해 복잡하고 End turn의 높이가 높아진다는 단점이 있다.6) 하지만 집중권보다 짧은 슬롯 피치의 길이와 슬롯의 위상차로 인해 고조파가 감소되고 고조파에 의해 발생되는 영구자석 와전류 손실 또한 감소되어 고속 영역에서 높은 효율을 가지는 장점이 있다.7) 더 나아가 권선법은 전절권(Full pitch winding)과 단절권(Short pitch winding)으로 구분할 수 있으며 전절권은 코일 피치와 극 피치가 동일하다.
그에 반해 단절권은 코일 피치가 극 피치보다 작아 전절권에 비해 전동기의 소음 및 진동에 주요 원인인 토크 리플과 제어의 정확성에 영향을 주는 역기전력의 THD가 더 낮으며 End-turn 부분에서 누설 인덕턴스 성분도 적다는 장점이 있다.8) 하지만 한 상의 권선에 쇄교되는 자속량이 적어 전절권에 비해 기자력의 크기가 작다.9) 따라서 단절권을 고출력이 요구되는 모빌리티용 IPMSM의 권선 방식으로 사용하기 위해서는 평균 토크 향상에 관한 연구가 필요하다.
평균 토크를 향상시키기 위한 연구들로 영구자석의 매입 형태 및 각도에 따른 토크 비교, 회전자 배리어의 형상 최적화 등 다양한 연구들이 있다. 그중에서 회전자 구조에 영향을 주는 회전자 배리어의 형상이 변함에 따라 마그네틱 토크와 릴럭턴스 토크가 변하기 때문에 배리어 형상을 변경하여 영구자석의 Q(Quadrature)축 자로를 확보해 릴럭턴스 토크를 증가시켜 평균 토크를 향상시키는 연구,10) 새로운 배리어 형태를 만들어 평균 토크를 향상시키는 연구11) 등 배리어 형상 최적 설계 연구가 활발히 진행되고 있다. 하지만 기존 연구들에서는 전기자동차 구동모터로서 요구되는 중요한 특성인 토크 리플, 역기전력의 THD 등이 최적 설계에 고려되지 못하였다. 토크 리플과 역기전력의 THD는 전동기의 소음 및 진동, 제어에 큰 영향을 주기 때문에 최적 설계 시 고려할 필요성이 있다.12,13)
최적 설계 방법은 예측 모델인 메타 모델을 사용하는 방법과 최적화 알고리즘을 직접 결합하는 방법으로 구분할 수 있다. 메타모델 기반 최적설계 기법은 실험계획법을 기반으로 하여 설계 공간 전체를 효과적으로 탐색하고, 다항 회귀 분석, 크리깅(Kriging), 신경망(Neural network) 등 다양한 메타모델링 기법을 활용하여 실제 해석 모델의 입력 변수와 출력 반응 간의 관계를 수학적 함수로 근사화한 후 최적화 알고리즘과 결합하여 최적해를 찾게 된다. 따라서 고비용 또는 시간이 많이 소요되는 실제 해석 모델을 대체할 수 있다.14) 하지만 근사화 함수로 만들어진 예측 모델이기 때문에 예측 성능이 좋지 않은 메타모델을 사용할 경우 실제 해석값과 예측값의 오차가 크게 발생할 수 있다. 따라서 예측 성능이 뛰어난 메타 모델을 만드는 것이 중요한 사항이다.15)
하지만 기존 연구들에서는 주로 단일 메타모델링 기법을 사용하여 메타 모델을 생성하였다.16-18) 설계 문제마다 적용하는 메타모델링 기법에 따라 메타 모델의 예측 성능이 상이할 수 있기 때문에 가장 적합한 메타모델링 기법을 선정하기 위해서는 다양한 메타모델링 기법을 적용하여 검토해야한다.19)
따라서, 본 논문에서는 메타모델의 예측 성능을 높이기 위해 단일 메타모델링 기법이 아닌 11가지 메타모델링 기법 중 메타모델 예측 성능 평가 지수인 Predicted R2을 활용해 가장 예측 성능이 우수한 메타모델링 기법을 선정하였으며, 최적화 알고리즘과 결합하여 평균 토크를 향상시키기 위해 단절권을 사용한 매입형 영구자석 동기전동기의 회전자 배리어 형상 최적 설계를 진행하였다. 또한 전기자동차 구동 모터로서 중요하게 요구되는 토크 리플, 역기전력의 THD 특성들을 고려하여 최적 설계를 진행하였다.
2. 최적화 설계
2.1 초기 모델
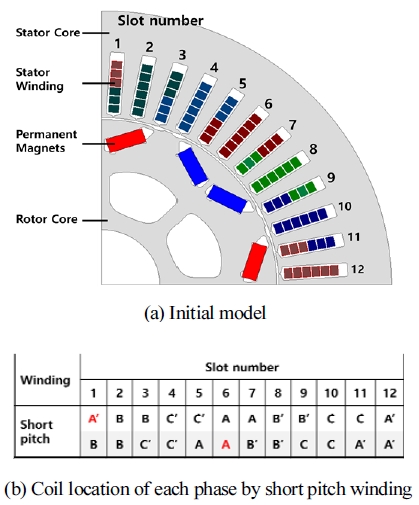
Fig. 1의 (a)는 단절권을 사용한 영구자석 동기전동기의 초기 모델의 형상이며, 제원은 Table 1과 같다. 모델은 8극 48슬롯이며, 평각동선을 사용하였다. 평각동선은 환형동선보다 슬롯 내에 불필요한 공간을 줄일 수 있어 점적률이 높고 그로 인해 출력 밀도와 효율을 향상시킬 수 있다.20) 본 모델의 권선 방식은 한 상을 다수의 슬롯에 분포되도록 구성하는 분포권과 코일 피치가 극 피치보다 작은 단절권을 사용하였으며, 권선 배치는 Fig. 1의 (b)와 같다. 고정자와 회전자는 와전류가 발생되는 공간을 축소시켜 와전류손을 저감하기 위해 일반적으로 많이 사용하는 0.5 mm 두께의 전기강판이 아닌 0.35 mm의 두께를 가지는 35JN440 등급의 전기강판을 사용하였다. 영구자석은 N45SH 등급의 NdFeB를 사용하였으며 출력 밀도를 증가시키기 위해 자속을 집중시키는 V-type으로 매입하였다.
2.2 최적 설계 과정
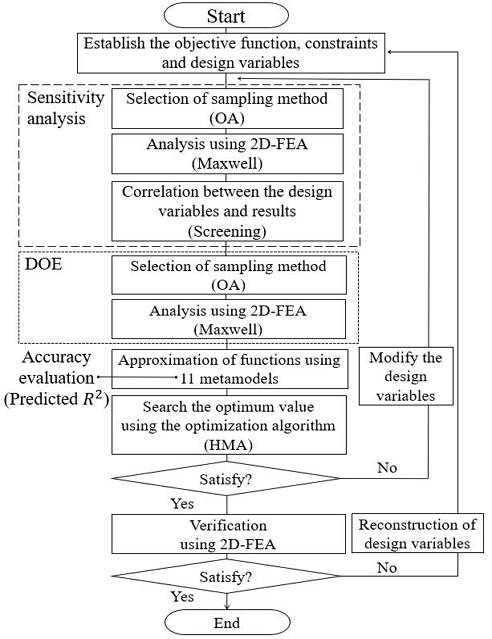
본 논문에서는 유한요소해석 프로그램인 Ansys Maxwell과 PIDOTECH의 PIAnO(Process Integration, Automation and Optimization)를 사용하였다. PIAnO는 최적 설계 프로그램으로, 실험계획법, 민감도분석, 메타모델링, 메타모델 기반 최적 설계 등 최적 설계에 필요한 기능들을 제공한다.21) 먼저 최적 설계를 위해 목적 함수와 제약 조건을 설정하였고 유의한 최적 설계 변수를 선정하기 위해 PIAnO의 Screening 기법을 활용하여 민감도 분석을 수행하였다. OA(Orthogonal Array) 기법을 통해 18개의 실험점을 선정하였으며, 선정한 18개의 실험점 데이터를 바탕으로 11가지 메타모델링 기법을 각각 사용하여 출력 변수별 11개의 메타모델을 생성하였다. 이후, 예측 성능 평가 지수인 Predicted R2을 활용해 출력 변수별 가장 적합한 메타모델링 기법을 선정하였다. 생성된 메타모델과 전역 최적화 알고리즘인 HMA(Hybrid Metaheuristic Algorithm)를 결합하여 메타모델 기반으로 한 전동기의 회전자 배리어 형상 최적 설계를 진행하였다. Fig. 2는 매입형 영구자석 동기전동기의 최적 설계 과정이다.22)
2.3 설계 문제 정식화 및 설계 변수
최적 설계를 진행하기 전에 설계 문제 정식화를 위한 목적 함수와 제약 조건을 설정해야 한다. 기자력의 크기가 전절권에 비해 작은 단절권의 단점을 보완하기 위해 목적 함수는 평균 토크 최대화로 설정하였으며, 제약 조건은 토크 리플, 역기전력의 THD, 효율로 선정하였다. 역기전력의 THD와 효율은 초기 모델과 동일한 수준으로 유지되도록 각각 8.13 % 이하, 94.97 % 이상으로 설정하였으며 토크 리플은 전기자동차용 견인 전동기의 허용 가능한 토크 리플 수준인 10 % 미만으로 제약 조건을 설정하였다.23)
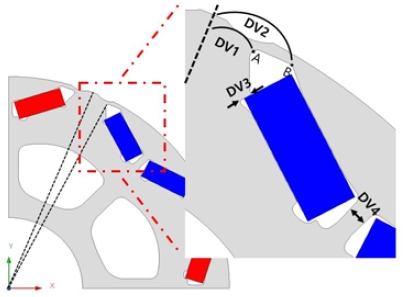
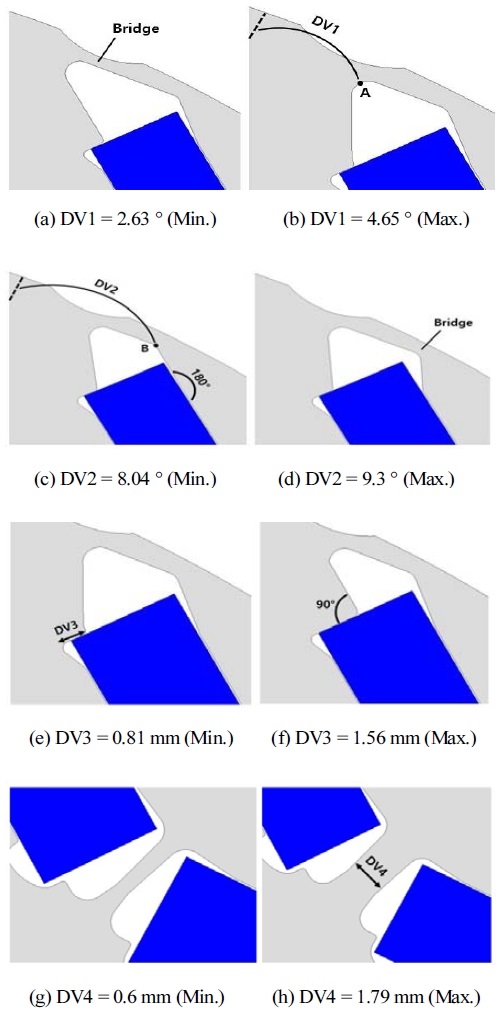
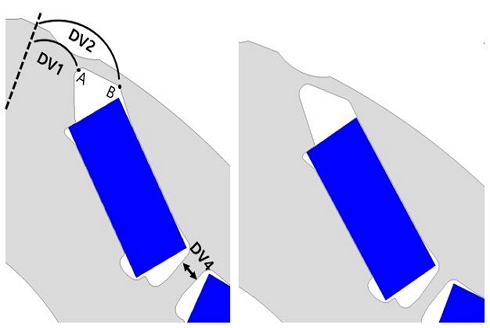
목적 함수와 제약 조건을 만족시키기 위한 설계 변수는 Fig. 3에 나타내었다. 설계 변수인 DV1과 DV3의 형상 변화에 따라 Bridge의 두께, 영구자석의 Q축 자로가 변하게 되어 토크, 역기전력, 효율 등 전동기의 전반적인 특성에 영향을 미치게 되고, DV2의 형상 변화에 따라 쇄교자속과 자속의 분포가 변하게 되어 전동기의 토크 및 토크 리플 특성이 변하게 된다.24,25) 또한 DV4의 값이 변하게 되면 DV4를 통과하는 자속 밀도가 변하게 되어 공극 자속에 영향을 미치기 때문에 설계 변수로 선정하였다.26) 설계 변수의 범위는 Table 2에 정리하였으며 설계 변수의 범위가 최소, 최대일 때 형상은 Fig. 4와 같다. 설계 변수의 범위를 선정할 때 전기적인 특성, 제작 생산성, 기계적 강성 등을 고려해야 한다. 또한 범위를 너무 크게 선정하면 최적점을 찾기까지 시간이 오래 소요될 수 있으며, 반대로 범위를 작게 선정하면 도출된 최적점이 정확한 최적점이 아닐 수도 있다. 따라서 설계 변수의 범위를 잘 선정해야 한다.15)
설계 변수 DV1은 Barrier outer이며 회전자 중점에서 자석 N극과 S극 사이 중점을 가로지르는 기준선과 Fig. 3에 표시된 점 A의 사잇각이다. DV1의 최솟값은 금형 공정에서 필요한 최소 기준 치수인 0.5 mm와 허용 공차인 0.1 mm를 고려하여 Fig. 4의 (a)에 표시한 Bridge가 0.6 mm가 되는 2.63 °를 최솟값으로 선정하였다. 최댓값은 Bridge 두께에 따른 전기적인 특성을 고려하였다. Bridge의 두께는 얇아질수록 전동기의 전반적인 특성이 향상되지만 반대로 두꺼워지면 전동기의 특성은 저하된다.27) 따라서 DV1이 커질수록 Bridge가 두꺼워지기 때문에 초기 모델의 기존값인 4.65 °를 최댓값으로 선정하였다. DV2는 Barrier Inner로 회전자 중점에서 자석 N극과 S극 사이 중점을 가로지르는 기준선과 Fig. 3에 표시된 점 B의 사잇각이다. 따라서 DV2의 최솟값은 Fig. 4의 (c)에 표시한 각도가 180 °에 이를 때, DV2의 각도인 8.04 °를 최솟값으로 선정하였다. DV2의 사잇각이 커질수록 Fig. 4의 (d)에 표시한 Bridge의 두께가 얇아진다. 따라서 금형 제작 생산성을 고려하여 Bridge의 길이가 0.6 mm가 될 때의 각도인 9.3 °를 최댓값으로 선정하였다. DV3은 Magnet fixture이며 고속 회전 시 원심력에 의한 영구자석 비산을 방지하는 구조이다. 따라서 최솟값은 기존값인 0.81 mm이며 최댓값은 Fig. 4의 (f)에 표시한 각도가 90 °일 때 길이인 1.56 mm로 선정하였다. 표시한 각도가 90 °보다 작아질 경우 해당 부분은 돌출 되어있는 형태로 되어 회전 시 응력이 집중되거나 제작 공정 중에 해당 부분이 깨질 수 있다. DV4는 Center bridge로 최솟값은 기계적 강성과 금형 제작에 필요한 최소 기준 치수인 0.5 mm 및 허용 공차 0.1 mm를 고려하여 최솟값을 0.6 mm로 선정하였다. 또한 DV4가 기존값보다 더 커지게 되면 DV4의 자속 밀도가 감소하게 된다. 이로 인해 더 많은 영구자석의 자속이 DV4를 통해 흐르게 되어 공극 자속이 줄어들기 때문에 기존값인 1.79 mm를 최댓값으로 선정하였다.26)
2.4 민감도 분석
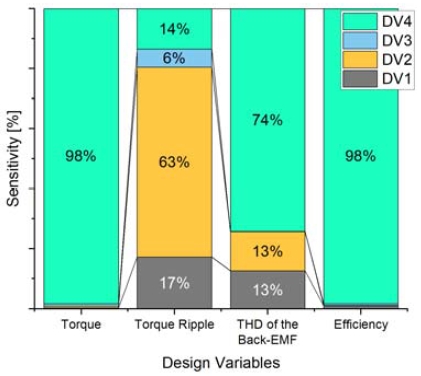
선정된 설계 변수와 출력 변수 간의 상관관계를 분석하기 위해, FFD(Full Factorial Design) 기법 중 하나인 OA 기법을 이용하여 실험점을 선정하였으며, PIAnO의 screening 기법을 활용하여 민감도 분석을 진행하였다. OA 기법은 직교성을 만족하는 직교 배열을 사용하여 설계 변수 간의 교호 작용을 파악하고 인자들의 효과가 함께 나타나 각 인자의 개별효과를 알 수 없는 등 무시할 수 있는 교호 작용들은 배재하는 기법이다. 이로 인해 FFD 기법보다 적은 실험회수로 설계 변수와 출력 변수 간의 상관관계를 분석할 수 있다는 장점이 있다.28) 4개의 설계 변수에 대해 3수준으로 직교성을 만족하는 총 18개의 실험점을 선정하였고 유한요소해석을 수행하였다. 이후, 실험점에 대한 유한요소해석 값을 이용하여 민감도 분석을 진행하였고 Fig. 5는 민감도 분석 결과이다. 민감도 분석을 통해, 설계 변수 중 Center bridge (DV4)가 목적 함수인 평균 토크와 제약 조건에 가장 큰 영향을 미치는 설계 변수임을 확인하였다. 반면 Magnet fixture(DV3)는 출력 변수 중 토크 리플에만 6 %의 영향을 미치는 것으로 나타났으며, 나머지 출력 변수에 대한 영향도는 1 % 미만으로 확인되었다. 따라서, Magnet fixture(DV3)는 최적 설계 변수에서 제외하였고, 유의하다고 판단된 Barrier outer(DV1), Barrier inner(DV2), Center bridge(DV4) 총 3개의 최적 설계 변수만을 가지고 메타모델링을 진행하였다.
2.5 실험계획법 및 메타모델링
실험계획의 횟수는 설계 변수의 수에 따라 결정되며 메타모델의 정확성을 고려하기 위해서 다음 식 (1)을 통해 필요한 실험점의 수를 구할 수 있다.21) nEXP는 실험점의 수이며, nDV는 설계 변수의 수를 의미한다.
| (1) |
즉, 민감도 분석을 통해 선정된 최적 설계 변수가 3개이므로 식 (1)을 통해 계산하면 실험점이 15개 이상이어야 한다. 샘플링 기법으로는 민감도 분석에서 사용한 OA 기법을 사용하였다. OA 기법은 직교배열을 이용하기 때문에 직교성을 만족해야 한다. 따라서 직교성과 메타모델의 정확성에 필요한 실험점의 수를 고려하여 실험점을 18개로 선정하였다. 또한 메타모델을 생성하기 위해 18개의 실험점에 대한 유한요소해석을 수행하였다. 메타모델링 기법에는 다양한 기법들이 있다. 어떠한 메타모델링 기법을 사용했는가에 따라서 메타모델의 정확도가 달라지기 때문에 설계 문제에 적합한 메타모델링 기법을 선정하는 것은 중요하다. 따라서 전역 모델과 국부 편차의 합을 이용하여 심한 비선형성까지 나타낼 수 있는 Kriging과 기저함수와 신경망을 결합해 근사함수를 생성하는 RBF(Radial Basis Function), 최소 자승법을 사용해 다항식의 계수를 구하여 메타모델을 생성하는 PRG(Polynomial Regression), 예측값을 나타내는 여러 개의 결정 트리 (Decision Tree)의 평균값으로 예측 모델을 형성하는 EDT(Ensemble of Decision Trees), 딥러닝 알고리즘의 한 유형으로 실제값과 다층 퍼셉트론을 통하여 예측한 값의 오차를 최소화하도록, 반복적으로 학습시키는 MLP(Multi-layer Perceptron) 기법 등 총 11가지의 메타모델링 기법을 각각 적용하여 PIAnO에서 제공하는 메타모델 생성 기능을 통해 메타모델을 생성하였다.29-32) 이후, Predicted R2을 이용하여 메타모델의 정확도를 평가하는 PIAnO의 메타모델 평가 기능을 통해 생성된 메타모델들의 정확도를 평가하였다. Predicted R2 는 메타모델의 예측 성능에 대한 정확도를 평가하는 지표이며 다음 식 (2)을 통해 정의된다.21)
| (2) |
여기서 y(xi)는 i번째 실험점의 실제 값, 는 i번째 실험점을 제외하고 구성한 모델의 i번째 실험점에 대한 예측 값, 는 실제 값의 평균이다.
Predicted R2는 정량화된 오차 값을 제공하는 기존의 R2와 달리 교차 검증을 통해 각 실험점을 독립적으로 검증하며 모델을 평가한다. 그로 인해 메타모델의 예측 성능을 기존의 R2 보다 더 정확히 평가할 수 있다.21) Predicted R2는 0과 1의 사잇값을 가지며 1에 가까울수록 메타모델과 실제 모델 간의 오차가 적음을 나타낸다. 출력 변수별 생성된 11가지 메타모델의 Predicted R2값을 Table 3에 정리하였다. 평균 토크는 PRG(Forward Step) 기법, 역기전력의 THD는 PRG(Backward Step) 기법, 토크 리플과 효율은 Kriging 기법을 사용했을 때 메타모델의 정확도가 가장 우수하여 최적 메타모델링 기법으로 선정되었다.
2.6 메타모델 기반의 최적 설계
출력 변수별 최적 메타모델링 기법으로 생성된 메타모델들은 전역 최적화 알고리즘인 HMA와 결합시켜 최적화를 진행하였다. HMA는 적합도에 따라 독립적으로 취급되는 상위 집단과 하위 집단으로 분할하여 상위 집단에서 Rank-iMDDE(Improved constrained defferential evolution), 하위 집단에서는 MCS(Modified Cuckoo Search)기법을 사용하여 최적해를 찾는 방법이다. Rank-iMDDE 및 MCS 기법의 이점을 결합하여 사용하기 때문에 다른 전역 최적화 알고리즘에 비해 빠르게 최적해를 찾을 수 있다.15) 최적 설계 결과는 Table 4에 나타내었다. HMA를 통해 도출된 예측값과 FEA의 검증 값에 대한 오차율을 비교한 결과, 토크는 0.01 %, 토크 리플은 0.74 %, 역기전력의 THD는 1.47 %, 효율은 0.0 %로 예측 성능이 우수한 메타모델임을 확인할 수 있다. 역기전력의 THD의 도출된 예측값은 8.15 %로 제약 조건이었던 8.13 %를 초과하였지만 최적설계프로그램인 PIAnO에서 허용되는 오차율을 고려해 + 0.3 %까지는 제약 조건을 만족한다고 판단한다. 토크 리플은 초기 모델 대비 9.51 %에서 9.59 %로 0.08 % 증가하였지만 제약 조건인 10 % 미만을 만족한다.
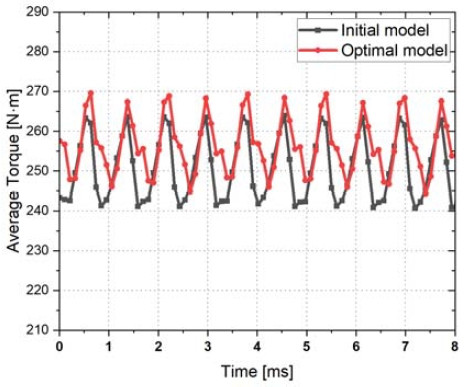
역기전력의 THD는 8.13 %에서 8.27 %로 0.14 % 증가하였으며 이는 DV4가 줄어들어 자속이 중앙으로 집중됨에 따라 공극 자속 밀도가 변화하였기 때문이다. 효율은 94.97 %에서 95.11 %로 초기 모델보다 향상되었다. 목적 함수였던 평균 토크는 초기 모델 대비 249.97 N⋅m 에서 255.86 N⋅m로 약 2.3 % 증가하였다. Fig. 6은 초기 모델과 최적 모델의 평균 토크 파형이며 형상은 Fig. 7에 나타내었다.
2.7 고찰
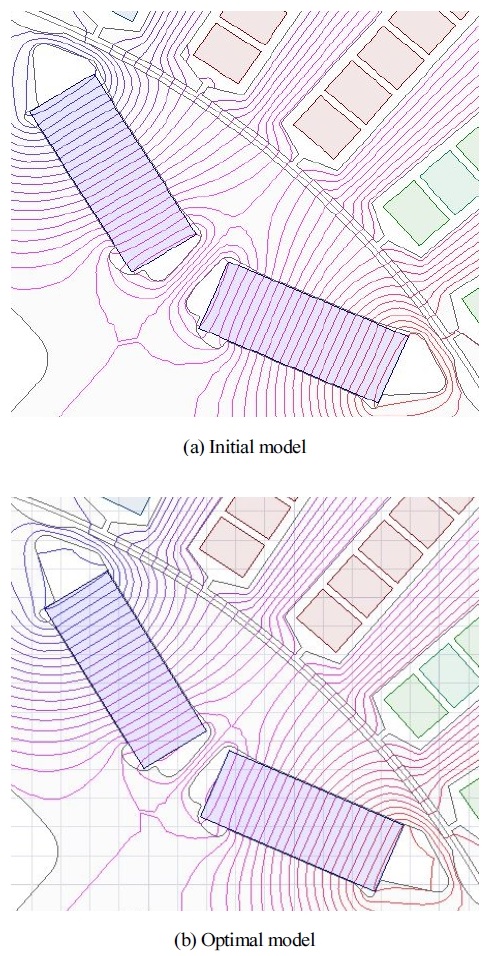
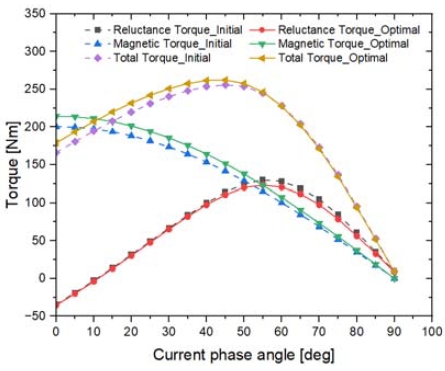
민감도 분석을 통해 평균 토크에 가장 영향을 미치는 설계 변수는 Center Bridge (DV4)임을 알 수 있었다. 또한 최적 설계 결과인 Table 4를 보면 Center Bridge (DV4)가 기존 1.79 mm에서 1.03 mm로 변경됨을 알 수 있다. Fig. 8은 초기 모델과 최적 모델의 자속 선도이다. 초기 모델과 최적 모델의 자속 선도를 비교하면 최적 모델에서 자속선이 더 증가하였고 고정자 치의 누설 자속 또한 감소했음을 알 수 있다. Fig. 9는 초기 모델과 최적 모델의 릴럭턴스 토크, 마그네틱 토크 파형이며 최적 모델의 마그네틱 토크가 증가함에 따라 전체 토크가 증가하였음을 알 수 있다. 따라서 배리어의 형태가 자속의 흐름을 원활하게 만들고 Center Bridge(DV4)의 길이가 줄어들수록 자속을 집중시켜 토크 향상에 큰 영향을 미친다는 것을 확인할 수 있었다. 또한 도출된 최적점 예측값과 유한요소해석 값의 오차율이 1.5 % 미만으로 출력 변수별 11가지 메타모델링 기법 중 가장 적합한 메타모델링 기법을 선정하는 것이 예측 성능이 우수한 메타모델을 생성하는데 유용하다는 것을 알 수 있었다.
3. 결 론
본 논문에서는 메타모델 기반의 최적 설계를 통해 매입형 영구자석 동기전동기의 회전자 배리어 형상 최적화를 수행하였다.
- 1) 전절권에 비해 기자력 크기가 작은 단절권의 단점을 보완하고자 목적 함수를 평균 토크 최대화로 설정하였고, 제약 조건은 토크 리플, 역기전력의 THD, 효율로 설정하였다. OA 기법을 활용한 민감도 분석을 통하여 목적 함수와 제약 조건에 유의미한 설계 변수를 도출하였다.
- 2) 11가지의 메타모델링 기법 중 메타모델 정확도 평가 방법인 Predicted R2을 활용하여 출력 변수별 가장 적합한 메타모델링 기법을 도출하여 메타모델을 생성하였다.
- 3) 전역 최적화 알고리즘인 HMA와 생성된 메타모델을 결합하여 최적 설계를 진행하였으며 목적 함수와 제약 조건에 만족하는 최적점을 도출하였다.
한 가지 메타모델링 기법만이 아닌 11가지의 메타모델링 기법을 검토하여 가장 적합한 메타모델링 기법을 선정함으로써 예측 성능이 우수한 메타모델을 생성할 수 있었으며, 유한요소해석을 통해 예측값과 실제 해석 값의 오차율이 1.5 % 미만임을 확인하여 설계 결과의 타당성을 검증하였다.
따라서 메타모델 기반의 회전자 배리어 형상 최적 설계가 단절권 매입형 동기전동기의 토크 향상에 유용함을 알 수 있었다.
Nomenclature
| IPMSM : | interior permanent magnet synchronous motor |
| SPMSM : | surface permanent magnet synchronous motor |
| THD : | total harmonic distortion |
| HMA : | hybrid metaheuristic algorithm |
| Back-EMF : | back electromotive force |
| FEA : | finite element analysis |
Acknowledgments
A part of this paper was presented at the KSAE 2023 Fall Conference and Exhibition
이 논문은 2024년도 정부(교육부, 산업통상자원부)의 재원으로 한국연구재단의 기초연구사업(No.2021R1I1A3060525)과 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0020536, 2024년 산업혁신인재성장지원사업).
References
-
J. Park, C. Kim and T. Kim, “An Analysis of the Research Trend on Smart Mobility: Topic Modeling Approach,” The Journal of the Korea Institute of Intelligent Transport Systems, Vol.21, No.2, pp.85-100, 2022.
[https://doi.org/10.12815/kits.2022.21.2.85]

-
G. Jeong, C. B. Park, H. W. Lee, S. D. Lee and J. Lee, “A Study on the Design of a 130kW-class IPMSM for Propulsion of Tram-Train,” Journal of the Korean Society for Railway, Vol.19, No.4, pp.427-435, 2016.
[https://doi.org/10.7782/JKSR.2016.19.4.427]

- D. Y. Han, Y. T. Kim, C. S. Hahn and K. C. Kim, “Characteristic Analysis of Parameters for the Performance Simulation of Interior Permanent Magnet Synchronous Motor,” KSAE Spring Conference Proceedings, p.1338, 2014.
-
M. Lee, I. Kim and C. S. Lee, “Characteristic Comparison of Brushless Motor Type for EPS System,” Transactions of KSAE, Vol.20, No.1, pp.53-60, 2012.
[https://doi.org/10.7467/KSAE.2012.20.1.053]

-
R. Dutta and M. F. Rahman, “Design and Analysis of an Interior Permanent Magnet (IPM) Machine With Very Wide Constant Power Operation Range,” IEEE Transactions on Energy Conversion, Vol.23, No.1, pp.25-33, 2008.
[https://doi.org/10.1109/TEC.2007.905061]

- J. H. Bahn, S. Kwon, S. H. Ha and J. P. Hong, “Investigation on Characteristics of Interior Permanent Magnet Synchronous Motor According to Pole-Slot Combination,” The Korean Institute of Electrical Engineers, pp.771-772, 2006.
-
J. H. Seo, S. Y. Kwak, S. Y. Jung, C. G. Lee, T. K. Chung and H. K. Jung, “A Research on Iron Loss of IPMSM with a Fractional Number of Slot Per Pole,” IEEE Transactions on Magnetics, Vol.45, No.3, pp.1824-1827, 2009.
[https://doi.org/10.1109/TMAG.2009.2012786]

-
M. Silberberger, D. P. Morisco, H. Rapp and A. Möckel, “Calculation of End-Winding Leakage Inductance for Hairpin Winding High Power Density Traction Machines Using the PEEC Method,” IEEE International Electric Machines & Drives Conference (IEMDC), pp.1-7, 2021.
[https://doi.org/10.1109/IEMDC47953.2021.9449550]

-
M. Ooshima, “Analyses of Rotational Torque and Suspension Force in a Permanent Magnet Synchronous Bearingless Motor With Short-Pitch Winding,” IEEE Power Engineering Society General Meeting, pp.1-7, 2007.
[https://doi.org/10.1109/PES.2007.386135]

-
K. D. Lee and J. Lee, “Shape Design Method for High Torque in the Flux-Weakening Range of the IPMSM,” The Transactions of The Korean Institute of Electrical Engineers, Vol.64, No.4, pp.629-633, 2015.
[https://doi.org/10.5370/KIEE.2015.64.4.629]

-
W. Zhao, F. Zhao, T. A. Lipo and B. -I. Kwon, “Optimal Design of a Novel V-Type Interior Permanent Magnet Motor with Assisted Barriers for the Improvement of Torque Characteristics,” IEEE Transactions on Magnetics, Vol.50, No.11, pp.1-4, 2014.
[https://doi.org/10.1109/TMAG.2014.2330339]

- C. Kim, S. Lee and S. Y. Jung, “Design of Cogging Torque and Torque Ripples Reduction for High Precision Controlled SPMSM,” The Transactions of the Korean Institute of Electrical Engineers, Vol.58, No.10, pp.1923-1929, 2009.
-
D. Jung, “Design of Driving Motor for Small Electric Vehicle Using Low Voltage Battery,” Transactions of KSAE, Vol.30, No.1, pp.83-89, 2022.
[https://doi.org/10.7467/KSAE.2022.30.1.083]

- S. Jin, K. -B. Park and J. -H. Seong, “Metamodel Based Design Optimization of Railway for Improving Vibration,” The Korean Society for Railway, pp.1054-1059, 2012.
-
Y. M. You, “Shape Optimization of PMSM Based on Automated Design of Experiments and Multi-layer Perceptron,” Journal of Next-generation Convergence Technology Association, Vol.4, No.5, pp.478-484, 2020.
[https://doi.org/10.33097/JNCTA.2020.04.05.478]

- J. H. Kim, M. H. Sung, G. T. Park, S. H. Jeong and M. S. Lim, “A Study on the Optimal Design of the Air-cooled Outer Rotor In-Wheel Traction SPMSM Using Kriging Surrogate Model,” KSAE Spring Conference Proceedings, pp.755-759, 2023.
-
M. Djami, M. Hage-Hassan, C. Marchand, G. Krebs, P. Dessante and L. A. Belhaj, “Kriging Metamodel for Electric Machines: A Drive Cycle Approach,” International Conference on Electrical Machines (ICEM), pp.251-256, 2022.
[https://doi.org/10.1109/ICEM51905.2022.9910946]

-
J. -G. Bu, M. Zhou, X. -D. Lan and K. -X. Lv, “Optimization for Airgap Flux Density Waveform of Flywheel Motor Using NSGA-2 and Kriging Model Based on MaxPro Design,” IEEE Transactions on Magnetics, Vol.53, No.8, pp.1-7, 2017.
[https://doi.org/10.1109/TMAG.2017.2702758]

-
Y. M. You, “Optimal Design of PMSM Based on Automated Finite Element Analysis and Metamodeling,” Energies, Vol.12, Paper No.4673, 2019.
[https://doi.org/10.3390/en12244673]

- J. Yoon, “Design of EPS Motor Applied Hair-Pin Winding Using Rectangular Wire,” KSAE Annual Conference Proceedings, pp.662-663, 2019.
- PIDOTECH Inc., PIAnO User’s Manuals and Tutorials, PIDOTECH Inc., Seoul, Korea, 2019.
- D. H. Kim and Y. M. You, “Optimal Design of Rotor Shape of Interior Permanent Magnet Synchronous Motor,” KSAE Annual Conference Proceedings, pp.1238-1239, 2023.
-
K. T. Chau, Electric Vehicle Machines and Drives: Design, Analysis and Application, 1st edn., Wiley-IEEE, Hoboken, p.243, 2015.
[https://doi.org/10.1002/9781118752555]

- H. -W. Kim, Y. -G. Min, D. -H. Jung, H. -S. Seol, H. -J. Lee, S. -J. Kim and J. Lee, “Torque Analysis of V-type IPMSM According to Asymmetric Barrier for Electric Motorcycle Traction,” The Korean Institute of Electrical Engineers, pp.661-662, 2018.
- J. -M. Yeon, B. Xia and C. -S. Koh, “Barrier Shape Optimization Design of Double-layer Interior Permanent Magnet Synchronous Motor for Improvement of Torque Characteristics,” The Korean Institute of Electrical Engineers, pp.72-74, 2015.
-
L. Liu, H. Li and D. Ban, “Multi-Objective Optimization of IPMSM Based on Subspace Division,” 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, pp.1-4, 2017.
[https://doi.org/10.1109/ICEMS.2017.8056374]

- J. W. Jung, T. Lee, J. J. Lee, G. H. Lee, J. P. Hong and K. N. Kim, “Shape Design of IPMSM for HEV Traction Motor to Reduce Usage of Permanent Magnet and to Ensure Maximum Output Power,” The Korean Institute of Electrical Engineers, pp.607-608, 2009.
-
Y. Chang, C. Low and C. -J. Wu, “Optimal Design of Discrete-Value Passive Harmonic Filters Using Sequential Neural-Network Approximation and Orthogonal Array,” IEEE Transactions on Power Delivery, Vol.22, No.3, pp.1813-1821, 2007.
[https://doi.org/10.1109/TPWRD.2007.899780]

-
L. Lebensztajn, C. A. R. Marretto, M. C. Costa and J. -L. Coulomb, “Kriging: A Useful Tool for Electromagnetic Device Optimization,” IEEE Transactions on Magnetics, Vol.40, No.2, pp.1196-1199, 2004.
[https://doi.org/10.1109/TMAG.2004.824542]

-
B. Mulgrew, “Applying Radial Basis Functions,” IEEE Signal Processing Magazine, Vol.13, No.2, pp.50-65, 1996.
[https://doi.org/10.1109/79.487041]

-
S. Bal and R. Radha, “Prediction of Heat Transfer Performance Using Polynomial Regression,” Second International Conference on Artificial Intelligence and Smart Energy (ICAIS), Vol.7, No.1, pp.1735-1740, 2022.
[https://doi.org/10.1109/ICAIS53314.2022.9742910]

-
D. H. Wang, J. H. Lee, S. J. Kim, M. C. Kim and I. S. Lee, “Fault Diagnosis of Induction Motor Using an Ensemble Method of Decision Tree and Multilayer Neural Network,” The Journal of Korean Institute of Information Technology, Vol.20, No.3, pp.47-55, 2022.
[https://doi.org/10.14801/jkiit.2022.20.3.47]