유한요소해석과 다목적 최적화를 이용한 타이어 설계
Copyright Ⓒ 2024 KSAE / 225-04
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In this paper, a sensitivity analysis between a Tire Design Parameter(TDP) and a Functional Tire Characteristics(FTC) was conducted by using FE simulation data, and a multi-objective optimal design was derived by using an optimization algorithm. By introducing variation on 21 TDPs, 43 virtual tire models were designed to analyze the sensitivity of TDPs on FTCs. FE simulations were performed to calculate the FTCs of the virtual tires, and a sensitivity analysis was conducted to identify the primary TDPs for each FTC. Multiple linear regression equations for each FTC were derived and would be used as surrogates. Then, Pareto solutions to optimize the FTCs were obtained by using NSGA-II(Non-dominated Sorting Genetic Algorithm) and the surrogate model. Furthermore, multi-dimensional Pareto solutions can be mapped onto a two-dimensional space, and will be clustered by using SOM(Self-Organizing Map). This framework can derive the optimal tire design solution efficiently for the given functional requirements.
Keywords:
Multi-objective optimization, Non-dominated sorting genetic algorithm, Self-organizing map, FE simulation, Sensitivity analysis, Tire design키워드:
다목적 최적설계, 비지배 정렬 유전 알고리즘, 자기조직화지도, 유한요소해석, 민감도 분석, 타이어 설계1. 서 론
차량의 발전에 따라 시장에서 타이어에 요구되는 성능이 다양해지고 수준이 증가하고 있다. 타이어는 핸들링, 연비, 제동 등 차량의 다양한 성능에 영향을 주기 때문에,1-3) 타이어 설계 시에 각 성능 별 영향도가 높은 TDP(타이어 설계인자)를 도출하여 조정하는 것이 필요하다. 특정 TDP들은 2개 이상의 FTC(타이어 특성치)에 동시에 상반되는 영향을 주며, 이로 인해 성능 간 상충관계가 발생한다.4) 따라서 설계자는 성능 간 상충관계를 고려하여 종합적인 성능 목표를 달성하기 위한 TDP의 최적 조합을 찾기 위해 노력한다. 이 과정은 타이어 설계, 제작, 평가 및 검증을 통해 진행되며, 여러 시행착오로 인한 시간과 비용이 많이 발생하고 있다.
FEA(Finite element analysis)의 기술발전으로 인하여 타이어 설계 및 평가가 가상의 공간에서 많은 부분 진행되고 있다.5-7) CAD(Computer-Aided Design) tool을 사용하여 Virtual tire를 모델링하고, CAE(Computer-Aided Engineering) tool을 통해 Virtual tire의 FTC를 FE simulation data로 얻는다. 이를 통해 타이어 설계자는 실물 제작 없이 TDP 조합별 목표 성능 달성 여부를 확인할 수 있으므로, 시간과 비용을 절약할 수 있다.8) 하지만 검토해야 하는 TDP가 많은 경우 TDP의 조합을 구성하기 위한 시행착오 과정이 길어져 비효율적인 설계가 진행될 수 있다.
최근 컴퓨터의 발전으로 다목적 최적화 알고리즘이 개발되었으며, 타이어 설계 과정에 유전알고리즘과 SOM(Self-Organizing Map)을 이용하여 다목적 최적해를 선정하는 것이 가능해졌다.9) 이 과정에서 NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm-Ⅱ)의 적합도 평가를 위하여 각 타이어 성능을 예측할 수 있는 Surrogate model이 필요하였다. 기존 방법에서는 예측 정확도를 위해 풍부하게 축적된 데이터와 경험적인 지식 등이 필요하지만 데이터나 지식이 부족하여 예측 모델이 확보되지 않은 규격에는 사용에 제한이 있다.
본 연구에서는 FE simulation을 통해 새로운 Data를 생성하여 민감도 분석을 한 후 FTC 예측 모델과 최적화 알고리즘을 사용하여 종합 성능 목표를 고려한 최적 설계안을 도출하는 것을 목적으로 하였다.
2. 최적화 프로세스
본 논문에서 타이어의 최적 설계안 도출을 위해 진행한 프로세스는 Fig. 1과 같다. Virtual tire를 모델링하고 FE simulation을 통해 TDP와 FTC가 포함된 Data를 생성하였다. 해당 Data를 기반으로 민감도 분석을 진행하고, FTC 예측 모델을 생성하였다. 그리고 다목적 최적화를 위해 최적화 알고리즘을 사용하여 Pareto 최적해를 구한 후, 다차원의 Pareto 최적해를 차원축소 및 군집화를 하여 최종 설계안 도출을 용이하게 하였다.
3. 민감도 분석
3.1 Tire Design Parameter
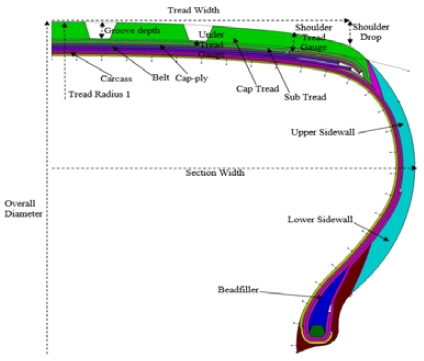
본 연구에서 설계한 타이어의 사이즈는 275/55R20이다. Table 1과 같이, 민감도 분석을 위하여 프로파일, 구조, 물성 등이 포함되어 있는 21개의 TDP를 선정하였으며, 각 TDP별로 기준값, 최대값, 그리고 최소값을 설정하여 설계 범위를 정하였다. 설계 범위는 규격 기준과 제조성 등을 고려하여 설정하였고, 반제품의 물성값은 각 TDP의 기준 물성값을 100 %로 설정한 후 특정 배율을 적용하여 범위를 설정하였다. Fig. 2는 선정된 TDP들의 타이어 단면상에서의 위치를 표현하였다. 해당 TDP들을 조합하여 총 43개의 Virtual tire 설계안을 도출하였으며, 설계 내용은 Table 2와 같다. TDP들의 기준값(Base value)의 조합으로 이루어진 Base virtual tire를 설계하였다. 그리고 각 TDP마다 최대값(Max value), 최소값(Min value)을 적용한 2개의 Virtual tire를 설계하였다. 또한, 민감도 분석을 위하여 각 설계인자를 독립적으로 변경하여 Virtual tire를 생성하였다. 예를 들어, TDP7은 타이어의 Tread depth이고, 설계범위는 8 mm ± 1 mm로 설정을 하였다. Tread depth를 변경한 2개의 Virtual tire의 경우, 각각 최대값 9 mm와 최소값 7 mm의 Tread depth가 적용되었고, 나머지 TDP는 기준값을 갖도록 하였다.
3.2 Functional Tire Characteristics
본 연구에서는 총 5개의 차량 성능과 관련된 FTC를 선정하여 성능 최적화를 수행하였다. 각 차량 성능 별로 선정한 FTC 항목은 Table 3과 같다. 차량의 연비 성능과 관련 있는 FTC는 타이어 주행 시 발생한 회전저항계수로 선정하였고, 핸들링 성능과 연관 있는 FTC는 Slip angle에 의해 발생하는 코너링 강성으로 선택하였다. 승차감 성능 관련 FTC는 타이어 진동 시 발생한 주행방향(x방향) 힘의 Peak to Peak값으로 선정하였다. NVH 성능 관련 FTC로는 타이어 노면 가진 시 휠의 중앙에서 발생하는 x,z방향 힘의 RSS(Root Sum Square)값을 사용하였고, 제동 관련 FTC로는 Slip ratio에 의해 발생한 최대마찰계수를 이용하였다.
각 FTC는 차량 성능을 향상시키기 위한 보편적인 설계 방향이 존재한다. 본 논문에서는 FE simulation으로 얻은 FTC값을 지표화를 함으로써, 각 FTC의 지표 값이 커질수록 유리한 방향임을 의미하도록 하였다. FTC 설계 방향이 ‘증가’인 경우 FTC의 지표 값은 FTC값/(Base virtual tire의 FTC값)이고, FTC 설계 방향이 ‘감소’인 경우(Base virtual tire의 FTC값)/FTC값을 지표로 사용하였다. 또한 각 FTC별 지표는 FTC차량성능으로 표기하였다.
3.3 FE Simulation
Simulation database 생성을 위하여, Virtual tire를 모델링한 후 FE simulation을 수행하였다. 이 과정에서 Table 2의 Virtual tire list에 해당하는 43개의 Virtual tire를 카티아(CATIA V5)를 사용하여 모델링하였다. 그리고 Abaqus와 In-house FE simulation 소프트웨어를 사용하여 FE simulation을 진행하였다. In-house FE simulation 소프트웨어는 비선형 점탄성 모델과 온도 변화를 고려한 Explicit FE simulation을 사용하여 예측 정확도를 향상하였다.10)
3.4 피어슨 상관계수
피어슨 상관계수는 두 변수간의 선형 상관 관계를 나타내는 수치이다. X와 Y라는 변수가 있을 때, 다음과 같은 피어슨 상관계수가 주어진다.
상관계수의 값의 범위는 –1에서 +1 사이이 상관계수의 값의 범위는 -1에서 +1 사이이며, 절대값의 크기는 상관관계의 강도를 의미한다. 또한, 상관계수의 부호는 상관관계의 방향을 의미한다. 예를 들어, 두 변수 X와 Y의 상관계수가 +1이면, 양의 상관관계를 이루므로 X값이 클수록 Y값이 커지는 경향이 있다.
3.5 민감도 분석 수행 및 결과
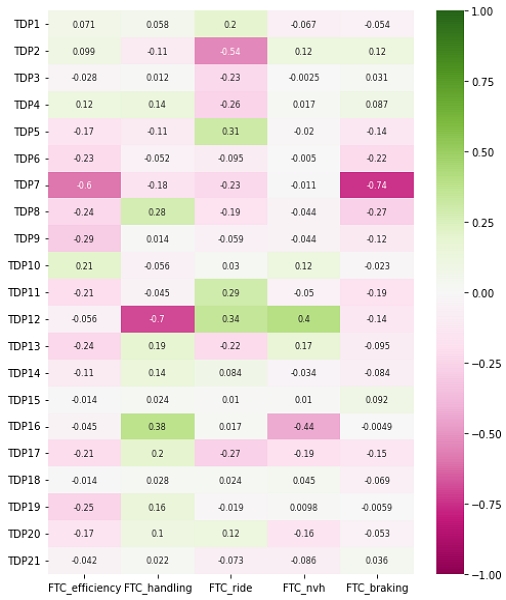
Fig. 3은 FE simulation database를 활용하여 TDP와 FTC 간의 상관관계를 Heatmap으로 표현한 결과이다. 가로축은 FTC, 세로축은 TDP로 나열하였다. Heatmap 안에 있는 Data는 인자 간 상관계수이며, 색깔이 진할수록 상관관계의 강도가 높음을 의미하도록 하였다. 또한, 양의 상관관계는 녹색으로 표현하였고, 음의 상관관계는 핑크색으로 표현하였다.
Heatmap에서 색깔의 진하기로 각 FTC별로 민감도가 높은 TDP를 확인 가능하며, 색깔의 종류로 설계 방향을 알 수 있었다. FTCefficiency의 경우, Tread depth가 가장 민감도가 높으며, Under Tread Gauge, Beadfiller height순으로 주요한 설계인자였다. 해당 3개의 TDP 모두 FTCefficiency와 음의 상관관계를 이루므로, FTCefficiency를 유리하게 설계하기 위해서는 해당 TDP들을 작게 설계하는 것이 필요하였다. Tread depth는 FTCbraking의 주요 TDP이기도 하므로, Tread depth를 작게 설계함으로써 FTCefficiency와 FTCbraking를 동시에 유리하게 할 수 있었다. FTChandling을 유리하게 하기 위해서는 Belt angle을 감소시키는 것이 가장 민감도가 높았다. 하지만 Belt angle의 감소는 FTCride와 FTCnvh를 불리하게 하는 경향이 있으므로, Belt angle 변경 시에 상충관계를 이루는 FTC가 존재하는 것을 확인 할 수 있었다.
위와 같은 방법으로 각 FTC별로 민감도가 높은 TDP의 설계방향을 도출하고, 특정 TDP를 변경하였을 때 FTC 간 상충관계가 존재하는지도 확인하였다. 이를 통해 설계자는 상충관계를 고려하여 TDP를 선정하고 변경하는 것이 가능하였다. 예를 들어, FTChandling의 개선을 위해 Belt angle을 감소시키고, Section width 감소를 통해 FTCride를 보완하는 것을 검토할 수 있었다.
FTC에 대한 민감도를 종합적으로 검토를 진행하였을 때, Tread depth, Cap Tread Modulus, Belt angle, Cap-ply Modulus 등이 여러 FTC에 영향도가 높은 주요 설계인자인 것을 알 수 있었다. 결과적으로 민감도 분석을 통해 설계를 진행하는 것은 설계 우선순위를 고려하여 체계적인 설계가 가능하다는 장점이 있었다.
4. 예측 모델
본 연구에서는 제 3항에서 생성한 FE simulation database를 학습하여 다중선형회귀(Multiple linear regression)를 진행하여 FTC 예측모델을 생성하였다. 파이썬 라이브러리 ‘Scikit’11)을 사용하여 각 FTC의 다중선형회귀식을 도출하였다.
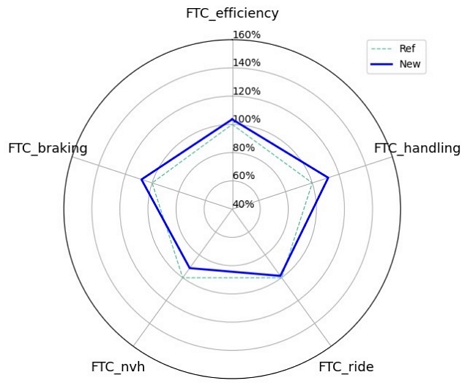
학습에 사용된 FE simulation data는 21개 TDP의 독립적인 증감 효과를 포함하고 있기 때문에 TDP와 FTC간의 선형적인 민감도가 반영된 FTC 예측모델을 생성할 수 있었다. 또한 해당 모델을 사용하여 새로운 TDP 조합의 FTC 예측값을 구하였다. 예시로, FTCefficiency와 FTChandling의 증가를 위하여, Fig. 3의 민감도 분석 결과를 통해 Tread depth와 Belt angle을 감소시킨 설계안을 도출하였다. 나머지 TDP들은 Base virtual tire와 동일하게 한 후, 다중선형회귀식으로 FTC 예측값을 구하였다. Fig. 4에 새로운 설계안(New)의 FTC 예측값과 Base virtual tire(Ref)의 FTC값을 표현하였다. Tread depth의 감소에 의해 FTCefficiency와 FTCfbraking이 증가하였으며, Belt angle의 감소에 의해 FTChandling은 증가하고 FTCride와 FTCride가 감소되었다.
5. 다목적 최적화
5.1 목적함수와 제한조건
본 연구에서는 5개의 FTC에 대한 다목적 최적화를 진행하였다. 각 FTC의 지표를 최대화하는 5개의 목적함수를 설정하고, 각 TDP별 설계 범위를 제한조건으로 설정하였다.
5.2 비지배 정렬 알고리즘(NSGA-II)
유전알고리즘은 자연계의 진화과정을 모방하여 최적해를 찾는 알고리즘이다. 세대를 거듭하면서 부모 세대 중 우수한 적합도(Fitness)를 가진 개체(Individual)만 선택되고 교배(Crossover)와 돌연변이(Mutation)를 통해 변형되면서 진화가 진행된다.
다목적 최적화를 진행할 때 모든 목적함수를 동시에 만족하는 해는 일반적으로 존재하지 않으며, 목적 함수 간에 상충하는 경우가 생긴다. 최적해를 찾는 방법 중 하나는 Pareto 최적해를 구하는 것이다. Pareto 최적해는 후보해 중에서 지배되지 않는 해들의 집합을 의미한다. NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm)은 유전알고리즘 중에 하나이며, 빠른 비지배 분류(Fast-non-dominated-sorting)를 수행하고 밀집도 거리(Crowding distance) 개념을 적용한다. 비지배 순위를 계산하여 Pareto 최적해를 구분한 후 우선 순위가 높은 개체를 선택하고 같은 우선순위 내 개체 중에서는 밀집도 거리가 큰 개체를 선택하여 새로운 부모 개체군을 만든다. 세대를 거듭하여 유전 알고리즘 과정을 반복하면서 최종 Pareto 최적해를 도출한다.12)
5.3 다목적 최적화 수행 및 결과
본 연구에서는 NSGA-Ⅱ를 사용하여 5개의 목적함수에 대한 Pareto 최적해 도출을 진행하였다. 이 과정에서 파이썬(Python) 라이브리 ‘DEAP’13)을 사용하였으며, Hyperparameter는 Table 4와 같이 설정하였다. 각 객체는 21개의 TDP 조합으로 이루어져 있으며, 적합도 평가 시에 필요한 5개의 FTC차량성능값은 제 4항에서 생성하였던 다중선형회귀모델을 사용하여 계산되도록 설정하였다.
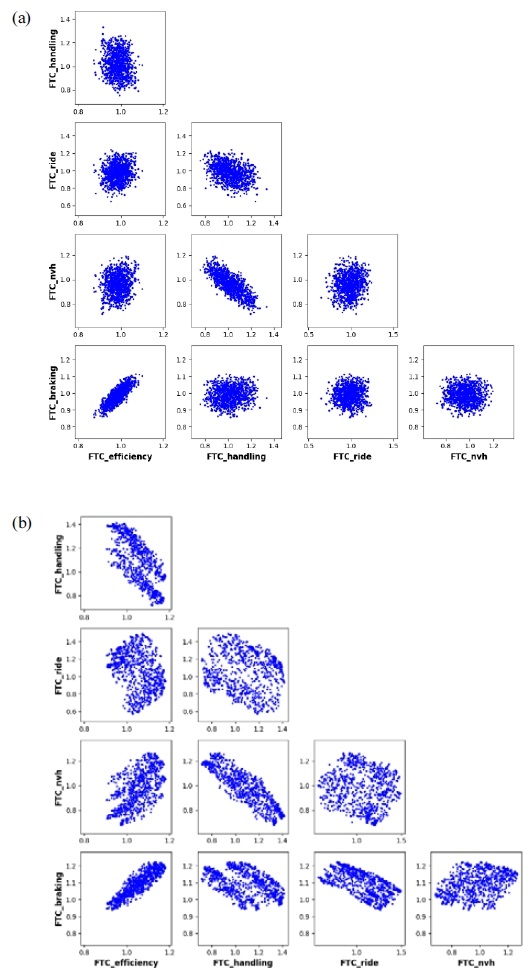
NSGA-Ⅱ 알고리즘을 통해 구한 5개 FTC에 대한 Pareto 최적해는 Fig. 5와 같다. Fig. 5에서 각 축은 FTC 항목으로 나열하였고, 객체들의 FTC 산포도를 표현하였다. 초기 세대에서는 Fig. 5(a)와 같이 임의의 FTC값을 갖는 객체들이 생성되었지만, 세대를 거치면서 최종적으로 Fig. 5(b)와 같은 다목적 Pareto 최적해를 구할 수 있었다. Fig. 5(a)와 Fig. 5(b)를 비교했을 때, 각 FTC별로 목적함수에 부합하는 해가 구해진 것을 확인할 수 있었다. 예를 들어, 초기 세대에서 FTCefficiency와 FTCbraking의 값이 1.2이상인 객체는 존재하지 않지만, 최종 세대에서는 1.2이상의 값을 갖는 객체들이 존재하였다.
Pareto 최적해의 산포도를 분석함으로써 FTC 간의 상충관계 여부를 확인할 수 있었다. Fig. 6은 Fig. 5(b) 그래프 중의 일부 산포도를 표현하였다. Fig. 6(a)에서 FTCefficiency와 FTCbraking은 양의 상관관계 분포를 이루어, 최적화 과정에서 동시에 성능이 향상하는 경향을 보였다. 그러므로 2개 FTC의 최적해를 선정할 때 그래프 내 우측 상단에 있는 해를 선정하는 것이 적절하였다. 반면, Fig. 6(b)에서 FTChandling와 FTCnvh는 음의 상관관계를 이루어, 최적화 과정에서 상충관계를 보였다. 상충관계가 존재하는 경우, 2개 FTC의 목적을 동시에 만족하는 최적해를 찾는 것은 불가능하므로, 2개 중 최소 1개의 FTC를 희생하는 최적해를 선정하는 것이 필요하였다. FTChandling를 극대화한다면 그래프 내 우측 하단에 위치한 해를 선정하고, FTCnvh를 극대화한다면 그래프의 좌측 상단에 위치한 해를 선택해야 하였다. 중앙의 상단에 위치한 해를 선정한다면 균형 있는 설계안을 도출할 수 있었다.
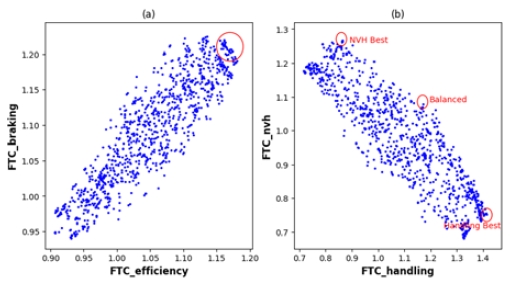
The parts of Fig. 5(b) (a) x-axis : FTCefficiency, y-axis : FTCbraking (b) x-axis : FTChandling, y-axis : FTCnvh
위와 같은 방법으로 NSGA-Ⅱ 알고리즘을 통해 Pareto 최적해들을 도출한 후 설계 우선순위를 고려하여 최적 설계안을 선정하는 것이 가능하였다.
6. 다목적 최적해 군집화
6.1 자기조직화지도(Self-Organizing Map)
SOM은 다차원의 데이터를 2차원으로 차원축소를 시켜주는 신경회로망이며, 군집화(Clustering) 방법으로 많이 사용된다. SOM은 비지도학습(Unsupervised learning) 기법을 진행하기 때문에, 사전지식이 없어도 복잡한 연관관계가 있는 데이터를 쉽게 군집화가 가능하다는 장점이 있다.
SOM은 입력층과 출력층으로 구성되어 있다. 입력층에는 입력 벡터가 전달이 되며, 경쟁 층에서는 경쟁층 노드들과 입력 벡터 사이의 유클리드 거리를 계산하고 가장 가까운 노드가 승자 노드로 선택된다. 승자노드가 선택되면 해당 노드와 이웃 노드들의 가중치 값을 조정하면서 학습이 진행된다. 학습이 끝나면 비슷한 성격의 입력벡터 값을 가지는 데이터들은 출력층의 특정 노드에 매핑이 되면서 군집화가 진행된다.14,15)
6.2 Pareto 최적해 군집화 수행 및 결과
2차원과 3차원의 데이터는 평면이나 공간에 시각화하는 것이 가능하다. 하지만 4차원 이상의 데이터는 시각화를 하는 것이 쉽지 않다.
제 5항에서는 NSGA-Ⅱ을 사용하여 5개 FTC에 대한 Pareto 최적해들을 구하였다. 이 중에서 성능 상충관계를 고려하여 최종적인 설계안을 선정을 해야 하기 때문에, 5차원의 데이터를 종합적으로 비교 분석할 수 있는 용이한 방법이 필요하였다. 이를 위해 SOM을 사용하여 5차원의 데이터를 군집화를 진행하여 시각적 분석을 진행하였다.
본 연구에서는 파이썬 라이브러리 ‘Minisom’16)을 사용하여 SOM을 진행하였으며, 군집(Cluster)의 개수는 9개로 설정하였다. Minisom 라이브러리를 사용하기 위한 Hyperparameter는 Table 5와 같다.
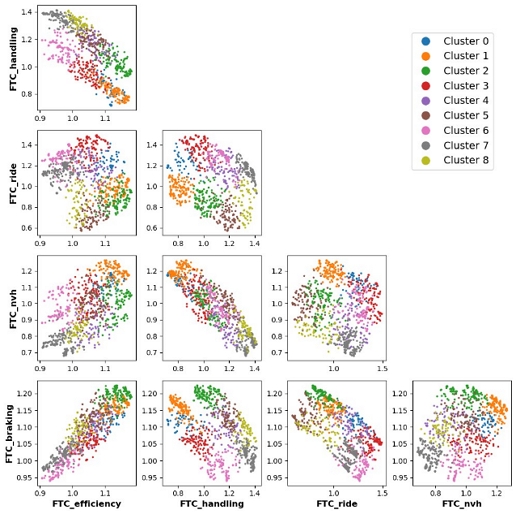
SOM을 통해 Fig. 5에서 표현되었던 5개 FTC pareto 최적해를 군집화한 후 시각화하여 표현한 결과는 Fig. 7과 같다. 각 2차원 평면 내에서 비슷한 FTC값을 가지는 객체들끼리 군집을 이루는 것을 확인하였고, 해당 군집이 여러 2차원 평면 내 어느 영역에 위치하는지 시각적으로 확인이 가능하였다.
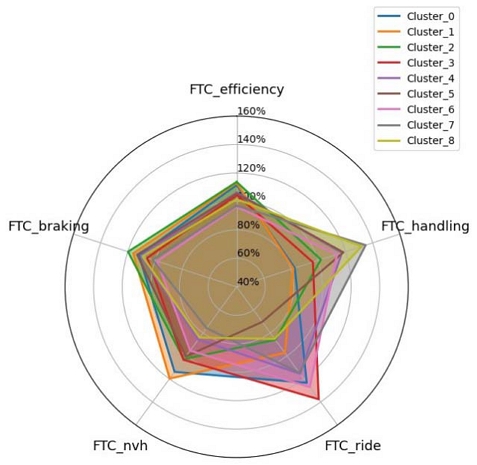
하나의 평면 내에서 군집들의 특징을 비교분석하기 위하여, 각 군집 내 객체들의 FTC 평균값을 계산하여 비교를 진행하였다. 군집의 FTC 평균값들을 Radar chart로 Fig. 8과 같이 표현할 수 있으며, 각 군집의 특징을 파악하고 목표하는 성능 우선순위에 부합하는 집단을 선택하는 것이 가능하였다. 예를 들어, Cluster0, Cluster1, Cluster2는 FTCefficiency와 FTCbraking이 우수한 집단이며, 타 성능에서 각각 다른 장점을 가졌다. Cluster0은 FTCride, Cluster1은 FTCnvh, Cluster2는 FTChandling이 상대적으로 우수하였다. FTCefficiency, FTChanlding 순으로 우선순위가 높다면, 설계자는 Cluster2를 선택하는 것이 적절하였다. 만약 FTChanlding의 우선순위가 제일 높다면 Cluster7 또는 Cluster8이 적합하고, FTCride의 우선순위가 높은 경우 Cluster3 또는 Cluster6이 적합하였다.
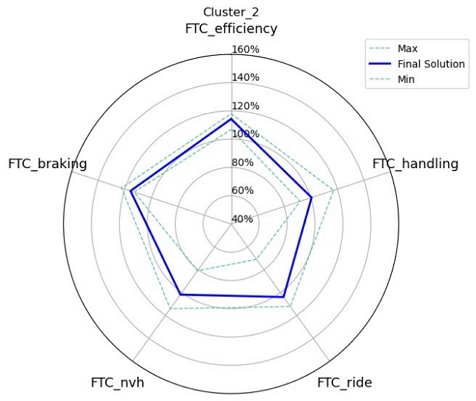
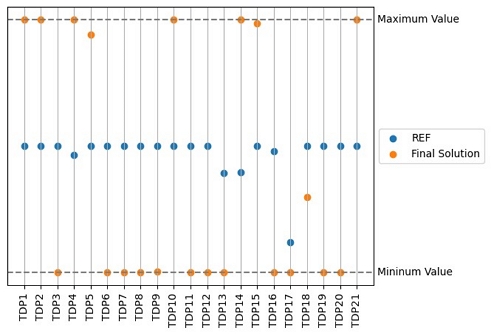
Cluster를 선택함으로써 객체들이 가지는 FTC 값의 범위는 성능 우선순위에 부합하게 설정되었다. 해당 Cluster 내에서 최종적인 객체를 선택하여 용이하게 최적 설계안(Final solution)을 도출할 수 있었다. 예를 들어, FTCefficiency와 FTChanlding순의 우선순위에 따라 Cluster2를 선택하였을 때, 군집 내 객체들이 이루는 FTC의 범위는 Fig. 9에서 확인할 수 있었다. 해당 범위 내 객체들 중에서 Base virtual tire 대비 FTCefficiency와 FTCbraking이 10 %이상 우수하고 타 성능의 상충관계를 극복한 최적 설계안을 선택할 수 있었다. Fig. 10은 해당 최적 설계안의 21개 TDP값을 Base virtual tire의 설계정보와 비교하여 표시한 그래프이다. 해당 그래프를 통해 최적화된 성능을 구현하기 위한 각 TDP의 설계값을 확인하였다. 예를 들어, Tread depth는 최소값인 7 mm를 적용하고, Overall diameter는 최대값인 812 mm로 설정하는 것이 필요하였다.
7. 결 론
본 연구에서는 FE simulation data를 기반으로 민감도 분석과 예측 모델과 최적화 알고리즘을 사용한 다목적 최적 설계를 진행하였다. 독립적으로 TDP를 변경한 Virtual tire를 설계하여 FE simulation을 수행하였으며, 해당 Data를 활용한 TDP와 FTC 간의 민감도 분석을 통해 주요 TDP를 선정하고 설계 방향을 도출할 수 있었다. 또한, 다중선형회귀예측 모델을 생성함으로써, 설계자는 새로운 TDP 조합에 대한 FTC 예측값을 얻을 수 있음을 확인하였다.
일반적으로 다목적 최적화 문제에서는 모든 목적함수를 동시에 만족하는 해를 구하는 것이 불가능하기 때문에, 후보해들을 구한 후 적절한 최적해를 선정하는 것이 필요하였다. 이를 위해 NSGA-Ⅱ와 SOM을 사용하여 5개의 FTC에 대한 다목적 최적화를 수행하였다. 이를 통해 다음과 같은 결론을 얻었다.
- 1) NSGA-Ⅱ을 사용하여 5개 FTC에 대한 Pareto 최적해를 도출하였으며, 각 FTC별로 기존 대비 1.2배 이상 유리해지는 후보해들을 확인하였다.
- 2) Pareto 최적해의 산포도를 분석하여, 설정된 설계 범위 내에서 FTC 간의 상충관계 확인이 가능하였다. FTCefficiency와 FTCbraking는 양의 상관관계를 이루는 반면, FTChandling와 FTCnvh는 상충관계를 이루었다.
- 3) SOM을 사용하여 Pareto 최적해를 차원축소 및 군집화함으로써, 최적 설계안을 최종 선택하는 것이 용이하였다. 이를 통해 타 성능의 손실 없이 FTCefficiency와 FTCbraking이 10 %이상 개선할 수 있는 타이어 설계안을 도출하였다.
본 논문에서 진행한 최적 설계 과정은 FE simulation과 최적화 알고리즘을 사용하여 진행하였기 때문에 실물 제작 없이 가상의 환경에서 타이어의 설계가 가능하였다. 하지만 선형적인 민감도 분석을 위한 최소한의 Virtual tire의 Data를 기반으로 선형회귀예측모델을 만들었다는 점에서 한계가 있다. 해당 모델에는 TDP 조합에 따른 FTC의 교호작용의 효과가 반영되어 있지 않기 때문에, FTC 예측값과 실제값 사이에는 Error가 발생할 수 있다. 정확한 예측 성능을 위하여, 교호작용을 반영하는 예측 모델 생성을 위한 Virtual tire 생성 방법과 예측 모델 생성 방법 등에 대한 연구가 필요하다.
Acknowledgments
본 논문은 현대자동차와 한국타이어앤테크놀로지의 공동 연구과제로 수행되었으며 지원에 감사드린다.
References
- Y. H. Lee, S. I. Kim, M. W. Suh, D. Y. Kim and D. R. Kim, “Influence of Tire Cornering Stiffnesses on the Steering Characteristics of a Four-Wheel Steering Vehicle,” Transactions of KSAE, Vol.3, No.4, pp.115-125, 1995.
-
S. D. Lee and J. M. Ko, “A Study on the Influence of Tire Rolling Resistance Coefficient on Vehicle Fuel Consumption and CO2 Emissions,” Transactions of KSAE, Vol.26, No.3, pp.402-406, 2018.
[https://doi.org/10.7467/KSAE.2018.26.3.402]

- Y. R. Oh, “Effects of Tire Inflation Pressures on Tire Characteristics or Vehicle Performance,” Auto Journal, KSAE, Vol.40, No.7, pp.25-31, 2018.
- Y. K. Kang, G. H. Kim, I. S. Jang and Y. J. Oh, “A Study on Tire Labeling Performance for Tire Stiffness Design,” Proceedings of the KSNVE Annual Autumn Conference, pp.265-267, 2013.
- H. W. Kim and K. Z. Cho, “A Study for the Prediction of a Tire Cornering Characteristics Using a Finite Element Method,” Transactions of KSAE, Vol.6, No.1, pp.151-162, 1998.
- H. U. Kim, Y. H. Kim and J. B. Park, “Tire Blocked Force Simulation Development and Sensitivity Research,” KSAE Fall Conference Proceedings, pp.2544-2548, 2022.
-
P. N. Zitelli, G. N. Curtosi and J. Kuster, “Rolling Resistance Calculation Procedure Using the Finite Element Method,” Tire Science and Technology, Vol.48, No.3, pp.224-248, 2020.
[https://doi.org/10.2346/tire.19.170158]

- H. G. Kwak and J. H. Kim, “An Introduction to Computer Aided Engineering of Tire,” Auto Journal, KSAE, Vol.31, No.3, pp.47-53, 2009.
-
D. Mosnier, F. Gillot and M. Ichchou, “Integrated Workflow for Multi-Objective Evolutionary Optimization of the Vehicle Tyre Parameters,” Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, Vol.227, No.2, pp.222-233, 2012.
[https://doi.org/10.1177/0954407012450821]

-
J. C. Cho and J. Y. Huh, “Improved Prediction of Tire Cornering F&M by Using Nonlinear Viscoelasticity and Transient Thermal Analysis Through Explicit FEM,” 7th International Munich Chassis Symposium, pp.899-910, 2016.
[https://doi.org/10.1007/978-3-658-14219-3_56]

- Scikit-learn, LinearRegression, https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html, , 2023.
-
K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A Fast and Elitist Multi-Objective Genetic Algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, Vol.6, No.2, pp.181-197, 2000.
[https://doi.org/10.1109/4235.996017]

- GitHub, DEAP, https://github.com/deap/deap, , 2023.
-
T. Kohonen, “The Self-Organizing Map,” Proceedings of the IEEE, Vol.78, No.9, pp.1464-1480, 1990.
[https://doi.org/10.1109/5.58325]

-
J. Vesanto and E. Alhoniemi, “Clustering of the Self-Organizing Map,” IEEE Transactions on Neural Networks, Vol.11, No.3, pp.586-600, 2000.
[https://doi.org/10.1109/72.846731]

- GitHub, MiniSom, https://github.com/JustGlowing/minisom, , 2023.