교합 장치를 장착한 전기 모터 구동형 궤도차량의 2단 변속 시스템 성능 제어

1. 서 론

최근 친환경적인 연구가 전 세계적으로 많은 관심이 집중되고 있고, 자동차 업계에서는 배기가스 배출량을 줄이기 위하여 전기 모터를 사용하는 다양한 구조의 차량 개발이 많이 이루어지고 있다.^1-4) 전기 모터를 사용하는 차량은 배터리의 충전에너지만을 사용하는 순수 전기차와 엔진의 배터리 충전을 포함하는 하이브리드 차량으로 나눌 수 있다.

소형차 분야에서 시작된 전기 모터 구동형 차량의 개발 영역은, 중대형 상용차와 트럭의 범위뿐만 아니라 군용차량의 범위까지 포함하고 있다. 특히, 직렬형 하이브리드 타입의 군용 차량 시스템은 바로 군사적인 용도로 사용하기에는 부족함이 있으나 주행 시 저소음과 높은 가속 성능 등의 강점이 있기 때문에, 미국, 영국, 일본 등을 중심으로 오래전부터 꾸준한 연구가 진행되어 왔다.^5,6)

본 논문의 연구 대상 차량은 2단 변속기를 장착한 전기 모터 구동형 궤도 차량 시스템이며, 구동 모터 2개, 조향 모터 1개, 교합 장치(Cross-Drive)로 구성되어 있어서 전투 시 구동 모터 1개와 조향 모터가 파손되더라도 안전하게 부대로 복귀할 수 있는 특징이 있다.

노면의 주행 부하 모델은 직진 시의 주행 부하 모델과 선회 시의 주행 부하 모델을 결합하여 개발하였다. 특히 선회 주행 시 주행 부하 모델은, 많은 성능 파라미터들을 필요로 하는 복잡한 모델보다는 개발 초기의 적은 성능 파라미터들로 구현되는 혹스모델(Hock’s model)을 이용하여 개발하였다.

변속 시, 속도 동기화 없이 갑작스러운 클러치 결합을 진행하게 되면 파워트레인에 충격이 가해질 수 있다. 이러한 파워트레인의 충격을 줄이기 위하여 모터와 변속기 출력축 속도의 동기화 및 변속 충격 최소화 로직도 구성 적용하였다.

성능 분석을 위해 개발한 시뮬레이터에 개발된 변속 및 조향 제어 로직을 적용하여, 다양한 주행 상태(직진, 경사, 제자리 선회(Pivot), 조향 반경(β)에 따른 선회 등)에 대해 시뮬레이션을 진행하였다.

2. 차량 시스템 모델링

2.1 파워트레인 모델링

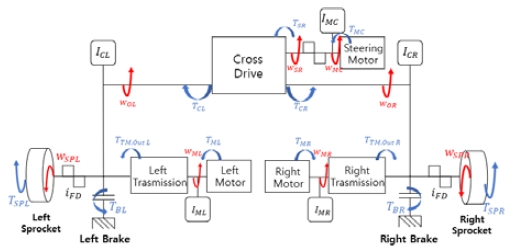
연구 대상 차량의 파워트레인은 Fig. 1과 같이 좌, 우측 출력축을 구동하는 구동 모터 1개와 2단 변속기 1개가 좌우 1쌍으로 장착되어 있다. 조향 모터 1개는 선회 운동 시에만 토크를 전달하는 교합장치에 장착되어 있다. 교합장치에 입력으로 들어온 조향 모터의 토크(T_SR)는 교합 장치 내부 장치들을 통하여 좌우측 출력축에 같은 크기를 가지지만 반대 부호를 가지는 값(T_CR, T_CL)으로 출력된다. Fig. 1에서 정의된 운동 변수들을 이용하여 연구 대상 파워트레인의 과도상태 이산계 성능 모델링을 수행하였다. 차량 관성은 등가화를 통하여 개수를 최소화하여 모델링을 진행하였다. Fig. 1의 5개의 회전 관성(I_MC, I_OR, I_OL, I_MR, I_ML)에 대한 각 회전속도와 토크에 관한 운동 방정식을 정리하면 식 (1)과 같다.

$\[ \left\{\begin{array}{c}{I}_{MC}\dot{{\omega }_{MC}}=T_{MC}-T_{SR}/i_{MC}\hfill \\ I_{CR}{\dot{\omega }}_{OR}=T_{CR}+T_{TM,Out,R}-T_{BR}-T_{SPR}/i_{FD}\hfill \\ I_{CL}{\dot{\omega }}_{OL}=T_{CL}+T_{TM,Out,L}-T_{BL}-T_{SPL}/i_{FD}\hfill \\ I_{MR}{\dot{\omega }}_{MR}=T_{MR}-T_{TM,Out,R}/i_{RIGHTMM}\hfill \\ I_{ML}{\dot{\omega }}_{ML}=T_{ML}-T_{TM,Out,L}/i_{LEFTTM }\hfill \end{array}\right. \]$

(1)

Fig. 1

Lumped modeling of 2-speed transmission

변속 제어로직에 따라 좌우 측의 2개의 변속단을 어떻게 선택할지가 달라지는데, 변속에 의한 클러치 체결 형태에 따라 파워트레인의 운동방정식이 달라진다. 좌우 측 변속 단수를 고려하여 등속 상태에서의 운동방정식들을 정리하면 식 (2)와 같다.

$\[ \left\{\begin{array}{c}{i}_{RIGHTTM}{T}_{MR}+T_{MC}{i}_{MC}{i}_{Cross Drive }=T_{BR}+\frac{T_{SPR}}{i_{FD}}\hfill \\ i_{LEFTTM}{T}_{ML}-T_{MC}{i}_{MC}{i}_{Cross Drive }=T_{BL}+\frac{T_{SPL}}{i_{FD}}\hfill \end{array}\right. \]$

(2)

2.2 주행 부하 모델링

2.2.1 직진 주행부하 모델링

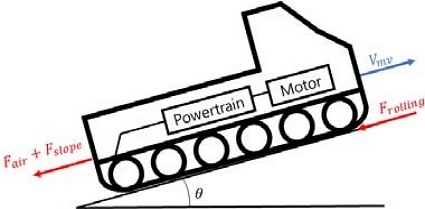
본 연구에서는 차량 주행 시 직진 주행 부하를 기본적으로 고려하였고, 선회 시에는 선회 주행 부하를 추가하는 방식으로 차량 부하 모델을 개발하였다. 구체적인 차량 부하 모델은 식 (3) ~ (8)와 같다. 직진 주행 부하는 구름 저항력(F_rolling),경사 저항력(F_slope), 공기저항력 (F_air)의 합으로 표현된다.

$\[ V_{mv}=\frac{V_1+V_2}{2} \]$

(3)

$\[ F_{load}=F_{st,load}+F_{hokes} \]$

(4)

$\[ F_{st,load }=F_{rolling }+F_{slope }+F_{air } \]$

(5)

$\[ F_{rolling }=f_{r}mg\text{cos}\theta \]$

(6)

$\[ F_{slope }=mg\text{sin}\theta \]$

(7)

$\[ F_{air }=\frac{1}{2}\rho A{C}_d{V}_{mv}^2 \]$

(8)

Fig. 2

Load model of track vehicle in a straight forward

2.2.2 선회 주행부하 모델링(Hock’s Model)

궤도 차량의 조향 부하 분석 시, 노면에 대한 궤도의 슬립을 고려하면 차량의 실제 주행 속도와 회전 반경을 추정하기 어려워지고 해석의 난이도가 급격히 증가하게 된다. 차량 개발 초기 단계에서 보다 쉽게 조향 부하를 예측하기 위해서, 원심력에 의한 궤도의 횡방향 슬립과 구동 및 제동력에 의한 궤도의 종방향 슬립을 무시하는 혹스모델을 이용하는 것이 효과적이다.⁷⁾ 그 외에도 궤도 차량의 부하 분석을 진행하는 Kitano와 Kuma,⁸⁾ Wong과 Chiang⁹⁾ 등의 연구자들의 자세한 모델이 있지만 실시간 시뮬레이션에서 활용도가 높은 혹스 모델을 통하여 연구를 진행했다.

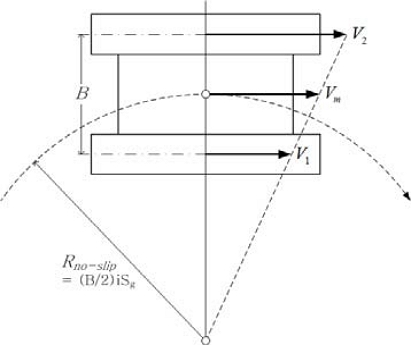
본 연구에서는 혹스모델을 이용하여, 평지에서의 저속 등속 선회 주행을 기준으로 궤도 차량의 조향 부하 모델링을 진행하였다. 식 (9)와 Fig. 3은 혹스모델을 이용하여 분석한, 선회 주행 궤도차량의 iS_g(조향 기어비)에 따른 회전 반경(R_no-slip)을 나타내고 있다.

$\[ i{S}_g=\frac{V_2+V_1}{V_2-V_1}=\frac{R_{no-sip}}{B/2} \]$

(9)

Fig. 3

Velocity distribution of both track during low-speed turn

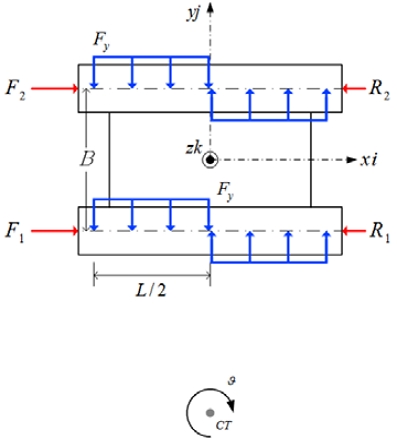
Fig. 4는 궤도차량이 저속 평지 선회 운동을 하는 경우, 혹스모델에 의한 궤도 작용력들을 나타낸 것이고, 식 (10)은 해당되는 조향 운동 시의 마찰 저항 모멘트(M_G)를 나타내고 있다.

$\[ M_G=2{\mu }_w\left(\frac{W_n}{2L}\right)\left(\frac{L}{2}\right)\left(\frac{L}{2}\right)=\frac{{\mu }_w{W}_{n}L}{4} \]$

(10)

Fig. 4

Force of the track during a low-speed turn

따라서 조향 운동 시 궤도 좌우측에 요구되는 구동력은 다음과 같이 결정된다.

$\[ \left\{\begin{array}{c}{F}_1=\frac{W_n}{2}\left(sign\left({\omega }_1\right)f_r-\frac{{\mu }_{w}L}{2B}\right)\hfill \\ F_2=\frac{W_n}{2}\left(sign\left({\omega }_2\right)f_r+\frac{{\mu }_{w}L}{2B}\right)\hfill \end{array}\right. \]$

(11)

식 (11)에서 μ_w는 조향 마찰계수를 의미하며 구체적으로는 식 (12)와 같이 표현된다.

$\[ {\mu }_w=\frac{{\mu }_{w0}}{{\left(1+i{S}_g\right)}^{0.2}}\left(1-\frac{i{S}_g}{i{S}_{g,infinite}}\right) \]$

(12)

여기서 μ_w,0는 제자리선회 상태(iS_g=0)에서의 횡방향 마찰계수 값을 의미하는데, μ_w,0가 클수록 거친 노면이라고 할 수 있다. 또한 iS_{g ,infinite}는 직진 시의 iS_g값을 의미하는데, iS_g값이 약 1,600 이상이면 직진 상태와 다름없다고 가정하여 iS_g,infinite는 1,600으로 설정한다.

2.3 차량 시뮬레이터 모델링

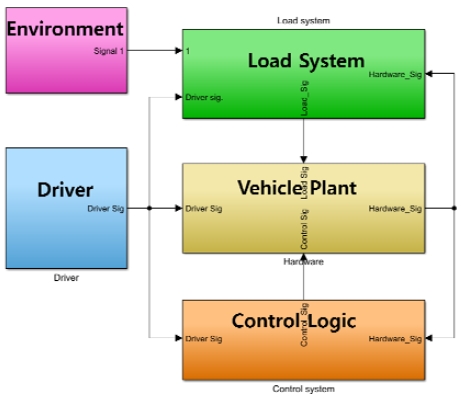
본 연구에서는 앞에서 언급한 이론 모델들을 이용하여 Fig. 5와 같이 성능 시뮬레이터를 구성하였다. 시뮬레이터는 Environment, Driver, Load system, Vehicle plant, Control logic으로 구성되어 있다. Environment는 경사와 같은 노면과 같은 환경 입력 신호를 구성하는 시스템이고, Driver는 APS, BPS 등 구동계에 대한 운전자 명령 값을 결정한다. Vehicle plant는 모터, 파워트레인 등의 시스템 요소들로 구성되어 있고, Control logic은 변속, 선회 제어로직을 담당하는 시스템이다.

Fig. 5

Simulator structure

3. 제어로직 모델링

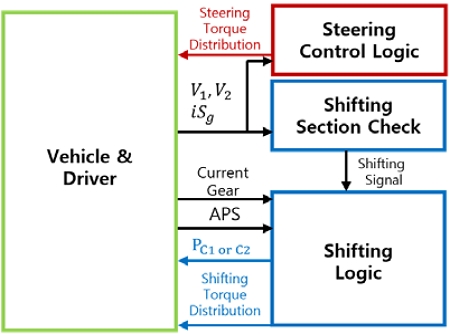
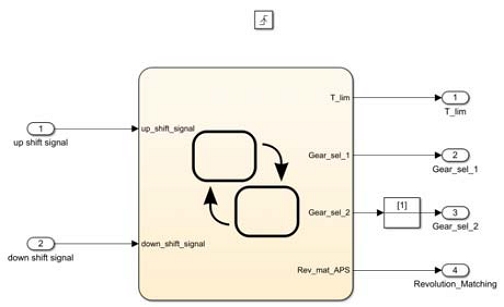
본 연구에서는 시스템 전체 제어로직을 Fig. 6과 같이 변속 제어로직과 선회 제어로직으로 나누어 구성하였다. 변속 제어로직은 차량 하드웨어에서 차량 속도와 iS_g를 입력 받아 변속 가능 구간을 확인한 후, 변속 신호를 출력하게 하였다. 변속 신호를 입력받은 변속 제어기는 변속 충격을 최소화하기 위하여 속도 동기화를 진행하며 부드러운 변속이 이루어지게 하였다.

Fig. 6

Simulator control logic

연구 대상 차량은 교합 장치와 조향 모터를 활용하는 방식이며, 선회 제어로직도 이에 맞게 설계하였다. 개발된 제어 로직들은 HILS(Hardware In Loop System)에서도 활용이 가능하도록 이산 시간 신호(Discrete time signal)로 설계하였다.

3.1 변속 제어로직

3.1.1 변속 가능 구간 확인

기본적으로 모터 구동 차량의 변속 시점은 모터의 효율과 구동력을 향상시키는 관점에서 결정하게 된다. 하지만 본 연구 대상 시스템의 구동 모터와 조향 모터들은 교합 장치에 의해 연결되어 회전하기 때문에, 차량의 주행속도와 조향 상태에 따라 구동 모터와 조향 모터의 작동 영역이 제한된다. 따라서 본 연구에서는 임의의 구동 및 조향 상태에서 모터 작동이 가능한 영역들을 분석하고, 해당 작동 영역의 최고 속도 점에서의 변속 특성을 분석하였다.

차량 선회 시에는 양측 궤도 속도가 달라지고 교합 장치로 인해 모터 최대 회전속도(ω_MR,max)를 기준으로 차량의 주행 최대 속도(V_mv,max)가 제한된다. 구동모터가 최고 회전 속도일 때 조향기어비 iS_g에 의해 제한되는 주행 가능한 최고 차속은 식 (13)에 의해 결정된다.

$\[ V_{mu,\text{max}}=\frac{r_{sp}{\omega }_{MR,\text{max}}}{i_{FD}{i}_{Transmission }}\frac{i{S}_g}{i{S}_g-1} \]$

(13)

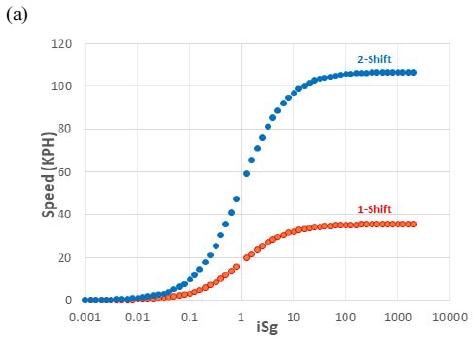
Fig. 7은 식 (13)을 이용하여, 변속 단수(1단, 2단)별로 구동모터가 최대 속도로 회전할 때, 조향기어비 iS_g의 변화에 따른 최고 차속을 나타낸 그래프이다. 빨간색 선도 아래의 영역은 1, 2단의 변속이 모두 가능하지만 빨간색과 파란색 선도 사이의 구간은 2단 변속만 가능하다. 따라서 1↔2단 변속이 가능한 1단의 최대속도 선도 이하 영역을 1단 주행 가능 구간으로 고려하였다.

Fig. 7

Vehicle speed area according to maximum speed of each shift motor

3.1.2 변속 제어로직 구성

변속 과정에서 측정되는 신호만으로 변속을 판단하는 경우에는 순간적인 상, 하단 변속 등의 오류가 발생할 수 있기 때문에, 본 연구에서는 상하단 변속시점의 히스테리시스(Hysteresis)를 적용하여 이 문제를 해결하였다. 또한 운전자가 의도하지 않는 변속이 발생하지 않도록 APS, 현재 기어단수, 차량 가속도 등의 변수들을 이용하여 변속 신호를 제어하였고, 이들 신호를 받는 변속 제어기에서는 변속 시의 클러치 상대속도 (∆ω_up, ∆ω_down)를 감소시키는 제어를 하여 변속 충격을 최소화하였다.

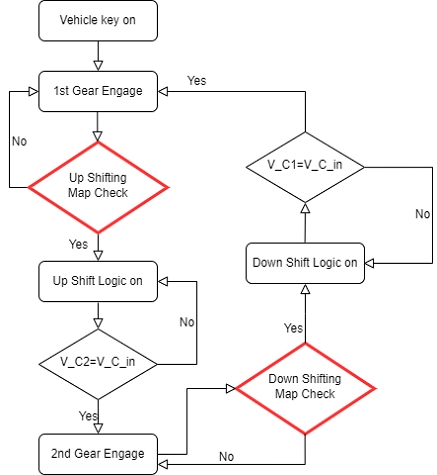
변속 로직의 알고리즘은 아래의 Fig. 8과 같다. 차량의 시동이 걸리면 1단 클러치를 결합하여 1단으로 주행하다가 iS_g와 차량 속도에 따라 변속 가능 구간에서 상단 변속 신호를 발생시킨다. 이때, 구동 모터는 역 토크를 발생시켜 ∆ω_up을 감소시키고, ∆ω_up의 최소값에서 2단 클러치를 체결한다.

Fig. 8

Shift control logic flow chart

Fig. 9

Shift control logic in simulator

하단 변속도 상단 변속과 동일하게 변속 가능 구간 확인을 통하여 하단변속 신호를 결정하고, ∆ω_down을 줄이기 위하여 모터의 토크를 Full throttle 기준으로 작동시켜 레브매칭(Revolution matching)을 진행한다. 그에 따라 모터 속도가 증가하며 ∆ω_down의 최소값에서 1단 클러치를 체결한다.

3.2 선회 제어로직 구성

본 연구 대상 차량은 궤도차량이므로 차량이 선회하기 위해서는 양측 궤도의 속도 차이를 발생시켜야한다. 선회 반경이 클 때는 양측 구동 모터의 토크 차이를 발생시켜 선회할 수 있다. 선회 반경이 작은 급격한 선회는 조향 모터를 추가적으로 사용하여 선회를 진행해야 한다.

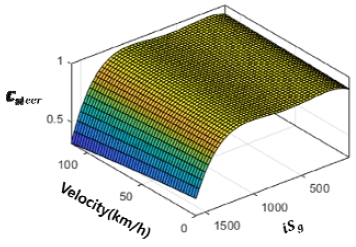
본 장에서는 선회를 진행할 때, 요구 선회 반경과 양측 궤도 속도에 따라 변화하는 조향 모터의 출력 토크를 결정하는 게인 값(C_steer)을 설계하였다. C_steer은 0~1 사이의 값으로 조향 모터 최대 토크 값에 곱해진다. C_steer는 선회 시 양측에 걸리는 부하토크(T_SPR,T_SPL)와 차량 주행 시 회전체 관성에 의한 부하 토크(T_load,add)를 고려하여 식 (14)로 나타낼 수 있다.

$\[ C_{steer }=\frac{T_{BR}+\frac{T_{SPR}+T_{load,add}/2}{i_{FD}}-T_{TM,out,R}}{T_{MC,max }{i}_{MC}{i}_{Cross - Drive }} \]$

(14)

식 (1)의 I_CR, I_CL에 관한 운동방정식을 C_steer을 포함한 식으로 표현하면 식 (15)와 같다. 식 (15)를 활용하여 C_steer를 Fig. 10에 iS_g와 차량 속도에 따른 Map 형태로 표현하였다.

$\[ \left\{\begin{array}{c}{I}_{CR}\dot{{\omega }_{OR}}=\begin{array}{l}{T}_{TM,Out,R}-T_{BR}-T_{SPR}/i_{FD}\hfill \\ +T_{MC,\text{max} }{i}_{MC}{i}_{CrossDrive }{C}_{steer }\hfill \end{array}\hfill \\ I_{CL}\dot{{\omega }_{OL}}=\begin{array}{l}{T}_{TM,Out,L}-T_{BL}-T_{SPL}/i_{FD}\hfill \\ -T_{MC,\text{ max} }{i}_{MC}{i}_{CrossDrive }{C}_{steer }\hfill \end{array}\hfill \end{array}\right. \]$

(15)

Fig. 10

Output torque gain(Csteer) map of steering motor

4. 모델 시뮬레이션

앞에서 설명한 차량 하드웨어의 모델과 실시간 제어가 가능한 제어 로직들을 바탕으로 제어 성능 시뮬레이터를 구성하였다. 시뮬레이션은 다양한 주행 상황들(단일 변속단 직진, 선회 주행, 우측 모터 파손 주행과 변속 직진 주행)에 대하여 진행하였다.

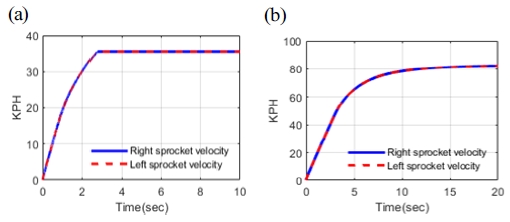
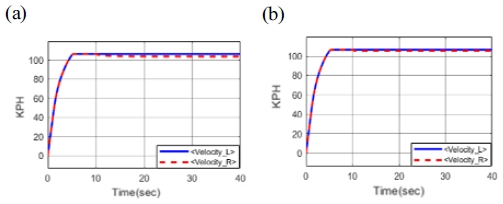
먼저 단일 변속단 직진 주행의 시뮬레이션 결과를 Fig. 11에 나타냈다.

Fig. 11

Single-stage driving simulation (a) 1-shift (b) 2-shift

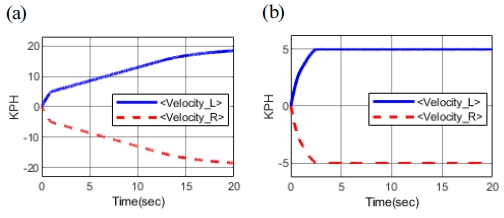
다음으로 Fig. 12에는 1단 조향 반경 별 선회 주행 시뮬레이션 결과를 나타냈다. Fig. 13에는 2단 조향 반경 별 평지 선회 주행 시뮬레이션 결과를 나타냈다. Fig. 14는 각 단별 제자리 선회 시뮬레이션을 진행하여 결과를 나타냈다.

Fig. 12

Simulation of a turn at speed of 35 km/h with 1 st shift Steering radius (a) 50 m (b) 150 m

Fig. 13

Simulation of a turn at speed of 105 km/h with 2nd shift Steering radius (a) 50 m (b) 150 m

Fig. 14

Simulation of Pivot (a) 1-Shift (b) 2-Shift

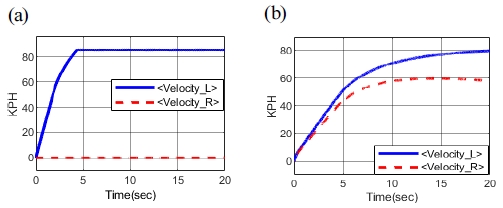
다음으로 평지 주행 중 우측 모터가 파손되었을 때, 교합 장치가 없는 차량과 있는 차량을 비교하여 시뮬레이션을 진행하였고 그 결과를 Fig. 15에 나타냈다. 교합 장치가 없는 차량의 경우, 좌우측 동력 단절로 인하여 한쪽 모터 파손 시 반대쪽 궤도의 속도만 발생하였다. 교합 장치가 있는 차량인 경우, 좌우측 동력이 교합 장치를 통해 연결되어 있다. 한쪽 모터가 파손되어도 교합 장치를 통하여 조향모터와 반대쪽 모터를 이용하여 차량 구동이 가능함을 확인하였다.

Fig. 15

Vehicle simulation with damaged right motor (a) Cross-Drive X (b) Cross-Drive O

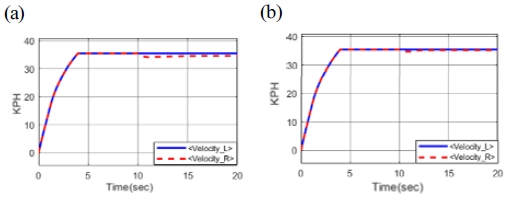
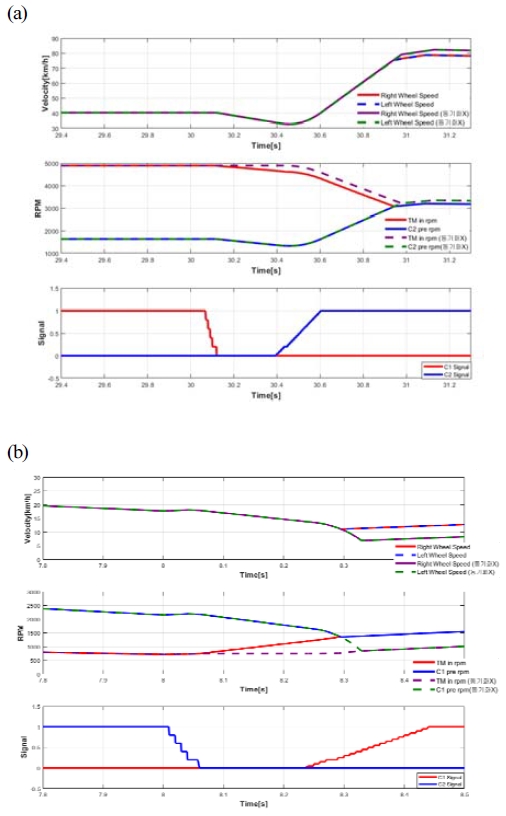
다음으로 Fig. 9의 제어 로직을 활용하여 변속 클러치 상대속도를 감소시켜 변속 충격을 감소시키는 상하단 변속을 진행하였다. 클러치 입력축과 출력축의 상대속도가 약 500 RPM 감소하였고 상하단 변속 시간이 약 50 ms 감소하는 것을 확인할 수 있었다. 변속 로직을 적용하기 전과 후 결과를 Fig. 16에 나타냈다.

Fig. 16

Shift optimization simulation (a) Up-shift (b) Down-shift

5. 결 론

• 1) 2단 변속기와 교합장치를 장착한 전기 모터 구동형 차량의 모터, 파워트레인, 교합장치 모델링을 진행하였다.
• 2) 혹스 모델 기반의 부하 모델 모델링을 진행하였다.
• 3) 교합 장치가 장착된 궤도 차량의 변속 가능 구간을 모터 회전 속도 작동 영역 관점으로 설계하였다.
• 4) 전기 모터를 사용하는 궤도차량의 상하단 변속 시 상대속도를 최소화하여 변속 충격을 최소화하는 제어로직을 설계하였다.
• 5) 3개의 모터(양측 구동모터, 조향 모터)와 교합장치를 사용하는 궤도 차량의 선회 제어로직 모델을 설계하여 구동모터와 조향모터의 토크 양을 결정하였다.
• 6) MATLAB/SIMULINK를 사용하여 차량 제어로직 모델과 플랜트 모델을 설계하여 모터 파손 주행 등 몇 가지 주행 시뮬레이션을 진행하였다.

Acknowledgments

이 논문은 2023년 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(KRIT-CT-21-025).

References

• D. H. Sung, H. Y. Lee, W. S. Lim and S. W. Cha, “The Study on the Applicability of Energy Control Strategy Based on Fuel Economy Optimization of Hybrid Vehicle,” KSAE Annual Conference Proceedings, p.98, 2018.
• D. K. Kim, J. M. Yun, J. Y. Lee, S. H. Chun and W. S. Lim, “Optimization of Shift Hydraulic Pressure Pattern for HEV,” KSAE Spring Conference Proceedings, p.105, 2023.
• C. H. Zheng, Y. I. Park, W. S. Lim and S. W. Cha, “A Study on Battery SOC Estimation by Regenerative Braking in Electric Vehicles,” Transactions of KSAE, Vol.20, No.1, pp.119-123, 2012. [https://doi.org/10.7467/KSAE.2012.20.1.119]
• J. R. Jeong, H. K. Kim, K. Y. Kim, W. S. Lim and S. W. Cha, “Evaluation of Fuel Economy and Performance for 2WD and 4WD Hybrid Electric Vehicle Based on Backward Simulation,” Transactions of KSAE, Vol.22, No.1, pp.174-182, 2014. [https://doi.org/10.7467/KSAE.2014.22.1.174]
• M. K. An, B. M. Ku and K. S. Choi, “R&D Trends and Future Prospects of Hybrid Military Vehicle,” KSAE Annual Conference Proceedings, pp.1282-1286, 2020.
• K. H. Kwon and J. S. Lee, “Multi-Objective Optimization of Powertrain System for Tracked Hybrid Electric Vehicles Considering Equivalent Inertia,” KSAE Annual Conference Proceedings, p.1161, 2020.
• W. Ehlert, B. Hug and I. C. Schmid, “Field Measurements and Analytical Models as a Basis of Test Stand Simulation of the Turning Resistance of Tracked Vehicles,” Journal of Terramechanics, Vol.29, No.1, pp.57-69, 1992. [https://doi.org/10.1016/0022-4898(92)90014-B]
• M. Kitano and M. Kuma, “An Analysis of Horizontal Plane Motion of Tracked Vehicles,” Journal of Terramechanics, Vol.14, No.4, pp.211-225, 1977. [https://doi.org/10.1016/0022-4898(77)90035-0]
• J. Y. Wong and C. F. Chiang, “A General Theory for Skid Steering of Tracked Vehicles on Firm Ground,” Institution of Mechanical Engineers, Vol.215, No.3, pp.343-355, 2001. [https://doi.org/10.1243/0954407011525683]