[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 32, No. 3, pp.281-288

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Mar 2024

Received 14 Nov 2023 Revised 19 Dec 2023 Accepted 20 Dec 2023

DOI: https://doi.org/10.7467/KSAE.2024.32.3.281

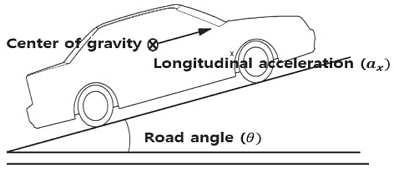
도로 등판각 추정 기반 알고리즘 및 시스템 설계

김민수¹⁾ ; 정대이^*^{, 2)} ; 김동규³⁾ ; 윤태민³⁾

1)군산대학교 고등기술융합연구원 기계융합연구본부
2)군산대학교 기계자동차공학부
3)이씨스 연구소

Road Slope Angle Estination Based Algorithm and System Design

Minsu Kim¹⁾ ; Daeyi Jung^*^{, 2)} ; Donkyu Kim³⁾ ; Taemin Yoon³⁾

1)Kunsan National University Advanced Techonology Insitute for Convergence, Sandannambuk-ro, Gunsan-si, Jeonbuk 54001, Korea
2)Department of Mechanical and Automotive Engineering, Kunsan National University, Kunsan-si, Jeonbuk 54150, Korea
3)R&D Team, ESSYS Company, 55 Gaetbeol-ro, Yeonsu-gu, Incheon 21999, Korea

Correspondence to: ^*E-mail: dyjung@kunsan.ac.kr

Copyright Ⓒ 2024 KSAE / 220-04
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

The utilization of an Automatic Emergency Braking(AEB) system and Electronic Stability Control(ESC) in commercial vehicles, including large buses and trucks, can enhance driving stability by ensuring the weight of the vehicle, road surface conditions, and the estimation of road gradient. Particularly, this research focuses on road gradient estimation. Previous studies used various sensors and longitudinal vehicle dynamics models to estimate road gradient, but integrating them into production vehicles became challenging due to sensor costs. In this study, a model was developed to predict road gradient based on the vehicle’s Control Area Network(CAN) signals, thus eliminating the need for additional sensors. The estimation performance of various filters, including Low-Pass Filters(LPF), Kalman Filters(KF), and Recursive Least Squares(RLS) filters, were compared. The algorithm was implemented in MATLAB/Simulink, and the performance of each filter achieved estimations within a ±10 % error range.

Keywords:

Road slope angle, Low pass filter, Kalman filter, Rersuive Least Square, Commercial vehicle, Automatic emergency braking, Electronic stability control

키워드:

도로 등판각도, 저역필터, 칼만 필터, 회기 최소 자승기법, 상용차량, 자동 긴급 제동 시스템, 차량 자세 제어 시스템

1. 서 론

상용차의 제동 안정성을 확보할 수 있는 자동긴급제동(AEB) 시스템은 졸음운전, 밤길 운전 등 운전자 및 차량의 위험 상황을 감지하여 자동으로 차량을 제동하는 장치이다. 대형버스 및 트럭 등 상용차량은 사고 발생 시 승용차량에 비해 대형사고로 이어져 대형 인명 피해가 발생할 가능성이 높기 때문에, 차량추돌 및 차선이탈 등의 사고를 예방하기 위해서는 자동긴급제동을 통한 차량 제동 안정성 확보가 필수적이다.^1,2)

또한 자동긴급제동 시스템 구성으로 제동장치를 전자적으로 제어하는 전자 제어 브레이크시스템(ESC)을 통하여 차량의 주행 안정성을 확보할 수 있다.

이에 따라 차량의 주행 안정성을 확보하기 위해 차량의 무게, 도로 노면, 도로의 등판각 추정이 필수적인 요소로 작용한다. 본 연구에서는 도로 등판각 추정에 대한 연구를 진행하였다.

기존 도로 경사각을 추정하기 위하여 많은 연구들이 진행되어왔다. 종 경사각 추정기를 구현하는 방법은 차량의 다양한 센서와 종방향 차량 동역학 모델을 이용하여 개발되어 왔다. 종 경사각을 추정할 때 차량의 가속도계와 휠속력계, GPS를 이용하여 종방향 차량 동역학 모델을 이용하지 않고 개발되었으며, Hahn 등³⁾, Han 등⁴⁾이 제안한 적응 제어 기법은 횡 속도를 측정하는 센서를 이용하여 노면 경사각을 구하는 방법도 연구 되어왔다. 하지만 이와 같은 센서 자체가 고가이므로 판매용 차량에 이를 도입하는 것은 많은 어려움이 있다.

본 연구에서는 개발 알고리즘은 Matalb/Simulink 기반으로 구현하였으며, 별도의 추가 센서 부착 없이 차량의 CAN(Control Area Network)신호로 계측되는 가속도, 속도, 조향각센서(Steering angle sensor), Brake on/off Signal 등 취득한 데이터를 사용하였다.

등판각 추정 성능을 높이기 위하여 LPF, KF, RLS 필터 기반의 등판 각도를 예측할 수 있는 모델을 개발한 후 각 필터의 추정 성능을 비교하였다. 추 후 질량 추정 및 도로노면 추정 알고리즘을 포함한 통합 알고리즘을 개발하고자 한다.

2. 차량 모델 선정 및 종 경사각 추정기를 통한 등판각 추정

2.1 시험 대상 차량

본 연구에서는 실험 대상 차량 모델을 상용 트럭인 국내 H사의 Truck을 선정하였으며, 실험 대상 차량 모델은 1톤급이다.

Photo. 1

H Company truck(1 ton)

2.2 종 경사각 추정기 설계

CAN 신호로 계측되는 가속도, 속도계가 있으며, 종 방향 가속도계는 차량 종 방향 가속도와 중력으로 인한 가속도의 합이다. 종 경사각 식 (1) ~ (3)은 다음과 같이 계산할 수 있다.

a x, s = a x + g s i n θ

(1)

a x, s = V t + 1 - V t d t + g s i n θ

(2)

θ = a x, s - V t + 1 - V t d t g * s i n θ ≈ θ

(3)

Fig. 1

Defining road slope angle θ

여기서, a_x_,s는 가속도계 측정값, a_x은 종방향 가속도 추정값, V는 차량의 속도, g는 중력가속도이다. 또한 이때 가속도 및 속도, 조향각센서(Steering angle sensor), Brake on/off Signal은 차량 시험을 통하여 측정하였다.

이처럼 설계한 종 경사각 추정기를 LPF, KF, RLS에 따른 성능 비교한다.

도로 등판각을 추정 조건은 다음과 같은 시나리오를 통해 추정하였다.

1) 차량 속도 10 kph 이하로 주행(등판로 주행이 가능한 최소 속도)
2) 제동 중에는 모델이 불안정하기 때문에 Brake stat = 0 일 때 추정
3) 조향각센서(Steering angle sensor)는 30° 이하 일 때 추정

2.3 실차 시험 주행 조건

시험 대상 차량이 공차 무게일 때 6, 12, 18, 30 %의 도로 등판각을 주행하였으며, 차량의 속도는 10 kph이하로 주행하였다. 알고리즘에 필요한 차량의 속도, 가속도, 조향각센서(Steering angle sensor), Brake om/off Signal을 계측한다. 자세한 시험 주행 조건은 Table 1에 나타낸다.

Photo. 2

Actual vehicle test

Table 1

Algorithm variable

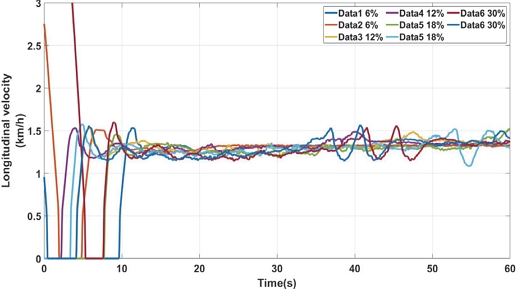
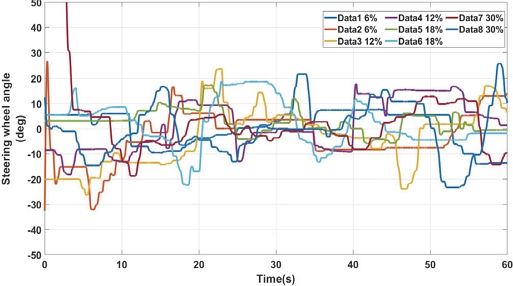
Fig. 2, Fig. 3은 주행 조건에 따른 Longitudinal velocity, 조향각센서(Steering angle sensor)이다.

Fig. 2

Longitudinal velocity of 6, 12, 18, 30 %

Fig. 3

Longitudinal velocity of 6, 12, 18, 30 %

3. 등판각 추정 알고리즘 구성 및 검증

3.1 등판각 추정 알고리즘 구성

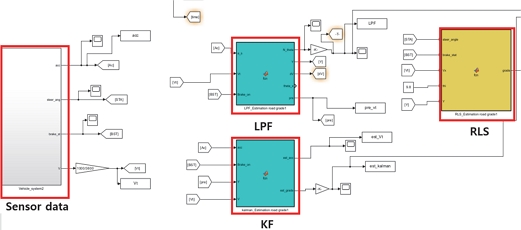
본 연구에서 제안한 등판각 추정기를 Matlab/Simulink 기반으로 구현하였으며, 실제 차량에서 취득한 데이터로 시뮬레이션 하여 LPF, KF, RLS 3가지 기반의 통합 알고리증 성능을 분석하였다.

실제 차량에서 취득한 가속도 센서, 속도 센서계 정보를 사용하여 등판각을 추정하였다.

Fig. 4

Matlab/Simulink based road slope angle estimation algorithm

등판각 추정 알고리즘 Logic on/off 조건은 다음과 같다.

Steering angle sensor ≤ 30 ∘

(4)

Brake stat ≈ 0

(5)

Longitudinal Velocity ≻ 0.01 k m / h

(6)

3.2 LPF(Low Pass Filter) 기반 알고리즘 설계 및 검증

LPF는 특정한 차단 주파수 이상 주파수의 신호를 감쇠시켜 차단 주파수 이하의 주파수 신호만 통과시키는 필터이다.

LPF를 사용하여 등판각을 추정하는 알고리즘은 가속도 및 속도에서 나오는 테이터의 노이즈를 제거하고 저주파 신호를 통과시킴으로써 신호를 부드럽게 만들어준다. LPF는 다음과 같이 표현된다.

y t = α ⋅ y t - 1 + 1 - α ⋅ x t

(7)

이 때, τ τ + t s = α

(8)

여기서 y(t)는 현재 시간 t에서의 LPF 출력이며, x(t)는 현재 시간 t에서의 입력신호, α는 필터링을 제어하는 매개변수로, 0에서 1사이의 값으로 설정되며 τ는 Time constant, T_s는 Sample time이다. α값이 작을수록 필터는 더 부드러운 출력을 생성하고, 높은 주파수 노이즈를 더 효과적으로 제거한다.

Fig. 5

LPF-based road slope angle 6 %(3.43°) results

Fig. 6

LPF-based road slope angle 12 %(6.84°) results

Fig. 7

LPF-based road slope angle 18 %(10.20°) results

Fig. 8

LPF-based road slope angle 30 %(16.69°) results

종 경사각 추정기 설계를 LPF에 적용하면 다음과 같다.

θ t + 1 = α ⋅ θ + 1 - α ⋅ a x, s - V t + 1 - V t d t g

(9)

등판각 추정 시 적절한 τ값 설정이 필요하다. 본 연구에서는 τ값을 다음과 같이 설정하였다.

α = τ τ + t s = 1 1 + 0.001

(10)

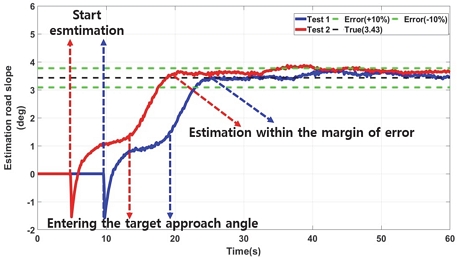
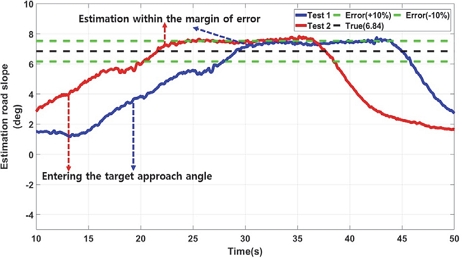
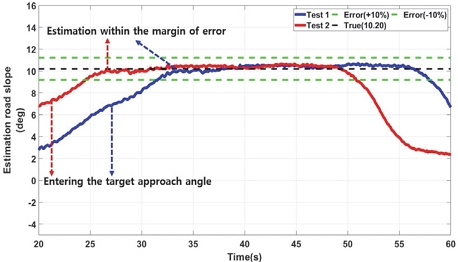
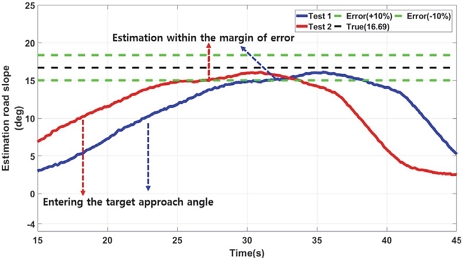
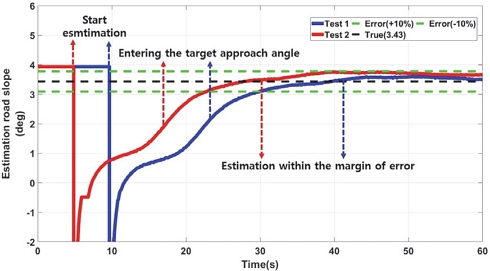
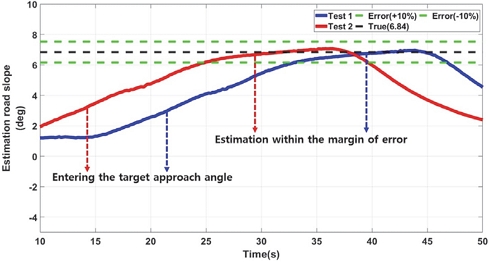
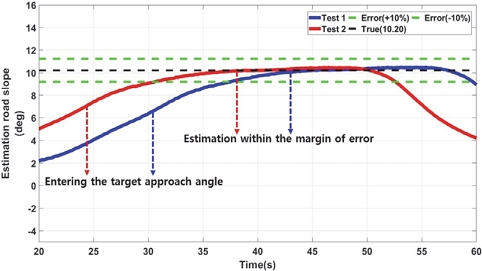
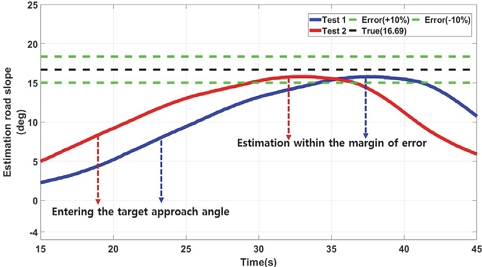
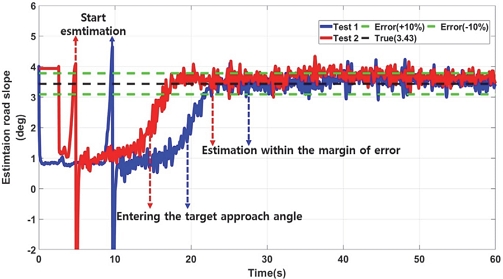
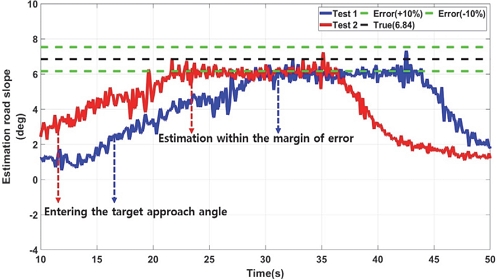
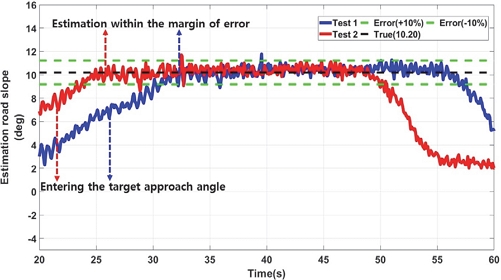
본 연구에서는 각 등판각 마다 실험을 2회씩 진행하였으며, LPF 기반의 등판각 추정 결과 오차 범위 ±10 % 내에 추정이 완료되었다.

3.3 RLS(Recursive Least Square) 기반 알고리즘 설계 및 검증

RLS 알고리즘은 회귀 분석 및 신호 처리 분야에서 사용되는 효과적인 최적화 알고리즘이다. 일반적으로 가중 최소 제곱(Weighted least squares) 기법을 기반으로 하며, 잡음이 포함된 입력 데이터와 해당 데이터에 대한 목표값을 사용하여 모델 파라미터를 조정하는 것을 목표로 한다.^5-7)

RLS 알고리즘의 갱신 규칙은 다음과 같다.

1) 초기에 모델 파라미터를 초기화
2) 각 데이터 포인트마다 다음과 같은 단계를 수행
3) 현재 데이터를 사용하여 모델의 예측값을 계산
4) 예측 오차를 계산하고 이를 사용하여 모델 파라미터 업데이트
5) 가중 최소 제곱 방법을 사용하여 파라미터를 업데이트할 때 이전에 계산한 파라미터와 현재 데이터 정보를 이용

Fig. 9

Method of least square

RLS 알고리즘은 매개 변수 추정을 위하여 회귀 처리의 형태인 식 (11) ~ (12)와 같이 표현된다.

y = ϕ T θ

(11)

V θ^= 12 ∑ i = 1 k y i - ϕ T i θ^2

(12)

이때 망각인자(Forgetting factor)를 갖는 RLS 알고리즘을 나타내면 식 (13) ~ (15)와 같이 나타낼 수 있다.

V θ^= 12 ∑ i = 1 k λ k - i y i - ϕ T i θ^k 2

(13)

L k = P k - 1 ϕ k λ + ϕ T k P k - 1 ϕ k - 1

(14)

P k = 1 - L k ϕ T K P k - 1 1 λ

(15)

θ k = θ k - 1 + L k L k - s e n s o r - ϕ k θ k - 1

(16)

위 식에서 y와 ϕ^T는 이미 알고 있는 파라미터 값이며, θ_k는 추정하고자 하는 예측값을 나타낸다.

식 (14)에서 이득 벡터(L(k))는 반복 계산 과정에서 이득 값이 도출되며, 망각인자는 RLS 알고리즘에서 사용되는 중요한 파라미터로, 이전 데이터의 영향력을 제어하는 역할을 한다. 망각인자의 값은 일반적으로 0보다 크고 1보다 작은 값을 가지며, 값이 작을수록 최신 데이터에 더 빨리 반응하게 된다. 즉 망각인자의 값이 작을수록 이전 데이터에 덜 의존하고 최신 데이터에 더 큰 가중치를 둔다. 반대로, 망각 인자의 값이 크면 이전 데이터에 더 의존하게 된다.

본 연구에서는 도로 등판각 추정 성능 연구를 위해 망각인자가 포함된 RLS 알고리즘을 구성하였다.

도로 등판각 추정을 위하여 식 (3)을 통해 각 변수를 다음과 같이 정의한다.

ϕ T k = g

(17)

L k - s e n s o r = a x, s - V t + 1 - V t d t

(18)

RLS 기반의 등판각 추정 결과 오차 범위 ±10 % 내에 추정이 완료되었다.

Fig. 10

RLS-based road slope angle 6 %(3.43°) results

Fig. 11

RLS-based road slope angle 12 %(6.84°) results

Fig. 12

RLS-based road slope angle 18 %(10.20°) results

Fig. 13

RLS-based road slope angle 30 %(16.69°) results

3.4 KF(Kalman Filter) 기반 알고리즘 설계

KF는 시스템의 상태를 추정하는데 사용되는 알고리즘으로, 시스템 모델에 노이즈가 포함된 경우에 사용되며 초기 추정치와 시스템의 다양한 입력 및 측정치를 사용하여 시스템의 현재 상태를 추정하고, 이러한 추정치를 지속적으로 업데이트 한다.

KF 알고리즘의 단계는 다음과 같다.

1) 현재 상태 추정치를 이전 상태 추정치를 이용해 예측하며, 이전 상태 추정치는 이전 시간 단계에서 추정
2) 시스템에서 얻은 실제 관측치(측정치)와 예측한 상태를 비교
3) 예측과 실제 측정치 사이의 오차를 계산하고, 이를 이용해 상태 추정치를 업데이트 함

KF는 예측과 업데이트 단계를 반복하면서 시스템 상태를 더 정확하게 추정하고 예측 오차를 최소화한다. 이 과정은 시스템 모델과 관측 모델에 기반하며, 노이즈 및 불확실성을 고려하여 최상의 상태 추정치를 계산한다.

(1) 초깃값 선정

x^0, P 0

(19)

(2) 추정값과 오차 공분산 예측

x^k = A x^k - 1

(20)

P k - = A P k - 1 A T + Q

(21)

(3) 칼만 이득 계산

K k = P k - H T H P k - H T + R - 1

(22)

(4) 추정값 계산

x^k = x^k + K k z k - H x^k * z k = 측정값

(23)

(5) 오차 공분산 계산

P k = P k - - K k H P k -

(24)

알고리즘에 변수는 Table 2와 같다.

Table 2

Algorithm variable

도로 등판각 추정을 위하여 식 (3)을 통해 각 변수를 다음과 같이 정의한다.

a c c = d V d t + g θ → V k + 1 - V k d t = a c c - g θ

(25)

V k + 1 = V k + a c c - g θ k d t, θ k + 1 = θ k

(26)

V k + 1 θ k + 1 = 1 - g d t 01 V k θ k + a c c × d t 0 ↓ ↓ ↓ ↓ X k + 1 = A k × X k + C k

(27)

Fig. 14

KF-based road slope angle 6 %(3.43°) results

Fig. 15

KF-based road slope angle 12 %(6.84°) results

Fig. 16

KF-based road slope angle 18 %(10.20°) results

Fig. 17

KF-based road slope angle 30 %(16.69°) results

KF 기반의 등판각 추정 결과 오차 범위 ±10 % 내에 추정이 완료되었다.

3.5 각 필터의 추정 성능 비교

동일한 시나리오에 대한 LPF, RLS, KF의 추정 성능 비교를 진행하였다. 각 필터의 목표 등판각 수렴시간은 Table 3과 같다.

Table 3

Filter convergence time comparsion

각 필터의 수렴시간을 비교한 결과 RLS 필터는 다른 두 필터에 비해 수렴시간이 늦었으며, LPF, KF는 수렴 시간이 비슷하게 추정되었다.

4. 결 론

본 연구에서는 상용차의 자동긴급제동(AEB) 시스템을 개선하여 차량의 주행 안전성을 향상시키기 위해 도로 등판각 추정에 초점을 맞춘 연구를 진행하였다. 별도의 센서 부착 없이 차량의 CAN 신호를 활용하여 등판각 예측 모델을 개발하였으며, LPF, KF, RLS 필터 등을 사용하여 개발한 모델의 성능을 비교 분석하였다.

1) 차량 등판각 추정 알고리즘을 Matalb/Simulink로 구성하였으며, 실제 차량의 데이터를 활용하여 개발 알고리즘을 검증하였으며, 주요 파라미터는 조향각센서(Steering angle sensor), Longitudinal velocity, Acceleration, Brkat on/off 이다.
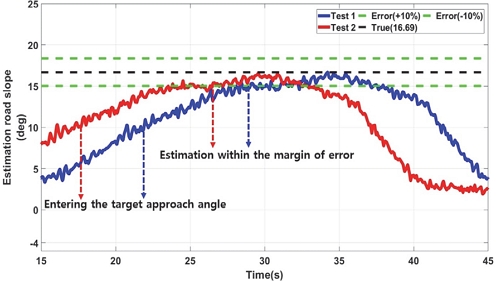
2) LPF, RLS, KF 등을 사용하여 개발 모델의 성능을 비교 분석하였으며, 등판각 진입 후 10~12 m 정도 지난 후 정확한 값을 추정하게 되며, 각 필터의 성능 추정 결과 오차 범위 ±10 % 이내 추정이 완료되었다.
3) 본 연구에서는 개발 모델을 기반으로 질량 추정과 도로 노면 추정 알고리즘을 통합하여 더욱 정확하고 효과적인 자동긴급 제동 시스템을 개발하고자 한다.
4) 이러한 연구는 대형 차량 사고 예방 및 운전 안전성 향상에 기여할 것이다.

Nomenclature


α_x_,s :	longitudinal acceleration sensor, m/s²
α_x :	longitudinal acceleration estimate, m/s²
g :	gravitational acceleration, m/s²
V :	vehicle speed, m/s
t :	sampling time, s
θ :	road slope, °
τ :	time constant, -
T_s :	sample time, s

Subscripts


LPF :	low pass filter
KF :	kalman filter
RLS :	recursive least square
CAN :	control area network
GPS :	global positioning system
AEB :	automatic emergency braking
ESC :	electronic stability control
SAS :	steering angle sensor

Acknowledgments

본 연구는 2023년도 산업통상자원부 및 한국산업기술진흥원(KIAT) 연구비 지원에 의한 연구임(‘P0018565’).

References

V. Trent and M. Greene, “A Genetic Algotithm Predictor for Vehicular Rollover,” 28th Annual Conference of the Industrial Electronics Society, pp.1752-1756, 2002.
A. Hac, “Rollover Stability Index Including Effects of Suspension Design,” SAE Transactuions, pp.1403-1413, 2002. [https://doi.org/10.4271/2002-01-0965]
J. O. Hahn, R. Rajamani, S. -H. You and K. I. Lee, “Real-Time Identifications of Road-Bank Angle Using Differential GPS,” IEEE Transactions on Control Systems Technology, Vol.12, No.4, pp.589-599, 2004. [https://doi.org/10.1109/TCST.2004.825131]
K. J. Han, I. K. Kim, S. K. Kim and K. S. Huh, “Real-Time Vehicle Mass Estimator for Active Rollover Prevention Systems,” Transactions of the Korean Society of Mechanical Engineers A, Vol.36, No.6, pp.673-679, 2012. [https://doi.org/10.3795/KSME-A.2012.36.6.673]
M. Kim, G. Choi and M. Hong, “Vehicle Mass Estimation Algorithm Using Recursive Least Square Method with Forgetting and Lopass Filter,” Transactions of KSAE, Vol.27, No.11, pp.833-838, 2019. [https://doi.org/10.7467/KSAE.2019.27.11.833]
G. Tejas, Estimation of Vehicle Mass and Road Slope, M. S. Thesis, Clemson University, United States of America, 2008.
Y. S. Yoon, Y. G. Park and H. J. Kim, “Study on Online Estimation of Vehicle Mass and Road Slope Using A Recursive Least Squares Method with Multiple Forgetting Factors,” KSAE Annual Conference Proceedings, pp.1816-1819, 2010.

Road slope angle	Velocity	SAS	Number of test
6, 12, 18, 30 %	0~10 kph	-30~+30°	12

Variable purpose	Variable
External input	z_k (측정값)
Final output	$x^k$ (추정값)
System model	A, H, Q, R
Internal cacilation	$x^k, P k -, P k, K k$

Table 3

Filter convergence time comparsion

	LPF	RLS	KF
Test1 6 %	25.5 sec	38 sec	25 sec
Test2 6 %	20 sec	28 sec	19 sec
Test1 12 %	32 sec	39.5 sec	30.5 sec
Test2 12 %	24.5 sec	31.5 sec	21.5 sec
Test1 18 %	33.5 sec	44 sec	32.5 sec
Test2 18 %	26.5 sec	37.5 sec	25 sec
Test1 30 %	30.5 sec	37 sec	29 sec
Test2 30 %	27 sec	32 sec	24.5 sec