상대 차량 효용 추정 기반 게임이론을 활용한 자율주행차의 차선 변경 알고리즘 개발
Copyright Ⓒ 2024 KSAE / 218-13
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper presents an interaction algorithm that can be used in lane change scenarios through a game theory based on estimated opposing vehicle utility. General game theory-based interaction algorithms are valuable in implementing interaction mechanisms that consider the utility of related vehicles. However, they may become inefficient due to uncertainties of the utilities of opposing vehicles. The primary concept behind estimating utility is defining it as a function of achieving driving goals and ensuring safety, which are universal considerations in changing lanes. Weights for each objective in the utility function are determined based on the driver’s driving characteristics. The proposed algorithm estimates opposing vehicle utility by adjusting driving characteristics through driving patterns. Finally, the Stackelberg game, which is grounded in updated utility, offers an optimal lane change strategy after considering the opponent’s real-time actions. The proposed algorithm was then validated, and could provide a beneficial strategy based on safety, traffic flow, and individual driving preferences.
Keywords:
Autonomous vehicle, Lane change strategy, Game theory, Utility estimation, Interaction키워드:
자율주행차, 차선 변경 전략, 게임 이론, 효용 함수 추정, 상호작용1. 서 론
환경 센서 기술과 판단 기술의 발전으로 완전 자율주행차량의 일반 공도 주행이 가능하게 할 것으로 예상되고 있다. 하지만 여전히 자율주행차량(Autonomous vehicles)과 유인운전차량(Human-driven vehicles)이 혼재하는 상황에서 자율주행차량의 구현에는 여러 문제점이 존재한다. 그 중 하나는 자율주행차량과 유인운전차량 간의 상호작용 구현이다.1) 기존의 자율주행차량은 안전 확보를 위하여 과도하게 방어적으로 주행한다.2,3) 그러나 이러한 인간답지 않은 주행 패턴은 인간운전자들과 상호작용할 때 혼란을 야기할 수 있으며 전체적인 교통 흐름의 저해 및 심지어 사고를 유발할 수도 있다.4,5) 교통 흐름을 효율적으로 유지하면서 안전을 보장하기 위해서는 자율주행차량이 인간운전자처럼 자신의 선택으로 상대 차량이 어떤 행동을 취할 것인가를 예측하는 상호작용을 통해 최적의 주행을 위한 의사 결정 기술 개발이 필요하다.6,7)
대부분의 자율주행차량과 유인운전차량 간의 상호작용 연구는 게임 이론을 기반으로 한다.8-13) 게임 이론은 합리적인 의사 결정을 하는 각 게임 참가자가 자신의 의사 결정에 따른 다른 참가자들의 효용을 예측하고 자신의 이익을 극대화하는 수학적 이론이다.14,15) 유인운전차량과 자율주행차량을 주행 환경에 대한 게임 참가자로 고려하고, 이익을 자신의 주행 목표, 안전성, 교통 흐름 등의 함수로 정의한다면, 게임 이론을 통해 추출된 최적의 주행 전략은 상호작용 기반 최적의 의사 결정이 될 것이다.
그러나 상대의 효용을 정확하게 예측하는 것은 어렵다. 따라서 게임 참가자들은 상대방의 효용을 자신의 효용과 유사하게 정의하거나 사전에 주어진 형태로 정의하여 게임을 진행한다. 이러한 부정확한 효용 예측은 잘못된 의사 결정을 초래할 수 있으며16) 특히 자율주행차량의 경우 교통 흐름 방해나 사고와 같은 문제를 야기할 수 있다.11,17)
본 연구는 상대 차량의 효용 추정을 통해 상대방의 불확실성에 대응 가능한 게임 이론 기반 상호작용 알고리즘을 제안한다. 주행 시나리오는 관련된 차량 수가 제한되어 있으면서 상호작용 발생률이 높은 차선 변경에 대해서 고려한다. 게임 이론으로의 차선 변경 시나리오 적용은 게임 참가자들 간 서로의 효용을 고려한 최적의 상호작용 기반 차선 변경 전략 수립을 가능하게 한다. 제안하는 알고리즘의 주요 핵심인 상대 차량에 대한 효용 추정은 상대 차량의 실제 행동 관측을 통해 운전자 성향을 추정함으로써 이루어진다. 이를 위해 효용을 운전자가 차선 변경 시 고려하는 보편적인 가치 기반 함수로 정의하고 운전자 성향에 따라 조정 가능하도록 설계한다. 제안하는 알고리즘은 사전 예측한 운전자 성향 기반 거동과 실제 관측된 거동 간의 차이를 통해 운전자 성향을 조정함으로써 효용을 실시간으로 갱신하여 최종 상호작용 기반 차선 변경 전략을 도출한다. 기존의 실용적이지 않은 게임 이론 기반 주행 전략의 단점을 극복한 실시간 추정된 효용 함수가 반영된 게임 이론 기반 차선 변경 알고리즘은 여러 시뮬레이션 검증을 통해 안전성, 전체 교통 흐름, 자 차량의 주행 목표 면에서 효율적인 차선 변경 전략을 제시한다.
2. Stackelberg 게임 기반 차선 변경 전략 설계
일반 교통 환경에서 차선 변경 전략 수립 시 운전자는 타 차량의 행동을 보고 차선 변경 의사를 결정한다. 즉, 차선 변경 상황은 계층적, 순차적 게임이라고 가정할 수 있다. 따라서 게임 참가자를 리더와 팔로워로 나누고, 리더가 먼저 행동한 후 팔로워가 행동하는 것을 가정한 계층적이며 순차적인 게임 이론인 Stackelberg 게임을 차선 변경 시나리오에 도입한다. 게임 이론 적용을 위한 차량 모델 및 기본 전략, 그리고 게임 참가자가 취하는 Action에 대해 정의한다.
2.1 Stackelberg Game
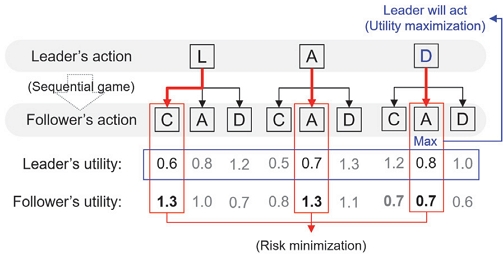
Stackelberg 게임 이론의 기본 전제는 리더가 먼저 행동하고 팔로워는 관측된 리더의 행동을 바탕으로 자신의 행동을 결정한다(Sequential game). 이때 리더는 팔로워가 리더의 효용을 가장 최소화하면서 본인의 효용을 최대화하는 의사 결정을 한다는 가정(Risk minimization)하에 본인의 효용이 가장 높은 행동 후보지를 선택(Utility maximization)한다.15) 팔로워는 리더의 선제적 행동을 관측한 후 주어진 상황에서 자신의 효용을 최대화할 수 있는 행동 후보를 선택한다.
Fig. 1은 리더와 팔로워가 각각 L, A, D 세 가지 행동과 C, A, D 세 가지 행동 선택지를 가지며 각 선택지에 따른 효용은 그림과 같이 제시되었을 때의 Stackelberg 게임의 예시를 보여준다. 리더는 자신의 행동 L, A에 따라, 팔로워가 리더의 행동에 따른 본인의 효용이 가장 높은 C, A의 선택지를 선택하리라고 예측할 것이다. 만약 리더의 행동이 D일 경우, 팔로워는 본인의 효용이 최대인 두 가지 선택지 C, A 중 리더의 효용이 더 낮은 A를 선택하리라고 예측된다. 리더의 행동에 따른 팔로워의 반응이 {L-C, A-A, D-A} 쌍으로 예측되는 가운데, 리더는 Stackelberg 게임 이론이 제시하는 팔로워의 행동에 대한 가설에 따라 팔로워가 A의 행동을 할 것이라 예측을 하고 본인의 효용을 가장 높이는 D의 행동을 취한다.
Stackelberg 게임 이론의 장점 중 하나는 리더의 입장에서 상대 행동의 불확실성에 대한 위험을 최소화하도록 선택을 유도한다는 것이다. 차선 변경 상황에서 차선 변경을 시도하려는 차량을 리더로, 리더가 가려는 차선에 달리고 있는 차량을 팔로워로 설계하면, 게임 수행 동안 자신의 효용 함수를 최대화하려는 리더의 차선 변경 행동이 타 차량과의 상호작용이 반영된 자율주행차의 최적의 차선 변경 전략이 된다.
2.2 Vehicle Dynamics Model
차량은 문제를 간략화하기 위해 질점으로 가정하며 순차적인 Stackelberg 게임에 적용하기 위한 이산화된 차량의 동역학 모델은 다음과 같다
| (1) |
- where,
이 때 X와 Y는 차량의 종 방향 및 횡 방향 위치이며, vx와 vy는 차량의 종 방향 및 횡 방향 속도, ax는 차량의 종 방향 가속도, dt는 샘플링 시간을 의미한다. 운전자의 입력은 차량의 종 방향 가속도 ax와 조향에 따른 횡방향 속도 vy로 표현되며 이는 게임 이론을 통해 결정되는 운전자의 의도이다.
2.3 Action Space
Stackelberg 게임에서 차선 변경에 관련된 차량들이 취할 수 있는 행동 후보지는 다음과 같다.
이때 a와 b는 임의로 설정된 종방향 가속도 크기 및 횡속도 크기이다.
차선 변경 시나리오에서 차선 변경하려는 차량인 리더는 종⋅횡방향에 대한 거동이 둘 다 고려되어야 하며 차선을 유지하는 차량인 팔로워는 종방향에 대한 거동만 고려한다. 따라 리더가 선택 가능한 주행 전략은 종방향의 행동 후보 {C, A, D}와 횡방향에 대한 행동 후보 {LC, LK}의 조합, 총 6가지이며, 팔로워가 선택 가능한 주행 전략은 종방향의 행동 후보 {C, A, D} 3가지이다.
2.4 Driving Strategy
설계된 게임 이론 기반의 차선 변경 주행 전략은 리더와 팔로워가 충분히 상호작용하는 구간 내에서 리더의 의사 결정에 적용된다. 차선 변경 시나리오에서 상호작용은 리더의 위치 xl이 팔로워의 위치 xf보다 앞서 있으면서 두 차량이 서로를 인식할 수 있는 범위 xth 내에 있을 때 발생한다. 즉, Stackelberg 게임 기반 주행 전략은 다음과 같은 구간에서 작동한다.
| (2) |
상호작용 발생 시에는 게임 이론을 기반으로 운전자들이 정해진 규칙에 따라 합리적인 판단을 하지만, 상호작용이 발생하지 않는 일반적인 상황에서 각 차량은 교통 흐름에 따라 속도를 제어한다. 이러한 일반적인 주행 전략을 모사하기 위하여 차선 변경 게임 진행 전후에는 Intelligent driver model(IDM) 전략을 적용하여 차량의 종방향 움직임을 제어한다.18)
| (3) |
- where,
여기서 v는 실제 자 차량 속도, vdes는 목표 주행 속도, Δv는 타차량과의 상대 속도, amax는 최대 가속도, δ은 가속도 지수, s는 타차량과의 상대 거리를 의미한다. sdes는 원하는 타 차량과의 간격을 의미하며, 최소 안전 거리 s0, 자 차량의 속도 v, Time headway T, 상대속도 Δv, 가속도 amax와 타겟 감속도 bdes의 함수로 정의된다. 전방 차량이 없는 경우 sdes는 무시된다. IDM 주행 전략은 상대 차량과의 상호작용이 없을 때, 즉 리더가 차선 변경을 완료하거나 차선 변경을 시도하더라도 팔로워와의 상대 거리가 멀어 상호작용이 굳이 필요하지 않을 때 적용된다.
3. 효용 함수 정의 및 상대 효용 가치 추정
게임 이론에서는 게임 참여자 모두를 합리적인 의사결정을 하는 주체라고 고려하며 합리적인 의사결정이란 자신의 의사 결정에 따른 상대방의 효용을 예측하여 자신의 효용을 높이기 위한 결정을 의미한다. 차선 변경 시나리오에 맞춰 설계된 게임을 수행하기 위하여 차선 변경 시 고려되는 가치들을 기반으로 효용 함수를 정의한다. 또한 상대 운전자의 운전 성향에 따른 불확실성에 강건한 의사 결정을 위하여 관측된 상대 차량의 의도로부터 상대 차량의 효용 가치를 추정한다.
3.1 효용 함수 정의
차선 변경 시나리오에 관여하는 합리적인 운전자들은 주행 목표 달성과 안전 확보 두 종류의 가치를 고려하며 의사 결정을 하게 된다. 주행 성능 목표 달성 가치는 운전자가 원하는 대로 주행하고자 하는 욕구를 의미하며, 원하는 속도로 주행하려는 종 방향에 대한 목표와 타 차선으로 변경하고 싶은 횡 방향에 대한 목표로 구성된다. 안전 확보 가치는 안전감을 확보하려는 욕구를 의미하며, 충돌 회피와 앞 차량과의 안전 거리 확보로 구성된다. 효용 함수 U는 이러한 가치들을 고려하여 패널티 개념으로 정의된다.
| (4) |
- where,
이 때 Uv, Ulc, Uc, Uh는 각각 종방향에 대한 주행 욕구, 횡방향에 대한 주행 욕구, 충돌에 대한 안전 확보, 앞 차량과의 거리에 대한 안전 확보에 대해 정의된 효용 함수다.
종방향에 대한 주행 욕구를 나타내는 효용 Uv는 운전자 행동에 의한 속도 v가 원하는 종 방향 속도 vdes를 추종하도록 정의되었다. 횡방향에 대한 주행 욕구를 나타내는 효용 Ulc는 차선 변경 시 차선 변경을 하지 않는 LK 상태 이거나 차선 변경이 끝났음에도 불구하고 차선 변경을 하는 LC 상태인 경우, 즉 차선 변경 의도와 차량 상태가 어긋난 경우에 대하여 패널티를 부과하도록 정의되었다. 충돌에 대한 안전 확보 효용 Uc는 충돌 c의 발생 여부에 따라 정의되었다. 앞 차량과의 안전 거리 확보에 대한 효용 Uh는 특정 거리 hth 앞에 있는 차량이 인식될 경우 현재 앞차와의 거리 h가 원하는 안전 거리 hdes를 추종하도록 정의되었다.
wv, wlc, wc, wh는 각 효용 함수에 대한 가중치로 운전자 개개인의 성향 및 주행 상황에 따라 결정된다. 예를 들어, 충돌 위험에 대한 두려움보다 속도를 유지하려는 욕구가 큰 공격적인 성향을 가진 운전자의 경우 wc 대비 wv가 크게 설정되도록 설계한다. 또한 차선을 변경하지 않으려는 차량, 즉 설계된 시나리오에서의 팔로워의 경우 차선을 변경하려는 의도가 없기 때문에 wlc는 0으로 설계된다.
3.2 상대 차량 효용 함수 추정
이상적인 상호작용을 위해서는 자 차량의 의사 결정에 따른 상대 차량의 효용을 정확하게 알아야한다. 본 연구에서 설계된 효용은 운전자의 주행 목표 달성 욕구와 안전 확보 욕구와 같이 일반적인 운전자의 보편적인 가치로 구성되었으므로 각 차량의 효용은 주행 목표 욕구와 안전 확보 욕구에 대한 운전자 성향, 즉, wv, wlc, wc, wh에 의해 결정된다. 그러므로 상대 차량의 효용을 정확하게 알아야 한다는 것은 상대 운전자의 wv, wlc, wc, wh를 파악해야 한다는 것을 의미한다.
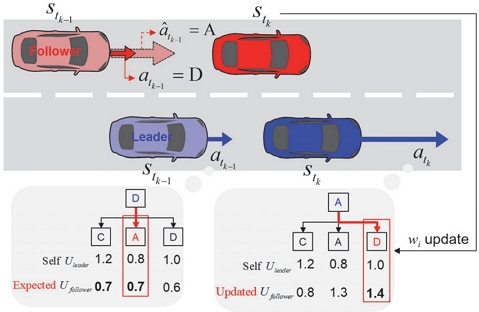
하지만 운전자 성향은 운전자의 내적인 것이므로 관측이 불가능하다. 관측 가능한 정보는 자 차량의 의사 결정에 따른 상대 차량의 실제 거동, 즉, atk-1에 따른 Stk 다. 일반적으로 게임 참가자는 상대 게임 참가자가 동일한 효용 가치, 즉 동일한 운전 성향을 갖는다고 가정하고 상대의 효용 가치(Expected U)를 계산하여 그에 맞게 본인의 행동 atk을 결정한다. 교통 환경에서 상대 운전자의 운전 성향에 대한 단순한 가정에 따른 의사 결정은 예기치 못한 사고 및 교통 흐름 방해 등을 불러일으킬 수 있다. 따라서 상대 차량의 운전 성향이 내포된 상대 차량의 실제 거동으로부터 상대 차량의 효용 함수를 조정할 필요가 있다.
Fig. 2는 측정된 상대 차량의 거동을 기반으로 효용 함수를 조정하여 자 차량의 행동을 결정하는 개념을 보여준다. 차선을 변경하는 차량인 리더는 자신의 성향에 따라 계산된 본인의 효용 Self Uleader과 기대하는 팔로워의 효용 Expected Ufollower을 기반으로, 팔로워가 라고 행동할 것이라는 가정하에 본인의 거동 atk-1을 결정한다. 하지만 팔로워의 실제 거동 atk-1이 리더가 예측한 거동과 다르게 나타날 경우, 리더는 관측된 팔로워의 atk-1에 따른 stk를 바탕으로 다음과 같이 팔로워의 운전 성향, 즉 효용 함수의 가중치를 갱신하여 Updated Ufollower를 기반으로 atk를 결정한다. 효용 함수의 가중치 갱신은 다음과 같이 보편적인 운전자 성향에 대한 가정을 기반으로 설계되었다.
- ⟶ 공격적인 주행 성향을 가진 운전자는 안전 확보에 대한 효용 대비 주행 목표 달성 욕구에 대한 효용이 높다.
- ⟶ 보수적인 주행 성향을 가진 운전자는 안전 확보에 대한 효용 대비 주행 목표 달성 욕구에 대한 효용이 낮다.
- ⟶ 상대 차량이 자 차량 운전자의 예상보다 빠르게 가속하는 경우 상대 운전자는 공격적인 주행 성향을 가졌을 확률이 높다.
- ⟶ 상대 차량이 자 차량 운전자의 예상 대비 감속하는 경우 상대 운전자는 보수적인 주행 성향을 가졌을 확률이 높다.
- ⟶ 상대 차량이 자 차량 운전자의 예상과 다르게 차선 변경을 하는 경우 상대 운전자는 공격적인 성향을 가졌을 확률이 높다.
- ⟶ 상대 차량이 자 차량 운전자의 예상과 다르게 차선 유지를 하는 경우 상대 운전자는 보수적인 성향을 가졌을 확률이 높다.
- ⟶ 종 방향의 속도를 유지하는 경우 상대 운전자의 운전 성향을 파악하는 것은 모호하다.
제시된 가정을 바탕으로 상대 차량의 실제 거동 atk-1과 자 차량 운전자가 예측한 거동 간의 확연한 차이가 나타날 경우, 상대 운전자의 성향을 나타내는 효용 함수의 가중치들은 다음과 같이 갱신된다.
| (5) |
여기서 dwi는 가중치를 갱신하는 값이며 정의된 Action space에 따른 운전자의 성향을 구분하는 기준은 Table 1에 제시되어 있다. 모호한 경우에는 운전자의 성향을 갱신하지 않는다. 갱신된 가중치 wi를 기반으로 수정된 효용 함수를 통해 리더는 tk 시간에서의 거동 를 최종 결정한다.
4. 검증 및 고찰
4.1 주행 시나리오
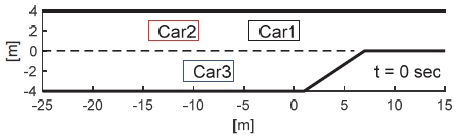
차선 변경에 대한 Stackelberg 게임은 Fig. 3과 같이 차선 변경에 대한 효용을 고려하기 좋도록 차선 병합 구간에서의 주행 시나리오에 대해 검증한다. 해당 시나리오에서 합류지점이 임박함에 따라 Car3는 반드시 차선을 변경해야 한다. 그러나 변경하려는 차선에 같은 방향으로 주행하고 있는 2대의 차량 Car1과 Car2의 간격이 좁아 Car2와 상호작용하지 않고는 차선 변경이 불가능하다. 이때 이미 Car3보다 앞서 주행 중인 Car1은 상호작용 대상이 되지 않는다. 따라서 Car3는 본인을 리더로 Car2를 팔로워로 고려하여 정의된 Action space와 효용 함수 기반의 Stackelberg 게임 전략을 통해 차선을 변경하는 전략을 수립하게 된다.
각 차량들의 초기 위치 조건 (x0, y0)은 Table 2에 제시되었으며 초기 속도 v0는 모두 동일하며 모든 차량은 다른 차량들의 행동을 관측 가능하다고 가정한다. 또한 Action space에 정의된 행동 후보지에 필요한 파라미터 a, b는 각각 1.5와 2로 설정하였다.
4.2 주행 전략 조건
설계된 게임 이론 기반 차선 변경 주행 전략은 Car3와 Car2가 충분히 상호작용이 일어나는 구간 내에서 Car3의 의사 결정 시 동작한다. 그 이외에는 Table 3에 제시된 파라미터 기반의 IDM 전략으로 차량들이 제어된다. 이때 두 차량이 서로를 인식할 수 있는 범위 xth는 7.5 m로 설정하였다.
상호작용 시 리더인 Car3의 주행 성향, 즉 효용 함수를 이루는 가중치는 [wv, wlc, wc, wh]leader = [1, 1, 5, 3]으로 설정되었다. 리더가 생각하는 팔로워 Car2의 주행성향은 [wv, wlc, wc, wh] follower = [5, 0, 0.5, 3]로 설정되었다. 이는 리더인 Car3 본인이 다소 보수적인 주행 성향을 가지며 리더가 생각하기에 상대 차량은 자신보다 공격적인 주행 성향을 가지고 있다고 여기는 것이다.
리더가 생각하는 팔로워 효용 함수 가중치는 리더가 예측한 팔로워의 거동 과 팔로워의 실제 거동 atk-1의 차이가 극명히 드러날 때 다음과 같이 갱신된다.
이때 리더는 팔로워가 종 방향 거동만 하며 최소 안전 거리에 대한 효용은 변하지 않는다고 가정한다. dwv와 dwc는 모두 0.05로 설정하였다. 효용 함수 계산 시 요구되는 원하는 종 방향 속도 vdes, Uh를 고려할 때 사용되는 특정 거리 hth, 원하는 안전 거리 hdes는 각각 2.5 m/s, 1 m, 1 m로 설정하였으며, 이는 리더 본인의 효용 함수 및 리더가 생각하는 팔로워의 효용 함수에 동일하게 적용된다.
상호작용 시 팔로워인 Car2는 운전자 성향에 따라 0.3 m/s2으로 가속하거나 -0.3 m/s2으로 감속하도록 설계되었다. Car3의 게임 이론 기반 의사 결정에 대해 상대 차량 효용 추정에 대한 효과를 명확하게 살피기 위해, Car3가 상대 차량을 공격적인 주행 성향을 가진다고 생각하였으므로, 상호작용 시 Car2는 보수적으로 -0.3 m/s2으로 감속하도록 설정하였다. 리더인 Car3가 이미 Car2의 주행 차선으로 넘어온 경우 Car2의 주행 전략은 IDM으로 변경된다.
4.3 검증 결과
Fig. 4, Fig. 5는 리더의 팔로워에 대한 효용 함수 추정 알고리즘 적용 여부에 따른 차선 변경 결과 그래프를 제시한다. 이때 시뮬레이션의 샘플링 시간 dt는 상호작용이 전개됨에 따라 리더가 충분히 팔로워의 효용 함수 수렴성을 확보할 수 있도록 0.01초로 설정되었다.
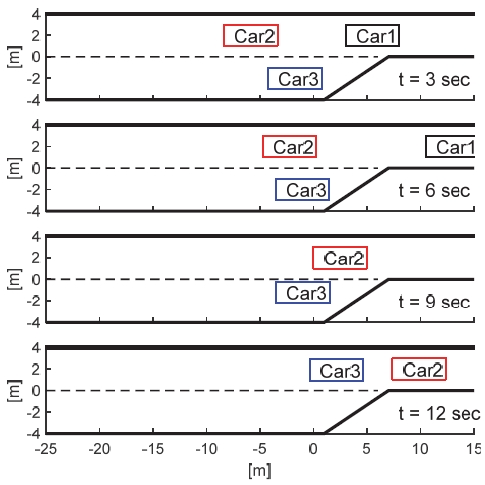
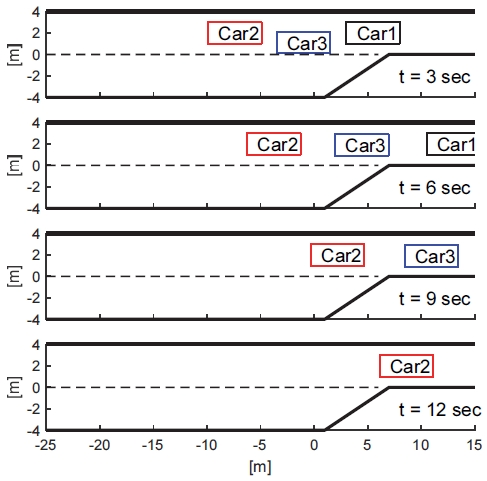
Fig. 4에서 보이는 것처럼 제안하는 알고리즘이 적용되지 않은 경우 Car3는 공격적인 운전 성향을 가진 Car2가 자신의 차선 변경 행동에 대해 비양보적으로 가속할 것이라고 예측하여 충돌을 회피하기 위해 대기하다가 Car2의 뒤로 진입하는 결과를 보였다. 그 결과 Car3는 어떠한 충돌 없이 차선 변경을 완수하였다. 하지만 Car3의 예상과 달리 Car2가 감속하였기에 전체적인 차선 변경 시간이 10.9초가 소모되었다.
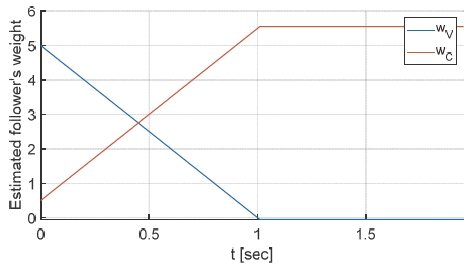
반면 Fig. 5와 같이 제안하는 알고리즘을 적용한 경우 Car2가 Car3의 예상과 달리 감속하며 양보하는 행위 관측을 통해 Car3는 실시간으로 Car2의 운전 성향을 갱신한다. Fig. 6은 Car2 실제 거동에 따라 Car3가 갱신한 Car2의 운전 성향 가중치를 보여준다. 처음에 Car3는 Car2가 [wv, wc] = [5, 0.5]를 가진다고 효용을 계산하였지만 거동관측을 통해 실시간으로 가중치를 갱신한다. Car2의 예측 거동과 실제 거동이 일치되는 1초 이후에는 운전자의 성향을 제대로 파악하였다고 가정하고 더 이상 가중치는 갱신되지 않고 최종 [wv, wc] = [-0.05, 5.55]로 수렴된다. 실시간 갱신된 가중치 기반으로 효용을 계산하여 차선 변경 판단 결과 장기간 대기하지 않고도 3.4초 내에 안전하게 차선 변경을 완수하였다. 즉, 제안하는 알고리즘은 상대 운전자의 운전 성향을 실시간으로 조정함으로써 훨씬 효율적으로 차선 변경 전략을 제시 가능하게 한다.
4.4 고찰
현재 차선 변경을 포함한 자율주행차량용 기술들은 인간 운전자가 공격적인 성향을 가진다고 가정하여 보수적으로 설계되고 있다. 그러나 실제 인간 운전자가 예상과 다르게 보수적인 거동을 구현하더라도 그에 대한 대책이 없어 시스템 전체적으로 보면 교통 흐름을 저해할 수 있다. 제안하는 알고리즘은 실제 운전자의 행동이 예측한 운전 성향과 다른 경우 상대 운전자의 운전 성향을 조정하여 자율주행차량이 안전을 유지하면서도 빠르게 차선 변경을 완료할 수 있도록 도와준다.
제안한 알고리즘은 다른 시나리오에 대해서도 기존 알고리즘보다 운전자 성향을 반영한 효율적인 차선 변경 전략을 제공한다. Fig. 7은 리더인 Car3의 효용 함수를 이루는 가중치가 [wv, wlc, wc, wh]leader = [5, 1, 3, 1]일 때, 즉 리더가 공격적인 주행 성향을 가지고 있을 때 [wv, wlc, wc, wh] follower = [5, 0, 3, 1]의 공격적일 것이라고 여겨진 팔로워 Car2가 리더의 예상과 달리 감속한 경우에 대하여 효용 함수 추정 알고리즘 유무에 따른 차선 변경 결과를 보여준다. 그 외 모든 조건은 위와 동일하다. 제안한 알고리즘이 적용된 결과의 경우에 대해서는 실선으로, 적용되지 않은 결과의 경우에 대해서는 점선으로 표시하였다.
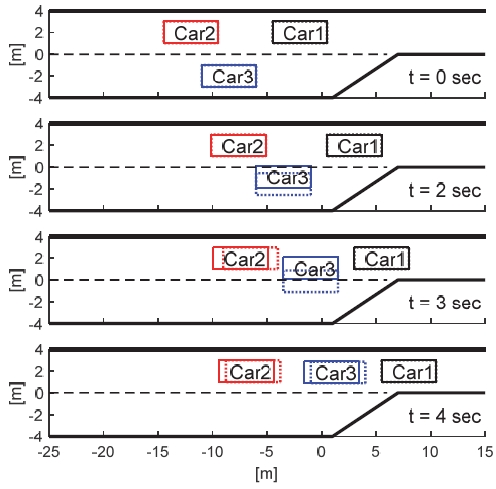
Simulation results for a scenario in which a follower predicted to be aggressive adopts conservative driving behavior
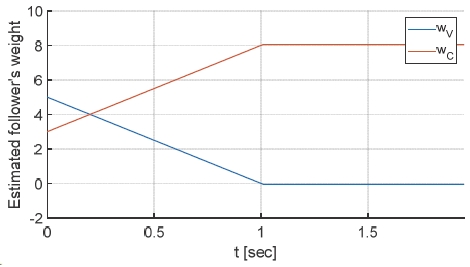
두 경우 모두 처음 t = 1.5초 정도 까지는 차량들이 동일하게 거동하며, Car3의 경우 차선 병합 지점이 점점 다가옴에 따라 차선 변경을 시작하려고 한다. 추정 알고리즘을 적용한 경우 Car3는 Car2가 자신과 비슷하게 공격적인 운전 성향을 가지고 있다고 판단하였다. 하지만 상대방의 보수적인 거동을 관측하여 Fig. 8과 같이 Car2에 대한 운전 성향 가중치를 갱신하면서 더 적극적으로 차선 변경을 시도한다. 그 결과 추정 알고리즘을 적용하지 않은 경우 Car3의 차선 변경이 4.01초에 완료된 반면 추정 알고리즘을 적용한 경우 3.4초에 차선 변경이 완료되었다. 그러나 t = 4초일 때 제안된 알고리즘을 적용하였을 때의 결과가 그렇지 않았을 때의 결과보다 종 방향 진행 위치가 더 느리게 나타난다. 이는 차선 변경 완료에 따른 IDM 주행 전략으로의 변경 시점이 다르기 때문이다. 제안된 알고리즘의 경우 Car3는 이미 차선 변경을 완료하였기 때문에 IDM 주행 전략을 기반으로 Car1과 적절한 거리를 유지한 채 주행하고 있다. 반면 제안된 알고리즘이 적용되지 않은 경우 t = 4.01초일 때 차선 변경이 완료되었으므로 IDM 주행 전략으로의 변경이 늦어져 Car1과의 거리 유지 명령이 늦게 전달된다. 그 결과 Car3는 앞 차량과의 안전 거리를 확보하기 위해 제안된 알고리즘이 적용된 경우보다 훨씬 큰 감속도로 급 감속을 수행하며, 그 여파가 Car2에까지 영향을 미치는 것을 확인할 수 있다. 따라서 상호작용이 발생하는 동안에는 제안된 운전자 성향 추정 알고리즘이 더 시간 효율적인 주행 전략을 제공한다는 것을 알 수 있다.
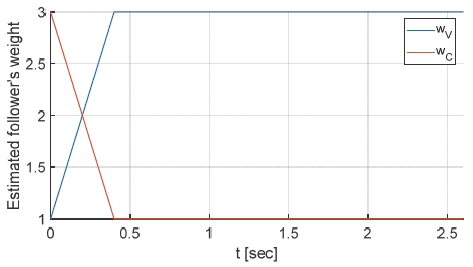
Fig. 9는 리더인 Car3의 효용 함수를 이루는 가중치가 [wv, wlc, wc, wh]leader = [5, 1, 2, 1]일 때, 즉 리더가 공격적인 주행 성향을 가지고 있을 때 [wv, wlc, wc, wh] follower = [1, 0, 3, 1]의 보수적인 성향이라고 여겨진 팔로워 Car2가 (x0, y0) = (-12.8, 2) m인 위치에서 리더의 예상과 달리 가속한 경우에 대하여 효용 함수 추정 알고리즘 유무에 따른 차선 변경 결과를 보여준다. 그 외의 모든 조건 역시 위와 동일하다. Car3 본인이 공격적인 주행 성향을 가지고 있는데 상대적T으로 멀리 떨어진 Car2가 보수적일 것으로 추측하여 제안하는 추정 알고리즘이 없는 경우 Car3는 바로 차선 변경을 시도한다. Car3가 Car2의 차선으로 진입 후, IDM 전략으로 주행 전략을 전환한 Car2는 Car3와의 간격 유지를 위한 급격한 감속을 수행하면서 Car3의 차선 변경을 허용함에 따라 Car3는 1.95초 내에 차선 변경을 완료하였다. 하지만 Car2의 운전 성향 예측 실패에 따른 Car3의 행동 결정은 t = 1초에서의 차량 궤적에서 볼 수 있듯이 충돌 위험성이 상당히 높다. 반면 추정 알고리즘이 적용된 경우 Fig. 10에서 볼 수 있듯이 Car2가 실제로는 공격적인 주행성향을 가졌음을 0.4초 내에 확신하고 t = 1초에서 Car2의 주행에 대해 좀 더 신중하게 거동함을 확인할 수 있었다. 그 결과 4.06초 내에 차선 변경을 완료하였다. 즉, 제안된 알고리즘 적용 결과 Car3는 Car2의 공격적인 운전 성향을 반영하여 본인이 공격적인 주행 성향을 가지고 있더라도 전체적인 충돌 효용을 고려하여 차선 변경에 대한 욕구를 양보하는 경향을 보였다.
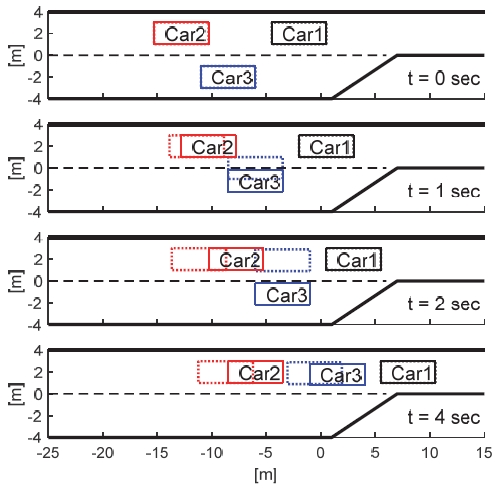
Simulation results for a scenario in which a follower predicted to be conservative adopts aggressive driving behavior
여러 시나리오에 대한 검증을 통해 제안하는 알고리즘은 단순히 리더 본연의 운전 욕구 충족을 위해 시간면에서만 효율적인 차선 변경 전략을 제공하는 것이 아니라 상대 운전자의 운전 성향에 맞춰 시스템 전체에서의 안전과 리더 운전자 개인의 운전 성향에 맞는 차선 변경 전략을 제공한다는 것을 알 수 있다. 즉, 자율주행차량이 상대 차량에 대해 무조건 보수적인 거동만 하는 것이 아닌 시스템 전체의 효율적인 면을 고려하여 주행을 하는 전략을 가질 수 있도록 설계 가능하다.
5. 결 론
본 연구는 관측된 상대 차량의 실제 거동으로부터 추정된 효용 함수를 활용한 Stackelberg 게임 기반의 차선 변경 알고리즘을 제안한다. 상호작용이 반영된 의사 결정 모델 개발 시 가장 널리 사용되는 게임 이론은 리더가 상대방의 효용을 정확히 파악해야 한다는 가정을 기반으로 하여, 실제 교통 환경으로의 적용에 어려움이 존재했다. 제안하는 방법론의 핵심은 효용을 주행 목표 달성과 안전 확보와 같은 운전 시 필요한 보편적인 가치 기반 함수로 정의하는 것이다. 어떤 보편적인 가치를 더 중요하게 여기는지에 대한 운전자의 성향은 각 가치들의 가중치로 여겨질 수 있다. 그리고 상대 차량의 예상 운전 성향과 관측된 상대 차량의 실제 거동을 비교하여 상대 운전자의 가중치들을 재조정함으로써 본인 전략에 맞는 효용을 실시간으로 갱신한다. 최종적으로 제안하는 알고리즘은 리더에 해당하는 차선 변경 차량에 대하여 실제 상대 차량의 거동과 전체 교통 흐름, 그리고 자신의 주행 성향에 최적인 주행 전략을 제시한다. 다양한 시나리오에서 제안하는 알고리즘을 적용한 결과 훨씬 시간 효율적이면서 안전한 전략을 제시한다는 것을 확인하였다.
본 연구는 운전자 성향에 대한 가중치 갱신에 따른 효과를 파악하였다. 만약 리더 입장에서의 팔로워 차량의 초기 운전자 성향 결정 및 갱신되는 운전자 성향 가중치가 신뢰성 있게 설계된다면 제안된 알고리즘의 적용 가능성을 높일 수 있다. 또한 리더의 차선 변경에 대해 팔로워의 행동 후보지에 횡방향 속도를 추가한다면 더 다양한 차선 변경 전략을 구사할 수 있다. 추가 연구를 통해 다양한 시나리오에 대해 상대 차량의 운전자 성향을 반영한 차선 변경 전략 알고리즘을 완성한다면 기존의 안전 중심 자율주행 기술을 넘어 상대 차량의 행동을 고려하여 안전과 주행 목표 성능을 동시에 극대화하는 상호작용 기반 의사 결정 모델로 활용될 수 있을 것으로 기대된다.
Acknowledgments
이 논문은 2020년도 국방기술품질원의 재원으로 방산혁신클러스터의 지원을 받아 수행된 연구 일부임(DCL2020L, 2020년 방산혁신클러스터 방산 소재 부품 연구실 사업).
References
-
N. Chater, J. Misyak, D. Watson, N. Griffiths and A. Mouzakitis, “Negotiating the Traffic: Can Cognitive Science Help Make Autonomous Vehicles a Reality?,” Trends in Cognitive Sciences, Vol.22, No.2, pp.93-95, 2018.
[https://doi.org/10.1016/j.tics.2017.11.008]

-
T. Y. Oh, W. I. Son, T. W. Ahn, Y. K. Lee and K. H. Park, “Development of Automated Lane Change Algorithm Considering Safety of Surrounding Vehicles,” Transactions of KSAE, Vol.29, No.5, pp.391-405, 2021.
[https://doi.org/10.7467/KSAE.2021.29.5.391]

-
K. S. Oh and S. C. Oh, “Model Predictive Steering Control Algorithm for Lane Change of Autonomous Vehicles Using Control Input Based Predicted Longitudinal Velocity,” Transactions of KSAE, Vol.29, No.7, pp.655-666, 2021.
[https://doi.org/10.7467/KSAE.2021.29.7.655]

-
E. R. Teoh and D. G. Kidd, “Rage Against the Machine? Google’s Self-Driving Cars Versus Human Drivers,” Journal of Safety Research, Vol.63, pp.57-60, 2017.
[https://doi.org/10.1016/j.jsr.2017.08.008]

-
N. Evestedt, E. Ward, J. Folkesson and D. Axehill, “Interaction Aware Trajectory Planning for Merge Scenarios in Congested Traffic Situations,” 2016 IEEE 19th International Conference on Intelligent Transportation Systems(ITSC), pp.465-472, 2016.
[https://doi.org/10.1109/ITSC.2016.7795596]

- K. J. Chang and S. M. Yoo, “A Study on Autonomous Vehicle Lane Change Method Using Cooperative Maneuver,” The Journal of the Korea Contents Association, Vol.21, No.1, pp.139-146, 2021.
-
S. Gupta, M. Vasardani and S. Winter, “Negotiation Between Vehicles and Pedestrians for the Right of Way at Intersections,” IEEE Transactions on Intelligent Transportation Systems, Vol.20, No.3, pp.888-899, 2018.
[https://doi.org/10.1109/TITS.2018.2836957]

-
H. Zhang, Y. Su, L. Peng and D. Yao, “A Review of Game Theory Applications in Transportation Analysis,” 2010 International Conference on Computer and Information Application, pp.152-157, 2010.
[https://doi.org/10.1109/ICCIA.2010.6141559]

-
A. Ji and D. Levinson, “A Review of Game Theory Models of Lane Changing,” Transportmetrica A: Transport Science, Vol.16, No.3, pp.1628-1647, 2020.
[https://doi.org/10.1080/23249935.2020.1770368]

- K. T. Ji and K. S. Han, “Development of a Lane Merging Strategy for the Self-driving Car using Stackelberg Game Theory,” KSAE Fall Conference Proceedings, pp.506-512, 2020.
- J. H. Yoo and R. Langari, “A Stackelberg Game Theoretic Driver Model for Merging,” ASME 2013 Dynamic Systems and Control Conference, 2013.
-
H. Yu, H. E. Tseng and R. Langari, “A Human-Like Game Theory-Based Controller for Automatic Lane Changing,” Transportation Research Part C: Emerging Technologies, Vol.88, pp.140-158, 2018.
[https://doi.org/10.1016/j.trc.2018.01.016]

-
A. Talebpour, H. S. Mahmassani and S. H. Hamdar, “Modeling Lane-Changing Behavior in a Connected Environment: A Game Theory Approach,” Transportation Research Procedia, Vol.7, pp.420-440, 2015.
[https://doi.org/10.1016/j.trpro.2015.06.022]

- R. Gibbons, A Primer in Game Theory, Prentice Hall, Hoboken, New Jersey, 1992.
-
T. Başar and G. J. Olsder, Dynamic Noncooperative Game Theory, SIAM, Philadelphia, 1998.
[https://doi.org/10.1137/1.9781611971132]

-
A. M. Colman, “Cooperation, Psychological Game Theory, and Limitations of Rationality in Social Interaction,” Behavioral and Brain Sciences, Vol.26, No.2, pp.39-153, 2003.
[https://doi.org/10.1017/S0140525X03000050]

-
K. T. Ji, M. Orsag and K. S. Han, “Lane-merging Strategy for a Self-driving Car in Dense Traffic Using the Stackelberg Game Approach,” Electronics, Vol.10, No.8, Paper No.894, 2021.
[https://doi.org/10.3390/electronics10080894]

-
M. Treiber, A. Hennecke and D. Helbing, “Congested Traffic States in Empirical Observations and Microscopic Simulations,” Physical Review E, Vol.62, No.2, Paper No.1805, 2000.
[https://doi.org/10.1103/PhysRevE.62.1805]