노면 경사에 강건한 차량 질량 추정 방법에 대한 연구

1. 서 론

차량의 질량은 차량 운동 성능을 결정하는 중요한 인자로 차량 안정성 제어와 추정에 가장 많이 활용되는 파라미터 중 하나이다.^1-3) 하지만 차량 질량은 탑승객의 인원수나 탑재된 짐의 무게에 따라 수시로 변하는 값으로 직접 계측할 수 없어 이를 추정하기 위해 많은 연구들이 수행되어왔다. 타이어의 압력 센서나 GPS와 같이 차량 내 센서가 아닌 추가적인 센서를 이용하여 차량의 질량을 추정하는 연구들이^4,5) 있는 반면 차량 내 센서를 이용해 차량 종 방향 동역학에 기반한 질량 추정 연구들도 많이 수행되어 왔다.^6-10) 차량 종 방향 동역학에 기반한 추정은 노면 종 경사각에 대한 정보가 매우 중요하기 때문에 대부분의 연구들이 질량과 노면 종 경사각을 같이 추정하는 방법들이 제안되고 있다. 망각인자 회기 최소 자승법을 이용한 질량 추정 방식이나,⁶⁾ 칼만 필터를 이용한 질량 추정 방식을⁸⁾ 대표적으로 들 수 있다.

본 연구에서는 차량 질량을 실시간으로 추정하기 위한 연구를 수행하였다. 기존 연구들과 유사하게 차량의 종 방향 동역학을 기반으로 계측 가능한 신호를 이용하여 질량 추정 로직을 개발하였다. 기존 연구는 차량 질량을 추정하기 위해 노면의 종 경사각을 같이 추정하였지만 제안하는 추정 방식은 노면 종 경사에 대한 정보 없이 추정할 수 있는 방안을 제안했다는 것이 가장 큰 특징이라 할 수 있다. 차량에서 계측 가능한 종 가속도 신호는 관성 센서를 통해 계측된다. 그렇기 때문에 종 가속도 신호에는 가속도, 원심력, 그리고 차량 종 경사(피치각)에 의한 중력 성분을 모두 포함하고 있다. 이러한 가속도 센서의 특성을 이용하여 노면 종 경사에 관계없이 질량 추정이 가능한 종 방향 동역학 기반의 질량 추정 알고리즘을 제안하고 있다.

본 논문의 구성은 다음과 같다. 2장에서는 질량 추정 컨셉을 기술하여 노면 종 경사에 관계없이 질량 추정이 가능한 이유에 대해 설명하고, 3장에서 추정 알고리즘에 대해 상세히 설명한다. 4장에서는 설계된 추정 알고리즘의 시뮬레이션 검증을 다루며 5장에서는 결론을 맺는 것으로 구성되어 있다.

2. 질량 추정 컨셉

서론에서 언급한 바와 같이 본 연구에서 제안한 질량 추정 알고리즘은 노면 경사에 강건한 추정 성능을 확보하기 위해 차량 종 방향 동역학에 기반하여 개발하였다. 아래 식 (1)은 평면 운동에 대한 차량 종 방향 동역학 수식을 나타내고 있다.

여기에서 ΣF_x는 차량이 입력 받는 총 종 방향 힘으로 아래 식 (2)와 같이 나타낼 수 있다.

여기에서 F_x.i (i = FL, FR, RL, RR)는 제/구동 토크로 인해 발생되는 각 휠의 종 방향 타이어 힘을, F_air는 속도에 의한 공기 저항력을, 그리고, F_slope는 노면 경사에 의한 외력을 나타낸다.

식 (1)과 (2)로부터 종 가속도(a_x)와 총 종 방향 힘(Σ F_x)을 안다면 질량이 추정 가능함을 알 수 있다. 종 가속도의 경우 차량에서 계측되는 신호이지만 관성 센서를 사용하기 때문에 센서 계측 값은 아래와 같은 성분을 포함하고 있다.

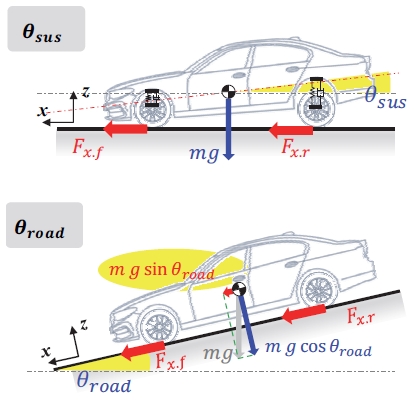
여기에서 θ_sus는 서스펜션 피치 각을 그리고 θ_road는 노면 경사에 의한 피치 각을 나타낸다. 이 두 요소 모두 차량의 피치 각을 의미하지만 물리적인 차이는 분명하다. Fig. 1은 서스펜션 피치 각과 노면 경사에 의한 피치 각의 차이를 나타내고 있다. 서스펜션 피치 각의 경우 차량의 종 방향 외력에 아무런 영향을 주지 않는 반면 노면 경사에 의한 피치 각은 mgsin(θ_road)만큼의 외력이 작용함을 알 수 있다. 또한 해당 외력은 식 (2)의 F_slope와 같다.

Fig. 1

Difference between suspension pitch angle and road slope pitch angle

식 (1)과 (2) 그리고 노면 경사와 노면 경사에 의한 외력 관계(F_slope = mgsin(θ_road))를 정리하면 아래와 같이 표현 할 수 있다.

식 (4)와 (2)를 통해 아래와 같은 수식을 도출 할 수 있다.

식 (5)를 통해 서스펜션 피치 각, 각 휠의 타이어 힘, 그리고 공기 저항력에 대한 정보를 알고 있으면 계측된 종 가속도 센서를 이용하여 노면 경사에 관계없이 차량의 질량을 추정할 수 있음을 알 수 있다.

3. 질량 추정 로직 설계

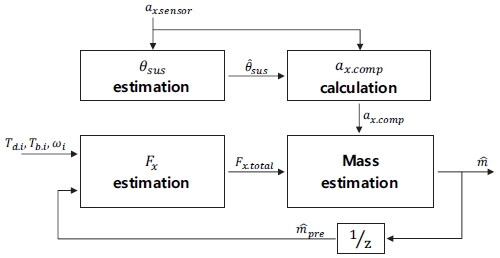
Fig. 2는 질량 추정 로직의 기능 아키텍처를 나타내고 있다. 질량 추정 로직은 크게 서스펜션 피치 각(θ_sus) 추정 모듈, 추정된 서스펜션 피치 각을 이용해 계측된 종 가속도 신호를 보정하는 보정 종 가속도(a_x.comp) 계산 모듈, 차량에 인가되는 총 종 방향 힘(F_x.total) 추정 모듈, 그리고 질량 추정 모듈 이렇게 4개의 주요 모듈로 구성되어 있다. 지금부터 각 모듈들에 대해 상세히 기술하도록 한다.

Fig. 2

Architecture of mass estimation logic

3.1 θ_sus Estimation

차량의 서스펜션 피치 각은 서스펜션 롤 각을 추정한 기존 연구를 응용하여 개발할 수 있다.¹¹⁾ 서스펜션 피치 각 추정을 위해 우선 스프링, 댐퍼, 그리고 피치 회전관성으로 이루어진 피치 2차 운동방정식을 구하고 이 2차 모델에서 상대적으로 영향도가 적은 상태 변수를 제거하고 중요한 모델의 특성만을 보존하는 방식인 Balanced truncation 방법론을 적용하면 아래 식 (6)과 같이 계측된 종 가속도에 대한 1차 시스템으로 서스펜션 피치 각을 추정할 수 있다.

$\[ {\hat{\theta }}_{sus}=\frac{K}{\tau s+1}{a}_{x.sensor} \]$

(6)

여기에서 K와 τ는 DC gain과 시정수를 각각 의미한다. 이 두 값은 모두 시험을 통해 튜닝하는 값으로 K는 계측 종 가속도에 의해 발생되는 서스펜션 피치 각의 크기를 조절하는데 사용되고 τ는 계측 종 가속도와 서스펜션 피치 각 사이의 위상을 조절하는데 사용된다. 이렇게 개발된 서스펜션 피치 각 추정 알고리즘을 검증하기 위해 시뮬레이션 해석을 Carsim, Matlab/Simulink를 이용하여 실시하였다. Table 1은 시뮬레이션 대상 차량의 제원을 나타내고 있다.

Table 1

Vehicle specification

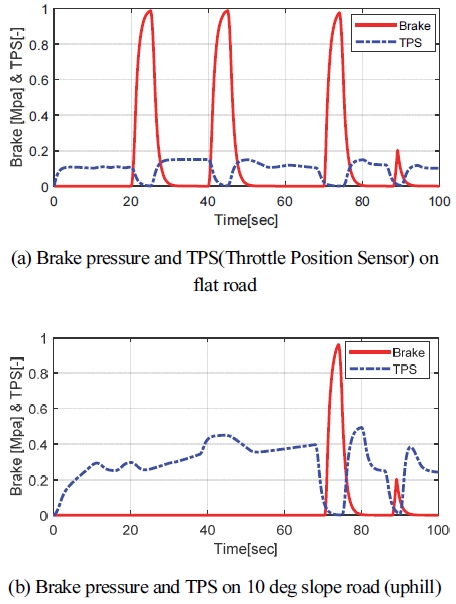
시뮬레이션 시나리오는 초기 속도 60 kph에서 임의의 직진 가/감속을 한 상황으로 차량에 인가된 제동 압력과 가속 페달은 아래 Fig. 3과 같다. Fig. 3(a)는 평지 도로에서 가/감속을 한 결과이고, (b)는 노면 경사가 10 deg 오르막 길인 상황에서 가/감속을 한 결과이다.

Fig. 3

Acceleration and deceleration inputs applied to the vehicle

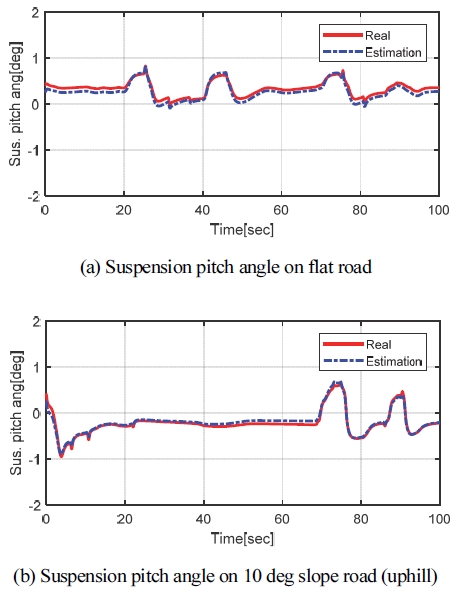
Fig. 4는 Fig. 3 시나리오에서의 서스펜션 피치 각 추정 결과로 빨간색 실선은 실제 서스펜션 피치 각을 그리고 파란색 점선은 추정된 서스펜션 피치 각을 나타낸다. 노면 경사에 관계없이 서스펜션 피치 각이 잘 추정됨을 보이고 있다.

Fig. 4

Simulation results for suspension pitch angle estimation

3.2 a_x.comp Calculation

해당 모듈은 보정된 종 가속도(a_x.comp) 값을 계산하는 모듈로 보정 종 가속도란 계측된 종 가속도 신호에 포함되어 있는 서스펜션 피치 각 성분을 제거한 가속도를 의미한다. 보정 종 가속도를 계산하는 이유는 2절 질량 추정 컨셉에 상세히 기술되어 있다. 보정 종 가속도는 식 (5)로부터 아래와 같이 간단히 구할 수 있다.

$\[ a_{x.comp}=a_{x.sensor}+gsin\left({\hat{\theta }}_{sus}\right) \]$

(7)

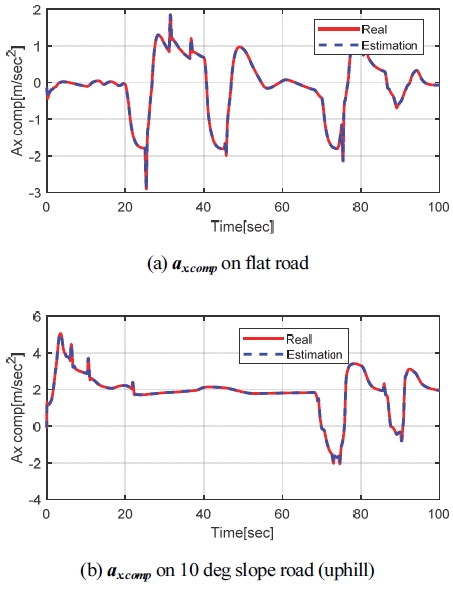
보정된 종 가속도에 대한 정합성 검증을 위해 시뮬레이션 해석을 실시하였다. Fig. 3과 동일한 시나리오로 앞 절에서 추정된 서스펜션 피치 각을 이용해 구한 보정된 종 가속도와 실제 서스펜션 피치 각을 이용해 구한 보전된 종 가속도를 비교하였다. Fig. 5는 시뮬레이션 결과를 나타내고 있다. 보는 바와 같이 추정된 보정 종 가속도(파란색 실선)와 실제 보정 종 가속도(빨간색 실선)가 거의 동일함을 확인할 수 있다.

Fig. 5

Simulation results for ax.comp

3.3 F_x Estimation

본 절에서는 노면 경사로 인해 받는 외력인 F_slope를 제외하고 차량이 받는 모든 종 방향 외력들의 합(F_x.total)을 추정하는 모듈이다. 노면 경사에 의한 외력을 제외하면 차량이 받는 외력은 제/구동에 의한 각 휠의 타이어 힘(F_x.i)과 공기 저항력(F_air)이 있다.

$\[ F_{x.total}={\sum }_{i=FL..RR}{F}_{x.i}-F_{air} \]$

(8)

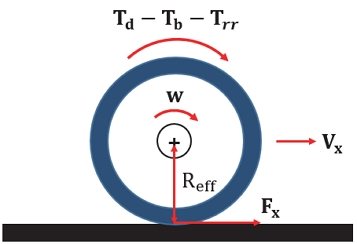
F_x.total를 추정하기 위해선 각 휠의 타이어 힘과 공기 저항력을 각각 추정해야한다. 우선 각 휠의 타이어 힘은 구동 토크(T_d)와 제동 토크(T_b)를 알고 있다는 가정하에 휠 동역학 모델을 이용해 구할 수 있다. Fig. 6은 휠 동역학 모델을 나타내고 있다.¹²⁾

Fig. 6

Simplified wheel dynamics model

Fig. 6을 통해 아래와 같이 휠 동역학 모델을 구할 수 있다.

$\[ I_{\omega ,i}\cdot {\dot{\omega }}_i=T_{d,i}-T_{b,i}-T_{rr,i}-R_{eff}\cdot F_{x,i} \]$

(9)

여기에서 i = FL, FR, RL, RR을 의미하고, $$ I_{\omega ,i},{\dot{\omega }}_i$$, 그리고 R_eff 각각 휠의 회전 관성모멘트, 휠의 각가속도, 휠의 유효반지름을 의미한다. T_d, T_b, T_rr, F_x은 각각 구동 토크, 제동 토크, 구름 저항 모멘트, 종 방향 타이어 힘을 나타내고 있다. 식 (9)를 통해 종 방향 타이어 힘 F_x,i를 아래와 같이 추정할 수 있다.

$\[ F_{x,i}=\frac{T_{d,i}-T_{b,i}-T_{rr,i}-I_{\omega }\cdot {\dot{\omega }}_l}{R_{eff}} \]$

(10)

하지만 구름 저항 모멘트(T_rr)은 모르는 값이기 때문에 $$ \frac{T_{rr,i}}{R_{eff}}$$를 구름 저항력인 F_rr,i로 표현하여 정리하면 다음과 같다.

$\[ F_{x,i}=\frac{T_{d,i}-T_{b,i}-I_w\cdot {\dot{w}}_l}{R_{eff}}-F_{rr,i} \]$

(11)

식 (11)에서 알 수 있듯이 휠 동역학 모델을 통해 계산된 타이어 종 방향 힘은 구름 저항력이 포함된 힘을 계산하게 된다.

식 (12)는 공기 저항력 F_air 추정 근사식을 나타내고 있다.

$\[ F_{x,air}=\frac{1}{2}{C}_{d}A\rho V_x{}^2 \]$

(12)

여기에서 C_d, A, 그리고 ρ는 각각 차량 공기저항 계수, 차량 전면 부 면적, 공기 밀도로 아는 값으로 가정한다.

식 (11)과 식 (12)을 식 (9)에 대입하면 노면 경사에 의한 외력을 제외한 차량이 받는 전체 외력을 아래와 같이 추정 할 수 있다.

$\[ F_{x.total}=\begin{array}{l}{\sum }_{i=FL..RR}\frac{T_{d,i}-T_{b,i}-I_w\cdot {\dot{w}}_l}{R_{eff}}-{\sum }_{i=FL..RR}{F}_{rr,i}\\ -\frac{1}{2}{C}_{d}A\rho V_x{}^2\end{array} \]$

(13)

F_x.total를 구하기 위해선 구름 저항력을 알아야 한다. 본 논문에서는 구름 저항력은 아래와 같은 근사 식을 이용해 구하였다.

$\[ {\sum }_{i=FL..RR}{F}_{rr,i}={\mu }_{rr}\cdot {\hat{m}}_{pre}\cdot g \]$

(14)

여기에서 μ_rr은 구름 저항 계수를 그리고 $$ {\hat{m}}_{pre}$$은 차량의 질량인데 이는 직전 스텝에서 추정된 질량을 사용한다.

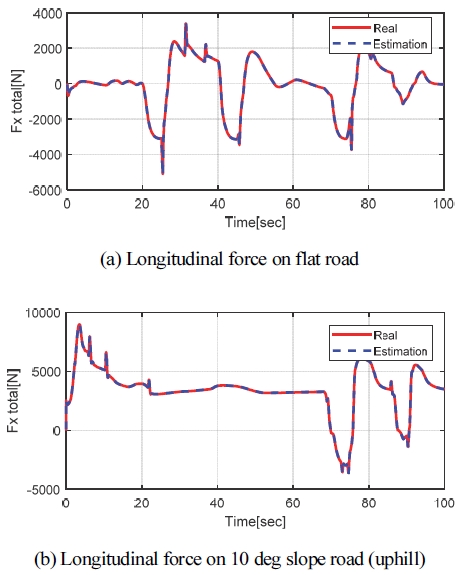
이렇게 개발된 종 방향 외력 추정 알고리즘을 검증하기 위해 Fig. 3과 동일한 조건에서 검증을 수행하였다. Fig. 7은 검증 결과를 나타내고 있다. 보는 바와 같이 노면 경사에 강건히 종 방향 외력을 잘 추종함을 확인할 수 있다.

Fig. 7

Simulation results for longitudinal force estimation

3.4 Mass Estimation

차량 질량은 앞 절에서 추정한 보정 종 가속도($$ {\hat{a}}_{x.comp}$$)와 계산한 종 방향 외력(F_x.total) 그리고 식 (5)의 관계를 기반으로 Adaptation law를 적용하여 추정할 수 있다. 질량 추정을 위해 우선 아래와 같이 Lyapunov function과 그 Condition을 정의한다.

$\[ L=\frac{1}{2}{\left(m-\hat{m}\right)}^2 \]$

(15)

$\[ \dot{L}=-K{\left(F_{x.total}-{\widehat{F}}_{x.total}\right)}^2, K>0 \]$

(16)

여기에서 m은 실제 차량의 질량을, $$ \hat{m}$$은 추정 질량을, 그리고 F_x.total는 앞 절에서 계산한 종 방향 외력을 의미하고, $$ {\hat{F}}_{x.total}$$는 아래와 같이 구한다.

$\[ {\hat{F}}_{x.total}=\hat{m}\cdot a_{x.comp} \]$

(17)

식 (15)와 (16)을 통해 Lyapunov function의 Condition을 만족시키기 위한 추정 질량($$ \hat{m}$$)을 찾게 되면 추정 질량은 실제 질량을 추종함을 알 수 있다. 식 (15)를 시간에 대해 미분하면 아래와 같이 나타낼 수 있다.

$\[ \dot{L}=-\dot{\hat{m}}\cdot \left(m-\hat{m}\right) \]$

(18)

m의 경우 주행 중에는 무게가 변하지 않기 때문에 $$ \dot{m}$$은 0으로 가정한다. 식 (16), (17), 그리고 (18)을 정리하면 아래와 같이 표현할 수 있다.

$\[ \dot{\hat{m}}=K{a}_{x.comp}\left(F_{x.total}-\hat{m}{a}_{x.comp}\right) \]$

(19)

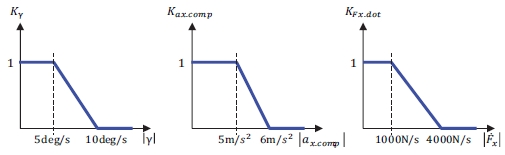
여기에서 K는 튜닝 변수로 추정 속도를 결정한다. 따라서 질량 추정이 잘되는 주행상황에서는 K를 크게 설정하여 질량 추정 업데이트가 잘 되도록 하고, 질량 추정이 잘 안되는 주행상황에서는 K를 작게 설정하여 기존에 업데이트한 질량을 유지하도록 한다. K는 아래와 같이 총 3개의 튜닝 Map의 곱으로 표현할 수 있다.

$\[ K=K_{\gamma }\cdot K_{ax.comp}\cdot K_{Fx.dot} \]$

(20)

K_γ, K_ax.comp, 그리고 K_Fx.dot는 Fig. 8과 같이 Map으로 설정하였다. K_γ는 차량이 선회하는 상황에서는 질량 추정 업데이트를 하지 않기 위한 튜닝 변수이다. 제안 추정 로직은 종 방향 동역학에 기반한 추정 방식으로 차량이 선회 시 발생하는 감속을 반영하지 않고 있다. 따라서 차량이 선회를 할 경우 식 (13)에서 계산한 종 방향 외력은 정확도가 떨어지게 되고 이는 질량 추정 오차를 발생 시키는 요인이 된다. K_ax.comp은 현재 종 가속도 크기에 따른 튜닝 변수로 가속도가 클 경우 추정 업데이트를 하지 않도록 한다. 큰 가속도는 휠의 과 슬립을 발생시킬 위험이 있다. 본 로직은 휠 슬립을 고려하지 않기 때문에 과 슬립이 발생하는 상황에서는 추정 정확도가 떨어지게 된다. 마지막으로 K_Fx.dot은 계산된 종 방향 외력의 변화율이 큰 경우 추정을 하지않게 하기 위한 튜닝 변수이다. 힘 변화율이 크다는 것은 급 가/감속 상황임을 의미하고 이는 식 (13)에서 계산한 종 방향 외력의 정확도가 떨어질 수 있다는 것을 의미한다. 그렇기 때문에 급 가/감속 상황에서는 추정 업데이트를 최소화해야 한다. 이렇게 튜닝 된 Map은 직진 상황이고 크지 않은 가/감속 상황을 판단하기 위한 Map으로 대상 차량이 바뀌어도 변경할 필요는 없다.

Fig. 8

Tuning gain K

4. 시뮬레이션 검증

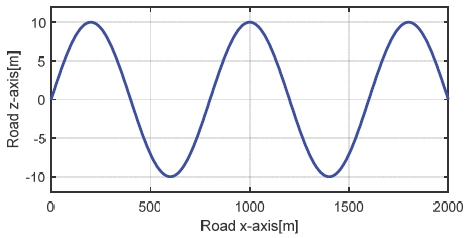
앞서 개발한 차량 질량 추정 로직 성능을 검증하기 위해 시뮬레이션 해석을 Carsim과 Matlab/Simulink를 이용하여 실시하였다. 아래 표와 같이 3가지 Case의 노면에 대해서 임의의 직진 가/감속 시뮬레이션을 수행하였다. Case 1은 평지 노면, Case 2는 10 deg 오르막인 경사 노면, 그리고 Case 3은 진폭이 10 m인 sin 파 형태의 노면이다. Fig. 9는 case 3의 도로 정보를 나타내고있다. 차량의 기본 하중은 1,500 kg으로 가정하였고 실제 하중은 이보다 330 kg 무거운 1,830 kg으로 설정하였다. 즉, 1,500 kg은 차량 제원으로부터 알 수 있는 하중이고 1,830 kg은 추정해야 할 실제 하중이다.

Table 2

Driving scenarios for estimating vehicle mass

Fig. 9

Road shape for case 3

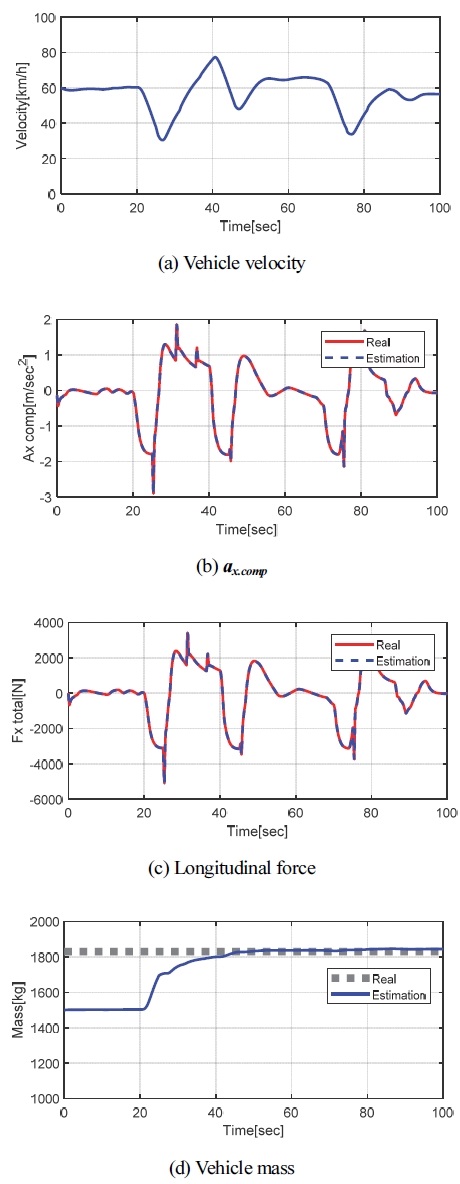
Fig. 10은 Case 1에 대한 시뮬레이션 결과를 나타내고있다. Fig. 10(a)는 차속을, (b)는 보정 종 가속도(a_x.comp)를, (c)는 종 방향 외력(F_x.total)을, 그리고 (d)는 질량 추정 결과를 각각 나타내고있다. 시뮬레이션 초반(0 ~ 20초)에 60 kph 정속 주행을 하고 그 이후에는 임의의 가/감속을 하였다. 보정 종 가속도나 종 방향 외력의 경우 앞 장의 결과와 동일하게 잘 추정됨을 보이고 있다. 질량 추정의 경우 정속 주행 중인 0초에서 20초 사이에는 질량 추정 업데이트가 이루어지지 않음을 보이고 있다. 이는 질량 추정 업데이트가 보정 종 방향 가속도 크기에 비례하기 때문으로 식 (18)을 통해 확인할 수 있다. 20초 이후에 차량에 가/감속이 발생하며 질량이 정상적으로 추정됨을 보이고 있다.

Fig. 10

Simulation results for case 1

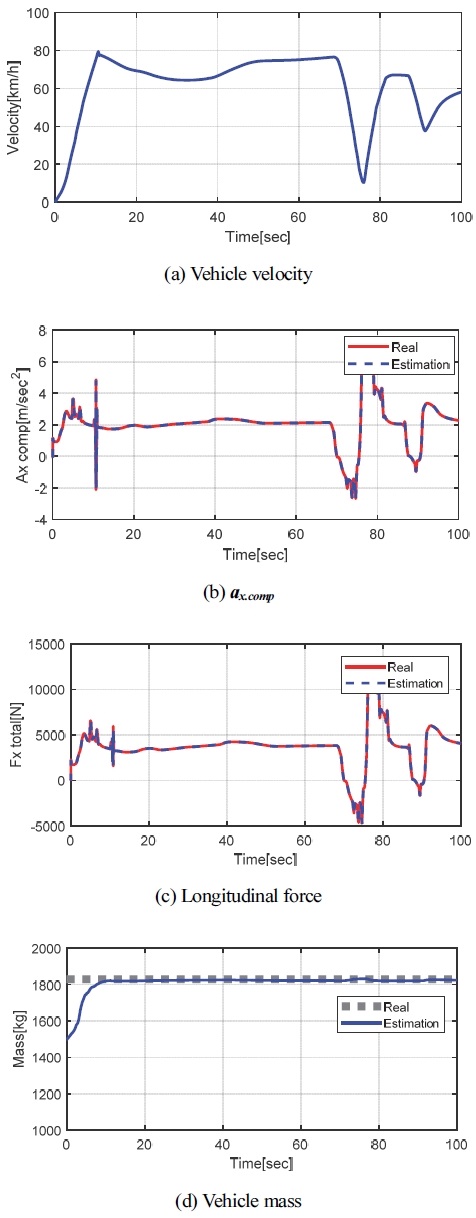
Fig. 11은 10 deg 오르막 노면인 Case 2에 대한 시뮬레이션 결과이다. 보정 종 가속도, 종 방향 외력, 그리고 질량 추정 모두 case 1의 결과인 Fig. 10과 동등 추정 성능을 보이고 있다. 그리고 해당 시나리오는 시뮬레이션 시작과 동시에 정지 상태에서 가속하는 상황으로 질량이 바로 추정됨을 보이고 있다.

Fig. 11

Simulation results for case 2

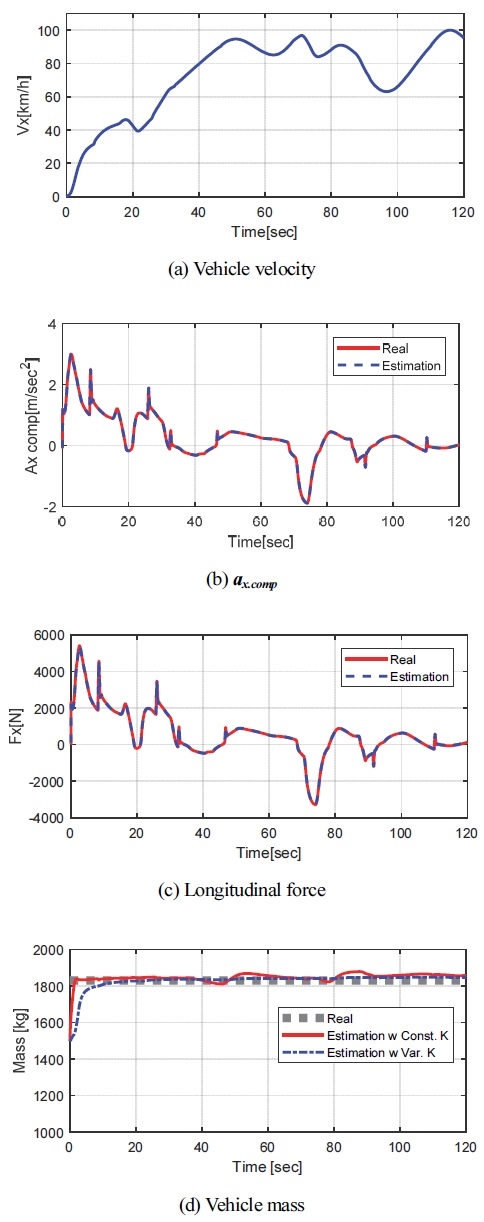
마지막으로 Fig. 12는 case 3에 대한 시뮬레이션 결과이다. 해당 시나리오는 주행 중 노면 경사가 임의로 변하여도 질량 추정에 문제가 없음을 보이기 위한 시나리오로 시뮬레이션 결과 임의로 변하는 노면 경사에도 질량이 강건하게 추정됨을 보이고 있다. 그리고 질량 추정 결과의 경우 두 가지 추정 결과를 나타내고 있는데 빨간색 실선의 경우 Adaptation law 적용 시 튜닝 변수 K를 고정 값을 사용한 결과이고 파란색 점선은 식 (19)에서 제안한 튜닝 변수를 사용한 결과이다. 고정 K를 사용한 경우 제안 방식보다 빠르게 추정되나 가/감속력이 변하는 구간에 추정 로직이 민감하게 반응하여 추정 오차를 보이고 있다.

Fig. 12

Simulation results for case 3

5. 결 론

본 논문에서는 차량 안정성 제어에 매우 중요한 정보 중 하나인 질량을 차량 종 방향 동역학에 기반하여 추정하는 연구를 수행하였다. 종 방향 가속도 센서에 서스펜션 피치 각 성분을 제거하면 직진 가/감속 상황에서는 노면 경사에 관계없이 질량 추정이 가능함을 2장에서 언급하였다. 이 원리를 이용하여 질량 추정 로직은 서스펜션 피치 각 추정, 종 가속도 보정, 종 방향 외력 추정, 그리고 질량 추정 이렇게 4개의 주요 모듈로 설계하였다. 질량 추정의 경우 Gradient 방법 기반의 Parameter adaptation 기법을 이용하였고 주행 상황 별 Adaptation gain을 차별화하여 질량을 추정하였다. 해당 로직은 선회 상황이나 타이어 종 방향 슬립을 고려하지 않기 때문에 선회 상황이나 과 슬립이 발생할 수 있는 큰 가/감속 상황에서는 Adaptation gain을 감소시켜 질량 추정 업데이트를 하지 않도록 하였다. 제안한 추정 로직은 Carsim 시뮬레이션을 통해 평지 노면 상황, 10 deg 오르막 노면 상황, 그리고 경사가 Sine wave로 매 순간 노면 경사가 바뀌는 상황에서 그 성능을 확인하였다. 향후에는 개발된 로직을 실차 환경에서 검증할 예정이다.

Acknowledgments

본 연구는 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2022R1A2C1004405, No.2021R1F1A1050200). 본 연구는 2023학년도 한국기술교육대학교 교육연구진흥과제 지원을 받아 수행된 연구임. 본 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(‘20024837’).

References

• S. Oh, M. Kim, B. Lee and K. Oh, “Integral Action Based Model Predictive Fault-Tolerant Control for Yaw Rate Tracking of 4-Wheel Independent Steering Vehicle with Multiple Constraints,” Transactions of the KSAE, Vol.29, No.6, pp.493-505, 2021. [https://doi.org/10.7467/KSAE.2021.29.6.493]
• J. Song, “Integrated Dynamics Control System for SUV with Front Brake Force and Front Steering Angle,” Journal of the Korean Society of Manufacturing Process Engineers, Vol.21, No.5, pp.22-27, 2022. [https://doi.org/10.14775/ksmpe.2022.21.05.022]
• S. Y. Lee, K. Nakano and S. K. Kim, “Real-Time Estimation of Yaw Moment of Inertia of a Traveling Heavy Duty Truck,” Transactions of the Korean Society of Mechanical Engineers A, Vol.41, No.3, pp.205-211, 2017.
• H. Fechtner, U. Spaeth, E. Patelkos and B. Schmuelling, “Optimization of Driver and Driving Assistance Systems of Electric Vehicles by a Static Vehicle Mass Estimation,” 6th Hybrid and Electric Vehicles Conference(HEVC 2016), London, UK, 2016. [https://doi.org/10.1049/cp.2016.0977]
• H. S. Bae, J. Ryu and C. Gerdes, “Road Grade and Vehicle Parameter Estimation for Longitudinal Control Using GPS,” Proceedings of the IEEE Conference on Intelligent Transportation Systems, pp.166-171, 2001.
• M. Kim, G. Choi and M. Hong, “Vehicle Mass Estimation Algorithm Using Recursive Least Squares Method with Forgetting and Lowpass Filter,” Transactions of KSAE, Vol.27, No.11, pp.833-838, 2019. [https://doi.org/10.7467/KSAE.2019.27.11.833]
• A. Jo, Y. Jeong, H. Lim and K. Yi, “Vehicle Mass and Road Grade Estimation for Longitudinal Acceleration Controller of an Automated Bus,” Journal of Auto-vehicle Safety Association, Vol.12, No.2, pp.14-20, 2020.
• S. Hao, P. Luo and J. Xi, “Estimation of Vehicle Mass and Road Slope Based on Steady-state Kalman Filter,” 2017 IEEE International Conference on Unmanned System(ICUS), Beijing, China, 2017. [https://doi.org/10.1109/ICUS.2017.8278412]
• S. Lim, J. Jung, D. Hong, S. Han, K. Huh and H. Cho, “Development of a Vehicle Mass Estimation Algorithm for an Adaptive Roll Stability Control,” KSAE Fall Conference Proceedings, Vol.2, pp.745-751, 2006.
• D. Wu, C. Zeng and J. Luo, “Research on Joint Estimation Algorithm of Intelligent Vehicle Mass and Road Grade,” 2023 4th International Conference on Computer Engineering and Application (ICCEA), Hangzhou, China, 2023.
• C. Joen, H. Na and S. H. You, “Development of Vehicle Roll Model for Active Suspension Control System,” Transactions of KSAE, Vol.28, No.2, pp.109-115, 2020. [https://doi.org/10.7467/KSAE.2020.28.2.109]
• W. Cho, J. Yoon and K. Yi, “Estimation of Tire Forces and Tire-road Friction Coefficient for Application to a Unified Chassis Control,” KSAE Fall Conference Proceedings, pp.618-623, 2009.