[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 32, No. 1, pp.59-68

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jan 2024

Received 12 Oct 2023 Revised 31 Oct 2023 Accepted 01 Nov 2023

DOI: https://doi.org/10.7467/KSAE.2024.32.1.59

정상유동 장치에서 CI 기관 유동의 특성(1) : SI 포트와의 비교

박용우¹⁾ ; 엄인용^*^{, 2)}

1)서울과학기술대학교 융합과학대학원 에너지시스템공학과
2)서울과학기술대학교 기계⋅자동차공학과

Flow Characteristics of CI Engine in Steady Flow Bench(1) : Comparison with SI Port

Yongwoo Park¹⁾ ; Inyong Ohm^*^{, 2)}

1)Department of Energy System Engineering, Graduate school of Convergence Science, Seoul National University of Science and Technology, Seoul 01811, Korea
2)Department of Mechanical & Automotive Engineering,, Seoul National University of Science and Technology, Seoul 01811, Korea

Correspondence to: ^*E-mail: iyohm@seoultech.ac.kr

Copyright Ⓒ 2024 KSAE / 218-06
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

In this study, the steady flow characteristics of 27 port opening cases in CI engines were evaluated and compared with existing SI results to determine the macroscopic characteristics and differences between two engines. For this purpose, the swirl ratios were evaluated from 1.75 B to 6.00 B, using an impulse swirl meter and a particle image velocimetry. Then, the average of these values was calculated for each port and evaluation method so that changes in value can be analyzed, depending on the measurement location. Through this approach, the following results were obtained. Overall, the flow characteristics of the CI indicated less changes and remained consistent than SI, regardless of measurement location and method. Opening both ports simultaneously is very similar to the case of opening the tangential port. In the ISM evaluation, swirl decreased toward the downstream for both CI and SI, and the decrease was greatest in the case of the opened helical port. In the PIV evaluation, the swirl of the CI decreased as it went downstream, but SI exhibited different characteristics, depending on the shape of the combustion chamber. Additionally, in the PIV evaluation, if the axial velocity is assumed to be proportional to the planar velocity, swirl was at its highest. In the CI, the value was closest to the ISM evaluation, whereas, in SI, it varied, depending on the shape of the combustion chamber and the port. When the PIV evaluation was at its highest in CI, TVO closely matched ISM, starting at 3.00 B, FVO was always lower than ISM, and BVO matched well with ISM across the entire plane. Lastly, in the case of a pent roof combustion chamber in SI, the relative swirl ratio increased significantly as it went downstream. However, when a semi-wedge combustion chamber was adopted, the change in relative swirl ratio according to the measurement position was like that of CI.

Keywords:

Steady flow bench, CI, SI, Swirl, Impulse swirl meter, PIV, Tangential port, Filling port

키워드:

정상유동장치, 압축점화, 불꽃점화, 스월, 충격식 스월 측정기, 입자영상유속계, 접선형 포트, 충전 포트

1. 서 론

정상유동 평가는 현재까지 내연기관의 유동 특성을 정의하는데 가장 유효한 방법이며 널리 사용되고 있다. SI(Spark ignition) 기관을 대상으로 정상유동 평가 방법에 대해 논의한 여러 이전 연구들 통하여 살펴본 바와 같이, 실린더 내부 유동에 대한 지배적인 설계 변수는 밸브각도, 연소실 형상, 포트 형상으로 볼 수 있으며, 이들의 조합에 의해 유동 특성이 결정된다.^1-12)

한편 거의 절대 다수의 직분식 CI(Compression Ignition) 기관은 연소실이 피스톤 보울(Bowl)에 형성되고 밸브가 직립되어 있으며, 헤드 측의 연소실 형상이 평면으로 매우 단순하기 때문에 SI에서 고려되었던 밸브각도와 연소실 형상의 영향을 배제할 수 있다. 따라서 포트의 기하학적 배치와 형상만 실린더 유동에 영향을 주기 때문에 이 두 파라미터의 영향이 SI보다 지배적이며 명확히 드러난다.

소형 직분식의 경우, 유동과 분사장치의 특성이 성능에 지배적 영향을 미치므로, 기관 성능 개발에서 가장 중요한 요소는 유동과 분사 징치와의 적절한 조화인데, 일반적으로 분사 장치가 고도화될수록 유동의 역할은 줄어든다.

한편 SI를 대상으로 한 이전 연구에서,^1-12) 현재 통용되는 측정위치에서 ISM 측정의 문제점을 지적하였고, 측정위치를 변경하며 PIV 결과와 비교함으로써 적절한 측정 위치의 선정을 정상 유동의 전개와 결부하여 논의 하였다. 여기서 비교적 유동에 영향을 주는 변수가 SI보다 적지만, 유동에 대한 의존성이 SI보다 큰 CI에서도 이러한 문제점이 내재되어 있는지 검증할 필요가 있다.

본 연구에서는 형상 및 배치가 서로 다른 2개의 포트가 있는 상용 엔진 9개를 대상으로 SI 기관을 대상으로 평가하였던 방법 즉 측정위치에 따른 유동 특성의 변화를 입자영상유속계(PIV, Particle Image Velocimetry)와 충격식 스월 측정기(ISM, Impulse Swirl Meter)로 각각 평가하고 비교하여 유동 특성을 분석하고자 한다. 이 때 개별 포트의 특성 그리고 2 포트 동시 사용의 특성을 4개의 측정위치에 대해 평가하였으므로 총 108개의 물리적 조합이 존재한다. 동시에 각각의 평가에 대해 축 방향 속도 및 중심 설정에 따라 PIV평가에서 4가지 그리고 여기에 ISM 평가를 추가하여 총 540 경우의 평가 결과를 얻었다. 이를 바탕으로 본 연구에서는 개별적인 포트 특성에 대한 논의는 배제하고, 기존에 논의하였던 SI 기관의 결과(120 경우)^1-12와 비교하면서 평가 결과를 전체적으로 조망해 보고자 한다.

2. 실험 장치 및 방법

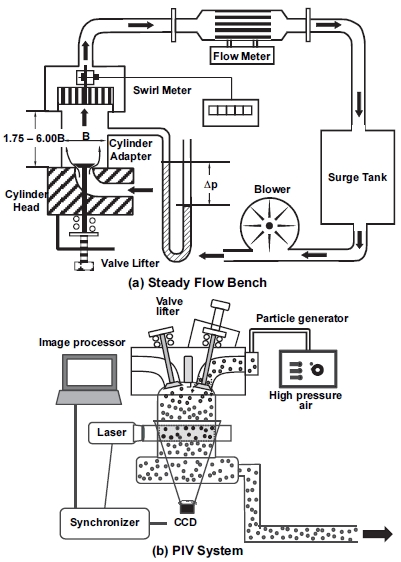
본 연구 대상인 모든 소형 직분식 CI 기관은 두 개의 포트로 구성되는데, 기본적으로 직선형 형상을 가지고 실린더 벽과의 기하학적 배치를 통해 스월 거동을 유도하는 접선(Tangential)포트와 충전(Filling) 포트로 구성되어 있다. 충전 포트는 대부분 포트에서 스월 유동을 형성시키는 나선형(Helical) 형상을 채택하고 있다. 각 포트의 출구에는 유량과 스월의 미세 조정을 위해 오프셋 챔퍼(Offset chamfer)가 적용되어 있다.

Fig. 1에 본 연구에 사용된 9개 엔진의 포트 형상 사진, Table 1에는 간략히 그 특성을 제시하였다.

Fig. 1

Port shapes of 9 commercial ports

Table 1

Port composition and cylinder specification

실험장치의 개략도를 Fig. 2에 나타내었는데, 이전 연구^1-12)에서와 마찬가지로 ISM(G. Cusson사 P7,300/200)은 통상적인 ISM 측정위치인 1.75 B(헤드 하면에서 보어의 1.75배 하류)를 포함하여 3.00, 4.50, 6.00 B에 장착하였고, 동일 위치에서 PIV 측정도 병행하였다. 실험 조건과 기타 PIV 시스템의 사양은 Table 2에 나타내었는데 차압을 포함하여 밸브 리프트 변경(1 mm 간격)은 ISM과 PIV 모두 동일하다. 자세한 장치의 설명과 실험방법은 이전 논문^1-6)에서 다루었기 때문에 생략하고 주요한 결과 식만 제시하기로 한다.^13-15)

Fig. 2

Schematics of (a) steady flow bench and (b) PIV system

Table 2

Experimental conditions and specifications of PIV

실린더 내 유동의 유속(Momentum flux)의 모멘트 즉 토크(Torque, moment of momentum flux)는

T = ∫ 0 B / 2 ∫ 0 2 π ρ ⋅ v z r, θ ⋅ v θ r, θ ⋅ r 2 d r d θ

(1)

ISM의 경우 축방향 속도가 일정하다고 가정하였으므로 이 경우 토크는

T I S M = ρ v z ω c ∫ 0 B / 2 ∫ 0 2 π r 3 d r d θ = 18 m ˙ ω c B 2

(2)

PIV 측정속도를 기반으로 한 토크는 각각 유동요소에서 구한 토크의 합이므로 직교 좌표계에서 구분 구적법을 적용하여

T P I V = ∑ i ρ i v z, i r i v θ, i Δ x Δ y = ∑ i ρ i v z, i r i v y, i c o s ⁡ θ - v x, i s i n ⁡ θ Δ x Δ y

(3)

이때 앞서 언급한 바와 같이 PIV의 경우 중심 설정과 축 방향 속도에 따라 4가지 경우로 가정하여 평가할 수 있다. 즉 축 방향 속도가 ISM과 같이 일정하다고 가정한 경우와 그렇지 않은 경우 그리고 스월의 중심을 실린더 중심과 같이 두는 경우와 실제 스월의 중심에 두는 경우이다.

반경의 경우 실린더 중심 및 스월 중심으로부터의 거리를 반영해 주면 되지만, 축 방향 속도는 실제로 측정을 하지 않았으므로 다음과 같이 구하여 적용하였다.

먼저 축 방향 속도가 일정하면 속도 v_z는 체적 유량을 실린더 단면적으로 나눈 축 방향 평균 속도를 사용하였다. 평균 속도를 기반으로 개별 유동 요소에서 축 방향 속도가 평면 속도에 비례한다고 가정하면

v z, i = v z v i / v ¯

여기서 $v ¯$ 는 평균 평면속도이고 v_i와 v_z_,i는 각각 개별 유동요소의 평면속도와 축 방향 속도이다.

따라서 식 (3)에 축 방향 속도 및 중심 설정에 따라 r_i 및 v_z_,i를 달리 사용하여 토크를 계산하였고, Table 3에 이를 간략히 제시하였다. 여기서 ISM의 실제 측정값과 측정 원리상 가장 일치하는 것은 C_A로 볼 수 있다.

Table 3

Momentum according to evaluation method

다음으로 각각의 리프트에서 무차원 스월 계수는

N r = ω c ⋅ B ⋅ m ˙ v 0 ⋅ m ˙ = 8 T m ˙ v 0 B

(4)

전체 흡입 행정에서 일종의 평균적인 스월비를 나타내는 스월 비 R_s는 기관의 크랭크 각속도에 대한 스월의 각속도로 다음과 같다

R s = ω c ω e = B S π n D 2 ∫ α 1 α 2 C f N r d α ∫ α 1 α 2 C f d α 2

(5)

마지막으로 본 연구에서는 각 포트의 개별적인 유동특성보다 다수의 포트를 대상으로 평가 방법 및 측정위치에 따른 전체적인 변화 특성에 대해 논의하는 것이 목적이다. 따라서 각 포트의 최종 특성이라 할 수 있는 식 (5)를 통해 구한 스월 비가 주요 논의 대상이다. 이때, 측정 위치가 변화하면 마찰¹⁾ 및 속도 분포의 변화⁶⁾ 등으로 스월 비 R_s도 변하기 때문에 절대 값의 변화를 관찰하는 것도 중요하지만 스월 비는 개별 포트 특성에 따라 크게 다른 값을 보여주므로 이를 근거로 논의하는 것은 최소화하고자 한다. 아울러 동일 위치에서 ISM과 PIV 평가 값의 상대적인 비의 변화를 관찰하는 것이 더 유효한 방법이며 추가적인 정보를 얻을 수 있다고 판단된다. 이에 따라 ISM 평가대비 PIV 평가 값의 비를 다음과 같이 구하였고, 이 상대 스월 비를 바탕으로 방법 및 위치에 따른 변화도 논의하기로 한다.

R S, R e l a t i v e = R S, P I V R S, I S M

(6)

3. 결과 및 검토

3.1 측정 평면에 따른 ISM 평가 스월 비

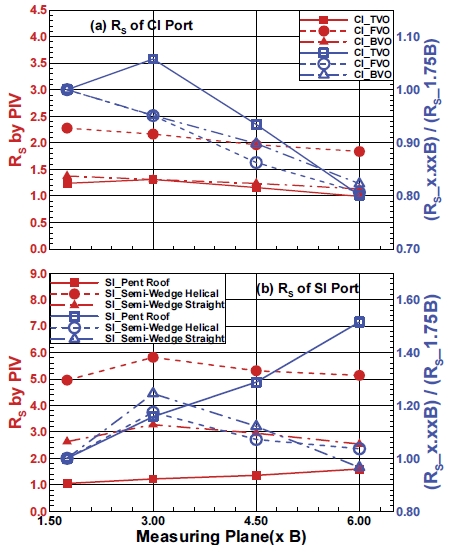
Fig. 3에 본 연구의 기준이 되는 ISM 방식으로 평가한 스월 비의 측정위치에 따른 변화를 나타내었다. 그림에서 SI 지붕(Pent roof)형은 모두 직선형 포트를 그리고 반 쐐기(Semi-wedge)형은 직선형과 나선형을 모두 채택하고 있다. 스월 비 또는 실린더 내 정상유동 특성은 앞서 언급한 바와 같이 포트 및 연소실 형상 밸브각도 등에 따라 크게 달라져서, 실제 개별 포트별로 보면 CI의 경우 0.5 ~ 4.2 그리고 SI의 경우^5,11) 2.5 ~ 9.0 사이에 분포한다.

Fig. 3

Average swirl ratio as a function of estimating plane by ISM when (a) CI and (b) SI port

그러나 이들 개별 포트의 특성을 일일이 논의하는 것은 본 연구의 목적이 아니므로, 그림에서는 포트 형상, 포트 사용 및 연소실 형상에 따라 이를 분류하고 평균하여 나타내었다. 즉 CI의 경우 접선 포트 개방(TVO, Tangential port open), 충전 포트 개방(FVO, Filling port open), 두 포트 동시개방(BVO, Both port open)에 대해 각 평면에서 9개 그리고 SI의 경우 포트 형상 및 연소실 형상에 따라 2 ~ 4개의 개별 포트 측정값의 평균과 1.75 B 측정값의 비를 도시하였다.

ISM 평가 값의 측정위치에 따른 변화를 전체적으로 살펴보면, 이전 연구에서도 관찰되었듯이 측정 위치가 하류로 갈수록 감소하는데, 이는 유동의 진행에 따라 벽면 마찰을 포함하여 각종 손실이 발생하기 때문에,¹⁾ 동시에 불완전한 유동 전개에 의해 특히 상류일수록 ISM 측정값이 과대평가되기 때문이기도 하다.^1-6,9,10) 이 때 포트 및 연소실 형상 등에 따라 그 절대 값은 크게 차이가 나고, 스월 비가 클수록 하류로 진행하면서 그 감소가 큰데. 이는 스월이 강할수록 그 만큼 벽면 마찰이 증가하기 때문인 것으로 판단된다. 1.75 B 대비 6.00 B에서의 상대적 감소는 20 ~ 40 % 수준이다.

먼저 Fig. 3(a)에 도시된 CI의 경우를 보면, 대체로 나선형인 충전포트 개방(FVO)이 직선형인 접선포트 개방(TVO)보다 높은 스월 비를 가지고 있다. 그러나 측정 위치가 하류로 이동하면서 FVO는 초기(3.00 B)에 TVO보다 크게 감소하고 이후 6.00 B최종적인 감소도 TVO보다 크다.

두 포트 동시 개방(BVO,)에서 절대 값은 TVO와 매우 유사한 값을 보이고 있지만, 평면 변경에 따른 감소는 앞의 두 경우와 비교해 매우 적고 특히 하류에서의 감소가 크지 않음을 알 수 있다.

BVO의 이러한 특성을 분석하면 다음과 같다.

이전 연구^7.8,11,12)에서 보았듯이 스월은 주로 실린더 벽면 근처의 유동에 의해 지배된다. 실제로 두 포트를 동시에 사용하면 유동의 상호 간섭에 의해 개별 포트의 특성이 많이 희석되지만, 포트 배치 및 형상 측면에서 주로 벽면을 따른 유동을 유도하는 접선 포트가 충전 포트보다 전체적인 스월에 더 크고 지배적인 영향을 주었기에 BVO와 TVO의 스월 비가 매우 근접한 값을 보여준다고 판단된다.

한편 접선 포트에 비해 상대적으로 실린더 중심을 따르는 유동을 유도하고 동시에 스월 거동이 강한 충전 포트에 의해, 벽면과 중심 사이 중간 부분을 흐르는 유동도 단독 포트 사용보다 강하게 형성된다. 이에 따라 접선 포트에 의해 벽면 근처를 흐르는 유동은 하류로 갈수록 마찰 등으로 약화되지만 운동량 교환 등으로 비교적 강한 중심 부분의 유동에 의해 꾸준히 보완된다. 동시에 벽면과 중심 사이의 중간 부분 유동도 접선 포트보다 강하기 때문에, 벽면 근처의 유동에 비해 스월에 미치는 영향은 적지만 일정 부분 스월 증가에 기여하기 때문이다.

SI의 경우(Fig. 3(b)), 포트 및 연소실 형상이 모두 스월 비에 영향을 주고 있다. 여기서 나선형은 기본적으로 높은 스월을 유도하므로 논외로 치더라도, 동일한 직선형 포트에서도 반 쐐기 형을 채택한 경우가 지붕 형을 채택한 경우보다 스월 비가 매우 높게 나타난다. 반 쐐기 형과 지붕 형에서 이러한 큰 차이가 나는 것은 다음과 같이 설명할 수 있다.

흡입유동이 직접 실린더로 진입하는 CI와 달리 SI는 연소실의 대부분이 헤드 측에 형성되고, 흡입 유동도 일단 헤드 측 연소실을 경유하여 실린더로 진입하므로 이 형상이 실린더 내 유동에 영향을 준다. 또한 밸브 주변의 흡입유동은 벽면에 의해 유동이 제한이 되는 실린더 벽면 방향보다 실린더 중심방향으로 주 유동이 형성되며, 일단 연소실에 진입한 이후 연소실 벽면을 따라 거동하다 실린더 영역으로 진입한다.^16-18) 이때 연소실 벽면과 실린더 사이의 각도에 따라 실린더 진입방향이 달라진다.¹⁰⁾

실린더 벽면과 헤드 측 연소실 벽면이 이루는 각도의 최솟값은 90°이고 대부분의 CI가 이에 해당한다. SI 다 밸브(Multi-valve)의 경우, 이 각도는 배기 밸브각도에 따라 달라지는데 이 배기 밸브각도의 실용 범위는 0 ~ 30°이고, 이 각도가 작을수록 CI에 가깝다. 본 연구에서 지붕 형의 경우 흡입 및 배기 밸브각도는 동일하며 11 ~ 26° 범위이고, 반 쐐기 형은 흡입 25°, 배기 4°이다.

따라서 반 쐐기 형에서는 CI와 매우 유사한 거동을 보여 스월이 증가한 반면, 지붕 형의 경우 이 각도가 클수록 실린더 벽면을 추종하는 유동 외에 강한 축 방향 유동 및 재순환 유동 등이 발생하여^5,6,11) 스월 거동이 왜곡된다. 추가로 지붕 형의 경우도 대체로 밸브각도가 클수록 스월이 약화되는 경향을 보여 주어, 이 분석을 뒷받침 한다고 사료된다.

SI에서 측정 위치 변경에 따른 상대 스월 비의 변화를 보면, 스월이 강한 반 쐐기 형의 경우 CI의 FVO와 마찬가지로 마찰 및 ISM 측정 왜곡 등에 의해 초기에 크게 감소하고 이후 대체로 직선적으로 감소한다. 최종 감소는 CI 보다 크다.

반면 지붕 형의 경우 하류로 가면서 상대적으로 완만하게 직선적으로 감소하는데, 감소 형태만 보면 CI의 TVO와 유사하지만 그 기구는 다르다고 판단된다. SI 특히 지붕 형인 경우 CI와 달리 정상유동에서 유동의 전개가 늦게 진행되고, 이에 따라 하류에서 축 방향 운동량의 접선 방향 운동량의 변환이 상대적으로 많이 발생한다.⁶⁾ 이러한 이유로 하류에서 마찰에 의한 손실을 운동량 변환이 일정 부분 보상한 것이 원인으로 판단된다.

3.2 측정 평면에 따른 PIV 평가 스월 비

Fig. 4에는 PIV 측정 속도를 기반으로 평가한 스월 비의 변화를 나타내었다. 이것은 중심 설정과 축 방향 속도에 따른 4가지 평가 방법으로 구한 값을 모두 평균한 것이다. 따라서 이를 근거로 방법에 따른 구체적 분석은 불가능하고, 여기에서는 개괄적 특성만 다루겠다. 평가 방법에 따른 차이와 분석은 이후 데이터를 제시하며 후술한다.

Fig. 4

Average swirl ratio as a function of estimating plane by PIV when (a) CI and (b) SI port

그림을 보면 전체적으로 ISM 평가와는 매우 다른 특성이 나타나는데 이 결과를 ISM 방식과 비교하며 논의하면 다음과 같다.

Fig. 4(a)의 CI 결과를 보면, 측정 위치가 하류로 가면서 감소하는 것은 ISM과 같지만, 대체적으로 ISM보다 낮게 평가되고 있으며 특히 상류 그리고 FVO에서 이러한 특징이 두드러진다. 그러나 그 감소의 구배는 ISM 보다 낮은데, 이에 따라 하류로 가면서 ISM 평가 값과의 차이가 줄어들고 있다. 1.75 B와 6.00 B를 비교해 보면, 포트에 따라 ISM 방식에서는 22 ~ 35 % 감소하지만, PIV에서는 18 ~ 20 % 정도로 감소폭이 적고 동시에 포트 별 차이도 거의 없음을 알 수 있다. 이것은 앞서 언급한 바와 같이^1-6,11,12) 상류일수록 ISM 평가가 왜곡되기 때문이다.

TVO의 경우 예외적으로 3.00 B에서 1.75 B 대비 오히려 소폭 증가하는데, 이는 TVO는 유동 전개가 3.00 B 부근에서 완료되고 전개에 의한 효과가 마찰 등에 의한 손실을 상쇄하고도 남아 소폭 증가를 가져온 것으로 판단되며, 이에 대해서는 속도 데이터 등을 제시하며 후속 논문에서 논의하도록 하겠다.

Fig. 4(b)의 SI 결과를 보면, 앞의 여러 경우와 다른 경향이 관찰되는데, 연소실 형상에 따라 동일한 특성을 보여준다. 먼저 스월 비 절대 값은 지붕 형 연소실에서는 측정 평면이 하류에 위치할수록 증가하는데, 이는 기본적으로 지붕 형에서는 흡입 밸브와 가까운 상류에서의 유동은 스월로 거동이 매우 왜곡되어 나타나고, 하류로 가면서 지속적으로 유동의 전개가 진행되어 이상적 분포에 가까워져서^3,4) 평가 값이 증가하기 때문이다.

반 쐐기 형의 경우 앞서 언급한 바와 같이 흡입 초기 거동이 CI의 접선형과 유사하므로 포트 형상과 관계없이 3.00 B에서 모두 최고가 되고 이후 진행에 따라 감소한다.

3.3 포트 개방 방법에 따른 상대 스월 비

Fig. 5에 CI 포트의 개방 방법별로 평가 위치 및 PIV 평가 방법에 따른 상대 스월 비(R_S_,Relative)의 변화를 나타내었다. 먼저 전체적인 특성을 관찰하면 다음과 같다.

Fig. 5

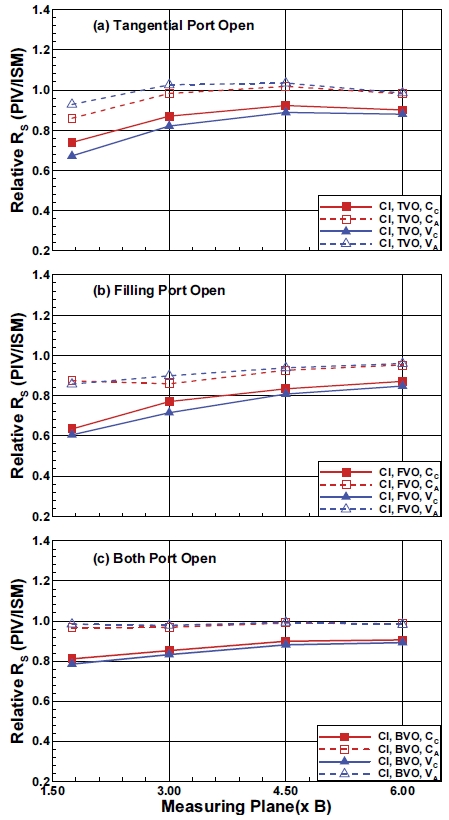
Relative swirl ratio of CI as a function of estimating plane according to method when (a) tangential, (b) filling and (c) both port open

평가 방법에 관련하여, 축 방향 속도 가정이 중심 설정보다 스월 값에 훨씬 큰 영향을 주며, 축 방향 속도를 고려하는 경우 스월 비가 가장 높고 동시에 ISM 평가 값과도 가장 잘 일치한다. 중심 설정도 영향을 주지만 그 영향은 매우 미미하다. 이것은 CI의 경우 비교적 이상적 분포에 가까운 평면 속도 분포를 가지기 때문에, 설정된 중심에서 유동 요소까지의 거리 및 접선 속도 차이가 줄어들어 중심 설정이 큰 영향을 주지 않고, 축 방향 속도를 고려하면 벽면 근처 유동 성분의 운동량 평가 값이 증가하여 스월 값을 증대시키기 때문이다.

두 번째, 1.75 B에서 ISM 대비 PIV 평가가 가장 낮으며 이후 차이가 줄어든다. 이는 SI 평가에서 논의하였듯이^1-6,9,10) 상류일수록 유동의 전개가 충분치 않아 발생하는 ISM 평가방법에 내재된 문제에 의한 것이다. 즉 상류일수록 ISM 방법이 스월 값을 과대평가하기 때문이며, SI에서와 동일한 현상이 발생하지만 유동 전개가 더딘 SI와는 정도의 차이만 있다고 볼 수 있다.

다음, 축 방향 속도 일정 가정에서는 모든 경우 실린더 중심이, 그리고 축 방향 속도와 평면속도의 비례 가정에서는 대부분의 경우 스월 중심이 미세하나마 높게 평가된다. 이것은 스월 중심과 실린더 중심은 일치하지 않고 어느 정도 편심이 생기는데, 이에 의해 스월 중심에서 가장 먼 벽면 근처의 유동 요소가 축 방향 속도 가정에 따라 스월에 기여하는 정도가 서로 다르기 때문이다.^7,8,11,12)

마지막으로 축 방향 속도가 일정하다고 가정한 경우에는 모든 측정 평면에서 항상 ISM보다 낮다. 그러나 하류로 진행하면서 평가 값의 증가는 축 방향 속도를 고려한 경우보다 더 커서 6.00 B에서 차이가 가장 적은데, 이는 하류에서의 유동 전개로 평면 내 축 방향 속도의 차이가 감소하기 때문이다.

이어서 포트 개방에 따른 특성을 관찰해 보면, Fig. 5(a)의 TVO에서, 1.75 B 평면에서는 평가 방법에 따라 상당한 차이가 있지만 이후 하류로 진행할수록 방법 간의 차이가 감소한다. 이것은 하류로 갈수록 유동의 전개가 진행되어 이상적 속도분포에 가까워지기 때문이다. 축 방향 속도 가정과 관계없이 1.75 ~ 3.00 B 사이 증가가 가장 크고, 축 방향 속도를 고려한 경우 3.00 ~ 4.50 B에서 ISM과 매우 근접하며 6.00 B에서 소폭 감소한다.

Fig. 5(b)의 FVO를 보면, 전체적으로 항상 ISM 보다 낮고 평가위치가 하류로 갈수록 꾸준히 증가하여 최곳값은 6.00 B에서 나타난다. TVO와 달리 1.75 B에서 방법 간 차이는 축 방향 속도 가정에 의한 것만 두드러지게 나타난다. 축 방향 속도를 고려한 경우 1.75 B에서 3.00 B 평면 사이의 증가는 TVO와 다르게 증가가 미미하다.

BVO를 도시한 Fig. 4(c)를 보면, 앞의 ISM 평가 결과에서 보았듯이 TVO 및 FVO와는 매우 다른 특성이 나타난다.

일단 축 방향 속도를 고려한 경우 전체 평면에서 ISM 평가와 매우 잘 일치한다. 동시에 축 방향 속도일정 가정에서도 다른 포트와 달리 1.75 B에서도 상대적으로 높은 값을 보여주고 있으며, 이후 하류로 갈수록 증가의 형태도 직선적이고 구배도 크지 않다. 동시에 축 방향 속도 가정이 같은 경우, 중심 설정에 의한 차이도 매우 적다. BVO의 이러한 특성은 앞의 ISM 결과에서 논의한 바와 같이 TVO와 HVO 특성이 적절히 조합되어 벽면 근처 유동은 접선 포트에 의해 지배되고 벽면과 중심 사이 중간 영역은 충전 포트에 의해 강화되어 나타난 것으로 판단된다.

Fig. 6에는 이전에 진행한 SI 기관의 정상유동특성을 연소실 형상 및 포트 형상에 따라 구분하여 나타낸 것이다.

Fig. 6

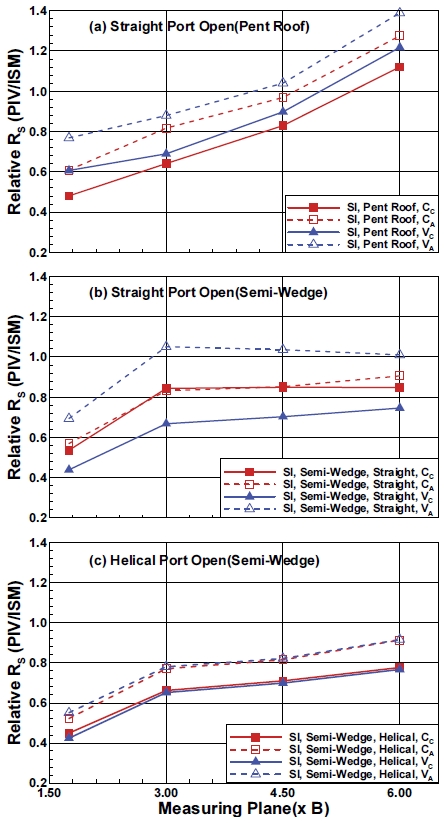
Relative swirl ratio of SI as a function of estimating plane according to method when (a) pent roof straight, (b) semi-wedge straight and (c) semi-wedge helical port open

전체적으로 살펴보면, SI는 CI와 매우 다른 특성을 보여주고 있는데, 이는 실린더 유동에 영향을 주는 파라미터가 CI 보다 많고 이들의 상호 작용이 매우 복잡하게 발생하기 때문이다. 이에 따라 CI에서는 상당히 많은 공통적 특징이 발견되지만, SI에서는 축 방향 속도를 고려할 때 스월 중심으로 평가한 경우가 가장 높다는 것 외에는 없다. 그러나 동일 연소실 형상 내에서는 평면 변경에 따른 변화에서 공통적 특성이 관찰된다.

지붕 형 연소실에 직선형 포트를 적용한 결과를 보면, 우선 방법 간의 차이가 뚜렷이 나타난다. 구체적으로 축 방향 속도를 고려하면 그리고 스월 중심인 경우 높은 값을 보인다. 그리고 상류인 1.75 B에서 PIV 평가는 ISM 대비 매우 낮지만, 이후 꾸준히 증가하여 4.50 B에서 V_C는 ISM 평가보다 높게 나오고 이후 6.00 B에서는 모든 방법이 ISM보다 높다. 이는 Fig. 4, Fig. 5에서 관찰된 바와 같이 하류로 가면서 ISM 평가는 낮아지고 PIV 평가는 증가하기 때문이다.

반 쇄기 형 연소실에서는(Fig. 6(b), (c))에서는 포트 형상과 평가 방법에 관계없이 1.75 B에서 3.00 B로 이동할 때 대폭 증가하고, 이후 동일 수준을 유지하거나 증가의 구배가 크게 줄어든다. 이러한 변화 형태는 직선형의 경우 CI의 TVO 그리고 나선형의 경우 CI의 FVO와 상당히 유사한데, 이는 앞서 언급한 바와 같이 반 쐐기 형의 경우 CI에 가까운 유동을 유도하기 때문이다. CI와 차이점은 1.75 ~ 3.00 B 평면 사이에서 ISM 평가(Fig. 3(b))에서는 감소가 크고 반면 PIV 평가 (Fig. 4(b))에서는 소폭 증가한다는 것인데, 이것은 앞서 논의한 바와 같이 상류에서 ISM 평가가 과대평가되는 특성에 기인한다.

포트 별로 살펴보면, 직선형 포트(Fig. 6(b))에서 실린더 중심인 경우 축 방향 속도의 영향이 거의 없는 반면, 스월 중심의 경우에는 각각 최대 및 최소를 보여주며 매우 크다는 것이다. 이것은 이전 연구¹⁰⁾에서 관찰된 바와 같이 스월 거동 중심이 실린더 중심에서 벗어난 정도를 나타내는 편심도(Eccentricity)가 직선형의 경우 나선형보다 매우 크기 때문에 나타나는 현상이다. 즉 편심도가 커서 중심에서 먼 벽면 근처의 유동 성분의 운동량이 축 방향 속도 가정에 따라 크게 달라지기 때문이다. 실린더 중심으로 평가한 경우 중심에 대한 접선 속도가 매우 복잡한 분포를 지니기 때문에 서로 방향이 달라 상쇄되는 경우가 많아 축 방향 속도의 가정이 큰 영향을 주지 못하였다.^10,12)

반 쐐기 형 연소실에서 나선형의 경우, 중심 설정보다는 축 방향 속도 가정이 지배적 영향을 준다. 앞서 언급한 1.75 ~ 3.00 B 평면 사이의 급격한 증가를 제외하면 대체로 CI 포트의 변화 상태와 유사하다.

지금까지 기술한 내용에 더해 추가적으로 논의를 하면 다음과 같다.

CI의 경우 헤드 측의 연소실 형상은 단순하지만 포트는 매우 다양한 형태와 배치를 가지고 있고 기관마다 목표로 하는 스월 비도 다르다, 더구나 SI는 이에 더해 다양한 연소실 형상을 가지고 있다. 따라서 이들에 의해 발생하는 스월 비는 기관 및 포트에 따라 넓은 범위에 걸쳐 있고, 이를 기계적으로 평균하여 일종의 대표 값으로 삼는 것에는 많은 문제점이 있다.

그러나 이러한 단순 평균을 통해 살펴 본 두 기관의 유동 특성과 차이가 상당히 일관성 있는 경향을 보여 주므로, 이를 분석함으로써 CI 포트의 개방 방법에 따른 차이와 SI와의 차이 그리고 SI에서 연소실 형상의 영향을 정성적으로 파악할 수 있었다고 판단된다.

전체적으로 보면 CI의 측정 위치에 따른 유동특성의 변화가 측정 위치 및 방법에 관계없이 SI 보다 변화가 적고 일관된 경향을 보여준다. 이는 비교적 간단한 헤드 측 연소실 형상에 의해 유동 특성을 지배하는 변수가 줄어들었기 때문이다.

동시에 유동에 대한 가정을 달리하며 여러 평가 방법을 사용하여 비교하였는데, 축 방향 속도가 평면 속도에 비례한다는 가정이 비교적 합리적 방법으로 판단된다. 실제로 ISM 평가에서 축 방향 속도가 일정하다는 가정이 가장 큰 오차의 원인으로 지적이다.¹⁹⁾ 아울러 평가 방법에 따른 차이가 가장 적은 경우, 실린더 내 유동이 이상적 분포에 가깝다고 볼 수 있다. 이러한 측면에서 CI는 SI보다 비교적 상류에서부터 단순한 형태의 조직적 유동이 존재하고 이후 이 상태가 하류까지 지속된다. 반면, SI는 상류에서 복잡한 유동하게 전개된 유동이 하류로 가면서 정돈되는데, 이 정돈도 연소실 형상의 영향을 크게 받아, 반 쐐기 형이 지붕형 보다 CI에 가까운 특성을 나타낸다.

후속 연구에서는 CI 기관에서 포트 별로 나누어 측정 및 평가 결과를 제시하며 그 구체적 특성에 대해 논의하고자 한다.

4. 결 론

CI 포트의 형상, 개방 방법 및 평가 위치에 따라 스월 비를 구하고 이를 SI와 비교한 결과 다음과 같은 결론을 얻었다.

1) 전체적으로 CI의 유동특성이 측정 위치 및 방법에 관계없이 SI 보다 변화가 적고 일관된 경향을 보여주며, 두 포트를 동시 개방한 경우의 유동 특성은 접선포트를 개방한 경우와 매우 유사하다.
2) ISM 평가에서 CI 및 SI 모두 하류로 갈수록 스월이 감소하고, 나선형 포트를 사용한 경우 감소가 가장 크다.
3) PIV 평가에서 하류로 갈수록 CI의 스월은 작아지지만 SI는 3.00 B에서 증가하고 이후 연소실 형상에 따라 지붕 형에서는 계속 증가하고 반 쐐기 형에서는 감소한다.
4) PIV 평가에서 축 방향 속도가 평면 속도에 비례한다고 가정한 경우 스월이 가장 높게 평가되는데, CI는 ISM 평가와 가장 가까운 반면 SI에서는 연소실과 포트 형상에 따라 달리 나타난다.
5) CI에서 PIV 평가가 ISM에 가장 접근하는 경우, TVO는 3.00 B부터 ISM과 거의 일치하고 FVO는 ISM보다 항상 낮으며, BVO는 전 평면에 걸쳐 ISM과 잘 일치한다.
6) SI에서 지붕 형 연소실의 경우 하류로 갈수록 ISM 평가는 낮아지고 PIV 평가는 증가하여 상대 스월 비가 크게 증가하지만, 반 쐐기 형 연소실을 채택하면 측정위치에 따른 상대 스월비의 변화는 CI와 유사하다.

Nomenclature


B :	bore, m
C :	cylinder center
C_f :	mean flow rate coefficient
$m ˙$ :	mass flow rate through port, kg/s
N_r :	Non-dimensional rig swirl
R_s :	swirl ratio
r :	distance from center to element area
S :	stroke, m
T :	torque(moment of momentum flux), N⋅m
Q :	volumetric flow rate, m³/s
V :	swirl center
v :	velocity, m/sec
v₀ :	theoretical velocity across port, m/sec
$v ¯$ :	average planar velocity, m/sec
α₁ :	crank angle of intake valve opening, rad
α₂ :	crank angle of intake valve closing, rad
ρ :	density of air, kg/m³
ω_c :	angula swirl velocity at induction end, rad/sec
ω_e :	angula crank velocity, rad/sec

Subscripts


C :	constant axial velocity
i :	element area
ISM :	based on ISM
PIV :	based on PIV
A :	variable axial velocity(proportional to planar velocity)
x, y, z :	x, y, z direction in cartesian coordinate
θ :	θ direction in cylindrical coordinate

Acknowledgments

이 연구는 서울과학기술대학교 교내연구비의 지원으로 수행되었습니다.

References

C. Park and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(1)-Raising Issue,” Transactions of KSAE, Vol.23, No.1, pp.88-96, 2015. [https://doi.org/10.7467/KSAE.2015.23.1.088]
C. Park and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(2)-Comparison of ISM and PIV Measurement,” Transactions of KSAE, Vol.23, No.1, pp.139-147, 2015. [https://doi.org/10.7467/KSAE.2015.23.1.139]
C. Park, J. Sung and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(3)-Velocity Profile(1),” Transactions of KSAE, Vol.24, No.2, pp.169-182, 2016. [https://doi.org/10.7467/KSAE.2016.24.2.169]
C. Park, J. Sung and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(4)-Velocity Profile(2),” Transactions of KSAE, Vol.24, No.2, pp.242-254, 2016. [https://doi.org/10.7467/KSAE.2016.24.2.242]
S. Cho and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(5)-Effect of Evaluation Position,” Transactions of KSAE, Vol.25, No.2, pp.179-189, 2017. [https://doi.org/10.7467/KSAE.2017.25.2.179]
C. Yang and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(6)-Effect of Axial Velocity,” Transactions of KSAE, Vol.26, No.2, pp.174-186, 2018. [https://doi.org/10.7467/KSAE.2018.26.2.174]
C. -H. Lim, J. -H. Hyun and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(7)-Torque Distribution along Radial Direction(1),” Transactions of KSAE, Vol.28, No.1, pp.75-86, 2020. [https://doi.org/10.7467/KSAE.2020.28.1.075]
C. -H. Lim, J. -H. Hyun and I. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(8)-Torque Distribution along Radial Direction(2),” Transactions of KSAE, Vol.31, No.1, pp.29-42, 2023. [https://doi.org/10.7467/KSAE.2023.31.1.029]
H. Kim and I. Ohm, “Effects of Port Shape on Steady Flow Characteristics in an SI Engine with Semi-Wedge Combustion Chamber(1)-Velocity Distribution(1),” Transactions of the Korean Society of Mechanical Engineers B, Vol.40, No.7, pp.417-427, 2016. [https://doi.org/10.3795/KSME-B.2016.40.7.417]
I. Yoon and I. Ohm, “Effects of Port Shape on Steady Flow Characteristics in an SI Engine with Semi-Wedge Combustion Chamber(2)-Velocity Distribution(2),” Transactions of the Korean Society of Mechanical Engineers B, Vol.41, No.2, pp.97-107, 2017.
J. Hyun and I. Ohm, “Effects of Port Shape on Steady Flow Characteristics in an SI Engine with Semi-Wedge Combustion Chamber(3)-Comparison of Evaluation Method and Position,” Transactions of the Korean Society of Mechanical Engineers B, Vol.42, No.10, pp.631-643, 2018. [https://doi.org/10.3795/KSME-B.2018.42.10.631]
W. -T. Kim and I. Ohm, “Effects of Port Shape on Steady Flow Characteristics in an SI Engine with Semi-Wedge Combustion Chamber(4)-Distribution Characteristics along the Radial Direction,” Transactions of the Korean Society of Mechanical Engineers B, Vol.46, No.8, pp.427-439, 2022. [https://doi.org/10.3795/KSME-B.2022.46.8.427]
Superflow Corporation, Superflow 600 Instructions, Appendix I, Colorado Springs, 1988.
Richard Stone, Introduction to Internal Combustion Engines, 2nd Edn., pp.183-185, McGraw-Hill, Hong Kong, 1992. [https://doi.org/10.1007/978-1-349-22147-9]
J. Heywood, Internal Combustion Engine Fundamentals, 1st Edn., pp.225-227, McGraw-Hill, Singapore, 1988.
I. Ohm and C. Park, “In-Cylinder Intake Flow Characteristics according to Inlet Valve Angle,” Transactions of KSAE, Vol.14, No.3, pp.142-149, 2006.
I. Ohm and C. Park, “In-Cylinder Intake Flow Characteristics of Helical Port Engines with Wide Valve Angle,” Transactions of the Korean Society of Mechanical Engineers B, Vol.32, No.10, pp.761-768, 2008. [https://doi.org/10.3795/KSME-B.2008.32.10.761]
I. Ohm and C. Park, “Effect of Inlet Valve Angle on In-Cylinder Swirl Generation Characteristics(I),” Transactions of KSAE, Vol.16, No.6, pp.148-156, 2008.
SwRI, Cylinder Head Port Design, Presentation, 1999.

	Port Shape		Bore	Stroke
	Tangential	Filling	(mm)
P01	Straight	Helical	76.0	82.5
P02	Straight	Helical	86.0	94.0
P03	Straight	Helical	81.0	95.5
P04	Semi-Helical	Semi-Helical	81.0	95.5
P05	Straight	Semi-Helical	80.0	79.5
P06	Straight	Semi-Helical	77.2	84.5
P07	Straight	Helical	85.4	96.0
P08	Helical	Helical	77.0	85.8
P09	Straight	Helical	83.0	92.3

Laser pulse	Separation	25 µsec
	Frequency	5 Hz
	Width	≪100 µm
Sampling raw data No.		200
Pressure drop		15" H₂O(383 mmH₂O)
CCD camera		KODAK Megaplus ES 1.0
Lens		85 mm PC-E Micro Nikkor
Processing		50 % Overlap,16 ×16 pixel
Atomizer		TSI_SIX-JET 9306
Particle	Size	≪1 µm
	No. density	10⁷ particle/cm³
	Stokes No.	≪1
Software		TSI_Insight

Method	Center	Axial velocity assumption
C_C	Cylinder	Constant (v_z,_i = v_z, Q/A)
C_A	Cylinder	$v z, i = v z ⋅ v i / v ¯$
V_C	Swirl	Constant
V_A	Swirl	$v z, i = v z ⋅ v i / v ¯$