차량의 횡 안정성 제어를 위한 노면 마찰계수 추정에 관한 연구
Copyright Ⓒ 2023 KSAE / 217-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper describes a method of estimating the tire-road friction coefficient used in vehicle lateral stability control. The estimated tire-road friction coefficient is used to calculate a target yaw rate to maintain vehicle lateral stability control. The tire-road friction coefficient used for the target yaw rate should be estimated at a constant value, though there might be some errors, rather than accurately estimating the current road status. The estimation algorithm is developed by integrating two estimation methods: estimation based on the magnitude of the current lateral acceleration, and estimation applied with the Bayesian tracking method. To apply the Bayesian tracking method, the yaw rate calculated by the current lateral acceleration and the reference yaw rates for each tire-road friction coefficient are used. Simulation tests using Carmaker and Matlab/Simulink are then conducted to study the feasibility and performance of the proposed estimation algorithm under various road conditions.
Keywords:
Tire-road friction coefficient, Vehicle lateral stability control, Target yawrate, Lateral acceleration, Bayesian tracking키워드:
노면 마찰계수, 차량 횡 안정성 제어, 목표 요레이트, 횡 가속도, 베이지안 트레킹1. 서 론
차량의 운동 성능은 타이어에서 발생되는 힘에 의해 주로 결정되고 타이어 힘은 타이어와 노면 사이의 접지력에 의해 결정된다. 그렇기 때문에 접지력에 지배적인 역할을 하는 노면 마찰계수는 차량 핸들링이나 안정성 제어 관점에서 매우 중요한 정보라 할 수 있다. 하지만 노면 마찰계수는 직접적으로 계측할 수 없는 정보이기 때문에 노면 마찰계수를 추정하기 위해 많은 연구들이 수행되어왔다. Brush 타이어 모델과 같이 노면 마찰계수 정보를 포함하지만 비교적 간단한 타이어의 수학적 모델을 이용한 노면 마찰계수 추정에 관한 연구,1,2) 노면 마찰계수와 타이어 슬립 각을 동시에 추정하기 위해 적응형 강건 추정 방식을 제안한 연구,3) 마찰계수에 따른 종방향 타이어의 μ-slip curve를 이용한 연구,4) 타이어 뉴메틱 트레일 정보를 활용한 연구5) 등 다양한 방식의 마찰계수 추정 방법들이 제안되고 있다.6,7)
이러한 기존 연구들은 현재의 노면 마찰계수를 보다 정확히 추정하는 것을 목표로 하고 있다. 하지만 노면 마찰계수의 정보가 차량 안정성 제어에 어떻게 쓰이는지에 따라 요구되는 마찰계수의 추정 성능은 다를 수 있다. 일반적으로 안정성 제어나 핸들링 제어는 차량의 요레이트를 제어해 안정성을 확보하는데 해당 제어기들은 대부분 목표 거동, 제어기, 그리고 분배기로 구성되어 있다.8) 해당 모듈 중 노면 마찰계수 정보는 주로 목표 거동과 분배기 모듈에 활용이 된다. 분배기 모듈에서 노면 마찰계수 정보는 현재 마찰 한계를 계산하고 이 한계 범위 내에 제어 시스템이 구동되도록 제한하는 역할을 한다. 그렇기 때문에 분배기 모듈에서 사용되는 노면 마찰계수는 정확히 추정된 값이어야 한다. 목표 거동 모듈에서 노면 마찰계수 정보는 목표 요레이트를 연산하는데 활용된다. 식 (1)과 (2)는 목표 요레이트의 계산 과정을 나타내고 있다. γss는 Bicycle 차량 모델로부터 산출된 정상상태 요레이트이고 γtar는 질점 역학의 원심력 원리에 따라 정상상태 요레이트에 노면 최대 마찰에 의한 물리적 제한을 준 최종 목표 요레이트이다.2) 식 (2)를 통해 마찰계수 정보가 정상상태 요레이트의 크기를 제한하는 데 사용됨을 알 수 있다.
| (1) |
| (2) |
안정성 제어가 필요한 대부분의 주행 상황은 운전자의 과도한 조향으로 발생되기 때문에 이때 연산된 목표 요레이트는 마찰계수에 의해 제한된다. 정확히 추정된 노면 마찰계수는 센서의 노이즈, 불 균일한 노면 정보 등을 포함하고 있기 때문에 일정한 값으로 추정되지 않는다. 이를 사용하여 정상상태 요레이트를 제한할 경우 목표 요레이트는 떨림이 발생되고 이는 차량의 안정성을 확보해 줄 순 있지만 차량 거동의 떨림을 발생시키게 된다. 그리고 식 (2)는 강체인 차량을 질점으로 가정하여 제한한 방식이기 때문에 일부 제한 오차를 허용할 수 있다. 이를 바탕으로 목표 거동 모듈에서 사용되는 노면 마찰계수는 일부 추정오차가 존재하더라도 일정한 값으로 추정되어야 한다는 요구사항을 얻을 수 있다. 또한 목표 요레이트는 일반적인 노면에서 운전자가 생각하는 이상적인 거동이다. 여기에서 일반적인 노면은 아스팔트 노면(고 마찰 노면)이라 할 수 있다. 그렇기 때문에 고 마찰 노면 상황에서 마찰계수 추정 오류로 인해 차량이 이상 거동을 보이는 것은 운전자가 납득할 수 없다. 반면 저 마찰 노면 상황은 일반적인 상황이 아니기 때문에 해당 노면에서 추정 오류로 인한 차량의 순간적인 이상 작동은 운전자가 납득할 수 있다. 물론 이상 작동 시간은 최소화되어야 한다.
본 연구에서는 현재 노면 마찰계수를 정확히 추정하기 위한 기존 연구와는 달리 목표 요레이트 계산에 사용될 노면 마찰계수 추정에 대한 방법을 제안하고 있다. 앞서 언급한 바와 같이 해당 노면 마찰계수는 현재 상태를 정확히 추정하기보단 일부 오차가 존재하더라도 일정하게 추정되어야 하고 저 마찰 노면을 고 마찰 노면으로 추정하는 것은 일부 수용이 되지만 고 마찰 노면을 저 마찰 노면으로 추정해서는 안 된다. 이러한 요구성능을 만족시키기 위한 추정 로직을 개발하고 그 성능을 시뮬레이션을 통해 확인하였다.
2. 노면 마찰계수 추정기 설계
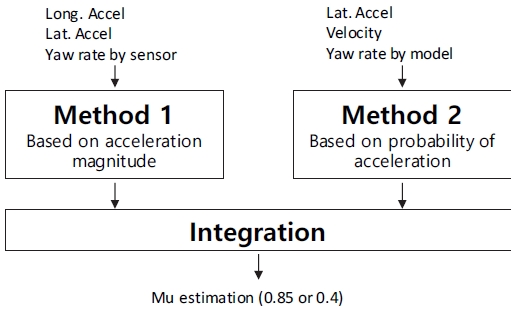
Fig. 1은 노면 마찰계수 추정기의 구조를 나타내고 있다. 해당 로직은 Method 1과 Method 2 이렇게 2개의 추정 모듈과 통합 모듈로 구성되어 있다. Method 1은 차량 가속도(종/횡 가속도)의 크기에 기반한 추정 방식이고, Method 2는 횡 가속도 신호를 이용해 확률적 방식(Bayesian tracking)을 적용한 추정 방식이다. Method 1의 경우 선회 초반에 고 마찰 노면을 저 마찰 노면으로 오 추정하는 문제가 있고, Method 2는 과도 주행 시 선회 중반에 고 마찰 노면을 저 마찰 노면으로 오 추정하는 문제가 있다. 각 방식들의 추정 문제를 해결하기 위해 두 추정치를 통합함으로써 최종 추정 로직을 개발하였다. 지금부터 각 모듈들에 대해 상세히 기술하도록 한다.
2.1 Method 1
Method 1은 차량의 종 가속도와 횡 가속도의 크기를 이용해 노면 마찰계수를 추정하는 방식이다. 차량의 가속도는 노면 마찰계수의 영향을 가장 직접적으로 받는 신호임을 식 (3)으로부터 알 수 있다.
| (3) |
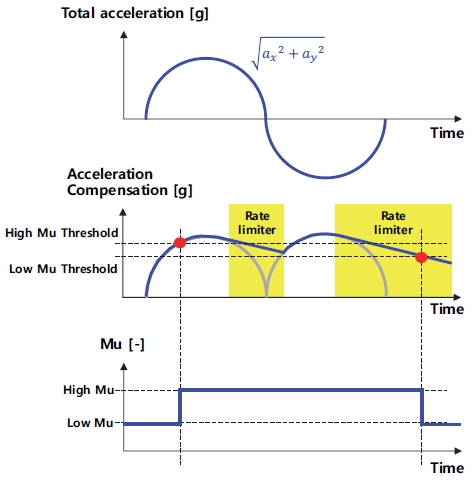
식 (3)은 Friction circle 관계에서 질량(m)을 소거하고 중력가속도(g)을 양변에 나눠주어 도출된 식으로, 차량이 낼 수 있는 중력 가속도 단위의 총 가속도는 노면 마찰계수 크기를 초과할 수 없다는 것을 의미한다.3) 따라서 차량의 총 가속도의 크기(중력 가속도 단위)가 노면 마찰계수라 할 수 있다. 하지만 이 방식은 차량이 마찰 한계까지 주행해야 추정 정확도를 보장할 수 있다. 또한 마찰 한계까지 주행하더라도 Single lane change나 Slalom 같은 Transient 한 주행일 경우 좌(우) 선회에서 우(좌) 선회로 바뀌는 상황에서는 차량의 횡 가속도는 0을 지나게 되어 추정 정확도가 떨어지게 된다. Method 1에서는 이러한 문제점들을 보완하여 노면 마찰계수를 추정한다. Fig. 2는 Single sine 정속 주행 상황에서 Method 1 추정 방법에 대한 개념을 보여주고 있다. 총 가속도에 절댓값을 취하고 Transient 주행 상황을 고려하여 절댓값에 기울기 제한을 준다. 서론에서 언급한 바와 같이 고 마찰 노면을 저 마찰 노면으로 오 추정하는 것을 최대한 방지하기 위해 감소 기울기만을 제한한다. 그리고 이 값을 기준으로 노면 마찰계수를 추정한다.
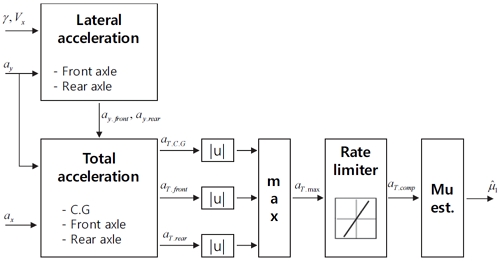
Fig. 3은 Method 1의 알고리즘 구조를 나타내고 있다. 우선 횡 가속도, 차속, 그리고 요레이트 센서 신호를 입력받아 전륜과 후륜의 횡 가속도를 연산한다. 전륜 횡 가속도는 빠른 노면 마찰계수를 추정하기 위함이고, 후륜 횡 가속도는 Transient 한 주행 시 횡 가속도 감소를 늦추기 위함이다. 이렇게 계산된 전/후륜 횡 가속도와 센서로 계측된 횡 가속도 그리고 종 가속도를 이용하여 전륜, 후륜, 그리고 무게 중심에서의 총 가속도를 각각 계산한다. 그 이후에는 절댓값, Max 함수, 그리고 기울기 제한 등을 통해 노면 마찰계수를 추정한다.
전륜과 후륜의 횡 가속도는 아래와 같이 계산할 수 있다.
| (4) |
식 (4)의 결과를 기반으로 전륜, 후륜, 그리고 무게 중심에서의 총 가속도는 중력 가속도 단위(g)로 다음과 같이 구할 수 있다.
| (5) |
식 (5)의 결과에 절댓값을 취한 후 최대 가속도를 산출한다.
| (6) |
최대 가속도에 감소 기울기를 제한하여 보정 가속도(aT.comp)를 산출한다.
| (7) |
여기에서 ∆는 내려가는 기울기 제한 값으로 고 마찰 노면에서 저 마찰 노면으로 바뀌는 상황에서 문제가 될 수 있다. 그렇기 때문에 μ jump(고 마찰 → 저 마찰) 상황에 대한 실차 시험을 통해 안정성 제어가 문제없이 수행되도록 설정해야한다. 본 논문에서는 시뮬레이션을 통해 1 g/sec로 설정하였다.
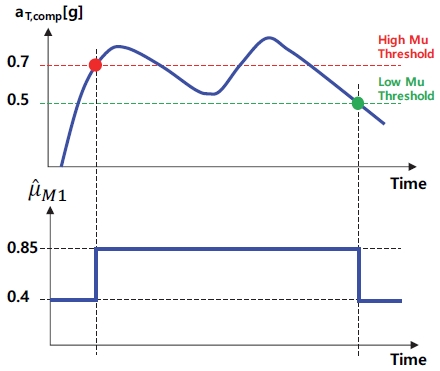
이렇게 계산된 보정 가속도를 기준으로 노면 마찰계수()가 추정된다. 서론에 언급한 바와 같이 본 추정기는 노면 마찰계수의 정확한 추정보다는 일부 오차가 있더라도 일정한 값으로 추정하는 것을 목표로 하고 있다. 따라서 보정 가속도를 이용해 Fig. 4와 같은 기준으로 노면 마찰계수를 추정하였다. 보는 바와 같이 보정 가속도가 0.7 g 이상일 경우 고 마찰 노면()으로 추정하고, 0.5 g 이하이면 저 마찰 노면()으로 추정한다.
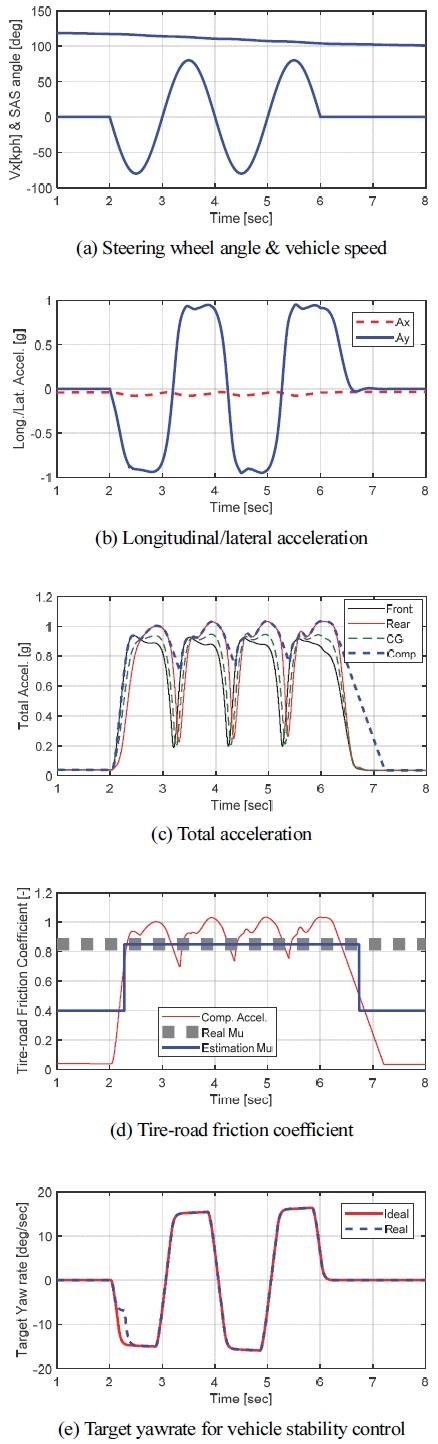
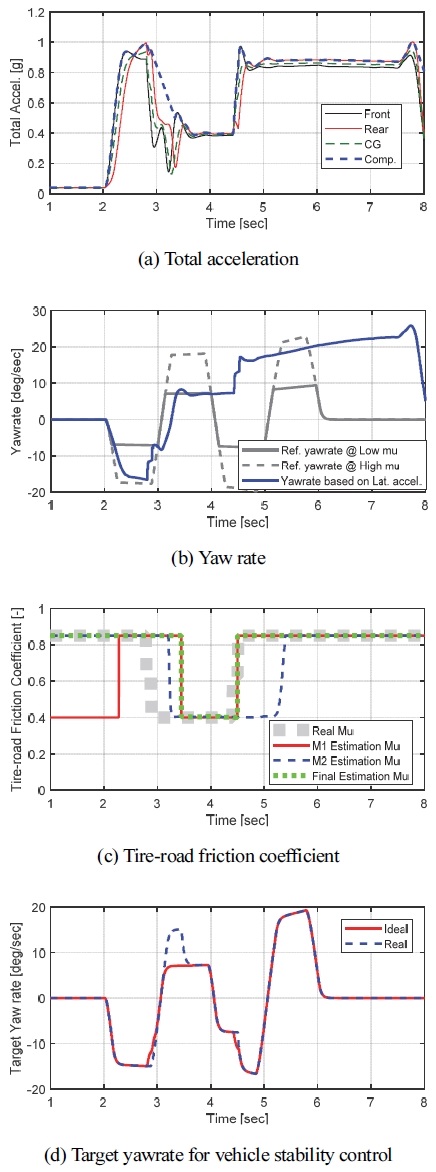
이렇게 개발된 Method 1 추정 방식의 성능을 확인하기 위해 시뮬레이션 해석을 Carmaker, Matlab/Simulink를 이용하여 실시하였다. 시뮬레이션 시나리오는 고 마찰 노면(μ = 0.85)이고 차량 속도가 120 kph인 상황에서 Single sine 조향(± 80 deg)을 한 경우로 안정성 제어가 필요한 한계 주행 상황이다. Fig. 5는 시뮬레이션 결과를 나타내고 있다. Fig. 5(a)는 주행 시나리오로 차속과 운전자 조향각을 나타내고, (b)는 종/횡 가속도를, (c)는 전/후륜 그리고 무게 중심에서의 총 가속도(aT.front, aT.rear, aT.C.G)와 이를 보정한 총 가속도(aT.comp)를, (d)는 보정된 총 가속도를 통해 추정된 노면 마찰계수를, 그리고 (e)는 추정된 노면 마찰계수를 통해 연산 된 목표 요레이트(Real)를 나타내고 있다. (d)를 통해 차량이 마찰 한계까지 주행을 하면 안정적으로 고 마찰 노면을 추정함을 확인할 수 있다. 하지만 마찰 한계까지 주행을 해야 정확한 추정이 가능하기 때문에 해당 방식으로 추정된 노면 마찰계수를 활용하여 목표 요레이트를 연산할 경우 선회 초반(2 ~ 3초 사이) 고 마찰 노면을 저 마찰로 오 추정하여 정상적인 목표 요레이트를 연산하지 못하는 것을 (e)를 통해 확인할 수 있다.
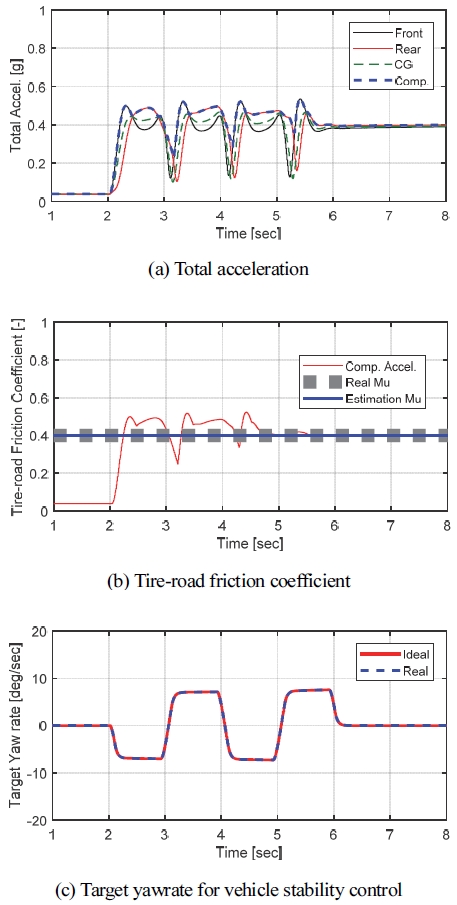
Fig. 6은 Fig. 5(a)와 같은 주행 상황을 저 마찰 노면(μ = 0.4)에서 시뮬레이션한 결과를 나타내고 있다. 해당 시나리오는 차량이 Spin-out 되어 차량이 직진으로 수렴하지 못함을 Fig. 6(a) 총 가속도 결과를 통해 확인할 수 있다. 차량이 Spin-out이 되어도 저 마찰 노면 상황에서는 해당 방식이 전 주행 구간에서 노면 마찰계수를 정확히 추정하여 목표 요레이트가 정상적으로 연산 됨을 확인할 수 있다.
2.2 Method 2
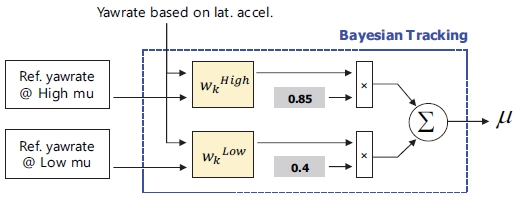
Method 2는 차량의 횡 가속도 신호를 기반으로 계산된 요레이트와 마찰계수 별(μ = 0.4, 0.85) 기준 요레이트 간의 비교를 통해 Bayesian tracking 방식을 적용하여 확률적으로 추정한다. Fig. 7은 Method 2 추정 방식의 구조를 나타내고 있다. 보는 바와 같이 센서로 계측된 횡 가속도에 기반한 요레이트와 마찰계수 별 기준 요레이트 간 크기 비교를 통해 현재 노면이 고 마찰 노면일 확률(wkHigh)과 저 마찰 노면일 확률(wkLow)을 계산하여 최종 노면 마찰계수를 추정한다.
횡 가속 기반 요레이트는 식 (8)과 같이 횡 가속도의 Kinematic 한 관계식을 통해 계산할 수 있다.
| (8) |
위 식에서 롤 각(ϕ)과 횡 속도 미분 값을() 작다고 가정하면 횡 가속도 기반 요레이트는 아래와 같이 간단히 계산할 수 있다.
| (9) |
마찰계수 별 기준 요레이트의 경우 식 (1)에서 나타낸 정상상태 요레이트(γss)를 이용하여 계산할 수 있다. 식 (1)로부터 계산된 정상상태 요레이트를 식 (10)와 같이 마찰계수에 대한 제한을 두어 마찰계수 별 기준 요레이트를 계산한다.
| (10) |
여기에서, i는 고 마찰 노면과 저 마찰 노면을 의미한다. 고 마찰 노면의 경우 μi를 0.85로 저 마찰 노면의 경우 0.4로 설정하여 마찰계수 별 차별화된 크기 제한을 가진 기준 요레이트를 계산할 수 있다. 최종 노면 마찰계수는 아래와 같이 고 마찰 노면 값(μHigh = 0.85)과 저 마찰 노면 값(μLow = 0.4)의 가중치의 합으로 추정할 수 있다.
| (11) |
여기에서, μHigh = 0.85, μLow = 0.4이고 가중치인 와 는 앞서 계산한 요레이트 값들로부터 확률적으로 아래와 같이 계산할 수 있다.
| (12) |
여기에서, i = High μ, Low μ를 의미하고 Zk = [γay.0 ⋯ γay.k-1 γay.k] 로 현재까지(0 ~ k step) 측정한 횡 가속도 기반 요레이트를 의미한다. 따라서 위 식 (12)는 횡 가속도 기반 요레이트를 입력받았을 경우 i 일 확률을 의미한다. 식 (12)을 Recursive form으로 표현하면 아래와 같다.
| (13) |
식 (13)에 Bayes’s rule을 적용하면 아래와 같이 정리할 수 있다.9)
| (14) |
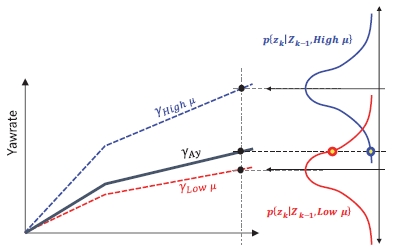
위 수식에서 p{zk|Zk-1, i}는 Conditional probability function으로 i (Low μ또는 High μ)에서 zk(횡 가속도 기반 요레이트γak.y)가 나올 확률로 식 (15)와 같이 Gaussian으로 가정한다. Fig. 8은 해당 방식의 개념을 나타내고 있다.
| (15) |
여기에서 는 마찰계수 별 기준 요레이트로 식 (10)에서 계산된 요레이트(γHigh μ, γLow μ)를 의미한다. S는 Error covariance로 크게 설정할 경우 추정 속도는 느리나 모델 오차에 둔감하게 반응하여 기준 요레이트가 실제 차량과 오차가 존재하더라도 안정적으로 추정된다는 장점이 있고 작게 설정할 경우 추정 속도는 빠르나 모델 오차에 민감하게 반응한다는 단점이 있다. 따라서 S는 일부 오차가 존재하더라도 일정하게 추정되어야 한다는 요구 성능과 기준 요레이트의 정확도를 종합적으로 고려하여 실차 시험 시 튜닝해야 할 파라미터이다. 본 논문에서는 S를 0.15로 설정하였다.
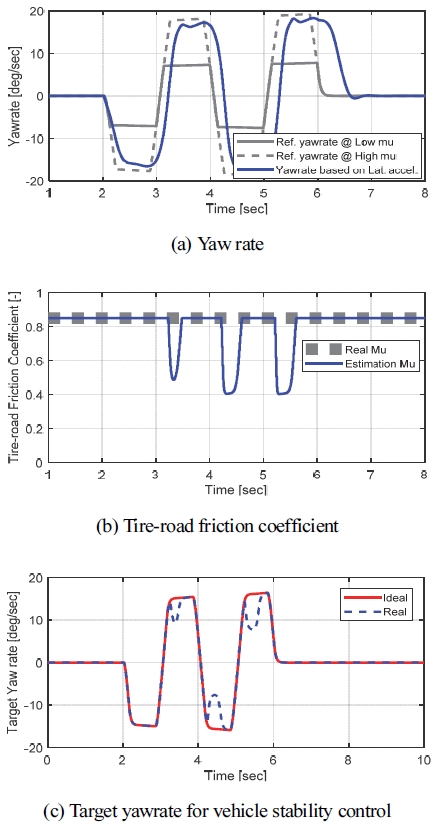
Method 2 추정 방법에 대한 성능을 확인하기 위해 앞 절과 동일한 조건에서 시뮬레이션을 수행하였다. Fig. 9는 고 마찰 노면에서의 시뮬레이션 결과를 나타내고 있다. Fig. 9(a)는 횡 가속도 기반 요레이트와 마찰계수 별 요레이트를 나타내고 있다. 고 마찰 노면이기 때문에 횡 가속도 기반 요레이트와 고 마찰 노면에 대한 기준 요레이트가 크기 면에서 유사한 경향이 있음을 알 수 있다. 하지만 선회 중반 이후로 갈수록 이 두 신호 간 위상 차이가 크게 발생하며 마찰계수 추정에 오차가 발생함을 (b)를 통해 알 수 있다. 또한 이러한 추정 오차로 인해 정상적인 목표 요레이트를 연산하지 못함을 (c)를 통해 확인할 수 있다.
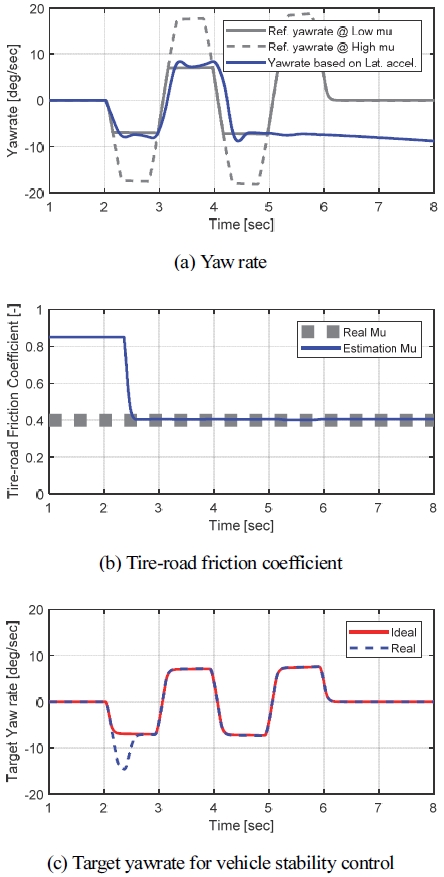
Fig. 10은 저 마찰 노면에서 시뮬레이션 결과들을 나타내고 있다. 선회 초반 순간적으로(0.5초 내외) 저 마찰 노면을 고 마찰 노면으로 오 추정하는 결과를 보이고 있다. 이는 서론에서 언급한 저 마찰 노면을 순간적으로 고 마찰 노면으로 오 추정해도 된다는 요구사항에 만족되는 결과로 추정 성능에 문제가 없다고 볼 수 있다.
2.3 Integration
앞 절에서 서술한 Method 1과 2의 성능 결과를 정리하면 다음과 같다. 우선 고 마찰 노면 상황에서 Method 1의 경우 차량이 마찰 한계까지 주행을 해야 정확한 마찰계수가 추정이 가능하기 때문에 선회 초반 고 마찰 노면을 저 마찰 노면으로 잘못 추정하는 문제가 있다. 이는 서론에서 언급한 추정기 요구사항을 만족시키지 못하게 된다. 반면 Method 2는 선회 초반 추정엔 문제가 없으나 선회 중반 이후 추정 오차가 발생되는 문제를 보이고 있다. 저 마찰 노면 상황에서 Method 1의 경우 전 구간 정확히 저 마찰 노면으로 추정함을 확인하였고 Method 2는 선회 초반 순간적으로 저 마찰 노면을 고 마찰 노면으로 잘못 추정하나 이는 추정기 요구사항을 불만족하지 않는 성능임을 확인하였다. 즉, Method 1은 선회 초반 추정기 요구사항을 만족시키지 못하고 Method 2는 선회 중반에 요구사항을 만족시키기 못하는 경우가 존재한다.
앞서 서술한 각 방식 별 성능 특성을 바탕으로 두 추정 값들 중 큰 값을 사용할 경우 추정기 요구사항을 모두 만족함을 알 수 있다. 따라서 Integration 모듈에서는 식 (16)과 같이 두 추정 값들의 최댓값을 취함으로써 최종 노면 마찰계수를 구할 수 있다.
| (16) |
3. 시뮬레이션 기능 검증
노면 마찰계수 추정 로직을 평가하기 위해 시뮬레이션 해석을 앞 장과 동일하게 Carmaker, Matlab/Simulink를 이용하여 실시하였다. 총 2가지 Case로 시뮬레이션을 수행하였는데 첫 번째 Case는 노면 마찰계수 추정 성능 자체를 검증한 경우로 고 마찰 노면, 저 마찰 노면, 그리고 μ jump(고 마찰 → 저 마찰 → 고 마찰) 상황에 대해 추정 성능을 확인하였다. 두 번째 Case는 본 논문에서 제안한 추정 로직이 차량 제어에 충분히 활용될 수 있음을 보이기 위해 첫 번째 case와 동일한 주행 상황에서 추정된 마찰계수를 이용해 횡 안정성 제어를 실시한 경우이다.
3.1 노면 마찰계수 추정 성능 검증
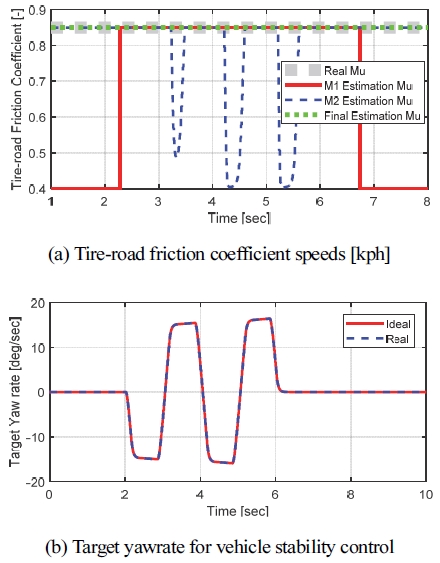
본 절에서는 노면 마찰계수 추정 성능 자체를 검증하기 위해 고 마찰 노면, 저 마찰 노면, 그리고 μ jump(고 마찰 → 저 마찰 → 고 마찰) 상황에 대해 시뮬레이션을 수행하여 그 성능을 검증하였다. 주행 상황은 120 kph에서 Single sine 조향(± 80 deg)을 한 경우로 Fig. 5(a)와 동일하다. 아래 Fig. 11은 고 마찰 노면 상황에서의 시뮬레이션 결과를 나타내고 있다. Fig. 11(a)는 추정된 노면 마찰계수의 결과를, 그리고 (b)는 추정된 노면 마찰계수를 이용해 연산된 목표 요레이트를 나타내고 있다. 최종 추정된 노면 마찰계수가 실제 노면 마찰 계수와 정확히 일치되어 목표 요레이트를 정상적으로 연산함을 확인할 수 있다.
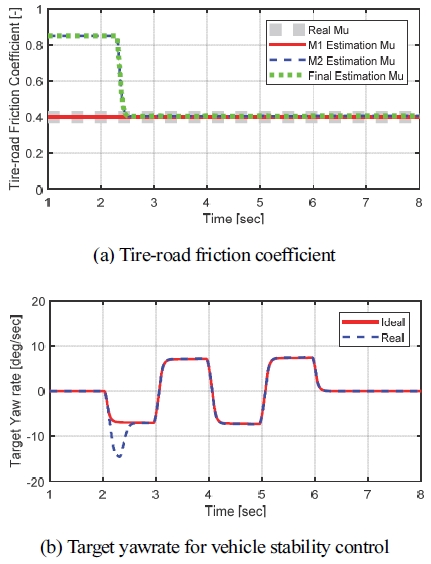
Fig. 12는 저 마찰 노면 상황에서의 시뮬레이션 결과를 나타내고 있다. 선회 초반 저 마찰 노면을 고 마찰 노면으로 오 추정하여 추정 값을 이용해 연산한 목표 요레이트(Real)가 이상적인 목표 요레이트(Ideal) 보다 크게 연산 되지만 0.5초 내에 이상적인 목표 요레이트와 동일해지는 것을 확인할 수 있다.
Fig. 13은 μ jump 상황에서의 시뮬레이션 결과를 나타내고 있다. Fig. 13(a)는 Method 1 추정 방식에 사용된 총 가속도를, (b)는 Method 1 추정 방식에 사용된 요레이트를, (c)는 추정 노면 마찰계수를, 그리고 (d)는 목표 요레이트를 각각 나타내고 있다. 앞선 결과와 동일하게 고 마찰 노면인 경우 오차 없이 바로 추정이 되고 저 마찰 노면으로 바뀌는 경우 초반에 오 추정이 되지만 0.5초 내에 정상 추정이 되어 μ jump 상황에서도 목표 요레이트 연산에 문제가 없음을 확인할 수 있다.
3.2 추정 노면 마찰계수 활용 안정성 제어 검증
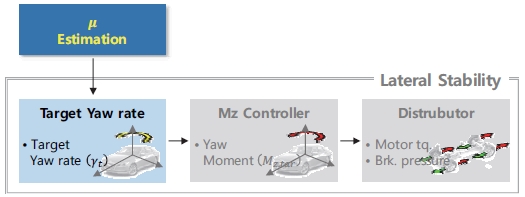
앞 절에서는 다양한 노면 상황에서 노면 마찰계수 추정 성능과 이를 이용한 목표 요레이트의 연산 결과를 확인하였다. 본 절에서는 앞 절에서 계산한 목표 요레이트를 이용하여 차량 횡 안정성 제어를 수행한 결과를 보여준다. 횡 안정성 제어 알고리즘은 인휠 모터 시스템을 이용한 연구 결과를 활용하였다.8) Fig. 14는 횡 안정성 제어 알고리즘의 구조를 나타내고 있다. 해당 제어는 목표 요레이트, Mz 제어기, 분배기로 구성되어 있다. 서론에선 언급한 바와 같이 본 연구에서 개발한 노면 마찰계수 추정 알고리즘은 목표 요레이트 모듈에 활용된다. 안정성 제어 알고리즘은 기존 연구를 활용하였기 때문에 각 모듈에 대한 설명은 생략한다. Table 1은 제어 대상 차량의 제원을 나타내고 있다.
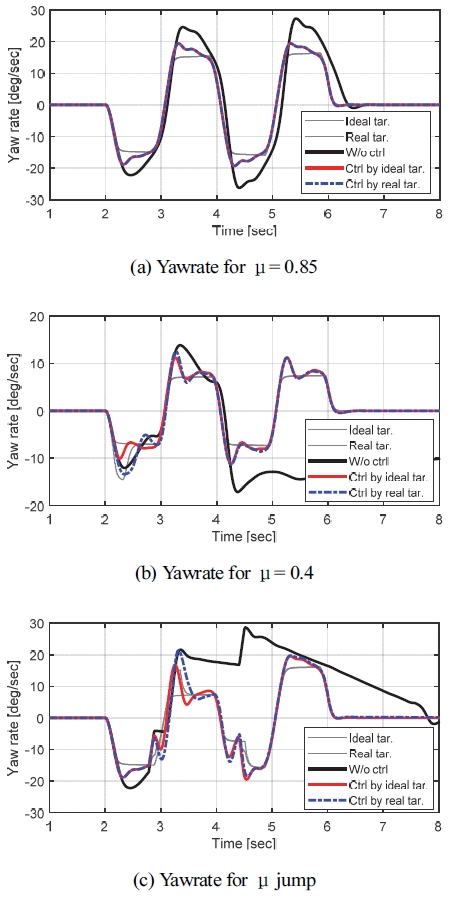
Fig. 15는 안정성 제어 결과로 요레이트를 나타내고 있다. Fig. 15(a)는 고 마찰 노면에서의 결과를, (b)는 저 마찰 노면에서의 결과를, 그리고 (c)는 μ jump 상황에서의 결과를 각각 나타내고 있다. 각각의 그래프에 얇은 회색 실선 2개는 이상적인 목표 요레이트와 추정된 노면 마찰계수를 이용해 연산 된 목표 요레이트를 나타내고 있다. 목표 요레이트에 대한 결과는 앞 절에서 이미 보여주었고, 이를 이용한 제어 결과를 보는 것이 본 절의 목표이기 때문에 목표 요레이트들을 같은 선으로 표현하였다. 검은색 실선은 미 제어 시의 차량 요레이트이고, 빨간색 실선은 이상적인 목표 요레이트로 제어했을 때의 요레이트, 그리고 파란색 점선은 추정된 노면 마찰계수를 이용해 연산한 목표 요레이트로 제어했을 때의 요레이트를 나타내고 있다. 고 마찰 노면 상황에서는 이상적 목표 요레이트와 연산된 목표 요레이트가 동일하기 때문에 제어된 요레이트의 성능이 동일함을 알 수 있다. 그리고 저 마찰 노면이나 μ jump 상황에서는 저 마찰 노면 초반에 순간적인 오 추정으로 이상적인 제어 결과보다 Overshoot이 크게 발생해 약간 불안정적인 모습을 보이나 바로 정상 추정이 되며 안정성이 확보됨을 확인할 수 있다.
4. 결 론
본 논문에서는 차량 안정성 제어에 매우 중요한 정보 중 하나인 노면 마찰계수를 추정하는 연구를 수행하였다. 차량 안정성 제어기는 기본적으로 목표 거동, 제어기, 그리고 분배기 모듈로 구성되었다. 해당 모듈 중 노면 마찰계수 정보는 주로 목표 거동과 분배기에 활용된다. 목표 거동에서는 목표 요레이트에 제한을 주기 위해 활용되고 분배기에서는 마찰 한계를 알기 위해 활용된다. 각 모듈 별 노면 마찰계수 정보의 활용 목적이 다르기 때문에 각 모듈에서 요구하는 마찰계수 추정 성능의 요구사항이 다르다. 분배기 모듈은 현재 노면 마찰계수를 정확히 추정해야 한다는 요구사항이 있는 반면, 목표 거동 모듈에서는 차량의 선형적인 거동 제어를 위해 추정 오차가 일부 존재하더라도 일정한 값으로 추정되어야 하고 저 마찰 노면을 고 마찰 노면으로 오 추정되는 것을 일부 허용하되 고 마찰 노면을 저 마찰 노면으로 오 추정되어서는 안된다는 요구사항이 있다. 본 연구에서는 목표 거동 모듈에 활용할 수 있는 노면 마찰계수 추정기를 제안하였다. 해당 추정기는 횡 가속도 크기 기반의 추정 방식(Method 1)과 횡 가속도 기반으로 계산된 요레이트와 마찰 계수 별 기준 요레이트를 이용해 확률적 방식(Bayesian tracking)을 적용한 추정 방식(Method 2)를 통합하여 개발하였다. 제안한 추정 로직은 Carmaker 시뮬레이션을 통해 고 마찰 노면 상황, 저 마찰 노면 상황, 그리고 μ jump 상황에서 그 성능을 확인하였고, 추정된 마찰계수 정보를 활용하여 안정성 제어 수행 시 문제없이 차량 안정성이 확보됨을 검증하였다. 향후에는 개발된 로직을 실차 환경에서 검증할 예정이다.
Nomenclature
| ax : | longitudinal acceleration |
| ay : | lateral acceleration |
| g : | gravity acceleration |
| Lf : | distance from the center of gravity(CG) to front axle |
| Lr : | distance from the CG to rear axle |
| Cf : | front tire cornering stiffness |
| Cr : | rear tire cornering stiffness |
| Vx : | vehicle longitudinal velocity |
| Vy : | vehicle lateral velocity |
| δf : | tire steer angle |
| μ : | tire-road friction coefficient |
| ϕ : | vehicle roll angle |
Acknowledgments
본 연구는 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2022R1A2C1004405, No.2021R1F1A1050200). 본 연구는 2022학년도 한국기술교육대학교 교육연구진흥과제 지원을 받아 수행된 연구임. 본 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(‘20024837’), 본 연구는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 3단계 산학연협력 선도대학 육성사업(LINC 3.0)의 연구결과임.
References
- K. Park, S. J. Heo, I. Paik and K. Yi, “Estimator Design for Road Friction Coefficient and Body Sideslip Angle for Use in Vehicle Dynamics Control Systems,” Transactions of KSAE, Vol.9, No.2, pp.176-184, 2001.
-
K. B. Singh and S. Taheri, “Estimation of Tire–road Friction Coefficient and Its Application in Chassis Control Systems,” Systems Science & Control Engineering, Vol.3, No.1, pp.39-61, 2015.
[https://doi.org/10.1080/21642583.2014.985804]

-
C. Ahn, H. Peng and H. E. Tseng, “Robust Estimation of Road Frictional Coefficient,” IEEE Transactions on Control Systems Technology, Vol. 21, No.1, pp.1-13, 2013.
[https://doi.org/10.1109/TCST.2011.2170838]

-
J. Y. Park, W. Shim and S. J. Heo, “A Study of Tire Road Friction Estimation for Controlling Rear Wheel Driving Force of 4WD Vehicle,” Transactions of KSAE, Vol.24, No.5, pp.512-519, 2016.
[https://doi.org/10.7467/KSAE.2016.24.5.512]

-
K. Han and S. Choi, “A Study on Lateral Tire-road Friction Coefficient Estimation Using Tire Pneumatic Trail Information,” Transactions of KSAE, Vol.24, No.3, pp.310-318, 2016.
[https://doi.org/10.7467/KSAE.2016.24.3.310]

-
J. Hu, S. Rakheja and Y. Zhang, “Tire-Road Friction Coefficient Estimation under Constant Vehicle Speed Control,” ScienceDirect, Vol.52, No.8, pp.136-141, 2019.
[https://doi.org/10.1016/j.ifacol.2019.08.061]

-
C. H. Hsu, S. P. Ni and T. Hsiao, “Look-Up Table-Based Tire-Road Friction Coefficient Estimation of Each Driving Wheel,” IEEE Control Systems Letters, Vol.6, pp.2168-2173, 2022.
[https://doi.org/10.1109/LCSYS.2021.3137722]

-
I. G. Jang, S. H. You, S. H. Hwang and W. Cho, “Lateral Stability Control of a 4-Wheel Independent Drive Electric Vehicle Using the Yaw Moment Contour Line Concept,” IEEE Access, Vol.9, pp.136892-136904, 2021.
[https://doi.org/10.1109/ACCESS.2021.3117295]

-
C. Shen, H. Li and M. J. Brooks, “Classification-Based Likelihood Functions for Bayesian Tracking,” 2006 IEEE International Conference on Video and Signal Based Surveillance, p.33, Sydney, NSW, Australia, 2006.
[https://doi.org/10.1109/AVSS.2006.33]