MR 유체와 댐퍼 형상 및 물성을 고려한 MR 댐퍼 감쇠력 예측 프로그램
Copyright Ⓒ 2023 KSAE / 217-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Magneto-Rheological(MR) fluid-based dampers provide different damping forces, depending on the magnetic field generated by an electromagnet. This study aims to develop a damping force prediction program for MR dampers by modelling the properties of MR fluids and the magnetic properties of MR damper designs. Through the characterization and analysis of MR fluid properties, this study aims to establish a framework to understand the behavior of MR dampers and their impact on vehicle dynamics. Then, the developed program can be used to predict the damping force at the design stage, enabling efficient design and optimization of MR dampers in automotive applications.
Keywords:
MR damper, MR fluid, Magnetic flux density, Yield point, Bi-plastic Bingham model키워드:
MR 댐퍼, MR 유체, 자속밀도, 항복점, 이중 소성 빙햄 모델1. 서 론
차량용 현가장치는 불규칙적인 노면에 의해 발생하는 외란을 최소화하여, 승차감과 주행 안정성을 향상시켜 주는 장치이다.1) 현가장치는 에너지의 입력 없이 동작하는 수동형, 에너지의 입력이 들어가는 능동형, 능동형 중에서 시스템에 에너지의 입력 없이 전자적으로 특성이 변화하는 반 능동형으로 나뉜다. MR 댐퍼는 자기유변(Magneto-rheological) 유체를 이용하여 노면 상태 및 주행 환경에 따라 감쇠력을 유동적으로 제어할 수 있으므로, 반 능동 현가장치에 널리 이용된다.2) MR 댐퍼는 불규칙한 노면에서 승차감(Ride) 성능을 향상시키며, 감쇠력 제어를 통하여 조향(Handling)시 차량의 차체 거동을 개선할 수 있다고 기대된다.3,4) MR 댐퍼 개발 과정의 효율화를 위해 설계 인자로부터 MR 댐퍼의 감쇠력 특성을 예측하는 것이 필요하다.
MR 댐퍼의 형상, 코일(Coil)의 수, 유로의 넓이 등은 댐퍼 감쇠력에 영향을 준다.5) 감쇠력 특성을 유추하기 위해 MR 유체의 전단 특성을 Bi-plastic Bingham 모델로 근사하였고, 댐퍼의 형상 및 재질에 따른 자기장 해석을 위해 오픈소스(Open-source)인 FEMM(Finite Element Method Magnetics)6) 소프트웨어를 사용하였다.
본 연구에서는 형상 인자(전자석 설계부 길이, 코일 수, 유로의 넓이 등)를 입력하면 내부적으로 자기장을 해석하고, Bi-plastic Bingham 모델로부터 도출된 MR 유체의 항복응력 비(δ), 점도 비(γ)와 같은 유체 특성 인자를 추가하여 감쇠력을 계산하는 프로그램을 개발하였다. 유체 특성으로 표현할 수 없는 관로 저항과 마찰력의 영향도 고려하였다. 연산 및 GUI(Graphi User Interface)는 MATLAB 소프트웨어(Software)를 활용하여 제작하였다.
시뮬레이션 프로그램의 신뢰성을 확인하기 위해 프로그램으로부터 출력 받은 감쇠력의 결과값과 실제 실험 데이터를 비교하였다.
2. 이론적 배경
MR 유체는 현탁액으로, 자기장이 가해졌을 때 입자간의 Chain을 형성하고 강한 인력을 가지게 된다.7) 이러한 MR 유체의 특성은 자기장에 따라 달라지며, 감쇠력 계산에 유체 특성을 고려하기 위해서는 유체의 거동을 설명하는 모델이 필요하다.
2.1 유체 모델
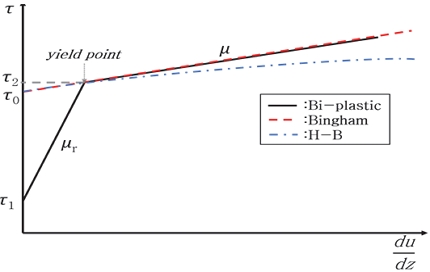
일반적으로 자기 유변 유체의 특성을 고려하기 위해 Bingham plastic, Bi-plastic Bingham, Herschel-Burkley (H-B) 모델이 많이 이용된다. 이 외에도 MR 유체의 비선형 유변학적 특성을 설명하기 위한 Eyring, Casson, Papanastasious, Papanastasious-Herschel-Bulkley와 같은 모델8)들이 있지만 많은 매개변수, 복잡한 특성 및 복잡한 계산으로 인하여 댐퍼 설계 단계에서 이용하기엔 적합하지 않은 모델들이다. 따라서, 본 연구에서는 MR 유체의 특성을 모델링하기 위해 Bingham plastic, Bi-plastic Bingham, H-B 모델을 검토하였다. 3가지 모델을 이용한 전단응력 방정식은 각각 식 (1), 식 (2), 식 (3)으로 주어진다.
| (1) |
| (2) |
| (3) |
τ0는 항복 전(Pre-Yield) 영역의 정적 항복응력, τ1은 항복 후(Post-Yield) 영역의 정적 항복응력, τ2는 항복 후 영역의 동적 항복응력, μ는 항복 전의 유체 점도, μr는 항복 후의 유체 점도(Viscosity), m은 유동 거동 지수(Flow index)이다. 3가지 모델이 보이는 전단률-전단응력 관계는 Fig. 1로 확인할 수 있다.
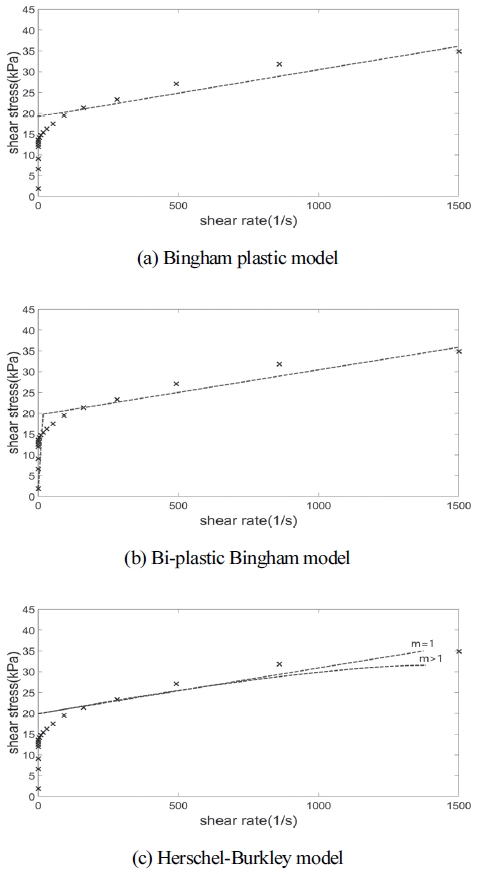
Fig. 2는 개발 중인 MR 유체의 전단률-전단응력 실험 데이터와 모델링의 비교 검증 결과이며, MR 유체의 전단응력 실험 결과는 점으로, 모델은 점선으로 표시하였다.
Fig. 2(a)와 식 (1)에서 Bingham plastic 모델은 저전단률에서 신뢰성을 확보할 수 없는 것을 확인하였다. Fig. 2(c)와 식 (3)의 H-B 모델은 유동 거동 지수(m)으로 전단 박화/ 농화 효과를 설명할 수 있으나, 실험 결과가 m=1에 가까워서 큰 의미가 없다.
Fig. 2(b)와 식 (2)의 Bi-plastic Bingham 모델은 Bingham plastic 모델에 항복응력 비를 추가한 모델이고 근사적으로 전단 박화/농화 효과를 보인다. MR 유체의 실험 데이터로 확인할 수 있듯이 MR 유체는 항복 전, 후로 전단응력의 변화 특성이 다르다. Bi-plastic Bingham 모델은 항복(Yield point) 전, 후의 전단응력의 변화 특성을 비교적 잘 설명할 수 있다. 또한, 무차원 변수를 이용한 감쇠력 방정식을 얻을 수 있어, Bi-plastic Bingham 모델이 MR 유체의 특성을 나타내는 데에 용이함을 확인하였다.9)
2.2 모델을 통한 감쇠력 도출
MR 유체를 모델링하여 전단률-전단응력 실험값에서 속도-힘 관계를 얻기 위해서는 일련의 과정이 필요하다. 본 연구는 댐퍼의 감쇠력 예측을 위해 Goldasz 등9)의 모델링 과정을 참고하였다. 복잡한 유동 방정식을 간단하게 만들기 위해 무차원 변수를 활용한다. 식 (4)의 변수는 압력 변수(Pressure number), 가소 변수(Plastic number)이다.
| (4) |
여기서, L은 전자석 몸체의 축 방향 길이, Qa는 유량(Volume Rate), w는 전자석 몸체의 원주 둘레이다. 체적 유량, 압력 구배를 무차원 매개변수와 댐퍼의 대칭성 등을 이용하여 피스톤의 Bi-plastic Bingham 모델의 유로의 입 출구 압력차를 구할 수 있다.10)
| (5) |
위 식은 각각 S<S0(항복 전), S≥S0(항복 후)구간에서 유로의 압력의 차이이다. 여기서 γ는 점도 비(μ/μr), δ는 항복응력 비(τ1/τ2), S0는 γ(2 − 3δ + δ3), x, y, x′, y′는 식 (6)으로 주어진다.
| (6) |
식 (5)를 실제 유로 면적에 적용하여 얻은 감쇠력에 마찰력, 관로저항을 추가한다면 최종적으로 다음의 항복 전, 후로 댐퍼 감쇠력 수식을 얻을 수 있다.
| (7) |
여기서Fdamp는 댐퍼의 감쇠력, Vp는 피스톤의 속도, Cp는 관로 저항계수, μ0는 자기장을 가하지 않았을 때의 유체의 점도, h는 유로의 폭, Aeff는 유로의 면적,La는 코어에서 전자석을 제외한 길이, Ff는 마찰력이다.
3. 형상 및 물성을 고려한 감쇠력 시뮬레이션
설계 프로그램 개발에 있어 가장 중요한 목표는 실험 데이터와의 유사성이다. 따라서, 현재 유체 파라미터들의 중요성과 영향에 대해 파악하고, 실험과 프로그램 F-v 선도를 비교하는 과정을 보이고자 한다.
감쇠력 곡선에 영향을 미치는 요소는 다양하다. 댐퍼의 유로 형상은 압력 강하에 영향을 미치고, 댐퍼 재료의 물성, 코일의 수 등은 자속밀도에 영향을 주어 댐퍼의 감쇠력에 영향을 준다.
감쇠력은 유체의 자속밀도(B)-자계(H) 특성, 자속밀도(B)-전단응력(τ) 특성, 점도 비(γ), 항복 응력 비(δ) 등에 의해서도 영향을 받는다. 이때 다양한 전류에서 MR 유체에 가해지는 자기장의 산출은 감쇠력 예측에 가장 첫 단계의 과정이다.
3.1 댐퍼 형상
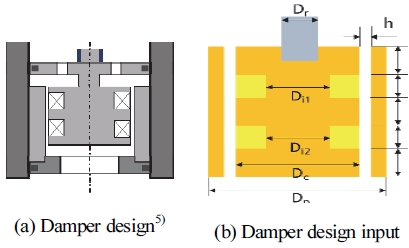
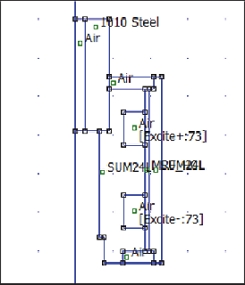
댐퍼의 형상은 유로의 폭, 피스톤(Piston)의 직경, 코일의 직경, 로드(Rod)의 직경 등으로 결정된다. 본 연구에서는 설계 형상을 기반으로 자기장 해석을 진행하기 때문에 댐퍼의 설계 파라미터를 입력으로 받아 감쇠력 예측 및 자기장 해석의 기본 환경을 구축한다. Fig. 3(a), Fig. 3(b)은 각각 듀얼 타입 댐퍼 형상과 자기장 해석에서 사용하는 형상 입력 치수이다.
3.2 재료 물성 및 자기장 해석
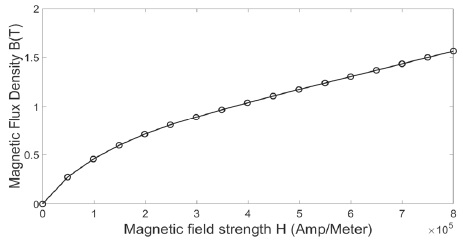
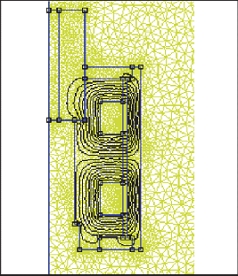
본 연구에서는 FEMM을 통해 입력된 댐퍼 형상에 따른 자기장을 해석하였다. FEMM은 기계 가공이나 열처리의 영향을 배제했기 때문에 높은 신뢰도를 확보하기 어렵지만11) 유체의 B-H 특성, 댐퍼 피스톤 형상의 재료 선정을 통해 대략적인 자속밀도를 효과적으로 얻어낼 수 있으므로, 설계 단계에서 예측값을 구하는 데에는 효율적일 것으로 판단하였다. FEMM에 입력된 MR 유체의 B-H 특성은 Fig. 4에 나타났으며, MR 댐퍼의 재료의 입력은 Fig. 5처럼 FEMM에 입력한다.
유체 특성, MR 댐퍼의 재료 및 형상 입력으로 유한요소 해석을 수행하면 Fig. 6의 자기장 해석 결과가 나타난다. 자기장 해석 수행 후 MR 유체가 통과하는 관로의 평균 자속밀도 값을 계산할 수 있다.
Table 1은 FEMM 해석 결과 Fig. 7의 결과로 얻은 전자석에 주어진 전류별 관로의 평균 자속밀도(B)이다.
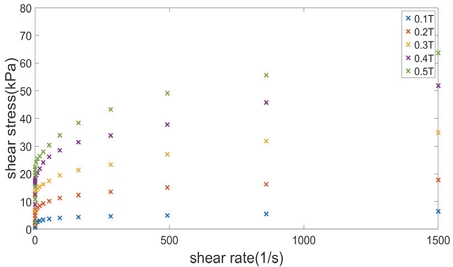
반면에 MR 유체 제작 업체로부터 제공받은 데이터 Fig. 7은 특정 자속밀도에 대한 전단률-전단응력 데이터로 한정되어 있다. 자속밀도 해석의 값과 일치하지 않으므로, 제한된 데이터에서 해석에 필요한 자속밀도의 전단률-전단응력 데이터를 얻는 것이 필요하다.12)
본 프로그램에서는 한정된 유체 데이터를 얻기 위해서 MATLAB을 사용해 Fig. 8과 같이 간단한 선형보간법을 사용하였다. Fig. 7에서 알 수 있듯이 비선형성이 높은 구간에서 더 정확한 예측을 위해서는 주어진 데이터 기반으로 가상 자속밀도에서의 전단률-전단응력 데이터를 얻기 위해 추가적인 연구가 필요하다.
3.3 Shear strain-Shear stress 데이터 비교
유체 실험 데이터의 모델링을 통해서 점성 비(γ), 항복응력 비(δ)을 얻기 위해서는 정확한 전단응력 데이터가 필요하다. 댐퍼의 작동속도를 고려하면 최소 1,000(1/s)에 근사하는 높은 전단률까지 필요하다. 또한, 낮은 전단률 구간에서 항복점이 결정되며, 0(1/s)에서 정적 항복응력(τ1)이 큰 영향을 미치기 때문에 저속 전단률 구간의 자세한 측정도 필수적이다.
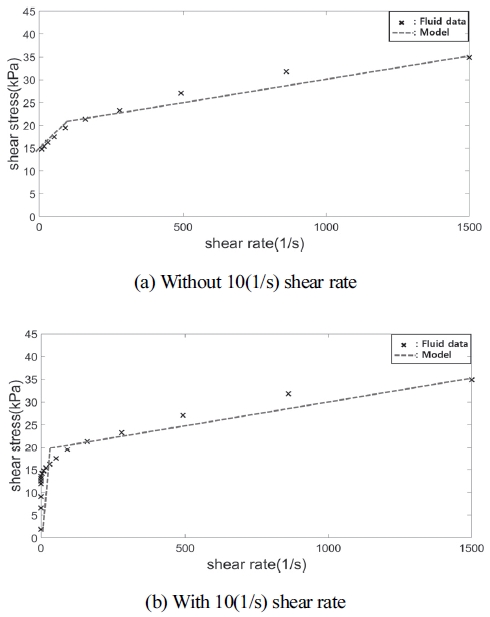
모델에서 항복점 지정과 정적 항복응력(τ1)은 점성 비(γ), 항복응력 비(δ)에 실질적인 영향을 가장 많이 준다. 실험 데이터에서는 명확하지 않은 항복점을 선정하여 항복 이전과 이후 구간으로 구분하는 데에는 정형화된 과정이 존재하지 않으며 연구자, 데이터마다 다양하며, 이에 따라 결과가 크게 달라진다.12) 실제로는 유체에서 정확한 저속 전단률의 필요성을 살펴보기 위해, 개발 중인 동일한 유체에 대해 두 번의 측정한 결과가 Fig. 9이다. Fig. 9(a)는 10(1/s) 이하 데이터가 없는 경우, Fig. 9(b)는 10(1/s) 이하 데이터가 있는 경우이다.
전체 데이터 영역에서 10(1/s)이하 데이터는 비교적 짧은 구간이지만, 점도 비(γ)에 큰 영향을 미친다. 정적 항복응력(τ1)은 실험 데이터 중 최저 전단률에서 근사적으로 구해지기 때문에 두 경우에서 큰 차이를 보여, 결과적으로 점도 비(γ)와 항복응력 비(δ)에 영향을 주게 된다.
3.4 항복점 선정에 따른 감쇠력 비교
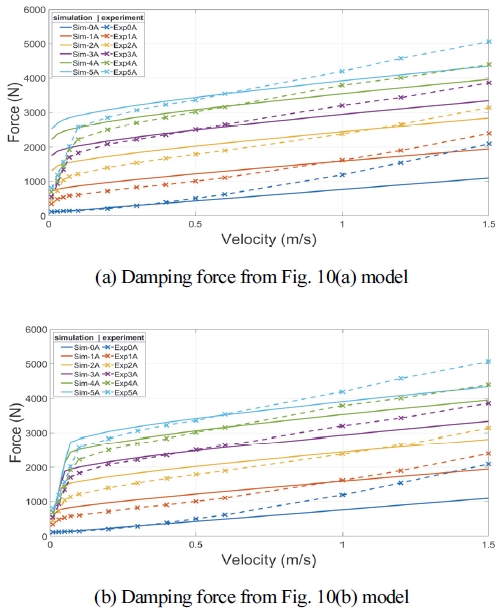
Fig. 10(a), (b)은 각각 Fig. 9(a), (b)의 모델을 2.2절의 과정을 통해 계산한 예측 감쇠력(실선)과 제작된 댐퍼의 실험에서 측정한 감쇠력(점선)이다. 식 (7)에서 댐퍼의 마찰력과 관로 저항은 고려하지 않았다. Fig. 10(a)의 예측 감쇠력은 저속에서 실험 감쇠력의 경향을 전혀 따라가지 못하지만, Fig. 10(b)은 비교적 높은 유사성을 보인다.
Fig. 9(a)에서는 항복점(Yield point)를 지정하기엔 한정적이고, 지정하더라도 항복 전 구간과 항복 후 구간의 점도(선형 기울기)의 차이가 크게 나지 않아, 점도 비가 큰 값을 가지고 항복 후 정적 항복응력(τ1)도 크기 때문에 항복응력 비도 큰 값을 가진다. 점도 비(γ)가 클수록 감쇠력(F-v)선도의 꺽이는 지점이 높아지는 영향이 있고, 항복응력 비(δ)가 클수록 0(m/s)에서 감쇠력이 증가하는 영향을 보인다. 전체 전단률에서 적은 영역의 유무가 미치는 영향을 보인 Fig. 10(a), Fig. 10(b)의 비교를 통하여 저전단률 구간의 중요성을 파악할 수 있다.
Fig. 10(b)도 약간의 오차를 보인다. 원인으로 추정되는 몇 가지 요인은 다음과 같다. MR 유체의 비선형성을 선형 모델링 과정의 한계, 전단률의 항복점 선정의 불명확성, 자기장 해석 오차 등에 따른 오차를 예상할 수 있다.
3.5 감쇠력 예측
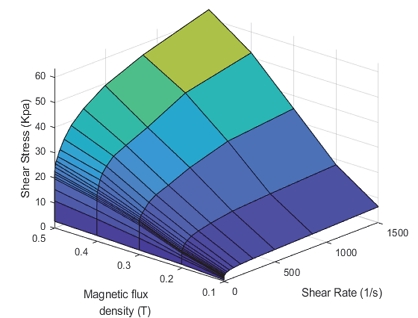
Table 2는 댐퍼의 마찰력과 관로저항 등을 고려하여 감쇠력 계산에 사용한 데이터이다. 점성 측정 장치에서 자속밀도(B)가 0.5 T 이상은 측정이 불가능하였기 때문에 그 이상의 자속밀도 영역은 특성 파라미터를 0.5 T와 동일하게 입력하였다.
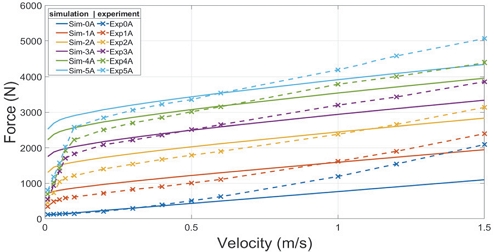
Fig. 11은 예측 감쇠력(실선)과 제작된 댐퍼의 실험에서 측정한 감쇠력(점선)으로 저속 부분에서 고속에서 비해 큰 차이를 보이나 정확한 유체 데이터를 확보한다면 보완할 것으로 예상된다. 설계 단계의 예측한 값으로는 적합한 수준으로 판단된다.
시뮬레이션으로 예측한 감쇠력과 제작된 댐퍼의 실험에서 측정한 감쇠력를 비교하면 Table 3과 같다.
4. 설계 프로그램 개발
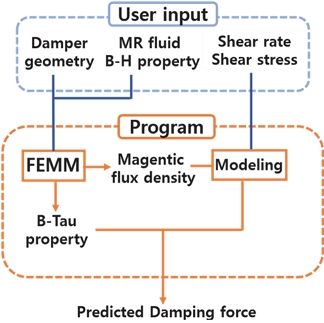
2절과 3절의 과정을 통합하여 단일 프로그램을 개발하였다. 프로그램의 구조는 사용자가 유체 특성, 댐퍼 형상 설계과 재료 물성을 입력 후, FEMM 해석과 모델링을 통한 유체 파라미터 입력으로 감쇠력을 얻는 MATLAB 프로그램 구조는 Fig. 12이다.
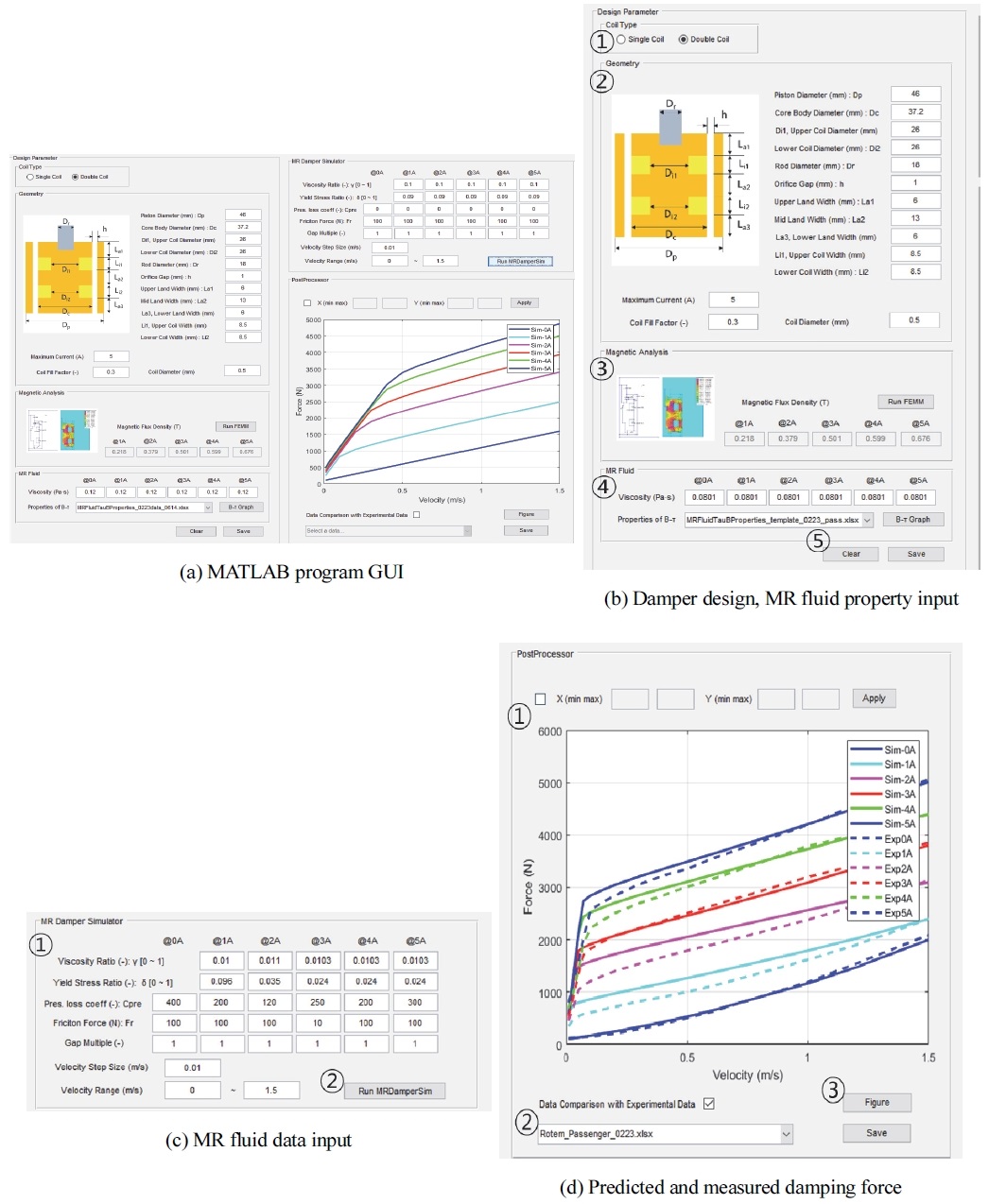
Fig. 13(a)로 MR 댐퍼 감쇠력 예측 프로그램의 전체적인 GUI를 확인할 수 있다.
Fig. 13(b)의 ①영역에서 전자석 종류를 Single, Double 중 선택이 가능하며, ②영역에서 내부 폴더에 저장된 댐퍼의 설계 파라미터들이 입력된다. ③영역에서 내부적으로 FEMM를 호출하여 평균 자속밀도를 얻은 후 ④영역에서 유체 특성을 입력하여 유체 정보 설정해준다. ⑤영역은 부가적으로 데이터 초기화 및 파라미터 데이터 저장이 가능하게 하였다.
Fig. 13(c)의 ①영역 유체데이터를 이용해 얻은 점도 비 γ(μ/μr), 항복응력 비 δ(τ1/τ2), 관로 저항 요소, 마찰 특성 요소를 입력하고, 해석 조건(속도 해석 단위 간격, 해석 범위)을 입력하면, 감쇠력을 계산하게 된다.
최종적으로 Fig. 13(d)에서 ①영역에 그래프를 생성할 수 있고 ②영역을 통해 데이터 파일(.xlsx)로 저장된 실제 댐퍼로부터 측정한 감쇠력 결과와 예측한 결과를 비교할 수 있다. ③영역의 부가 기능에서 신규 그래프 창 생성과 해석 결과 데이터 파일(.xlsx)로 저장 및 확인하도록 한다.
5. 결 론
본 연구에서는 MR 유체 특성과 댐퍼의 설계 데이터를 기반으로 MR 댐퍼의 성능을 예측하는 프로그램을 개발하였고, 실제 개발한 댐퍼의 성능 값과 비교 하였다. 자기장 해석 결과와 주어진 자속밀도의 차이로 선형 보간을 통해 유체 전단률-전단응력 데이터를 얻어 Bi-plastic bingham 모델을 이용하였다. 본 연구 과정의 결론은 다음과 같다.
- 1) 본 연구 과정에서 비선형성을 가진 MR 유체를 선형으로 모델링하는 경우, 항복지점의 선정에 주의가 필요하다. 항복지점의 선정에 따라 항복응력 비(δ), 점도 비(γ)가 매우 크게 변한다.
- 2) 유체의 응답 특성을 경험적으로 이상적인 모델로 변환하고, 가정을 통해 저속 전단률에서의 데이터의 중요성, 항복응력 비(δ) 등의 영향을 확인할 수 있었다. 항복응력 비(δ)이 증가할수록 0 m/s의 감쇠력이 증가하고, 점도 비(γ)가 증가할수록 감쇠력 항복 위치가 더 고속에서 형성된다.
- 3) 실험을 통한 감쇠력과 프로그램에서 예측한 감쇠력의 비교하여 유사성을 확인하였다. 평균 제곱근 편차를 기준으로 최대 오차는 350 N로 나타났다.
모델링 과정에서 우회(Bypass) 채널이나, 부동(Floating) 피스톤 등 고려되지 않은 요인이 많으므로, 정확성에 한계가 존재할 수밖에 없다. 그러나, 본 프로그램의 목적인 설계 단계에서 자기계나 유체의 특성을 통해 성능을 예측하는 것은 달성한 것으로 판단된다. MR 댐퍼 설계에서 프로그램을 이용한 감쇠력 특성을 예측할 수 있으므로, 제품 제작에 있어서 시행 착오를 줄이고, 효율적 설계가 가능할 것이다. 또한 추후 MR 유체의 동적 자속밀도 해석, 정확한 전단응력 시험이 보장된다면 더 높은 신뢰성을 보일 수 있을 것이다.
Acknowledgments
이 논문은 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20018369, 수소전기상용차 반능동 현가시스템용 공통요소부품기술개발).
References
-
D. Kim, D. Park, J. Lee, S. Shin, J. Choi, B. Choi and D. Choi, “Optimal Vehicle Rear Suspension through Integration of Analysis and Design Process,” Transactions of KSAE, Vol.22, No.4, pp.72-81, 2014.
[https://doi.org/10.7467/KSAE.2014.22.4.072]

- W. Baek, J. Lee and J. Sohn, “Dynamic Characteristics Modeling for A MR Damper Using Artifical Neural Neural Network,” Transactions of KSAE, Vol.12, No.3, pp.170-176, 2004.
-
H. Yoon, I. Moon, J. Kim, C. Oh and H. Lee, “Semi-Active Control of a Suspension System with a MR Damper of a Large-sized Bus,” Journal of the Korean Society of Manufacturing Technology Engineers Vol.21, No.4, pp.683-690, 2012.
[https://doi.org/10.7735/ksmte.2012.21.4.683]

- E. Rhee, S. Jin and J. Lee, “Evaluation of Driving Performance of Commercial Vehicle with MR Damper,” KSAE Annual Conference Proceedings, p.1182, 2021.
-
S. Ha, M. Seong, Q. Heung and S. Choi, “Optimal Design of MR Damper: Analytical Methodand Finite Element Method,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol.19, No.11, pp.1110-1118, 2009.
[https://doi.org/10.5050/KSNVN.2009.19.11.1110]

- D. Meeker, “Finite Element Method Magnetics,” FEMM, Vol.4, No.32, p.162, 2010.
- J. Park, M. Kim, N. Kim and E. Rhee, “Study on Design Parameters Optimization of MR Damper for Small Electric Vehicles,” KSAE Annual Conference Proceedings, pp.335-335, 2020.
-
Y. Peng, J. Yang and J. Li, “Parameter Identification of Modified Bouc–Wen Model and Analysis of Size Effect of Magnetorheological Dampers,” Journal of Intelligent Material Systems and Structures, Vol.29, No.7, pp.1464-1480, 2018.
[https://doi.org/10.1177/1045389X17740963]

-
J. Goldasz and B. Sapinski, “Nondimensional Characterization of Flow-mode Magnetorheological/electrorheological Fluid Dampers,” Journal of Intelligent Material Systems and Structures, Vol.23, No.14, pp.1545-1562, 2012.
[https://doi.org/10.1177/1045389X12447293]

-
J. Gołdasz and B. Sapiński, Insight Into Magnetorheological Shock Absorbers, Springer, Berlin, 2014.
[https://doi.org/10.1007/978-3-319-13233-4]

-
I. Jonkkari, E. Kostamo, J. Kostamo, S. Syrjala1 and M. Pietola, “Effect of the Plate Surface Characteristics and Gap Height on Yield Stresses of a Magnetorheological Fluid,” Smart Materials and Structures, Vol.21, No.7, Paper No.075030, 2012.
[https://doi.org/10.1088/0964-1726/21/7/075030]

-
I. Bahiuddin, S. A. Mazlan, M. I. Shapiai, F. Imaduddin, Ubaidillah and S. Choi, “A New Platform for the Prediction of Field-dependent Yield Stress and Plastic Viscosity of Magnetorheological Fluids Using Particle Swarm Optimization,” Applied Soft Computing, Vol.76, pp.615-628, 2019.
[https://doi.org/10.1016/j.asoc.2018.12.038]