후륜 2축 현가장치를 갖는 의료차량의 저자유도 모델 개발 및 검증

2.1 모델 구성 및 개요

차량의 저자유도 모델 개발 및 검증을 위해 MATLAB을 활용하였다. 본 연구의 대상인 의료차량은 특수목적을 위해 기존 차량에서 변경 설계가 이뤄진 차량이며, 기존 차량은 현대 자동차 파비스 모델이다.

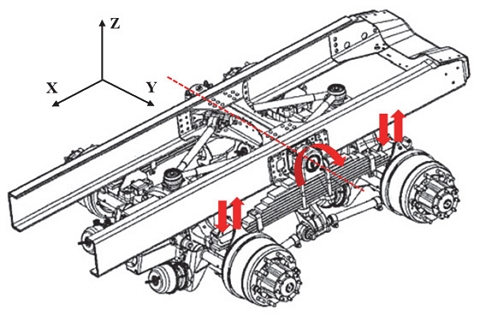
해당 모델의 전륜 현가장치는 에어 서스펜션을 활용하기 때문에 이에 맞는 스프링 및 댐퍼 값을 통해 간단히 모사가 가능하다. 하지만 후륜 현가장치는 Fig. 1과 같이 단일 현가장치에 2개의 구동축(Rigid axle)이 리프 스프링 각 끝단에 연결되어 있고 해당 스프링 중심이 차체에 고정되어 기계식 레버로 작용하기 때문에 단순히 스프링 및 댐퍼 값을 통한 모사가 불가하다. 추가로 후륜 2축은 리프 스프링을 포함하여 총 6개의 링크로 구속되어 있기 때문에 Fig. 1을 기준으로 X 방향 회전과 Z 방향 병진 운동만 허용된다. 후륜 리프 스프링은 2축이 모두 하중을 받을 경우 강성체로 작용하여 지면에서 발생하는 충격을 흡수하지만 노면 요철이 커서 후륜 각 축간 높이차이가 나는 경우 레버로 작용하여 한쪽 축에만 하중이 과하게 걸리는 현상을 억제시킨다. 그리고 각 휠 마다 댐퍼가 독립적으로 설치되어 후륜 현가장치에 총 4개의 댐퍼가 설치되어 있다.

Fig. 1

Example of twin-rear axle suspension(https://www.synthx.com/torsion-axle-walking-beam-suspension/)

대상 의료차량의 주된 주행환경은 고속도로를 포함한 양질의 포장로를 항속주행하는 환경이다. 이 경우 노면 요철에 의한 현가장치의 거동은 크지 않고 차량 하중에 의한 노면 변형도 무시할만 하다. 또한 개발하고자 하는 저자유도 모델은 차량 초기 개발 단계에서 현가장치의 구조 변화, 하중 변화에 의한 차체의 거시적인 거동을 간단하고 신속하게 보기 위한 것이기 때문에 모델 생성 전 아래와 같이 가정하였다.

• - 스프링 강성과 댐퍼 값은 선형적이다.
• - 지면은 차체 무게에 의해 변형되지 않고 유지된다.
• - 안티 롤바(Antiroll bar)에 대한 요소는 무시한다.
• - 엔진, 기어 박스 등 회전체에 의한 진동은 무시한다.
• - 주행시 차량 속도는 일정하게 유지된다.

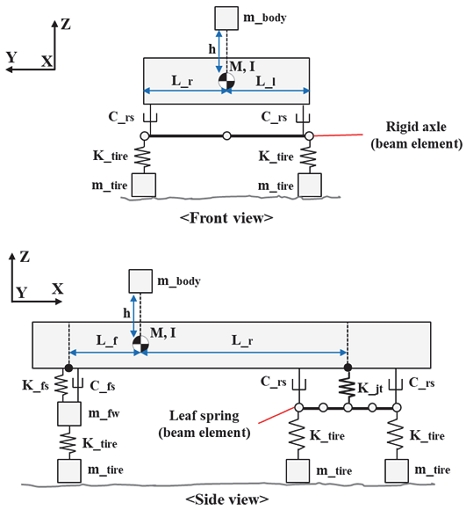
상기 가정들을 바탕으로 대상 차량의 저자유도 모델은 Fig. 2와 같이 생성되었다. 모델에서 차체는 강체로 모사되었으며 바운스(Z 방향 병진), 롤링(X 방향 회전) 및 피칭(Y 방향 회전)으로 총 3자유도를 갖으며, 전륜은 에어 서스펜션에 해당하는 스프링과 댐퍼로 모사된다. 후륜 현가장치에서 리프 스프링과 각 구동축은 빔 요소(Beam element)로 모사되었다. 리프 스프링 모사에 해당되는 빔은 Z 방향 병진과 Y 방향 회전 운동을 갖으며, 구동축에 해당되는 빔은 Z 방향 병진과 X 방향 회전 운동을 갖는다. 그리고 각 휠에 연결되는 타이어는 Z 방향 병진 운동만 갖는다. 이로써 모델은 차체(3 DOF), 전륜 휠 2개(2 DOF), 리프 스프링 2개(20 DOF), 구동축 2개(12 DOF) 및 타이어 6개(6 DOF)로 구성되어 총 43 DOF(Degree Of Freedom)를 갖는다.

Fig. 2

Schematics of reduced-order model for a vehicle with twin-rear axle suspension

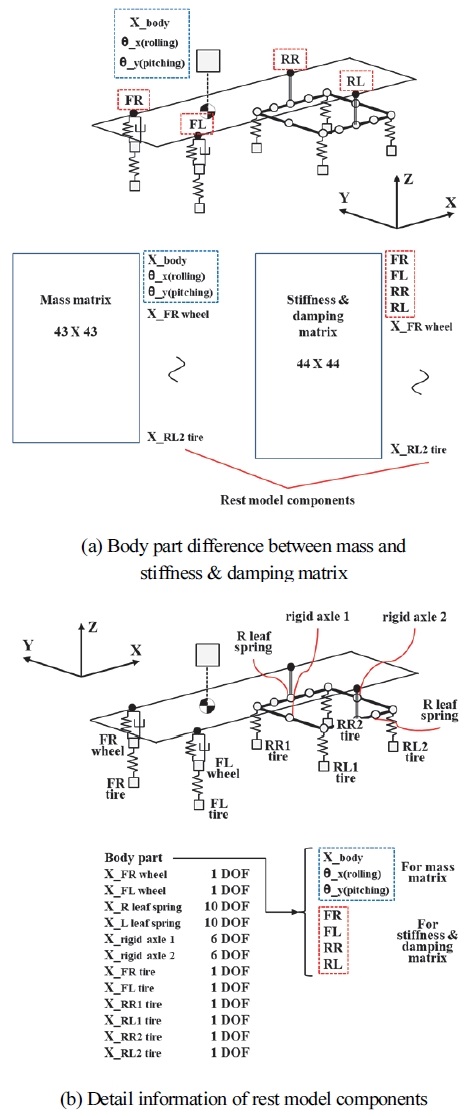
언급한 바와 같이 개발 모델은 43 DOF를 갖지만 강성 및 감쇠 행렬의 사이즈는 44 X 44이다. 이유는 강성 및 감쇠 행렬에 의한 힘을 도출하는 과정에서 각 현가장지와 차체 간 상호작용을 계산하기 위해 차체 내 각 현가장치 연결점의 위치(Suspension point on body)가 고려되기 때문이다. 강성과 감쇠 행렬에서 1 ~ 4번째 성분은 Fig. 3와 같이 각 현가장치 연결점(FR, FL, RR, RL)에 해당된다.

Fig. 3

3D schematics of the model and difference between mass and stiffness & damping matrix

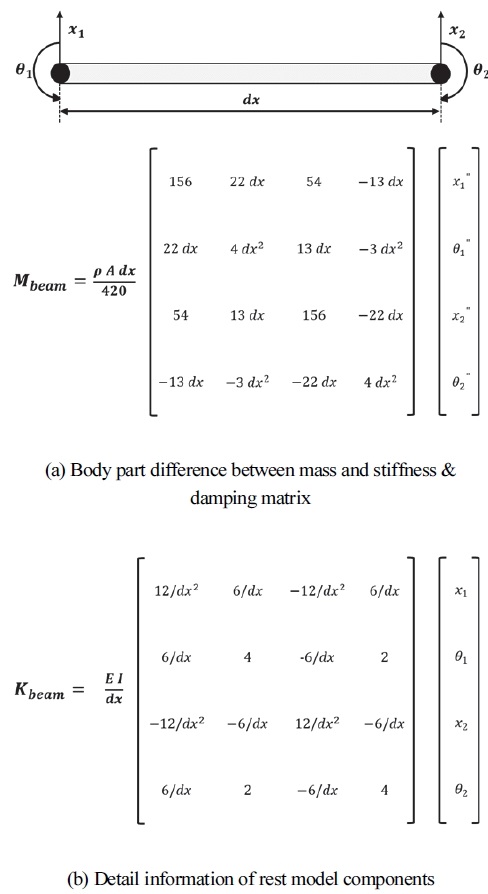
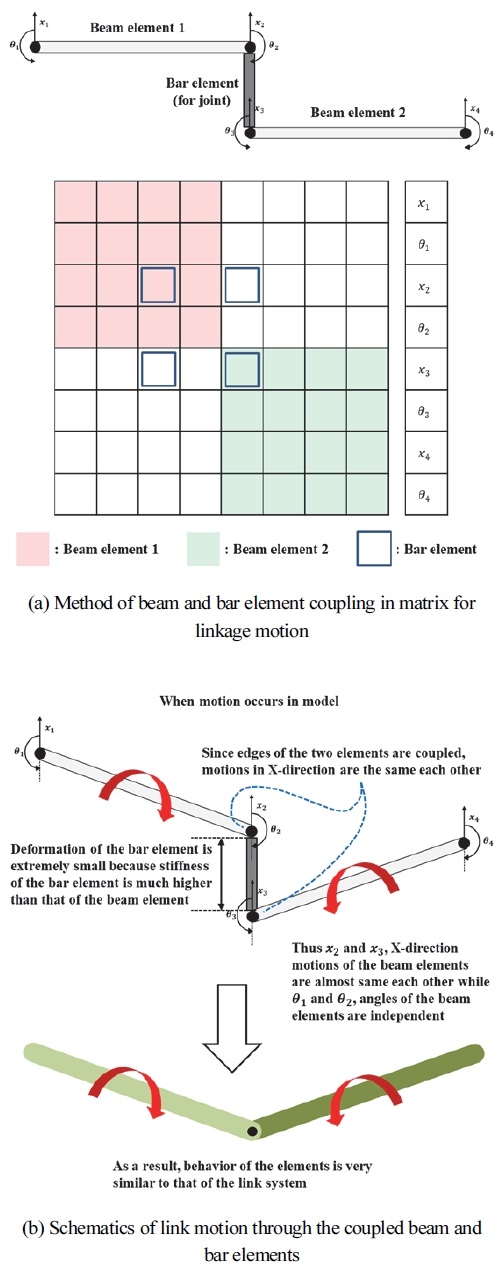
한편, 후륜 현가장치에서 리프 스프링 중앙은 차체에 연결되고 구동축의 좌우 끝단은 리프 스프링 앞뒤 끝단에 연결된다. 이와 같이 후륜 2축이 연계된 경우를 모사하기 위해 빔 요소가 활용되었으며, 이는 후륜 현가장치에서 Fig. 3에 표현된 리프 스프링(Leaf spring)과 강체 링크(Rigid axle 1 & 2)의 역할을 한다. 빔 요소는 구조물이 휘어지는(Bending) 변형을 모사하기 위해 사용되며 Fig. 4와 같이 각 절점마다 상하 및 회전 운동을 담당하는 2 자유도 성분으로 구성된다. 여기서 x와 θ는 각각 상하 및 회전 운동에 대한 자유도 성분을 의미한다. 빔 요소가 보 요소와 연결됨으로써 대상 차량의 후륜 현가장치와 같은 링크 시스템의 거동이 모사되는 원리는 다음과 같다. Fig. 5를 보면 2개의 빔 요소의 각 끝단이 보 요소에 의해 연결되어 있다. 보 요소는 상하 방향으로만 움직이며 빔 요소에서 상하 거동과 관련된 성분과 연결되기 때문에 연결부의 상하 거동은 동일하다. 그리고 보 요소의 강성은 현가장치의 스프링에 비해 상대적으로 매우 높기 때문에 변형이 매우 작다. 결과적으로 보 요소로 연결된 빔 요소들은 연결점들의 상하 거동은 동일한 한편 회전 운동은 독립적으로 발생한다. 이를 링크 기구 관점에서 보면 링크 간 체결 조건이 유지되는 것으로 볼 수 있다.

Fig. 4

Components and DOF(Degree Of Freedom) of beam matrix

Fig. 5

Method of describing linkage motion using beam elements

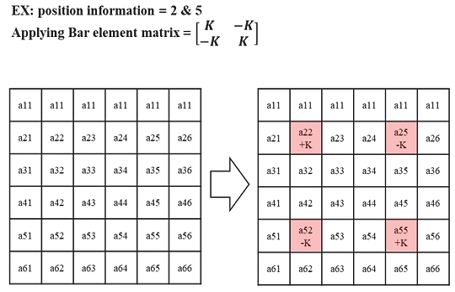
이와 같이 차체와 리프 스프링을 담당하는 빔 요소와 후륜 강체 링크를 담당하는 빔 요소들은 링크 시스템 거동을 모사하기 위해 각 연결부에 보 요소(Bar element)를 적용하였다. 모델의 전체 행렬에서 보 요소가 적용된 위치는 Table 1과 같으며 적용 방법은 Fig. 6에 표현 되었다.

Table 1

Connection point and position information for bar element application to entire stiffness and damper matrix

Fig. 6

Method of applying bar element to entire matrix according to position information

개발 저자유도 모델에서 강성 행렬은 앞서 기술한 과정으로 생성하였으며, 질량 행렬 생성시 차체, 전륜 휠 및 각 타이어는 집중질량(Lumped mass)로 간주하였고 리프 스프링과 구동축은 빔 요소에서 생성되는 질량 행렬을 활용하였다. 감쇠 행렬의 경우 차체와 전륜 및 후륜 각 휠 간 댐퍼만 모사하도록 생성하였다.

2.2 모델을 통한 동적거동 해석 과정

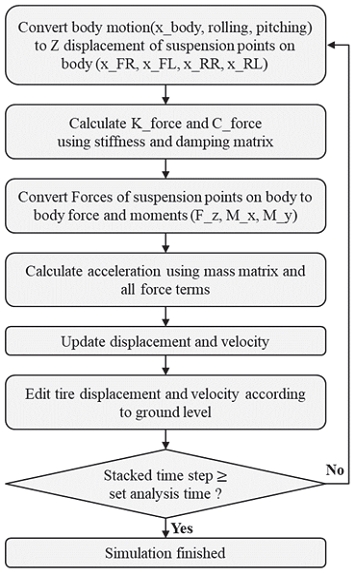
저자유도 모델의 각 행렬(질량, 강성 및 감쇠) 생성 후 Explicit dynamics method를 활용하여 주행 시뮬레이션이 수행되며, 구체적인 계산 과정은 Fig. 7에 표현되어 있다.

Fig. 7

Flow chart of dynamic analysis in the model

먼저 차체 거동(바운스, 롤링 및 피칭각) 정보를 통해 차체 내 각 현가장치 연결점들의 Z 방향 변위를 식 (1)을 통해 도출한다. 아래 식에서 차체 무게 중심으로부터 각 현가장치 연결점의 x와 y방향 위치는 l_x와 l_y로 표현되었으며 총 4개 값을 갖는다. 모델에 적용된 값은 부록에 기술되었다.

도출된 차체 내 현가장치의 변위와 전륜 휠로부터 타이어를 포함한 나머지 점들에 대한 변위 및 각도를 강성 행렬에 적용하여 차량 현가장치 스프링 및 강성에 의한 힘(K_force in Fig. 7)을 도출한다. 이와 유사하게 식 (1)을 통해 차체 내 현가장치 연결점들의 Z 방향 속도도 도출한 뒤 해당 속도와 전륜 휠부터 타이어를 포함한 점들의 속도 및 각속도를 감쇠 행렬에 적용하여 차량 현가장치 댐퍼에 의한 힘(C_force in Fig. 7)을 도출한다.

강성 및 감쇠 행렬을 통해 도출된 힘에서 1 ~ 4 성분은 차체 내 현가장치 연결점에 작용하는 Z 방향 힘이기 때문에 차체에 적용하기 위해 Z 방향 힘과 X 및 Y 방향 모멘트로 변환이 필요하며, 해당 과정은 식 (2)를 활용하여 진행한다.

차체에 적용되는 힘과 모멘트 및 기 도출된 나머지 힘 성분들(전륜 휠부터 타이어에 적용되는 힘)과 외력 및 질량행렬을 식 (3)에 적용시켜 매 Time step에 대한 가속도를 도출한다. 식 (3)에서 a, Inv(M), F_out, C_force 및 K_force는 각각 가속도, 질량 행렬의 역행렬, 외력(중력에 해당), 감쇠 행렬로 도출된 힘과 강성 행렬로 도출된 힘을 의미한다.

가속도 도출 후 식 (4)를 활용하여 매 Time step에 따른 속도 및 변위를 업데이트 한다.

한편, 차량 주행 중 타이어는 지면과 접촉(Contact)하게 되는데, 주행 상황에 따라 타이어는 공중에 뜬 후 낙하하여 지면에 재 접촉하는 상황이 발생한다. 개발 모델에서는 이러한 현상을 반영하기 위해 매 Time step 별로 타이어와 입력 노면의 Z 방향 높이를 비교한다. 만약 타이어가 노면보다 낮거나 같을 경우 이를 충격 후 접촉상황으로 간주하여 타이어 변위를 노면과 동일하게 변경하고 속도는 0으로 변경한다.

모델을 통한 차량의 동적거동 해석은 차체 현가장치 연결점의 Z 방향 변위 도출부터 타이어의 지면 접촉 조건에 따른 변위 및 속도 변경까지의 과정을 반복하여 진행된다.

2.3 큰 요철 노면 주행 시뮬레이션을 통한 모델의 후륜 현가장치 거동 타당성 조사

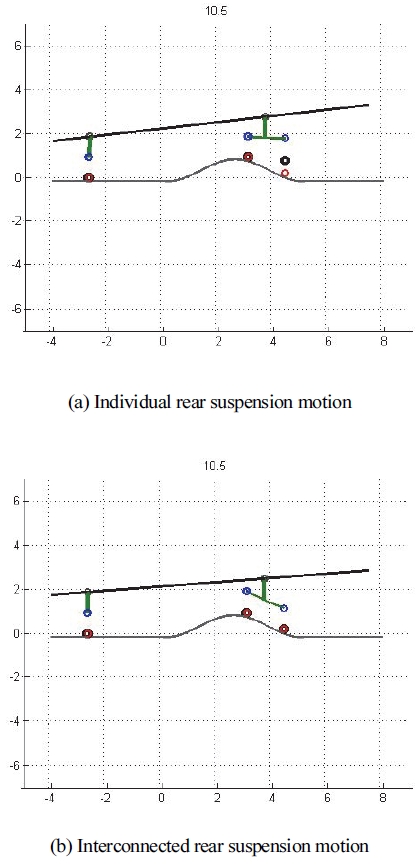
개발된 모델이 후륜 현가장치의 거동을 반영하는지 확인하기 위해 요철이 큰 노면에 대한 주행 시뮬레이션을 수행하였다. 모사한 후륜 현가장치의 경우 리프 스프링이 기계식 레버로 작용하기 때문에 후륜 각 휠은 노면 형상을 수월하게 추종할 것으로 예상된다.

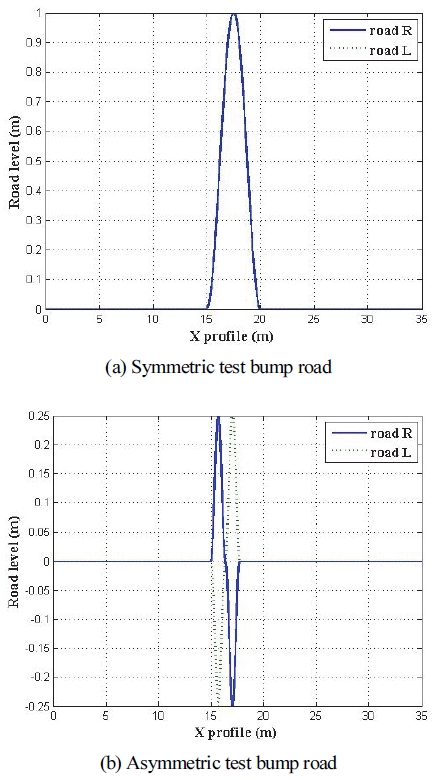
노면 요철은 Fig. 8과 같이 2개로 모사하였으며, 주행 시뮬레이션 수행 시 타이어와 지면의 접촉조건이 보장되도록 차량 속도는 1.2 m/s, 해석 시간은 20 s로 설정하였다. 또한 대상 차량을 모사하기 위해 모델에 입력한 상세 정보는 부록에 표기하였다.

Fig. 8

Test bump roads for suspension motion verification

대각 축이 연계된 후륜 현가장치의 하중 균일화 효과를 알아보기 위해 후륜 각 현가장치가 독립적으로 움직이는 경우와 주행 중 휠 하중을 비교하였다. 후륜 현가장치의 독립적 거동을 위해 개발 모델에서 리프 스프링의 중앙 노드에 해당하는 변위와 회전 모두 고정 조건을 적용하였다. 이 경우 리프 스프링은 더 이상 기계식 레버로 작용하지 않고 각 축에 독립된 스프링으로 작용한다.

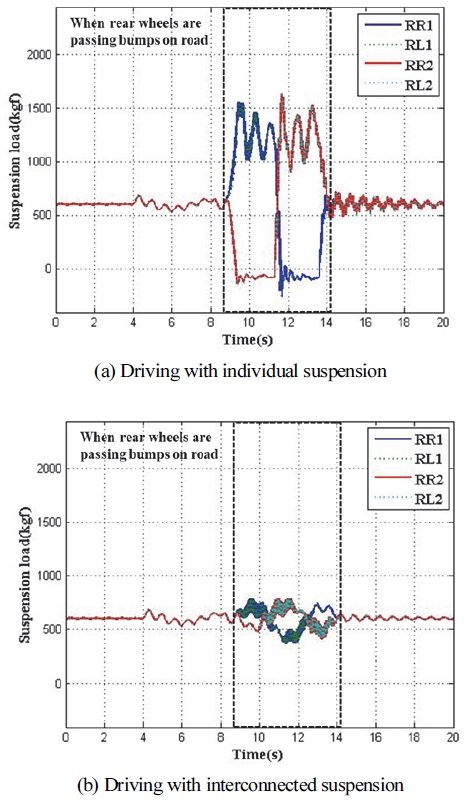
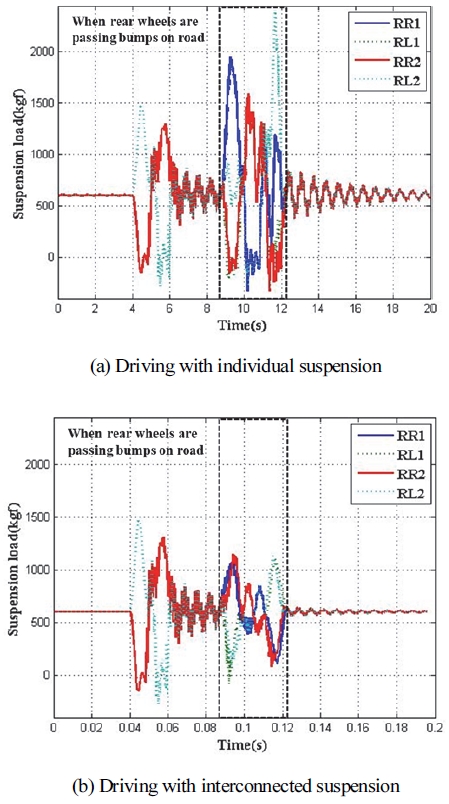
Fig. 9는 각 노면과 리프 스프링 회전 유무에 따른 후륜 현가장치의 거동을 보여주며, Figs. 10, 11은 각 경우에서 후륜 휠에 적용되는 하중을 보여준다. 후륜 현가장치가 연계된 경우 각 휠은 노면을 잘 추종하는 모습을 보이며 휠에 하중이 집중되는 현상도 효과적으로 억제된다. 반면 현가장치가 독립적으로 작용할 때 노면 요철에 의해 일부 휠이 공중에 뜨는 현상이 발생하고 노면과 접지된 휠에 과하중이 걸린다. 후륜이 주 요철 구간을 지날 때 각 상황별로 휠에 걸리는 최대 하중을 Table 2에 기술하였다. 요철을 지나기 전 평평한 노면에서 모든 타이어가 접지되었을 때 후륜 각 휠에 걸리는 하중은 600 kgf 인데, 이를 기준으로 최대 하중을 분석하면 현가장치가 연계되지 않은 경우 휠 하중은 기준 대비 2.72배에서 3.99배까지 증가하지만 현가장치가 연계된 경우 하중은 기준 대비 1.84배에서 1.93배 수준으로 과하중 현상이 크게 억제됨을 알 수 있다. 특정 노면을 통해 주행 시뮬레이션을 수행한 뒤 현가장치의 거시적 거동과 연계 여부에 따른 휠 하중을 조사한 결과 개발된 모델이 현가장치의 특성을 적절히 반영하는 것으로 판단된다.

Fig. 9

Motion of rear suspension on the symmetric test bump roads

Fig. 10

Rear suspension wheel load during simulation of symmetric test bump road

Fig. 11

Rear suspension wheel load during simulation of asymmetric test bump road

Table 2

Maximum load of wheel when rear tires goes over the bump on road

3.1 노면별 실차 주행 데이터 분석

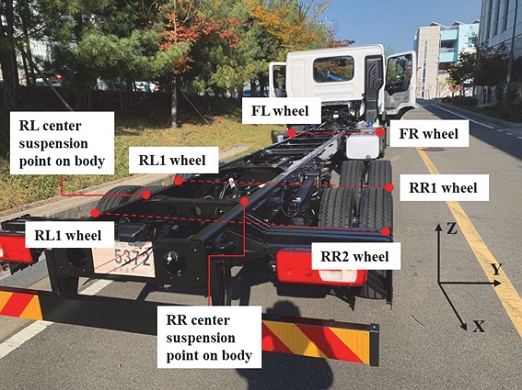
대상 차량의 주행 중 동특성 파악 및 모델 검증을 위해 주행 시험을 진행하였다. 대상 차량은 현대 자동차 파비스 모델로 총중량 19.9톤급이며, 시험 당시 차량은 Fig. 12와 같이 공차 상태로 화물이 실리지 않았다. 거동 측정을 위해 가속도 센서를 각 휠과 차체에서 후륜 현가장치가 설치된 중앙부 좌⋅우로 부착하여 총 8개점에 대한 Z 방향 신호를 획득하였다. 주행 시험을 위한 노면은 고속도로, 국도, 벨지안로이며 각 노면 주행 시 평균속도는 80, 60, 5 km/h 이다.

Fig. 12

Target vehicle for real driving test

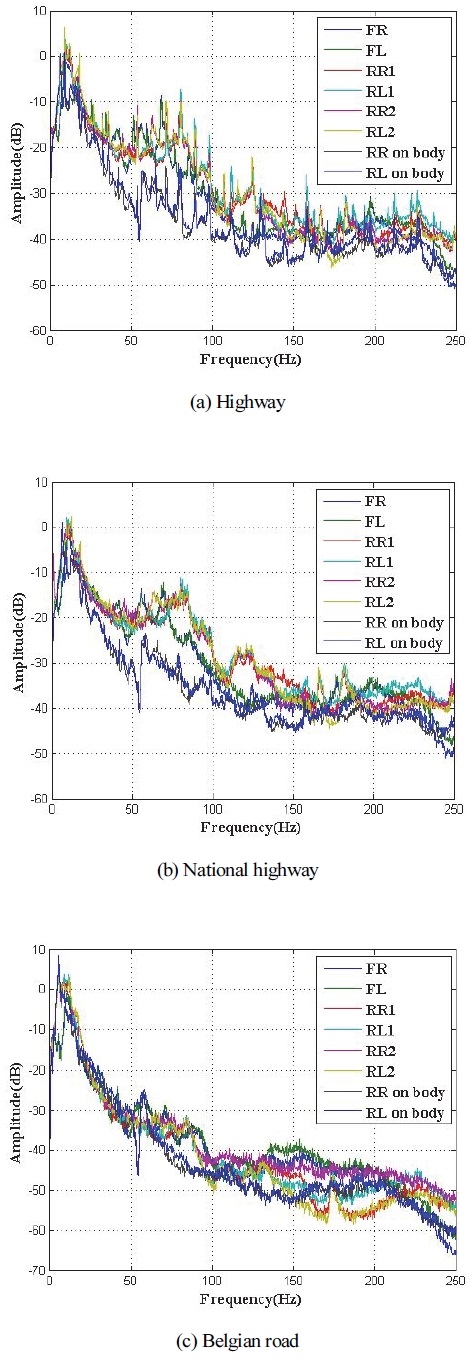
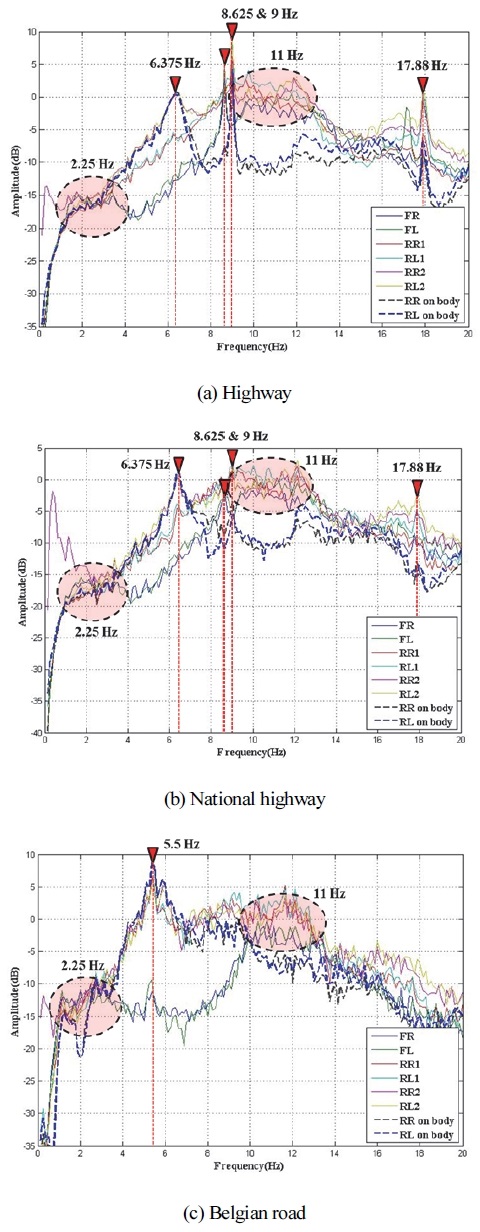
휠에서 측정된 가속도 신호의 주파수 성분은 Fig. 13에 나타나 있다. 주파수 성분 결과를 볼 때 전반적으로 3가지 노면 신호 모두 0 ~ 50 Hz 영역 내 성분이 주로 발생하며, 해당 영역 내에서 약 10 Hz 근방에서 모든 휠이 가장 큰 거동을 갖는다. 본 연구의 대상차량과 같이 다축 대형 차량의 경우 노면 요철에 의한 거동은 주로 20 Hz 이내에서 발생하기 때문에 Fig. 14와 같이 0 ~ 20 Hz 범위에서 주파수 성분에 대한 추가 분석을 수행하였다. 먼저 고속도로 주행 데이터를 분석한 결과 약 11 Hz 근방에서 거시적으로 큰 성분이 관찰되었으며, 이후 6.375, 8.625, 9 및 17.88 Hz에서 뚜렷한 성분들이 관찰된다. 다음 국도 주행 데이터의 경우 고속도로 주행 데이터와 유사하게 11 Hz 성분과 함께 6.375, 8.625, 9 및 17.88 Hz 성분들이 관찰된다. 벨지안로 주행 데이터는 이전 노면 주행 데이터와 달리 5.5 Hz 성분이 가장 크게 발생한다. 벨지안로 주행 환경은 저속에 큰 요철을 지나는 것을 고려하면 해당 5.5 Hz 성분은 차량 프레임 변형에 의한 진동 성분으로 판단된다. 이전 주행 데이터에서 언급된 11 Hz 성분도 2번째로 큰 성분으로 관찰되지만 다른 주행 데이터에서 관찰되는 6.375, 8.625, 9 및 17.88 Hz 성분들은 관찰되지 않는다. 고속도로와 국도 주행환경의 경우 60 ~ 80 km/h 속도로 주행하기 때문에 엔진 및 기어를 포함한 다양한 회전의 고속회전으로 인한 진동 성분이 비교적 크고 뚜렷하게 발생한다. 따라서 언급된 4개 성분들은 차량 내 회전체에 의한 성분으로 판단된다. 한편 모든 노면 주행 데이터에서 약 2.25 Hz 및 11 Hz 근방에서 뚜렷하진 않지만 공통적으로 2개의 성분이 관찰되었는데 이는 주행 중 차체 바운스와 휠의 상하 거동에 의한 성분들이다. 해당 성분들에 대한 주파수 선도가 뚜렷하지 않은 이유는 대상 차량에 설치된 현가장치의 높은 감쇠특성 때문이다.

Fig. 13

PSD of real driving data at wheel and body in range of 0 to 250 Hz

Fig. 14

PSD of real driving data at wheel and body in range of 0 to 20 Hz

3.2 실차 주행 데이터와 시뮬레이션 결과 비교를 통한 모델 검증

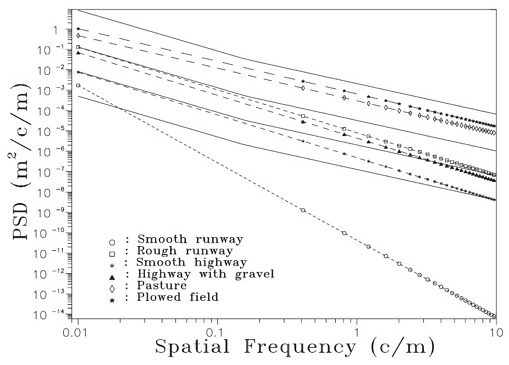
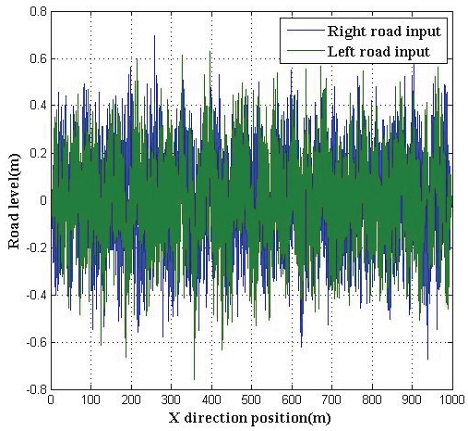
실 주행 데이터와 시뮬레이션 데이터 간 비교를 통해 모델 검증을 수행하고자 하였다. 신뢰성 있는 결과를 위해 실제 노면 데이터를 활용하는 것이 가장 타당하지만 고속 주행 중(60 ~ 80 km/h) 정밀하게 노면형상을 계측하는 것은 어렵다. 또한 휠 계측 데이터만으로 노면 형상을 추정하는 것은 재현성이 낮기 때문에 실제 노면의 특성을 고려한 가상의 노면 입력 데이터를 생성하는 것이 필요하다. 김광석¹⁰⁾은 주어진 노면 거칠기 특성을 나타내는 PSD 함수를 사용하여 2차원 노면을 생성한 뒤 이를 횡방향으로 확장시켜 3차원 가상 노면을 생성하는 연구를 진행하였다. 본 연구에서는 해당 연구에서 제시된 기법을 참고하여 가상의 노면 입력 데이터를 생성하였다. 벨지안로를 제외하고 고속도로나 국도와 같은 실제 도로는 불규칙한 형상을 갖기 때문에 먼저 랜덤 데이터를 생성하고 이후 적절한 노면 거칠기에 해당하는 PSD 함수를 적용하였다. 3.1절의 Fig. 13(a)와 (b)의 신호에서 주파수 성분의 크기는 고속도로와 국도 간 큰 차이를 보이지 않는다. 따라서 고속도로의 거칠기는 국도와 비슷하고 주행 시험 당시 국도의 노면은 거친 상태였기 때문에 두 주행로 모두 Rough runway로 간주하였다. PSD 함수 생성은 Fig. 15를 참고하였으며, Fig. 16은 생성된 좌.우 노면 입력 데이터를 보여준다.

Fig. 15

PSD of various roads based on ISO standard and Wong classification10,11)

Fig. 16

Road input data for driving simulation

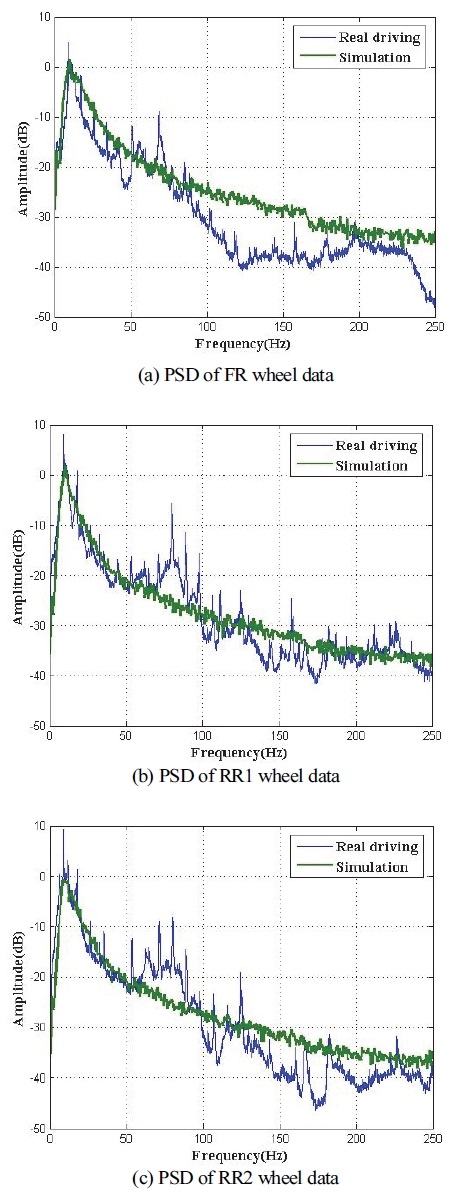
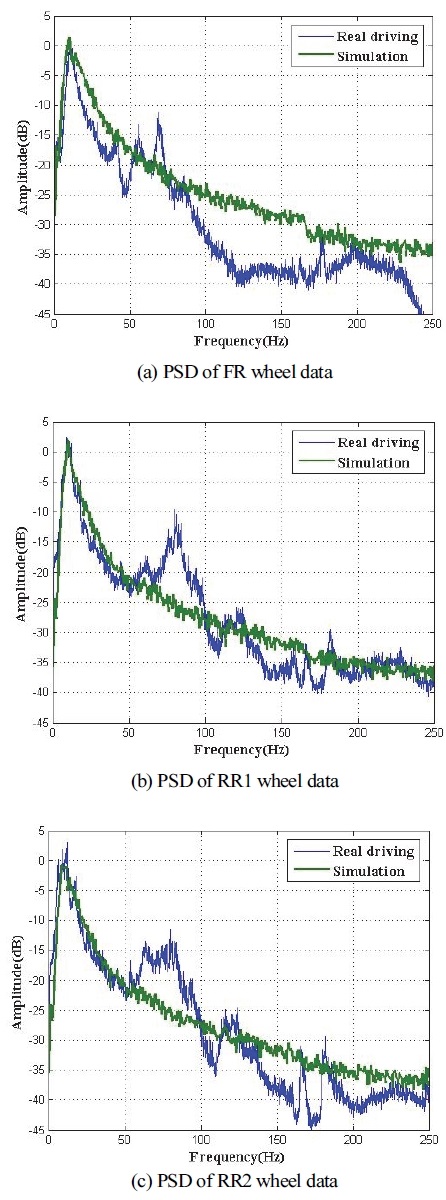
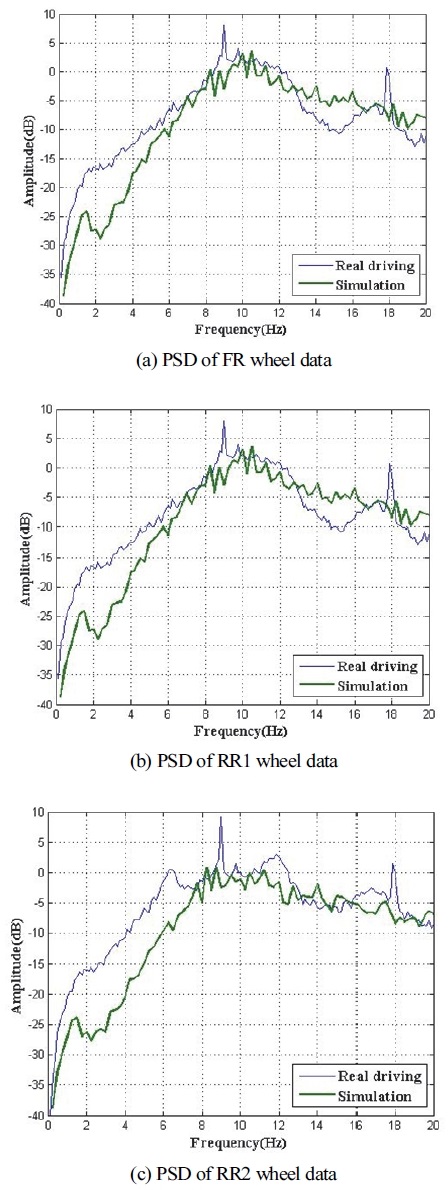
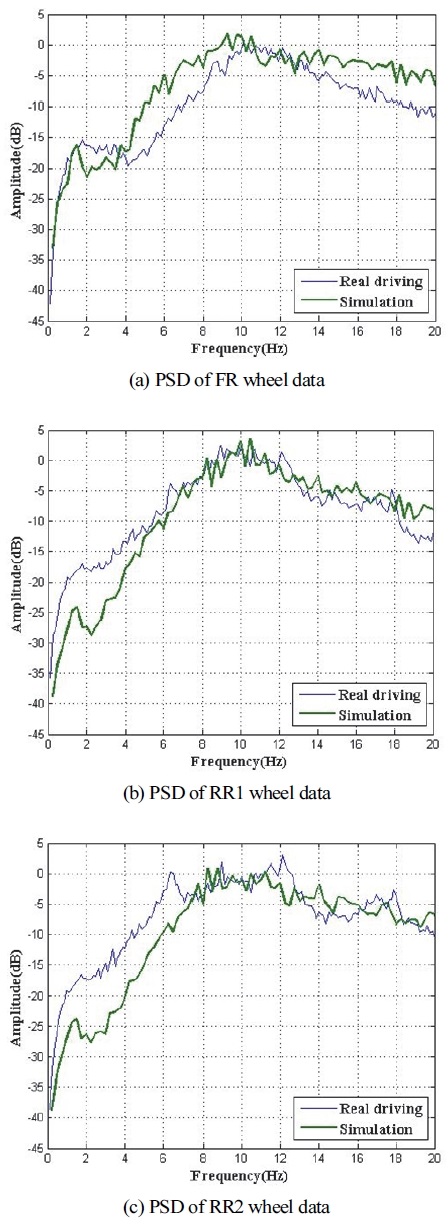
이후 모델을 통해 주행 시뮬레이션을 진행한 뒤, 실 주행 및 시뮬레이션을 통해 획득된 휠 계측 가속도 신호의 주파수 성분을 비교하였다. 먼저 Fig. 17 및 18과 같이, 고속도로 및 국도 시험 데이터와 시뮬레이션 결과를 0 ~ 250 Hz 영역에서 전반적인 주파수 선도의 경향을 비교하였다. 2개 노면 모두 전륜 휠은 시험 데이터와 시뮬레이션 결과 간 차이를 보이지만 후륜 휠의 경우 50 Hz 이하 영역에서 주파수 선도 형태와 크기가 서로 유사함을 알 수 있다. 다음으로 Fig. 19 및 20과 같이 0 ~ 20 Hz 범위에서 추가 분석을 수행하였다. 3.1절과 같이 실차 시험 데이터 분석결과 해당 범위에서는 차체 Bounce와 차량 휠 상하거동이 실제 차량과 개발된 모델에서 공통적으로 발생하기 때문에 2개 성분 비교에 주안점을 두었다.

Fig. 17

PSD of real driving and simulation data in range of 0 to 250 Hz(Highway VS simualtion)

Fig. 18

PSD of real driving and simulation data in range of 0 to 250 Hz(National highway VS simualtion)

Fig. 19

PSD of real driving and simulation data in range of 0 to 20 Hz(National highway VS simualtion)

Fig. 20

PSD of real driving and simulation data in range of 0 to 250 Hz(National highway VS simualtion)

먼저 고속도로 데이터와 시뮬레이션 결과 비교를 수행하였다. 모든 휠 데이터에서 차량 회전체 및 프레임 변형 등에 의한 성분은 시뮬레이션 결과에서 관찰되지 않고 차체 Bounce와 휠 상하 거동만 관찰된다. 차체에 의한 성분은 1.5 Hz, 휠에 의한 성분은 약 9.5 Hz로 시험 데이터의 2.25 Hz(차체 Bounce 성분)와 11 Hz(휠 상하 거동)에 비해 33 % 및 14 %가 낮게 도출된다. 다음으로 국도 데이터와 시뮬레이션 결과를 비교하였는데, 국도 데이터의 경우 고속도로에 비해 시뮬레이션 결과가 잘 일치하는 경향을 보인다. 이러한 이유는 시뮬레이션에서 모사한 노면 입력이 Rough way로 국도에 더 유사하기 때문이다. 전륜 휠의 경우 시뮬레이션에서 차체와 휠에 의한 성분이 시험 데이터에 비해 낮게 관찰되지만 후륜 휠의 경우 10 Hz 이후 영역에서 유사한 경향을 보인다.

개발된 모델의 특성상 실제 발생하는 차체 프레임의 변형, 차량 내 다양한 회전체 및 리프 스프링의 마찰 감쇠 등을 반영하지 않았고 실제 노면이 시뮬레이션의 노면 입력 간 차이로 인해 차이가 발생하였다. 하지만 차체 Bounce와 휠 상하 거동 성분이 20 Hz 이하 영역에서 발생한다는 점과 특히 국도 시험 데이터의 경우 10 ~ 50 Hz 영역에서 후륜 휠에 대한 주파수 성분이 시뮬레이션 결과와 매우 유사한 점은 주목할만하다. 모델 시뮬레이션 결과를 볼 때 주요 주파수 성분은 일치하며, 각 축이 연계된 후륜 현가장치의 특성을 잘 반영하기 때문에 추후 차량 변경에 따른 동특성 변화를 잘 반영할 것으로 기대된다.