Plenum의 공간 형상에 따른 공랭식 배터리 팩 냉각 유동 성능 연구

1. 서 론

내연기관 차량과 달리 하이브리드 자동차 및 전기차는 전기 모터 구동을 위해 배터리를 동력원으로 사용한다. 주로 이용되는 배터리는 자동차 가속 시, 순간적으로 높은 출력을 요구하기 때문에 고출력의 리튬 이온 배터리가 사용되고 있다. 이때 전동기는 큰 전류를 필요로 하고 배터리의 온도는 증가하게 된다.¹⁾ 배터리는 작동 온도에 따라 성능이 급격히 변화하게 되며, 특정 작동 온도 범위를 넘어서면 수명 감소, 화재 및 폭발의 위험성을 가지고 있다.^2,3)

위와 같이 배터리의 열적 문제를 해결하기 위해 다양한 연구가 진행되었으며, 냉각 방식에 있어서 크게 3가지로 공기 냉각(Air cooling), 액체 냉각(Liquid cooling) 그리고 상 변화 냉각(Phase change cooling)이 있다.⁴⁾ 공기 냉각 방식은 다른 냉각 방식보다 열전달 용량이 상대적으로 낮은 단점이 있지만, 저렴하고 가벼우며, 유지 보수가 편하다는 장점이 있다.⁵⁾

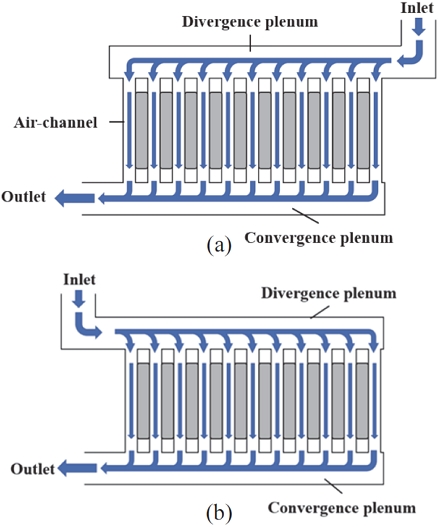
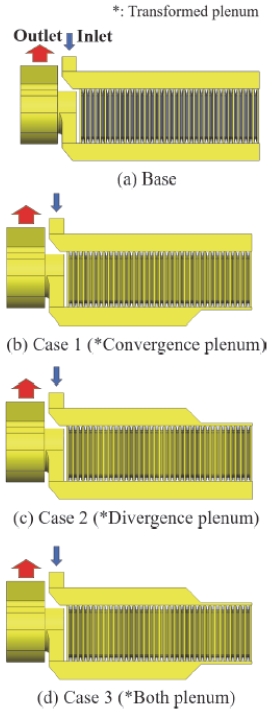
공랭식 냉각 방식의 형상은 배터리 팩 내부 공간에서 유체가 지나가는 경로에 따라 Fig. 1과 같이 Z-type, U-type 등으로 설명할 수 있다. Park⁶⁾은 Z-type과 U-type의 공랭식 배터리 냉각 시스템에 대해 최적화 연구를 진행했고 한쪽 방향으로 좁아지는 플레넘 형상에 대한 냉각 성능 효과를 전산 유체 역학을 활용하여 확인했다. 또한, 정석훈과 서현규⁷⁾는 EV 배터리 시스템의 냉각 성능 예측을 위해 시스템의 입ㆍ출구 면적 및 외부 Case의 형상을 변경하여 냉각 성능에 미치는 영향을 보여주었다. 이서근과 김한상⁸⁾은 방전율에 따른 공기 유량 산정에 관한 연구를 진행했다. 냉각을 위한 공기의 유량의 증가는 펌프 소모 동력의 증가로 이루어져 효율적인 냉각이 어려움을 확인하였다.

Fig. 1

Schematic of battery air-cooled management system (a) Z-type (b) U-type

본 연구에서는 Fig. 1과 같이 배터리 팩 내부의 유동경로 형태에 따라 Z-type과 U-type의 형상에서 직접 공기 냉각 방식 배터리 팩의 플레넘 파라미터 설계를 통해 Z-type과 U-type에서 효율적인 냉각 설계 규명을 목적으로 한다. 공랭식 배터리 팩을 구성하는 부품 중, 셀의 최고 관리 온도 이하를 유지하기 위해서 플레넘을 이용하며, 플레넘은 적절한 유동 공기 압력을 형성하여 각 채널에 유입되는 공기의 양을 균일하게 설정하도록 한다. Fig. 1과 같이 입구에서 공기가 들어와 각 공기 채널에 유입되는 공간인 Divergence plenum과 각 공기 채널에서 열교환을 마친 공기가 모이는 Convergence plenum의 설계 변경에 의한 배터리 팩의 냉각 성능을 규명하기 위하여 열 유동해석을 수행하였다.

Fig. 2

Air-cooled battery pack of fluid model (a) Z-type (b) U-type

2. 배터리 팩 내부의 열유동 해석 및 경계조건

2.1 Battery Cell 구조 및 형태

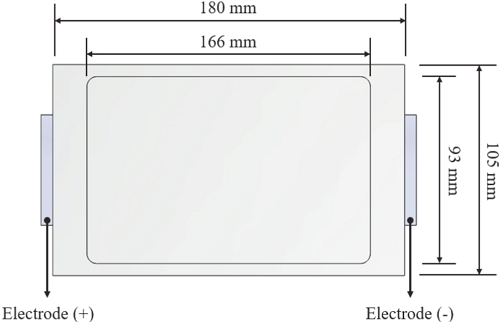
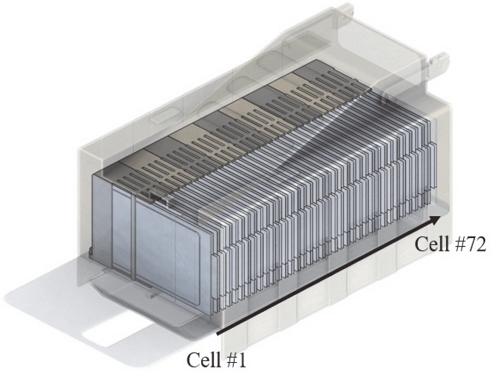
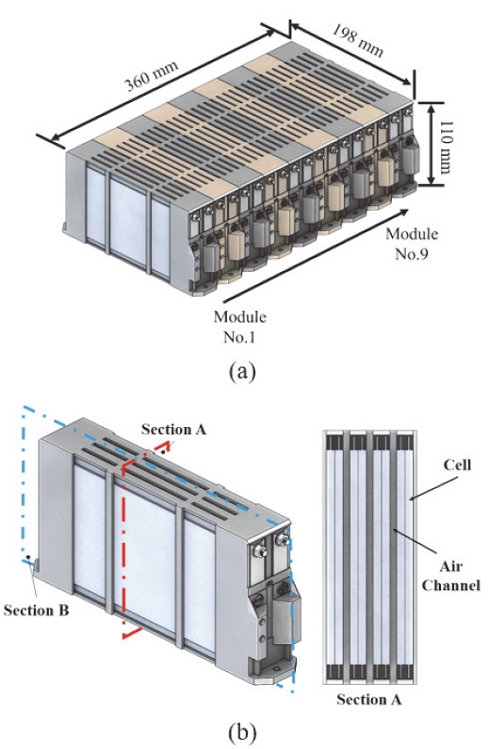
본 연구의 배터리 팩을 구성하는 배터리 셀은 Fig. 3에 나타난 것처럼 타입은 파우치 타입이다. 배터리 셀의 전체 크기는 180 × 105 × 3.5 mm이며, 한 개의 모듈에 8개의 셀이 조립되고 총 9 모듈이 하나의 배터리 팩을 구성한다. Fig. 4와 같이 본 연구에서 고려하는 배터리 팩은 총 72개의 셀이 사용되었다.

Fig. 3

Schematic diagram of battery cell

Fig. 4

Assembled cell in the battery pack

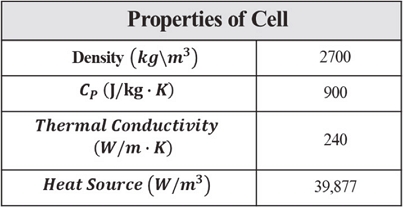
리튬-이온 배터리 팩과 모듈 모델은 Fig. 5와 같은 형상이며, Fig. 5(b)의 Section A에서 채널과 채널 사이에 2개의 셀이 조립됨을 알 수 있다. 해당 배터리 팩은 풀 하이브리드 차량에 사용되며, 배터리 팩의 정격 에너지는 약 1.4 kWh이다. 수치해석에 사용된 파우치 셀의 물성은 Table 1에 표기하였다.

Fig. 5

Schematic diagram of (a) battery pack and (b) battery module

Table 1

Properties of cell

2.2 Battety Pack 내부에서 Air Channel 구성

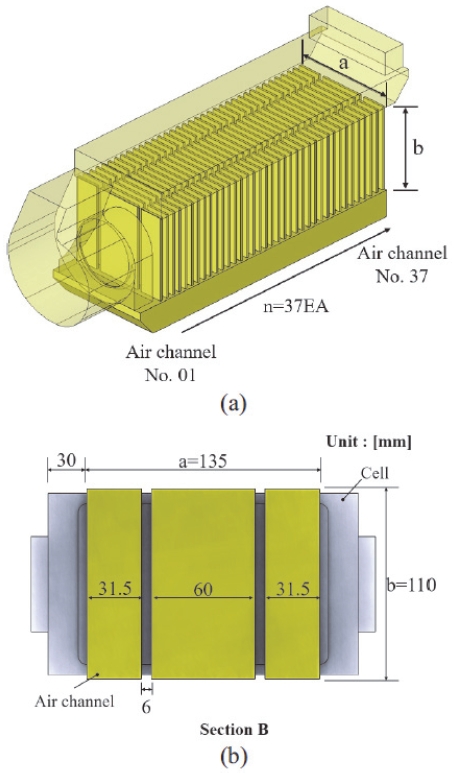
Aic-channel(공기채널)의 형태는 모듈 내부 공간, 모듈과 모듈 사이, 배터리 팩 내부 형상을 고려하며, 이러한 공간 사이에서 형성되는 냉각 공기에 대한 열 유동 수치 해석을 진행하였다. 채널의 번호는 블로워와 가장 가까운 공기 채널이 1번을 시작으로 수평 방향으로 37번까지 구성된다. 채널은 폭과 길이의 비, a:b = 1:1.23의 비율을 가진다. 자세한 치수 정보와 형상은 Fig. 6에 나타냈다.

Fig. 6

Fluid domain of air channels (a) Iso view, (b) Front view(Reference Fig. 5(b))

2.3 Plenum Space 형태 설계

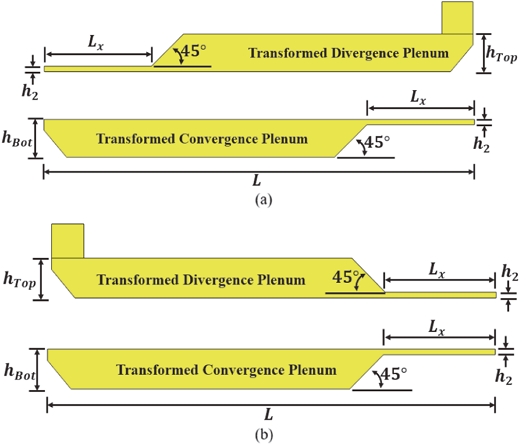
플레넘(Plenum)은 적절한 압력 형성을 통해 각 공기 채널 사이로의 유동량을 균일하게 제어해야 한다. 이 때 내부 압력과 공기 흐름은 플레넘의 형상에 따라 지배적으로 변한다.

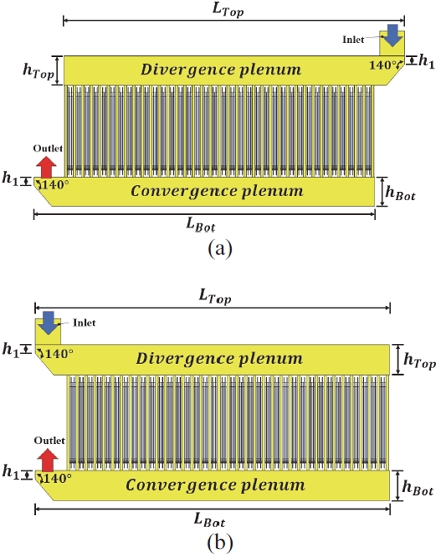
공랭식 배터리 팩에서 플레넘은 역할에 따라 유동공기가 공기채널로 공급하는 Divergence plenum과 공기 채널로부터 공기가 유입되는 Convergence plenum으로 분류할 수 있다. Fig. 7에서 (a)는 Z-type의 Base 플레넘이며, (b)는 U-type의 Base 플레넘을 보여주고 있다. 두 타입의 플레넘의 자세한 치수는 Table 2에 표시하였다.

Fig. 7

Fluid domain of design (a) Z-type, (b) U-type

Table 2

Plenum of design value

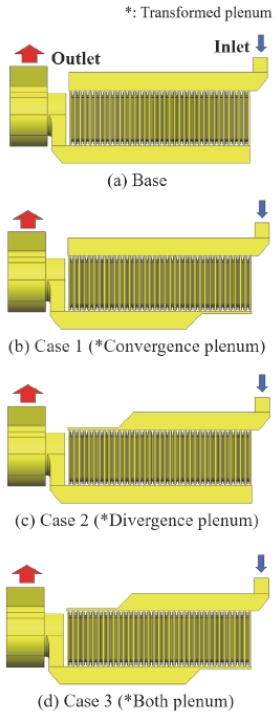
플레넘 공간 형태에 따른 Z-type과 U-type의 배터리 팩 형상 설계의 대상을 냉각 효율 향상에 적용하기 위해 가능한 설계 대상을 Fig. 8과 Fig. 9에 설정하였다.

Fig. 8

Z-type parameter design (a) Base (b) Case 1 (c) Case 2 (d) Case 3

Fig. 9

U-type parameter design (a) Base (b) Case 1 (c) Case 2 (d) Case 3

Fig. 8과 Fig. 9는 Z-type과 U-type의 설계 Case를 보여주고 있다. 각 Case는 Fig. 10과 같이 공기 유동 통로를 위하여 변형된 플레넘을 적용하여 배터리팩 유동 형태 및 플레넘 공간 형상이 배터리 팩 냉각 성능에 미치는 영향을 살펴보았다.

Fig. 10

Schematic diagram of transformed plenum (a) Z-type (b) U-type

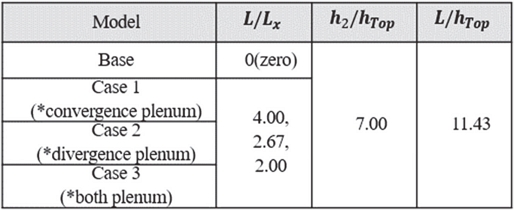
변형된 플레넘의 L_x/L의 비율은 2.00, 2.67, 4.00으로 설정하였다. L_x/L의 비율을 각 타입의 Case에 반영하여 최적 설계를 찾을 수 있도록 하였다. Lx는 플레넘의 전체 길이 L의 50 %를 넘지 않도록 하였으며 Table 3에 플레넘 설계 파라미터에 대한 비율을 표기하였다.

Table 3

The ratio of design parameters

2.4 공랭식 배터리 팩 내부 열 유동 해석

배터리 팩 내부 유체의 열 유동 해석은 상용 CFD 프로그램인 ANSYS FLUENT를 이용하여 수행했다. 연속 방정식(Continuity equation) (1)과 운동량 보존 방정식(Momentum conservation equations) (2)를 계산하여 각 채널의 유량 편차 및 압력을 분석하였다.⁹⁾

$\[ \frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }\mathit{t}}+\mathbf{\text{∇}}ㆍ\left(\mathit{\rho }\overrightarrow{\mathit{v}}\right)=0 \]$

(1)

$\[ \frac{\mathit{\partial }}{\mathit{\partial }\mathit{t}}\left(\mathit{\rho }{\overrightarrow{\mathit{v}}}_{\mathit{i}}\right)+\mathbf{\text{∇}}ㆍ\left(\mathit{\rho }\overrightarrow{{\mathit{v}}_{\mathit{l}}}\overrightarrow{{\mathit{v}}_{\mathit{l}}}\right)=-\mathbf{\text{∇}}\mathit{p}+\mathbf{\text{∇}}\left(\mathbf{\text{∇}}\overrightarrow{\stackrel{=}{\mathit{\tau }}}\right)+\mathit{\rho }\overrightarrow{\mathit{g}} \]$

(2)

발열원과 냉각 유체인 공기와의 열전달 현상을 분석하기 위하여 식 (3)인 에너지 방정식(Energy Equation)을 이용하여 계산하였다.¹⁰⁾

$\[ \begin{array}{c}\frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }\mathit{t}}\left(\mathit{\rho }\left(\mathit{e}+\frac{{\mathit{v}}^2}{2}\right)\right)+\mathbf{\text{∇}}\left(\mathit{\rho }\mathit{v}\left(\mathit{h}+\frac{{\mathit{v}}^2}{2}\right)\right)=\hfill \\ \mathbf{\text{∇}}ㆍ\left({\mathit{k}}_{\mathit{e}\mathit{f}\mathit{f}}\mathbf{\text{∇}}\mathit{T}-{\sum }_{\mathit{j}}{\mathit{h}}_{\mathit{j}}{\overrightarrow{\mathit{v}}}_{\mathit{j}}+{\mathit{\tau }}_{\mathit{e}\mathit{f}\mathit{f}}ㆍ\overrightarrow{\mathit{v}}\right)+{\mathit{S}}_{\mathit{h}}\hfill \end{array} \]$

(3)

모든 해석 조건에 대해서, 동일한 발열량과 토출구 공기 유량을 설정하였고 중력을 고려하여 비압축성 유동에 대한 정상상태 해석을 진행하였다. 내부 유동의 경우, 실제 배터리 팩 내부 유동을 모사하기 위하여 난류 모델 SST k-ω으로 선정했고 셀과 공기의 대류 열전달과 셀 내부 열 전도를 해석하기 위해 에너지 방정식을 계산하였다.

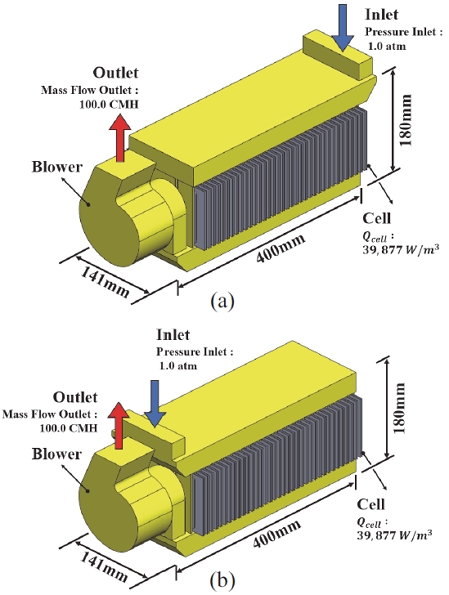
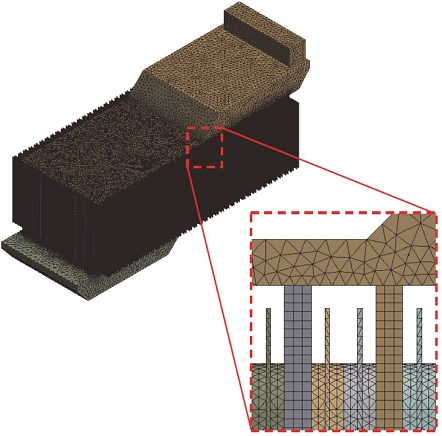
셀의 발열은 전기화학 반응과 줄(Jule) 열로 인해 셀 내에서 단위 부피당 발열이 발생하는 것으로 볼 수 있으며, 본 연구에서 셀의 단위 부피당 발열은 공간적으로 균일하다고 가정하였다.^11,12) 각 셀의 초기 온도와 유입 공기 온도는 상온인, 25 ^oC로 설정했으며, 블로워의 공기 토출 유량은 100 CMH(m³/h)로 설정하였다. 또한 각 Case는 각 Plenum의 냉각 효과 비교를 위해서, 입구 면적, 채널 형상 및 크기, 출구 면적을 동일하게 설정하였다. Fig. 11과 같이, 상대적으로 협소한 공기채널에 3개의 Hexahedral 격자를 구성하여 격자의 개수를 절약했으며, 플레넘이 변형되면서 생기는 좁은 공간에 4개 이상의 Tetrahedral 격자를 적용하여 정확도를 확보하고자 했다. 해석에 사용된 격자 수는 약 35,057,690개가 사용되었다.

Fig. 11

Mesh configured in air channel, narrow space and cells

3. 공랭식 배터리 팩 내부 열 유동 해석 결과

동일한 해석 조건에서, 각 Case의 변형된 플레넘의 적용 부위 및 플레넘 길이 방향 변수 Lx에 따른 냉각 특성을 확인하고자 한다. 변화 요인에 따라 어떤 영향을 미치는지 판단하기 위해 Z-type과 U-type에서 각 케이스의 평균 온도, 최대 온도, 최소 온도를 확인하고 각 채널에 유입되는 공기의 유량과 압력 강하 특성을 살펴본다.

3.1 Plenum 형상에 따른 냉각 특성

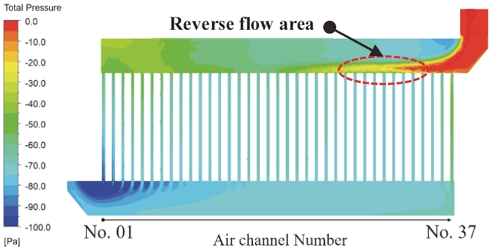
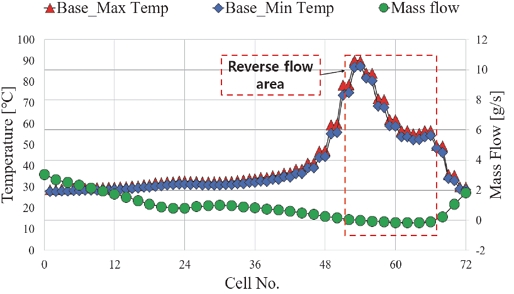
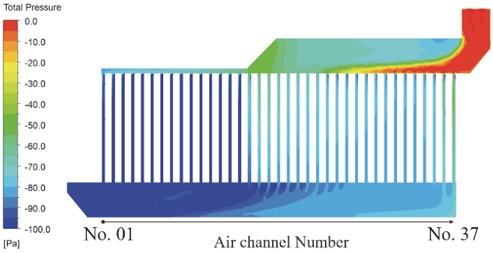
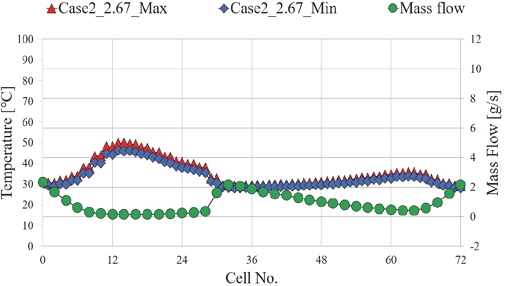
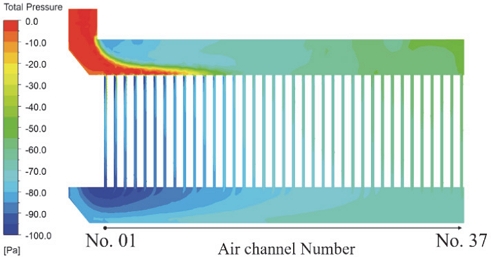
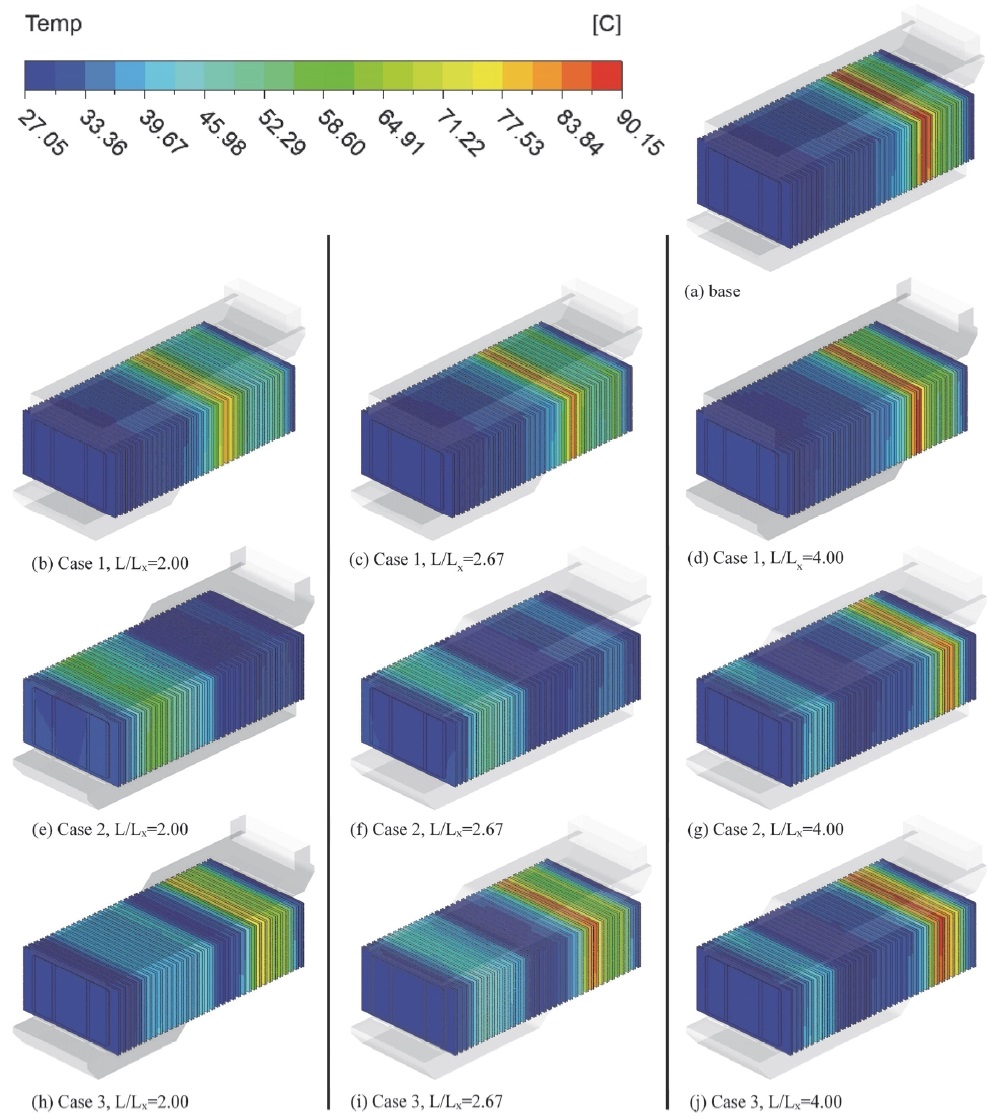
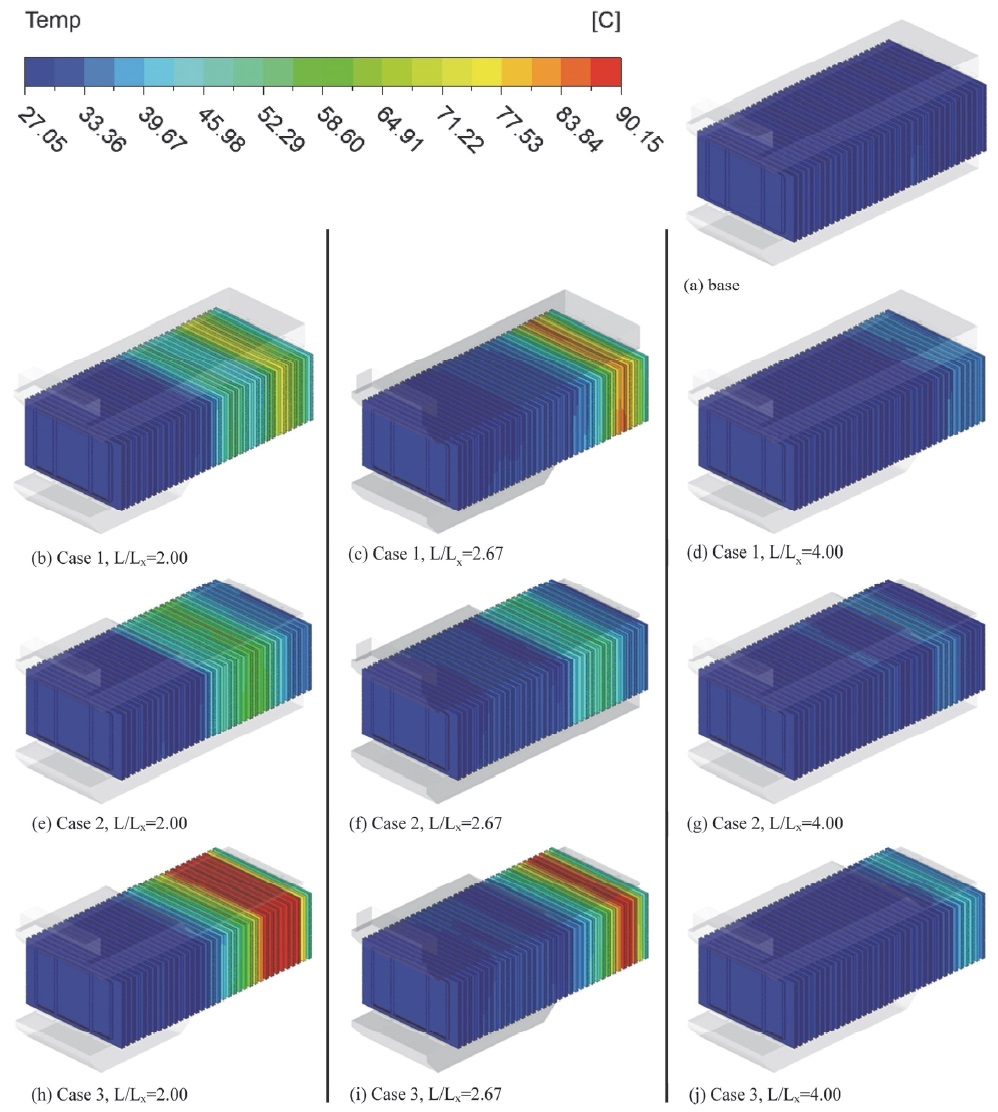
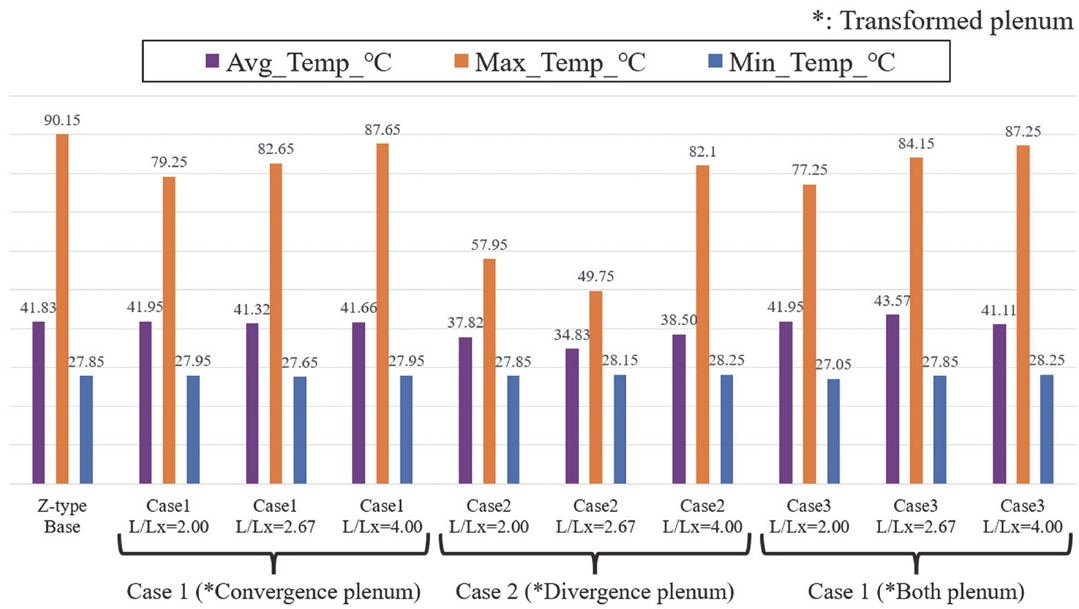
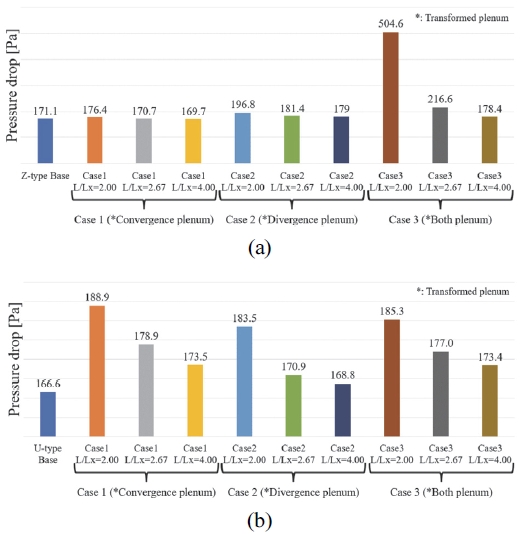
Z-type 배터리 팩에 대한 플레넘 형상에 따른 배터리 팩 내부 셀 온도 해석 결과에서 Z-type의 최대 온도 중 Base 모델이 가장 큰 온도 값인 90.15 ^oC이였으며 Case 2의 L/L_x=2.67에서 가장 낮은 온도인 49.75 ^oC를 보였다. Z-type Base 모델의 플레넘 전압 분포를 Fig. 12에 나타냈다. Base 플레넘은 유동 경로에 부적절한 압력이 형성되어 28번부터 34번 채널까지 역류가 발생했다. Fig. 13과 같이, 역류가 발생한 구간의 셀(약 50 ~ 68번)의 온도는 역류가 발생하지 않은 구간보다 크게 상승함을 해석을 통해 확인했다. 이와 다르게 가장 낮은 최대 온도를 보인 Z-type Case 2의 L_x/L=2.67에서는 Z-type base보다 개선된 압력이 플레넘에 형성되었고 어떤 채널에도 역류는 일어나지 않았다. 그 결과 최대 셀 온도는 Base 모델보다 약 40 ^oC 하락하였다. Z-type Case 2 L_x/L=2.67의 압력 분포와 셀 온도 및 채널에 유입되는 유량은 Fig. 14와 Fig. 15에 표시하였다.

Fig. 12

Non-uniform total pressure inside the battery pack of Z-type base model

Fig. 13

Effect of mass flow on cell temperature in Z-type base model

Fig. 14

total pressure inside Z-type case2 Lx/L=2.67

Fig. 15

Effect of mass flow on cell temperature in Z-type case2

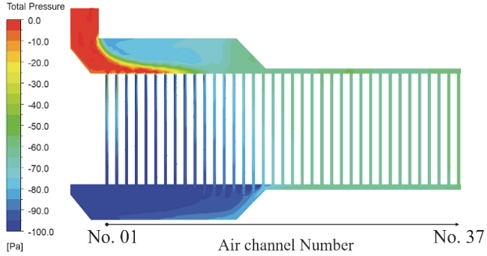
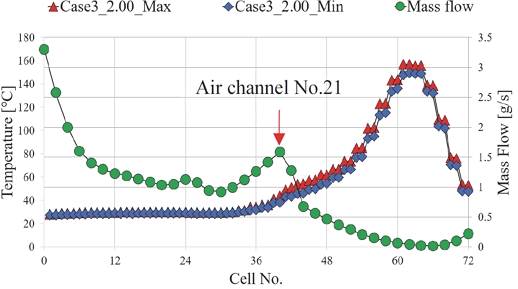
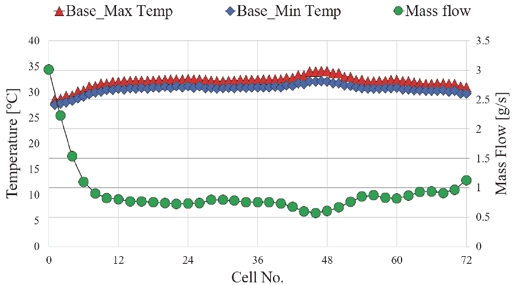
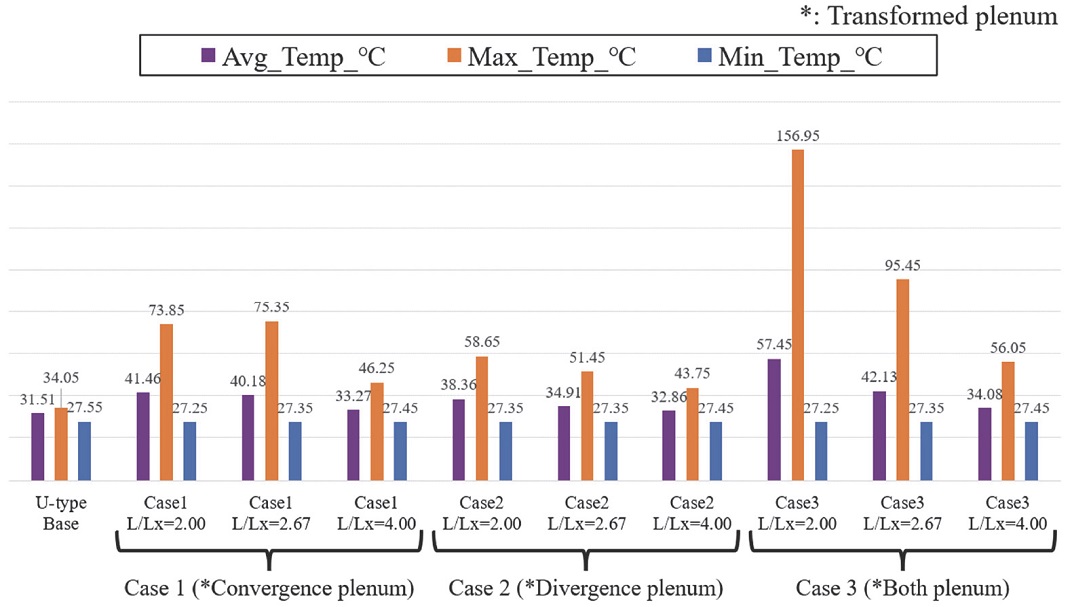
U-type 배터리 팩에 대한 케이스들의 온도 결과에서 가장 높은 셀 최대 온도를 보인 케이스는 U-type Case 3 L_x/L=2.00으로, 최대 온도는 약 156 ^oC이였으며, U-type base가 약 34 ^oC로 가장 낮은 셀 최대 온도를 보였다. Fig. 16과 Fig. 17에 U-type Case 3 L_x/L=2.00의 내부 전압과 유량에 따른 온도 그래프를 표시하였다. Case 3은 플레넘 공간이 최대로 줄어드는 채널 18번 이후로 유량 공급이 원활하지 못하기 때문에 셀의 온도가 급격히 상승한 것으로 보인다. 반면, 가장 낮은 최대 온도를 보인 U-type base의 경우, 유동 경로의 변화로 인해 Fig. 18과 같이 적절한 압력이 형성되어 Fig. 19와 같이 균일한 유량 공급되었다. 각 유동 경로 타입 별 Case의 셀 온도 분포는 Fig. 20과 Fig. 21에 표시하였고 Fig. 22와 Fig. 23은 Z-type과 U-type에서 각 Case 별 플레넘 형상에 따른 최대온도를 비교해서 나타내었다.

Fig. 16

Total pressure inside U-type case3 Lx/L=2.00

Fig. 17

Effect of mass flow on cell temperature in U-type case3 Lx/L=2.00

Fig. 18

Total pressure inside U-type base

Fig. 19

Effect of mass flow on cell temperature in U-type base

Fig. 20

Cell temperature distribution of Z-type battery pack according to the plenum shape of each case

Fig. 21

Cell temperature distribution of U-type battery pack according to the plenum shape of each case

Fig. 22

Cell temperature of Z-type according to each case

Fig. 23

Cell temperature of U-type according to each case

3.2 Plenum 형상에 따른 각 Channel의 유량

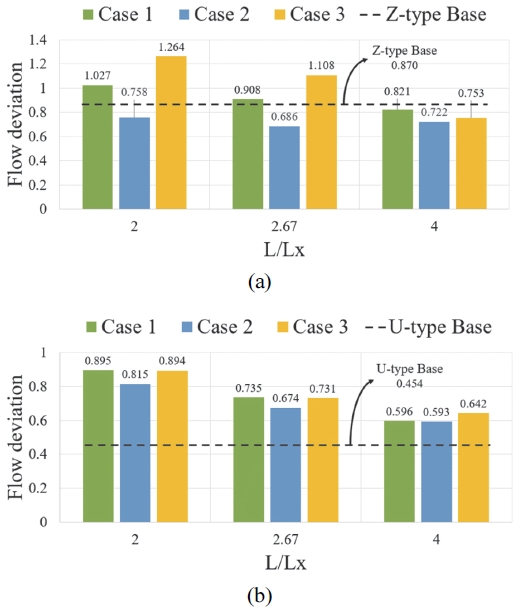
배터리 팩 내부의 각 셀의 균일한 냉각은 각 공기채널에 균등한 냉각 공기가 공급됨으로써 이루어질 수 있다. 플레넘 형상이 각 공기 채널로의 유량 편차 감소에 어떠한 영향을 미치는지 확인하기 위해 유동 경로 타입에 따른 각 채널의 유량 편차를 Fig. 24에 나타냈다. Fig. 24의 (a)에서 Z-type의 배터리 팩의 경우, Divergence plenum만 형상 변경이 이루어진 Case 2가 상대적으로 낮은 유량 편차를 보였다. 이를 통해, Z-type 배터리 팩 설계에서 Divergence plenum의 설계 변경은 유량 편차를 줄이는데 큰 효과를 보일 수 있음을 확인하였다. Fig. 24의 (b)는 U-type 배터리 팩의 플레넘 형상에 따른 유량 편차 그래프이며 Base 모델이 균일한 유량을 채널에 공급했다. U-type 배터리 팩에서 플레넘의 형상 변경은 오히려 불균일한 유량 공급을 불러올 수 있음을 알 수 있다.

Fig. 24

Results of flow deviation according to the plenum shape of each case (a) Z-type (b) U-type

3.3 Plenum 형상에 따른 압력 강하 특성

배터리 팩의 압력 강하는 블로워의 부하와 직결된다. 따라서 배터리 팩 냉각 설계 시, 압력 강하는 중요한 설계 요소이다. 공랭식 배터리 팩의 압력 강하 값을 산출하기 위해 인렛과 아웃렛 면에서의 평균 전압(Total pressure)의 차이를 계산하였다.

유동 경로 타입 별 Case의 압력 강하는 Fig. 25에 나타냈다. 플레넘의 공간이 작아질수록 압력 강하가 상승하는 경향을 Fig. 25의 (a)와 (b)에서 확인할 수 있다. Fig. 25의 (a)에서 Z-type base와 비교했을 때, Case 3에서 유독 큰 압력강하가 일어난 것을 알 수 있다. Case 3의 경우, Convergence plenum과 Divergence plenum 모두 변형되어 협소한 유동 공간을 가지고 있다. 따라서 협소한 유동공간의 특성으로 인해 Fig. 24의 (a)와 같이 Case 3은 상대적으로 큰 유량편차를 보였다. 큰 유량편차에 의해 좁은 공간에서 다량의 공기를 움직이기 위해서 유독 큰 압력 강하가 발생한 것으로 보인다. 이러한 이유로 가장 협소한 유동 공간을 가지는 Case 3 L_x/L=2.00에서 높은 압력 강하가 일어났다. Fig. 25의 (b)에서 U-type base와 가장 큰 압력강하 값과 비교했을 때, 약 4 Pa에서 약 22 Pa의 상승이 있었다.

Fig. 25

Results of pressure drop according to the plenum shape of each case (a) Z-type (b) U-type

큰 압력강하는 공기에 운동량을 부여하는 블로워에 더 많은 동력을 요구하게 된다. 이는 결국, 에너지 효율 관리가 중요한 HEV(Hybrid Electric Vehicle)혹은 BEV(Battery Electric Vehicle)에서 손실로 이어짐으로 압력 강하를 줄이려는 설계가 필요하다.

4. 결 론

본 연구는 냉각 공기 유동 경로 타입인 Z-type과 U-type 공랭식 배터리 팩에 Divergence plenum과 Convergence plenum 변경 및 조합에 따른 냉각 특성을 수치 해석을 통해 확인해 보았으며 이를 통해 얻은 결론은 아래와 같다.

• 1) 적절하지 못한 Plenum 설계는 배터리 팩 내부 유동에 역류를 발생시켜 역류가 발생되는 지점에서 배터리 온도 상승의 원인이 되는 것을 확인했다.
• 2) Z-type 배터리 팩의 경우, Divergence plenum의 설계 변경은 각 채널에 유입되는 공기를 상대적으로 균일하게 공급할 수 있도록 유도하는 것을 확인했다.¹³⁾
• 3) U-type 배터리 팩의 경우, 플레넘의 공간 감소는 각 채널의 유량의 균일화와 압력 강하에 부정적인 요인임을 확인했다.

향후 연구에서, 실제 배터리 발열 조건을 시뮬레이션에 적용하여 해석에 대한 신뢰성을 올리고 배터리 팩 구성 요소의 열 냉각 특성을 확인하는 것이 필요하다.

Acknowledgments

A part of this paper was presented at the KSAE 2022 Spring Conference

본 연구는 2022년도 정부(교육부)의 재원으로 한국연구재단의 BK21사업(5199990814084)지원과 한국연구재단(NRF #2018R1D1A1B07043950)의 지원을 받아 수행한 연구입니다.

References

• T. W. Kang, K. S. Yoo and J. H. Kim, “Analysis and Experiment Verification of Heat Generation Factor of High Power 18650 Lithium-ion Cell,” The Transactions of the Korean Institute of Power Electronics, Vol.24, No.5, pp.365-371, 2019.
• Y. Liu and J. Zhang, “Design a J-type Air-based Battery Thermal Management System Through Surrogate-based Optimization,” Applied Energy, Vol.252, P aper No.113426, 2019. [https://doi.org/10.1016/j.apenergy.2019.113426]
• C. E. Park, S. S. Yoo, Y. H. Jeong and K. B Kim, “Effect of Thermal Management of Lithium-Ion Battery on Driving Range of Electric Vehicle,” Journal of the Korea Academia-Industrial cooperation Society, Vol.18, No.5, pp.22-28, 2017.
• H. Fayaz, A. Afzal, A. D. M. Samee, M. E. M. Soudagar, N. Akram, M. A. Mujtaba, R. D. Jilte, Md. Tariqul Islam, Ü. Ağbulut and C. A. Saleel, “Optimization of Thermal and Structural Design in Lithium-Ion Batteries to Obtain Energy Efficient Battery Thermal Management System (BTMS): A Critical Review,” Archives of Computational Methods in Engineering, Vol.29, pp.129-194, 2022. [https://doi.org/10.1007/s11831-021-09571-0]
• H. Liu, Z. Wei, W. He and J. Zhao, “Thermal Issues About Li-ion Batteries and Recent Progress in Battery Thermal Management Systems: A Review,” Energy Conversion and Management, Vol.150, pp.304-330, 2017. [https://doi.org/10.1016/j.enconman.2017.08.016]
• H. Park, “A Design of Air Flow Configuration for Cooling Lithium-ion Battery in Hybrid Electric Vehicles,” Journal of Power Sources, Vol.239, pp.30-36, 2013. [https://doi.org/10.1016/j.jpowsour.2013.03.102]
• S. Jeong and H. Suh, “Predictions of the Cooling Performance on an Air-Cooled EV Battery System According to the Air Flow Passage Shape,” Transactions of the Korean Society of Mechanical Engineers B, Vol.40, No.12, pp.801-807, 2016. [https://doi.org/10.3795/KSME-B.2016.40.12.801]
• S. Lee and H. Kim, “A Study on the Estimation of Air Flow Rate with Discharge Rate for an Air-cooled Lithium-ion Battery Pack Using CFD Simulation,” Transactions of KSAE, Vol.30, No.4, pp.273-280, 2022. [https://doi.org/10.7467/KSAE.2022.30.4.273]
• G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge Univ. Press, Cambridge, England, 1967.
• ANSYS, Fluent Theory Guide, USA, 2022.
• M. Ryu, T. Kim, S. Park, J. Lee and S. Park, “A Study on the Characteristic of the Indirect Air Cooling System of a Lithium-ion Battery Module for Vehicle,” Transactions of KSAE, Vol.26, No.5, pp.663-675, 2018. [https://doi.org/10.7467/KSAE.2018.26.5.663]
• K. Shah, S. J. Drake, D. A. Wetz, J. K. Ostanek, S. P. Miller, J. M. Heinzel and A. Jain, “Modeling of Steady-state Convective Cooling of Cylindrical Li-ion Cells,” Journal of Power Sources, Vol.258, pp.374-381, 2014. [https://doi.org/10.1016/j.jpowsour.2014.01.115]
• G. H. Lee, H. K. Kim and S. Y. Jang, “Effect of Plenum on Cooling Performance in Air-cooled Z-type,” KSAE Spring Conference Proceedings, p.54, 2022.