자율주행 차량과 차량센서 교정을 위한 외부 시스템 구성에 관한 연구

1. 서 론

자율주행 분야는 크게 인지, 판단, 제어 분야로 나뉘어 연구가 활발히 진행 중에 있다. 인지 분야는 크게 검출과 측위 부분으로 나뉘어 연구가 진행 중에 있다. 판단 분야는 모션 판단, 주변 객체에 대한 궤적 예측 등을 수행하고 있다. 제어 분야는 판단을 기반으로 차량에 제어 명령을 수행한다. 최근 딥러닝 기술력과 높은 컴퓨팅 파워의 발전에 힘입어 기존 규칙기반 시스템보다 높은 성능의 자율주행 연구가 활발히 연구 중에 있다. 저자 Na 등¹⁾의 경우 계층 프레임워크를 이용하여 자율주행 차량 주변의 차량들에 대한 궤적을 예측하는 연구를 수행했으며, 주변 환경의 정보를 보다 정확히 인지하기 위해 Semantic segmentation을 이용한 주변 환경 인지에 대한 연구가 Jeong 등,²⁾ Park 등,³⁾ 송하민 등⁴⁾과 같이 활발히 연구 중에 있다. 하지만 자율주행 시스템은 각각 독립적 관계가 아닌 종속적 관계이다. 때문에 서로 신뢰할 수 있는 정보를 주고받아야 안전한 자율주행 시스템을 구성할 수 있다.

인지 분야는 센서 데이터를 토대로 검출 및 측위 연구가 수행된다. 판단 분야는 검출 및 측위 분야에서 제공하는 데이터(주변 객체 위치, 자차 위치 등)를 기반으로 제어 명령을 보낼 수 있다. 제어 분야는 판단 분야로부터 얻은 정보를 기반으로 최적의 차량 제어를 수행할 수 있다. 이런 종속적 관계를 구성하기 위해선 차량과 센서에 대한 외부 교정이 수행 되어야 한다. ROS에서는 이러한 관계 포맷을 URDF라고 정의한다. URDF는 Frame과 Frame 즉 Camera, LiDAR, GNSS/INS, Wheel 등의 좌표계를 하나의 기준 좌표계(e.g. base_print)로 나타낼 수 있다.

외부 교정(Extrinsic calibration)은 앞서 언급한 URDF를 구성할 수 있는 방법이다. 외부 교정이라 함은 각각의 센서 혹은 플랫폼이 가지고 있는 좌표계들의 위치, 자세 관계를 구하는 것이다. 외부교정은 수많은 연구가 수행되어져 왔다. 배종욱 등⁵⁾저자는 카메라-라이다(LiDAR) 센서 교정을 수행하기 위해 목표물 기반, 비 목표물 기반, 움직임 기반, 장면 기반, 딥러닝 기반 외부 교정 논문을 소개하며 실제 적용한 논문을 제시하였다. 일반적으로 카메라-라이다 센서의 목표물 기반 외부 교정은 Dhall 등,⁶⁾ Liu 등,⁷⁾ Beltrán 등,⁸⁾ Tsai 등⁹⁾처럼 높은 정교성을 보여주고 있다. 하지만 목표물 기반 외부 교정 시스템은 차량이 정지해 있는 상태에서 수행되기 때문에 INS 센서 교정이 불가능하다. 비 목표물 기반 연구는 주로 움직임기반 Kim 등¹⁰⁾과 Wang 등¹¹⁾처럼 외부 교정 연구를 수행하고 있다. 움직임 기반 교정의 경우 인지 센서(카메라, 라이다) 간 교정뿐만 아니라 INS 센서와 교정도 Kim 등,¹⁰⁾ Taylor와 Nieto¹²⁾과 같이 수행되고 있다. 하지만, 이런 비 목표물 기반의 연구는 일반적으로 초기값을 요구하고 있다.

앞서 언급한 바와 같이 딥러닝과 컴퓨팅 파워의 발전으로 인해 센서로부터 검출된 특정 객체의 위치 정확도나 차량의 위치 정확도, 주변 객체의 이동 예측 정확도가 상당히 높아진 것을 확인할 수 있다(Paperswithcode).¹³⁾ 그러나 각각의 분야에서 정확도가 높아지더라도 자율주행 시스템은 제어하고자 하는 차량이 정확하게 제어가 되는 것이 최종 목표이다. 최종 목표를 정확히 수행되기 위해서는 인지, 판단, 제어의 정확도뿐만 아니라 차량과 센서의 외부 교정 정확도 역시 매우 중요하다. 본 논문에서는 차량 좌표계와 차량 센서간의 외부 교정을 수행하기 위한 외부 시스템에 대해 소개하고 외부 시스템을 교정 공간 좌표계(Global coordinate system) 기준으로 자세를 구하는 방법을 제시하고자 한다.

2. 차량 자세를 추정하기 위한 외부 시스템

외부 시스템이라 하면 흔히 SfM(Structure from Motion)¹⁴⁾기법이나 LiDARCap¹⁵⁾ 기법과 같이 외부에 센서를 구축하여 특정 목표물을 3D로 구성하는 시스템이라 할 수 있다. 하지만 SfM 기법과 같이 외부에서 스캔하는 방식은 센서가 다양하게 움직이지 못하는 실내에서는 제약 조건이 존재한다. Motion capture¹⁶⁾ 방식은 마커와 주변에 수많은 센서를 이용하여 자세를 정교하게 측정하는 방법이 있다. 그러나 이런 방법 역시 많은 외부 센서를 요구하기 때문에 초기에 많은 비용이 발생한다.

차량 센서 교정 방법에 있어서 목표물 기반 외부 교정은 실내에서 수행이 이루어진다. 실내는 실외에 비해 센서 노이즈 원인 중 하나인 외부 요소(밝기의 변화 등)가 적기 때문에 좀 더 정교한 외부 교정 수행이 가능하다. 그러나 대부분 목표물 기반 센서 교정은 센서와 센서들의 교정을 수행할 뿐 차량과 외부 교정을 수행하지 않는다. 이를 해결하기 위해 나온 방법이 움직임 기반의 교정 방법이다. Kim 등¹⁰⁾과 Taylor와 Nieto¹²⁾는 다중 센서와 차량 움직임 기반의 교정방법에 관한 연구를 진행하였다. 하지만 이러한 방법들은 넓은 공간과 초기값을 요구하고 있다. 또한 차량 좌표계와 센서 간의 교정을 수행하기 위해 Dürr¹⁷⁾와 같이 기업에서는 외부 장비를 이용하여 차량과 센서들 간의 외부 교정을 수행하고 있다. 하지만 이러한 장비는 실내를 더 협소하게 만들 뿐만 아니라 높은 가격을 요구하며, Fig. 1과 같이 특정 위치(장비 위치)에서만 교정이 가능하다는 단점이 존재한다.

Fig. 1

Wheel alignment equipment18)

이번 장에서는 이러한 단점들을 해결하고자 센서 교정 공간의 조성 방법과 외부 시스템의 필요성에 대해 제시한다.

2.1 외부 시스템 및 차량 교정을 위한 공간 조성

외부 시스템 및 차량 교정 공간 이라 함은 Dürr¹⁷⁾과 같이 차량과 차량 센서간 교정을 수행하기 위한 공간이다. 하지만 본 연구에서는 Dürr¹⁷⁾같이 많은 장비를 필요로 하지 않는 교정 외부 시스템을 제시하고자 한다.

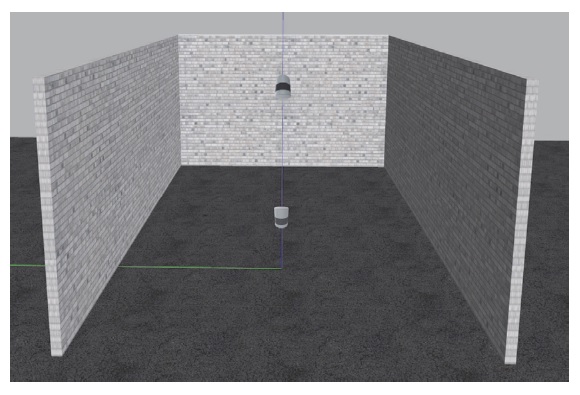
교정 공간은 주변 벽이 서로 수직으로 구성 되어 있는 일반적인 실내 공간이다. 실험 환경으로 사용할 교정 공간은 오픈소스 3D 로봇공학 시뮬레이터인 Gazebo를 이용하여 구축하였다. Gazebo에서 구축한 라이다의 경우 노이즈가 없는 센서로 구축 하였다. Fig. 2는 Gazebo를 이용하여 구축한 최종 교정 공간이다. 이때 주변 벽은 서로 수직 관계가 있으며 바닥은 수평 하다고 가정한다.

Fig. 2

Extrinsic calibration room in gazebo

앞서 언급한 바와 같이 차량 자세와 차량 센서의 위치 및 자세를 구하기 위해 교정 공간에 카메라와 라이다를 구축한다. 본 연구에서는 라이다 센서만을 구축하고자 한다. 그 이유는 라이다의 자세를 추정할 수 있으면 기존 존재하는 카메라-라이다간 외부 교정을 통해 카메라 자세를 구할 수 있기 때문이다.

구축된 라이다 센서는 추후에 차량과 차량에 장착된 센서 간의 교정을 수행할 수 있을 것으로 예상한다.

2.2 교정 공간에서의 외부 센서 구축 필요성

자율주행 차량은 차량에 장착된 센서와 차량 좌표계와의 교정이 필요하다. 이를 해결하기 위해서 기존에는 2장에서 언급한 움직임 기반 방법과 교정 장비 설치 방법이 존재한다. 하지만 움직임 기반 방법은 넓은 공간을 필요로 하는 단점이 있다. 또한 교정 장비 설치는 실내를 더욱 협소하게 만들 뿐만 아니라 초기 비용이 많이 발생한다.

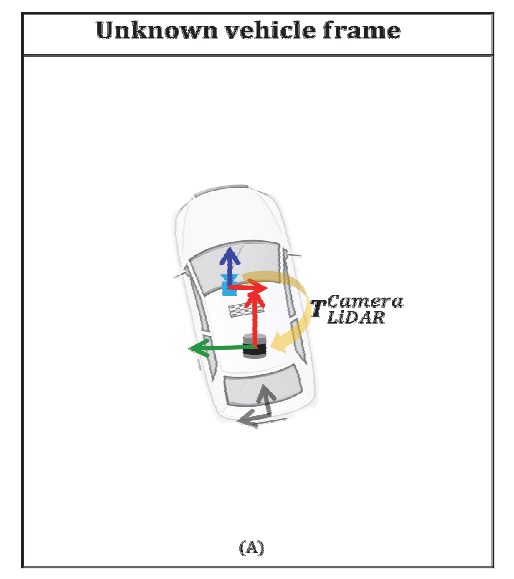
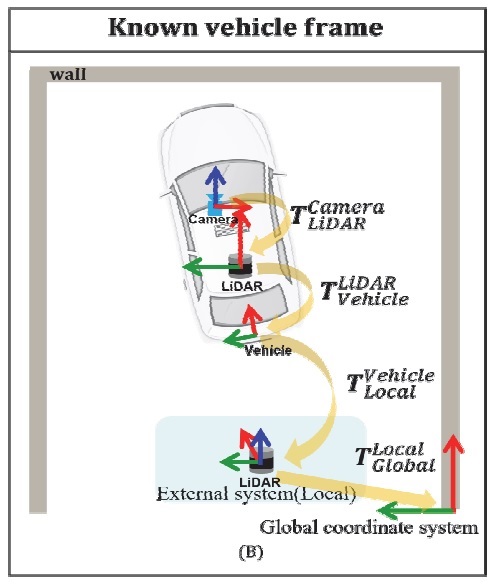
실내에서 움직임 없이 차량 자세를 추정하기 위해서는 차량의 자세를 구할 수 있는 외부 시스템이 필요하다. Fig. 3(a)와 같이 외부 센서가 없다면, 차량과 차량 센서들 간의 위치 관계를 구할 수 없다. 반면 Fig. 3(b)와 같이, 외부 시스템이 주어지면 교정 공간(Global coordinate system) 기준으로 Vehicle frame의 자세 정보를 구할 수 있다. 하지만 교정 공간에 외부 시스템이 구축 되어 있어도 교정 공간과 외부 시스템 간의 위치 자세($$ T_{Global}^{Local}$$, T=homogeneous transformation matrix)를 알 수 없으면 차량 자세는 외부 시스템 기준으로 나오게 되어 교정 공간 기준으로 구할 수 없다. 이를 해결하기 위해 3장에서는 외부 시스템으로 선정한 라이다의 자세를 교정 공간을 기준으로 구하는 방법에 대해 제시하고자 한다. 교정 공간은 향후 차량과 차량 센서간 교정 기준 점이 된다.

Fig. 3(a)

Unknown vehicle frame

Fig. 3(b)

Known vehicle frame

3. 외부 시스템의 자세 추정 방법

센서 교정 공간에 설치한 외부 시스템 라이다의 자세 추정 방법은 주변 교정 공간을 이용해서 추정할 수 있다. 이번 장에서는 주변 환경을 이용하여 외부 시스템인 라이다의 외부 교정값을 교정 공간 기준으로($$ T_{Global}^{Local}$$) 구하는 방법에 대해 설명하고자 한다.

3.1 SVD를 이용한 라이다 자세 추정

라이다는 임의의 자세로 구축했다고 가정한다. 라이다는 교정 공간을 기준으로 자세를 구하기 위하여 SVD를 활용한다. SVD는 임의의 m×n 행렬 A를 식 (1)처럼 분해할 수 있는 행렬 분해(Decomposition) 방법 중 하나이다. 쉽게 선형 변환 후에 크기는 변하지만 여전히 직교하는 직교 집합을 나타낸다. SVD의 특이값(Singular value)은 식 (2)처럼 크기가 큰 순서대로 정렬되며(σ₁>σ₂>σ₃), 그에 연관된 특이벡터(Singular vector) 또한 특이값 순서에 맞춰서 정렬된다. 이때 식 (4) V행렬의 특이 벡터 방향성을 이용하여 라이다의 자세를 구하고자 한다.

$\[ A=U\Sigma V^T \]$

(1)

$\[ \Sigma =\left(\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right) \]$

(2)

$\[ U=\left(\begin{array}{ccc}⋮& ⋮& ⋮\\ \overrightarrow{u_1}& \overrightarrow{u_2}& \overrightarrow{u_3}\\ ⋮& ⋮& ⋮\end{array}\right) \]$

(3)

$\[ V=\left(\begin{array}{ccc}⋮& ⋮& ⋮\\ \overrightarrow{v_1}& \overrightarrow{v_2}& \overrightarrow{v_3}\\ ⋮& ⋮& ⋮\end{array}\right) \]$

(4)

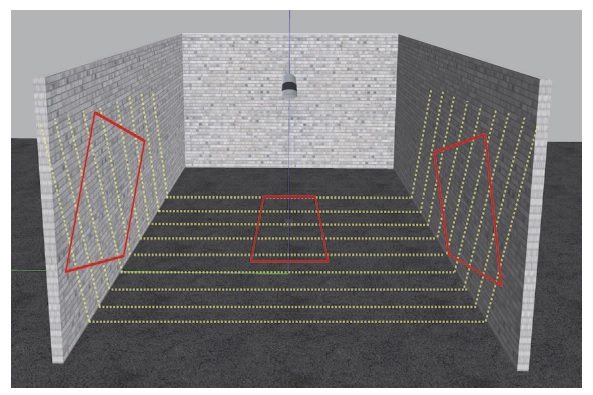
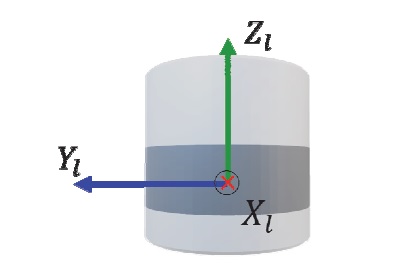
앞서 언급한 라이다의 자세를 구하기 위해 라이다 직교좌표계 특성을 이용하여 RoI를 구한다. 이때 RoI는 Fig. 4와 같이 라이다 센서 x, y축을 기준으로 구한다. 설치된 라이다의 좌표계는 Fig. 5와 같이 구성되어 있다.

Fig. 4

RoI position

Fig. 5

LiDAR coordinate system

RoI 영역을 구한 뒤 RoI에 존재하는 포인트 클라우드 데이터를 SVD를 통해 RoI 영역의 Normal vector를 구한다. SVD 특성을 이용하여 얻은 하나의 Normal vector는 라이다의 Roll, Pitch, Yaw 모두 구할 수 없다. 이 문제를 해결하기 위해서 우리는 서로 다른 방향의 Normal vector를 이용하여 라이다의 오일러 각(Euler angle)을 구하고자 한다. 본 논문에서는 Fig. 4와 같이 Ground normal vector와 Wall normal vector를 이용한다. 벽면 RoI, 바닥 RoI는 0.6 × 0.8(m) 크기로 정했다. 정해진 RoI 영역의 데이터들을 SVD 수행 후 V행렬을 구한다. SVD 수행 결과는 계산 방법에 따라 V행렬의 열벡터 순서가 다르게 나올 수 있다. 본 실험에서는 RoI 영역에 존재하는 포인트 클라우드 값의 편차를 이용하여 SVD를 수행했다. 이때 V의 세 번째 열벡터 $$ \overrightarrow{v_3}$$는 해당 RoI의 법선 벡터가 된다. 우리는 이런 특이벡터의 정의를 활용하여 라이다의 자세를 교정 공간 기준으로 구하고자 한다.

4. 실험 결과

이번 장에서는 3.2절에서 언급한 회전 순서에 따른 정확도를 검증하기 위하여 두 가지 시나리오를 구성했다. 첫 번째 시나리오는 Ground normal vector를 이용하여 얻은 Roll, Pitch값을 이용하여 회전 변환 후 Wall normal vector를 이용하여 라이다의 Yaw 값을 구한다. 두 번째 시나리오는 회전 변환 없이 Roll, Pitch, Yaw 값을 구했다.

4.1 회전 변환 유무에 따른 라이다 자세

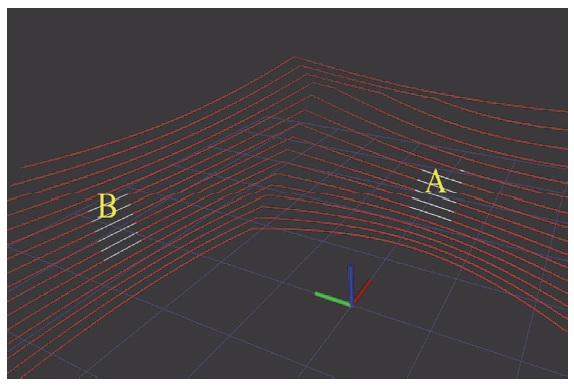
이번 절에서는 Roll, Pitch의 회전 변환 유무에 따른 라이다 자세 실험 결과를 나타낸다. 아래 Fig. 6은 Fig. 4의 Gazebo를 이용하여 얻은 데이터 모습이다. 이때 Fig. 6에 표기된 A는 Ground RoI이며, B는 Wall RoI이다.

Fig. 6

RoI in gazebo simulator

아래 Table 1은 초기 라이다 자세를 나타냈다.

Table 1

Initial pose of LiDAR sensor

A영역인 Ground RoI에 SVD를 이용하여 얻은 식 (4)의 $$ \overrightarrow{v_3}$$백터(Normal vector)를 이용하여 Pitch 와 Roll을 식 (6)과 식 (5)로부터 구하였다.

$$ \mathrm{p}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{ }={\mathrm{s}\mathrm{i}\mathrm{n}}^{-1}\left(\widehat{v_{31}}\right)=39.9965\left(\mathrm{d}\mathrm{e}\mathrm{g}\right)$$

$$ \mathrm{r}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{ }={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\widehat{v_{32}}}{\widehat{v_{33}}}\right)=9.9978591\left(\mathrm{d}\mathrm{e}\mathrm{g}\right)$$

아래에서 구한 $$ \widetilde{yaw}$$ 값은 Pitch, Roll의 회전 변환 없이 구한 Yaw 값이다.

$$ \widetilde{yaw}={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\widehat{v_{31}}}{\widehat{v_{32}}}\right)=7.6857\left(\mathrm{d}\mathrm{e}\mathrm{g}\right)$$

초기 라이다 Yaw값(10 deg)과 비교해보면 2.3143 (deg) 정도의 에러가 발생한 것을 확인할 수 있다.

아래 $$ \widetilde{yaw}$$값은 Pitch, roll 변환 후 Wall normal vector를 이용하여 얻은 Yaw 값이다.

$$ \widetilde{yaw}={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\widehat{v_{31}}}{\widehat{v_{32}}}\right)=9.99766\left(\mathrm{d}\mathrm{e}\mathrm{g}\right)$$

5. 결 론

본 연구에서는 차량 좌표계와 차량에 장착된 센서간의 외부 교정을 위한 외부 시스템을 소개하고, 외부 시스템을 교정 공간(Global) 기준으로 위치 및 자세를 구하는 방법에 대해 소개 한다.

이 연구에서는 외부센서로 라이다를 이용하였으며, SVD특성을 이용하여 교정 공간에 대한 라이다의 자세를 구하였다. 라이다 자세를 구하기 위해 기준점이 될 교정 공간의 벽과 땅은 서로 수직 관계가 있다고 가정하며, 실험 환경은 Gazebo simulator를 이용하여 구현하였다.

라이다센서 자세를 교정 공간 기준으로 구하기 위해 RoI영역에 속한 포인트 클라우드 데이터를 SVD 하였으며, SVD를 통해 구한 Normal vector를 이용하였다. 이 연구에서는 Ground normal vector를 이용하여 라이다의 Pitch, Roll 값을 구하였고, Pitch, Roll 순으로 회전 변환한 뒤 Wall normal vector를 이용하여 라이다의 Yaw 자세를 구하였다.

향후 외부 시스템은 차량 자세를 교정 공간 기준으로 구할 수 있을 것으로 예상한다. 뿐만 아니라 차량 좌표계와 차량에 장착된 센서간의 외부 교정을 외부 시스템을 이용하여 교정 될 수 있다. 향후 해당 외부 시스템이 구축된 교정 공간을 이용하여 차량에 장착된 센서와 차량 간의 외부 교정에 대한 연구를 진행할 계획이다.

Acknowledgments

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 연구되었음(과제번호 21AMDP-C161756-01).

References

• Y. Na, J. Lee and K. Jo, “Interaction-aware Trajectory Prediction of Surrounding Vehicles Based on Hierarchical Framework in Highway Scenarios,” IEEE Intelligent Vehicles Symposium (IV), pp.1060-1065, 2022.
• J. Jeong, H. Song, J. Park, P. Resende, B. Bradaï and K. Jo, “Fast and Lite Point Cloud Semantic Segmentation for Autonomous Driving Utilizing LiDAR Synthetic Training Data,” IEEE Access Vol.10, pp.78899-78909, 2022. [https://doi.org/10.1109/ACCESS.2022.3184803]
• J. Park, C. Kim, S. Kim and K. Jo, “PCSCNet: Fast 3D Semantic Segmentation of LiDAR Point Cloud for Autonomous Car using Point Convolution and Sparse Convolution Network,” Expert Systems with Applications, Vol.212, Paper No.118815, 2023. [https://doi.org/10.1016/j.eswa.2022.118815]
• H. Song, J. Cho, J. Ha, J. Park and K Jo “Camera-LiDAR Fusion-Based Point Cloud Semantic Segmentation through Voxel-Pixel Matching for Autonomous Driving,” Transactions of KSAE, Vol.30, No.10, pp.809-817, 2022. [https://doi.org/10.7467/KSAE.2022.30.10.809]
• J. Bae, Y. Lee, J. Koh, J. Lee and J. Choi “Multi-Sensor Calibration Techniques for Camera-LiDAR Sensor Fusion,” Transactions of KSAE, Vol.30, No.10, pp.849-858, 2022. [https://doi.org/10.7467/KSAE.2022.30.10.849]
• A. Dhall, K. Chelani, V. Radhakrishnan and K. M. Krishna “LiDAR-Camera Calibration Using 3D-3D Point Correspondences,” arXiv preprint arXiv:1705.09785, , 2017.
• Y. Liu, H. Schofield and J. Shan, “Fiducial Marker Detection in Multi-Viewpoint Point Cloud,” arXiv preprint arXiv:2209.01072, , 2022.
• J. Beltrán, C. Guindel and F. García, “Automatic Extrinsic Calibration Method for Lidar and Camera Sensor Setups,” IEEE Transactions on Intelligent Transportation Systems, Vol.23, No.10, pp.17677-17689, 2022. [https://doi.org/10.1109/TITS.2022.3155228]
• D. Tsai, S. Worrall, M. Shan, A. Lohr and E. Nebot, “Optimising the Selection of Samples for Robust Lidar Camera Calibration,” IEEE International Intelligent Transportation Systems Conference, pp.2631-2638, 2021. [https://doi.org/10.1109/ITSC48978.2021.9564700]
• H. Kim, S. N. K. Rangan, S. Pagad and V. G. Yalla, “Motion-based Calibration between Multiple Lidars and Ins with Rigid Body Constraint on Vehicle Platform,” IEEE Intelligent Vehicles Symposium (IV), pp.2058-2064, 2020. [https://doi.org/10.1109/IV47402.2020.9304532]
• W. Wang, S. NobuHara, R. Nakamura and K. Sakurada, “Soic: Semantic Online Initialization and Calibration for Lidar and Camera,” arXiv preprint arXiv:2003.04260, , 2020.
• Z. Taylor and J. Nieto, “Motion-based Calibration of Multimodal Sensor Arrays,” IEEE International Conference on Robotics and Automation (ICRA), pp.4843-4850, 2015. [https://doi.org/10.1109/ICRA.2015.7139872]
• Meta AI, Paperswithcode, https://paperswithcode.com/sota, , 2022.
• J. L. Schönberger and J. M. Frahm, “Structurefrom-Motion Revisited,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp.4104-4113, 2016. [https://doi.org/10.1109/CVPR.2016.445]
• J. Li, J. Zhang, Z. Wang, S. Shen, C. Wen, Y. Ma, L. Xu, J. Yu and C. Wang, “Structure-from-Motion Revisited,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp.4104-4113, 2016.
• A. M. Aurand, J. S. Dufour and W. S. Marras, “Accuracy Map of an Optical Motion Capture System with 42 or 21 Cameras in a Large Measurement Volume,” Journal of Biomechanics Vol.58, pp.237-240, 2017. [https://doi.org/10.1016/j.jbiomech.2017.05.006]
• Dürr, Multi Sensor Calibration, https://www.durr.com/en/products/final-assembly/testing-systems/autonomous-driving-passenger-cars/multi-sensor-calibration-test-stand-passenger-cars, , 2022.
• Turbosquid, https://www.turbosquid.com/ko/3d-models/3d-wheel-alignment-equipment-car-model-1608832, , 2022.