찢김 에너지를 이용한 고무 부시 내구 수명 해석

1. 서 론

고무는 복원력이 우수하고 진동 절연성이 좋아 차량의 방진 제품 재료로 많이 사용된다. 이러한 제품은 자동차의 NVH(Noise, Vibration, Harshness)성능에 큰 영향을 주기 때문에 특성 및 내구 성능 예측을 통한 설계 능력이 매우 중요하다. 그러나 고무 재료는 일반적인 금속 재료와 달리 복잡한 비선형 재료 거동으로 인해 유한 요소 해석(Finite Element Analysis, FEA)을 통한 수명 예측이 어렵다. 특히 피로 내구 해석에서는 고려해야 하는 변수가 많고 해석에 필요한 고무의 피로 수명 선도(S-N Curve, E-N Curve)에 대한 데이터 베이스(DB)확보가 어려워 신뢰할 만한 결과를 얻기가 힘든 것이 현실이다.

고무는 일반적으로 변형률이 100 ~ 500 % 이상의 대변형에서도 탄성을 유지하는 초탄성(Hyperelastic)성질을 가지고 있으며,¹⁾ 이러한 고무 재료의 거동을 나타내기 위해서 다양한 변형률 에너지 밀도 함수가 사용된다. 대표적으로 많이 사용하는 함수로 식 (1)과 같은 Yeoh^2,4)모델과 식 (2)와 같은 Ogden^2,5)모델을 예로 들 수 있다.

식 (1)의 I₁은 불변량의 함수이며, 식 (2)의 λ₁, λ₂, λ₃은 각 방향으로의 신장비를 의미한다. 그리고 식 (1)과 식 (2)의 C_i0, u_i, α_i는 재료 상수를 의미한다.

또한 고무의 큰 특징 중 하나로 뮬린스 효과(Mullins Effect)를 들 수 있다. 이 뮬린스 효과는 고무 재료에 하중 부하(Loading) 및 제하(Unloading)를 반복하는 과정에서 강성이 완화(Softening)되는 현상을 말하며, 이러한 거동은 Ogden-Roxburgh 모델^3,6)로 설명이 가능하다.

여기서 η는 응력 완화 비를 의미한다. 변형 이력 중 변형률 에너지 밀도(Strain Energy Density, W)가 가장 큰 값인 W_max는 최초 하중 부하 시 W=W_max로 η=1이 되어 응력 완화가 없는 반면, 제하 시에는 W<W_max로 η<1이 되어 기존 응력(S₀)에 η가 곱해진 응력 완화 거동이 표현되게 된다. η는 식 (4)와 같이 재료상수 r, m, β와 오차함수 erf(x)를 이용하여 표현할 수 있다.³⁾

이러한 함수식을 이용하면 고무의 거동을 예측하여 응력 및 변형률 데이터를 피로 내구 해석에 활용할 수 있다. 전통적인 내구 해석 방법은 Wöhler⁷⁾의 연구를 기반으로 한 응력 및 변형률과 수명의 관계를 이용하는 것이다. 일반적으로 최대 주 변형률(Maximum Principal Strain)과 변형률 에너지 밀도 등을 많이 이용하며, 시험 결과와 비교를 통해 관계식을 도출하고 이를 수명 예측에 이용한다. 이러한 내구 해석 방법은 실제 산업 현장에서 가장 많이 사용되고 있는 방법 중 하나이다. 우창수 등⁸⁾은 장구형 시편(Dumbbell Cylindrical Specimen)과 같이 비교적 간단한 형상으로 여러 하중 조건에서 시험을 진행하고 해석을 통해 얻은 변형률 값과 비교하여 피로 수명 선도를 작성하였으며, 이를 실제 제품에 적용하여 신뢰성 검증을 하였다. 그러나 이러한 해석 방법은 하중 조건이 비교적 단순하거나, 다양한 조건에 대한 수명 선도 DB가 구축되어 있는 경우로 국한된다. 실제로 하나의 수명 선도를 작성하기 위해서는 여러 하중 조건에서 시험을 해야 하며,⁷⁾ 최대 하중과 최소 하중의 비인 응력비(Stress ratio = $$ \frac{{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}$$, R-ratio)에 따라 수명 결과가 달라질 수 있고,⁹⁾ 주 변형 모드에 따라 수명 결과가 달라질 수 있다.^10,11) 그렇기 때문에 정확한 DB를 구축하기 위해서 여러 변수 조건을 고려해야 하며, 상당한 시간과 노력이 요구되는 단점이 있다.

한편 Griffith¹²⁾는 금속 재료를 에너지 해방률(Energy Release Rate, G)에 근거한 파괴 역학적 관점으로 피로 내구를 예측하였다. 물체에 외력이 가해지면 물체 내부에 탄성 변형 에너지가 축적되며, 균열이 생성됨에 따라 변형 에너지가 해방된다는 개념을 설명하며 식 (6)을 제시하였다.

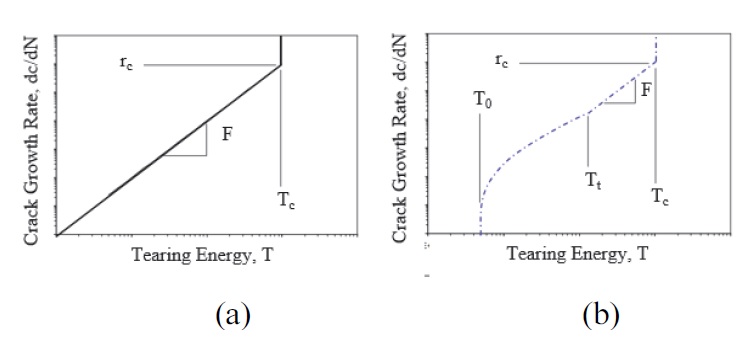
에너지 해방률은 찢김 에너지(Tearing Energy, T)라고도 하며, U는 균열 성장을 통해 방출되는 전체 탄성 포텐셜 에너지, A는 균열의 면적을 의미한다. Rivlin과 Thomas¹³⁾는 이러한 개념을 고무로 확장시켰다. Thomas¹⁴⁾는 찢김 에너지와 크랙 성장 속도와의 관계를 연구하여 Fig. 1(a)과 같이 나타내었다. Lake와 Lindley¹⁵⁾는 Thomas식을 확장시켜 모든 에너지 영역에서 찢김 에너지와 크랙 성장 속도와의 관계를 설명하기 위해 크랙이 일어나는 과정을 Fig. 1(b)와 같이 4구간으로 나누어 설명하였다.

Fig. 1

Typical fatigue crack growth rate curve(FCGR curve); (a) Thomas model, (b) Lake-lindley model

식 (7)의 크랙 성장 속도(dc/dN)는 식 (8)과 같이 크랙의 초기 결함 길이(C₀)와 최종 결함 길이(C_f)를 정의하여 적분을 통해 제품 수명(N_f)을 구하는데 활용된다.¹⁶⁾

Mars와 Fatemi¹⁷⁾는 응력비가 0이 아닌 하중 조건에서 고무 재료의 분자 사슬이 정렬된 상태에서 완전히 풀리지 않고 유지됨으로 인해 크랙의 성장을 방해하여 피로 수명이 올라가는 변형 결정화(Strain Crystallization)가 일어난다고 설명하였다. 이러한 현상은 응력비의 변화에 따라 찢김 선도(FCGR Curve)의 기울기가 달라지며, 그 차이에 해당하는 x(R)을 식 (9)와 같이 정의하여 설명하였다.¹⁸⁾

Fig. 2와 같이 변형 결정화 물성을 적용하면 응력비에 따라 찢김 선도의 기울기가 크게 차이가 나는 반면, 적용하지 않을 경우 응력비와 상관없이 하나의 찢김 선도가 나타나는 것을 확인할 수 있다.

Fig. 2

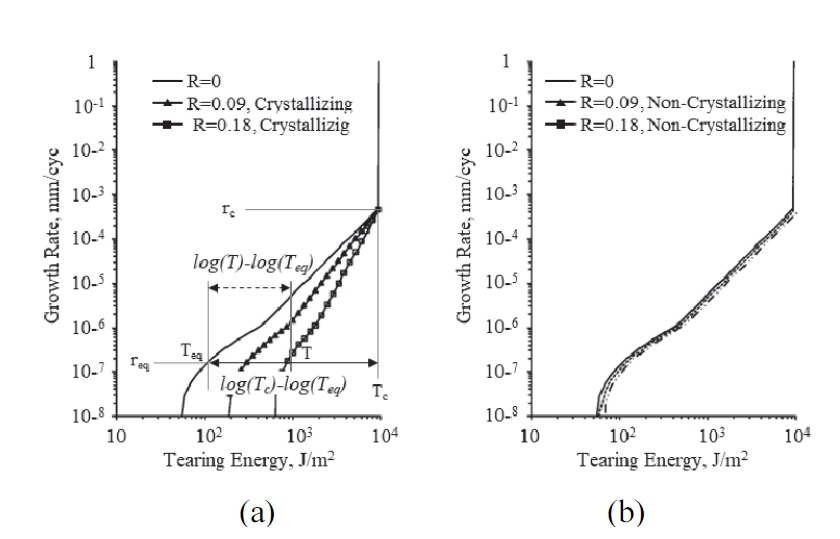
Non-relaxing fatigue crack growth behavior of rubber materials; (a) Strain-crystallization material, (b) Non-strain crystallization material19)

찢김 에너지를 이용한 내구 해석은 몇 가지의 시편 시험을 통해 물성 파라미터를 추출할 수 있어서 물성 DB가 충분하지 않은 상태에서도 해석이 가능하며 신뢰성 또한 우수하다는 장점이 있다. 그렇기 때문에 최근 많은 연구에서 전통적인 내구 예측 방법을 대체하고 있다. 김헌영과 김호²⁰⁾는 Thomas가 제안한 모델을 기반으로 찢김 에너지 식을 정식화하였고, 문형일 등²¹⁾은 정식화된 찢김 에너지 식을 자동차용 모터 마운트에 적용하여 검증하였다. 하지만 변형 결정화 현상을 반영하지는 않았다. Nyaaba 등²²⁾은 변형 결정화 현상을 고려하여 타이어 피로 내구 해석을 검증하였으며, 그 결과 크랙 위치와 수명 값에 차이가 발생한다는 것을 확인하였다.

본 논문에서는 수명 예측이 어려운 자동차용 고무 부시에 대하여 찢김 에너지를 기반으로 한 피로 수명 해석을 검증하였다. 이를 위해 고무 거동 해석이 가능한 ABAQUS^2,3)와 찢김 선도와 변형 결정화 물성을 반영하여 내구 해석을 할 수 있는 FE-SAFE/RUBBER²³⁾를 활용하였다. 먼저, 시편 물성 시험을 통해 고무의 거동을 나타내는 변형률 에너지 밀도 함수와 내구 물성을 나타내는 FCGR(Fatigue Crack Growth Rate) 파라미터, 변형 결정화를 나타내는 함수 x(R)을 추출하였다. 또한, 추출된 물성 데이터를 장구형 시편과 실제 고무 부시에 적용하여 내구 수명 해석을 진행하였고, 시험 결과와 비교를 통해 신뢰성을 검증하였다. 또한, 오차 발생 원인 및 신뢰성 향상 방안에 대해 제시하였다.

2. 재료 물성 시험

본 논문에서는 방진 제품의 재료로 많이 사용하는 천연고무(NR)가 주원료인 배합고무를 사용하였으며, 물성 시험은 미국의 Axle Products사에서 수행하였다.

2.1 초탄성 시험

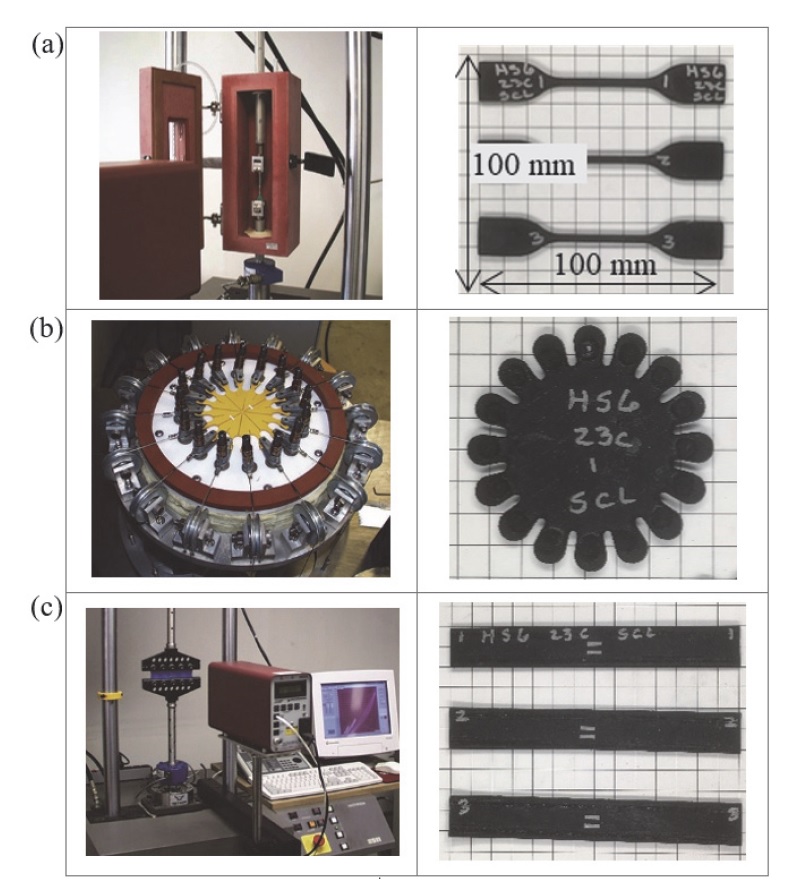
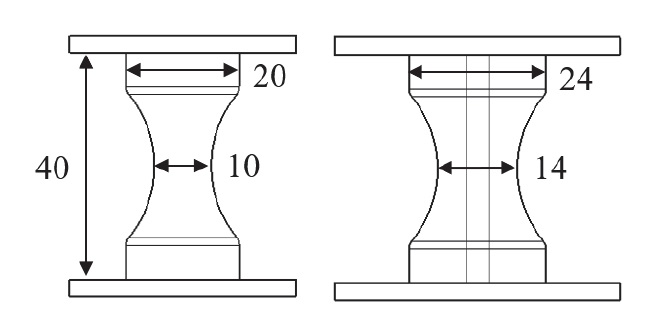
고무재료의 경우 변형모드에 따라 다른 거동이 나타나기 때문에 단순 인장, 이축 인장, 순수 전단 등 3가지 시험 데이터를 모두 활용하여 최적화된 물성 파라미터를 추출하는 것이 일반적이다.²⁾ 각 시험의 장비 및 시편형상은 Fig. 3과 같으며 한 눈금의 크기는 10 mm이다.

Fig. 3

Material test machine24) and specimen, (a) Uniaxial test, (b) Biaxial test, (c) Planar test

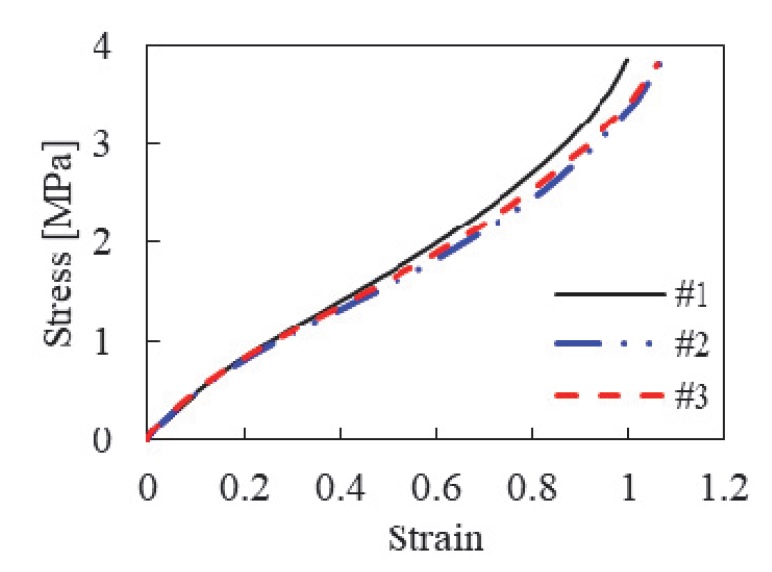
시험 방법은 정적 물성을 얻기 위해 시험 속도를 0.01 strain/s로 진행하였으며,²⁵⁾ 뮬린스 효과를 고려하여 하중 조건을 변형률 20 %, 50 %, 70 %, 100 %로 4가지 조건에 대하여 각 하중 당 5회씩 부하와 제하를 반복하여 실시하였다. 피팅 시에는 측정된 시험 데이터에서 각 변위 하중의 첫 번째 부하 곡선을 연결한 주 곡선, 각 변위 하중의 마지막 제하 곡선 4가지를 뮬린스 효과 곡선으로 추출하여 ABAQUS에서 피팅 데이터로 활용하였다. 본 논문에서는 변형률 에너지 밀도 함수의 대표 중 하나인 Yeoh모델과 뮬린스 효과의 거동을 나타내는 함수인 Ogden-Roxburgh모델의 재료 상수를 추출하였으며, 결과는 Fig. 4와 Table 1과 같다.

Fig. 4

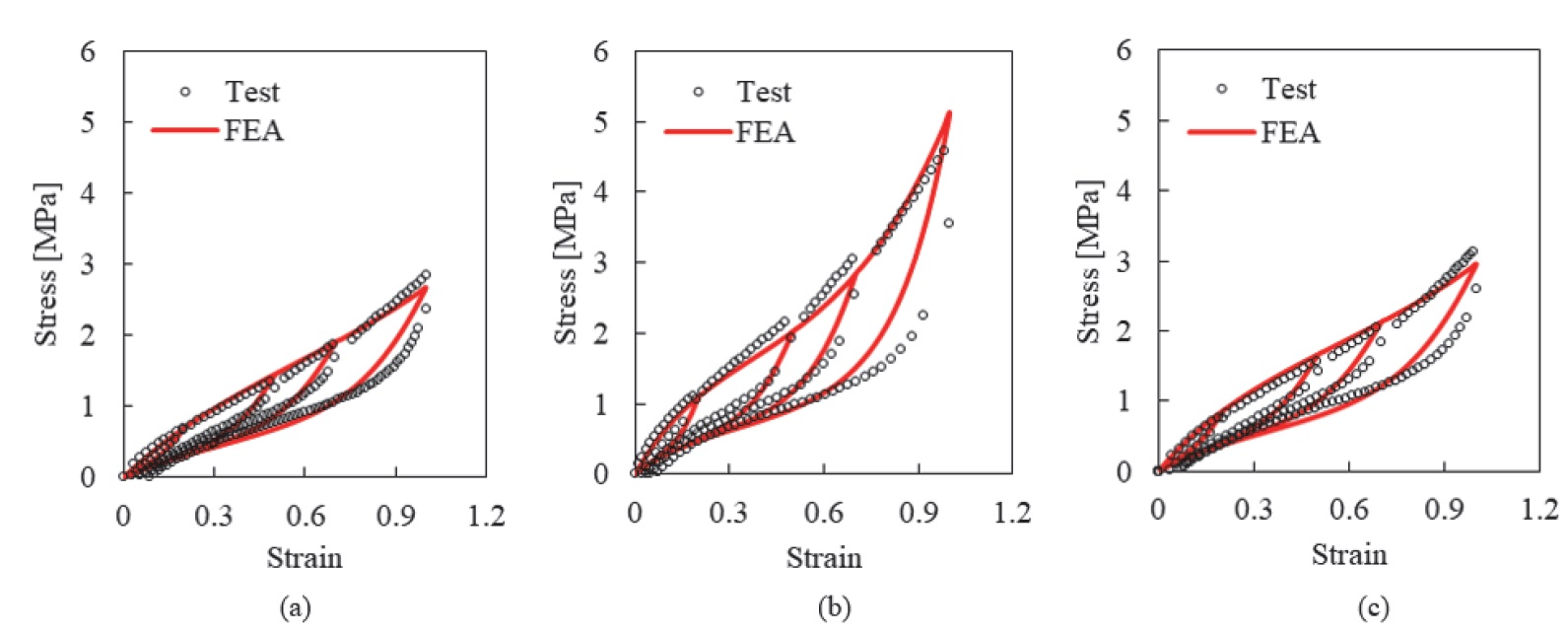
Comparison of test data and material fitting data, (a) Uniaxial test, (b) Biaxial test, (c) Planar test

Fig. 5

Tear strength test machine26) and planar specimens after test

Table 1

Yeoh model & mullins effect material parameter

2.2 찢김 강도 시험

찢김 강도 시험은 시편이 찢어질 때의 임계 찢김 에너지(를 추출하는데 목적이 있다. 시험은 에너지 해방률 계산이 비교적 간단한 전단 시편을 이용하였으며, 균열 성장 방향을 명확히 하기 위해 시편 앞에 25 mm가량의 크랙을 미리 만든 후 실시하였다. 시험 방법은 앞서 순수 전단 시험과 동일하게 0.01 strain/s의 속도로 진행하지만 반복 하중 없이 한번의 인장으로 시편이 완전히 찢어질 때까지 진행하였다. 임계 찢김 에너지는 식 (6)을 근거하여 식 (10)과 같이 표현이 가능하다.

$\[ T=-\frac{dU}{dA}=-\frac{Wh(l-(c+dc\left)\right)t-Wh(l-c)t}{(c+dc)t-ct}=Wh \]$

(10)

여기서 h는 시편의 높이, l은 길이, t는 두께, c는 크랙 길이를 의미하며, W는 시편이 받는 변형률 에너지 밀도를 의미한다. 시험 결과는 Fig. 6과 같으며, W는 그래프 아래 면적으로 구할 수 있다.

Fig. 6

Tear strength test data

2.3 크랙 성장 시험

크랙 성장 시험 역시 전단 시편을 사용하여 진행하였다. 시편에 25 mm의 크랙을 만든 후 점진적으로 증가하는 반복 하중을 가하여 반복 수(N)에 따른 크랙 길이(c)를 카메라로 측정하였고, 변형률, 응력, 찢김 에너지 등을 로드셀을 이용하여 측정하였다. 하중 조건은 응력비가 0인 완전 이완 조건(Fully Relaxing Condition)과 응력비가 0이 아닌 불완전 이완 조건(Non-Relaxing Condition) 총 2가지 조건에 대해 시험을 진행하였다.

Fig. 7

Fatigue crack growth experiments machine and planar specimen with Jig26)

2.3.1 Fully Relaxing Condition

완전 이완 조건은 Fig. 8(a)와 같이 최소 하중을 0으로 고정하고 최대 하중은 점점 증가하도록 시험을 진행하였다. 반복 수에 대한 크랙 길이는 Fig. 8(b)와 같이 거듭제곱의 형태가 보인다는 것을 확인하였으며, 이를 토대로 식 (11)과 같이 정의하였다. 이때의 변수 a와 b를 엑셀의 해 찾기 기능을 이용하여 구할 수 있다.

$\[ c=a{N}^b \]$

(11)

Fig. 8

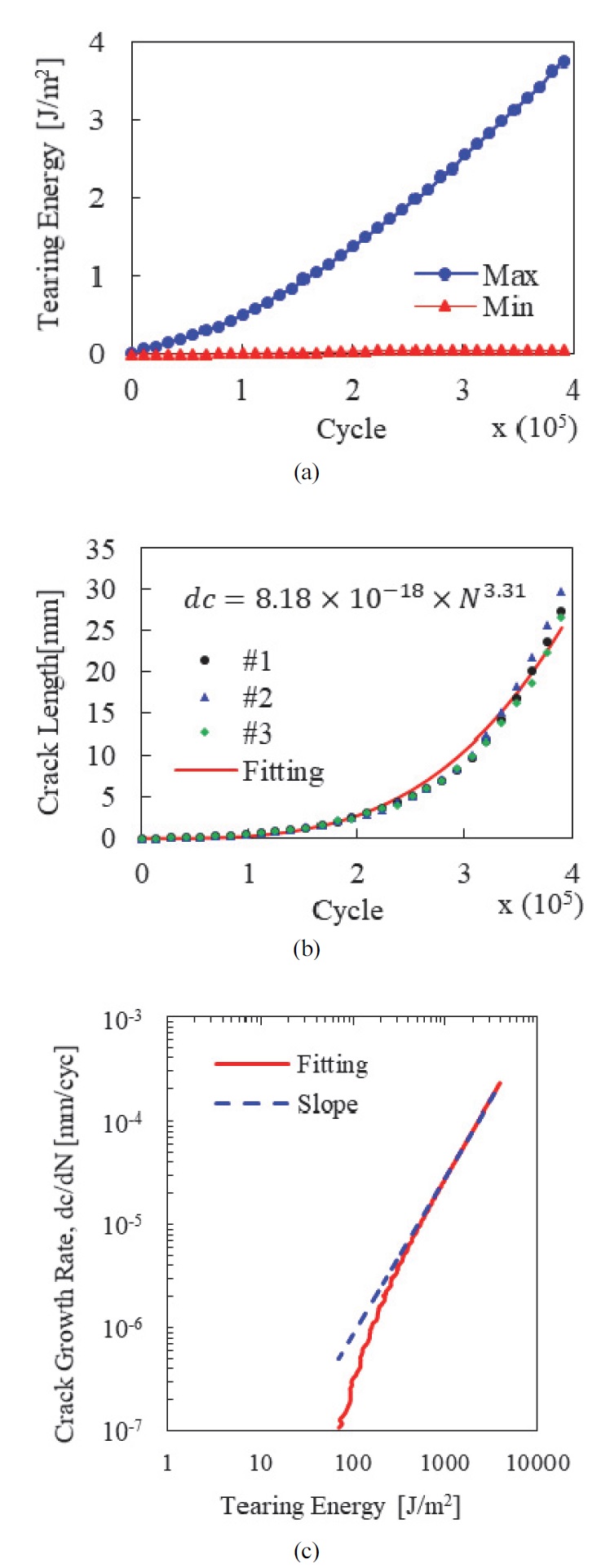
Fatigue crack growth test data(Fully relaxing); (a) Maximum & minimum tearing energy for cycles; (b) Comparison of test data and material fitting data: crack length for cycles; (c) Thomas model curve fitting result for test data

이후 식 (11)을 반복 수(N)에 대하여 미분하면 크랙 성장 속도(dc/dN)를 구할 수 있고, 시험을 통해 측정된 찢김 에너지와의 비교를 통해 식 (12)와 같이 표현할 수 있으며, 결과는 Fig. 8(c)와 같다. 여기서 내구 물성 파라미터인 FCGR(Fatigue Crack Growth Rate)의 F는 Fig. 8(c) 선도의 기울기이며, 임계 찢김 에너지 T_c에서의 크랙 성장 속도를 의미하는 r_c는 식 (13)과 같이 구할 수 있다. 식 (13)의 y는 찢김 선도의 Y절편을 의미한다.

$\[ \frac{dc}{dN}=ab{N}^{b-1}=r_c{\left(\frac{T}{T_c}\right)}^F \]$

(12)

$\[ r_c={10}^y\times {T_c}^F \]$

(13)

2.3.2 Non-Relaxing Condition

불완전 이완 조건은 Fig. 9(a)와 같이 처음에는 최소 하중을 0으로 고정하고 최대 하중을 증가시켜 R = 0 조건에서 반복 하중을 가하다가 일정 시간 이후 최대 하중을 고정하고 최소 하중을 점차 늘려 R > 0 조건으로 시험을 진행하였다. 여기서 크랙 길이와 반복 수의 관계를 살펴보면, R = 0에서는 선형적인 곡선을 보이고 R > 0에서는 기울기가 점점 작아지며 특정 길이에 수렴하는 형태의 곡선을 보인다. 이를 토대로 식 (14)와 같이 정의할 수 있으며, 시험 및 피팅 결과는 Fig. 9(b)와 같다.

$\[ c=kN(R=0) \]$

(14a)

$\[ c=c_1+\mathrm{\Delta }c\left(1-e^{-\frac{N-N_1}{\tau }}\right)(R>0) \]$

(14b)

Fig. 9

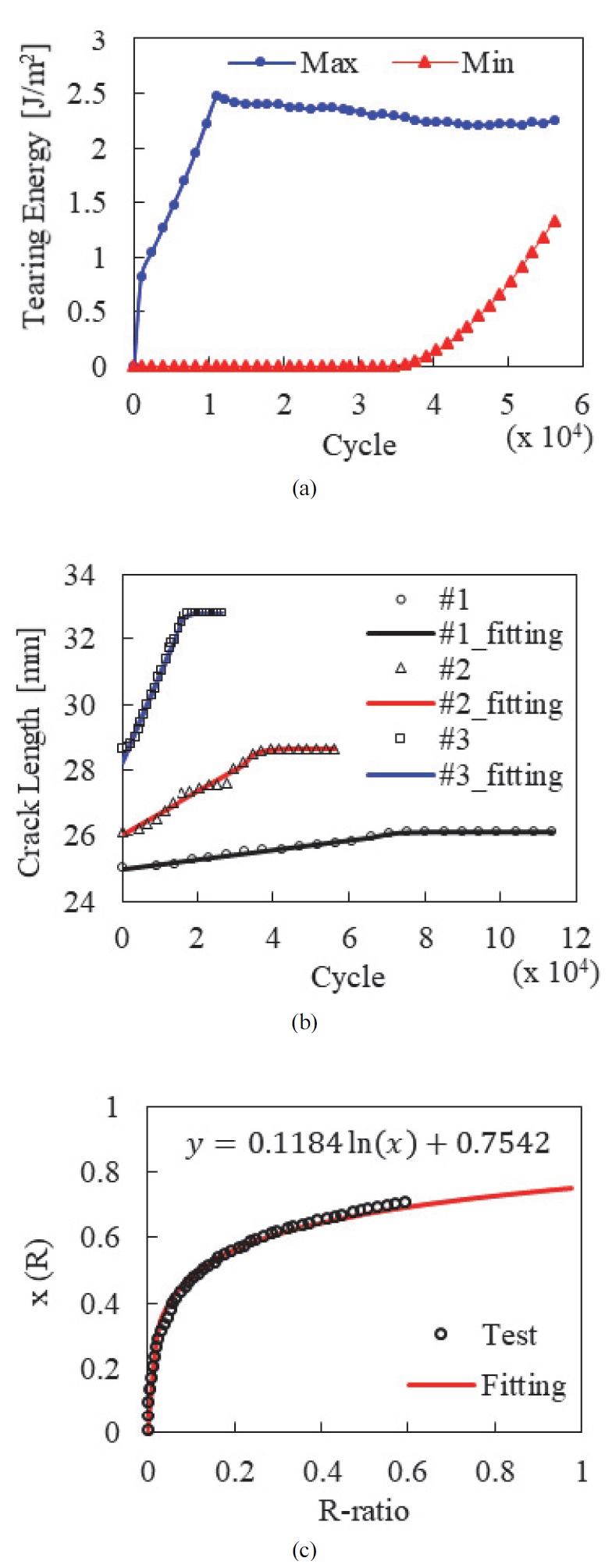
Fatigue crack growth test data(Non-relaxing); (a) Maximum & minimum tearing energy for cycles; (b) Comparison of test data and material fitting data: crack length for cycles; (c) Crystallization function x(R) fitting result

여기서 k는 R = 0일 때 크랙 길이와 반복 수의 비례상수를 의미한다. c₁과 N₁은 각각 선형구간이 끝나는 지점의 크랙 길이와 반복 수이며, ∆c는 최종 수렴되는 크랙 길이와 c₁의 차이, τ는 변수 파라미터를 의미한다. τ는 엑셀의 해 찾기 기능을 통해 정의할 수 있다. 이렇게 구한 식은 N에 대한 미분을 통해 식 (15)와 같이 표현할 수 있다.

$\[ \frac{dc}{dN}=k(R=0) \]$

(15a)

$\[ \frac{dc}{dN}=\frac{\mathrm{\Delta }c}{\tau }{e}^{-\frac{N-N_1}{\tau }}(R>0) \]$

(15b)

한편, 응력비에 따른 찢김 선도의 기울기 F(R)은 식 (7b)를 토대로 식 (16)과 같이 나타낼 수 있다.

$\[ F\left(R\right)=\frac{log(dc/dN)-log\left(r_c\right)}{log\left(T\right)-log\left(T_c\right)} \]$

(16)

여기서 찢김 에너지 T는 시험 데이터이고, dc/dN은 식 (15)에서 구하였다. 상수인, T_c, r_c값은 앞선 시험에서 추출된 값을 사용한다. 또한, 변형 결정화 함수 x(R)은 응력비가 0일 때의 기울기 F(0)와 R일때의 기울기 F(R)을 이용하여 식 (17)과 같이 나타낼 수 있으며,¹⁸⁾ 이렇게 구한 결과는 Fig. 9(c)와 같다.

$\[ x\left(R\right)=1-\frac{F\left(0\right)}{F\left(R\right)} \]$

(17)

2.4 초기 결함 측정 시험

초기 결함 측정 시험은 식 (8)의 C₀와 C_f를 구하기 위한 시험이다. 실제 고무 재료에서의 결함 분포와 크기는 산발적이기 때문에 정확한 결함 크기를 구하기 쉽지 않다. 따라서 시험과 해석의 비교검증을 통해 간접적으로 구하는 방법이 타당하다.

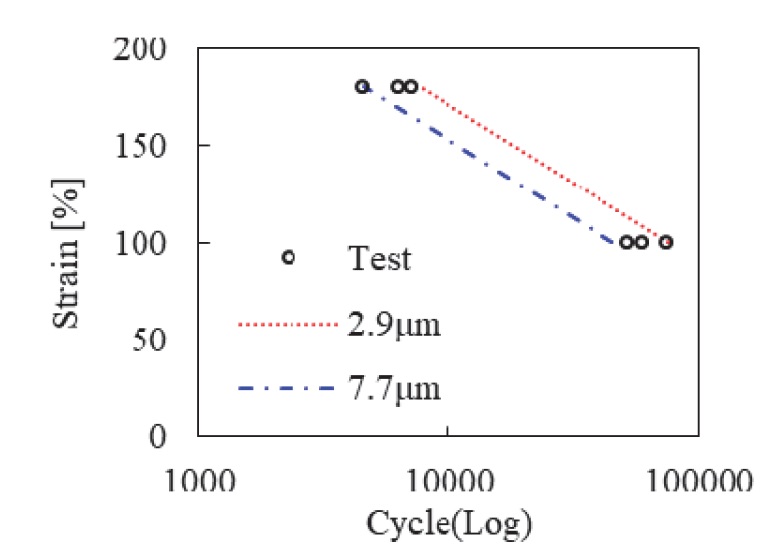
시험 방법은 Fig. 10과 같이 단순 인장 시편에 반복 하중을 가하여 수명을 측정한다. 하중 조건은 고무에 가해지는 변형률 크기와 수명의 관계가 로그스케일에서 선형적이라는 Mars와 Fatemi²⁷⁾의 고무 균열의 성장에 대한 연구를 근거로 변형률 100 %와 180 % 총 2가지 하중 조건에 대하여 시험을 진행하였다. 또한, 앞서 구한 FCGR 파라미터를 해석에 적용하고 C₀값 변화에 따른 해석과 시험 데이터를 비교하였다. C_f값은 5,000 μm로 고정하였는데 이는 일반적으로 크랙의 크기가 작을 때의 크랙 성장 속도가 크랙의 크기가 클 때의 크랙 성장 속도보다 수십 배는 작기 때문에 C₀의 변화에 민감한 반면, C_f값의 변화에는 큰 영향이 없기 때문에 임의로 육안으로 식별 가능한 크랙 사이즈로 정하였다.²³⁾

Fig. 10

Flaw size and crack nucleation test machine26) and simple tension specimens

해석/시험 검증 결과는 Fig. 11을 보면 알 수 있듯이, C₀값이 2.9 ~ 7.7 μm인 경우 시험 오차 범위 내에 들어온다는 것을 확인하였다.

Fig. 11

Flaw size and crack nucleation test and FEA result according C0

앞서 시험한 결과를 토대로 내구 물성 파라미터를 추출하면 Table 2와 같다.

Table 2

FCGR material parameter

3. 제품 시험/해석 검증

3.1 장구형 시편 검증

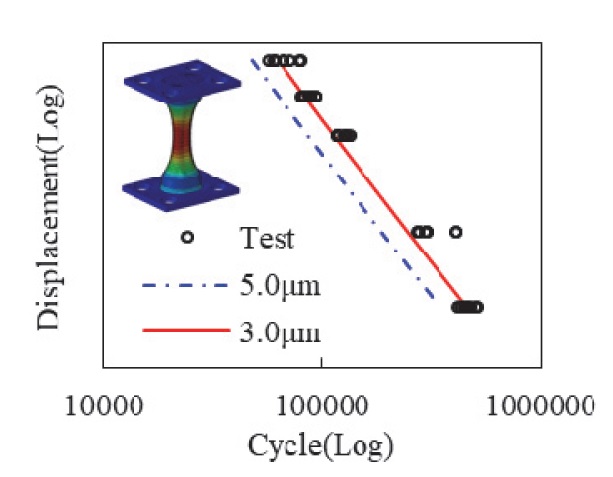
먼저 앞서 추출한 내구 물성 파라미터 신뢰성 검증을 위해 형상이 간단한 장구형 시편을 토대로 시험과 해석을 비교하였다. 하중 조건은 총 5가지 크기로 진행하였고, 각 하중 조건 당 12개의 시편으로 시험을 진행하였으며, 산포를 줄이기 위해 상/하위 각 2개씩의 데이터는 삭제하였다. 해석은 ABAQUS를 이용하여 시험 조건과 동일하게 반복 하중을 부여하였으며, 뮬린스 효과를 고려하여 위하여 2사이클에 대한 해석을 진행하였고 마지막 사이클에 대한 응력 및 변형률 이력을 이용하여 FE-SAFE/ RUBBER를 통해 수명 해석을 실시하였다.

Fig. 12

Dumbbell cylindrical specimen size

Fig. 13

1-Axle fatigue test of dumbbell cylindrical specimen

Fig. 14

Comparison of fatigue test and FEA for dumbbell cylindrical specimen

Table 3

Error rate of fatigue life analysis for dumbbell cylindrical specimen

해석 결과 값을 3.0 μm으로 적용하였을 때 시험과 가장 유사한 결과가 나타났으며, 약 8.16 %의 오차가 발생하였다.

3.2 실제품 검증

본 연구에서는 차량의 Front Lower Arm에 장착되는 G bush를 이용하여 시험/해석 검증을 실시하였다. 고무 부시의 경우 변형이 크기 때문에 수렴문제가 빈번하게 발생하고 해석 시간이 오래 걸리기 때문에 최적의 해석 조건을 찾는 것이 중요하다. 따라서 경험과 여러 시행착오를 통해 Table 4의 조건으로 해석을 진행하였다.

Table 4

FEA Modeling information of G bush

Fig. 15

Front lower arm and G bush

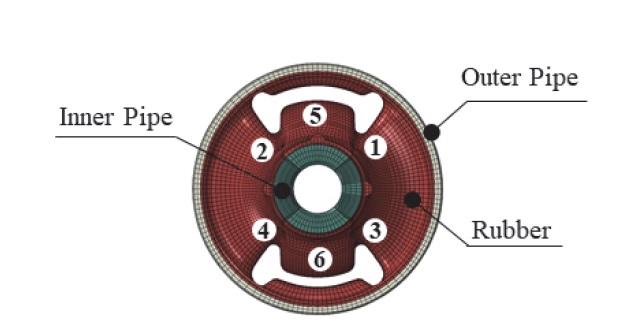
유한 요소 해석을 위한 모델링 결과는 Fig. 16과 같으며, 그림의 1 ~ 6번은 단품 및 실차 내구 시험에서 주로 파손되는 부위를 나타낸 곳이다.

Fig. 16

FEA model of G bush and weak points where failure occurs primarily

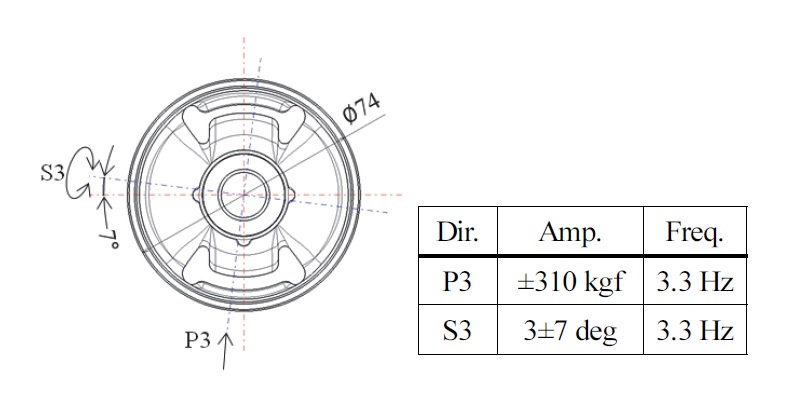
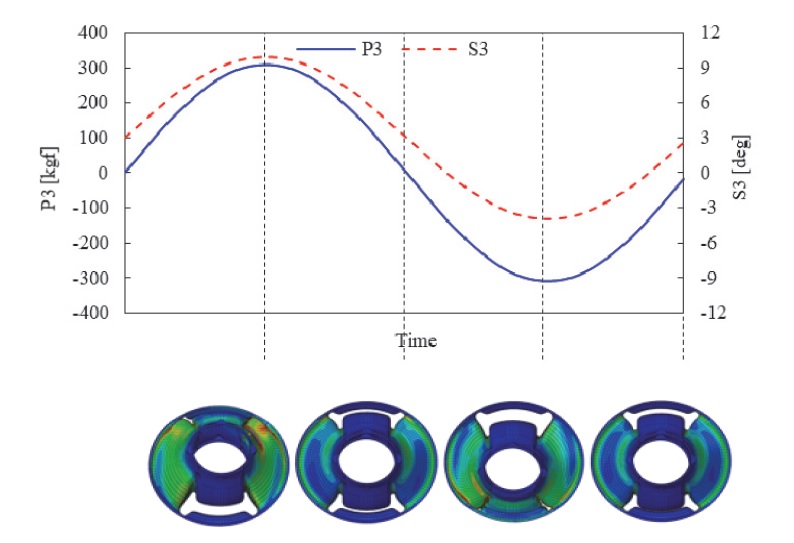
시험은 Fig. 17과 같이 7도 틸팅 장착 상태에서 P3방향 하중과 S3방향 비틀림 하중이 동시에 들어가는 하중 조건으로 2개의 샘플을 Fig. 18의 2축 내구 시험기를 이용하여 시험을 진행하였다.

Fig. 17

Load condition of G bush

Fig. 18

2-Axie fatigue test of G bush

해석은 시험과 동일한 하중 조건으로 Fig. 19와 같이 반복 하중에 대한 하중 이력 해석을 ABAQUS를 사용하여 진행하였다. 하중 이력 해석을 통해 추출한 변형 이력에 대한 응력 및 변형률 데이터는 FE-SAFE/RUBBER에서 피로 내구 해석에 활용하였으며, 내구 해석 시 변형 결정화 물성의 적용 여부에 따른 결과 차이를 비교해보았다.

Fig. 19

G bush deformations for cyclic load at 1/4, 2/4, 3/4, 4/4 time

먼저 시험 결과는 Fig. 20(a), (b)와 같이 Fig. 16의 1번 부위에 동일한 크랙이 발생하였고, 수명 값 또한 비슷한 수준으로 나타나는 것을 확인하였다. 이를 내구 해석 결과와 비교하였을 때, 변형 결정화 물성을 적용한 Fig. 20(c)는 시험 결과와 취약 부위가 일치하였으며 수명 값 또한 11.9 %의 근소한 오차가 나타났다. 그러나 변형 결정화 물성을 적용하지 않은 Fig. 20(d)는 Fig. 16의 4번 부위가 가장 취약한 것으로 나타났으며, 실제 크랙 부위인 1번 부위 수명 값을 비교하여도 34.3 %의 오차가 발생하는 것으로 나타났다.

Fig. 20

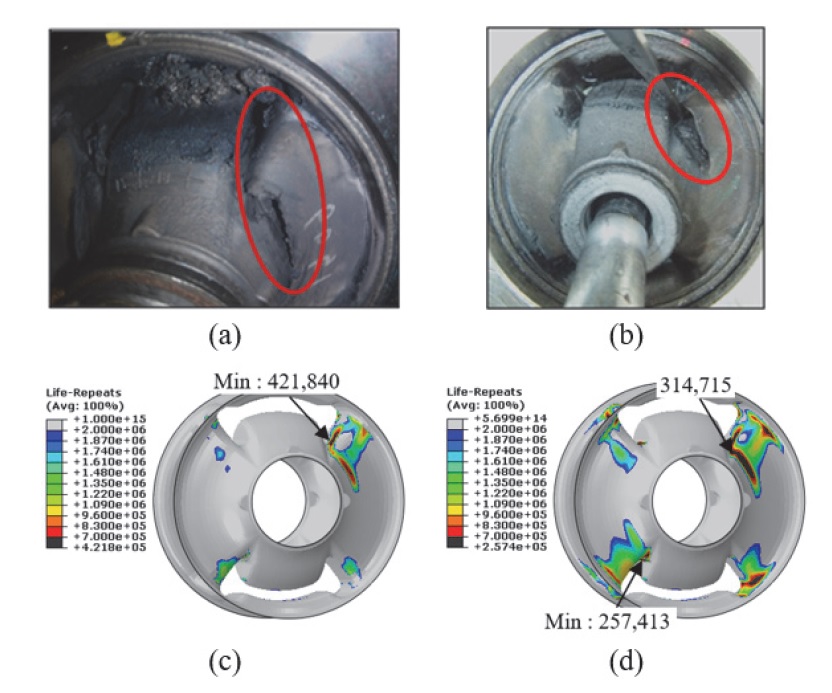
Fatigue test & FEA result of G bush; (a) Test result of sample No.1 : 500,037 Cycle; (b) Test result of sample No.2 : 457,999 Cycle; (c) FEA result with strain crystallization material properties; (d) FEA result without strain crystallization material properties

Fig. 21

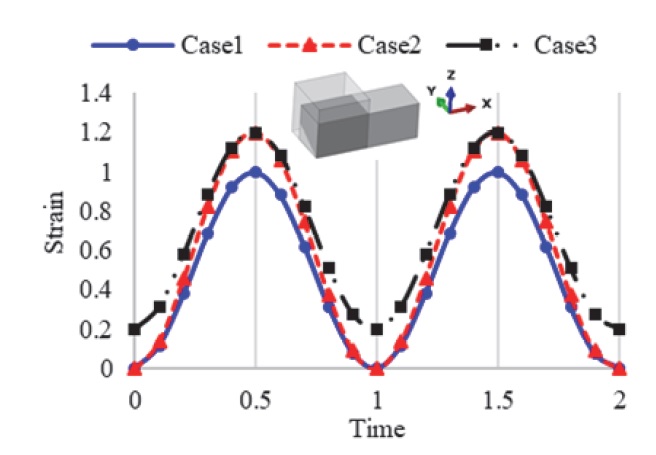
Uniaxial tensile deformation mode analysis of 1-Element for three load Cases; Case1: Strain 0 to 1, Case2: Strain 0 to 1.2, Case3: Strain 0.2 to 1.2

변형 결정화 물성의 영향을 자세히 분석하기 위해 1개의 요소를 이용하여 3가지 하중 조건에서 단순 인장 변형 모드에 대한 내구 해석을 진행하였으며, Fig. 22와 같이 각 하중 조건에 대해 변형 결정화 물성의 적용 여부에 따른 수명 값을 비교해 보았다.

Fig. 22

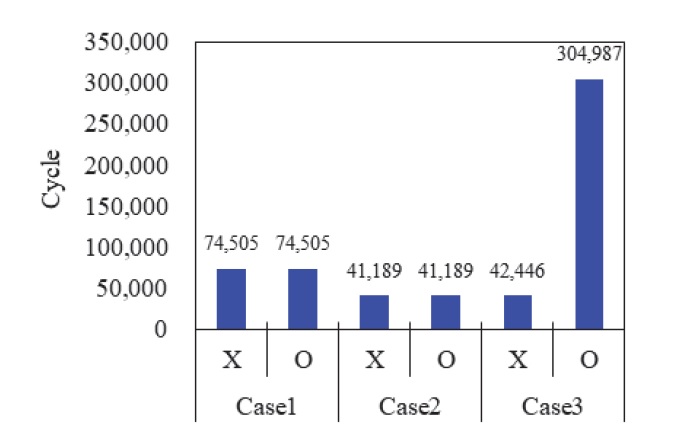
Fatigue analysis results of uniaxial tensile mode depending on whether strain crystallization properties are applied or not

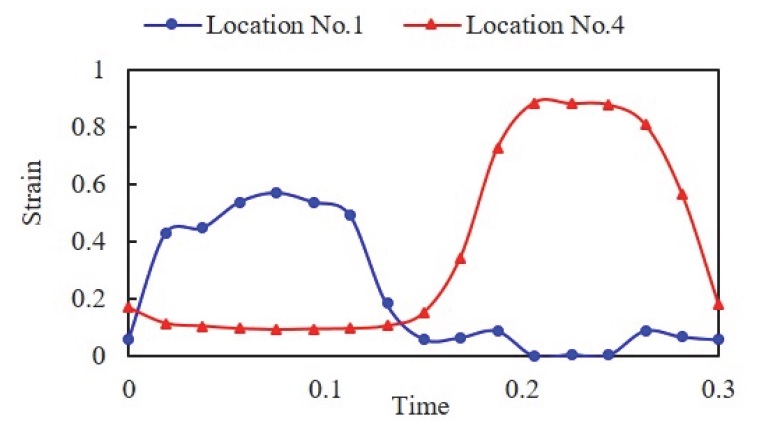
Case 1과 Case2의 경우에는 응력비가 0이기 때문에 변형 결정화 물성의 적용 여부와 관계없이 동일한 수명 값이 나타나며, 최대 변형의 크기가 더 큰 Case2의 수명이 상대적으로 작게 나타났다. 그러나 Case3의 경우에는 응력비가 0이 아니기 때문에 변형 결정화 물성의 적용 여부에 따라 해석 결과 차이가 크게 나타났다. 변형 결정화 물성을 적용하지 않은 경우에는 최대 변형률의 크기가 동일한 Case2의 수명과 비슷한 반면, 물성 적용 시에는 수명 값이 크게 증가하였다. 또한, Case1과 비교하였을 때 변형의 폭은 1로 동일하고 최대 변형률은 Case3이 큼에도 불구하고 내구에 유리한 것으로 나타났다. 실제로 Fig. 23과 같이 G Bush의 해석 결과에서 Fig. 16의 1번 부위와 4번 부위의 변형률 이력을 비교해보면, 최대 변형률은 4번 부위가 더 높게 나타나지만 최소 변형률이 일정 값 이상을 유지하여 변형 결정화 현상이 나타나 수명에 영향을 줬기 때문에 4번 부위가 아닌 1번 부위가 가장 취약하게 나타난 것으로 파악된다.

Fig. 23

Strain history for location No.1 & location No.4 during cyclic loading

이를 통해 최대 응력 및 변형률 결과만을 가지고 내구 수명을 판단하기 힘들며, 변형 결정화 현상이 내구 수 명에 영향을 미친다는 것을 확인할 수 있었다.

시험 결과의 평균치와 변형 결정화 물성을 적용한 해석 결과는 Table 5와 같다.

Table 5

Error rate of fatigue life analysis for G bush

4. 결 론

본 논문은 고무 부시의 내구 수명 해석을 찢김 에너지와 크랙 성장 속도와의 관계를 이용하여 수명을 예측하였으며, 다음과 같은 결론을 도출하였다.

• 1) 고무의 거동을 나타내는 에너지 밀도 함수를 구하기 위해 단순 인장, 이축 인장, 순수 전단 시험을 실시하였으며, 물성 피팅을 통해 Yeoh모델과 뮬린스 효과 물성 파라미터를 구하였다.
• 2) 내구 물성을 나타내는 FCGR(Fatigue Crack Growth Rate) 물성과 변형 결정화 물성을 추출하기 위해 찢김 강도 시험, 크랙 성장 시험, 초기 결함 시험을 진행하였으며, Thomas모델의 물성 파라미터와 변형 결정화 함수 x(R)을 도출하였다.
• 3) 추출한 물성 검증을 위해 장구형 시편으로 시험과 해석의 비교 결과, 8.16 %의 오차가 나타났다.
• 4) 실제품 검증 결과 내구 수명 해석에서 변형률 결정화 함수의 적용 여부에 따라 취약 부위와 수명 값이 달라진다는 것을 확인하였다. 변형 결정화 함수를 적용하였을 때 취약 부위가 시험과 일치하였고, 수명 값은 11.9 %의 오차가 나타났다. 또한 하중 이력 해석에서 응력 또는 변형률 값이 가장 높게 나타나는 부위가 반드시 내구에 가장 취약한 부위가 아닐 수 있다는 것을 확인하였다.
• 5) 오차 발생 원인으로는 실제품의 정확한 초기 크랙 시점을 찾기 힘든 점, 해석 상에서 큰 변형에 의한 왜곡이 발생하기 쉽다는 점, 해석의 수렴성과 소요 시간 등을 고려하여 요소의 사이즈를 충분히 작게 하지 못하였으며 ABAQUS Explicit를 이용하여 문제를 풀었다는 점 등으로 오차가 발생하였을 것으로 추정되며, 이를 고려하여 최적의 방법을 찾는 것이 필요할 것으로 보인다.

References

• L. G. Treloar, The Physics of Rubber Elasticity, Oxford University Press, 1975.
• ABAQUS Theory Manual, Hyperelastic, 2019.
• ABAQUS Theory Manual, Mullins Effect, 2019.
• O. H. Yeoh, “Some Forms of the Strain Energy Function for Rubber,” Rubber Chemistry and Technology, Vol.66, No.5, pp.754-771, 1993. [https://doi.org/10.5254/1.3538343]
• R. W. Ogden, “Large Deformation Isotropic Elasticity-on the Correlation of Theory and Experiment for Incompressible Rubberlike Solids,” Proceedings of the Royal Society A, Vol.326, No.1567, pp.565-584, 1972. [https://doi.org/10.1098/rspa.1972.0026]
• R. W. Ogden and D. G. Roxburgh, “A Pseudo–elastic Model for the Mullins Effect in Filled Rubber,” Proceedings of the Royal Society A, Vol.455, No.1988, pp.2861-2877, 1999. [https://doi.org/10.1098/rspa.1999.0431]
• A. Wöhler, “Wöhler’s Experiments on the Strength of Metals,” Engineering 4, pp.160-161, 1867.
• C. S. Woo, W. D. Kim and J. D. Kwon, “A Study on the Material Properties and Fatigue Life Prediction of Natural Rubber Component,” Materials Science and Engineering: A, Vol.483, No.1, pp.376-381, 2008. [https://doi.org/10.1016/j.msea.2006.09.189]
• S. M. Cadwell, R. A. Merrill, C. M. Sloman and F. L. Yost, “Dynamic Fatigue Life of Rubber,” Rubber Chemistry and Technology, Vol.13, No.2, pp.304-315, 1940. [https://doi.org/10.5254/1.3539515]
• B. J. Roberts and J. B. Benzies, “The Relationship between Uniaxial and Equibiaxial Fatigue in Gum and Carbon Black Filled Vulcanizates,” Proceedings of Rubbercon, Vol.77, No.2, pp.1-13, 1977.
• J. F. Roach, Crack Growth in Elastomers under Biaxial Stresses, Ph. D. Dissertation, The University of Akron, Akron, 1982.
• A. A. Griffith, “VI. The Phenomena of Rupture and Flow in Solids,” Philosophical Transactions of the Royal Society A, Containing Papers of a Mathematical or Physical Character, Vol.221, pp.582-593, 1921. [https://doi.org/10.1098/rsta.1921.0006]
• R. S. Rivlin and A. G. Thomas, “Rupture of Rubber. I. Characteristic Energy for Tearing,” Journal of Polymer Science, Vol.10, No.3, pp.291-318, 1953. [https://doi.org/10.1002/pol.1953.120100303]
• A. G. Thomas, “Rupture of rubber. V. Cut Growth in Natural Rubber Vulcanizates,” Journal of Polymer Science, Vol.31, No.123, pp.467-480, 1958. [https://doi.org/10.1002/pol.1958.1203112324]
• G. J. Lake and P. B. Lindley, “The Mechanical Fatigue Limit for Rubber,” Journal of Applied Polymer Science, Vol.9, No.4, pp.1233-1251, 1965. [https://doi.org/10.1002/app.1965.070090405]
• A. N. Gent, P. B. Lindley and A. G. Thomas, “Cut Growth and Fatigue of Rubbers. I. The Relationship between Cut Growth and Fatigue,” Journal of Applied Polymer Science, Vol.8, No.1, pp.455-466, 1964. [https://doi.org/10.1002/app.1964.070080129]
• W. V. Mars and A. Fatemi, “A Phenomenological Model for the Effect of R-ratio on Fatigue of Strain Crystallizing Rubbers,” Rubber Chemistry and Technology, Vol.76, No.5, pp.1241-1258, 2003. [https://doi.org/10.5254/1.3547800]
• W. V. Mars, “Critical Plane Analysis of Rubber,” Fatigue Crack Growth in Rubber Materials, Springer, pp.85-107, 2020. [https://doi.org/10.1007/12_2020_73]
• W. V. Mars, “Computed dependence of rubber’s fatigue behavior on strain crystallization,” Rubber Chemistry and Technology, Vol.82, No.1, pp.51-61, 2009. [https://doi.org/10.5254/1.3557006]
• H. Y. Kim and H. Kim, “Formulation of Tearing Energy for Fatigue Life Prediction of Rubber Like Material,” KSAE Spring Conference Proceedings, pp.938-943, 2005.
• H. I. Moon, H. Kim, C. S. Woo and H. Y. Kim, “Fatigue Life Prediction for Automotive Vibroisolating Rubber Component Using Tearing Energy,” Transactions of KSAE, Vol.20, No.6, pp.100-106, 2012. [https://doi.org/10.7467/KSAE.2012.20.6.100]
• W. Nyaaba, S. Frimpong and A. Anani, “Fatigue Damage Investigation of Ultra-large Tire Components,” International Journal of Fatigue, Vol.119, pp.247-260, 2019. [https://doi.org/10.1016/j.ijfatigue.2018.07.009]
• FE-SAFE/RUBBER Theory Manual, 2019.
• K. Miller, Axel Products, Inc., “Testing Elastomers for Hyperelastic Material Models in Finite Element Analysis,” http://www.axelproducts.com, .
• W. D. Kim, W. S. Kim, D. J. Kim, C. S. Woo and H. J. Lee, “Mechanical Testing and Nonlinear Material Properties for Finite Element Analysis of Rubber Components,” Transactions of KSME A, Vol.28, No.6, pp.848-859, 2004. [https://doi.org/10.3795/KSME-A.2004.28.6.848]
• Kurt Miller, Axel Products, Inc., “Fatigue and Failure Testing of Elastomers for Analysis,” http://www.axelproducts.com, .
• M. V. Mars and A. Fatemi, “Fatigue Crack Nucleation and Growth in Filled Natural Rubber,” FFEMS, Vol.26, No.9, pp.779-789, 2003. [https://doi.org/10.1046/j.1460-2695.2003.00678.x]