[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 30, No. 10, pp.849-858

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Oct 2022

Received 27 Jul 2022 Revised 19 Aug 2022 Accepted 19 Aug 2022

DOI: https://doi.org/10.7467/KSAE.2022.30.10.849

카메라-라이다 센서 융합을 위한 캘리브레이션 기법 소개

배종욱¹⁾

; 이영우¹⁾

; 고준호¹⁾

; 이재영²⁾

; 최준원^*^{, 1)}

1)한양대학교 전기공학과
2)한화디펜스 국방로봇사업부

Multi-Sensor Calibration Techniques for Camera-LiDAR Sensor Fusion

Jongwook Bae¹⁾

; Youngwoo Lee¹⁾

; Junho Koh¹⁾

; Jaeyoung Lee²⁾

; Junwon Choi^*^{, 1)}

1)Department of Electronic Engineering, Hanyang University, Seoul 04763, Korea
2)Department of Defense Robotics and Autonomous Systems Development, Hanwha Defense, 6 Pangyo-ro 319beon-gil, Bundang-gu, Seongnam-si, Gyeonggi 13488, Korea

Correspondence to: ^*E-mail: junwchoi@hanyang.ac.kr

Copyright Ⓒ 2022 KSAE / 203-09
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

In autonomous vehicles or robots, multiple sensors are used to achieve robust performance in a variety of perception tasks. Multi-sensor calibration is required to establish a spatial correspondence between different sensor coordinates. Camera-LiDAR calibration calculates the external parameters for transforming the representation of sensor data between the camera and LiDAR domains. In this paper, several camera-LiDAR calibration methods are reviewed and their practical applications are discussed. We demonstrate the application of the checkerboard-based camera-LiDAR calibration to a military armed vehicle equipped with Velodyne VLP-32C LiDAR sensor and Kaya Iron SDI 265 camera. We present the experimental results and discuss the practical tips for camera-LiDAR calibration.

Keywords:

Autonomous driving, Sensor fusion, Calibration, Deep-learning, Camera, LiDAR

키워드:

자율 주행, 센서 융합, 캘리브레이션, 딥러닝, 카메라, 라이다

1. 서 론

현재 자율 주행 시스템은 다양한 고성능 센서들의 개발과 함께 빠르게 발전하고 있다. 자율 주행을 위해서는 인지, 판단 그리고 제어의 각 단계가 수행되어야 한다. 인지 분야는 판단, 제어의 토대로써 객체 검출, 객체 추적, 영역 분할, 차선검출 등을 포함하게 된다. 인지 기능은 자율 주행의 안전성을 확보하기 위해 높은 정확성이 필요하다. 최근에는 자율 주행의 인지 기능에 딥러닝 기술을 적용하여 높은 인지 성능 향상을 이루었다. 특히 자율주행 차량에 장착된 카메라와 라이다 센서로부터 습득된 다양한 신호들을 융합하여 학습하는 모델은 큰 성능 향상 폭을 이루어낸다.

카메라-라이다 센서 융합 모델은 센서들의 장점을 이용하여 다른 센서의 단점을 보완하는 방식을 이용하여 높은 성능을 달성한다. 카메라는 색상, 질감 및 형상 정보를 얻을 수 있고 높은 해상도의 영상 데이터를 수집할 수 있으며 다른 센서들에 비해 가격이 저렴하나 조도에 쉽게 영향을 받고 거리 정보를 얻기 어려운 단점이 있다. 반면 라이다는 빛에 영향을 적게 받으며 상당히 정확한 거리 정보를 얻을 수 있다. 또한 라이다는 360도 회전을 통해 전 방위 데이터 획득할 수 있으므로, 카메라의 제한적인 FoV(Field of view)로 발생하는 음영지역을 보완할 수 있다. 하지만 라이더의 경우, 카메라에 비해 데이터의 분포가 희소하고 다른 센서들에 비해 가격이 높다는 단점이 있다. 따라서 완전한 자율 주행을 위한 보다 강인한 인지 성능 달성을 위해서는 상호보완적인 센서 융합 기술이 필요하다. 최근 들어 자율주행 차량 및 무인 주행 로봇 분야에서 카메라와 라이다의 장점을 살릴 수 있는 멀티 센서 시스템에 관한 연구가 활발히 진행되고 있다. 딥러닝 기반의 인지 알고리즘의 순위를 평가하는 자율 주행 데이터셋 KITTI dataset¹⁾과 nuScenes dataset²⁾ 및 Waymo open dataset³⁾의 알고리즘 성능을 살펴보면 최근에 센서 융합 객체 검출 모델들이 단일 센서 모델들과 비교하였을 때 높은 성능을 달성하는 것을 볼 수 있다. 높은 인지 성능뿐만 아니라 하나 이상의 센서를 사용하게 되면 하나의 센서의 성능이 저하되는 상황에서도 인지를 할 수 있기 때문에 열악한 상황에서 더욱 강인한 인지 성능을 달성할 수 있다.

센서를 통해 인지를 수행하기 위해서는 환경을 표현하는 외부의 3차원 좌표계와 센서 데이터가 표현되는 좌표계 간의 관계를 매칭시키는 캘리브레이션 과정을 거친다. 예를 들면 카메라의 영상 픽셀 영역 좌표계와 카메라 좌표계, 월드 좌표계의 관계는 카메라의 내부 파라미터와 외부 파라미터로 표현되며, 카메라 영상으로부터 이들을 추정해 내는 과정을 카메라 캘리브레이션이라고 한다. 특히 센서 융합 기술에서 이종 센서들을 통해 주변 환경에 대해 정보를 수집하고 이들을 융합하기 위해서는 각 센서 데이터가 표현되는 좌표계 간의 관계를 정확히 알아야 한다. 센서 융합 기술에서는 이처럼 이종 센서 간의 캘리브레이션 과정이 필수라고 할 수 있다. 이종 센서 캘리브레이션에서는 다중 센서로부터 데이터를 동시에 취득하여 데이터 간의 대응을 찾은 후에 서로 다른 센서 데이터 간의 상대적 좌표 관계를 나타내는 외부 파라미터들을 추정하는 과정을 수행한다.

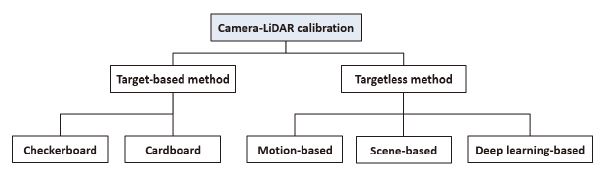
다양한 센서들 중 카메라-라이다 간 캘리브레이션 방법은 카메라 좌표계와 라이다 좌표계 사이의 변환 관계를 알아낸다. 이러한 변환 관계는 라이다와 카메라의 장착 위치와 방향에 의해 결정된다. 카메라-라이다 캘리브레이션 방법은 크게 목표물을 기반으로 하는 캘리브레이션 방법(Target-based calibration method)과 목표물을 사용하지 않는 캘리브레이션(Targetless calibration method) 방법으로 나눌 수 있다. 초기 카메라-라이다 캘리브레이션 방법은 목표물을 기반으로 한 방법이 주로 사용되었다. 목표물 기반 캘리브레이션에는 직사각 형태의 평면 판이나 체크 모양의 패턴이 있는 대상을 주로 사용하였으며 추가적인 캘리브레이션 성능 향상을 위해 원형 구멍 또는 기준 마커(Fiducial marker) 등을 추가하는 방법이 추후에 제안되었다. 이러한 목표물이 있는 장면에 대한 센서 데이터를 취득하여 목표물이 가진 있는 특징점에 대한 정합을 수행함으로써 좌표계 변환행렬을 얻어내게 된다. 비 목표물 기반 캘리브레이션 방법은 목표물 기반 캘리브레이션에 사용되는 특정 목표물 없이 주행 차량의 움직임(Motion-based) 또는 장면(Scene-based)을 기반으로 카메라-라이다 간 캘리브레이션을 수행하는 방법이다. 해당 방법은 장면마다 반복적으로 외부 파라미터를 최적화함으로써 더욱 정밀한 캘리브레이션이 가능하게 되었다. 최근 딥러닝 방식이 캘리브레이션에 도입되면서 비 목표물 기반 캘리브레이션의 초기 외부 파라미터에 대한 의존성 문제를 개선하는 방식도 도입되었다. 본 논문에서는 이러한 방법들의 장단점에 대해서 논의해 보고 실제 자율주행차에 캘리브레이션을 수행할 경우 고려해야 할 점들에 대해 살펴보기로 한다.

본 논문의 구성은 다음과 같다. 먼저, 카메라-라이다 캘리브레이션에 대한 원리를 설명하고 목표물 기반 캘리브레이션 방법, 비 목표물 기반 캘리브레이션 방법, 그리고 딥러닝 기반 캘리브레이션에 관해 소개한다. 마지막으로 본 연구팀에서 수행했던 카메라-라이다 캘리브레이션 과정을 간단히 소개하고자 한다.

Fig. 1

Classification of camera-LiDAR calibration

2. 카메라-라이다 캘리브레이션 원리

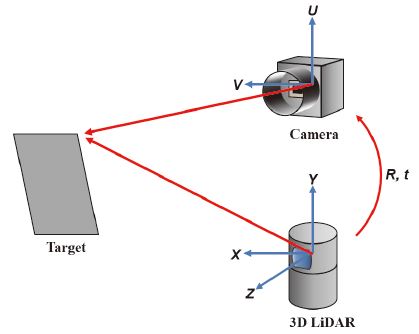
카메라 라이다 간 캘리브레이션은 Fig. 2와 같이 카메라-라이다의 상대적 회전 및 평행 이동을 의미하는 외부 파라미터 R, t를 정확하게 구하는 것을 목표로 한다. 우선 카메라 캘리브레이션을 통해 카메라의 내부 파라미터인 초점 거리(Focal length), 광학 중심(Optical center), 렌즈의 방사 왜곡 계수(Radial distortion coefficients of the lens)들을 구한다. 이러한 카메라 내부 파라미터로부터 동차좌표계로 표현되는 카메라 좌표계의 한 점 [X′ Y′ Z′ 1]^⊤을 카메라 영상 위의 한 점 [u υ 1]^⊤으로 투영하는 행렬 A를 얻게 된다. 한편, 카메라 좌표계의 한 점 [X′ Y′ Z′ 1]^⊤을 라이다 좌표계의 한 점 [X Y Z 1]^⊤으로 변환하기 위해서는 회전행렬 R과 평행이동벡터 t를 얻어내야 한다. 결국 카메라 영상위의 한 점 [u υ 1]^⊤과 라이다 좌표계의 한 점 [X Y Z 1]^⊤의 관계는 다음의 식 (1)과 같이 표현되며 카메라 라이다 캘리브레이션은 이러한 좌표계간 관계식을 이용하여 외부 파라미터 R, t 값을 추정한다.

s u υ 1 = f u s k e w * c c u 0 f υ c υ 001 X' Y' Z' 1 = A r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 X Y Z 1 = A R ∣ t X Y Z 1

(1)

Fig. 2

Schema of camera-LiDAR calibration

3. 목표물 기반 캘리브레이션

목표물 기반 캘리브레이션은 체크 모양의 패턴이 있는 사각형 평판이나 패턴이 없는 사각형 평판을 기준으로 카메라-라이다 간 외부 파라미터들을 얻는 과정을 말한다. 해당 방법은 각 데이터로부터 모서리, 중심점, 평면 등 어떤 특징을 추출하는지, 이러한 특징을 어떻게 추출하는지, 그리고 추출된 특징들의 관계를 통해 어떤 최적화 방식을 통해 외부 파라미터를 추정하는지에 따라 다양한 기법들이 제안되었다. 목표물 기반 캘리브레이션은 비 목표물 캘리브레이션에 비해 빠른 연산이 가능하며 4장에서 소개할 비 목표물 캘리브레이션의 초기화 문제를 해결하는데에 사용되기도 한다. 본 장에서는 목표물 기반 캘리브레이션 방식인 체커보드 기반 캘리브레이션(3.1장)과 카드보드 기반 캘리브레이션(3.2장)을 소개한다.

3.1 체커보드 기반 캘리브레이션

체커보드 기반 캘리브레이션은 Photo. 1과 같이 격자 문양 또는 체스판 형상이 그려진 사각형 목표물을 사용하여 이미지 및 포인트 클라우드 데이터로 체커보드에 대한 특징을 추출하여 이들 간의 관계를 통해 카메라-라이다 간 외부 파라미터를 구한다.

Photo. 1

Checker-board based camera-LiDAR calibration

Zhang과 Pless⁴⁾는 체커보드를 사용한 2차원 라이다-카메라 간 캘리브레이션을 제안하여 이후 소개할 3차원 라이다-카메라 간 캘리브레이션의 기반이 되었다. 2차원 라이다는 Laser Range Finder로도 불리며 바닥과 평행하게 설치되어 측정하고자 하는 목표물과의 거리를 측정하는 데 사용된다. 해당 방법은 2차원 라이다와 카메라에 체커보드가 전체가 보일 수 있는 다양한 위치와 자세로 체커보드의 위치를 설정하고 샘플 데이터를 수집한다. 수집한 이미지 데이터로부터 체커 문양의 교점을 추출하고 이로부터 카메라 좌표계를 얻고 포인트 데이터 중 체커보드 위에 존재하는 포인트들만 선택한다. 이때, 카메라 좌표계를 기준으로 한 포인트 P는 라이다 좌표계 P^f에 존재하므로 카메라 좌표계로부터 라이다 좌표계로의 변환은 다음과 같다.

P f = Φ P + △

(2)

Φ는 2차원 라이다 좌표에 대한 카메라 좌표계의 회전을 나타내는 행렬을, ∆는 평행이동을 나타내는 벡터를 나타낸다. 라이다로부터 얻은 포인트들은 카메라로 추정한 체커보드 평면 위에 존재해야 하는 관계에 따라 좌표변환에 대한 점-평면 간 제약조건을 얻을 수 있다. 이를 통해 다양한 자세와 위치의 샘플 데이터로부터 선형 방정식들을 얻어 Linear Least Square(LLS)로 외부 파라미터를 계산한다.

Kim과 Seo⁵⁾와 Unnikirishnan과 Herbert⁶⁾는 Zhang과 Pless⁴⁾가 제안한 2차원 라이다-카메라 간 캘리브레이션을 3차원 라이다에 확장 적용하였다. 특히, Unnikirishnan과 Herbert⁶⁾는 3차원 라이다로부터 얻은 포인트들에 Total Least Square(TLS)를 통해 평면을 추정한다. 이를 이미지 데이터로부터 추정한 체커보드 평면과의 일치 관계를 비선형 방정식으로 삼아 카메라-라이다 간의 좌표계를 추정한다. Zhang과 Pless⁴⁾가 R, t값을 한번에 추정하는 반면 해당 방법은 R, t 값을 독립적인 두 단계에 걸쳐 추정한다. 우선, 이미지와 포인트 클라우드를 통해 추정된 각 평면과 카메라의 원점 좌표와의 거리를 최소화하는 t를 추정한다. 그다음, 추정된 두 평면 간의 법선 벡터 간의 회전 값을 최소로 하는 R을 추정하여 카메라-라이다 간 외부 파라미터를 얻는다.

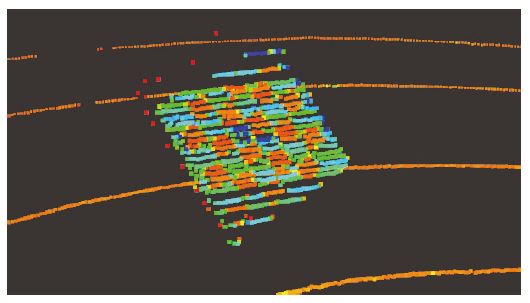
Zhou 등⁷⁾은 체커보드의 평면뿐만 아니라 외곽선도 추가로 사용하는 방식을 제안하였다. 기존에 제안된 방법들은 카메라 좌표계 추정에 격자무늬를 사용한 이미지 평면만을 제약조건으로 사용하여 최소 3개 이상의 샘플 데이터가 있어야 외부 파라미터 추정이 가능하다. 반면 Zhou 등은 체커보드 모서리를 추가 제약조건을 사용하여 단 한 개의 샘플 데이터만으로도 외부 파라미터 추정이 가능하다. 이미지 상의 체커보드의 모서리를 Line segmentation detector(LSD)⁸⁾를 이용하여 추출하고 이와 포인트 클라우드 상에서 평면과 모서리를 추출한다. 이미지와 포인트 클라우드에서 추출한 체커보드의 모서리를 통해 카메라 라이다의 상대적 방향과 위치를 나타내는 R, t에 대한 4개의 독립 제약조건과 각 데이터로 추정한 평면들을 통해 3개의 추가 제약 조건을 사용하여 R과 t를 계산한다. 특히 포인트들의 경우 Fig. 3과 같이 체커보드 경계에서 큰 노이즈를 포함하는 경우가 많은데 이를 RANSAC 알고리즘으로 제거하여 카메라-라이다 간 캘리브레이션의 정확성을 더욱 높였다.

Fig. 3

Point clouds from Velodyne VLP-32C

이후 Tsai 등⁹⁾은 Zhou 등⁷⁾이 제안한 캘리브레이션 기법에 샘플 선택 최적화 방식을 도입하여 전체 장면에 대해 일반화된 캘리브레이션 결과를 얻을 수 있게 되었다. 기존 캘리브레이션 기법들의 경우 샘플 수집 방식에 따라 특정 자세 및 위치에 과적합(Overfitting)이 발생할 수 있다. 이를 Tsai 등⁹⁾은 Variability of quality(VOQ) score를 도입하여 과적합을 방지하였다. 3개의 자세 샘플과 체커보드 면적 값을 통해 회전 매개변수의 품질과 위치 오륫값(Translation error)으로 VOQ score를 구성하고 다양한 샘플 데이터로부터 외부 파라미터를 일반화하여 전체 장면에 대해 일반화된 캘리브레이션 결과를 얻을 수 있다. 본 연구팀은 해당 기법을 카메라-라이다 캘리브레이션에 적용하여 5장에서 Tsai 등⁹⁾의 결과와 비교 분석한다.

3.2 카드보드 기반 캘리브레이션

카드보드 기반 캘리브레이션은 체커보드 기반 캘리브레이션과 달리 Fig. 2와 같은 문양이 없는 사각형 카드보드를 사용하거나 이에 원형 구멍 또는 각종 마커 등을 추가한 목표물을 통해 카메라-라이다 간 외부 파라미터를 추정한다.

Liao 등¹⁰⁾은 카드보드를 캘리브레이션 목표물로 사용하면서 모서리, 꼭짓점, 그리고 내부 포인트 제약조건을 활용하여 카메라-라이다 간 외부 파라미터를 추정한다. 해당 방법은 데이터 초기화, 특징 추출, 제약조건, 그리고 최적화 순으로 진행하며 데이터 초기화에는 각 데이터의 Time-stamp에 따른 동기화, 내부 파라미터를 통한 Image rectification(이미지 왜곡 보정)을 포함한다. 그다음 제약조건으로 사용될 꼭짓점, 모서리, 그리고 평면을 추출한다. 이미지 상의 모서리는 EDLines¹¹⁾를 통해 추출하며 이들의 교점으로부터 카드보드의 꼭짓점을 얻는다. 그리고 RANSAC 기법과 평면 모델을 통해 포인트 클라우드상 평면을 추출한다. 포인트들을 각 채널에 따라 나눈 뒤 각 채널의 양 끝점은 보드의 모서리를 나타내는 모서리 포인트 그룹으로, 나머지 포인트들은 카드보드 위의 포인트 그룹으로 나눈다. 그다음 이미지 상 모서리와 모서리 포인트 그룹을 통해 얻은 모서리 간 오차 함수와 이미지 상 꼭짓점과 포인트 클라우드 상 모서리와의 거리 함수를 조합하여 제약 조건을 설정한다. 최종적으로 앞서 구한 모서리 제약조건과 카드보드 위의 포인트들이 이미지로부터 추정한 평면 위에 있는지에 따른 오차 함수를 통한 내부 포인트 제약조건을 통해 외부 파라미터를 최적화한다.

Mishra 등¹²⁾은 카드보드를 캘리브레이션 목표물로 점-평면, 직선-직선 간의 일치를 제약 조건으로 외부 파라미터를 얻는다. 이미지 데이터에 LSD를 사용하여 모서리를 추출하고 이와 카드보드의 측정값을 PnP 문제에 적용하여 이미지 상 역투영 평면을 얻는다. 포인트 클라우드 데이터로부터 카드보드 모서리를 추정하기 위해 모서리 검출 알고리즘을 사용하여 모서리 주변의 포인트 클라우드를 필터링한다. 이에 평면 분할을 적용하여 이상치(Outliers) 제거 및 평면성을 강화한 다음 4개의 모서리에 포인트들을 맞추기 위해 RANSAC 기반 직선 검출 알고리즘 적용하여 카드보드 모서리를 추정한다. 이렇게 수집된 특징들을 Zhang과 Pless⁴⁾가 제안한 방식과 같이 점-평면 제약 조건을 통해 R, t 값을 얻는다. 그다음 라이다의 포인트 클라우드가 카드보드 모서리에 있고 이미지로부터 얻은 모서리와 일치하는 점-역투영 평면 간 제약 조건을 추가로 사용하여 외부 파라미터값 R, t 값을 정제(Refine)하여 더욱 정확한 캘리브레이션 결과값을 얻는다.

이후 단순 형태의 카드보드에 기준마커를 추가하여 이를 통해 카메라 좌표계를 추정하여 카메라-라이다 간 캘리브레이션을 수행하는 방식도 제안되었다.¹³⁾ 기준 마커는 바코드보다 간단한 내부 코드로 형상이 단순하여 카메라를 통한 인식이 용이하며 마커가 표기된 공간에 대한 정보를 제공한다. 이들 중 ArUCO 마커는 검은색 외각 테두리와 n×n 크기의 2차원 비트 패턴으로 구성되어 외각 테두리를 통해 마커의 모서리를, 2차원 비트 패턴을 통해 마커의 ID 값을 얻는다. 추출된 마커 모서리와 실제 마커 모서리의 길이, 그리고 카메라 내부 파라미터를 통해 카메라 좌표계를 얻을 수 있다.

Beltran 등¹⁴⁾은 ArUCO 마커를 카드보드의 각 모서리 부근에 추가하고 카드보드 가운데에 4개의 원을 뚫어 사용하는 방식을 제안했다. 다른 목표물 기반 캘리브레이션이 주로 모서리, 꼭짓점, 평면 등을 특징점으로 사용하는 반면 천공 원 4개의 중점을 기준점으로 하여 카메라-라이다 간 좌표계를 추정한다. 카메라를 통해 ArUco 마커들을 검출하여 카메라 좌표계 추정하고 이로부터 기준점들을 추정한다. 동시에 라이다를 통해 들어온 포인트들에 RANSAC 기법을 사용하여 카드보드의 평면 포인트들로 분할(Segmentation)한다. 이를 통해 카드보드를 검출한 다음 천공 원을 기준으로 포인트들을 재분할한 후 4개의 기준점을 추정한다. 각 데이터로부터 추정된 4개의 기준점들의 일치 조건을 통해 카메라와 라이다 간 외부 파라미터를 추정한다.

이처럼 카드보드 기반 캘리브레이션은 이미지 특징 추출을 위한 체커 무늬를 사용하는 대신 꼭짓점, 모서리 등의 다른 특징들과 제약조건으로 카메라-라이다 간 캘리브레이션을 수행한다.

4. 비 목표물 캘리브레이션

3장에서 설명한 목표물 기반 캘리브레이션 방법은 목표물과 센서와의 거리, 위치 구성 등에 의해 외부 파라미터의 결과가 목표물에 과적합 될 수 있다. 본 장에서는 이를 보완한 비 목표물 캘리브레이션 방법을 소개하고자 한다. 비 목표물 캘리브레이션은 목표물 기반 캘리브레이션과 달리 현재 장면에 존재하는 특징들을 이용하여 카메라와 라이다 간 외부 파라미터를 얻는 방식이다. 이는 사전에 설계된 목표물을 준비하지 않아도 되므로 비교적 다양한 환경에서 실시간 캘리브레이션이 가능하다는 장점이 있다. 비 목표물 캘리브레이션 방식에 해당하는 움직임 기반 캘리브레이션과 장면 기반 캘리브레이션을 각각 4.1장과 4.2장에서 소개한다. 또한 최근 다양한 컴퓨터 비전 분야에서 활용되는 딥러닝 기반 캘리브레이션에 관한 연구를 4.3장에서 소개한다.

4.1 움직임 기반 캘리브레이션

움직임 기반 캘리브레이션은 연속된 시간에서 카메라와 라이다의 움직임 정보를 활용하여 카메라와 라이다 간 외부 파라미터를 획득하는 방식이다. 본 논문에서는 움직임 정보를 활용하는 여러 가지 방법 중 Hand-eye 보정 기법¹⁸⁾과 Structure-from-Motion(SfM)¹⁹⁾ 방법 두 가지에 대해 소개한다.

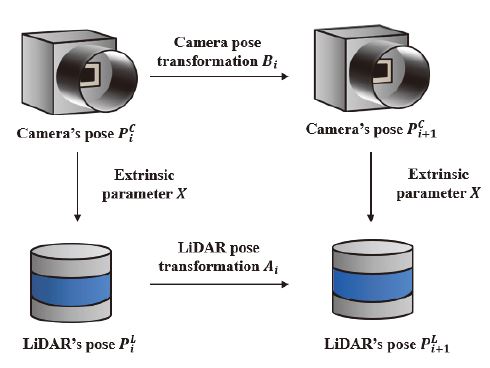
Ishikawa 등²⁰⁾은 Hand-eye 보정 기법을 적용하는 방식을 제안하였다. 우선 라이다와 카메라 센서의 움직임 변환 행렬 A_i와 B_i를 각각 AKAZE 알고리즘과 ICP 알고리즘을 통해 추정한다. 움직임 변환 행렬은 연속된 시간 i, i+1에서 센서가 부착된 차량 등의 움직임으로 인해 발생한 센서의 위치 이동(Translation) 및 회전 변환(Rotation)을 나타낸다. Hand-eye 보정 기법은 Fig. 4와 같이 A_i, B_i와 라이다 좌표계에서 카메라 좌표계로의 변환 행렬 X는 식 (3)과 같이 관계를 나타낼 수 있고, 이를 통해 카메라와 라이다 간의 초기 외부 파라미터를 추정한다.

B i ⋅ X = X ⋅ A i

(3)

Fig. 4

Hand-eye calibration

카메라는 라이다와 달리 거리 정보가 존재하지 않아 추정된 위치 이동 변환 행렬의 값이 부정확하다. 부족한 거리 정보를 보완하기 위해 포인트 클라우드를 초기 외부 파라미터를 통해 영상에 사영시켜 거리 정보를 융합한 후, 카메라 움직임 변환 행렬을 재추정한다. 이렇게 재추정된 카메라의 움직임 변환 행렬을 이용해 외부 파라미터를 보정하는 방식을 반복적으로 수행하여 최적화가 진행된다. 추정된 외부 파라미터를 통해 카메라의 부족한 거리 정보를 융합함으로써 최적화가 진행됨에 따라 정확한 외부 파라미터를 획득할 수 있다.

Yoon 등²¹⁾은 카메라의 움직임 정보를 이용하여 영상으로부터 SfM 기법을 통해 3차원 모델링을 시행하고 이와 포인트 클라우드 간의 변환 행렬을 추정하는 방식의 캘리브레이션 기법을 제안했다. 이들은 영역 분할(Segmentation)을 통해 분할된 연속적인 영상을 SfM 방법을 이용하여 물체 별 3차원 모델링을 진행한다. 3차원 모델과 포인트 클라우드에서의 물체를 ICP 알고리즘을 통해 3차원 공간에서 초기 외부 파라미터를 추정한다. 이후 분할된 영상과 포인트 클라우드에서 각각 물체마다 영상에서 물체의 외곽선 나타내는 외형 모델과 포인트 클라우드에서 물체의 3차원 그물형(Mesh) 모델을 생성한다. 추정된 초기 외부 파라미터를 이용하여 그물형 모델을 2차원 공간에 사영시켜 외형 모델과 사영된 그물형 모델의 일치성을 이용하여 외부 파라미터를 보정한다. 이 방법은 움직임 기반으로 초기 외부 파라미터를 추정하고 4.2장에 소개될 장면 기반 캘리브레이션 방법을 이용하여 외부 파라미터를 보정하는 방식으로 높은 정확도를 이루어냈다.

이러한 움직임 기반 캘리브레이션 방법은 센서가 장착된 대상의 충분한 회전 및 이동 궤적이 필요하므로 주행 공간이 충분히 확보되지 않을 경우 높은 정확성의 캘리브레이션 결과를 기대하기 어렵다.

4.2 장면 기반 캘리브레이션

장면 기반 캘리브레이션은 샘플 데이터에 존재하는 물체의 모서리(Edge), 혹은 영상과 포인트 클라우드의 강도(Intensity) 등의 특징들을 추출하여, 카메라와 라이다 좌표계에 존재하는 각 특징들을 일치시키는 방식으로 카메라와 라이다 사이의 외부 파라미터를 얻는 방법이다. 본 절에서는 Wang 등²²⁾이 제안한 의미론적 중심(Semantic centroid)을 특징으로 이용한 캘리브레이션 방법과 한계점, 그리고 이를 해결한 새로운 초기 외부 파라미터 추정 방식을 제안한 연구를 소개한다.

Wang 등²²⁾이 제안한 SOIC는 차량, 보행자 등의 객체 클래스 별 의미론적 중심을 특징으로 추출하여 영상 공간에서 일치시킴으로써 외부 파라미터를 추정한다. 의미론적 중심은 특정 클래스로 분할된 영상 및 포인트 클라우드 좌표의 평균으로 2차원과 3차원 공간에서 각각 얻어진다. 추출된 클래스 별 2차원, 3차원 공간의 의미론적 중심을 PnP 기법을 이용하여 일치시킴으로써 초기 외부 파라미터를 추정한다. 이후 물체 별로 분할한 포인트 클라우드와 영상의 일관성을 이용한 비용 함수를 최소화하는 방향으로 외부 파라미터를 보정해 가며 최적화한다. 하지만 장면에 존재하는 물체가 가려지거나, 많은 수의 물체가 존재할 경우 좌표의 평균을 통해 구해진 의미론적 중심은 서로 일치하지 않아 초기 외부 파라미터가 부정확한 결과를 얻는다는 한계점이 존재한다.

Ma 등²³⁾은 SOIC의 초기화 문제를 해결하기 위해 CRLF를 제안하였다. 이는 장면에 존재하는 도로 및 기둥 등 직선 형태의 특징을 추출하고 이를 매칭하여 캘리브레이션을 수행한다. 영상에서는 영역 분할 방법, 라이다에서는 포인트 클라우드의 강도를 이용하여 수직적인 특성을 가진 기둥 특징 1개와 차선과 같은 평행한 레인 특징 2개를 추출한다. 카메라와 라이다에서 각각 추출된 3개의 특징을 P3L 문제를 통해 초기 외부 파라미터를 추정한다. 이러한 CRLF의 초기화 방법은 기하학적인 제약 조건이 추가되어 강인한 초기 외부 파라미터를 구할 수 있다.

이처럼 장면 기반 캘리브레이션 방법은 초기 외부 파라미터 추정에 대한 높은 의존성으로 장면 내에 물체나 건물 등이 없어 추출할 특징이 부족할 경우 사용이 적합하지 않다.

4.3 딥러닝 기반 캘리브레이션

차량에 장착된 카메라와 라이다 센서는 주행 중에 발생하는 진동이나 충돌로 인해 센서의 위치가 변할 수 있다. 이는 기존에 획득한 외부 파라미터와 현재 센서 위치와의 차이를 발생시켜, 주기적인 캘리브레이션을 수행하여야 정확한 센서 융합이 가능하다. 하지만 앞서 소개한 방법들은 캘리브레이션을 수행하기 위해 체커 보드를 이용하거나 적합한 환경이 필요한 제한 사항이 있다. 본 절에서는 캘리브레이션의 실시간 반복 시행을 위한 딥러닝 활용 방법을 소개한다. 딥러닝 기반 캘리브레이션 방법은 카메라 영상과 라이다 포인트 클라우드를 입력으로 하여 두 센서 간의 외부 파라미터를 예측하기 위해 딥뉴럴네트워크를 사용한다. 이를 통해 목표물이나 상황에 구애받지 않고 카메라와 라이다에서 얻은 데이터만으로 지속적으로 캘리브레이션을 수행할 수 있다. 본 절에서는 딥러닝 기술을 적용한 3가지 캘리브레이션 연구를 소개한다.

Iyer 등²⁴⁾이 제안한 CalibNet은 영상과 캘리브레이션 되지 않은 포인트 클라우드를 입력으로 직접 외부 파라미터를 추정한다. 입력 영역을 일치시키기 위해 포인트 클라우드를 영상 평면에 사영시킨 희소 깊이 지도를 라이다 데이터의 입력으로 사용한다. 카메라 영상과 희소 깊이 지도를 입력으로 컨벌루션(Convolution) 계층으로 이루어진 네트워크를 통과하여 각각 특징 지도를 얻는다. 두 특징 지도를 연결(Concatenate)한 후 컨벌루션 층과 완전 연결 계층을 통과하여 외부 파라미터를 추정한다. 손실 함수는 추정된 외부 파라미터를 이용하여 영상 평면으로 사영된 희소 깊이 지도와 사전 캘리브레이션 된 GT 외부 파라미터를 이용하여 사영된 희소 깊이 지도(Sparse depth map)와의 측광 손실 함수와 3차원 공간에서 포인트 클라우드 사이의 거리를 손실 함수로 이용하여 네트워크를 학습하였다.

Shi 등²⁵⁾이 제안한 CalibRCNN은 CalibNet 네트워크에 LSTM 구조를 추가하여 연속적인 프레임 사이의 시간 영역 정보를 활용한다. 시간 영역을 네트워크에 추가함으로써 연속된 프레임 사이의 위치 변환에 대한 기하학 정보를 이용하여 이동 변환에 대한 오차를 크게 개선하였다. CalibNet의 손실 함수에 Epipolar 기하학 제약 조건을 이용한 손실 함수를 추가하여 네트워크를 학습시킴으로써 캘리브레이션 성능이 향상되었다.

마지막으로, LCCNet²⁶⁾은 희소 깊이 지도와 영상의 특징 지도의 유사도를 이용한 3D 비용 볼륨(Cost volume)을 이용하여 정확한 외부 파라미터를 추정한다. 먼저 희소 깊이 지도와 영상을 네트워크를 통해 특징 지도를 각각 추출한 후 이를 이용하여 3D 비용 볼륨을 구성하는 특징 매칭 계층으로 전해진다. 3D 비용 볼륨은 영상과 희소 깊이 지도로부터 추출된 특징 지도에서의 픽셀 위치 p₁과 p₂의 차이를 d로 제한하여 지역적인 3D 비용 볼륨을 구성한다. 이후 지역적인 비용 볼륨을 2개의 완전 연결 계층을 통해 각각 센서 간 외부 파라미터의 이동 변환과 회전 변환을 추정한다. LCCNet은 두 특징 지도 사이의 유사도를 이용하여 비용 볼륨을 구성함으로써 센서 간 정보를 융합시켜 외부 파라미터 추정 성능을 향상했다.

딥러닝을 이용한 캘리브레이션은 입력 데이터만으로 간편하게 외부 파라미터를 획득할 수 있어 주행 간 발생하는 센서의 위치 변화에 빠르게 대응할 수 있다. 하지만 네트워크 학습을 위해 캘리브레이션 된 데이터셋 구축이 선행되어야 한다는 단점이 있다.

5. 카메라-라이다 캘리브레이션 기법 적용

본 연구팀은 Photo. 2의 한화디펜스 사의 지능형 다목적 무인 차량 ‘ARION-SMET’전방에 설치된 카메라 및 라이다를 사용한 캘리브레이션을 수행하였다.

Photo. 2

Hanhwa defense ARION-SMET vehicle

야지 환경 주행을 목적으로 하는 무인 차량의 특성상 일반 도로 환경과 달리 장면 내에 추출할 특징이 적어 4.2 절에서 소개한 장면 기반 캘리브레이션 방법 적용은 적합하지 않았다. 또한 캘리브레이션 모델 학습을 위한 사전 데이터가 존재하지 않아 딥러닝 기반 캘리브레이션 방법 역시 적용 불가능하였다. 이에 체커보드 기반 캘리브레이션의 경우 캘리브레이션에 사용되는 체커보드를 카메라 내부 파라미터 추정에도 동일하게 사용 가능함을 고려하여 체커보드 기반 카메라-라이다 캘리브레이션 기법을 적용하였다. 공개된 캘리브레이션 toolkit 중 Tsai 등⁹⁾이 소개한 체커보드 기반 캘리브레이션 기법을 통해 카메라-라이다 간 외부 파라미터를 얻었다.

5.1 실험 환경

카메라-라이다 캘리브레이션을 위해 Photo. 1의 가로 700 mm, 세로 700 mm의 알루미늄 보드에 가로 100 mm, 세로 100 mm, 5 × 5 격자무늬 체커보드를 카메라 캘리브레이션 및 카메라-라이다 캘리브레이션에 사용했다. 캘리브레이션에는 Velodyne VLP-32C 라이다와 Kaya Iron SDI 265 단안 카메라를 사용하였으며 영상의 해상도는 1920 × 1080 pixel로 설정하였다. 실험은 실외 환경에서 광량이 충분한 낮 시간대에 진행하였으며 Robot Operating System(ROS)을 사용하여 이미지 토픽과 포인트 클라우드 토픽을 rosbag 형태로 저장하거나 실시간으로 사용하여 캘리브레이션을 진행하였다.

5.2 실험 과정

실험은 크게 두 가지 방법으로 진행하였다. 첫 번째 방법으로는 야지 환경에서 캘리브레이션 데이터를 rosbag 형태의 파일로 저장한 후 이를 재생하여 샘플을 선정 후 외부 파라미터를 얻는다. 두 번째 방법은 ROS를 통해 들어오는 영상 토픽과 포인트 클라우드 토픽을 이용하여 현장에서 실시간으로 샘플 선정 및 캘리브레이션을 진행한다.

카메라-라이다 캘리브레이션에 앞서 체커보드를 사용하여 카메라 내부 파라미터를 획득한다. 그다음 카메라-라이다 캘리브레이션을 위한 데이터 수집을 진행한다. 센서의 FoV를 고려하여 체커보드를 센서로부터 2∼10 m 영역에 다양하게 위치시킨다. 첫 번째 방법의 경우 rosbag 파일 형태로 데이터를 저장한 뒤 수집한 데이터를 재생하여 체커보드에 포인트 클라우드가 존재하는 영역을 설정한 뒤, 영상과 포인트 클라우드에서 체커 보드의 특징을 각각 추출한다. 두 번째 방법의 경우 실시간으로 들어오는 이미지 및 포인트 클라우드를 이용하여 동일한 방법으로 특징을 추출한다. 이때 샘플 수집 여부는 실물 체커보드의 외각 둘레 길이와 추정된 체커보드의 외각 둘레 길이의 차이를 나타내는 차수 오차(Dimension error) 값을 기준으로 시행한다. 첫 번째 방법의 경우 차수 오차가 50 mm 이하일 경우, 두 번째 방법의 경우 20 mm 이하일 경우 샘플로 선정하여 영상 및 포인트 클라우드 포즈 샘플 15쌍을 저장한다. 이후 수집된 서로 다른 포즈 샘플을 3개씩 그룹화하여 VOQ score와 외부 파라미터를 계산한다.

5.3 실험 결과

실험 결과 첫 번째 방법으로 저장된 데이터에서 얻은 샘플들 경우 평균 VOQ score는 53.82로 Tsai 등이 Velodyne VLP-16C를 사용한 캘리브레이션을 통해 얻은 가장 낮은 값 26.21보다 높은 값을 기록하였다. 반면, 두 번째 방법을 통해 실시간으로 들어오는 각 토픽을 이용해 얻은 샘플들의 경우 평균 VOQ score 15.54로 앞서 언급한 값보다 낮은 값을 얻을 수 있었다. 이는 실시간으로 치수오차를 확인하면서 자세 및 위치를 조정하여 더욱 낮은 치수오차를 가진 샘플들을 얻을 수 있었기 때문에 더욱 정확한 카메라-라이다 간 외부 파라미터를 얻을 수 있었다. 이를 통해 포인트 클라우드를 영상에 사영시킨 결과는 Photo. 3과 같다.

Photo. 3

Projection of point clouds to the image plane after camera-LiDAR　calibration

본 연구팀은 실험을 통해 카메라-라이다 간 캘리브레이션에 영향을 미치는 여러 요소 및 조건들을 확인할 수 있었다.

첫 번째로는 체커보드와 센서 간의 위치 및 거리 조건이다. 무인 차량에 설치된 Velodyne VLP-32 라이다의 특성과 설치된 위치, 카메라의 해상도와 체커보드의 크기 등을 고려했을 때 3 ~ 6 미터 내에 체커보드가 위치할 경우 영상 및 포인트 클라우드를 통한 특징 추출 및 낮은 차수 오차 값을 얻을 수 있었다. 체커 보드의 거리가 멀수록 포인트 클라우드 데이터의 밀도도 낮아지며 더욱 많은 노이즈가 발생하여 정확한 평면 추정이 어려워 높은 차수 오차의 원인이 되었다. 또한 카메라와 체커보드 간 거리가 8미터 이상의 경우 설정된 카메라 해상도에서 영상 상의 체커보드 특징점 추출이 불가능하였다.

두 번째로 캘리브레이션을 위한 체커보드의 자세에 대한 조건이다. 체커 무늬가 그려진 면의 방향이 과도하게 바닥으로 향할 경우 저조도 환경과 유사하게 체커보드에 조사되는 광량이 부족하여 영상으로부터의 특징점 추출이 잘 이루어지지 않았다. 반면 체커보드가 인쇄된 면이 카메라에 마주하는 방향 또는 약간 위를 향할 경우 높은 조도로 체커무늬의 교점 추출이 잘 이루어졌다.

다음으로 높은 습도가 캘리브레이션의 결과에 영향을 발생하는 요소로 작용하였다. 습도 80 % 이상의 환경에서 캘리브레이션을 수행할 경우 높은 습도로 인해 포인트 클라우드에 노이즈가 다량 발생하여 차수 오차가 높게 발생하거나 라이다 상의 체커보드 특징점 추출 자체가 불가능한 경우가 발생하였다.

6. 결 론

딥러닝의 도입으로 자율 주행 인지 기술이 빠르게 성장하고 있다. 특히 각 센서의 단점을 보완하고 장점을 살리는 다중 센서 융합 딥러닝 모델을 통해 객체 검출이 어려운 환경에서 더욱 강인한 검출이 가능하게 되었다. 이러한 센서 융합 모델을 사용하기 위해 센서 간 정확한 위치 관계를 얻어 동일한 주행 환경에 대한 인식이 필수적이다. 융합 센서로 주로 카메라와 라이다가 사용되고 있으며 이들 간의 캘리브레이션은 대상이 되는 목표물을 이용하는 방식과 움직임 또는 장면을 기반으로 설정한 목표물 없이 외부 파라미터를 얻는 다양한 방식이 제안되었다. 소개된 방법들은 각각 장단점이 존재하여 사용자의 센서 환경 및 사용 상황에 적합한 방법을 선택적으로 사용할 수 있다. 본 논문에서는 다양한 방법 중 체커보드 기반 방식을 이용하여 카메라-라이다 캘리브레이션을 재현해 보았다. 추후 구축할 데이터셋을 바탕으로 딥러닝 기반 카메라-라이다 간 캘리브레이션을 적용하여 각 결과를 비교 분석할 계획이다.

Subscripts


FoV :	field of view
u, v :	image coordinate
x, y, z :	LiDAR coordinate
R, t :	rotation matrix, translation matrix
f_u, f_υ :	focal length
c_u, c_υ :	principal point
skew_c :	skewness coefficient
A,B,C,P :	nodal point
SfM :	structure-from-motion
L, R :	left, right
ROS :	Robot operating system

Acknowledgments

본 논문은 “센서 융합 기반 야지환경 다중 객체 추적기술 연구”의 일환으로 한화디펜스의 지원을 받아 수행된 연구입니다.

References

A. Geiger, P. Lenz and R. Urtasun, “Are We Ready for Autonomous Driving? The Kitti Vision Benchmark Suite,” IEEE Conference on Computer Vision and Pattern Recognition, pp.3354-3361, 2012. [https://doi.org/10.1109/CVPR.2012.6248074]
H. Caesar, V. Bankiti, A. H. Lang, S. Vora, V. E. Liong, Q. Xu, A. Krishnan, Y. Pan, G. Baldan and O. Beijbom, “Nuscenes: A Multimodal Dataset for Autonomous Driving,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.11621-11631, 2020. [https://doi.org/10.1109/CVPR42600.2020.01164]
P. Sun, H. Kretzschmar, X. Dotiwalla, A. Chouard, V. Patnaik, P. Tsui, J. Guo, Y. Zhou, Y. Chai, B. Canie, V. Vasudevan, W. Han, J. Ngiam, H. Zhao, A. Timofeev, S. Ettinger, M. Krivokon, A. Gao, A. Joshi, Y. Zhang, J. Shlens, Z. Chen and D. Anguelov, “Scalability in Perception for Autonomous Driving: Waymo Open Dataset,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.2446-2454, 2020. [https://doi.org/10.1109/CVPR42600.2020.00252]
Q. Zhang and R. Pless, “Extrinsic Calibration of a Camera and Laser Range Finder(Improves Camera Calibration),” IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS), Vol.3, Cat. No.04CH37566, pp.2301-2306, 2004.
H. C. Kim and S. W. Seo, “Extrinsic Calibration of Camera, Lidar and Radar Sensor,” Summer Annual Conference of IEIE, Vol.43, No.1, pp.1696-1698, 2020.
R. Unnikirishnan and M. Herbert, “Fast Extrinsic Calibration of a Laser Rangefinder to a Camera,” Robotics Institute, Pittsburgh, PA, Tech. Rep. CMU-RI-TR-05-09, 2005.
L. Zhou, Z. Li and M. Kaess, “Automatic Extrinsic Calibration of a Camera and a 3D Lidar Using Line and Plane Correspondences,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp.5562-5569, 2018. [https://doi.org/10.1109/IROS.2018.8593660]
R. G. Von Gioi, J. Jakubowicz, J. Morel and G. Randall, “LSD: A Fast Line Segment Detector with a False Detection Control,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.32, No.4, pp.722-732, 2008. [https://doi.org/10.1109/TPAMI.2008.300]
D. Tsai, S. Worrall, M. Shan, A. Lohr and E. Nebot, Optimising the Selection of Samples for Robust Lidar Camera Calibration,” IEEE International Intelligent Transportation Systems Conference (ITSC), pp. 2631-2638, 2021. [https://doi.org/10.1109/ITSC48978.2021.9564700]
Q. Liao, Z. Chen, Y. Liu, Z. Wang and M. Liu, “Extrinsic Calibration of Lidar and Camera with Polygon,” IEEE International Conference on Robotics and Biomimetics (ROBIO). pp.200-205, 2018. [https://doi.org/10.1109/ROBIO.2018.8665256]
C. Akinlar and C. Topal, “Edlines: A Real-time Line Segment Detector with a False Detection Control,” Pattern Recognition Letters, Vol.32, No.13, pp.1633-1642, 2011. [https://doi.org/10.1016/j.patrec.2011.06.001]
S. Mishra, G. Pandey and S. Saripalli, “Extrinsic Calibration of a 3D-LIDAR and a Camera,” IEEE Intelligent Vehicles Symposium(IV), pp.1765-1770, 2020. [https://doi.org/10.1109/IV47402.2020.9304750]
V. Fremont and P. Bonnifait, “Extrinsic Calibration between a Multi-layer Lidar and a Camera,” IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, pp.214-219, 2008.
J. Beltrán, C. Guindel and F. García, “Automatic Extrinsic Calibration Method for Lidar and Camera Sensor Setups,” IEEE Transactions on Intelligent Transportation Systems, 2022. [https://doi.org/10.1109/TITS.2022.3155228]
J. K. Huang and J. W. Grizzle, “Improvements to Target-based 3D LiDAR to Camera Calibration,” IEEE Access, Vol.8, pp.134101-134110, 2020. [https://doi.org/10.1109/ACCESS.2020.3010734]
Q. Liao, Z. Chen, Y. Liu, Z. Wang and M. Liu, “Extrinsic Calibration of Lidar and Camera with Polygon,” IEEE International Conference on Robotics and Biomimetics(ROBIO), pp.200-205, 2018. [https://doi.org/10.1109/ROBIO.2018.8665256]
S. Mishra, G. Pandey and S. Saripalli, “Extrinsic Calibration of a 3D-LIDAR and a Camera,” IEEE Intelligent Vehicles Symposium(IV), pp.1765-1770, 2020. [https://doi.org/10.1109/IV47402.2020.9304750]
R. Y. Tsai and R. K. Lenz, “A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/eye Calibration,” IEEE Transactions on Robotics and Automation, Vol.5, No.3, pp.345-358, 1989. [https://doi.org/10.1109/70.34770]
R. Hartley and A. Zisserman, “Multiple View Geometry in Computer Vision,” Cambridge University Press, 2003. [https://doi.org/10.1017/CBO9780511811685]
R. Ishikawa, T. Oishi and K. Ikeuchi, “Lidar and Camera Calibration Using Motions Estimated by Sensor Fusion Odometry,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp.7342-7349, 2018. [https://doi.org/10.1109/IROS.2018.8593360]
B. H. Yoon, H. W. Jeong and K. S. Choi, “Targetless Multiple Camera-LiDAR Extrinsic Calibration Using Object Pose Estimation,” IEEE International Conference on Robotics and Automation (ICRA), pp.13377-13383, 2021. [https://doi.org/10.1109/ICRA48506.2021.9560936]
W. Wang, S. Nobuhara, R. Nakamura and K. Sakurada, “Soic: Semantic Online Initialization and Calibration for Lidar and Camera,” https://arxiv.org/abs/2003.04260, , 2020.
T. Ma, Z. Liu, G. Yan and Y. Li, “CRLF: Automatic Calibration and Refinement based on Line Feature for LiDAR and Camera in Road Scenes,” https://arxiv.org/abs/2103.04558, , 2021.
G. Iyer, R. K. Ram, J. K. Murthy and K. M. Krishna, “CalibNet: Geometrically Supervised Extrinsic Calibration Using 3D Spatial Transformer Networks,” IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS), pp.1110-1117, 2018. [https://doi.org/10.1109/IROS.2018.8593693]
J. Shi, Z. Zhu, J. Zhang, R. Liu, Z. Wang, S. Chen and H. Liu, “CalibRCNN: Calibrating Camera and LiDAR by Recurrent Convolutional Neural Network and Geometric Constraints,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp.10197-10202, 2020. [https://doi.org/10.1109/IROS45743.2020.9341147]
X. Lv, B. Wang, Z. Dou, D. Ye and S. Wang, “LCCNet: LiDAR and Camera Self-calibration Using Cost Volume Network,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp.2894-2901, 2021.