차량의 제동 요 안정성 향상을 위한 4륜 독립 조향 시스템의 비선형 모델 예측 제어 기반 간접 자가 동조 적분 제어 알고리즘

1. 서 론

차량의 브레이크 디스크 파손 및 변형, 브레이크 오일 누유 또는 브레이크 패드의 불균형적인 마모 등으로 인해 제동 장치가 손상되면 제동 시 차량이 한쪽으로 쏠리는 편제동 현상이 발생할 수 있다. 또한 경차의 경우 차량에 불균형적인 하중이 가해진 상태로 제동 입력을 인가할 경우 제동 쏠림 현상이 발생할 수 있다. 만약 주행 중 이러한 상황으로 인해 급작스러운 요 각속도가 발생한다면 운전자 의도 기반 조향 및 제동이 되지 않을 뿐만 아니라 큰 교통사고로 이어질 수 있다. 따라서 제동 장치의 안정성 향상 및 허용 제어 시스템 개발을 위한 노력이 필요하다. 차량의 요 안정성을 위해 ABS(Anti-lock Brake System), ESC(Electronic Stability Control) 등과 같은 상용화된 기술을 고도화하고 새로운 고장 허용 제어 기술 개발을 위한 많은 연구들이 진행 중이다.

구요한 등¹⁾은 AEBS의 횡방향 제동 불안정성을 보완하기 위해 목표 요 각속도을 유지하는 제동력 분배 알고리즘을 개발하였다. 나호용 등²⁾은 ESC의 한계점 보완을 위해 횡경사각을 포함한 요 각속도를 도출하여 제동력 제어를 수행하였다. Wang 등³⁾은 PID와 Fuzzy 제어기를 이용하여 후륜 제동력 기반 목표 물리량을 추종하는 EHB 시스템의 제어 방법론을 제안하였다. Huang 등⁴⁾은 AFS 기반 요 안정성을 위한 전륜 조향 입력을 도출하는 적응형 RPNN 알고리즘을 개발하였다. 위는 기존 상용 시스템 고도화를 위해 진행한 연구들이다. 차량의 제동 안정성을 향상시키기 위한 연구는 다음과 같다. 김기현 등⁵⁾은 선회 주행 중 타이어 모델 특성에 따른 제동 안정성을 평가하고 해석하였다. Sun 등⁶⁾은 인휠 모터의 회생 제동력을 이용하여 최적 제동력을 계산하여 제동 안정성을 향상시켰다. 고성연 등⁷⁾은 인휠 모터 차량의 마찰 유압 제동과 제동 협력 알고리즘을 개발하였다. Joa 등⁸⁾은 노면의 상태에 영향을 받지 않고 차량의 안정성을 유지하는 4륜 독립 제동 시스템 제어 알고리즘을 설계하였다. Shaohua 등⁹⁾은 6륜 차량이 선회하면서 정차하는 상황에서의 요 및 롤 안정성을 TCLP 모델을 이용하여 분석하였다. Zhileykin과 Skotnikov¹⁰⁾은 트레일러 트럭의 트레일러 제동 시스템 고장 시 조향 각 제어를 통한 제동 안정성을 확보하는 방법론을 제안하였다. 또한 주행 중 운전자의 의도와 다른 요 각속도가 발생하면 큰 사고로 이어질 수 있므로 이를 방지하고자 차량의 핸들링 성능 및 요 안정성 관점에서 많은 연구들이 진행되고 있다. 장문정 등¹¹⁾은 4륜 독립 조향 차량의 제동 안정성을 위해 MPC(MPC, Model Predictive Control) 기반 적분 제어 알고리즘을 개발하였다. He 등¹²⁾은 다양한 제동 시스템을 통합한 통합형 전자식 유압 제동 시스템을 설계하였다. Ren 등¹³⁾은 MPC 기반 인휠 모터 차량의 요 안정성을 위한 모터 토크 분배 알고리즘을 제안하였다. Falcone 등¹⁴⁾은 장애물 회피 및 차선 변경 시 안정적으로 조향 및 제동을 할 수 있는 제어 방법을 MPC를 이용하여 설계하였다. Zhu 등¹⁵⁾은 제동 및 선회 상황에서 차량의 종/횡력 및 요 각속도를 비선형 MPC를 이용하여 도출하는 알고리즘을 개발하였다. 대부분 차량의 제동력 제어를 위한 연구들은 주행 중 발생하는 타이어의 슬립을 제어하기 위해 노면의 상태를 고려해 제한된 환경에서만 적용이 가능하다는 한계점이 존재한다. 또한 제동 및 요 안정성을 위한 논문들은 다수 존재하지만 제동과 동시에 발생하는 제동 요 각속도를 제어를 위한 연구는 많이 이루어지지 않고 있다.

본 연구에서는 차량의 제동 시스템 고장으로 인해 편제동이 발생하였을 때 요 각속도 안정화 제어를 위해 MPC 기반 간접 자가 동조 적분 제어기(Indirect self-tuning integral control)를 제안한다. MPC는 시스템의 수학적 모델을 이용하여 상태를 예측해 최적의 제어 입력을 계산하는 제어 방법이다. 하지만 수학적 모델과 실제 시스템 간의 차이로 인한 불확실성이 존재하고 연산량이 많아 실시간 제어가 어렵다. 적분 제어는 목표 물리량과 실제 물리량 사이의 오차를 시간에 대해 적분하고 그 값에 적분 이득을 곱하여 제어를 수행한다. 적분 제어기는 단일 입출력 시스템(Single Input Single Output System)에서만 적용이 가능하기 때문에 여러 물리량을 고려하여 각 휠마다 다른 제어 입력을 계산하기 힘들다는 한계점이 존재한다. 따라서 본 논문에서는 MPC 제어 입력 변화량 기반 적분 제어 이득을 간접적으로 이용하여 자가 동조함으로써 합리적 제어 입력 분배 알고리즘을 개발하였다. 본 논문에서 제안하는 알고리즘의 성능 평가는 Matlab/Simulink 환경과 상용 소프트웨어(CarMaker)를 이용하여 차량의 직진 주행, 선회 주행 시나리오를 기반으로 수행하였다. 본 논문은 다음과 같이 구성되어 있다.

2장은 4륜 독립 조향 시스템에서의 제동 요 안정성을 위한 제어 알고리즘에 대해 기술하고, 3장에서 개발 알고리즘에 대한 성능 평가를 진행하였다. 4장은 결론 및 향후 계획으로 이루어져 있다.

2. 모델 예측 제어 기반 자가 동조 적분 제어

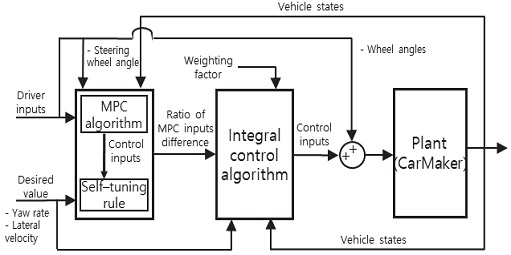
본 논문에서는 제동 시 발생하는 요 각속도를 보상하기 위한 MPC 기반 간접 자가 동조 적분 제어 알고리즘을 개발하였다. Fig. 1은 본 논문에서 제안하는 알고리즘의 모델 개략도이다. 운전자 조향 입력에 따라 결정되는 요구 물리량을 추종하기 위한 4개 휠의 조향각이 MPC를 통해 계산된다. MPC 제어 입력 변화량의 상대적 크기 비율을 이용하여 적분 제어기의 이득 값이 자동으로 계산되어 갱신되도록 설계하였다. 적분 제어를 통해 도출된 각 휠의 조향각은 운전자 조향 입력 기반 4륜 독립 조향 시스템에 인가된다.

Fig. 1

Model schematic for self-tuning Integral control based MPC

목표 물리량은 다음과 같다. 직진 주행 상황에서의 목표 요 각속도는 0 rad/s이다. 선회 주행 시 목표 요 각속도는 등속 원운동 공식을 기반으로 선회 반경과 차량의 종방향 속도를 이용하여 도출하였다. 이는 각각 식 (1)~(2)로 나타내었다. 회전 반경 R은 정상 원 선회 시나리오의 경우 고장이 없는 상태의 평가 데이터를 기반으로 이론적으로 도출하여 적용하였다.

본 논문에서 제안하는 알고리즘을 통해 최종적으로 차량에 인가되는 휠 조향각은 다음과 같다. 전륜은 MPC 기반 적분 제어기의 제어 입력과 운전자 조향 입력 기반 조향각의 합이다. 후륜 조향각은 제어기를 통해 도출된 제어 입력이다. 식 (3)~(4)를 통해 전륜과 후륜의 조향각 입력을 나타내었다.

2.1 모델 예측 제어 알고리즘

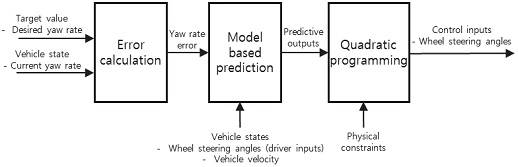
MPC는 수학적 모델을 이용하여 시스템의 상태 및 제어 입력을 예측하고 최적의 제어 입력을 도출하는 제어기이다. 다양한 물리량과 물리적 제약 조건을 반영하여 제어 입력을 도출할 수 있어 다중 입출력 시스템(Multi Input Multi Output System)및 과구동 시스템(Over-actuated system)의 제어에 적합하다. 본 논문은 단일 입출력 시스템에만 적용 가능한 적분 제어기의 적분 이득을 MPC 제어 입력을 기반으로 갱신함으로써 합리적 제어 입력 분배가 가능한 제어기를 제안한다. Fig. 2는 설계된 MPC의 모델 개략도이다.

Fig. 2

Model schematic for model predictive control

설계된 MPC는 목표 요 각속도와 현재 요 각속도를 이용하여 오차를 계산한다. 계산된 요 각속도 오차와 차량의 물리량을 이용하여 수학적 모델 기반 제어 입력 및 차량의 상태를 예측한다. 이후 2차 계획법(Quadratic programming)을 이용하여 물리적 제약 조건을 고려한 최적 제어 입력을 도출한다. 본 연구는 MPC 설계를 위한 수학적 모델로서 차량의 비선형 평면 모델을 이용하였고 식 (5)~(6)과 같이 횡방향 속도와 요 각속도 함수를 도출하였다.

$\[ \begin{array}{c}{f}_{v_y}=\frac{1}{m}\left[C_1\left({\delta }_1-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\cos {\delta }_1+C_2\left({\delta }_2-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\cos {\delta }_2\right.\hfill \\ \left.+C_3\left({\delta }_3-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\cos {\delta }_3+C_4\left({\delta }_4-\frac{v_y-l_f\dot{\psi }}{v_x}\right)\cos {\delta }_4\right]-v_x\dot{\psi }\hfill \end{array} \]$

(5)

$\[ \begin{array}{c}{f}_{\dot{\psi }}=\frac{l_f}{I_z}\left[C_1\left({\delta }_1-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\cos {\delta }_1+C_2\left({\delta }_2-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\cos {\delta }_2\right]\hfill \\ -\frac{l_r}{I_z}\left[C_3\left({\delta }_3-\frac{v_y-l_r\dot{\psi }}{v_x}\right)\cos {\delta }_3+C_4\left({\delta }_4-\frac{v_y-l_r\dot{\psi }}{v_x}\right)\cos {\delta }_4\right]\hfill \\ +\frac{t_w}{2I_z}\left[C_1\left({\delta }_1-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\sin {\delta }_1+C_3\left({\delta }_3-\frac{v_y-l_f\dot{\psi }}{v_x}\right)\sin {\delta }_3\right]\hfill \\ -\frac{t_w}{2I_z}\left[C_2\left({\delta }_2-\frac{v_y+l_f\dot{\psi }}{v_x}\right)\sin {\delta }_2+C_4\left({\delta }_4-\frac{v_y-l_f\dot{\psi }}{v_x}\right)\sin {\delta }_4\right]\hfill \end{array} \]$

(6)

도출된 횡방향 속도와 요 각속도 함수 및 차량의 물리량을 이용하여 횡방향 제어를 위한 상태 공간 방정식을 설계하였고 이는 식 (7)과 같다.

$\[ \dot{x}=Ax+Bu \]$

(7)

$\[ x=\left[v_y\dot{\psi }\right] \]$

(8)

$\[ A=\left[\begin{array}{cc}\frac{\partial f_{v_y}}{\partial v_y}& \frac{\partial f_{v_y}}{\partial \dot{\psi }}\\ \frac{\partial f_{\dot{\psi }}}{\partial v_y}& \frac{\partial f_{\dot{\psi }}}{\partial \dot{\psi }}\end{array}\right] \]$

(9)

$\[ B=\left[\begin{array}{cccc}\frac{\partial f_{v_y}}{\partial {\delta }_1}& \frac{\partial f_{v_y}}{\partial {\delta }_2}& \frac{\partial f_{v_y}}{\partial {\delta }_3}& \frac{\partial f_{v_y}}{\partial {\delta }_4}\\ \frac{\partial f_{\dot{\psi }}}{\partial {\delta }_1}& \frac{\partial f_{\dot{\psi }}}{\partial {\delta }_2}& \frac{\partial f_{\dot{\psi }}}{\partial {\delta }_3}& \frac{\partial f_{\dot{\psi }}}{\partial {\delta }_4}\end{array}\right] \]$

(10)

$\[ u={\left[{\delta }_{mpc,1} {\delta }_{mpc,2} {\delta }_{mpc,3} {\delta }_{mpc,4}\right]}^T \]$

(11)

식 (8)은 상태 벡터, 식 (9)와 (10)은 각각 시스템 행렬, 입력 행렬로 자코비안 행렬을 이용하여 횡방향 속도와 요 각속도 함수를 선형화하여 도출하였다. 식 (11)은 MPC 제어 입력을 나타내며, 제어 입력의 변화량 기반 적분 제어 이득 계산을 통해 MPC의 불확실성 극복 및 적분 제어기의 개별 제어 입력 분배가 가능하도록 알고리즘을 설계하였다. 목표 물리량 추종을 위해 오차를 식 (12)와 같이 정의하여 오차 동역학 모델을 도출하였고 이는 식 (13)~(16)과 같다.

$\[ e=x_d-x \]$

(12)

$\[ e\left(k+1\right)=A_{e}e\left(k\right)+B_{e}u\left(k\right)+F_e{w}_e \]$

(13)

$\[ y\left(k\right)=C_{e}e\left(k\right) \]$

(14)

$\[ C_e=\left(\begin{array}{cc}{w}_1& 0\\ 0& w_2\end{array}\right) \]$

(15)

$\[ A_e=A, B_e=-B, F_e=\left(A_d-A\right)x_d+B_d{u}_d \]$

(16)

식 (17)은 입력 행렬과 출력 행렬의 관계에 대한 예측 함수이다. 식 (18)~(25)는 식 (17)의 각 항에 대한 행렬 요소를 나타낸 수식이다.

$\[ Y_M=G_{M}e\left(k\right)+H_M{U}_M{F}_{M}u\left(k\right)+N_M{W}_M+K_M{w}_d\left(k\right) \]$

(17)

$\[ Y_M={\left[y_{N+1} y_{N+2} y_{N+3}\cdots y_{k+N}\right]}^T \]$

(18)

$\[ G_M={\left[C_{e}A C_e{A}^2\cdots C_e{A}^N\right]}^T \]$

(19)

$\[ H_M=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_e{B}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_e{A}_d^{N-2}{B}_d& C_e{A}_d^{N-3}{B}_d& \cdots & 0\end{array}\right] \]$

(20)

$\[ U_M={\left[u_{N+1} u_{N+2} u_{N+3}\cdots u_{k+N}\right]}^T \]$

(21)

$\[ F_M={\left[C_e{B}_d C_e{A}_d{B}_d\cdots C_e{A}_d^{N-1}{B}_d\right]}^T \]$

(22)

$\[ N_M=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_e{F}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_e{A}_d^{N-2}{F}_d& C_e{A}_d^{N-3}{F}_d& \cdots & 0\end{array}\right] \]$

(23)

$\[ W_M={\left[w_d\left(k+1\right) w_d\left(k+2\right)\cdots w_d\left(k+N\right)\right]}^T \]$

(24)

$\[ K_M={\left[C_e{F}_d C_e{A}_d{F}_d\cdots C_e{A}_d^{N-1}{F}_d\right]}^T \]$

(25)

MPC 제어 입력을 도출하기 위한 비용 함수는 식 (26)으로 정의하였다. r은 제어 입력에 대한 가중치이다.

$\[ J=Y_M^T{Y}_M+r{U}_M^T{D}^{T}D{U}_M \]$

(26)

$\[ D=\left[\begin{array}{cccccccc}1& 0& 0& 0& -1& 0& \cdots & 0\\ 0& 1& 0& 0& 0& -1& ⋮& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & 1\end{array}\right] \]$

(27)

MPC 제어 입력 도출을 위해 2차 계획법을 이용하였다. 2차 계획법은 2차 함수 개형의 비용 함수의 최솟값을 계산해 최적 제어 입력을 도출한다. 최적해를 도출하는 데에 있어 경계값 제약 조건(Boundary constraints), 부등호 제약 조건(Inequality constraints)을 적용하였다. 이는 각 휠의 최대 조향각 제한, 전/후륜 휠의 조향 변화 속도 제한이다. 본 논문에서는 조향 변화 속도 제한은 40 deg/s로 최대 조향각 제한은 40 deg로 적용하여 성능 평가를 진행하였다. 식 (28)~(30)은 식 (26)를 통해 도출된 2차 계획법에 이용된 비용 함수와 각 항을 나타낸 수식이다.

$\[ J=\frac{1}{2}{U}^{T}QU+f^{T}U \]$

(28)

$\[ Q={rD}^{T}D+H^{T}H \]$

(29)

$\[ f=H^T\left(Ge\left(k\right)+Fu+MW+K{w}_d\left(k\right)\right) \]$

(30)

본 연구에서 설계된 MPC는 식 (5)와 (6)에서 확인할 수 있듯이 슬립각 계산을 위하여 분모에 차량의 종방향 속도가 적용되었다. 그러므로 차량의 종방향 속도가 0 km/h에 가까울수록 함수의 값이 급격히 증가할 수 있으며, 이로 인하여 불안정한 제어 입력을 도출할 수 있는 한계점이 존재한다. 추후 언급된 한계점을 극복하기 위해 차량의 종방향 속도를 고려하는 비용 함수 설계를 통해 고도화를 계획하고 있다.

2.2 자가 동조 적분 제어

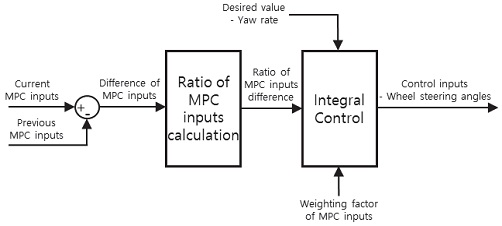
적분 제어는 기준 입력과 실제 출력의 차를 오차로 정의하고 이를 시간에 대해 적분한 값에 적분 이득을 곱하여 제어를 수행하는 방법이다. 적분 제어기는 제어 성능이 안정적이고 뛰어나기 때문에 본 연구에서는 MPC의 불확실성을 보완하고, 개별 적분 제어기의 합리적 제어 입력 분배를 위한 MPC의 제어 입력 기반 적분 이득 자가 동조 알고리즘을 설계하였다. 본 연구에서는 4륜 독립 조향 차량의 요 각속도 추종 제어를 위한 4 개의 적분 제어기가 적용되었고, 요 각속도 한 가지 물리량 추종 제어를 위해 적분 제어 이득을 MPC 제어 입력의 변화량을 이용함으로써 4개 휠에 합리적 제어 입력이 분배되도록 알고리즘을 설계하였다. Fig. 3은 본 논문에서 제안하는 제어기의 모델 개략도이다.

Fig. 3

Model schematic for MPC-based indirect self-tuning integral control

설계된 적분 제어기의 개별 이득은 계산된 MPC 제어 입력의 변화량을 이용하여 계산되었으며, 식 (31)과 (32)는 각각 MPC 제어 입력의 변화량과 적분 이득을 위한 제어 입력 변화량의 크기 비율을 계산하는 식을 나타낸다.

$\[ \Delta {\delta }_{mpc,i}={\delta }_{mpc,i}\left(k-1\right)-{\delta }_{mpc,i}\left(k\right) \]$

(31)

$\[ C_{r,i}=\frac{\left|\Delta {\delta }_{mpc,i}\right|}{\sum _{i=0}^4\left|\Delta {\delta }_{mpc,i}\right|} \]$

(32)

식 (33)과 (34)는 전륜과 후륜 적분 제어기의 적분 이득을 나타내며, 식 (32)의 제어 입력 변화량의 크기 비율과 역위상 조향을 만들 수 있는 부호 조건이 고려되어 계산되었다.

$\[ k_{int,cal,i}=k_s{C}_{r,i} \left(where, i=\mathrm{1,2}\right) \]$

(33)

$\[ k_{int,cal,i}={-k}_s{C}_{r,i} \left(where, i=3,4\right) \]$

(34)

앞서 2.1 절에서 언급된 것처럼 차량의 종방향 속도가 감소함에 따라 MPC는 불안정한 제어 입력을 도출할 수 있기 때문에 속도 임계값을 기준으로 개별 적분 이득이 가변(k_int,cal)되거나 이전 단계의 값으로 고정(k_int,fixed)되도록 알고리즘이 설계되었다. 설계된 속도 임계값 기준 적분 이득의 가변 또는 고정 알고리즘은 다음 식 (35)에서 확인할 수 있다. 속도 임계값은 30 km/h로 설정되었으며, 식 (36)은 설계된 적분 제어 입력을 나타낸다.

$\[ k_{int,i}=\left\{\begin{array}{ccc}{k}_{int,cal,i}\hfill & \hfill & \text{if}, v_x>v_{th}\hfill \\ k_{int,fixed,i}\hfill & \hfill & \text{if}, v_x\le v_{th}\hfill \end{array}\right. \]$

(35)

$\[ {\delta }_{int,i}=k_{int,i}{\int }_0^{t}edt \]$

(36)

2.3 안정성 증명

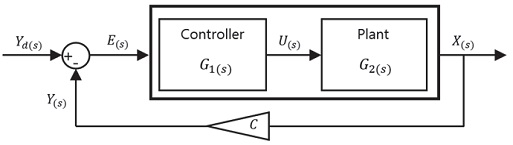
제안하는 MPC 기반 적분 제어기의 안정성 증명은 설계된 시스템 모델의 라플라스 변환을 통해 진행하였다. Fig. 4는 시스템 모델의 라플라스 함수를 기반으로 하는 폐회로 제어 시스템(Closed loop control system)의 모델 개략도를 나타낸다.

Fig. 4

Model schematics for closed loop control system

식 (7)에 표현된 상태 공간 방정식을 라플라스 변환하여 표현하고, 출력 행렬을 이용해 출력을 나타내면 각각 식 (37) 및 (38)과 같다. 요구 물리량과 현재 물리량의 오차는 (39)와 같이 표현할 수 있다.

$\[ \dot{X}\left(s\right)=AX\left(s\right)+BU\left(s\right) \]$

(37)

$\[ Y\left(s\right)=CX\left(s\right) \]$

(38)

$\[ E\left(s\right)=Y_d\left(s\right)-Y\left(s\right) \]$

(39)

각 블록의 전달 함수를 이용하여 적분 제어기와 플랜트의 입/출력 관계를 나타내면 각각 식 (40)과 (41)로 나타낼 수 있다. 본 연구에서는 적분 이득의 값은 상대적으로 크게 변하지 않는다고 가정하였다.

$\[ U\left(s\right)=G_1\left(s\right)E\left(s\right)=\frac{k_i}{s}E\left(s\right) \]$

(40)

$\[ Y\left(s\right)=G_2\left(s\right)U\left(s\right)=C{\left(sI-A\right)}^{-1}BU\left(s\right) \]$

(41)

플랜트의 전달 함수 G₂(s)는 시스템의 상태 공간 방정식 식 (37)을 이용하여 도출되었으며, 위 식을 이용하면서 적분 제어 입력을 적용하면 식 (42)와 같이 정리될 수 있다.

$\[ E\left(s\right)=\frac{Y_d\left(s\right)}{1+G_1\left(s\right)G_2\left(s\right)}=\frac{Y_d\left(s\right)}{1+\frac{CB}{\left(sI-A\right)}\frac{k_i}{s}} \]$

(42)

식 (42)를 기반으로 최종값정리(Final value theorem)를 이용하여 오차의 수렴성을 확인함으로써 안정성을 판단하였다. 목표 물리량 Y_d(s)가 계단 함수인 경우 라플라스 변환된 함수의 분모 차수가 1차이기 때문에 다음 식 (43)과 같이 최종값정리에 의해 오차가 0으로 수렴한다는 것을 확인할 수 있다.

$\[ e\left(\infty \right)=\underset{s\to 0}{\lim }E\left(s\right)=\underset{s\to 0}{\lim }\frac{Ms \left(sI-A\right)}{s^{2}I-As+CB{k}_i}=\frac{0}{CB{k}_i}=0 \]$

(43)

식 (43)의 최종값정리 식을 기반으로 계단 함수 외 경사 및 가속 함수가 목표 물리량으로 인가될 경우 제어 안정성을 확보하기 어렵다는 것을 확인할 수 있다. 그러므로 향후 적응형 비례-미분 제어 입력을 추가함으로써 주행 상황에서 설계된 다양한 목표 물리량을 추종할 수 있는 제어 알고리즘 고도화와 함께 적분 이득의 변화를 고려한 안정성 해석을 계획하고 있다. 본 연구에서는 일정 속도에서 일정 요 각속도를 목표 물리량으로 인가하는 직진 주행과 정상 원 선회 시나리오가 적용되었기 때문에 제안된 제어기 기반 제동 요 안정성을 확보할 수 있음을 확인할 수 있었다. 다음 장은 성능 평가 결과를 보여준다.

3. 성능 평가

본 논문에서 제안하는 알고리즘은 Matlab/ Simulink 환경과 상용 소프트웨어(CarMaker)를 이용하여 성능 평가를 진행하였다. 상용 소프트웨어는 차량의 조향 시스템에 대한 입력으로서 랙 변위를 이용한다. 따라서 설계된 제어기를 통해 도출된 각 휠의 조향각을 직접적으로 인가할 수 없으므로 휠 조향각 대비 랙 변위를 1차 함수로 근사하여 차량에 인가하였다. 성능 평가에 이용된 차량은 상용 소프트웨어에서 제공하는 BMW 5 Series를 이용하였고 이에 대한 제원은 Table 1에서 확인할 수 있다. 성능 평가 시나리오는 차량이 직진 등속 주행 중일 때와 일정한 선회 반경과 속력을 유지하며 정상 원 선회 주행 중 운전자가 제동 입력을 인가하는 상황을 적용하였다.

Table 1

Vehicle parameters

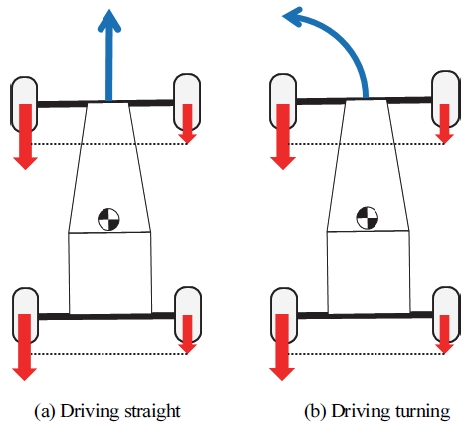
차량의 제동력 편차에 따른 편제동 현상을 재현하기 위해 상용 소프트웨어를 이용하여 좌측과 우측 휠의 제동 시스템에 다른 비율로 제동력이 인가되도록 하였다. Fig. 5는 성능 평가 시 차량의 휠에 적용된 제동력의 크기를 화살표를 이용하여 표현한 그림으로 좌측 대비 우측 휠에 더 적은 제동력이 인가된 것을 확인할 수 있다.

Fig. 5

Vehicle partial braking model

Fig. 5(a)는 우측 제동 시스템 고장으로 인해 좌측에 비해 적은 제동력이 인가된 상황이다. Fig. 5(b)는 우측 제동 시스템 고장으로 인해 좌/우 휠에 제동력이 불균형하게 인가된 상황이다. 각각의 상황은 직진 주행 상황과 선회 주행 상황에서의 성능 평가에 적용하여 진행하였다.

3.1 Case 1) 직진 주행

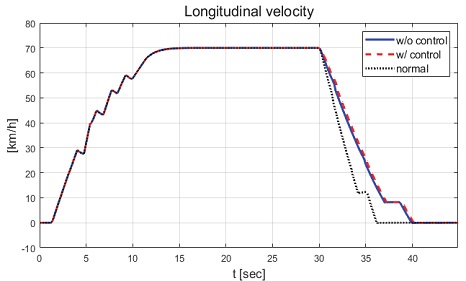
Case 1은 운전자가 약 70 km/h로 정속 직진 주행 중 30초에 제동 입력을 인가하는 시나리오를 기반으로 진행하였다. 총 성능 평가 시간은 45초로 차량은 70 km/h를 유지하며 주행 중 30초에 제동 입력을 인가한다. 성능 평가 그래프는 차량이 제동을 시작하는 30초 이후부터 차량의 종방향 속도가 임계값 이하로 감소하는 시점까지 나타내었다.

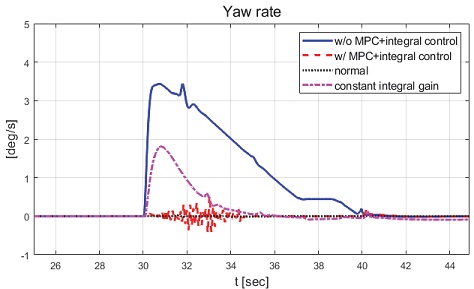
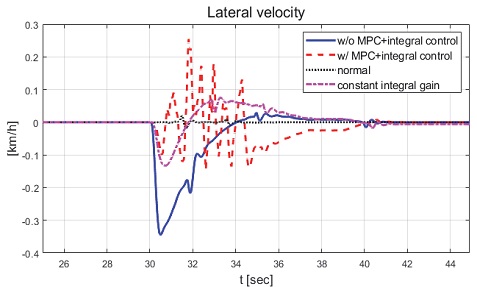
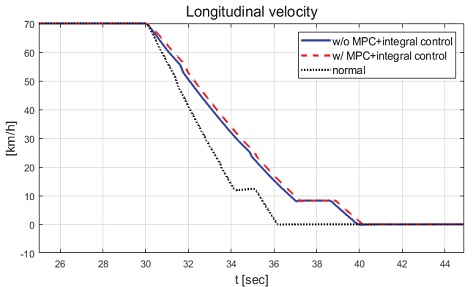
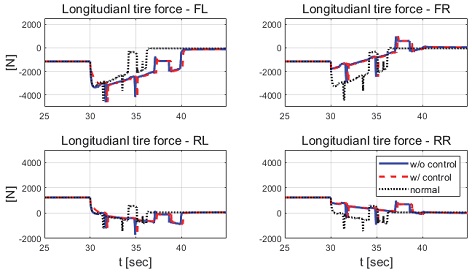
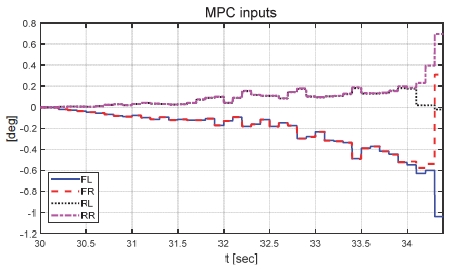
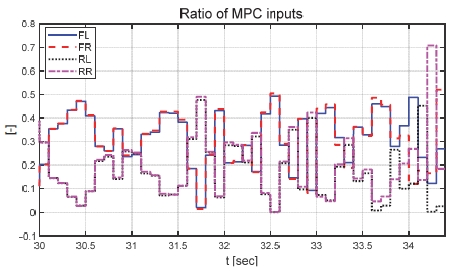
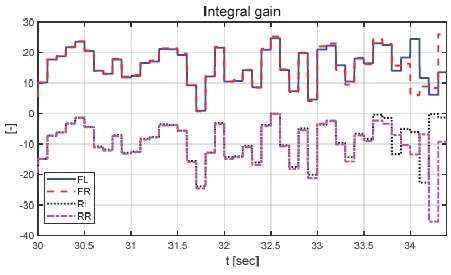
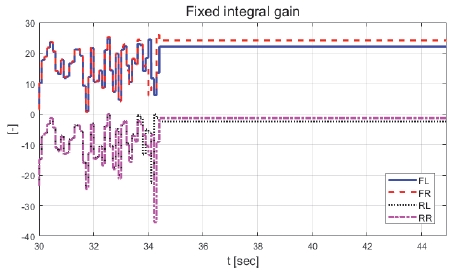
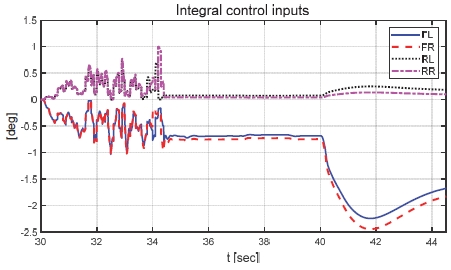
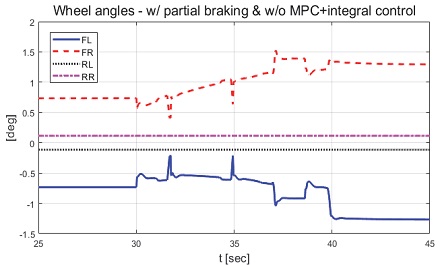
본 논문에서 제안하는 제어기의 성능을 비교하기 위해 일정한 적분 이득을 이용하는 적분 제어기를 이용하였다. 전륜과 후륜의 적분 이득은 0.1로 일정하게 인가하였으며 역위상 조향을 위해 부호를 반대로 계산하였다. Fig. 6은 전체 성능 평가 시간 동안 차량의 종방향 속도 그래프이다. 운전자는 70 km/h까지 가속 후 정속 주행 중 30초 이후부터 차량에 제동 입력을 인가한다. Fig. 7은 차량의 요 각속도 그래프로 제어 입력이 인가되었을 때는 인가되지 않았을 때에 비해 더 적은 요 각속도를 가지는 것을 확인할 수 있다. 또한 일정한 적분 이득을 가지고 있는 차량은 제안하는 제어기를 적용한 차량에 비해 더 큰 요 각속도를 나타냈다. 일정한 적분 이득을 적용할 경우 상황에 따라 적절한 이득 값 조절이 필요하다. 하지만 제안하는 알고리즘을 적용함으로써 물리량 변화를 반영한 제어 입력을 도출하는 것을 확인할 수 있다. Fig. 8은 차량의 횡방향 속도 그래프로 제동 이후 시점부터 제안하는 알고리즘이 적용된 경우 편제동이 존재하고 제어 입력이 인가되지 않은 경우에 비해 더 큰 횡방향 속도가 발생하였다. Fig. 9는 25초 이후의 종방향 속도를 나타낸 그래프로 편제동 현상이 일어난 경우 그렇지 않은 경우에 비해 제동력이 감소하여 더 느리게 감소하는 것을 확인할 수 있다. Fig. 10은 차량의 종방향 타이어 힘 그래프이다. 성능 평가에 이용된 차량은 후륜 구동 차량으로 후륜의 종방향 타이어 힘은 양수, 전륜은 음수로 나타난다. 또한 오른쪽 휠에 더 적은 제동력이 인가됨으로써 음의 방향으로 더 큰 타이어 힘이 발생한 것을 확인할 수 있다. Fig. 11은 MPC 제어 입력 그래프이다. 제동 입력이 인가된 이후부터 후륜은 양의 방향으로 전륜은 음의 방향으로 계산된 것을 확인할 수 있다. 이는 차량의 무게 중심이 후륜 축과 가까워 전륜에 더 큰 조향 입력을 인가하였을 때 더 큰 요 모멘트를 발생시킬 수 있기 때문이다. Figs. 12~13은 계산된 MPC 제어 입력 변화량의 상대적 크기 비율과 이를 기반으로 도출된 적분 제어 이득을 나타낸 그래프이다. Fig. 14는 최종적으로 계산된 적분 제어 이득을 나타낸 그래프로 차량의 종방향 속도가 속도 임계값 이하로 감소한 경우 일정한 제어 이득을 유지하는 것을 확인할 수 있다. Fig. 15는 최종적으로 차량에 인가된 적분 제어 입력이다. Figs. 16~19는 차량의 조향각 그래프로 Fig. 17을 통해 제안하는 제어기가 적용된 경우 제어 입력에 의해 전륜은 음의 방향으로 후륜은 양의 방향으로 조향한 것을 확인할 수 있다. Fig. 20은 각 휠의 조향각 비교를 위한 그래프이며, 설계된 대로 전륜과 후륜이 역위상 조향함으로써 요 각속도를 감소시킨 것을 확인할 수 있다. Fig. 21은 차량의 주행 경로를 나타낸 그래프이다. 편제동 현상이 발생한 차량은 정상 상태 차량 대비 최종 정차 위치 기준 횡방향으로 약 10 m 이상의 차이를 가지며 정차하였다. 또한 일정한 적분 이득을 이용하는 적분 제어기의 경우 정상 상태 차량의 최종 정차 위치 기준 약 4 m의 횡방향 오차를 가지고 있었다. 하지만 제안하는 알고리즘을 적용한 차량은 정상 상태의 차량과 유사한 경로로 정차하는 것을 확인할 수 있었다.

Fig. 6

Result: longitudinal velocity

Fig. 7

Result: yaw rate (25~45 [s])

Fig. 8

Result: lateral velocity (25~45 [s])

Fig. 9

Result: longitudinal velocity (25~45 [s])

Fig. 10

Result: longitudinal tire force (25~45 [s])

Fig. 11

Result: MPC inputs (30~34.4 [s])

Fig. 12

Result: ratio of MPC inputs (30~34.4 [s])

Fig. 13

Result: integral gain (30~34.3 [s])

Fig. 14

Result: fixed integral gain (30~45 [s])

Fig. 15

Result: integral control inputs (30~45 [s])

Fig. 16

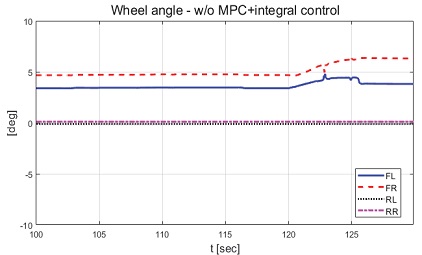
Result: wheel angles with partial braking and without control (25~45 [s])

Fig. 17

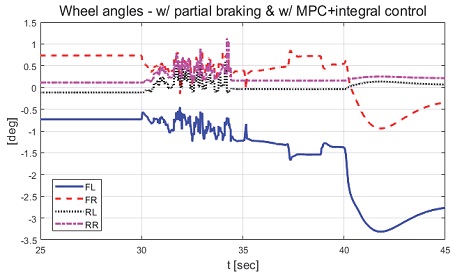
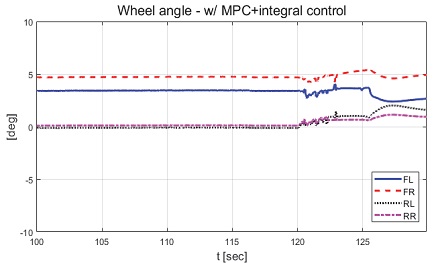
Result: wheel angles with partial braking and with control (25~45 [s])

Fig. 18

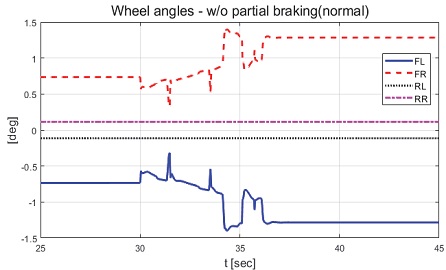
Result: wheel angels without partial braking (normal condition) (25~45 [s])

Fig. 19

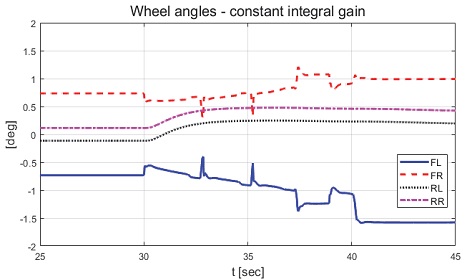
Result: wheel angels with partial braking with constant integral gain (25~45 [s])

Fig. 20

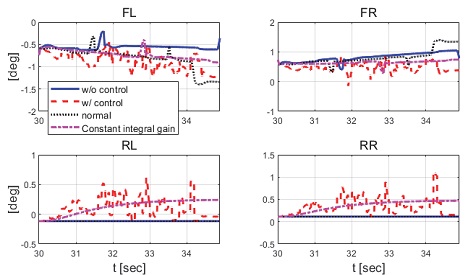
Result: wheel angles comparison (30~34.3 [s])

Fig. 21

Result: vehicle trajectory (25~45 [s])

3.2 Case 2) 선회 주행

Case 2는 운전자가 직진 주행 중 10초부터 조향 휠을 60도 회전시켜 약 50 km/h 속도를 유지하며 정상 원 선회 중 제동한 상황이다. 요 각속도와 종방향 속도가 일정하게 유지되었다고 판단된 시점 이후 시간인 100초부터 제어 입력이 인가되고 이후 120초에 운전자 제동 입력을 인가하였다. 그래프는 제어 입력이 인가되는 100초부터 종방향 속도가 임계값 이하로 떨어져 일정한 적분 이득이 인가되는 122.3초까지 나타내었다.

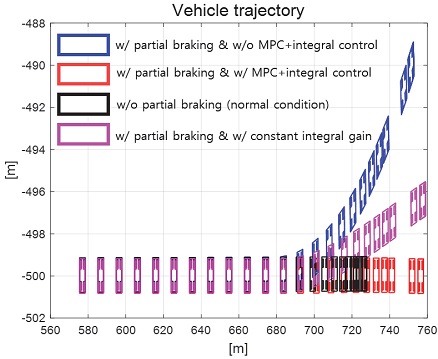
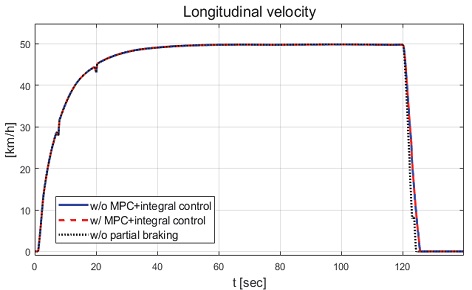
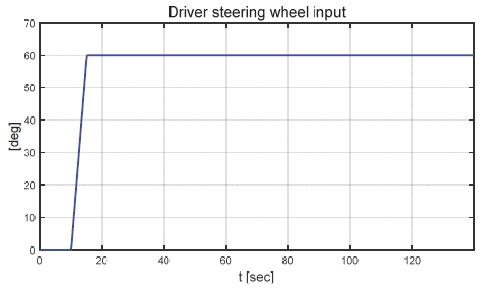
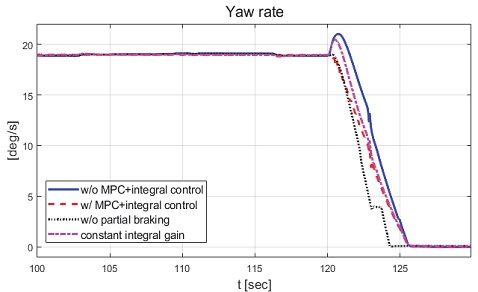
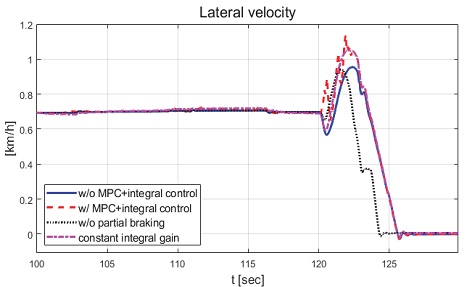
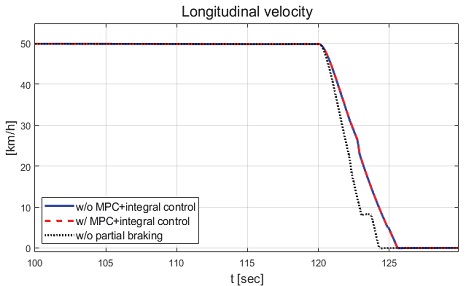
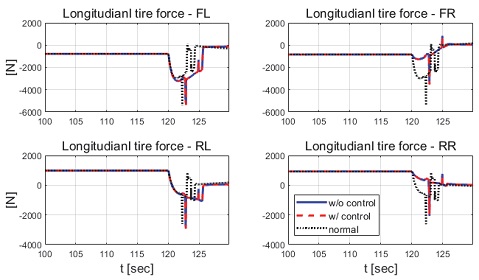
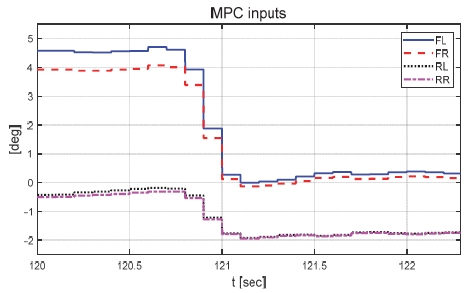
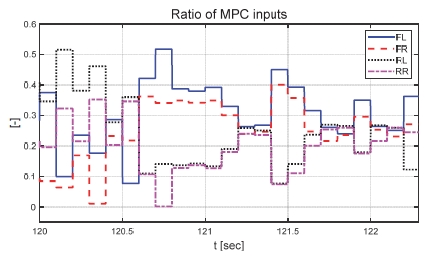
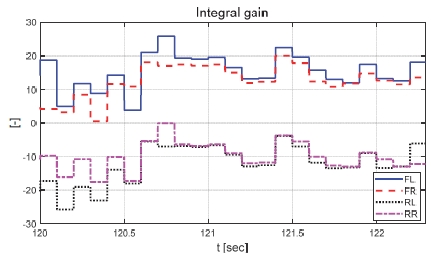
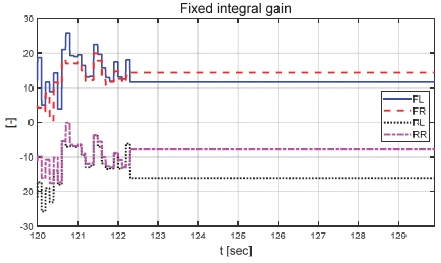
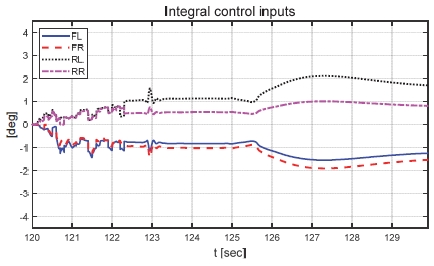
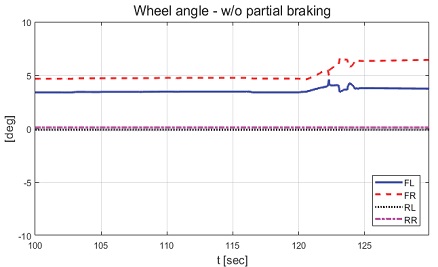
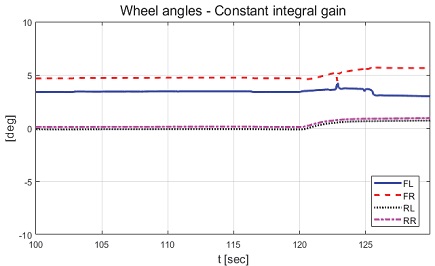
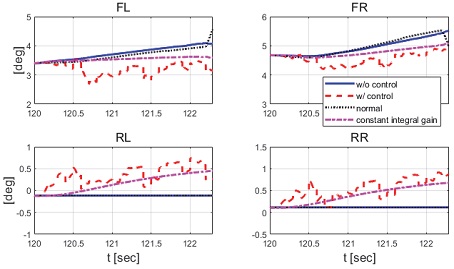
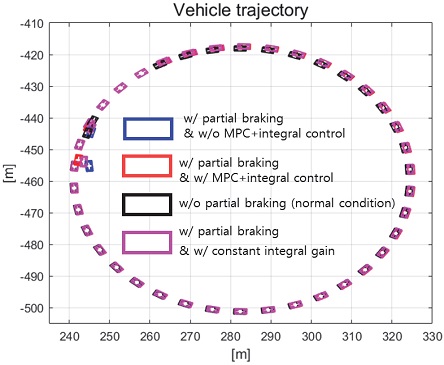
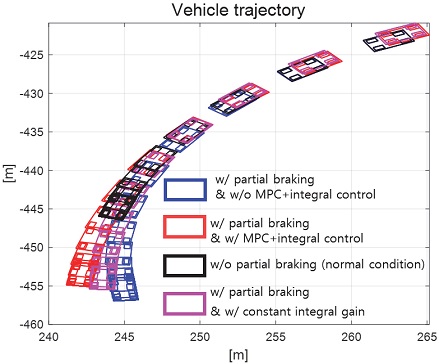
제안하는 제어기와 일정한 적분 이득을 이용하는 적분 제어기의 성능 평가 비교를 진행하였다. 일정한 적분 이득의 경우 전륜과 후륜의 적분 이득은 각각 0.1과 -0.1로 인가하였다. Fig. 22는 전체 성능 평가 시간 동안 차량의 종방향 속도 그래프이다. 운전자는 약 50초까지 50 km/h로 가속 후 정속 주행을 하면서 120초에 제동 입력을 인가한다. Fig. 23은 운전자 조향 휠 입력 그래프이다. 운전자 조향 입력은 10초부터 5초간 60 deg까지 조향 휠 입력이 인가되도록 설계하였다. Fig. 24는 차량의 요 각속도 그래프로 제안하는 알고리즘을 적용함으로써 종방향 속도에 비례하여 안정적인 요 각속도를 유지하며 감소하였고 일정한 적분 이득값을 가지는 적분 제어기에 비해 더 적은 오버슈트를 가지는 것을 확인할 수 있다. Fig. 25는 차량의 횡방향 속도 그래프로 제안하는 알고리즘이 적용된 경우 상대적으로 더 큰 횡방향 속도가 발생한 것을 확인하였다. Fig. 26은 차량의 종방향 속도 그래프로 편제동 현상이 일어난 경우 그렇지 않은 경우에 비해 종방향 감속도 크기가 작은 것을 확인할 수 있다. Fig. 27은 차량의 종방향 타이어 힘 그래프로 편제동이 있는 상태에서 제어가 적용된 경우와 적용되지 않은 경우 유사한 종방향 타이어 힘을 보이며 감소하는 것을 확인할 수 있었다. Fig. 28은 MPC 제어 입력을 나타내는 그래프이며, 양의 방향으로 발생한 요 각속도를 감소시키기 위해 후륜 조향 입력을 음의 방향으로 증가하시키는 제어 결과를 보였다. Figs. 29~30은 계산된 MPC 제어 입력 변화량의 상대적 크기 비율과 이를 기반으로 최종 도출된 적분 제어 이득을 나타낸 그래프이다. Fig. 31을 통해 차량의 종방향 속도가 임계값 이하로 감소하는 경우 이전의 적분 제어 이득을 유지하는 것을 확인할 수 있다. Fig. 32는 최종적으로 차량에 인가된 적분 제어 입력이다. 약 125.5초 이후 제어 입력이 급격히 증가하는 이유는 차량이 완전히 정차하면서 발생한 요 각속도 오차에 의한 것이다. Figs. 33~36은 차량의 조향각 그래프이다. Fig. 34를 통해 목표 요 각속도를 추종하기 위해 전륜은 음의 방향으로 후륜은 양의 방향으로 조향하는 것을 확인할 수 있다. Figs. 38~39는 차량의 주행 경로를 나타낸 그래프이다. 제안하는 알고리즘이 적용되지 않은 차량은 정상 상태 차량 대비 주행 경로를 상대적으로 크게 벗어나며 제동하였다. 제안하는 알고리즘이 적용된 차량은 정상 상태 차량과 비슷한 선회 반경을 가지며 제동하였고 최종 정차 위치 기준 제어기를 적용하지 않은 차량과 약 3 m 횡방향 차이를 보였다. 하지만 정상 상태 차량과 약 10 m의 제동 거리 차이가 존재하므로 추후 종방향 안정성을 위한 고도화가 필요하다.

Fig. 22

Result: longitudinal velocity

Fig. 23

Result: driver steering wheel input

Fig. 24

Result: yaw rate (100~130 [s])

Fig. 25

Result: lateral velocity (100~130 [s])

Fig. 26

Result: longitudinal velocity (100~130 [s])

Fig. 27

Result: longitudinal tire force (100~130 [s])

Fig. 28

Result: MPC inputs (120~122.3 [s])

Fig. 29

Result: ratio of MPC inputs (120~122.3 [s])

Fig. 30

Result: integral gain (120~122.3 [s])

Fig. 31

Result: fixed integral gain (120~130 [s])

Fig. 32

Result: integral control inputs (120~130 [s])

Fig. 33

Result: wheel angles with partial braking and without control (100~130 [s])

Fig. 34

Result: wheel angles with partial braking and with control (100~130 [s])

Fig. 35

Result: wheel angles without partial braking (normal condition) (100~130 [s])

Fig. 36

Result: wheel angels with partial braking with constant integral gain (100~130 [s])

Fig. 37

Result: wheel angles comparison (120~122.3 [s])

Fig. 38

Result: vehicle trajectory (100~130 [s])

Fig. 39

Result: vehicle trajectory (120~130 [s]) [zoom in]

본 논문에서는 등속 원 운동 공식을 기반으로 목표 요 각속도를 도출하였다. 하지만 선회 주행 중 발생하는 슬립으로 인해 제어를 수행한 차량과 그렇지 않은 차량의 주행 경로가 다른 것을 확인할 수 있었다. 따라서 수학적 모델 또는 환경 센서를 이용한 곡률 반경 추정 기반 목표 물리량 도출이 필요하다. 또한 주행 중 지속적인 제어 입력을 인가할 경우 운전자의 조향 의도가 반영되지 않을 수 있기 때문에 실 차량으로의 적용을 위해 운전자 입력 및 차량의 물리량 기반 제어 시점 판단 로직 개발을 계획하고 있다.

3.3 슬라이딩 모드 제어기를 이용한 성능 평가

슬라이딩 모드 제어기(SMC, Sliding Mode Control)는 외란에도 강건한 제어 성능을 가지고 있다. 하지만 채터링 및 외란 경계 영역 설계 등의 한계점과 과구동 시스템의 적절한 제어 입력 분배 문제가 존재한다. 본 성능 평가는 추후 MPC 기반 SMC 알고리즘 설계로의 고도화를 위해 SMC를 이용한 4륜 조향 제어기를 설계하여 진행하였다.¹⁸⁾ 제어기 설계를 위해 2 자유도 자전거 모델 기반 상태 공간 방정식을 식 (44)와 같이 설계하였다. 이를 통해 4개 휠의 SMC 제어 입력 δ_smc,i를 도출할 수 있다.

$\[ \begin{array}{c}{\dot{e}}_{\dot{\psi }}=A_{v_y}{e}_{v_y}+A_{\psi }{e}_{\psi }+A_{\dot{\psi }}{e}_{\dot{\psi }}+B_{{\dot{\psi }}_{des}}{\dot{\psi }}_{des}+B_{{\ddot{\psi }}_{des}}{\ddot{\psi }}_{des}\hfill \\ +\left[\frac{l_f{C}_f }{I}\frac{l_f{C}_f }{I}-\frac{l_r{C}_r }{I}-\frac{l_r{C}_r }{I}\right]{\left[{\delta }_{smc,1} {\delta }_{smc,2} {\delta }_{smc,3} {\delta }_{smc,4}\right]}^T\hfill \end{array} \]$

(44)

슬라이딩 표면 σ는 식 (45)와 같이 요 각속도 오차를 이용하여 정의하였다. 비용 함수는 랴푸노프 함수 기반 식 (46)과 같이 설계하였다.

$\[ \sigma ={\dot{\psi }}_{des}-\dot{\psi } \]$

(45)

$\[ J=\frac{1}{2}{e}_{\dot{\psi }}^2 \]$

(46)

주입항 v를 식 (47)과 같이 선택하고 외란의 절댓값이 항상 외란 경계 영역 L_b 보다 작거나 같다고 가정한다면 식 (48)과 같이 도출할 수 있다.

$\[ v=\left[\frac{l_f{C}_f }{I}\frac{l_f{C}_f }{I}-\frac{l_r{C}_r }{I}-\frac{l_r{C}_r }{I}\right]\left[\begin{array}{c}{\delta }_{smc,1}\hfill \\ {\delta }_{smc,2}\hfill \\ {\delta }_{smc,3}\hfill \\ {\delta }_{smc,4}\hfill \end{array}\right]=-\rho sign\left(e_{\dot{\psi }}\right) \]$

(47)

$\[ \dot{J}\le \left|\sigma \right|L_b-\left|\sigma \right|\rho =-\left|\sigma \right|\left(\rho -L_b\right) \]$

(48)

유한 시간 수렴 조건에 의해 비용 함수는 식 (49)와 같이 표현할 수 있다. 따라서 식 (48)과 (49)에 의해 주입항의 크기 ρ는 식 (50)과 같이 도출된다.

$\[ \dot{J}\le -\alpha J^{\frac{1}{2}}=-\frac{\alpha }{\sqrt{2}}\left|\sigma \right| \]$

(49)

$\[ \begin{array}{cc}\rho =L_b+\frac{\alpha }{\sqrt{2}}\hfill & where, \rho >0\hfill \end{array} \]$

(50)

SMC의 제어 입력은 비례 상수 R_f,R_r을 이용하여 전륜은 식 (51), 후륜은 식 (52)와 같이 설계하였으며, 식 (50)에 대입함으로써 제어 안정성을 확보하기 위한 비례 상수 관계식은 식 (53)과 같이 도출된다.

$\[ \begin{array}{cc}{\delta }_{smc,i}=\frac{I}{l_f{C}_f}{R}_f\left(L_b+\frac{\alpha }{\sqrt{2}}\right)sign\left(e_{\dot{\psi }}\right)\hfill & where, i=\mathrm{1,2}\hfill \end{array} \]$

(51)

$\[ \begin{array}{cc}{\delta }_{smc,i}=-\frac{I}{l_r{C}_r}{R}_r\left(L_b+\frac{\alpha }{\sqrt{2}}\right)sign\left(e_{\dot{\psi }}\right)\hfill & where, i=3,4\hfill \end{array} \]$

(52)

$\[ R_f+R_r=-0.5 \]$

(53)

설계된 SMC의 성능 평가는 Case 1 시나리오와 같은 직진 주행 시나리오를 기반으로 진행하였다. 비례 상수 R_f와 R_r은 각각 -0.25 적용함으로써 전륜과 후륜이 역위상 조향이 되도록 설계하였다. 다음은 성능 평가 결과이다.

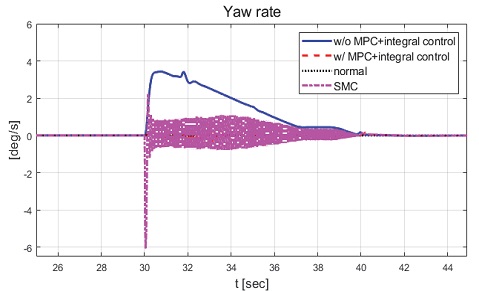
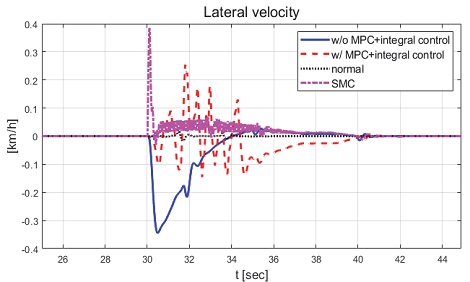
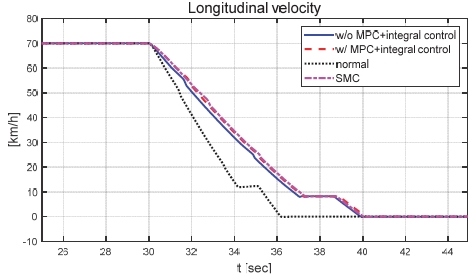
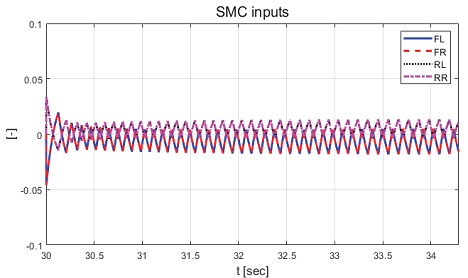
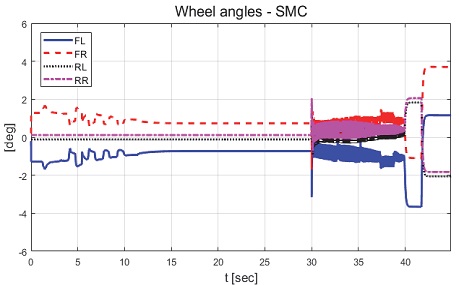
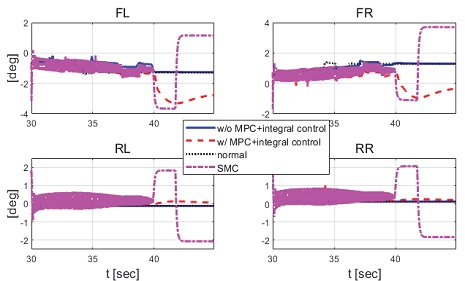
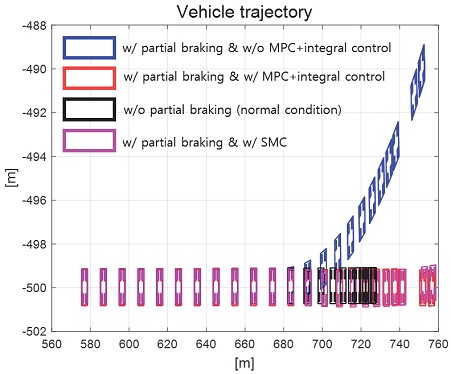
Fig. 40은 요 각속도 그래프로 제안하는 제어기에 비해 심한 채터링이 발생하면서 수렴하는 것을 확인할 수 있다. Fig. 41은 횡방향 속도 그래프로 제어 입력에 채터링 현상이 발생함에 따라 횡방향 속도 또한 채터링이 발생한 것을 확인할 수 있다. Fig. 42는 차량의 종방향 속도 그래프로, 이를 통해 편제동 현상이 발생한 경우 정상 상태 차량보다 작은 종방향 감속도를 보이는 것을 확인할 수 있다. Fig. 43은 SMC 제어 입력 그래프이다. 설계된 법칙에 따라 역위상 조향 제어 입력을 도출하는 것을 확인할 수 있다. Fig. 44는 최종적으로 차량에 인가된 휠 조향각 그래프이다. Fig. 45는 제안하는 MPC 기반 적분 제어기와 정상 상태의 차량 조향각, 편제동이 발생한 차량의 조향각, SMC를 이용하여 제어를 수행한 차량의 조향각을 비교한 그래프이다. Fig. 46은 차량의 주행 경로 그래프로 제안하는 제어기에 비해 차량이 양 옆으로 진동하면서 주행하지만 편제동이 발생하지 않은 차량과 비슷한 주행 경로를 가지며 제동하는 것을 확인할 수 있다.

Fig. 40

Result: yaw rate (25~45 [s])

Fig. 41

Result: lateral velocity (25~45 [s])

Fig. 42

Result: longitudinal velocity (25~45 [s])

Fig. 43

Result: SMC inputs (25~45 [s])

Fig. 44

Result: wheel angles with partial braking and with SMC (25~45 [s])

Fig. 45

Result: wheel angels comparison (30~45 [s])

Fig. 46

Result: vehicle trajectory (25~45 [s])

SMC의 경우 채터링 현상이 존재할 수 있고, 외란의 크기에 따른 제어 파라미터 조정이 필요하다. 또한 개별 최적 조향각을 도출하는 MPC에 비해 개별 조향각 도출 및 분배에 대한 한계점이 존재한다. 따라서 MPC 기반 적응형 SMC 설계를 통해 최적 제어 입력을 도출하는 강건 제어기를 설계함으로써 본 논문에서 제안하는 알고리즘 고도화를 진행할 예정이다.

4. 결 론

본 논문에서는 4륜 독립 조향 시스템에서 제동 요 안정성을 위한 MPC 기반 자가 동조 적분 제어 알고리즘을 제안하였다. MPC는 상태량 예측을 통해 최적의 제어 입력을 계산하지만 수학적 모델을 이용하기 때문에 제어 입력에 불확실성이 존재한다. 따라서 다수의 논문들이 적응형 MPC 설계를 통해 이러한 한계점을 극복하였다.^16,17) 적분 제어기는 제어 성능이 안정적이지만 시스템이 변할 경우 지속적인 이득 값 조절이 필요하다. 또한 단일 입출력 시스템에서만 적용이 가능하여 과구동 시스템 적용에 한계가 존재한다. 각 제어기의 단점을 보완하기 위해 MPC 제어 입력의 변화량을 이용한 간접 자가 동조 적분 제어 알고리즘을 개발하였다. 본 알고리즘의 합리성을 판단하기 위해 Matlab/Simulink 및 상용 소프트웨어(CarMaker)를 이용하여 직진 및 선회 상황에서의 성능 평가를 진행하였다. 성능 평가를 통해 제안하는 알고리즘을 적용한 차량의 경우 편제동 현상이 효과적으로 감소하는 것을 확인하였다. 또한 종방향 속도가 감소함에 따라 MPC 제어 입력이 불안정하게 도출되는 현상이 발생함에도 불구하고 자가 동조 규칙을 통해 이를 간접적으로 반영함으로써 안정적인 결과를 도출할 수 있었다. 향후에는 브레이크 페달, 조향 휠 입력 등을 이용하여 운전자의 조향 의도를 반영한 제어기 개입 시점이 합리적으로 지정되도록 고도화할 예정이다. 또한 수학적 모델을 이용함으로써 발생하는 MPC의 불안정성을 보완하기 위해 종방향 속도를 이용한 비용 불균형 보상 함수 설계 통해 한계점 보완을 계획하고 있다. 추후 실 차량 기반 검증을 위해 적응형 MPC 설계 및 최적 제어 입력 분배를 위한 시스템 모델 파라미터 추정 연구를 진행할 계획이다.

Acknowledgments

A part of this paper was presented at the KSAE 2020 Fall Conference and Exhibition

References

• Y. Koo, Y. Kang, D. Kim, T. Kang and K. Park, “A Study of Lateral Stability Securement during Autonomous Emergency Braking and Target Vehicle State Estimate using IMM,” KSAE Spring Conference Proceedings, pp.1058-1065, 2016.
• H. Na, K. Cho and S. You, “Robust Vehicle Lateral Stability Controller Against Road Bank Angles,” Transaction of the Korean Society of Mechanical Engineers, Vol.41, No.10, pp.967-974, 2017.
• M. Wang, X. Wang and Y. Xie, “Research on Accurate Adjustment of Braking Force and Vehicle Yaw Stability Control Strategy Based on New Electro-hydraulic Brake System,” In 2020 4th CAA International Conference on Vehicular Control and Intelligence, pp.374-379, 2020. [https://doi.org/10.1109/CVCI51460.2020.9338551]
• W. Huang, P. Wong, K. Wong, C. Vong and J. Zhao, “Adaptive Neural Control of Vehicle Yaw Stability with Active Front Steering using an Improved Random Projection Neural Network,” Vehicle System Dynamics, Vol.59, No.3, pp.396-414, 2021. [https://doi.org/10.1080/00423114.2019.1690152]
• K. Kim, J. Kim, K. Lee, C. Jung and M. Seo, “A Study on the Stability of Vehicles Considering Tire Characteristics in Brake-in-Turn Maneuvers,” KSAE Spring Conference Proceedings, pp.715-718, 2012.
• B. Sun, T. Zhang, S. Gao, W. Ge and B. Li, “Design of Brake Force Distribution Model for Front-and-Rear-Motor-Drive Electric Vehicle Based on Radial Basis Function,” Archives of Transport, Vol.48, No.4, pp.87-98, 2018. [https://doi.org/10.5604/01.3001.0012.8368]
• S. Ko, C. Song and H. Kim, “Co-operative Control between Motor and Hydraulic Friction Brake to Improve Vehicle Stability for an In-wheel Electric Vehicle,” KSAE Spring Conference Proceedings, pp.1241-1243, 2014.
• E. Joa, K. Yi, K. Sohon and H. Bae, “Four-wheel Independent Brake Control to Limit Tire Slip under Unknown Road Conditions,” Control Engineering Practice, Vol.76, pp.79-95, 2018. [https://doi.org/10.1016/j.conengprac.2018.04.001]
• L, Shuaohua, Y. Shaopu and C. Liqun, “Investigation on Cornering Brake Stability of a Heavy-duty Vehicle based on a Nonlinear Three-directional Coupled Model,” Applied Mathemetical Modelling, Vol.40, pp.6310-6323, 2016. [https://doi.org/10.1016/j.apm.2016.03.001]
• M. Zhileykin and G. Skotnikov, “The Method of Increasing the Stability of Trailer-trucks in Case of Emergency Braking in a Turn and Emergency Failure of the Trailer Brake System,” IOP Conference Series: Materials Science and Engineering, Vol.820, No.1, pp.12-17, 2020. [https://doi.org/10.1088/1757-899X/820/1/012017]
• M. Jang, M. Kim, B. Lee and K. Oh, “Development of a Self-Tuning Based Integral Control Algorithm Using MPC of 4-Wheel Independent Steering System for Braking Stability,” KSAE Fall Conference Proceedings, pp.443-444, 2020.
• X. He, K. Yang, X. Ji, Y. Liu and W. Deng, “Research on Vehicle Stability Control Strategy Based on Integrated-Electro-Hydraulic Brake System,” SAE 2017-01-15865, 2017.
• B. Ren, H. Chen, H. Zhao and L. Yuan, “MPC-based Yaw Stability in In-wheel-motored EV Via Active Front Steering and Motor Torque Distribution,” Mechatronics, Vol.38, pp.103-114, 2016. [https://doi.org/10.1016/j.mechatronics.2015.10.002]
• P. Falcone, H. Tseng, F. Borrelli, J. Agari and D. Hrovat, “MPC-based Yaw and Lateral Stabilisation Via Active Front Steering and Braking,” Vehicle System Dynamics, Vol.46, pp.611-628, 2008. [https://doi.org/10.1080/00423110802018297]
• J. Zhu, Z. Wang, L. Zhang and D. G. Dorrell, “Braking/steering Coordination Control for In-wheel Motor Drive Electric Vehicles based on Nonlinear Model Predictive Control,” Mechanism and Machine Theory, Vol.142, pp.611-628, 2019. [https://doi.org/10.1016/j.mechmachtheory.2019.103586]
• K. Pereida and A. Schoelling, “Adaptive Model Predictive Control for High-Accuracy Trajectory Tracking in Chainging Conditions,” 2018 IEEE/RSJ International Conference on Intelligent Robots and Systmes, pp.7831-78379, 2018. [https://doi.org/10.1109/IROS.2018.8594267]
• T. Song, H. Lee, M. Kim and K. Oh, “A Self-tuning Based Adaptive Model Predictive Control Algorithm for Improving Handling Performance of Four-wheel Independent Steering Vehicles,” Transactions of KSAE, Vol.28, No.8, pp.521-533, 2020. [https://doi.org/10.7467/KSAE.2020.28.8.521]
• L. Tan, S. Yu, Y. Guo and H. Chen, “Sliding-mode Control of Four Wheel Steering Systems,” 2017 IEEE International Conference on Mechatronics and Automation, pp.1250-1255, 2017. [https://doi.org/10.1109/ICMA.2017.8015996]