기계 학습을 활용한 구동 토크 예측 기반 차량 속도 프로파일 최적화
 ; Gihoon Kim2)
; Gihoon Kim2) ; Yoonyong Ahn2)
; Yoonyong Ahn2) ; Jihoon Sung2)
; Jihoon Sung2) ; Seokhun Choi2)
; Seokhun Choi2) ; Youngho Jun3)
; Youngho Jun3) ; Kunsoo Huh*, 2)
; Kunsoo Huh*, 2)
Copyright Ⓒ 2022 KSAE / 199-08
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
A number of studies have been proposed in order to obtain the optimal vehicle speed profile for a given route based on dynamic programming(DP). In general, solving optimization problems requires a vehicle dynamics model to accurately calculate energy consumption. However, this model cannot exactly reflect the real characteristics of various vehicles because of the nonlinearity of the rolling resistance, air resistance, and gradient resistance. Therefore, this study proposes vehicle speed optimization by using a machine learning network model that is trained from actual vehicle driving data. The performance of the proposed method is verified by simulation where the driving environment is duplicated corresponding to real driving conditions. The effectiveness of the proposed optimal speed profile is evaluated by comparing with conventional cruise control driving. As a result, driving with the optimal speed profile for a given route of 27.3 km significantly reduces battery energy consumption by 8.4 %.
Keywords:
Machine learning, Road-load, Optimal control, Dynamic programming, Electric vehicle, Eco drive키워드:
기계 학습, 주행 저항, 최적 제어, 동적계획법, 전기 자동차, 에코 드라이브1. 서 론
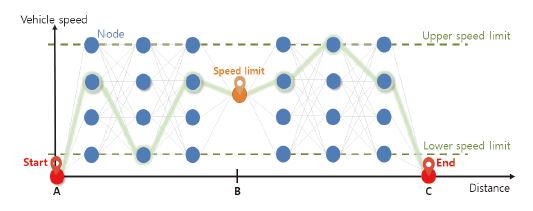
차량 주행 개선을 위한 주행 데이터, 도로/교통 인프라 정보 등을 활용한 차량 속도 최적화 기술은 연료 소비율/에너지 효율 그리고 동시에 주행 안전성까지 향상 시킬 수 있어 모빌리티 산업의 새로운 패러다임으로 제시되고 있다. 특히, 대중교통, 운송 차량 같이 동일한 경로를 반복적으로 주행하는 목적 기반 차량(PBV, Purpose Built Vehicle)에서 그 효과는 더욱 두드러지게 나타나며, 주행 구간에서 소모되는 에너지 총량을 보다 정확하게 예측할 수 있어 에너지 관리 측면에서도 이점을 갖는다.1) 효율적인 에너지 소비를 위한 최적 속도 프로파일은 노면 상태, 도로 구배, 교통 체증 등 여러 요인에 영향을 받을 수 있기 때문에 높은 연산 능력을 지닌 대용량 클라우드 시스템에서 주행 도로 형상 및 교통 상황을 고려한 집약적인 데이터 처리가 필요하다.2,3) 또한, 교통 체증과 다른 운전자의 행동과 같이 연료 소비와 차량의 이동시간에 큰 영향을 끼치는 인자들의 변동성을 확률적으로 고려하거나 주행 중인 차량의 시간과 위치에 따른 교통 신호 시스템과 도로의 고도와 곡률 역시 고려하여 주행을 개선할 수 있다.4-6) 이와 같은 빅 데이터, 기계 학습, 최적화 이론을 활용한 주행 개선 알고리즘은 실차 주행 혹은 시뮬레이션으로 검증된다. 최적화 문제를 풀기 위한 방법으로는 Dynamic Programming(동적계획법, 이하 DP)과 Pontryagin’s Minimum Principle(폰트리아긴 최소화 원리, 이하 PMP)가 주로 활용된다. DP의 경우 PMP에 비해 계산량이 많으나 전역 최적화가 가능하다. 반면, PMP의 경우 계산량이 DP에 비해 적으나 전역 최적화가 아닌 지역 최적화만 가능하다. 본 연구에서는 DP를 활용해 차량의 주행을 개선한다. DP를 활용한 최적 속도 프로파일 도출 알고리즘에 대한 개략도는 Fig. 1과 같다.
종방향 차량 동역학 모델을 통해 계산된 구동 토크를 활용하여 노드 간 이동에 필요한 에너지양과 구간별 소요시간을 고려한 목적함수를 설정한다. 그리고 DP를 이용해 시작점(Fig. 1 A지점)부터 도착점(Fig. 1 C지점)까지 목적함수의 총합이 최소가 되는 전역 최적 속도 프로파일을 도출한다. 그러나 종방향 차량 동역학 모델을 활용하여 도출한 구동 토크는 구름 저항, 공기 저항 그리고 구배 저항의 비선형성 때문에, 실차 주행을 통해 계측한 구동 토크와 비교하여 큰 오차를 갖는다. 그러므로 본 연구에서는 보다 정확한 에너지 소모량 계산을 위해 실차 주행 데이터로 학습된 구동 토크를 예측할 수 있는 기계 학습 네트워크 모델을 제안한다.7) 그리고 제안한 네트워크 모델로 예측된 구동 토크와 종방향 차량 동역학 모델로 도출된 구동 토크를 실차 데이터를 이용해 비교하여 네트워크 모델의 타당성을 검증한다.
최종적으로, 기계 학습 모델이 적용된 DP 연산의 성능평가를 위하여 실차와 동일한 주행 환경을 시뮬레이션 상에 구현한다. DP 연산에 도로의 곡률에 따른 요-레이트(Yaw-rate) 제한, 급 가/감속 제한, 과속 단속 카메라에 의한 속도 제한 등 여러 제한조건을 적용하여 도로 상황 및 주행 안정성을 확보한 최적 속도 프로파일을 도출한다. 도출된 최적 속도 프로파일은 일반 정속주행(Cruise control)한 대조군과 비교하여 본 연구의 효용성을 검증한다.
2. 기계 학습 네트워크 구축
2.1 데이터 세트(Data Set) 제작
기계 학습을 위한 데이터 세트 제작을 위해 현대 자동차의 아이오닉 EV(AE)8)의 주행 데이터를 CAN 통신과 GPS를 이용해 취득하였다(자동차안전연구원(KATRI) Proving ground 주행 데이터, 용산역에서 현대케피코까지의 실도로 주행 데이터 취득).
취득한 데이터는 MATLAB/Simulink를 활용하여, 샘플링 타임 조절 및 노이즈 필터링을 진행한다. 전처리가 완료된 데이터 세트들은 기계 학습의 성능을 확인하기 위해 무작위로 선정한 테스트 세트(TestX, TestY)와 이를 제외한 네트워크에 학습시킬 트레이닝 세트(TrainX, TrainY)로 분류한다.
2.2 기계 학습 네트워크
종방향 차량 동역학 모델은 동력원으로부터 동력 전달 계통을 통해 차량 바퀴(Drive wheel)에서 발생되는 구동력과 차량이 외부로 부터 받는 저항력으로 구분된다. 종방향 차량 동역학 모델을 통해 도출되는 구동 토크는 식 (1) ~ (6)으로 표현된다. 결론적으로 구동 토크는 가속도, 속도, 도로 구배에 의한 함수로 표현된다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
위 수식에서 υ는 차량 속도, Ftrac은 구동력, Froll은 구름 저항, Faero은 공기 저항, Fgrade은 구배 저항, Fbreak은 제동력, m은 차량 등가 질량, ηγ은 감속 기어 효율, γfd은 감속 기어비, Rwh은 휠 동반경, Ttrac은 구동 토크, Tmotor은 모터 토크, α는 도로 구배, r0, r1은 구배 저항 계수, Af는 차량 면적, Cd는 항력 계수 그리고 ρ는 공기 밀도이다.
종방향 차량 동역학식에 의거하여 구동 토크 예측을 위한 네트워크 모델에 차량의 속도 그리고 주행 구배를 입력인자로 선정하였다. 가속도의 경우 값이 작을 때, 노이즈로 인한 부호의 변화 등으로 예측 성능에 부정적인 영향을 미칠 수 있다. 따라서 가속도 값 대신 속도의 과거 값을 누적하여 사용함으로써 가속도의 성분을 네트워크가 유추할 수 있게 하였다. 이와 같은 방법으로 가속도의 변화가 작은 경우에도 구동 토크 예측 성능을 향상시킬 수 있다. 구동 토크를 예측하기 위해 사용한 네트워크 모델은 식 (7)과 같이 표현된다.
| (7) |
여기서 g는 시계열 데이터를 입력으로 받는 네트워크 모델이며, υ는 차량의 종방향 속도, α는 구배, h는 데이터를 쌓는 크기(Stack size)이고 t는 시간, Ttrac은 구동 토크를 의미한다.
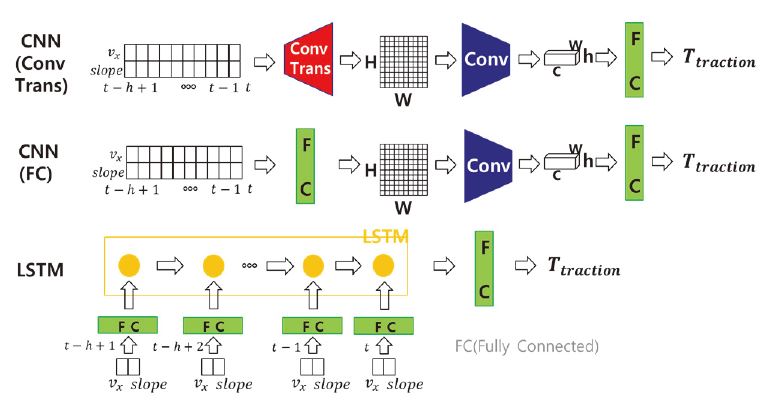
본 연구에서는 네트워크 모델 g의 후보를 CNN과 LSTM을 사용하고, CNN의 경우는 시계열 데이터를 2D-Array 형태로 가공하여 사용하였다(Fig. 2 참조).
2.3 네트워크 성능 비교 결과
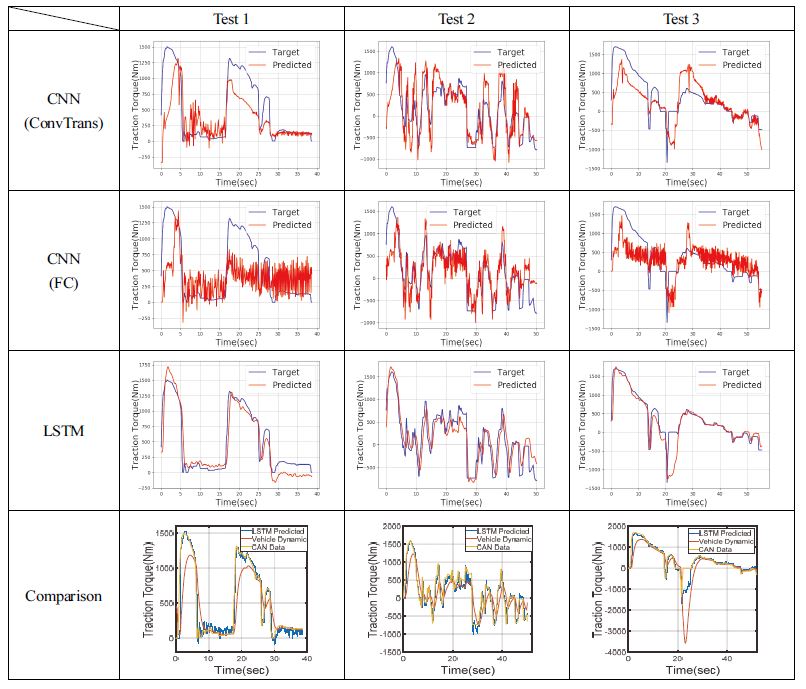
네트워크 성능 비교는 취득한 23개의 데이터들 중 학습에 사용하지 않은 3개의 데이터로 진행한다. Fig. 3은 네트워크 모델 별 구동 토크 예측 결과를 비교한 것이다. 네트워크의 입력은 과거 1초(h=10step)동안의 속도 및 구배 데이터이고, 출력은 구동 토크이다. 여기서 FC와 Conv Trans는 쌓아준 속도와 구배의 2행 데이터를 H행, W열 데이터로 확장시키는 과정에 차이가 있다. CNN(FC)가 예측 결과에 노이즈가 가장 많고 오차가 심하였다. CNN(Conv Trans)는 노이즈는 CNN(FC)에 비하여 줄었으나 부정확한 예측을 하는 곳이 존재한다. 반면, LSTM의 경우 예측 결과가 상대적으로 우수하였다. LSTM은 시계열 데이터의 처리에 강점이 있는 RNN을 개선한 모델이다. RNN의 경우 과거의 데이터를 은닉층에 저장하는 특징을 갖지만, Long-term dependency(장기 의존성) 문제로 과거의 데이터를 충분히 활용할 수 없는 한계가 있다. LSTM은 RNN과 달리 장기적으로 기억할 데이터와 단기적으로 기억할 데이터를 구분함으로써 중요한 과거 데이터를 충분히 활용할 수 있도록 한 구조이다. 본 연구에서는 구동토크 예측 성능이 가장 우수한 LSTM을 선정하여 네트워크 모델을 개발하였다.
2.4 기계 학습 사용 타당성 검증
일반적으로 차량 주행 에너지 소모량 예측은 종방향 차량 동역학 모델 기반이 사용된다. 그러나 동역학 모델 기반으로 도출한 구동 토크는 구름 저항, 공기 저항 그리고 구배 저항의 비선형적 특성 때문에 정확한 예측에 한계가 있다. 실차를 활용한 종방향 동역학 식 기반과 기계 학습을 활용한 요구 구동 토크 예측 비교 결과 그래프는 Fig. 3의 Comparison 부분과 같다.
차량 동역학 모델 기반으로 구동 토크의 값을 정확하게 예측하기 위해서는 구동 토크의 비선형 특성을 반영한 차량 동역학 모델이 필요하고, 차량의 내구가 진행됨에 따라 변화하는 차량 특성 인자가 동역학 모델에 반영되어야 하는 어려움이 있다. 반면, 기계 학습의 경우에는 주행 데이터를 이용하여 학습이 진행되므로, 누적되는 데이터를 통해 비선형성과 내구에 의한 인자 변화의 특성을 반영할 수 있어, 수식 기반의 동역학 모델 보다 상대적으로 유효한 결과를 도출할 수 있다. Test 3의 구동 토크가 급감하는 부분은 제동 성능 확인을 위한 주행을 한 부분으로 통상적인 주행과는 별개의 경우로 볼 수 있다. 그럼에도, 통상 주행이 아닌 경우 역시 동역학 모델에 비해서는 기계 학습 모델이 실측값에 근접한 것을 확인할 수 있다.
3. 최적 속도 프로파일 도출
3.1 동적 계획법
DP는 리처드 벨만(Richard E. Bellman)의 최적성의 원리(Principle of Optimality)에 근거하여 복잡한 시스템을 여러 개의 하위 시스템으로 나누어 문제를 해결하기 위한 모든 방법을 검토하고, 도출된 값을 결합하여 전체시스템의 최적 해를 구하는 해석기법이다. 일반적인 DP를 통한 최적화 문제는 식 (8)로 표현된다.
| (8) |
DP는 전역 최적값을 계산하기 위해, 다음 step에서 최종 step까지의 최적값을 참고하는 방법으로 진행되기 때문에 중복 계산을 피할 수 있다는 장점을 갖고 있다. 여기서 xk는 k step에서의 상태(State), uk는 k step에서의 입력, 는 k step에서 최종지점 N step까지의 최적값, Jk,k+1는 k step에서 k+1 step까지의 목적함수 값을 의미한다.
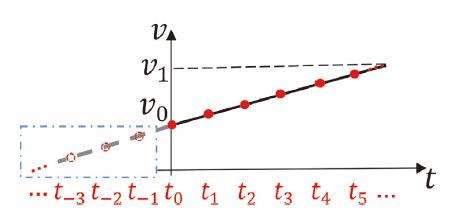
3.2 상태 이산화 그래프
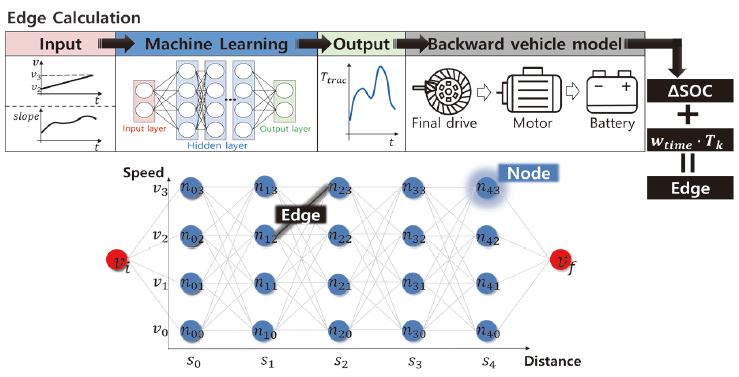
DP를 사용하기 위해서는 상태 이산화가 먼저 진행되어야 한다. 상태는 지점(Station)과 속도로 구성되며, 일정 간격으로 이산화한다. 이에 따라, x축은 지점, y축은 속도를 의미하는 그래프를 구성한다. 이산화된 각 상태는 원으로 표시되고(이하 노드(Node)) 각 노드와 노드를 잇는 선은(이하 Edge) 해당 구간을 지나는 동안의 목적함수 값을 의미한다(Fig. 4 참조). Edge는 우측의 방향성만을 가지며, 시작점부터 도착점까지의 Edge의 총합을 최소화하는 방향으로 최적화를 진행한다.
3.3 목적함수
DP에 사용될 목적함수는 노드와 다음 노드의 구간을 주행하며 소모되는 SOC(State Of Charge)와 소요되는 시간으로 구성된다. SOC 소모는 구동 토크 값에 지배적으로 결정되며, 본 연구에서 구동 토크는 기계 학습 네트워크를 통하여 예측한 값을 사용한다. 노드 간 이동은 등가속도 모델을 가정하여 속도 프로파일을 구한다. x축 방향 노드는 일정한 거리로 이산화했으므로, 노드 간 이동 시 걸리는 시간과 시간에 따른 이동 지점을 알 수 있고, 이에 따라 구배 프로파일을 네트워크의 입력으로 사용할 수 있다. 이후, Fig. 4와 같이 예측한 구동 토크로부터 SOC 소모 추정 모델을 사용하여 노드 간 이동에 필요한 에너지 소모량을 구한다. 본 연구에서 SOC 소모 추정 모델은 식 (9)로 표현되는 전류 적산법(Coulomb counting method)을 사용한다.
| (9) |
여기서 SOC0는 초기 시간 t0에서의 SOC, CN은 정격용량, t는 시간, η는 쿨롱 효율, I는 전류를 의미한다. 이 때, 초기 1초의 입력(h=10step)에 대해서는 구동 토크 예측 시 네트워크 입력으로 들어갈 초기 과거 데이터가 충분하지 않다. 그러므로 Fig. 5와 같이 미소 구간동안의 가속도는 일정하다는 가정을 통해, 부족한 과거 데이터를 생성한다. 유사한 방법으로 구배는 현재의 구배를 연장하여 사용한다.
SOC 소모만을 고려한 목적함수 사용 시 해당 값을 최소화하기 위해 저속으로만 주행하는 속도 프로파일이 생성되는 문제가 발생한다. 이를 해결하기 위해 식 (10)과 같이 목적함수에 주행시간을 고려한 항을 추가한다.
| (10) |
여기서 ΔSOCk는 SOC 소모량, wtime은 시간에 대한 가중치, Tk는 주행시간이다. 주행시간은 구간 이동거리와 평균속도에 의해 계산이 이뤄진다. 주행시간과 가중치를 곱한 항을 목적함수에 추가함으로써 주행 목적에 따라 가중치를 높여 주행시간에 비중을 더 크게 주거나, 가중치를 낮춰 적극적으로 전비 개선을 위한 주행을 할 수 있다.
3.4 제한 조건
최적 속도 프로파일을 도출 시 여러 제한조건을 고려할 수 있다. 본 연구에서는 주행구간의 도로 정보를 알고 있다는 가정 하에 구간별로 제한속도를 설정한다. 이는 과속카메라의 존재 혹은 구간별 교통상황에 의하여 결정된다. 주행 안정성을 위해서는 가속도와 요레이트(Yaw rate, ) 제한을 설정한다. 또한, 시작 지점과 도착 지점에서의 정차를 위한 제한조건을 추가한다. 언급한 모든 제한 조건들을 식으로 나타내면 식 (11)과 같다.
| (11) |
여기서 k는 step, υ는 차량속도, ds는 이산화한 지점간의 거리, R은 곡률반지름, N은 최종 지점 step을 의미한다.
4. 최적 주행 시뮬레이션
4.1 시뮬레이션 환경 구축
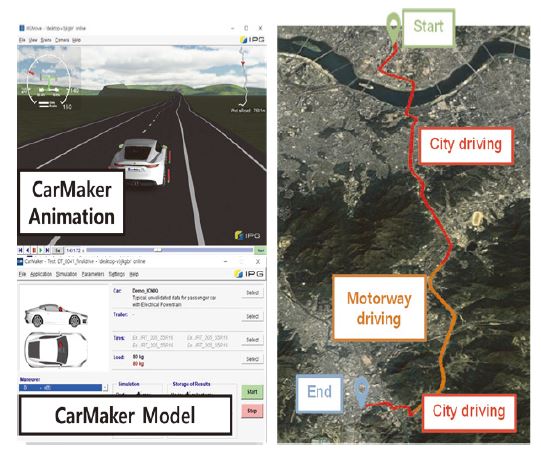
시뮬레이션 환경은 구글어스9)와 IPG사의 CarMaker를 활용한다. 용산역에서 현대케피코까지의 약 27.3 km의 도로를 실제 차량 주행을 통해 얻은 GPS 데이터를 활용하여 시뮬레이션 환경을 구축한다(Fig. 6 참조). 과속 단속 카메라들의 정보는 공공데이터 포털10)을 활용하였다.
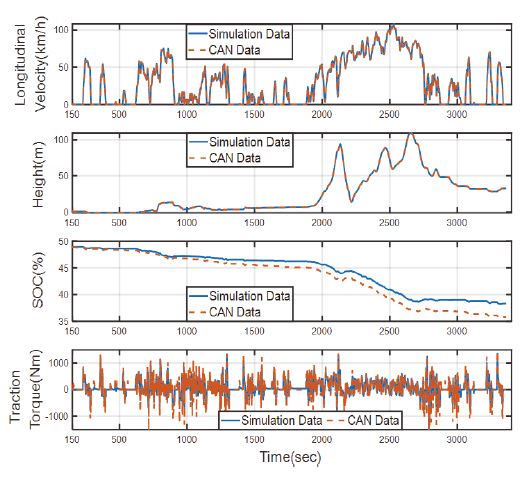
시뮬레이션에 사용된 차량 모델링은 아이오닉 EV(AE) 제원8)과 모터 특성 데이터를 활용하였다. 또한, 2장에서 언급한 실제 차량의 주행데이터와 동일한 성능의 차량이 시뮬레이션 상에서 주행될 수 있도록 CarMaker 내에서 파라미터를 보정하였다. Fig. 7에서 나타내는 바와 같이 차량모델이 실차 주행 데이터의 속도를 추종하기 위해 실차와 동일한 구동 토크가 발생하는 것을 확인할 수 있다. 여기서 SOC 소모량은 전장 부하에 의한 에너지 소모와 효율성 등은 고려하지 않았다.
4.2 최적 주행 시뮬레이션 결과
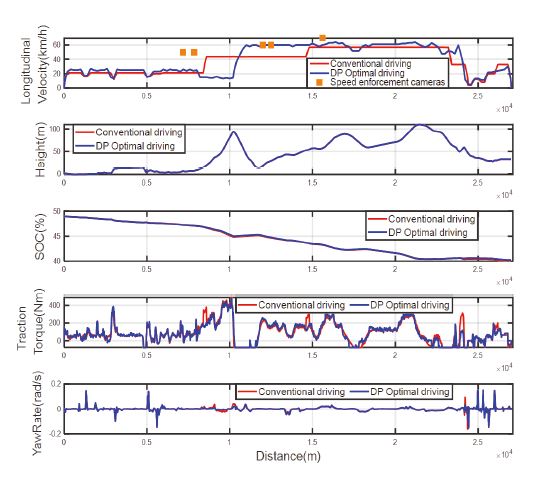
목적함수의 가중치 계수와 상태 이산화 그래프의 이산화 정도에 따라 차량의 최적 속도 프로파일은 다르게 도출된다. 본 장에서 분석할 시뮬레이션 대표 케이스는 신호 체계가 없는 전용도로를 주행하는 목적 기반 차량과 유사한 운송수단을 가정한다. 이를 고려하여, 대표 케이스의 상태 이산화 그래프는 x축(지점)은 200 m, y축(속도)는 1 km/h 간격으로 이산화하였다. Fig. 8은 시뮬레이션 상에 구축된 도로 약 27.3 km를 본 연구에서 제안한 방식으로 도출한 최적 속도 프로파일로 주행한 결과이다. 정속 주행 결과와 비교하기 위해, 동일한 교통 상황과 요레이트를 고려하고, 총 주행 시간이 58분으로 일치하도록 대조군을 설정하였다. 시뮬레이션 결과, 최적 속도 프로파일 주행을 통해 대조군 대비 배터리 에너지 사용량을 2,510 Wh에서 2,300 Wh로 감소시켜 약 8.4 %의 에너지를 절약한 효율적인 전비 주행을 하였다.
주행구간의 특성에 따른 속도 제한조건은 Table 1과 같다.
주행 안정성 확보를 위한 가속도 및 요레이트 제한조건은 Table 2와 같다.
5. 결 론
본 연구에서는 차량의 주행을 개선하기 위해 기계 학습을 통해 구동 토크를 예측하고, 이를 활용해 최적 속도 프로파일을 도출하고 시뮬레이션을 통해 본 연구의 효용성을 검증하였다. 최종적으로 정리된 연구 결과는 아래와 같다.
- 1)구동 토크 예측을 위해, CNN(Conv Trans), CNN(FC) 그리고 LSTM의 네트워크 모델을 구현하고, 기계 학습 네트워크 예측 성능을 평균 제곱근 오차를 통해 비교하였다.
- 2)차량 동역학 수식에 기반한 구동 토크 예측 모델은 인자들의 비선형 특성과 차량의 내구에 의한 차량 특성 변화 때문에 정확한 구동 토크 예측에 한계가 있다. 반면, 본 연구에서 제시하는 기계 학습 모델은 주행 데이터를 이용하여 학습이 진행되므로, 누적되는 데이터를 통해 비선형성과 내구에 의한 인자 변화의 특성을 반영할 수 있어, 보다 정확한 구동 토크 예측이 가능한 것을 확인하였다.
- 3)CarMaker와 MATLAB/Simulink를 활용하여 시뮬레이션 환경을 구축하고, 전비 성능 평가 시뮬레이션을 수행하였다.
- 4)시뮬레이션 결과, DP를 통한 최적 속도 프로파일 도출로 주행 구배가 고려되어 상승경사에서는 감속하고, 하강경사에서 선제적으로 속도를 상승시키는 방법으로 도로의 지리적 특성이 반영된 최적 속도 프로파일이 도출되었다.
- 5)DP를 통한 최적 속도 프로파일 도출 과정에서 과속 단속 카메라와 도로 교통 상황에 따른 속도 제한을 적용하여 교통 인프라와 연계된 속도 프로파일을 도출할 수 있었고, 도로의 곡률에 대한 요레이트 제한, 급 가/감속 제한 등의 제한조건을 추가하여 차량의 주행 안정성과 승차감을 확보한 최적 속도 프로파일을 도출할 수 있다.
- 6)최종적으로, 동일한 시간 동안 주행하는 최적 속도 주행과 정속 주행(Cruise Control)의 시뮬레이션 비교 평가 결과, 최적 속도 주행 결과의 전비가 약 8.4 % 상승하는 것을 확인하였다.
본 연구에서는 시뮬레이션 상의 최적 속도 프로파일을 DP를 통해 도출하였다. 하지만, 실제 주행에서의 DP는 연산 속도에 제한이 있기 때문에 주행 구간이 길어지면 특정 구간 별로 나누어야 한다. 또한, 전역 최적화는 불가능하나 DP에 비해 계산량이 적은 PMP를 향후 연구에 고려하여 실제 차량 주행을 통한 최적 속도 프로파일 도출과 실제 차량 주행의 에너지 소모량 개선 효과를 검증할 계획이다.
Nomenclature
| a : | acceleration, m/s2 |
| v : | velocity, m/s |
| α : | road slope, rad |
| R : | radius of curvature, 1/m |
Subscripts
| h : | stack size |
| t : | time |
| k : | step |
Acknowledgments
A part of this paper was presented at the KSAE 2021 Fall Conference and Exhibition
본 연구는 “현대자동차그룹의 재원”으로 지원받아 수행된 연구임.
References
-
A. Sciarretta, G. De Nunzio and L. L. Ojeda, “Optimal Ecodriving Control: Energy-Efficient Driving of Road Vehicles as an Optimal Control Problem,” IEEE Control Systems Magazine, Vol.35, No.5, pp.71-90, 2015.
[https://doi.org/10.1109/MCS.2015.2449688]

-
P. Olin, K. Aggoune, L. Tang, K. Confer and J. Kirwan, “Reducing Fuel Consumption by Using Information from Connected and Automated Vehicle Modules to Optimize Propulsion System Control,” SAE 2019-01-1213, 2019.
[https://doi.org/10.4271/2019-01-1213]

-
E. Ozatay, S. Onori, J. Wollaeger, U. Ozguner, G. Rizzoni, D. Filev, J. Michelini and S. D. Cairano, “Cloud-Based Velocity Profile Optimization for Everyday Driving: A Dynamic-Programming-Based Solution,” IEEE Transactions on Intelligent Transportation Systems, Vol.15, No.6, pp.2491-2505, 2014.
[https://doi.org/10.1109/TITS.2014.2319812]

-
K. Kim, C. Kang, W. Lim and S. Cha, “Optimization of Vehicle Speed in Urban Road Using Dynamic Programming,” Transactions of KSAE, Vol.27, No.9, pp.687-692, 2019.
[https://doi.org/10.7467/KSAE.2019.27.9.687]

- S. Choi and J. Lee, “Fuel Economy Improvement Cruise Control Algorithm Using Distance and Altitude Data of GPS in Expressway,” Transactions of KSAE, Vol.19, No.6, pp.68-75, 2011.
-
U. Vögele and C. Endisch, “Predictive Vehicle Velocity Control Using Dynamic Traffic Information,” SAE 2016-01-0121, 2016.
[https://doi.org/10.4271/2016-01-0121]

- B. Kim, G. Kim, Y. Ahn, J. Sung, S. Choi, Y. Jun and K. Huh, “Vehicle Speed Optimization Based on Predicted Traction Torque with Machine Learning,” KSAE Fall Conference Proceedings, pp.40-43, 2021.
-
D. Park, H. Song, D. Shin and N. Kim, “Performance Analysis of Electric Drive System on Hyundai Ioniq EV,” Transactions of KSAE, Vol.27, No.1, pp.69-76, 2019.
[https://doi.org/10.7467/KSAE.2019.27.1.069]

- Google, Google Earth, https://earth.google.com, /, 2021.
- Public Data Portal, https://www.data.go.kr, /, 2021.