회전저항 감소를 고려한 비공기입 타이어 형상 최적설계에 관한 연구

1. 서 론

비공기입 타이어(NPTs)는 경량화 및 유지보수성을 높일 수 있는 차세대 미래형 타이어로 주목 받고 있으며, 특히, 공기압의 유지 관리, 런 플랫(Run-flat) 및 실란트(Sealant) 기능이 필요 없으며, 주행 중 펑크로 인한 사고의 위험성이 없다는 장점들 때문이다.¹⁾ 비공기입 타이어는 단순화된 제조 공정으로 비교적 에너지 손실이 적은 재료를 활용하기 때문에 회전저항 줄이고, 연비 효율을 높일 수 있어 환경적 측면에서도 장점이 있다.

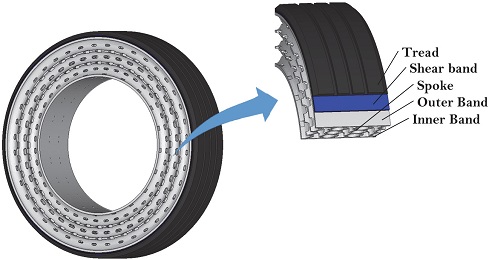
비공기입 타이어의 구조는 Fig. 1에 도시된 바와 같이 타이어와 동일한 기능과 형상을 가지는 트레드, 강철선의 벨트와 유사한 기능과 재료로 이루어진 전단 밴드(Shear band), 하중을 지지하는 스포크(Spoke), 이를 연결하는 외측 밴드(Outer band) 및 내측 밴드(Inner band)로 구성된다. 공기압의 역할을 대신하는 스포크는 설계에 따라 다양한 형상으로 설계가 가능하며, 그에 따라 비공기입 타이어의 성능이 변화되거나 결정된다.²⁾ 즉, 스포크 구조는 비공기입 타이어의 중요한 설계요소이다.

Fig. 1

Structure of Non-pneumatic tire with honeycomb spoke

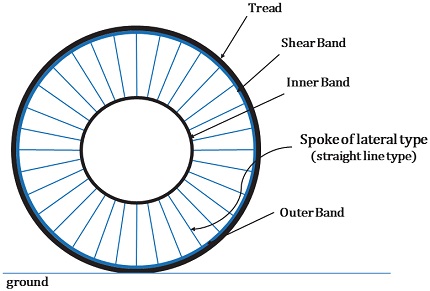
현재 승용차용 비공기입 타이어를 개발하는 연구자들은 스포크의 구조 설계를 통한 강성, 소음, 진동, 회전저항 등의 성능을 높임으로써 승용차에 적용할 수 있는 특성 연구를 집중적으로 수행해왔다. 특히, 타이어 라벨 제도의 시행으로 에너지 효율 등급을 만족하는 타이어만이 상용화가 될 수 있기 때문에 회전저항 성능을 선제적으로 개선하기 위한 연구가 우선시 되었다. Jin 등³⁾은 3가지 형상의 벌집형 구조(Honycomb structure)의 스포크를 갖는 비공기입 타이어를 대상으로 동적 거동 해석(Transient analysis)를 수행하였다. 그 결과 벌집형 셀(Honeycomb cell)의 각도 변화에 따라 스포크의 변형이 작을수록 회전저항이 개선된다는 결과를 해석적으로 확인하였다. 하지만 단일 요인에 의해서만 회전저항을 고려하였기 때문에 스포크의 복잡한 구조적 특성을 반영해서 여러 인자들을 복합적으로 고려하는 연구를 수행할 필요가 있다. 이에 Veeranurthy 등⁴⁾은 Fig. 2와 같이 측면형 일자 스포크를 대상으로 회전저항을 최소화하기 위한 최적설계를 진행했다. 스포크의 두께 및 곡률반경을 설계 변수로 선정했으며 2D 동적 거동 해석을 기반으로 DOE와 RSM(Response Surface Method)을 활용한 최적설계를 수행하였다. 그 결과 스포크의 두께와 전단 밴드의 두께가 두꺼워 질수록 회전저항이 감소한다는 사실을 해석적으로 밝혀냈다. Veeranurthy 등⁴⁾의 연구에서 제안하는 스포크 구조는 Fig. 2와 같이 타이어의 원주방향으로 스포크가 연속적이지 못하기 때문에 고속 주행 시 소음진동에 취약할 수 있다. 또한, 선행 연구들의 해석 기법은 과도한 해석 시간을 요하는 동적 거동 해석 기법을 활용하고 있기 때문에 해석을 기반으로 DOE를 활용하는 연구에서는 해석 시간이 오래 걸리는 단점이 있다. 최근 타이어 해석에서는 해석 시간을 보다 효율적으로 활용하고자 정상상태 회전(Steady State Rolling, SSR) 해석 기법을 활용한다. 김성래 등⁵⁾은 SSR 해석 기법을 활용하여 공기압 타이어의 회전저항을 해석적으로 평가하고, 실제 회전저항 시험과 비교 검증을 통해 SSR 해석 기법의 신뢰성을 확인한 바 있다.

Fig. 2

Non-pneumatic tire of spoke with type of straight line

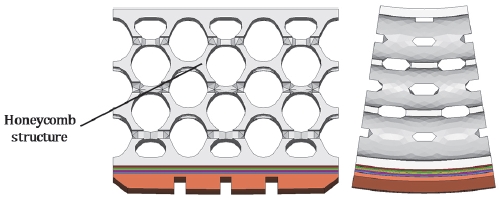
본 연구에서는 Fig. 3과 같이 측면형 스포크의 단점을 개선하고자 원주 방향으로는 벌집형 구조를 갖고, 측면에는 주기적인 타원형 구멍을 갖는 혼합형 스포크 구조를 제안한다. 제안한 비공기입 타이어의 회전저항을 평가하기 위해 SSR 해석 기법을 활용한 유한요소해석 모델을 구축하고, 회전저항 시험 데이터와 비교하여 해석 기법의 신뢰성까지 확보하고자 한다. 최종적으로, 구축된 해석모델을 활용하여 DOE를 통한 스포크의 구조 최적설계를 수행하고 회전저항 저감을 할 수 있는 설계의 방향성을 제안한다.

Fig. 3

Section of Non-pneumatic tire with honeycomb spoke of mixed type

2. 회전저항 시험

유한요소해석을 활용한 비공기입 타이어의 회전저항 해석 기법을 제안하고, 해석 모델의 신뢰성을 확보을 위해 회전저항 시험을 수행한다. 회전저항 시험은 ISO(International Standard Organization)에서 규정한 ISO28580(Passenger car, truck and bus tyre rolling resistance measurement method)에 명시된 시험법으로 수행하며, 시험 조건은 Table 1과 같다.

Table 1

Operating conditions of rolling resistance test

회전저항 계산법으로는 힘법(Force method), 토크법(Torque method) 및 동력법(Power method) 등이 있으며, 본 연구에서는 힘법을 적용한다. 힘법을 이용한 회전저항 측정은 이미 선행 연구들에서 공기압 타이어의 회전저항 측정을 위해 사용되어오던 검증된 방법이다.^5,6)

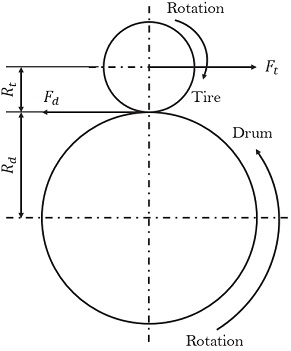
회전저항 산출 과정은 Fig. 4에 도시된 바와 같이 시험 중 타이어의 회전축에서 발생하는 반력(F_t)을 측정하여 식 (1)에 의해 드럼과 타이어의 접촉면에서의 회전저항(F_d)으로 계산한다. 하지만, 실제 타이어의 회전저항은 평면상에서 발생하기 때문에 드럼의 곡면 상에서의 회전저항과 차이가 존재한다. 따라서, 식 (2)를 통해 곡면상의 회전저항(F_d)을 평면상의 회전저항(F_rf)으로 계산한다. 최종적으로 식 (3)을 통해 시험 하중 값으로 나눈 회전저항 계수(RR_c)를 산출하여 회전저항을 평가한다.

• where F_d : reaction force in a drum surface (N)
• 　　　F_t : reaction force in a center of tire (N)
• 　　　F_rf : rolling resistance force (N)
• 　　　F_z : test load (kN)
• 　　　R_t : dynamic loaded radius (m)
• 　　　R_d : radius of a drum (m)
• 　　　RR_c : rolling resistance coefficient

Fig. 4

Force method for measurement of rolling resistance in a drum

3. 유한요소해석을 이용한 비공기입 타이어의 회전저항 해석 및 평가

본 절에서는 SSR해석 기법을 활용한 회전저항 해석 기법을 제안하고, 해석 기법의 신뢰성을 확보하고자 초탄성 및 점탄성의 비선형 재료의 물성 모델을 고려하여 접지압 특성의 시험⋅해석 결과를 비교하고자 한다.

3.1 스포크 및 트레드의 물성 모델

3.1.1 초탄성 물성 모델

스포크의 재료는 폴리에스터계 열가소성 탄성체(Thermoplastic Polyether-Ester Elastomer)인 TPEE를 사용한다. TPEE 재료의 기계적 물성 특성을 유한요소해석 모델에 반영하고자 단축 인장 시험을 수행하여 응력-변형률 데이터를 확보하고, 해석 상용 프로그램 ABAQUS의 비선형 물성 평가 기능을 활용하여 스포크의 초탄성 물성 모델을 선정한다. 본 연구에서는 Ogden 모델을 적용하고자 한다. 식 (4)는 Ogden 초탄성 모델 함수이며, Table 2는 Ogden 재료 상수를 명시하고 있다.

$\[ W\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\sum _{i=1}^N\frac{{\mu }_i}{{\alpha }_i}\left({\lambda }_1^{{\alpha }_i},{\lambda }_2^{{\alpha }_i},{\lambda }_3^{{\alpha }_i}-3\right) \]$

(4)

• where W : strain energy density
• 　　　μ_i, α_i : coefficients of material
• 　　　λ_1,2,3 : principal stretches
• 　　　N : the number of set of coefficients

Table 2

Coefficients of equation (4) for TPEE

동일한 방법으로 트레드 고무 재료는 Ogden 초탄성 물성 모델을 선정하여 유한요소해석 모델에 적용하고자 한다. 트레드의 재료 상수는 Table 3과 같다.

Table 3

Coefficients of equation (4) for a rubber

3.1.2 점탄성 물성 모델

비공기입 타이어의 히스테리시스 손실로 인해 발생하는 회전저항을 해석적으로 구현하기 위해서는 재료의 점탄성 물성 데이터가 필요하다. 이를 위해, 시간 영역에서 스포크 재료인 TPEE와 트레드 고무의 응력 완화(Stress-relaxation) 데이터를 측정하고자 한다.⁷⁾ 측정된 데이터는 프로니 급수(Prony series) 함수의 커브 피팅(Curve fitting)을 통한 점탄성 재료 상수를 산출하여 스포크와 트레드의 유한요소해석 모델에 적용한다. 식 (5)는 프로니 급수로 표현된 시간 영역에서의 응력 완화 함수이고, Table 4는 프로니 상수이다.⁸⁾

$\[ g_R\left(t\right)=1-\sum _{i=1}^N\overline{g_i^p}\left(1-e^{-\frac{t}{{\tau }_i^G}}\right) \]$

(5)

• where g_R : stress
• 　　　$$ g_i^P$$, $$ {\tau }_i^G$$ : prony coefficients
• 　　　t : time

Table 4

Coefficients of equation (5) for TPEE and a rubber

3.2 비공기입 타이어의 해석 모델

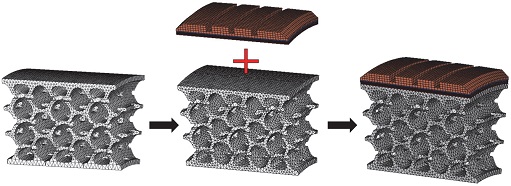
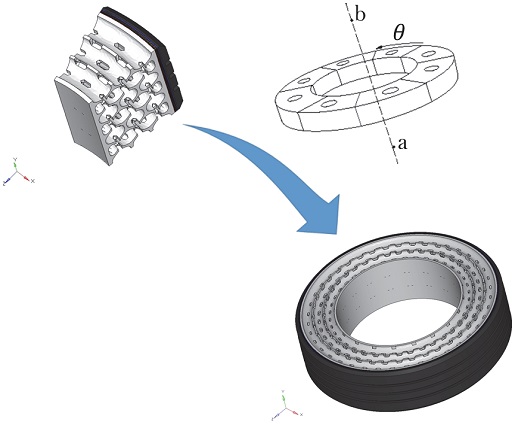
본 절에서는 비공기입 타이어의 유한요소해석 모델 구축에 관해 서술하고자 한다. 비공기입 타이어의 전체적인 구조는 타이어의 회전축을 기준으로 축 대칭 형상을 갖는다. 스포크 구조는 원주방향으로 벌집형 구조를 가지며, 측면에는 주행 중 발생하는 타이어의 발열로 인한 성능 저하를 방지하기 위해 타원형의 구멍이 주기적으로 위치한 대칭구조이다. 이와 같은 특징을 이용하여 Figs. 5, 6에 도시된 바와 같이 모델 구축 시 전체 360°중 일부분(18°, Degree)을 3D 유한요소 모델로 구축한 후 점 a와 b로 연결된 타이어의 회전축을 기준으로 360°회전시켜 비공기입 타이어의 전체 3D 모델을 구축하는 과정을 거친다. 이 과정은 해석 시 ABAQUS의 Symmetric generation model 기능을 활용하여 구현된다. 해당 기능은 회전저항 해석 시 SSR 해석 기법과 함께 전체 해석 모델을 구축하지 않고도 일부분만 구축하여 비공기입 타이어의 회전 해석을 구현하고 해석 시간을 절감할 수 있다는 장점이 있다.

Fig. 5

Generation model of one part(18°, Degree) for a spoke

Fig. 6

Model generation of non-pneumatic tire using symmetric generation model

비공기입 타이어의 유한요소 모델 정보로써 트레드와 전단 밴드의 요소 타입은 육면체 하이브리드 솔리으 요소(Hybrid solid element, C3D8H)를 사용하며, 스포크는 복잡한 벌집형의 연속적인 구조 특성으로 사면체 하이브리드 솔리드 요소(C3D4H)를 사용한다. 강철선(Steel cord)의 벨트 층은 강철선이 격자구조를 가진 층으로 되어 있어 쉘 요소 중 리바 요소(Rebar layer element, SPM3D4)를 사용하여 구현한다.

3.3 비공기입 타이어의 해석 모델 검증

앞서 구축한 비공기입 타이어의 유한요소 모델을 기반으로 접지압 해석 기법을 제안하고, 해석 모델의 검증을 위한 접지압 시험과 해석 결과를 비교⋅분석을 수행한다. 타이어의 접지 특성으로 해석 모델을 검증하는 이유는 타이어가 지면과 접지할 때 접지 형상 및 응력 분포 등의 특성이 강성 및 회전저항 성능과 직결되기 때문이다. 따라서, 타이어 설계 시 접지압 특성을 통한 해석 모델의 검증 과정은 필수이다.⁹⁾

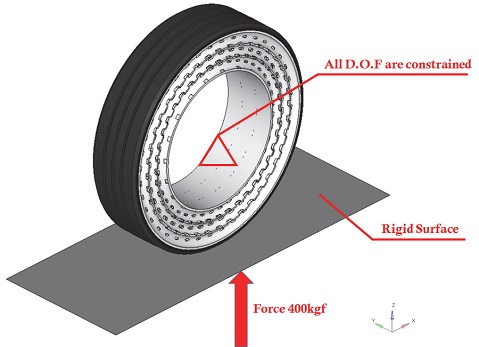
접지압 시험(Foot print test)은 비공기입 타이어가 공차 상황에서 지면과 접지 할 때의 접지 형상, 접지 폭, 접지 길이, 수직 변위 및 수직 강성 등을 측정한다. 접지압 해석 조건은 Fig. 7에 도시한 바와 같이 강체 지면(Rigid surface)을 Analytical surface를 활용하여 생성하고, 400 kgf의 공차 하중을 적용한다. 이때, 비공기입 타이어의 중심 자유도는 모두 구속한다.

Fig. 7

Boundary condition of foot print analysis

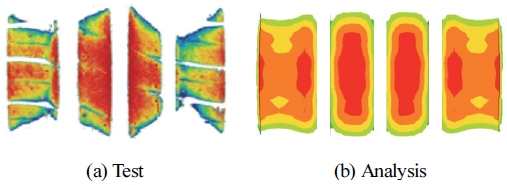
접지압 시험 및 해석 결과 Fig. 8 및 Table 5에 명시한 바와 같다. 수직 변위는 7 % 이내의 오차율을 보이고 있으며, 수직 강성, 접지 폭 및 길이는 3 % 이내의 오차율을 나타내면서 현재 적용된 타이어 해석 기법 및 모델을 신뢰할 수 있다고 판단된다. 특히 응력 분포가 전체적으로 중앙 그루브와 숄더부에 집중되는 점이 정확하게 구현된 것을 확인할 수 있다.

Fig. 8

Foot print result of non-pneumatic tire loaded 400 kgf

Table 5

Comparison between analysis and test of foot print test

3.4 비공기입 타이어의 회전저항 해석 결과

본 절에서는 비공기입 타이어의 회전저항 해석 기법에 관해 서술한다. ISO28580 회전저항 시험법을 해석적으로 구현하기 위해서 시간을 효율적으로 활용할 수 있는 SSR 해석 기법을 적용한다.

3.4.1 정상상태 회전 해석 기법

SSR해석 기법은 축 대칭 구조를 갖는 타이어의 정상상태 회전을 구현하는데 유용한 기법이다. Mixed Eulerian-Lagrangian을 기본으로 해석을 수행하며, 주행 상황 구현 시 타이어를 오일러 도메인(Eulerian domain)으로 간주하여 회전 중 발생하는 물성치, 에너지, 구속 및 하중 조건 등을 수치적인 값으로만 계산한다. 이때 발생 되는 물리적인 변형 값 또한 수치적으로만 계산하고 메쉬(Mesh)는 변형되거나 움직이지 않는다. 라그랑지안 도메인(Lagrangian domain)은 그 물리적인 타이어의 변형 값을 메쉬의 변형으로 구현시킨다. 이처럼 정상상태 회전은 오일러과 라그랑지안 도메인을 반복한 수치적 계산으로 구현된다. SSR해석의 장점은 동적 거동 해석을 수행하지 않고, 내연적(Implicit) 해석 기법을 활용한 타이어의 주행 중 거동을 빠른 시간에 구현할 수 있다는 장점이다.^5,10)

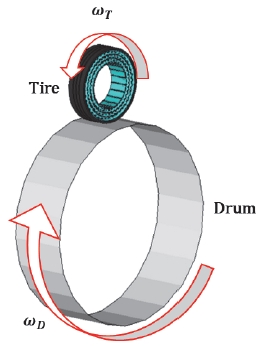
Fig. 9는 SSR을 활용한 비공기입 타이어의 정상상태 회전해석 모델로써 드럼은 Analytical surface를 통해 구현하며, 비공기입 타이어는 Symmetric generation model 기능을 활용하여 구축한다.ω_T는 비공기입 타이어의 각속도, ω_D는 드럼의 각속도이다.

Fig. 9

Steady state rolling analysis of a non-pneumatic tire

3.4.2 비공기입 타이어의 회전저항 해석 및 결과

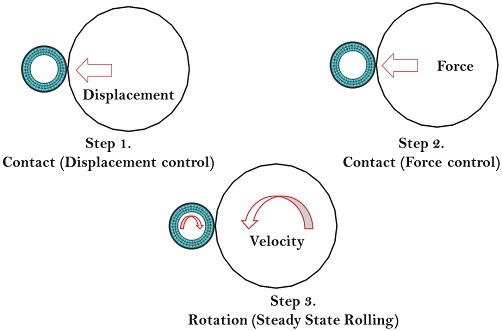
비공기입 타이어의 회전저항을 해석적으로 구현하고, 평가하기 위해 해석의 단계는 총 3단계로 구성된다. Fig. 10에 도시된 바와 같이 Step 1과 Step 2에서는 정적 해석을 수행한 후 마지막으로 SSR 해석을 수행하는 순차적인 해석 방법이다.

Fig. 10

The procedure of rolling resistance analysis method

Step 1은 타이어와 드럼의 변위 하중을 적용한 접촉 해석이다. 초기에는 드럼과 타이어가 접촉 상태가 아니기 때문에 하중을 부여하기 전 수치적 불안전성을 줄이기 위한 단계이다. Step 2는 타이어가 하중을 받는 상태를 구현하기 위한 단계로 비공기입 타이어의 회전 중심축의 모든 자유도를 구속하고, 드럼 중심에 차량의 공차 하중인 400 kgf를 적용한다. Step 3은 비공기입 타이어와 드럼이 80 km/h의 같은 선 속도를 가지도록 각속도를 적용한 SSR 해석 단계로써 비공기입 타이어의 중심에서 반력(F_t)을 결괏값으로 도출하여 회전저항을 산출한다.

회전저항 해석 결과와 실제 회전저항 시험 결과 비교는 Table 6과 같다. 해석을 통해 계산된 회전저항은 실제 회전저항 시험으로 계산된 값보다 12.5 % 높은 결과를 보이고 있다. 이와 같은 차이는 스포크와 트레드 재료 물성의 원인으로 판단된다. 실제 타이어는 주행 시 주기적인 인장과 압축으로 동적 하중을 받는 부품이기 때문에 스포크와 트레드 재료 물성의 주기적인 변형률로 인해 응력이 완화되는 뮬린스 효과(Mullins effect)를 고려하여 재료 물성 시험을 수행하고 해석에 반영해야 한다.

Table 6

Comparison between analysis and test for rolling resistance

4. 비공기입 타이어의 스포크 구조 최적설계

본 절에서는 비공기입 타이어의 회전저항을 저감하기 위하여 실험계획법을 이용한 스포크의 구조 최적설계를 수행한다. 최적설계 과정은 다음과 같이 총 4가지 단계로 구성된다.

• 1) 스포크 형상의 최적설계 문제 정식화
• 2) 직교 배열표를 이용한 실험계획 및 회전저항 성능 해석 수행
• 3) 평균 분석 및 분산 분석 수행
• 4) 설계 변수의 민감도와 유의성 검증을 통한 최적설계 도출

4.1 최적설계 문제 정식화

스포크의 구조 최적설계 문제 정식화는 목적함수, 설계 변수 및 제한조건을 정의하는 과정으로 비공기입 타이어의 회전저항 성능 최적화를 위해서는 기본적이고 필수적인 과정이다.

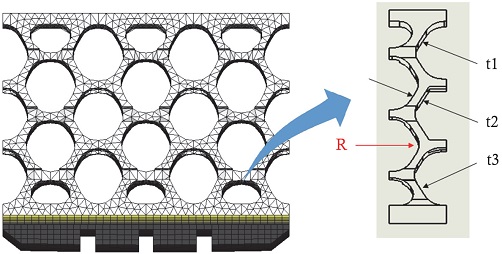
목적함수는 비공기입 타이어의 회전저항 최소화이다. 설계 변수는 Fig. 11에 도시된 바와 같이 회전저항 성능에 영향을 미칠 것으로 판단되는 스포크의 구조로서 벌집형 셀 구조의 두께 변수(t₁, t₂, t₃) 3개와 벌집형 셀의 형상을 결정하는 곡률 변수(R) 1개로 총 4개의 설계 변수를 선정한다. 제한조건은 비공기입 타이어의 수직 강성(VSR)과 최대 접지압(CP)으로 정의된다. 스포크 구조 최적설계 문제 정의는 식 (6)에서 식 (11)과 같다.

Fig. 11

Design variables of honeycomb spoke

스포크의 수직 강성과 최대 접지압력을 제한조건으로 정의한 이유는 비공기입 타이어의 회전저항이 최소화되는 과정에서 강성 특성에 영향을 주지 않는 최적설계안을 도출해야 하기 때문이다. 그러한 이유는 스포크의 강성 특성은 비공기입 타이어의 강성과 접지 특성을 결정짓는 설계 요소이며, 회전저항 성능이 변화할 때 강성 특성과 관련된 차량의 승차감과 하중을 견뎌내는 성능이 유지되어야 하기 때문이다.

$\[ \begin{array}{ccc}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{d}& & t_1,t_2,\end{array}{t}_3,R \]$

(6)

$\[ \begin{array}{ccc}\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}& & R{R}_c\left(t_1,t_2,t_3,R\right)\end{array} \]$

(7)

$\[ \begin{array}{ccc}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}& & 43kgf/mm\le VSR\le 52kgf/mm\end{array} \]$

(8)

$\[ \begin{array}{ccc}& & 0.48MPa\le CP\le 0.53MPa\end{array} \]$

(9)

$\[ \begin{array}{ccc}& & 9mm\le R\le 11mm\end{array} \]$

(10)

$\[ \begin{array}{ccc}& & \begin{array}{cc}3.5mm\le t_i\le 4.55mm& i=\mathrm{1,2},3\end{array}\end{array} \]$

(11)

• where t_i : the cellular thickness of spoke (mm)
• 　　　R : the radius of curvature of cellular (mm)
• 　　　VSR : vertical spring ratio (kgf/mm)
• 　　　CP : maximum contact pressure (MPa)
• 　　　RR_c : rolling resistance coefficient (N/kN)

4.2 실험계획법을 활용한 스포크 구조 최적화

본 연구에서 실험계획법을 활용하는 목적은 회전저항에 대한 스포크 구조 설계 변수의 영향도와 상관성을 규명하는 것이며, 이를 통해 회전저항을 최소화하는 스포크 구조의 설계의 방향성을 제안하는 것이다.

4.2.1 직교 배열표를 이용한 실험계획

직교 배열표(Orthogonal array)를 이용한 실험계획법은 주어진 설계 변수에 대한 목적함수의 변화를 파악하는데 유용하며, 이에 필요한 최소한의 실험횟수와 설계 변수 값들을 체계적으로 결정할 수 있는 기법이다.¹¹⁾ 가장 확실한 실험계획법은 모든 설계 변수의 경우의 수를 고려하여 목적함수를 평가하는 것이지만, 본 논문에서는 Table 7에 명시된 바와 같이 3수준 4요인이므로 총 81(3⁴)의 경우의 수를 고려해야 하기 때문에 이 모든 경우의 수를 고려할 경우 비효율적인 실험계획이 된다. 따라서, 스포크 구조 최적화를 위해 L₉(3⁴) 직교 배열표를 구성하여 3수준 4요인에 해당하는 설계 변수와 수준의 조합을 서로 독립적인 실험으로 정리한다. 각 열들이 독립성을 갖는 실험계획법은 경우의 수를 줄이고 설계 변수들의 수준에 따른 목적함수를 평가하고 분석하여 유효한 설계 변수를 찾는데 효과적이다. 따라서 본 연구의 복잡한 스포크 구조의 최적화 문제에 적합하다고 판단한다. Table 8은 L₉(3⁴)직교 배열표로서 실험 계획에 따른 9개의 해석을 수행하고 회전저항, 수직 강성 및 최대 접지압 값을 명시하고 있다.

Table 7

Design variables level

Table 8

Table of orthogonal arrays with analysis results

4.2.2 평균 분석(ANOM) 및 분산 분석(ANOVA) 해석

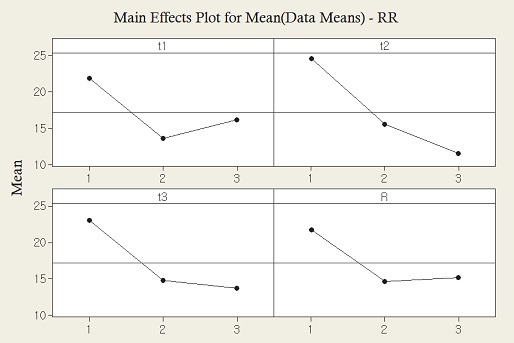
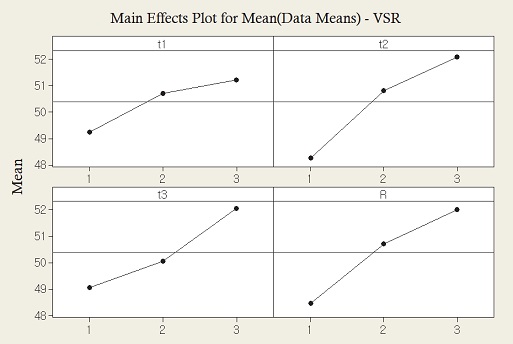
스포크 구조의 설계 변수 수준이 회전저항과 수직 강성에 미치는 영향을 파악하기 위해서는 평균 분석(Analysis of mean)을 수행하고, 분석의 유의성을 검증하기 위해서 분산 분석(Analysis of variance)을 수행한다.¹²⁾ Fig. 12 및 Fig. 13은 회전저항과 수직 강성의 평균분석 결과를 보여주고 있다.

Fig. 12

Sensitivity analysis of rolling resistance for design variables(ANOM)

Fig. 13

Sensitivity analysis of vertical spring ratio for design variables(ANOM)

평균 분석에서는 총 4개의 설계 변수 중 t₂, t₃이 회전저항에 큰 영향을 주는 것으로 판단된다. 특히, 스포크 구조의 두께(t₂, t₃)가 두꺼워 질수록, 벌집형 셀의 곡률 반경(R)이 커질수록 회전저항 감소에 유리한 설계의 방향임을 알 수 있다. 반대로 수직 강성은 증가하는 경향을 나타낸다. 이와 같은 설계 변수의 영향은 비공기입 타이어의 스포크가 높은 강성을 가지고 있을 때 주행 중 변형이 상대적으로 작게 발생함으로써 회전저항 성능에 유리하다는 결과이다. 분산 분석에서는 Table 9에 명시된 바와 같이 t₁을 제외한 t₂, t₃ 및 R의 3가지 설계 변수에 대해서는 90 % 이상의 유의 수준을 갖는 결과를 보이고 있으며, t₂는 95 % 이상의 유의 수준을 갖는 결과를 나타낸다. 결과적으로, 90 % 유의 수준에서 t₂, t₃ 및 R 순서로 비공기입 타이어의 회전저항 성능에 유효한 설계 변수이다.

Table 9

ANOVA results of rolling resistance for design variables

앞선 분석 결과를 반영하여 직교 배열표를 살펴보면 3번 실험 해석 모델의 회전저항 성능이 가장 낮지만 수직 강성이 구속조건인 52 kgf/mm를 초과하였다. 이와 같은 결과는 비공기입 타이어의 강성이 과하게 증가할수록 회전저항 성능은 개선되지만 지면에서 올라오는 충격 흡수력이 약해기지 때문에 승차감이 저하될 우려가 있으며, 트레드의 중앙 부분만 노면에 닿게 돼 트레드 안쪽이 쉽게 파열될 가능성이 있다. 또한, 지면과의 접지 면적이 감소하여 젖은 노면에서의 제동 성능(Wet grip)이 악화될 우려도 있다. 결과적으로, 수직 강성과 최대 접지압 2가지의 제한조건을 모두 만족하면서 회전저항이 기존 모델 대비 13.95 % 개선된 6번 모델을 최적설계 모델로 결정하고자 한다.

Table 10

Comparison rolling resistance between original and optimum designs

5. 결 론

본 연구 목적은 회전저항 성능이 향상된 승용차용 비공기입 타이어를 설계하고자 한다. 이를 위해, 회전저항 성능 평가 해석 모델을 구성하고 실험계획법을 통한 실험계획법을 활용한 스포크 구조의 최적설계를 수행하였다. 본 연구에서 얻어진 주요 결과는 다음과 같다.

• 1) 비공기입 타이어 해석 모델의 신뢰성을 확보하고자 접지압 해석과 시험 결과를 비교⋅분석하였다. 그 결과 하중-처짐은 7 %, 수직 강성 및 접지 면적은 3 % 이내의 오차율을 보이면서 비공기입 타이어의 유한요소 해석 모델을 검증하였다. 특히 접지력 분포가 전체적으로 중앙 그루브와 숄더부에 집중되는 현상을 동일하게 구현하였다.
• 2) 해석 방법은 국제 타이어 회전저항 시험법인 ISO28580의 시험 환경에 따라 해석적으로 구현하였다. 실제 회전저항 데이터와 해석 결과를 비교했을 때, 12.5 %의 차이를 보임으로써 비공기입 타이어를 대상으로 회전저항 성능평가 해석 기법의 신뢰성을 확보하였다.
• 3) 실험계획법의 평균 분석 및 분산 분석을 통해서 스포크 구조 설계 변수와 회전저항 사이의 영향을 파악하고, 설계 변수의 유효성을 판단하였다. 그 결과 스포크 두께 설계 변수(t₂, t₃)와 벌집형 셀의 곡률(R)이 커질수록 회전저항이 감소하고 강성이 증가하는 유의미한 경향을 보여주었다. 이와 같은 결과는 스포크의 구조 변화로 비공기입 타이어의 강성이 증가한다면 주행 중 타이어의 변형량이 줄어들고, 히스테리시스 손실 감소로 이어져 회전저항이 개선될 수 있다는 결론을 얻었다.
• 4) 비공기입 타이어의 스포크를 대상으로 구조 설계 변수(벌집형 셀 구조의 두께 및 곡률)를 변화시켜 회전저항 성능이 개선될 수 있다는 것을 해석적으로 규명하였다. 최종적으로, 평균 분석을 통한 스포크 최적설계안은 초기 모델과 비교했을 때 수직 강성과 최대 접지압의 제한 조건을 만족하면서 회전저항이 13.95 % 감소한 결과를 도출하였다.
• 5) 향후 연구에서는 비공기입 타이어의 회전저항 성능뿐만 아니라 경량화, 고속내구 및 Wet grip 성능 등을 고려한 다목적 최적설계를 연구할 필요가 있다.

Acknowledgments

본 연구는 국토교통부(MOLIT)의 지원으로 수행되었습니다(22HBST-C158067-03).

본 연구는 2022년도 산업통산자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구입니다(20013794).

References

• T. B. Rhyne and S. M. Cron, “Development of a Non-pneumatic Wheel,” Tire Science and Technology, Vol.34, No.3, pp.150-169, 2006. [https://doi.org/10.2346/1.2345642]
• S. W. Hwang and K. W. Kim, “Feasibility Study on Non-pneumatic Tire Having Innovative Spoke Structure,” Auto Journal, KSAE, Vol.41, No.10, pp.19-25, 2019.
• X. Jin, C. Hou, X. Fan, Y. Sun, J. Lv and C. Lu, “Investigation on the Static and Dynamic Behaviors of Non-pneumatic Tires with Honeycomb Spoke,” Composite Structures, Vol.187, No.4, pp.27-35, 2018. [https://doi.org/10.1016/j.compstruct.2017.12.044]
• M. Veeramurthy, J. H. Ju, L. L. Thompson and J. D. Summers, “Optimization of Geometry and Material Properties of a Non-pneumatic Tyre for Reducing Rolling Resistance,” International Journal of Vehicle Design, Vol.66, No.2, pp.193-216, 2014. [https://doi.org/10.1504/IJVD.2014.064567]
• S. R. Kim, K. G. Lee, B. C. Song and K. D. Song, “The Development of Rolling Resistance Estimation Method of Tires Using Steady-state Rolling Analysis Method,” KSAE Annual Conference Proceedings, pp.1645-1649, 2010.
• M. Veeramurthy, Modeling, Finite Element Analysis, and Optimization of Non-pneumatic Tire(NPT) for the Minimization of Rolling Resistance, M. S. Thesis, Clemson University, South Carolina, 2011.
• D. M. Kim, H. Heo, M. S. Uddin and J. H. Ju, “Optimization of Nonpneumatic Tire with Hexagonal Lattice Spokes for Reducing Rolling Resistance,” SAE 2015-01-1515, 2015.
• ABAQUS Analysis User’s Manual, Version 6.4, Dassault Systemes-Simulia Corp, USA, 2003.
• W. D. Kim, W. S. Kim, D. J. Kim, C. S. Woo and H. J. Lee, “Mechanical Testing and Nonolinear Material Properties for Finite Element Analysis of Rubber Components,” Transactions of the Korean Society of Mechanical Engineers-A, Vol.28, No.6, pp.848-859, 2004. [https://doi.org/10.3795/KSME-A.2004.28.6.848]
• T. Tang, D. Johnson, R. E. Smith and S. D. Felicelli, “Numerical Evaluation of the Temperature Field of Steady State Rolling Tires,” Applied Mathematical Modelling, Vol.38, Nos.5-6, pp.1622-1637, 2014. [https://doi.org/10.1016/j.apm.2013.08.033]
• H. U. Mun, H. Y. Lee, J. D. Chung, H. R. Hong, N. T. Jeong, G. S. Lee and M. W. Suh, “Study on Optimum Design of Conical Rubber Spring by Design of Experiment,” Journal of the Korea Society for Railway, Vol.22, No.2, pp.118-128, 2019. [https://doi.org/10.7782/JKSR.2019.22.2.118]
• H. U. Mun, H. Y. Lee, J. D. Chung, H. R. Hong, N. T. Jeong, G. S. Lee and M. W. Suh, “Study on Optimum Design of Conical Rubber Spring by Design of Experiment,” Journal of the Korea Society for Railway, Vol.22, No.2, pp.118-128, 2019. [https://doi.org/10.7782/JKSR.2019.22.2.118]